Геометрические модели объектов изготовления

Лекция 6 ММ ТП в маш.

Геометрические модели объектов изготовления

При математическом моделировании технологических процессов изготовления и сборки изделий машиностроения возникает необходимость в математическом описании предметов труда – объектов изготовления (ОИ): деталей и сборочных единиц.

Введем ряд определений.

Изделие – любой предмет или набор предметов, подлежащих изготовлению на предприятии. Устанавливаются следующие виды изделий:

1) детали;

2) сборочные единицы;

1. комплексы;
2. комплекты.

Изделия, в зависимости от наличия или отсутствия в них составных частей делят на неспецифицированные и специфицированные . Неспецифицированные изделия – детали не имеют составных частей, специфицированные изделия – изделия состоящие из двух и более составных частей.

Деталь – изделие, изготовленное из однородного по наименованию и марке материала, без применения сборочных операций. Например, валик , изготовленный из одного куска метала; пластина из биметаллического листа; печатная плата; отрезок кабеля или провода и. п. и эти же изделия, подвергнутые покрытиям, независимо от вида, толщины и назначения или изготовленные с применением сварки, пайки, склейки, сшивки и тп.

Сборочная единица – изделие, составные части которого подлежат соединению между собой на предприятии-изготовителе сборочными операциями (свинчиванием, клепкой, сваркой склейкой, развальцовкой, укладкой и т.п). а также изделия, для которых предусмотрена разборка на предприятии-изготовителе, например, для удобства транспортирования и хранения; совокупность сборочных единиц и (или) деталей имеющих общее функциональное назначение и совместно устанавливаемых на предприятии-изготовителе в другой сборочной единице (например, электрооборудование станка, автомобиля; комплект составных частей врезного замка и.п.).

Комплекс – два и более специфицированных изделия, не соединенных на предприятии-изготовителе сборочными операциями, но предназначенных для выполнения взаимосвязанных эксплуатационных функций (например, изделие, состоящее из метеоракеты, пусковой установки и средств управления).

Комплект – два и более изделия, несоединенных на предприятии изготовителе сборочными операциями и представляющих набор изделий, имеющих общее эксплуатационное назначение вспомогательного характера (например, комплект запасных частей; комплект инструментов и т.п.).

Каждому ОИ (объекту изготовлении) - детали или сборочной единице может быть сопоставлено множество моделей М и отношений R. Традиционными геометрическими моделями М до появления САПР и в настоящее время является представление ОИ в виде набора проекций, разрезов и сечений на плоскости чертежа, которые в совокупности позволяют создать пространственное изображение изделия. Базовое множество М состоит из нульмерных и одномерных объектов на плоскости (точек, отрезков прямых, дуг окружностей т.п.) которые называются примитивами.

Множество отношений R в этом случае чрезвычайно громоздко и трудно поддается формализации, так же как и восстановление пространственного объекта на основе примитивов и их расположения на плоском носителе. Поэтому указанные модели объектов изготовления при автоматизированном проектировании не используются.

Геометрические модели ОИ различают в зависимости от решаемых задач проектирования, начиная от создания его конструкции и кончая технологией изготовления. Поэтому необходимо преобразование геометрической информации при переходе от одного этапа проектирования к другому. В настоящее время проблема автоматизированной передачи геометрической информации не нашла своего окончательного решения, возможно лишь частичное решение с использованием ограничений на процесс проектирования детали с предварительным оформлением поверхностей в виде блоков и слоев.

Учитывая естественную иерархическую структуру сборочной единицы (сборочная единица – деталь – поверхность – элемент) , рассмотрим геометрические модели ОИ с учетом их отношений принадлежности. При этом геометрические модели объектов учитывают особенности их использования при дальнейшем построении технологических процессов изготовления.

Язык описания машиностроительной делали

Язык описания машиностроительной детали методами математической логики обладает достаточной универсальностью и широко используется при трехмерном геометрическом моделировании. Универсальность языка описания состоит в том, что он позволяет выявить все геометрические свойства делали (поверхности, плоскости, оси вращения и др.), необходимые при проектировании технологического процесса, Другая особенность языка состоит в том, что его примитивы совпадают с объектами обработки ТП (технологических процессов).

Геометрическая модель детали может быть представлена в виде:

(6.1)

где М – множество поверхностей, ограничивающих рассматриваемую деталь;

R – множество отношений на М.

Эти отношения можно разбить на две группы:

- унарные отношении R, каждое из которых определяет свойство поверхностей (геометрические параметры и параметры расположения);

- бинарные отношения, которые образуются с помощью логических операций & () – и, () – или, - не.

Первая составляющая описания – логическая, относится к условиям взаимодействия полупространств, с помощью которых осуществляется «конструирование» делали.

Вторая составляющая – алгебраическая относится к механизму построения полупространств с помощью поверхностей базового множества.

Описание плоской детали

Пусть задана плоская деталь квадратной формы. Для простоты положим, что сторона квадрата 1. Построить ее МО (математическое описание).

Базовое множество М геометрической модели содержит ограничивающие прямые , уравнения которых имеют вид:

(6.2)

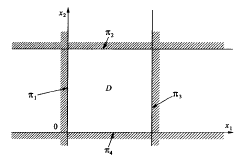
Рисунок 6.1 Выпуклая плоская деталь

Эти прямые порождают полуплоскости, которые получаются из (2), если равенства заменить цепочкой неравенств

В дальнейшем полупространства будем обозначать через . В нашем случае под деталью D будем понимать геометрическое место точек, которые удовлетворять условиям (2). Слово «одновременно» эквивалентно использованию связки или & над указанными условиями:

(6.3)

Отношения (2) и (3) являются логико-алгебраическим представлением детали D. К ним необходимо добавить условие выпуклости. Множество точек детали D обладает свойством выпуклости , если для любой пары точек все внутренние точки соединяющего их отрезка также принадлежат :

.

Рассмотрим математическое описание квадратной детали без четверти (рисунок 2).

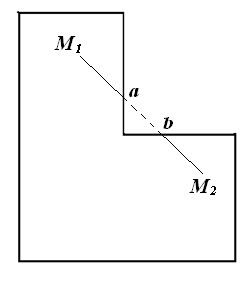
Рисунок 6.2 Невыпуклая плоская деталь

Базовое множество М должно содержать еще два ограничения

(6.4)

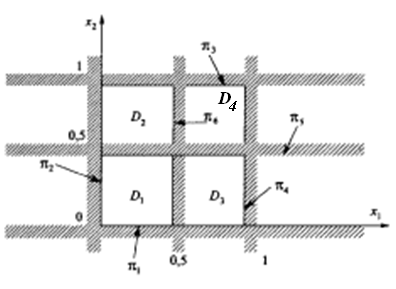
Рисунок 6.3

МО (математическое описание) детали D можно построить различными способами используя логические операции - (конъюнкции, дизъюнкции и отрицания):

(6.4)

где

Перечисленные формы (4) представления детали D эквивалентны в том смысле, что все они содержат одно и тоже геометрическое место точек на плоскости.

Проверим, что любая точка , например,

обеспечивает следующие значения для условий при этом , поэтому функция D(A) принимает значения

= т.е. .

Любую из формул алгебры логики можно преобразовать, используя преобразования формул математической логики. Например, преобразование первой формулы (4) во вторую:

. (6.5)

Это преобразование использует соотношения:

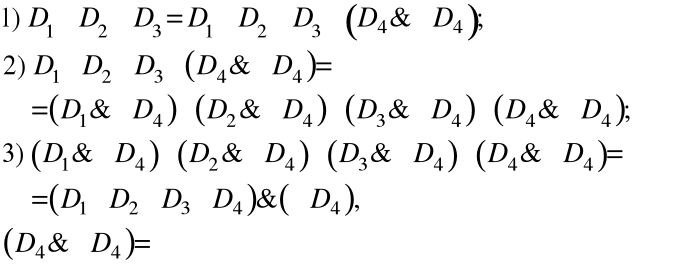
При этих преобразованиях учитывалось, что

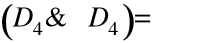. (6.6)

Пространственный случай описания детали

При построении базового множества М для трехмерных деталей возникают технические трудности определения уравнений поверхностей в трехмерном пространстве в случае произвольной ориентации их относительно координатных осей. Ввиду того, что логико-алгебраическое описание деталей предполагает аналитическую форму представления поверхностей, то это представление будем называть внутренним. Для пользователя более удобным является кодирование параметров поверхностей на основе использовании информации с чертежа, которая полностью определяет уравнение рассматриваемой поверхности. Такую форму представления поверхностей называют внешней. Внешнее представление поверхности зависит от ее вида: плоскость, цилиндрическая, коническая, сферическая, тороидальная, составная поверхность.

Рассмотрим возможности внешнего представления перечисленных выше поверхностей, которые имеют наибольшее распространение при образовании машиностроительных деталей.

Плоскость.

Плоскость в трехмерном пространстве определяется тремя точками, не лежащими на одной прямой. Возможны различные способы внешнего представления плоскости.

1. Заданы три точки не лежащие на одной прямой, которые в совокупности определяют девять параметров плоскости. Координаты точек могут быть получены чертежа. Например, плоскость скоса (рисунок 6.4) призматической детали определяются точками

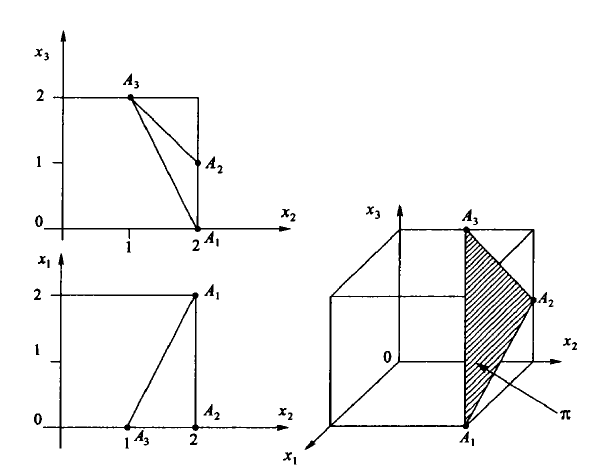
Рисунок 6.4

1. Заданы точка и нормаль к плоскости в точке А. Плоскость скоса призматической детали D определяется шестью параметрами: тремя координатами точки А и тремя направляющими косинусами нормали (рисунок 6.5).

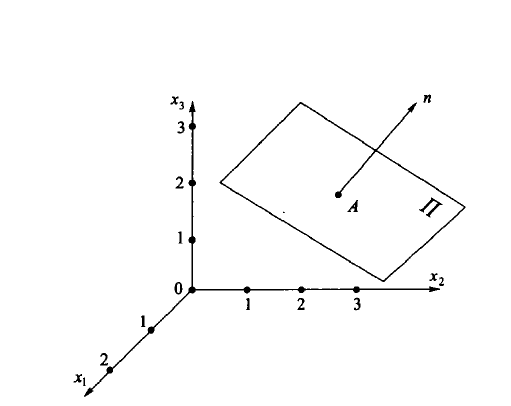
Рисунок 6.5

1. Частные случаи расположения плоскости параллельно координатным плоскостям. В этом случае параметры плоскости

Определяются непосредственно коэффициентами ее уравнения. Например, уравнение плоскости, параллельной координатной плоскости и смещенной на две единицы по координате (рисунок 6.6) будет иметь вид:

Рисунок 6.6

Цилиндрическая поверхность

Цилиндрическая поверхность в трехмерном пространстве определяется семью параметрами: координатами двух несовпадающих точек на оси вращения цилиндра и радиус окружности пересечения цилиндрической поверхности и плоскости, перпендикулярной оси вращении (рисунок 6.7)

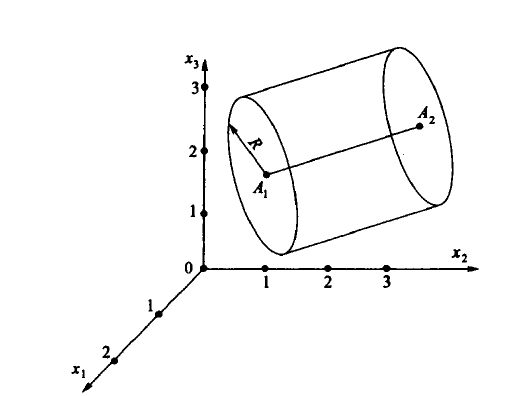
Рисунок 6.7

Сферическая поверхность

Сферическая поверхность определяется четырьмя параметрами – тремя координатами центра и радиусом R (рисунок 6.8)

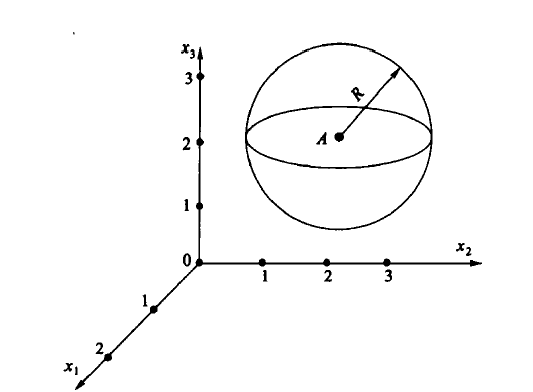
Рисунок 6.8

Тороидальная поверхность

Тороидальная поверхность (рисунок 6.9) определяется восемью параметрами: три координаты центра большой окружности и его радиус R; радиус малой окружности r и три направляющих косинуса нормали к плоскости центров.

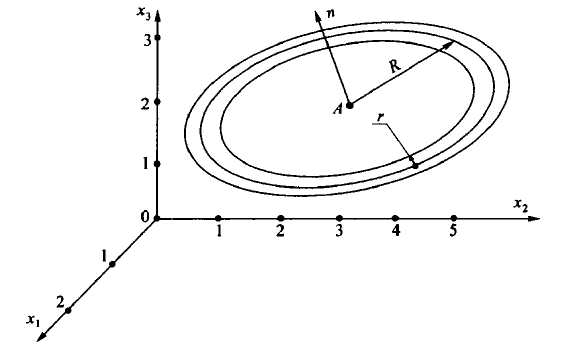
Рисунок 5.9

Коническая поверхность

Коническая поверхность определяется восемью параметрами: шесть координат центров оснований А1 , А2 , радиусов R1 , R2 окружностей пересечения плоскостей, проходящих через точки А1 , А2 и перпендикулярных оси вращения конической поверхности (рисунок 6.10)

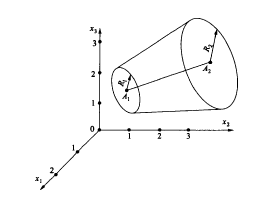
Рисунок 6.10

Поверхность общего вида может быть получена в результате аппроксимации сплайнами, в частности, сплайнами второго порядка.

Преобразование из внешнего представления во внутреннее.

Для получения аналитического уравнения поверхности П на основе параметров ее внешнего представления используется матрица М преобразования координат из относительной системы в абсолютную.

Преобразование производится в следующей последовательности.

1. Выбор собственной системы координат, связанной с поверхностью П.
2. Получение уравнения поверхности П в собственной системе координат:

1. Вычисление матрицы М преобразования координат: на основе внешнего представления поверхности.
2. Вычисление обратной матрицы М-1 преобразования координат:
3. Пересчет уравнения поверхности в абсолютную систему координат с учетом матрицы М-1 преобразования координат:

Рассмотрим матрицы М преобразования координат из относительной системы в абсолютную для плоского и пространственного случаев и расчет обратной матрицы М-1.

Плоский случай

Задана точка в относительной системе координат и положение относительной системы координат в абсолютной системы, которое определяется вектором смещения точек начала координат и углом поворота .

Требуется вычислить координаты точки в абсолютной системе

, (6.7)

где

(6.8)

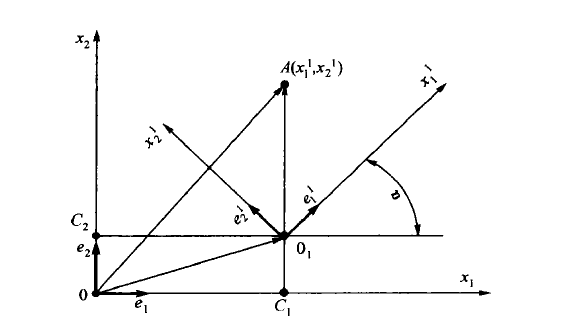
Рисунок 6.11

Орты в абсолютной системе координат определяются таким образом

(6.9)

Знак угла является положительным, если поворот совершается против часовой стрелки.

Подставляя соотношения (8) в (7) после соответствующих преобразований, получим

.

(6.10)

Приравнивая координаты при в правых и левых частях (10), получаем связь между абсолютными и относительными координатами точки А:

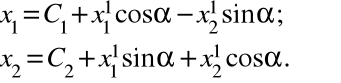(6.11)

Соотношения (11) можно записать в матрично-векторной форме:

(6.12)

Матрица для плоского случая имеет размерность (33), ее можно представить в виде произведения матрицы - матрицы параллельного переноса начала относительной системы координат на величину вектора и матрицы поворота относительной системы координат относительно абсолютной :

, (6.13)

где

(6.14)

Обратная матрица преобразований

(6.15)

Пространственный случай

Для пространственного случая матрица преобразований строится по аналогии с плоским случаем, предполагая, что переход от относительной системы координат к абсолютной получается в результате последовательных движений:

- параллельного переноса вдоль вектора

- поворота осей координат абсолютной системы соответственно на углы - матрицы поворота .

Существенное значение имеет последовательность движений:

(6.16)

.

После перемножения матриц , матрица преобразования примет вид

(6.17)

где

Обратная матрица имеет вид

(6.18)

Обратная матрица поворота - это тоже матрица поворота вокруг той же оси на тот же угол поворота, но в отрицательном направлении; она получается из матрицы поворота путем транспонирования, то есть

.

Например,

и т.д.

PAGE \* MERGEFORMAT 1

Геометрические модели объектов изготовления