Установление изоморфных отображений между геометрическими моделями деталей
Лекция 8 ММ ТП в маш
Установление изоморфных отображений между
геометрическими моделями деталей
Одна и та же деталь может иметь неограниченное множество геометрических моделей, каждая из которых предпочтительна при решении задач отображения и проектирования ТП при проектировании сквозных САПР (конструкция – технология – изготовление или CAD-CAM-CAE), большое теоретическое и практическое значение имеет установление связей (интерфейсов) между геометрическими моделями. Решение этой проблемы позволяет автоматизировать процесс передачи геометрической информации от одного типа проектирования к другому, а также устанавливать обратные связи от более поздних этапов проектирования к более ранним. Последнее имеет особое значение, так как конструктор-проектировщик имеет возможность отрабатывать конструкции изделия на технологичность на ранних стадиях проектирования. Особое место в множестве геометрических моделей занимают модели логико-алгебраического типа.
Важность логико-алгебраической модели определяется тем , что с ее помощью устанавливаются гомоморфные отображения с проблемными геометрическими моделями (МТП, МТО, МСАП ЧПУ ) (рисунок 8.1). В частности, логико-алгебраическая модель М позволяет определить необходимые свойства поверхностей, необходимые для проектирования ТП механической обработки, а так же все геометрические свойства обрабатываемой заготовки, требуемые для расчета управляющих программ ЧПУ, т.е. модель М обладает свойствами универсальности.
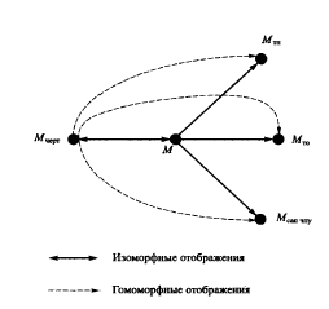
Рисунок 8.1
Попытки устанавливать прямые связи между моделями чертежа и проблемными моделями бесперспективны, потому что указанных связей должно быть столько, сколько разновидностей проблемных моделей. Поэтому с изменением геометрических моделей каждый раз возникает необходимость разработки соответствующих программных интерфейсов.
Из сказанного следует необходимость установления изоморфных связей между геометрическими моделями чертежа и логико-алгебраической модели.
Напомним, что модели М и M’ называются изоморфными, если между ними можно установить такое взаимно-однозначное соответствие, при котором для любых элементов a, b из М и соответствующих им элементов a’ и b’ из M’ сумме a + b соответствует сумма a’ +b’, а произведению ab соответствует произведение a’b’.
Модели M и M’ называются гомоморфными, если между ними можно установить такое отображение , при котором всякому элементу ставящее в соответствие однозначно определенный элемент , из M’ () и если для имеет место .
Очевидно, что потребовав от гомоморфизма дополнительно взаимную однозначность отображения , получим изоморфизм.
Отображение – закон, по которому каждому элементу х некоторого заданного множества Х сопоставляется однозначно определенный элемент у другого заданного множества У (при этом Х может совпадать с У). Такое соотношение между элементами и записывается в виде:
Говорят, что отображение f действует из X в Y и пишут:
или .
Если X и Y числовые множества (элементами этих множеств являются некоторые числа), то отображение f называется функцией.
Если множество Х – числовое множество, а множество Y – функциональное множество (множество, элементами которого являются функции), то отображение f называется функционалом.
Если X и Y являются функциональными множествами, то отображение f называется оператором.
Отношение – произвольное подмножество R множества всех кортежей (упорядоченных наборов) вида где элементы некоторого множества ; в этом случае говорят, что R есть п – местное (п – арное) отображение
При п =0 - нульарное отношение; п = 1 - унарное отношение; п = 2 – бинарное отношение; п = 3 – тернарное отношение и т.д. .
Понятие отношения служит в математике для выражения на теоретико-множественном языке связей между объектами. Обобщением понятия «отношение» является соответствие.
Возвращаясь к установлению изоморфных связей между геометрическими моделями чертежа Мчерт и моделями логико-алгебраического типа отметим, что где - базовое множество элементов (отрезки прямых, дуги, окружности, полулинии и другие одномерные многообразия на плоскости); - множество отношений. Множество можно разбить на две группы:
- унарные отношения (свойства) R(1) элементов множества ;
- парные отношения R(n) (n 2).
Рассмотрим эти группы отношений на примере фланца (рисунок 8.2)
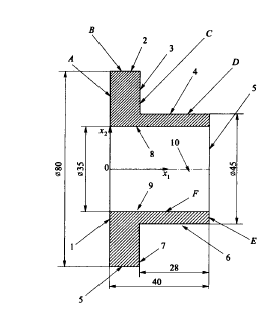
Рисунок 8.2
Первая группа отношений определяет свойства элементов, регламентированных графической системой: типы цветов и линий. К этой группе относятся унарные отношения, определяющие значения координат на плоскости (параметров) на плоскости:
-четыре координаты двух точек отрезка прямой на плоскости или шесть
координат в пространстве;
- координаты центра и радиус окружности;
- координаты трех точек дуги.
Начало координат в абсолютной системе имеет координаты (50, 100). Все отрезки прямых пронумерованы от 1 до 10. Каждый отрезок характеризуется шестью геометрическими параметрами: три координаты начальной точки и три координаты конечной точки отрезка. Например , отрезок LINE9 содержит шесть координат двух точек: первая точка (50, 82.5); вторая точка (90, 82.5); отрезок 10 имеет тип CENTER, а отрезки LINE1 … LEINE9 имеют тип CONTINUOS.
Вторая группа отношений получается на основе использования элементов модели и , а также правил преобразования отношений с использованием формул аналитической геометрии. Множество отношений второй группы потенциально неограничено, поэтому необходимо выделить из них те, которые связаны с образованием модели М.
Примером выделенных отношений R могут служить
- перпендикулярность БЭФов, параллельность, соосность и др.;
- принадлежность элементов поверхности.
Поверхности, ограничивающие деталь, показаны буквами латинского алфавита ABCDF. При построении логико-алгебраической модели М на основе модели Мчерт необходимо установить связь (интерфейс) между множеством чертежных примитивов 1…10 множеством поверхностей A…F. Эта задача относится к задачам классификации объектов, которая формулируется так: требуется выполнить разбиение исходного множества Мчерт на подмножества (классы) i , каждый из которых определяет поверхность i , ограничивающую рассматриваемую деталь D, так чтобы выполнялись соотношения
При построении модели используются п–арные отношения, связанные с образованием поверхностей 1 … 10 . К унарным отношениям (R(1)) относятся на множестве М модели М относятся тип поверхности, ее размеры, ориентация в пространстве. К п-арным отношениям R(n) относятся характеристики относительного расположения поверхностей, такие как отношения перпендикулярности, параллельности, соосности и др. Очевидно, п-арность отношения связана с типом образующей поверхности и правилами вывода отношения R(n).
Рассмотримосновные правила, лежащие в основе образования п-арных отношений модели М.
Правило образования отношения R(1) (торец А) можно сформулировать так: два примитива и образуют один класс (торец), если выполняются соотношения
Эти правила следует понимать так: существует осевая линия mj (свойство) и отрезок сплошной прямой линии mi (), перпендикулярный mj (условие 4) и симметричный mj (условие 1…3).
Приведенное правило позволяет объединить примитивы (1,10) а также (5, 10) в один класс – торец.
Если кольцевой торец образован двумя отрезками прямых, то правило образования класса «торец» усложняется:
В этом случае добавляется условие параллельности двух отрезков (cb) и (mn) (пункт 5).
Правило образования отношения R(n) (цилиндрическая поверхность n) можно сформулировать так: три примитива mi є Mчерт образуют один класс (цилиндрическая поверхность), если выполняются соотношения:
Это правило следует понимать так: существует осевая линия mj (свойство ) такая, что отрезки сплошных прямых линий mi и mk параллельны mj (условия 3,4) и симметричны относительно осевой линии mj (условие 5).
В таблице 8.1 показано содержание каждого множества из одномерных примитивов.
Таблица 8.1

Язык описания сборочных единиц
Геометрическая информация о сборочной единице (изделии) содержится в сборочном чертеже. Одной и той же сборочной единице (СЕ) может соответствовать неограниченное множество моделей М.
Рассматриваемая геометрическая модель СЕ предназначена для решения следующих задач проектирования ТП:
- моделирование силового замыкания с целью выявления сборочных размерных
цепей (СРЦ) и назначение допуска на составляющие звенья (детали);
- выявление геометрических свойств СЕ и элементов, позволяющие распоз-
навать условия базирования деталей;
- выявление возможности установления промежуточных СЕ и последова-
тельности сборки;
- выявление свойств элементов СЕ с целью определения условия базирования;
- определение характеристик точности относительного расположения поверхно-
стей замыкающего звена.
Исходя из служебного назначения СЕ и составляющих элементов следует, что передача силовых потоков осуществляется с помощью контактов базовых поверхностей, т.е. вспомогательных поверхностей базовой детали и основных баз присоединяемой детали, поэтому геометрическая модель СЕ имеет двухуровневую иерархическую структуру:
где базовое множество, состоящее из деталей СЕ;
множество отношений на ;
,
где базовое множество поверхностей, ограничивающих деталь D;
множество отношений на МD.
Таким образом, элементы базового множества МСЕ модели МСЕ , в свою очередь, представляют модель МD , которая содержит в качестве базового множества элементы нижнего уровня – ограничивающие поверхности. Отсюда иерархическая структура модели МСЕ определяется следующими уровнями элементов базового множества: сборочная единица – деталь – поверхность.
Рассмотрим множество отношений RCE , которые разбиваются на следующие группы:
- Унарные отношения которые характеризуют свойства элементов СЕ – деталей.
- Бинарные отношения на множестве МСЕ, которые характеризуют взаимосвязи между деталями сборочной единицы.
- Унарные отношения элементов базового множества МD.
- Бинарные отношения на множестве всех поверхностей деталей.
- п-арные отношения, которые определяют свойства подмножеств множества М быть сборочной единицей; эти отношения задаются в неявном виде с использованием правил вывода.
Отношения первой группы
Унарные отношения определяющие следующие свойства деталей, принадлежащих СЕ:
- характеристики, указанные в спецификациях сборочного чертежа (шифр детали, наименование, марка конструкционного материала, масса, габаритные размеры);
- параметры расположения делали в системе координат, связанной с СЕ (параллельный перенос собственной системы вдоль координатных осей и вращение вокруг этих осей).
Унарные отношения, определяющие параметры расположения детали, могут задаваться как в явном виде путем непосредственного считывания размеров деталей с чертежа, так и в неявном – путем указания поверхностей контакта со смежными деталями.
Отношения второй группы
Это бинарные отношения на множестве деталей, принадлежащих СЕ, устанавливают для каждой пары деталей Di и Dj факт их взаимодействия при функционировании сборочной единицы.
Будем говорить, что детали Di и Dj находятся в отношении если они взаимодействуют друг с другом в СЕ.
Моделью отношения может служить граф взаимосвязей G «деталь – деталь», который определяется так
где Р – множество вершин (входящие детали и сборочные единицы нижнего уровня);
U – множество дуг, соединяющие пары вершин.
На рисунке 8.3 показан кондуктор для сверления радиальных отверстий, а соответствующий ему граф G взаимодействия «деталь-поверхность) на рисунке 8.4, на рисунке 8.5 показан граф связей «деталь-деталь».

Рисунок 8.3
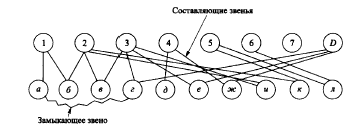
Рисунок 8.4
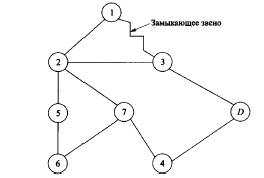
Рисунок 8.5
Рассмотренное бинарное отношение широко используется при разработке алгоритмов выявления сборочных размерных цепей.
Отношения третьей группы
Унарные отношения на множестве МD поверхностей детали. Эти отношения определяют свойства поверхностей детали, которые не отражены в модели М, то есть свойства поверхностей быть основной или вспомогательной базой. Эти свойства поверхностей можно выявить лишь с позиции СЕ, включающей рассматриваемую деталь.
Говорят, что поверхности i и j деталей Dk и Dl находятся в отношении
R(2)(Dk, Dl), если они взаимодействуют между собой в сборочной единице.
Для кондуктора, изображенного на рисунке 8.3 свойства R(1) (тип базы) поверхностей деталей отражены в таблице 8.2.
Таблица 8.2
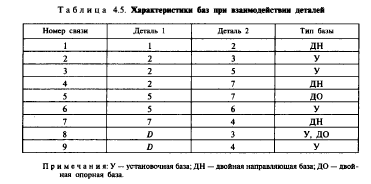
Унарные отношения третьей группы можно дальше детализировать до количества степеней свободы с учетом ориентации детали. К этим отношениям относятся также тип и точность посадки сопряжения рассматриваемой детали со смежными деталями.
Отношения четвертой группы
Это бинарные отношения на множестве всех поверхностей и деталей, принадлежащих СЕ.
Отношение может быть представлено в виде графа
где Р – множество вершин () , где - множество деталей; - множество поверхностей; - множество дуг; uij = (pi , pj), если . причем дуга имеет ориентацию от к .
Отношения пятой группы
п-арные отношения, позволяющие определить, является ли произвольное подмножество множества М деталей сборочной единицей или нет. Эти отношения невозможно определить в явном виде, но можно установить лишь алгоритмически с использованием правил вывода. К важнейшим свойствам относятся свойства базирования и доступности.
Расчет параметров расположения по условиям
сопряжения поверхностей
Пусть заданы две детали Dk и Dl и матрицы Мк и Мl преобразования координат из собственных систем в абсолютную систему, а также уравнения поверхностей
и - уравнения поверхностей и .
Используя соотношения и , получаем уравнения сопрягаемых поверхностей в абсолютной системе координат и их сопряжения:
Последняя уравнение отражает условия совпадения уравнений сопрягаемых поверхностей и (вспомогательной базы базовой детали и основной базы присоединяемой детали) в абсолютной системе координат. Решение этого уравнения позволяет автоматически синтезировать конструкцию сборочной единицы из заданных деталей на основе согласования свойств сопрягаемых поверхностей и осуществлять построение ее модели в виде графа связей «деталь-деталь».
PAGE \* MERGEFORMAT 1
Установление изоморфных отображений между геометрическими моделями деталей