ИССЛЕДОВАНИЕ ВЛИЯНИЯ СХЕМ КАЛИБРОВКИ И ИЗМЕРЕНИЙ НА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ЧЕТЫРЕХПОЛЮСНИКОВ СВЧ ВЕКТОРНЫМ АНАЛИЗАТОРОМ ЦЕПЕЙ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «КубГУ»)
Физико-технический факультет
Кафедра оптоэлектроники
Допустить к защите в ГАК
_____ . ____ . 2014 г.
Заведующий кафедрой
д-р техн. наук, профессор
_______________Н. А. Яковенко
ДИПЛОМНАЯ РАБОТА
ИССЛЕДОВАНИЕ ВЛИЯНИЯ СХЕМ КАЛИБРОВКИ И ИЗМЕРЕНИЙ НА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ЧЕТЫРЕХПОЛЮСНИКОВ СВЧ ВЕКТОРНЫМ АНАЛИЗАТОРОМ ЦЕПЕЙ
Работу выполнил_________________________ Третьяков Алексей Михайлович
Специальность 010801.65 – Радиофизика и электроника
Научный руководитель
канд. физ.-мат. наук, доцент _____________________________ А. С. Левченко
Нормоконтролёр инженер __________________________ И. А. Прохорова
Краснодар 2014
Реферат
Дипломная работа 65 с., 37 рис., 10 табл., 11 источников
ВЕКТОРНЫЙ АНАЛИЗАТОР ЦЕПЕЙ, СХЕМА КАЛИБРОВКИ, КОЭФФИЦИЕНТ ОТРАЖЕНИЯ, КОЭФФИЦИЕНТ ПЕРЕДАЧИ, ЭТАЛОННАЯ НАГРУЗКА, ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ПАРАМЕТРОВ ЧЕТЫРЕХПОЛЮСНИКА
В результате выполнения дипломной работы были получены экспериментальные данные измерения параметров нагрузок СВЧ и на их основе проведены исследования
В работе экспериментально и математически исследованы погрешности калибровки векторного анализатора цепей РК4-74 новым патентованным методом калибровки, возникающих из-за не идеальности калибровочных мер и нестабильности работы самого анализатора цепей, а так же влияние как математической, так и функциональной части самой методики калибровки. Проведено сравнение полученных погрешностей прибора с характеристиками аналогичных векторных анализаторов цепей: Р4М-18 производства «Микран» и 37000D производства «Antritsu».
Содержание
|
Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
4 |
|
1 Классификация и анализ известных методов калибровки векторных анализаторов цепей . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
6 |
|
2 Новый метод калибровки векторных анализаторов цепей СВЧ . . . . . . . . . . . . |
13 |
|
3 Практическое применение нового алгоритма . . . . . . . . . . . . . . . . . . . . . . . . . . . |
37 |
|
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
64 |
|
Список использованных источников . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . |
65 |
Введение
Измерения являются одним из основных объектов обмена при совместном решении научно-технических проблем. Особенно это требуется при разработке, создании и настройке различных СВЧ устройств. При этом основными параметрами в задачах измерения являются комплексные коэффициенты (амплитуда и фаза) коэффициентов отражения и передачи N – полюсников СВЧ.
Одной из первичных задач при измерениях является калибровка векторного анализатора цепей. Она заключается в нахождении собственных S – параметров его измерительных портов, как комплексных величин, характеризуемых модулем и фазой. Для этого зачастую применяется SOLT метод, то есть используется три типа эталонных мер – нагрузок ХХ, КЗ, СН (с паспортными данными). Меры являются необходимой и, фактически, основной составной частью комплекса средств измерения в части обеспечения единства измерений ККО. Так же как для метрологического оборудования, для самих мер необходима оценка погрешностей. Уровень точности эталонных и образцовых мер определяет уровень точности средств измерения параметров СВЧ устройств. Пути повышения точности за счет совершенствования технологии изготовления СВЧ анализаторов к настоящему времени практически исчерпали себя. На передний план вышли пути повышения точности измерителей за счет применения предварительной их калибровки, что требует высокоточных методик выполнения измерений. Ввиду бурного развития СВЧ техники данное направление является очень актуальным. При этом задачей разработки является создание, как физических элементов ГЭ (Генераторов, калибровочных мер, анализаторов, индикаторов), так и оценка погрешностей воспроизведения единицы волнового сопротивления, комплексного коэффициента отражения и передачи их размеров нижестоящим средствам.
На данный момент существует большое количество методов калибровки векторных анализаторов цепей.
Самыми распространенными для калибровки при измерениях коэффициентов отражения является TRL, SOLR и SOLT, при этом именно точность параметров калибровочных мер ограничивает точности калибровки. Для уменьшения влияния погрешностей значений эталонных мер на погрешность вносимую в процессе калибровки предлагается новый метод[4].
В работе экспериментально и математически исследованы погрешности калибровки векторного анализатора цепей РК4-74 новым патентованным методом калибровки, возникающих из-за не идеальности калибровочных мер и нестабильности работы самого анализатора цепей, а так же влияние как математической так и функциональной части самой методики калибровки. Проведено сравнение полученных погрешностей прибора с характеристиками аналогичных векторных анализаторов цепей: Р4М-18 производства «Микран» и 37000D производства «Antritsu».
1 Классификация и анализ известных методов калибровки векторных анализаторов цепей
При тестировании исследуемых устройств (ИУ) с целью высокоточного измерения их параметров рассеяния (S-параметров) при помощи векторных анализаторов цепей (ВАЦ) очень важно минимизировать систематическую погрешность измерений. С возрастанием частоты зондирующего сигнала, как правило, ухудшаются свойства тракта распространения. Это проявляется возрастанием КСВН аксессуаров, увеличением частотной неравномерности передачи элементов тракта, появлением различных паразитных проникновений сигналов. Все перечисленные явления вносят вклад в систематическую погрешность измерений. Для определения составляющих (факторов) систематической погрешности используется процедура калибровки ВАЦ. Для исключения погрешности применяется математическая коррекция результатов измерений. При разработке ВАЦ диапазона частот до 20 ГГц и тем более до 50 ГГц или выше нельзя не учитывать то, каким образом будет выполняться калибровка прибора. Чтобы правильно выполнить проектирование прибора и калибровочных средств для него, необходимо четко представлять современные достижения в области калибровки и коррекции в ВАЦ.
В данной главе обобщается опыт применения наиболее распространенных в настоящее время методов калибровки ВАЦ [1, 2]. При этом не делается акцент на то, каким именно способом выполняется калибровка: с помощью механического набора мер, с помощью электронного калибратора, в автоматическом режиме на зондовой станции или еще как-то. И прежде приведем краткую классификацию существующих типов калибровки ВАЦ, а именно
– нормировка для измерения коэффициента отражения (КО);
– нормировка для измерения коэффициента передачи (КП);
– однопортовая векторная калибровка;
– двухпортовая калибровка в одном направлении;
– полная двухпортовая калибровка.
Все эти калибровки предполагают измерение комплексных частотных характеристик различных одно- или двухпортовых устройств. Кроме этого, для выполнения высокоточных измерений при помощи ВАЦ можно использовать преобразование частотного описания цепей во временное и обратно. Например, можно проводить тестирование ИУ через идеальные отрезки линий передачи достаточной длины с последующим выделением отклика ИУ во временной области. Так, при работе ВАЦ до 50 ГГц разрешение по времени при известных условиях может достигать 6 мм.
При построении аппарата калибровки и коррекции измерений полагают, что существует идеальная (неискажающая) часть ВАЦ, а все погрешности сводят в линейные искажающие адаптеры (ИА). Очевидно, что параметры искажающих адаптеров не должны меняться во времени.
Существуют как минимум две модели ВАЦ, пригодные для получения алгоритмов калибровки. Эти модели изображены на рисунке 1 и рисунке 2. На рисунках факторы (составляющие) систематической погрешности обозначены через ` (наличие штриха означает изменение соответствующей составляющей для порта, который работает в режиме приема зондирующего сигнала). Приемники ВАЦ измеряют комплексные амплитуды сигналов , и при прямом зондировании (из первого порта во второй) и , и – при обратном (из второго порта в первый). Опорные приемники измеряют сигналы a, измерительные – b. Полученные амплитуды определяют некорректированные (измеряемые) S-параметры:
, , , (1)
Индексы F (от Forward – прямой) и R (от Reverse – обратный) определяют направление зондирования.
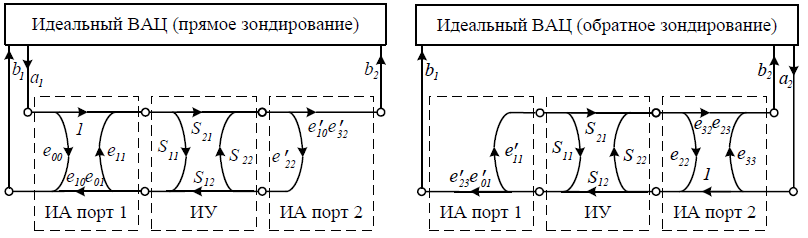
Рисунок 1 – Графы 10-параметрической модели ВАЦ: прямое и обратное зондирование
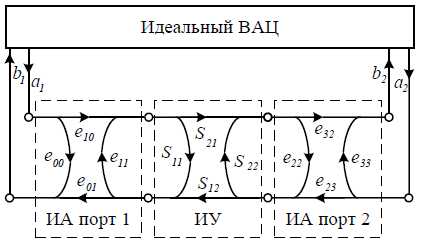
Рисунок 1 – Граф 8-параметрической модели ВАЦ
Неизвестными в 10-параметрической модели являются: , , , , , , и ; в 8-параметрической: , , , , , , и .
Существует модель с 16 параметрами, которая получается из 8-параметрической модели путем добавления ветвей графа, описывающих всевозможные паразитные проникновения сигналов. По этой причине такую модель следует использовать в ВАЦ в составе зондовых станций, особенно на частотах до 50 ГГц или выше. Очевидно, что из упомянутых наиболее полной является именно 16-параметрическая модель ВАЦ, так как она учитывает наибольшее число факторов систематических погрешностей измерений 4 S-параметров двухпортового ИУ. В настоящей работе данная модель детально не анализируется.
Модель с 8 параметрами может быть преобразована в модель с 10 параметрами путем привлечения дополнительных измерений в схеме с 4 приемниками (a2 при прямом зондировании и a1 при обратном). В свою очередь, к 10 параметрам можно добавить два основных паразитных проникновения сигнала и в результате получить основную для современных ВАЦ 12-параметрическую модель. Данная модель показана на рисунке 3 и является базовой для алгоритма коррекции измерений, который дается ниже. В таблице 1 приведены названия и обозначения для всех факторов систематической погрешности.
Факторы погрешности имеют определенный физический смысл и моделируют отражения и искажения сигналов при прохождении цепей внутри прибора, различных кабельных сборок и переходов вне его вплоть до разъёма, к которому подключается ИУ. Например, частотную неравномерность трактов формируют цепи передачи сигнала между точками ответвлениями сигнала в опорный и измерительный приемники. Направленность складывается из сигналов, поступающих на вход измерительного приемника до их отражения от ИУ.
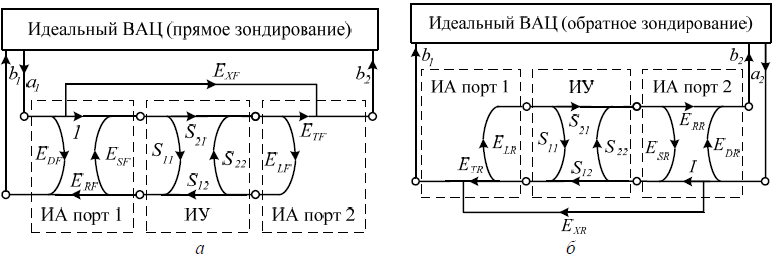
Рисунок 3 – Графы 12-параметрической модели ВАЦ: a – прямое; б – обратное зондирование
Таблица 1 – Факторы систематической погрешности ВАЦ
|
Тип |
Название |
||
|
1. Паразитное проникновение |
Направленность |
ED |
EDF= EDR= |
|
Изоляция |
EX |
EXF= EXR= |
|
|
2. Паразитное отражение |
Рассогласование источника сигнала |
ES |
ESF= ESR= |
|
Рассогласование нагрузки |
EL |
ELF= ELR= |
|
|
3. Частотная неравномерность |
Неравномерность тракта отраженного сигнала |
ER |
ERF= ERR= |
|
Неравномерность тракта передаваемого из порта в порт сигнала |
ET |
ETF= ETR= |
Измеренные S-параметры (как решение соответствующих потоковых графов, рисунок 3) равны:
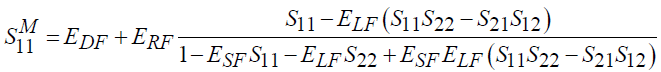 , (2)
, (2)
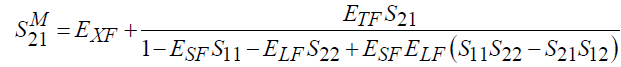 , (3)
, (3)
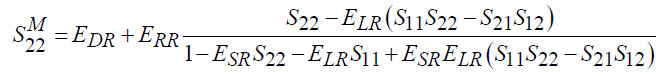 , (4)
, (4)
 , (5)
, (5)
Для исключения влияния ИА на результаты измерений S-параметров необходимо провести коррекцию, т.е. решить (2)–(5) относительно истинных значений S-параметров. Коррекция или оценка действительных значений S-параметров выполняется по формулам:
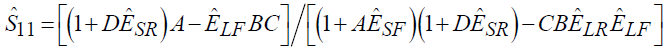 , (6)
, (6)
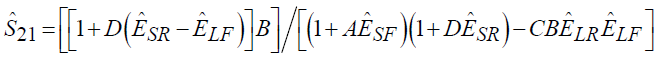 , (7)
, (7)
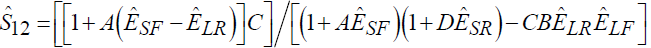 , (8)
, (8)
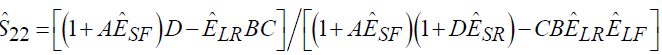 , (9)
, (9)
В настоящей работе рассмотрим два семейства полных векторных двухпортовых калибровок условно SOLT и TRL, отличающихся способом определения оценок E (или e). При рассмотрении алгоритмов калибровок из указанных семейств на первом этапе будем полагать, что выходные разъемы портов ВАЦ таковы, что возможно непосредственное подключение портов друг к другу. Всегда оценки факторов изоляции e30 и e03 либо приравниваются 0, либо измеряются как параметры S21 и S12 при подключении к обоим портам ВАЦ согласованных нагрузок.
Семейство калибровок SOLT. Основой для всевозможных калибровок из семейства SOLT (от первых букв слов: Short – короткозамкнутая нагрузка (КЗ), Open – нагрузка холостого хода (ХХ), Load – согласованная нагрузка (СН) и Thru – перемычка между портами) является 10-параметрическая модель ВАЦ, которая приведена на рис. 1. Обозначение SOLT отражает суть метода и полностью определяет только одну основную калибровку данного семейства. Тем не менее существует одно важное обстоятельство, которое объединяет основную калибровку со всеми остальными из данного семейства. Заключается оно в том, что для определения неизвестных факторов систематических погрешностей процедура калибровки разбивается на три этапа:
- Однопортовая калибровка первого порта (условно SOL).
- Однопортовая калибровка второго порта (условно SOL).
- Калибровка на проход (условно T).
Известны следующие типы однопортовых калибровок, отличающиеся техническими деталями при получении данных для вектора измерений:
– с использованием нагрузок КЗ, ХХ и фиксированной СН;
– с использованием нагрузок КЗ, ХХ и рассогласованной нагрузки (РН) с известным КО;
– с использованием нескольких (трех или более) нагрузок КЗ с разной, известной длиной;
– с использованием нагрузок КЗ, ХХ и подвижной СН;
– с использованием нагрузки КЗ и двух подвижных нагрузок с разными КО.
Независимо от типа калибровки в рамках рассматриваемого семейства одинаковым является
этап № 3. Точность калибровок SOLT существенно зависит от точности априорной информации о действительных значениях S-параметров калибровочных стандартов, от их стабильности во времени в
процессе эксплуатации, от качества изготовления нагрузок и соединителей. Алгоритмы TRL калибровок не требуют такого большого объема априорной информации.
Семейство калибровок TRL. Семейство TRL (от первых букв слов: Thru – перемычка между
портами, Reflect – мера отражения, Line – линия передачи между портами) объединяет двухпортовые калибровки ВАЦ, использующие 8-параметрическую модель, содержащую факторы: e00 , e11, e10 , e01, e33 , e22 , e32 и e23 (рисунок 2). Данную 8-параметрическую модель ВАЦ, которую, как было сказано ранее, можно преобразовать в 10-параметрическую, несложно нормализовать и получить 7 неизвестных параметров. Знание 7 параметров достаточно для восстановления всех факторов E,которые используются для выполнения коррекции измерений в соответствии с (6)–(9). Для этого должны быть привлечены дополнительные измерения в схеме ВАЦ с 4 приемниками. То есть для двухпортового ВАЦ с общим опорным приемником применение аппарата TRL затруднительно.
Воздушные линии являются эталонами волнового сопротивления. Качество калибровки TRL фактически определяется качеством изготовления воздушной линии. В результате алгоритмы TRL могут обеспечить максимальную точность определения факторов систематической погрешности, а значит – максимальную точность измерений среди всех известных алгоритмов калибровки. В зависимости от специфики ИУ, имеющегося набора мер и требуемого частотного диапазона следует выбирать тот или иной алгоритм из таблицы 1. Сложно обеспечить работу в широкой полосе частот, имея в калибровочном наборе только одну воздушную линию. Как правило, приходится комбинировать методы и даже меры, например, использовать в начале частотного диапазона СВЧ алгоритм TRM, а затем алгоритм TRL с двумя или более различными линиями. Существуют методы калибровки, предполагающие использование нескольких линий (multiline) на одних и тех же частотах. Основой метрологии векторных измерений являются прецизионные воздушные линии вместе с теорией TRL. Применение специальных динамометрических ключей обеспечивает повторяемость и единство измерений.
Современные приборы типа ВАЦ позволяют получить высокую точность измерений комплексных S-параметров различных устройств. Это достигается применением разнообразных методов калибровки. Чтобы эффективно использовать возможности прибора и разнообразных калибровочных наборов, необходимо ориентироваться в существующем многообразии алгоритмов.
Тем не менее, в настоящий момент имеются перспективные алгоритмы калибровки отечественной разработки, которые позволяют одновременно с измерениями оценить величину погрешностей, вызванных как не идеальностью калибровочных мер, так и влиянием самого векторного анализатора цепей, как сложного устройства. Далее в дипломной работе будет изложена как теория, так и практическое применение данного алгоритма.
2 Новый метод калибровки векторных анализаторов цепей СВЧ
Прежде чем исследовать метод аттестации, давайте определим, что именно с помощью этого метода нам предстоит определять.
Согласно общим представлениям, блок-диаграмма четырёхканального анализатора цепей может быть представлена в виде приведённом на рисунке 1.
Рисунок 4 – Блок диаграмма четырёхканального анализатора цепей
Исследуемый четырёхполюсник (DUT – device under test) и в принципе любая другая нагрузка может быть подключена между первым и вторым портом анализатора цепей. Измерения, возможно, проводить в прямом и обратном направлении, для этого выходной порт нагружается на согласованную нагрузку, а через входной подают СВЧ (RF) сигнал с генератора. Направленные ответвители используются для выделения пропорциональной части мощности падающего, отраженного и прошедшего сигнала для обоих направлений включения, как прямого, так и обратного. Смесители используются для преобразования СВЧ сигнала в сигнал ПЧ (IF). Частота LO=RF+IF.
-параметры исследуемого четырёхполюсника могут быть определены, если известны , , , , как :
– при измерении в прямом направлении (RFPort1DUTPort2Zo)
– при измерении в прямом направлении (RFPort1DUTPort2Zo)
– при измерении в обратном направлении (RFPort2DUTPort1Zo)
– при измерении в обратном направлении (RFPort2DUTPort1Zo)
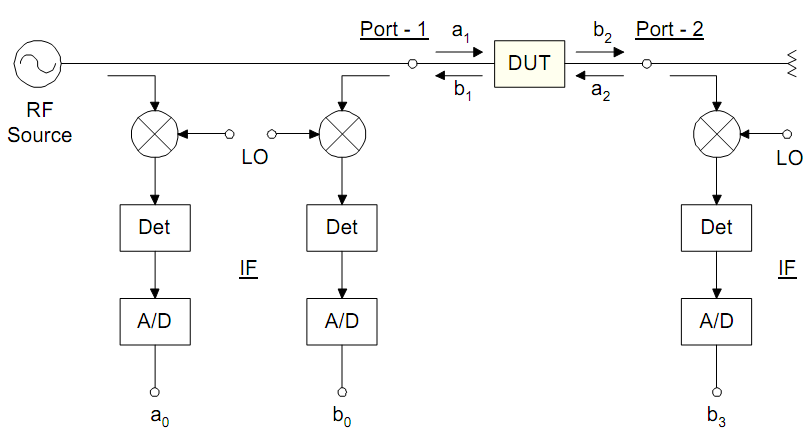
Рисунок 5 – Блок диаграмма четырёхканального анализатора цепей
включенного для измерений в прямом направлении
Блок диаграмма четырёхканального анализатора цепей включенного для измерений в прямом направлении приведена на рисунке 5. Естественно, что каждый IF сигнал детектируется и оцифровывается (Analog/Digital), тем самым позволяя измерять действительную и мнимую составляющую сигнала. Из этих комплексных детектированных данных представляется возможным рассчитать амплитуду и фазу сигналов. Результат оцифрованных сигналов , , является пропорционально уменьшенным значением электромагнитного излучения через DUT (, , ).
Для блок диаграммы четырёхканального анализатора цепей включенного по схеме измерений в прямом направлении в литературных источниках приводится ориентированный граф модели погрешностей всевозможных путей прохождения электромагнитного излучения, изображенная здесь на рисунке 6.
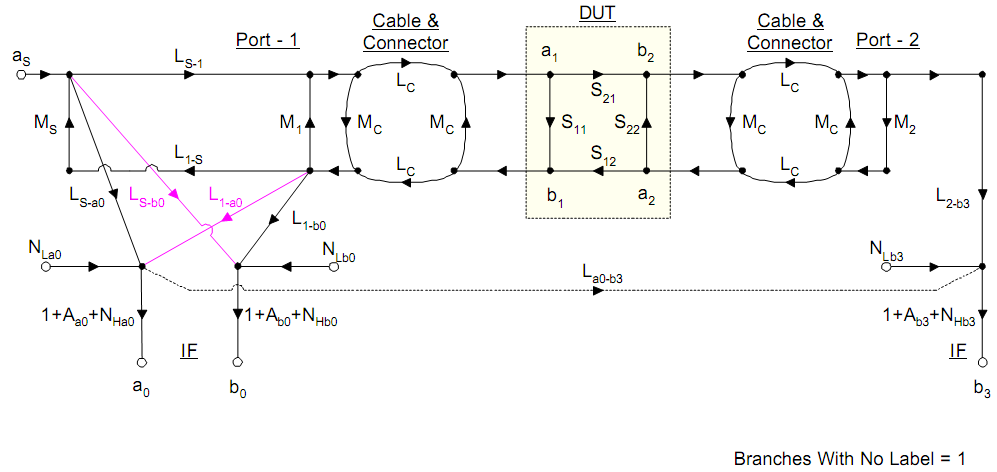
Рисунок 6 – Модель влияния погрешностей при прямом включении –
ориентированный граф всевозможных путей прохождения электромагнитного излучения
Указанные на графе пути включают не только искомые сигналы, но и потери, ошибки рассогласования волновых сопротивлений, и ошибки вызванные утечками (рассеянием). Так же, модель ориентированного графа включает (учитывает) нелинейность смесителей, цифрового преобразования и детекторов, а так же возникающие в системе анализатора цепей шумы. Ниже приведено описание обозначений используемых на рисунке 6.
|
– падающий сигнал из порта-1 – отраженный сигнал в порт-1 – падающий сигнал из порта-2 – поступающий сигнал в порт-2 – порт источника RF сигнала – измеряемый падающий сигнал – измеряемый отраженный сигнал – измеряемый проходящий сигнал – потери от источника RF до порта-1 – потери от порта-1 до источника RF – потери от источника RF до – потери от источника RF до – потери от порта-1 до – потери от порта-1 до – потери от порта-2 до – потери от до – потери в кабелях |
– коэфф. отражения DUT в порт-1 – коэфф. передачи в прямом направ. –коэфф. передачи в обратном направ. – коэфф. отражения DUT в порт-2 – согласование порта-1 – согласование порта-2 – согласование источника RF – согласование кабелей – низкоуровневый шум на – низкоуровневый шум на – низкоуровневый шум на – шум высокого уровня на – шум высокого уровня на – шум высокого уровня на – динамическая точность на – динамическая точность на – динамическая точность на |
Стоит отметить, что в иностранных источниках и называют направленностью, – рассеянием или утечкой, а динамические точности , и считают линейными.
Тем не менее, из-за сложности полной модели её уменьшают исключением в ориентированном графе некоторых факторов, получая граф, изображенный на рисунке 7. Этот граф не уступает в точности по систематической погрешности графу выше приведённому на рисунке 6, так как он получается в результате уменьшения путей за счет упрощения и расщепления путей [1].
Однако, эта модель (изображенная на рисунке 7) не учитывает: возникающие при измерениях шумы , , , , , ; динамическую точность , , ; дрейф после коррекции систематической погрешности; стабильность после коррекции систематической погрешности, а также повторяемость результатов и ошибки параметров калибровочных мер (стандартизированных эталонов).
Естественно, что стабильность, дрейф и другие ошибки ухудшают эксплуатационные качества прибора, они изменяются со временем, а это означает, что для достижения требуемой точности необходима перекалибровка прибора через определённый интервал времени, зависящий от нагрузки на прибор, окружающей среды (к примеру от температуры и влажности) и от некоторых других факторов.
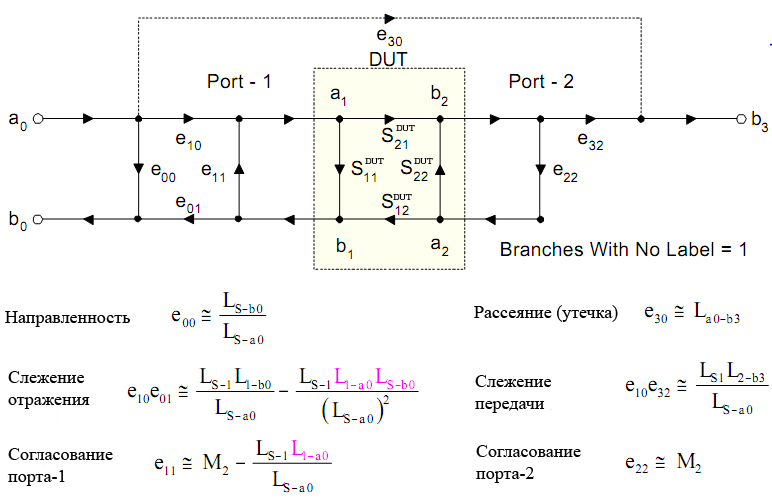
Рисунок 7 – Модель ориентированного графа при включении в прямом направлении измерения четырёхканального анализатора цепей учитывающий 6 систематических погрешностей
В любом случае и для четырёхканального (имеющего два порта) и для двуканального анализатора цепей (имеющего один порт) применяется процедура калибровки самого порта. Входе этой калибровки определяются параметры порта (или раздельно двух портов для четырёхканального анализатора цепей): – направленность, – согласование и – разбаланс (слежение), согласно модели изображенной на рисунке 8, являющейся частью модели, изображенной на рисунке 7.
Как видно, разбаланс представленный в ориентированных графах на рисунке 7 и рисунке 5 не совпадает по начертанию. Это следствие того, что произведение присутствует во всех вычислениях (и раздельно обычно не встречается) и для простоты написания формул граф представляют в виде в котором разбаланс можно представить одной буквой и не тягать по формулам их в отдельности (т.е. это просто математический трюк – финт ушами).
В дальнейшем параметры порта мы будем обозначать следующим образом:
– параметр направленности (соответствует )
– параметр согласования (соответствует )
– параметр разбаланса или слежения (соответствует произведению )
В наших обозначениях стандартный метод калибровки порта анализатора цепей, а точнее ориентированный граф для этого метода представлен на рисунке 8. Сам же метод калибровки заключается в измерении коэффициентов отражения от трёх различных нагрузок с известными коэффициентами отражения, называемыми эталонными мерами, в качестве которых обычно выступают: нагрузка короткого замыкания с коэффициентом отражения , согласованная нагрузка – и нагрузка холостого хода –.
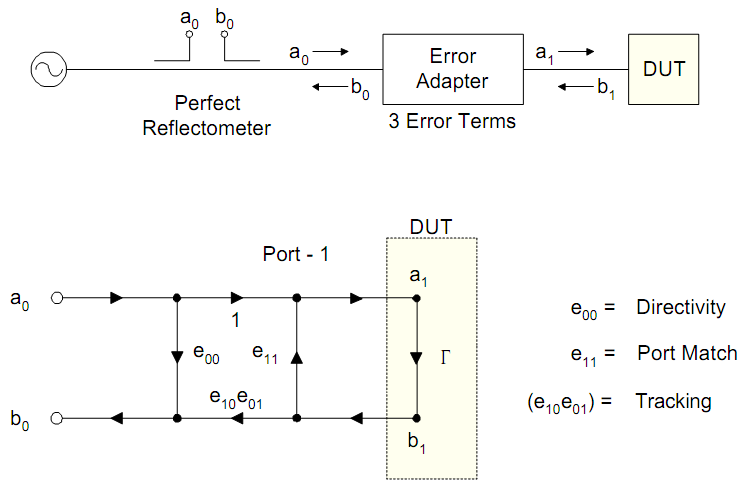
Рисунок 8 – Модель влияния параметров порта на систематическую ошибку измерения коэффициента отражения нагрузки
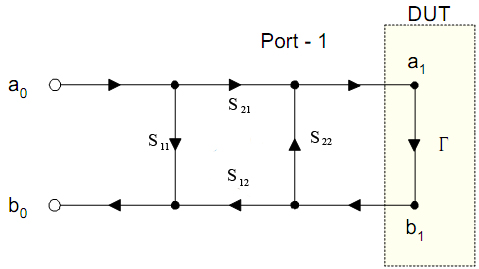
Рисунок 9 – Модель влияния параметров порта на систематическую ошибку измерения коэффициента отражения нагрузки с используемыми в дальнейшем обозначениями
Соотношения измеренного коэффициента отражения и реального значения коэффициента отражения эталонной нагрузки согласно ориентированному графу хорошо известны [4,5]:
(10)
(11)
Все три параметра порта , , могут быть определены при трёх измерениях от трёх различных с известными значениями коэффициентов отражения (эталонных мер) нагрузок с дальнейшим составлением системы из трёх уравнений по формуле (1) для каждой из нагрузок. Результатом решения составленной системы уравнений и будут значения параметров порта , , .
Однако, сами значения эталонных нагрузок, как правило, необходимо либо измерить на каком-то эталонном оборудовании более высокого класса точности, что невозможно в случае потребности откалибровать само эталонное оборудование; либо необходимо рассчитать параметры эталонных нагрузок с необходимой точностью, что достижимо лишь частично для узкого класса нагрузок, а именно нагрузок короткого замыкания (это связано с тем, что значения нужны в полосе частот, а конструктивно выполнить условия возможно только для одной частоты, либо в очень узком интервале частот). Естественно, погрешности в изначальной информации о значениях коэффициентов отражения (модуля и фазы) эталонных нагрузок увеличивают при стандартном методе калибровки анализатора цепей погрешность определения параметров порта , , , а значит и дальнейших измерений с его помощью.
Поэтому первоочередной задачей является разработка методов калибровки, для которых нет необходимости в изначальной информации о точных значениях коэффициентов отражения (модуля и фазы) эталонных нагрузок как минимум и , с целью уменьшения систематических погрешностей измерений, согласно выше изложенному.
Так как любой метод аттестации будет в любом случае иметь как математическую, так и методологическую ошибки (не считая возникающие при измерениях шумы, динамическую точность, дрейф после коррекции систематической погрешности и стабильность после коррекции) то, во-вторых – необходимо оценивать влияние на результаты измерений как математической, так и методологической ошибки.
В силу того, что рассматриваемая модель нового способа калибровки VNA[X], согласно рисунку 6, позволяет минимизировать только лишь систематическую ошибку измерений, но не в состоянии скомпенсировать возникающие при измерениях: шумы, динамическую точность, дрейф после коррекции систематической погрешности и стабильность после коррекции; перед нами стоит задача оценка основнх составляющих абсолютной погрешности измерений и сравнении полученной абсолютной величины погрешности с погрешностями метрологической точности эталонных нагрузок полученных другими методами.
Отметим, что в следующей главе метод калибровки будет исследоваться в общем, однако его оценка будет осуществляться на основе измерений проведённых при относительно стабильной температуре и в непродолжительный интервал времени (максимально для определения стабильности работы после включения в течение пяти часов) для конкретного РК4-74. Из этого следует, что исследования на влияние температуры, а так же стабильность после коррекции (проведения калибровки – аттестации) более чем на три часа без выключения прибора в этом отчете – не представлены.
Математическое описание метода и части алгоритма.
Измерительный порт включает в себя входной разъём и связанный с ним внутренний тракт измерителя характеристик четырёхполюсников СВЧ. Для определения (измерения и вычисления) собственных -параметров применяют режим аттестации (калибровки). Аттестация измерителя характеристик четырёхполюсников СВЧ заключается в вычислении собственных -параметров его измерительных портов, как комплексных величин, характеризуемых модулем и фазой. Для аттестации применяют эталонные нагрузки короткого замыкания (КЗ), холостого хода (ХХ) и согласованную нагрузку (СН), зависимости модуля и фазы коэффициентов отражения которых в диапазоне частот, при калибровке эталонной аппаратуры, известны лишь условно (приблизительно).
Естественно, погрешности в изначальной информации о значениях коэффициентов отражения (модуля и фазы) эталонных нагрузок при стандартном методе калибровки анализатора цепей (описанном в прошлой главе) увеличивают погрешность определения параметров порта , , , а значит и дальнейших измерений с его помощью.
Поэтому новый «способ аттестации собственных – параметров устройств, для измерения комплексных коэффициентов передачи и отражения четырехполюсников СВЧ», оформленный виде патента (авторы: К.С. Коротков, А.С. Левченко, Д.Н. Мильченко, И.Н. Шевченко), позволяющий повысить точность определения -параметров портов анализаторов цепей, таким образом уменьшив систематическую ошибку измерений с их помощью параметров четырёхполюсников, является весьма актуальным шагом на пути к созданию нового класса метрологических систем калибровки VNA.
С измерительной части способ заключается в том, что дважды измеряют коэффициенты отражений трёх эталонных нагрузок: короткого замыкания, холостого хода и согласованной нагрузки, присоединяя их один раз непосредственно к аттестуемому измерительному порту (рис. 7а), а второй раз присоединяя каждую из них к аттестуемому измерительному порту через линию передачи калиброванной длины (рис. 7б) называемую мерой волнового сопротивления (МВС).
Таким образом, для каждого из шести соединений согласно формуле (1) имеем:
(12)
(13)
где: , и – параметры измерительного порта;
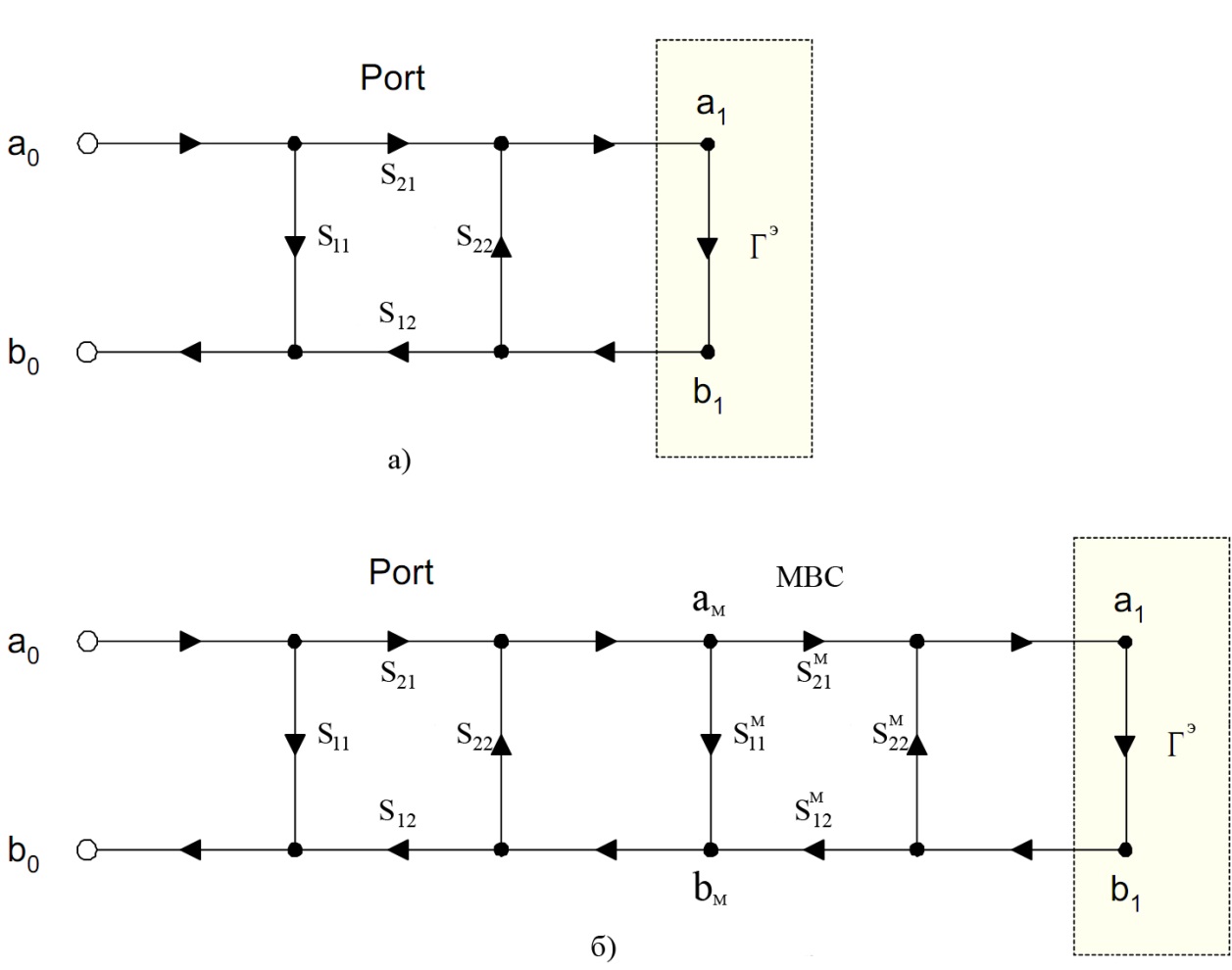
Рисунок 10 – Модель подключения эталонных нагрузок к аттестуемому порту для проведения его калибровки а) непосредственно, б) через МВС – меру волнового сопротивления
, и – измеренные коэффициенты отражения (рисунок 10) от подключенных непосредственно к порту нагрузок КЗ, ХХ и СН соответственно;
, и – истинное значение коэффициентов отражения от нагрузок КЗ, ХХ и СН соответственно;
, и – измеренные коэффициенты отражения (рисунок 10) от подключенных через МВС к порту нагрузок КЗ, ХХ и СН соответственно;
, и – значение коэффициентов отражения от МВС совместно с присоединённой нагрузкой КЗ, ХХ или СН соответственно (т.е. согласно рисунку 10);
Для значений , и коэффициентов отражения от присоединённых к МВС нагрузок КЗ, ХХ и СН согласно рисунку рисунок 10 так же справедлива формула (1):
, (14)
где , и – -параметры меры волнового сопротивления рассматриваемой в виде четырехполюсника.
И так, значения , , и , , определяются непосредственно в результате измерений и, следовательно, являются известными величинами. Все остальные – , , , , , , , , в общем случае, не известны. Таким образом, совместная система уравнений (3) и (4) с учетом (5) состоит из шести уравнений.
Отметим, что МВС подключается к порту анализатора цепей только однократно в процессе всей аттестации, а вот нагрузки КЗ, ХХ и СН поочерёдно подсоединяются, сначала к порту измерителя, а потом и к МВС. Следовательно, неодинаковость соединений внесёт дополнительную погрешность в определение искомых величин , , и в дальнейшем в погрешность измеряемых величин самим анализатором цепей. Математически это возможно учесть несколькими эквивалентными друг другу вариантами. Один из вариантов: параметры МВС во всех трех формулах уравнения (5) различны на величину равную тому, в какой мере различаются параметры соединения с портом измерителя и с параметрами соединения этого же типа нагрузки с МВС; а для коаксиальных МВС и отличие так же учитывается. Поэтому, этот факт будем иметь в виду, для учета в ходе дальнейших рассуждений возникающей при этом погрешности, а само явление назовём погрешностью зажима. Устранить эту погрешность никак нельзя, но возможно минимизировать конструктивной точностью выполнения соединительных разъёмов и применением ключей с калиброванным усилием для непосредственного соединения.
Вспомним, что аттестация анализатора цепей проводится в некотором, вполне определённом диапазоне частот, заведомо известном исходя из конструктивных особенностей аттестуемого прибора. Поэтому, для уменьшения количества неизвестных в первую очередь, в заданном диапазоне частот и с заданной точностью, возможно, рассчитать параметры короткозамкнутой нагрузки и использовать её для аттестации. К примеру, будем считать, что используемая нагрузка КЗ для полых волноводов имеет коэффициент отражения:
, (15)
и может быть изготовлена с точностью до пятого знака после запятой. Данное обозначение в место указывает, что значение является расчетной величиной с вполне определяемой погрешностью.
Так же, для уменьшения количества неизвестных оценим степень влияния и т.е. «разъёмов» МВС на соотношения (5). Минимальное их влияние на общие результаты измерений должно наблюдаться, когда длина МВС обеспечит разность фаз между отраженными от неоднородностей и волн в , что выполняется только для вполне определённых частот. Поэтому, используемая в методе МВС должна изготавливаться длиной таким образом, что бы указанные выше частоты попадали как можно ближе к краям рабочего диапазона анализатора цепей и присутствовали в достаточном количестве вдоль всего диапазона, но при этом не должна быть настолько длинной, чтобы заметно вносить затухание в проходящую мощность (заметное – это больше, чем неоднородность соединения). Эти частоты станут опорными для дальнейших расчётов. Поэтому точки различных зависимостей соответствующих этим частотам мы будем называть «реперными».
Таким образом, для выше указанных частот отраженные от неоднородностей и волны противофазно накладываясь, гасят друг друга (стоит отметить, что в этих точках так же минимально влияние погрешности зажима, так как погрешность зажима неявно входит в величину ), иными словами – минимизируются «биения» вдоль МВС.
При компенсации и математически эквивалентно к их отсутствию:
(16)
С учетом замены произведения на :
, (17)
с точностью до погрешности зажимов, степени компенсации и , и только для «реперных» точек:
(18)
Так как, системы уравнений (3) и (4) решаются в диапазоне частот, то с целью указания, области допустимого использования формул (8), при переходе к расчетам в диапазоне частот заменим для наглядности , и на , и соответственно, а также , и на , и соответственно. То есть, , и - это значения в диапазоне частот эталонных нагрузок, но уже не истинное, а с набором ограничений и условностей, которые напрямую сводятся к истинным (с точностью до погрешностей) только лишь в частотах соответствующих «реперным» точкам, при других частотах пренебрежение и даст заведомо отличный от истинного значения результат определяемый «биениями» возникающими вдоль МВС
. (19)
Таким образом, исходя из (3–9) и учитывая введённые обозначения (10) получим систему из шести уравнений с шестью неизвестными:
(20)
где неизвестны , , , , , .
Из трех уравнений в левой части системы уравнений (11) выразим параметры измерительного порта:

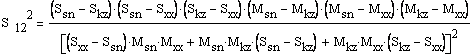 (21)
(21)
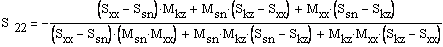
А из трех уравнений в правой части системы уравнений (11) выразим значения коэффициентов отражения нагрузок подключенных совместно с МВС:

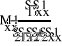 (22)
(22)
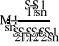
Подставив в систему уравнений (13) выражения для параметров порта из системы уравнений (12) получим систему уравнений (14) в которой значения коэффициентов отражения нагрузок подключенных совместно с МВС зависят только от , , , , , (известных измеренных значений), и , (на данном этапе двух искомых) и не зависит от параметров порта.

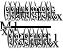 (23)
(23)
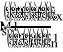
Естественно, что воспользовавшись системой уравнений (10), если бы мы точно знали параметр и значения , (эквивалентны , ), то правые и левые части уравнений не сошлись бы на величину, определяемую выбранными нами ограничениями , и погрешностями зажима. Поэтому согласно Приложению 1, мы можем представить это несоответствие в виде четырёхполюсника погрешностей включенного в схему и будем описывать параметры этого четырёхполюсника через - параметры (остаточные параметры):
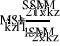
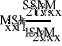 (24)
(24)
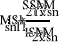
Расхождение будет обусловлено погрешностями зажимов вносящее вклад для всех параметров . Физический смысл остаточных - параметров порта – это параметры четырехполюсника погрешностей, отличающиеся от S` - параметров идеально согласованного по входу и выходу четырехполюсника без потерь (у которого в общем виде S`11 и S`22 равны нулю, а произведение S`11S`22 равно единице) на величину погрешностей аттестации, включающую как величины погрешностей калибровки коэффициентов отражения эталонных нагрузок ХХ, СН и отличие расчётного коэффициента передачи МВС от реального, включая погрешности разъемных соединений.
Так как МВС стараются сделать как можно лучше, то есть минимизировать значения и из-за несовпадения геометрических размеров и неоднородностей при соединении, то, как учитывая формулу (7) так из условия минимизации погрешностей – рассматриваемый четырёхполюсник погрешностей должен представлять собой, устройство с параметрами
, а и (25)
что соответствует отсутствию четырехполюсника погрешностей (идеальный случай).
Таким образом, из системы (15) выражаем остаточные - параметры:
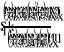
 (26)
(26)

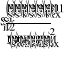
применяя соотношения (16) к системе уравнений (17), а так же заменив выражениями из системы уравнений (14) и учитывая, что знаменатель не может быть, строго равным нулю получим из первого и третьего уравнения:

(27)

где:  ,
,
 ,
,
 ,
,
В этой системе уравнений (18) всего две неизвестные и .
Второе уравнение из (17) даст возможность при знании и определить :
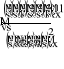 (28)
(28)
В принципе, строго математически эти соотношения (18) и (19) получаются при прямой подстановке системы уравнений (14) в систему уравнений (10), но тогда небыли бы введены остаточные - параметры, которые в дальнейшем понадобятся.
Если решить систему (18) относительно и , и восстановить по ним истинные и , то подставив восстановленные значения в систему уравнений (3) (или (12), но вместо и нужно подставлять истинные и ) возможно определить искомые , и – параметры измерительного порта анализатора цепей.
Пример калибровки по рассматриваемой методике и работа алгоритма калибровки
Аналитическое решение системы (18) относительно и , при измерениях для прямоугольного волноводного порта VNA представлено на рис-8, как пример. Как видно, хотя коэффициенты отражения от этих нагрузок должны быть гладкими мы наблюдаем резкие периодические всплески, они вызваны тем, что для формирования системы уравнений (18) мы воспользовались переходом от уравнения (7) к уравнению (9), а это осуществимо только в реперных точках – и то лишь условно. Поэтому между реперными точками влияние и увеличивается по мере приближения к частотным точкам, отстоящим ровно посередине между реперными, т. е. мы наблюдаем максимальное влияние пренебрежением и в решаемой системе уравнений вызываемое «биениями» вдоль МВС.
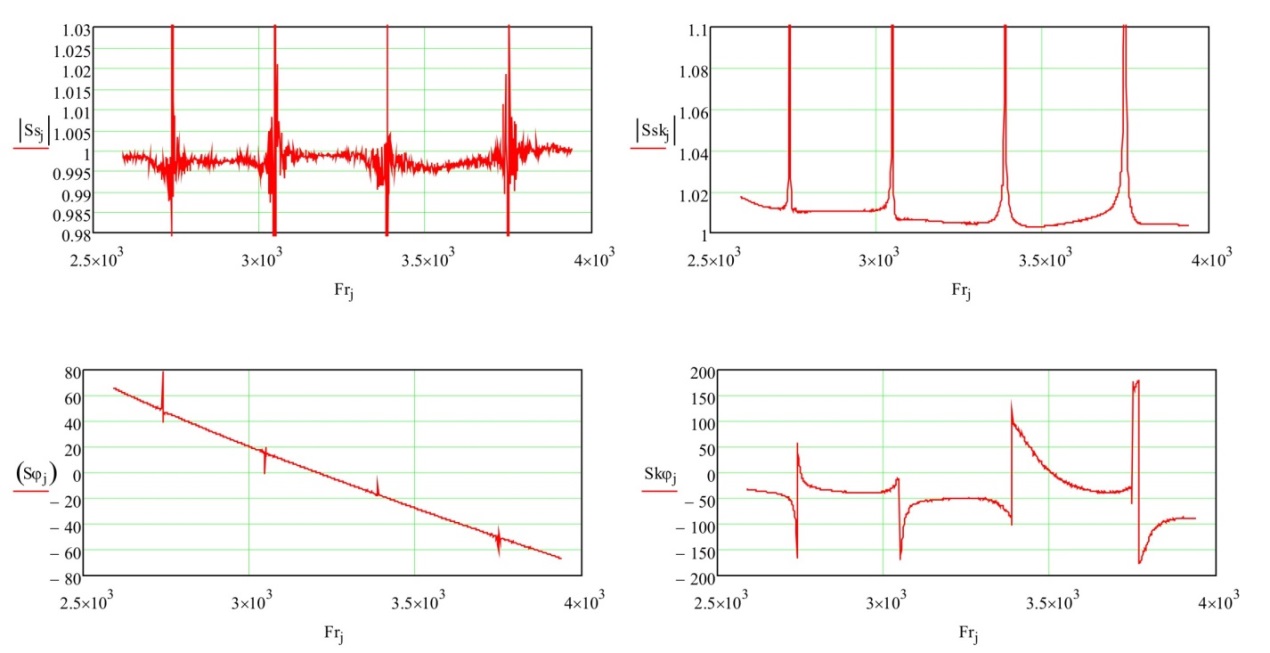
Рисунок 11 – Частотные зависимости амплитуды (сверху слева) выраженной в КСВн и фазы (снизу слева) в градусах; амплитуды (сверху справа) и фазы (снизу справа) в градусах. Частота в МГц
Однако, так как в формуле (19) присутствуют фактически только разностные составляющие коэффициентов отражения от различных нагрузок, то и по амплитуде и по фазе возникающие искажения «математически» компенсируются (это видно и по таблице 1 – для всех вариантов решения уравнения 18 значения для амплитуды и фазы МВС были одинаковыми). Таким образом, подставив в формулу (19) найденные значения и получим значения , для примера представленные на рисунке 12.
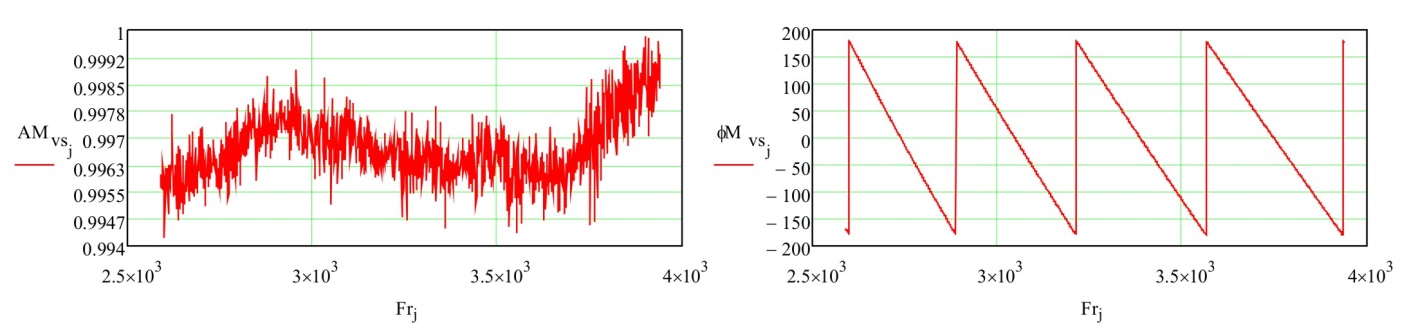
Рисунок 12 – Частотные зависимости амплитуды и фазы параметра
Из графика ФЧХ представляется возможным найти частоты соответствующие реперным точкам - когда длина МВС обеспечит разность фаз между отраженными от неоднородностей и волн в . Однако заметим что в отличие от фазы частот нагрузки «воздушной линии» представленной в [11] эти точки отстоят не на одинаковом расстоянии друг от друга. Это объяснимо в основном тем, что зависимости приводятся для МВС в виде прямоугольного волновода и длина волны внутри волновода отличается от длины волны которую выдаёт генератор; для проверки построим фазовую зависимость от относительной частоты сигнала в волноводе – рисунок 11.
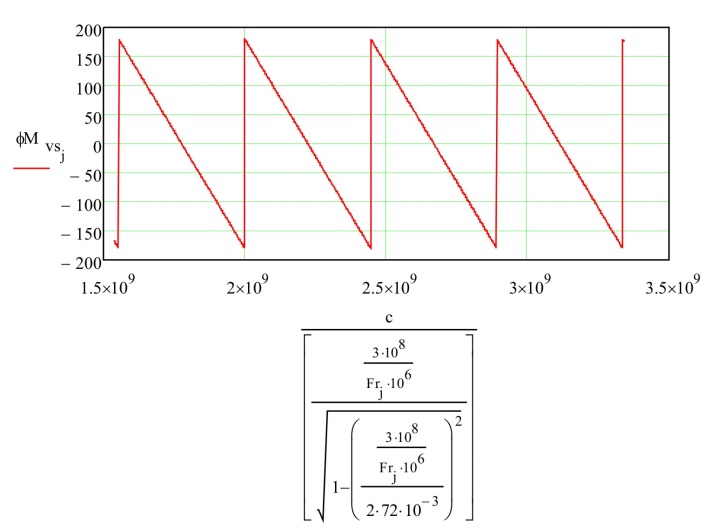
Рисунок 11 – Фазо-частотная зависимость, где частота пересчитана относительно длины волны в волноводе в ГГц
Шумы амплитуды изображенной на рис. 9 обусловлены множеством факторов, среди которых – ошибки аналого-цифрового преобразования сигналов с детекторов, частотная нестабильность генератора, а так же сделанное нами предположение по формуле (7) и (9).
Теперь необходимо скомпенсировать в промежуточных и точках пренебрежением и вызванным применением перехода от (7) к (9).
Для этого воспользуемся данными и в малой окрестности реперных точек, – найдём по ним производную функций и в каждой реперной точке. Производная определяется по наклону прямой являющейся результатом аппроксимации, по методу наименьших квадратов, зависимости значений функции в окрестности реперной частотной точки.
По значениям функций и в реперных точках и по найденным значениям производной функций в этих точках становится возможным построить аппроксимирующие функции Эрмита - и [10].
Отметим, что все вычисления мы проводим только в комплексном виде без перевода в амплитуды и фазы, так как последнее привело бы к накоплению погрешностей измерений при каждом переводе. Аппроксимацию мы так же проводим раздельно для мнимой и действительной части комплексного числа. Основная причина – изначальные данные измерений приведены в комплексном виде. Поэтому только лишь для визуальной оценки и понятного представления мы используем графики с амплитудно-частотной и фазо-частотной зависимостью, но не как не для вычислений.
Результаты и аппроксимации и представлены на рисунке 13.
Рисунок 13 – Зависимости АЧХ и ФЧХ (в градусах) функций и ( КСВн) являющихся результатом аппроксимации и соответственно также приведённых на графиках
Следующим этапом является определение искомых , и – параметров измерительного порта анализатора цепей. Для этого подставим восстановленные значения и в систему уравнений (3) (или эквивалент (12), но вместо и нужно подставлять истинные и ), в результате определяем искомые – параметры измерительного порта, к примеру представленные на рисунке 14.
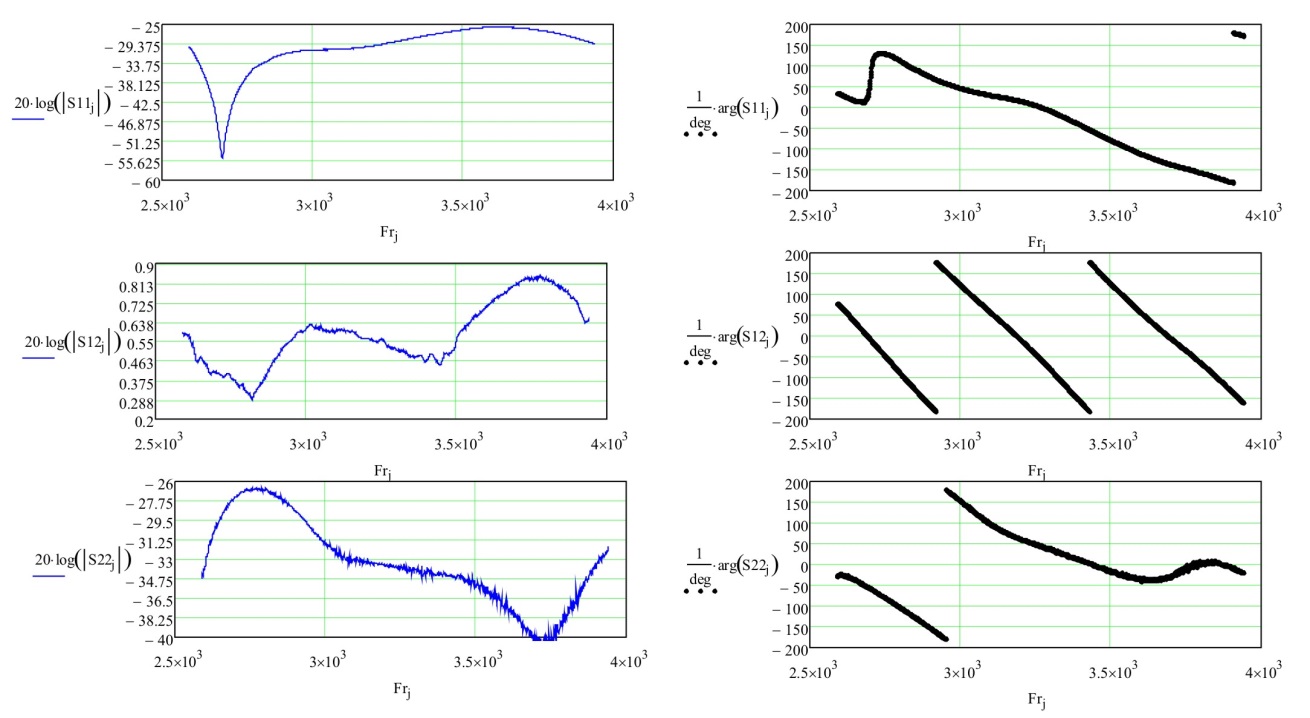
Рисунок 14 – Пример рассчитанных АЧХ (дБ) и ФЧХ (градусы) – параметров измерительного порта анализатора цепей – , и
Естественно, что мы хотим проверить наши расчеты и для этого применяем нехитрую формулу
(29)
Для отыскания Sk – «остаточных параметров порта», где значения коэффициентов отражения нагрузок подключенных совместно с МВС хотим вычислить по формуле (13) подставив в неё найденные параметры порта. Это всё эквивалентно использованию формулы (17) совместно хоть с (13) хоть с (14), но с заменой в них и на и
После проведения аппроксимации рис. 11, мы можем подставить найденные значения и в первую формулу системы уравнений (17). Действительно, формально параметр от – не зависит, тогда получившийся пример зависимости изображен на рисунке 15.
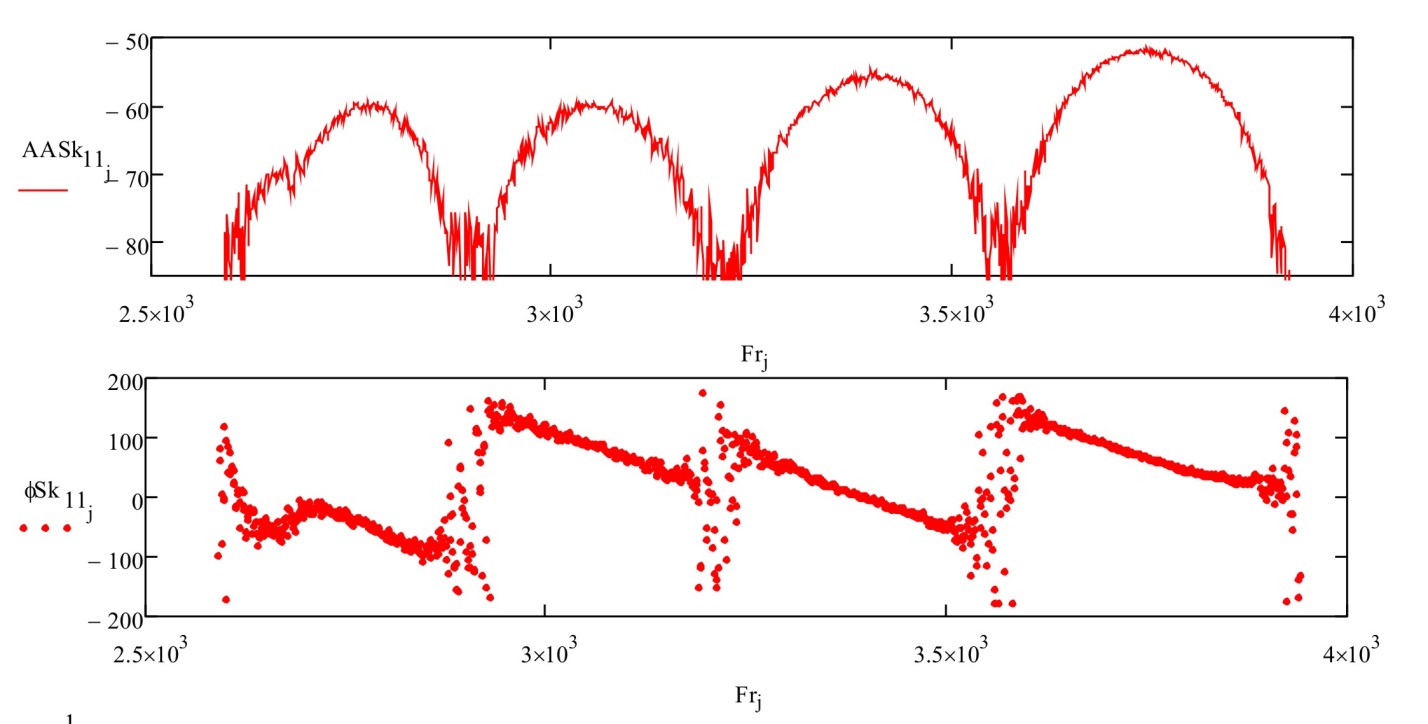
Рисунок 15 – Пример рассчитанных АЧХ (дБ) параметра при подстановке и в первую формулу системы уравнений (17)
Второе уравнение формулы (17) при подстановке и даст нам возможность определить . Пример приведен на рисунке 16.
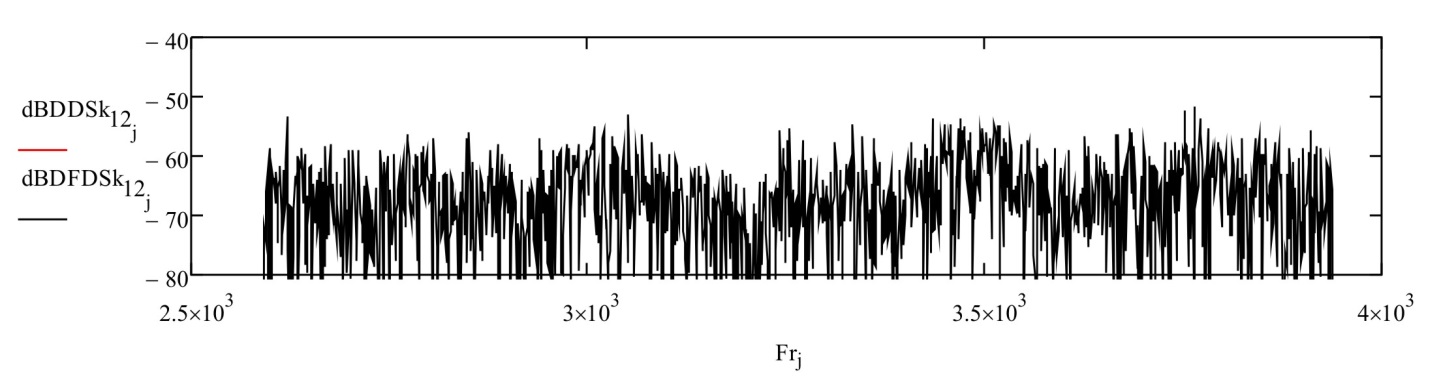
Рисунок 16 – АЧХ функции - т.е. график показывает в диапазоне частот отличие амплитудного значения параметра от единицы в дБ
При подстановке найденных значения и в третью формулу системы уравнений (17) для определения соответственно с аппроксимацией .
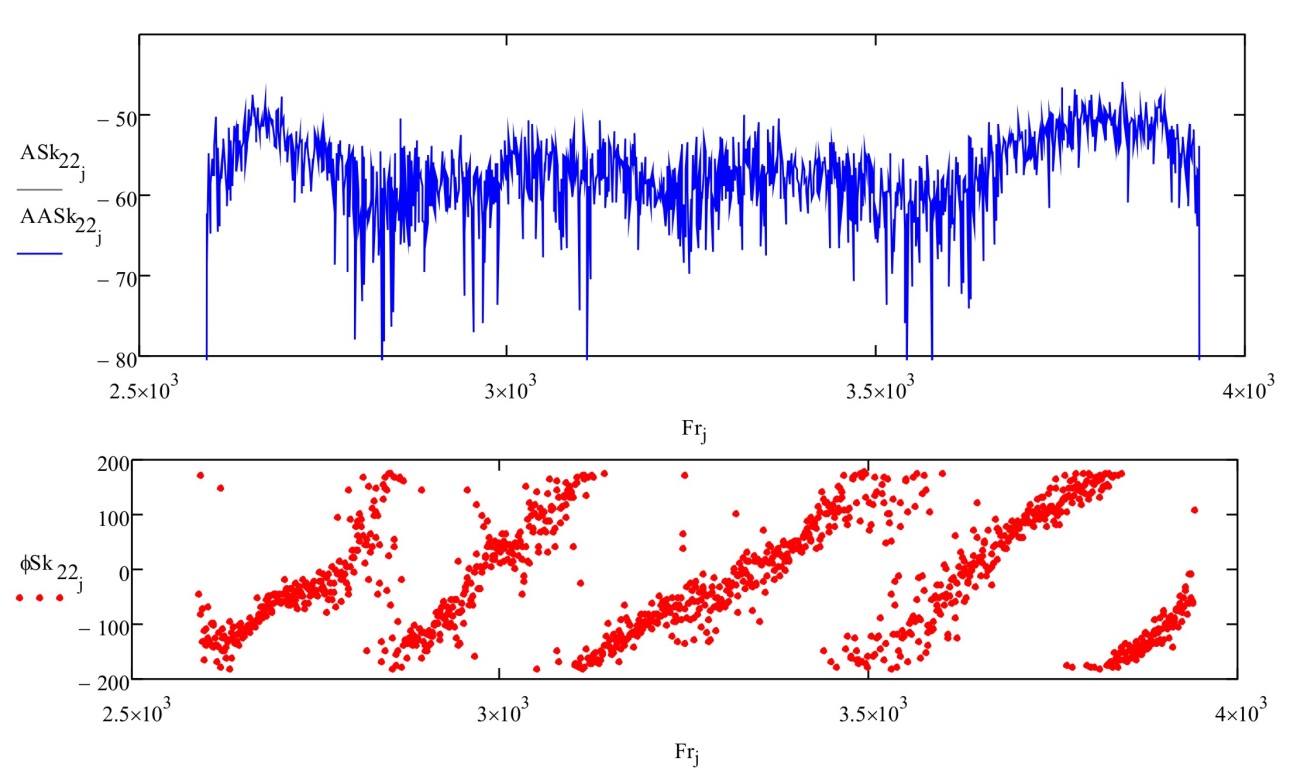
Рисунок 17 – Пример рассчитанных АЧХ (дБ) и ФЧХ (градусы) параметра при подстановке и в третью формулу системы уравнений (17) одинаковы при аппроксимации и без аппроксимации
параметрами – это параметры, отличающиеся от -параметров идеально согласного по входу и выходу четырёхполюсника без потерь (у которого в общем виде и равны нулю, а произведение равно единице) на величину погрешностей аттестации, включающую как величины погрешностей калибровки коэффициентов отражения эталонных нагрузок ХХ, СН и отличие расчётного коэффициента передачи МВС от реального, включая погрешности разъёмных соединений. Таким образом, величины, на которые параметры и отличаются от нуля, а от единицы, являются погрешностями аттестации. Если погрешности калибровки отсутствуют, то и должны быть равны нулю, а произведение должно быть равно единице, что соответствует идеальному случаю отсутствия погрешностей калибровки. (уберём неточности определения в третей главе).
Определение смысла остаточных параметров порта и анализа для абсолютной погрешности представленного во второй главе способа аттестации проведём исследование, описание которого и результаты приведены в главе 3.
3 Практическое применение нового алгоритма
Любая аппаратура работает не стабильно, однако значение нестабильности у разного класса аппаратуры могут отличаться на несколько порядков.
В исследовании на влияние схем калибровки и измерений на погрешности определения характеристик четырехполюсников СВЧ векторным анализатором цепей будем учитывать три составляющие погрешности:
– Погрешность, вызванная методологией калибровки (в данном случае из-за не идеальности стыков и, следовательно, точности соединений)
– Погрешность, вызванная джитером сигнала (с детекторов, A/D преобразователей, плавание частот, шумах в каналах) как по амплитуде, так и по фазе.
– Погрешность неточности знания значений КЗ
В любом случае, так как конечные параметры порта определяются математически, то все эти погрешности должны учитывать влияние математических преобразований при использовании рассматриваемого метода.
Погрешность, вызванная методологией калибровки, основывается на остаточных параметрах порта. Если при измерениях рассматривать значения получаемые аттестованным (откалиброванным и использующим для измерений соответствующие математический аппарат и формулы для вычисления конечных значений) векторным анализатором цепей, то из-за метода калибровки эти значения будут известны с точностью, до виртуально присутствующего четырехполюсника погрешности между измерительном портом и исследуемой нагрузкой. На рисунке 16 схематически показан четырехполюсник остаточных параметров в составе измерительного порта.
Рисунок 16 – Ориентированный граф измерительного порта
Сам прибор измеряет сигнал в точках a и b – падающую и отраженную волну; при компенсации параметров порта, калибровочный прибор выдает в качестве результата измерения Гu эквивалентно равной отношению падающей и отраженной волн в точках а’ и b’ соответственно. Но измеренное значение от реального будет отличаться на величину:
, (30)
Домножив числитель и знаменатель второго слагаемого на величину получим следующее выражение:
. (31)
В векторных анализаторах цепей метрологического класса менее 35 дБ, а измеряемое . Уровень точности векторных анализаторов цепей такого класса лежит в пределах 60 дБ, поэтому с запасом на несколько порядков (так как эта погрешность становиться существенной только при менее -30 дБ) слагаемым можно пренебречь и формула (Х) примет следующий вид:
, (32)
Отклонение или погрешность с учетом необходимых подстановок примет вид:
, (33)
Зачастую в векторных анализаторах цепей рассматриваемого класса менее –40 дБ, поэтому во многих случаях формулу (33) можно свести к
(34)
Стоит заметить, что в дальнейшем проведенных экспериментах будет использована формула (34), а для отличая вида погрешности будем обозначать ее в дальнейшем .
Оценка погрешности вызванной влиянием джитера в аппаратуре должна быть совмещена с выбранным алгоритмом на точность определения параметров порта. Для этого необходимо проводить серию измерений: будем обозначать эти серии I1 и I2.
I1 – это измерение с подключенными, непосредственно к измерительному порту, нагрузок ХХ, КЗ и СН. Причем, для каждой подключенной нагрузки проводим по N однотипных измерений не отсоединяя нагрузку от измерительного порта анализатора цепей (т. е. подсоединения для каждой нагрузки – одно, а по n раз повторяется зондирование сигналом во всем измеряемом диапазоне частот).
I2 – это измерение с подключенными к измерительному порту нагрузок ХХ, КЗ и СН, но уже через МВС. Причем, для каждой подключенной нагрузки проводим по n однотипных измерений не отсоединяя нагрузку от МВС, а сама нагрузка МВС во всех измерениях I2 и для всех нагрузок не отсоединяя от измерительного порта анализатора цепей (т. е. МВС подсоединили один раз, а потом к ней поочередно подсоединяем три нагрузки, причем подсоединение для каждой нагрузки одно, а по n раз повторяется зондирование сигналом во всем измеряемом диапазоне частот).
При этом стоит, опираясь на методику проведения эксперимента и дальнейшую математическую часть поиска параметров порта, описанную в главе 2, уточнить следующее:
а) так как при измерениях I1 подсоединения нагрузок к порту производилось однократно, то параметры «не идеальности» стыка соединительных фланцев раздельно составной частью входят в значения каждого коэффициента отражения от присоединяемых нагрузок и не одинаково для разных типов нагрузки.
б) при измерении I2, МВС подсоединяется к порту однократно, и эnо соединение используется для всех дальнейших измерений, значит параметр «не идеальности» стыка соединительных фланцев является постоянной величиной и составной частью входит в
значение параметра МВС.
в) при измерении I2 подсоединения нагрузок к порту МВС однократно, то параметры «не идеальности» стыка соединительных фланцев будут уже различаться от описанных в пункте а). Причем для каждой из нагрузок это различие будет свое, но постоянное.
Таким образом, через анализируемые данные I1 и I2 по средствам функциональных зависимостей мы сначала можем получить средние значения искомых величин и погрешность этих величин, вызванную джитером, но не учитывающим погрешность неодинаковости присоединения КЗ, XX и СН к измерительному порту и МВС.
И так, в I1 и I2 для каждого подключения необходимо провести по n измерений. Так как исходные данные с прибора представлены в комплексной форме, то будем рассчитывать погрешности, вносящие вклад в общую погрешность, для действительной и мнимой частей - независимо друг от друга. Это в общем случае справедливо, так как система измерителя с большим числом степеней свободы.
Погрешность будем брать с доверительной вероятностью (достоверность) т.е. для коэффициента Стьюдента t в соответствии с количеством проводимых измерений.
Среднее значение сигналов с детекторов будем вычислять как: для действительных частей и – для мнимых, где n – число измерений. В результате для каждой из пяти измерений получим среднее значение . Соответственно шесть частотных зависимостей: для I1 – , , и три для I2 – , , .
Отклонение от среднего значения так же вычисляем отдельно для действительной и мнимой частей:
дисперсия – ,
отклонение – ,
Для удобства хранения результатов будем его записывать и хранить в виде . Результат программы расчета средних значений и отклонений (приложение) разумно хранить в файлах cvs в виде:
Таблица 2 – Результат программы расчета средних значений и отклонений
|
вид данных |
f |
||||||
|
номер столбца |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
Таблица 3 – Результат программы расчета средних значений и отклонений
|
вид данных |
f |
||||||
|
Номер столбца |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
В каждой ячейке данные представлены в комплексной форме для каждой частотной точки.
Именно эти средние значения будут использованы в качестве данных для расчета собственных параметров измерительного порта и остаточных параметров порта.(т. е. Четырехполюсника погрешностей), с целью исключения завышения значения погрешности из-за зависимости этих параметров при калибровке от всех составляющих погрешностей; однако нам необходимо считать все эти три составляющие погрешности независимыми друг от друга.
Естественно, что изменения во входных значениях I1 и I2 вызванных джитером накладывает на аппроксимирующую функцию свой отпечаток, так как меняются не только амплитуды реперных точек, но и значения в их окрестности, а значит производных в реперных точках. Изменения аппроксимирующей функции влечет различие вычисляемых коэффициентов отражения эталонных нагрузок, а это в свою очередь приводит к изменению в получаемых значениях как собственных параметров порта, так и в их остаточные параметры.
В данном случае, необходима корректная обработка косвенных измерений. Будем рассматривать математический метод поиска собственных параметров порта и его остаточных параметров, а так же параметров Гхх и Гсн, как некую, весьма сломанную, функцию.
Функциональную зависимость , значения величин переменных находятся прямыми измерениями. Тогда, как уже отмечалось, действительные значения , , и определяются как:
(35)
Если зафиксировать значение всех аргументов, кроме одного, например , то прирощение функции при изменении ее аргумента имеет вид:
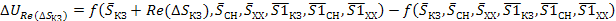
Величина характеризует погрешность, обусловленную погрешностью , т. е. джитером влияющим на измерение реальной части КЗ прикрученой к измерительному порту.
Аналогично, другие погрешности аргументов прямых измерений вызванных джитером
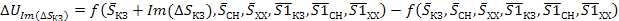
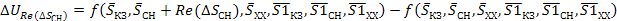
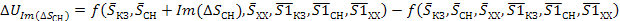
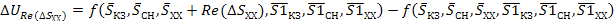
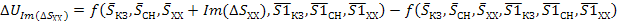
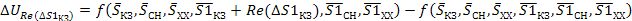
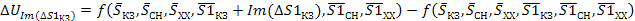
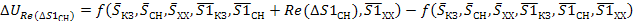
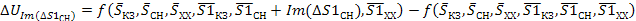
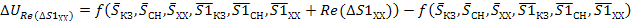
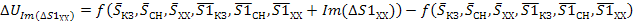
(37)
Полная погрешность косвенных измерений вычисляется либо с помощью квадратичного суммирования, либо суммирования по модулю ее составляющих, вносимых каждым аргументом. Так, как погрешность аргументов (т. е. джиттер) обусловлена влиянием многих факторов, среди которых нет преобладающего, а погрешности аргументов статистически не связанны, то:
(38)
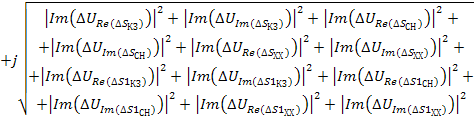
Однако в рассматриваемой функциональной зависимости значения КЗ было взято за эталон, при этом, как известно, КЗ задано всегда с какой-то точностью. Поэтому, аналогично предыдущему исследованиям, необходимо определить погрешности вызванные неточностью значения КЗ, но уже суммированием по модулю составляющих погрешностей .
(39)
Для применения вычисленных погрешностей и наглядного представления результатов их действия необходимо перевести комплексные значения погрешностей в значения погрешностей амплитуды и фазы.
Для амплитуды:
(40)
Погрешность фазы рассчитывается из следующих графических представлений
Рисунок 17 – Пояснения к расчету по формуле (41) погрешности фазы через известное значение погрешности амплитуды
Таким образом, для расчета погрешности фазы будем использоваться следующую формулу:
(41)
Суммарную погрешность от трех составляющих: остаточные параметры порта, джитер, погрешность знания КЗ; в силу независимости их значений, будем рассчитывать по формуле:
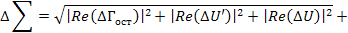
(42)
Заметим, что все расчеты ведутся в алгебрологической комплексной форме, дабы не увеличивать погрешность математическими переводами записей из алгебрологической формы в показательную, а затем обратно.
Все расчеты при этом являются частото-зависимыми , а так же зависимыми от модуля коэффициента отражения измеряемого объекта., поэтому результаты обычно представляют в виде представленном на рис А и Б
Для построения зависимостей от коэффициентов отражения будем, зачастую, пользоваться стандартной формулой
(43)
Которая дает возможность выразить , как функциональную зависимость
(44)
И так, как по выше описанному алгоритму мы сможем найти , , , то рассматривая эту зависимость как
(45)
Погрешность будем искать аналогично через отдельные части для мнимых и действительных составляющих
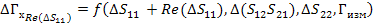
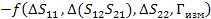
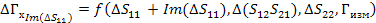
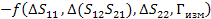
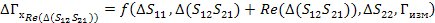
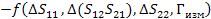
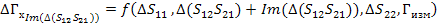
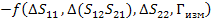
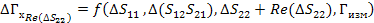
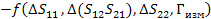
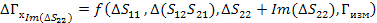
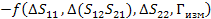
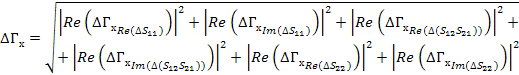
(46)
Для сравнения наших исследований будем сличаться с метрологическим оборудованием ведущих производителей: Antritsu и Микран.
У Микрана есть измеритель комплексных коэффициентов передачи и отражения Р4М-18 со следующими параметрами представленными в таблице 4 и на рисунке 18.
Таблица 4 – Эффективные параметры системы
|
Направленность |
0,5…10 ГГц 10…20 ГГц |
не хуже 44 дБ не хуже 40 дБ |
|
Согласование источника |
0,5…10 ГГц 10…20 ГГц |
не хуже 37 дБ не хуже 30 дБ |
|
Согласование нагрузки |
0,5…10 ГГц 10…20 ГГц |
не хуже 37 дБ не хуже 35 дБ |
|
Частотная неравномерность коэффициента отражения (трэкинг отражения) |
0,5…10 ГГц 10…20 ГГц |
< 0,05 дБ < 0,1 дБ |
|
Частотная неравномерность коэффициента передачи (трэкинг передачи) |
0,5…10 ГГц 10…20 ГГц |
< 0,15 дБ < 0,2 дБ |
Продолжение таблицы 4
|
Изоляция между портами |
0,5…10 ГГц 10…20 ГГц |
> 120 дБ > 110 дБ |
Таблица 5 – Погрешность измерения коэффициента отражения «Микран»
|
в диапазоне частот |
в диапазоне уровней |
модуль |
фаза |
|
0,5…10 ГГц |
0,018…0,06 0,06…0,18 0,18…0 |
< 0,007 < 0,008 < 0,03 |
< 22° < 7° < 3° |
|
10…20 ГГц |
0,018…0,06 0,06…0,18 0,18…0 |
< 0,012 < 0,015 < 0,06 |
< 35° < 12° < 5° |
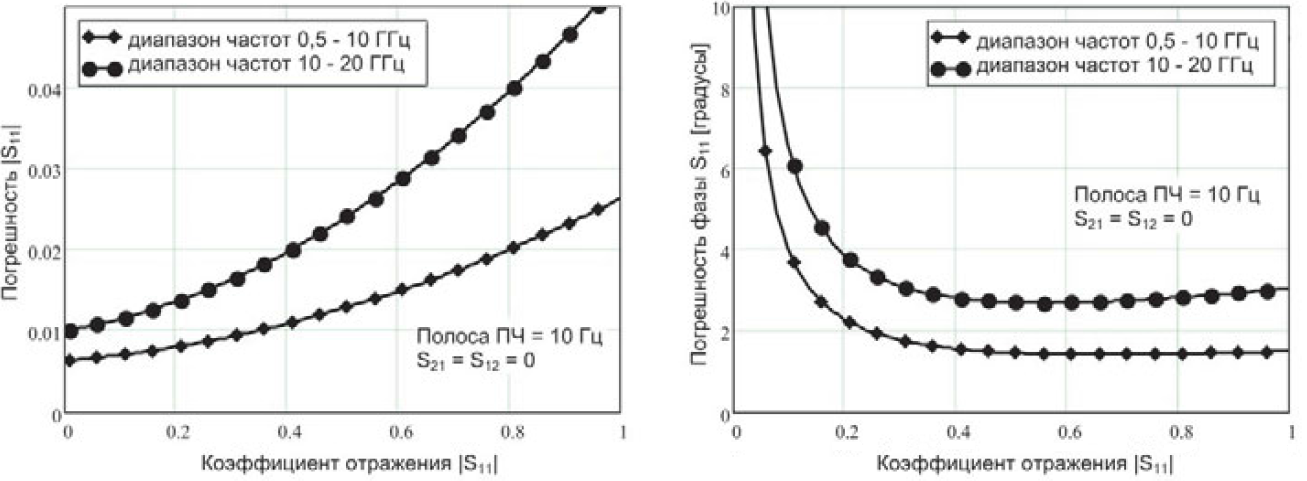
Рисунок 18 – Погрешность измерения коэффициента отражения
А у Antritsu будем рассматривать погрешности указанные в таблице 6
Таблица 6 – Погрешность измерения коэффициента отражения «Antritsu»
|
Частота |
Амплитуда, дБ |
Фаза, градусы |
|
40 МГц – 20 ГГц |
<0.04 |
<0.5 |
Таблица 7 – Погрешность измерения «Antritsu»
|
Коннектор |
Частота, ГГц |
, дБ |
, дБ |
, дБ |
Отражение, дБ |
Передача, дБ |
, дБ |
|
K (2.92 мм) |
0.04 |
>42 |
>40 |
>42 |
±0.005 |
±0.030 |
>105 |
|
2 |
>42 |
>40 |
>42 |
±0.005 |
±0.030 |
>105 |
|
|
20 |
>42 |
>38 |
>42 |
±0.005 |
±0.070 |
>110 |
Естественно, что температурную нестабильность исследовать не будем, хотя для метрологического это необходимо оформлять.
Экспериментальная часть. Волновод
Исследуем влияние схем калибровки и измерений на погрешность определения характеристик четырехполюсников СВЧ (в данном случае коэффициентов отражения) векторными анализаторами цепей РК4-74 для волноводного тракта прямоугольным сечением 72х34 мм в диапазоне частот 2.59 – 3.94 ГГц. Длина МВС равна 33.5 см.
При расчетах методом калибровки частотные параметры , и получились такими, как представлено на рисунке 17, рисунке 18 и рисунке 19 соответственно.
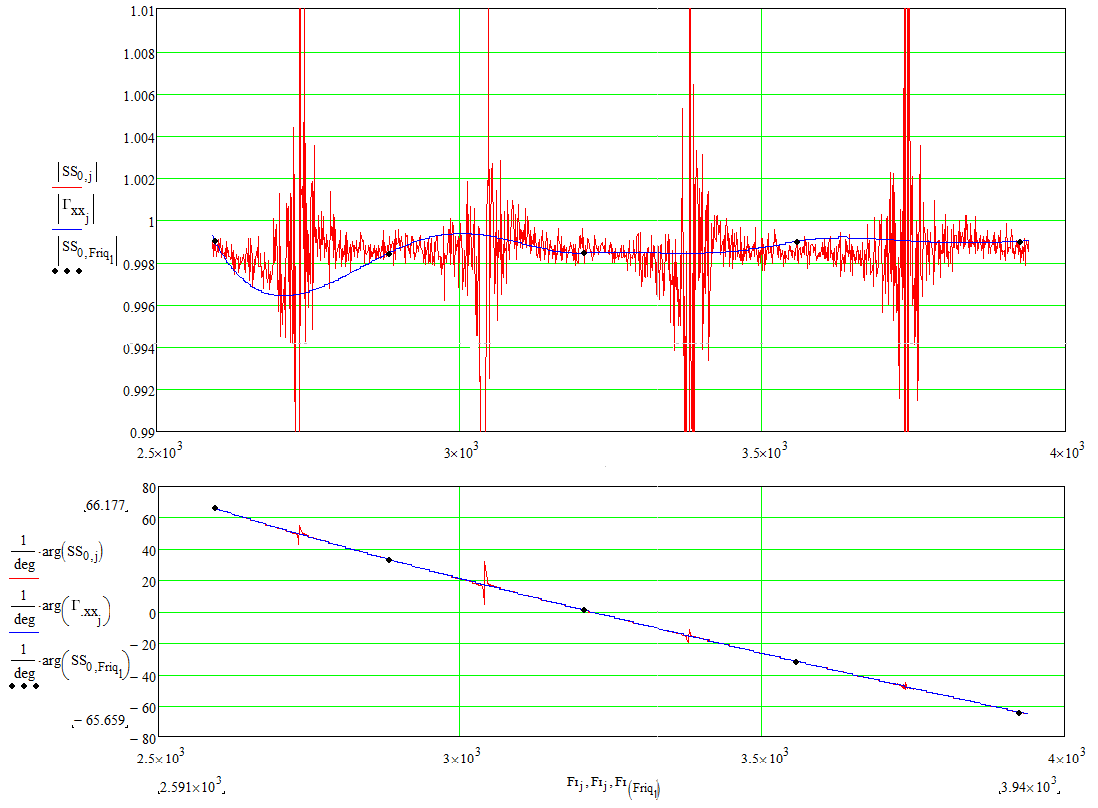
Рисунок 17 – Расчетах методом калибровки частотного параметра
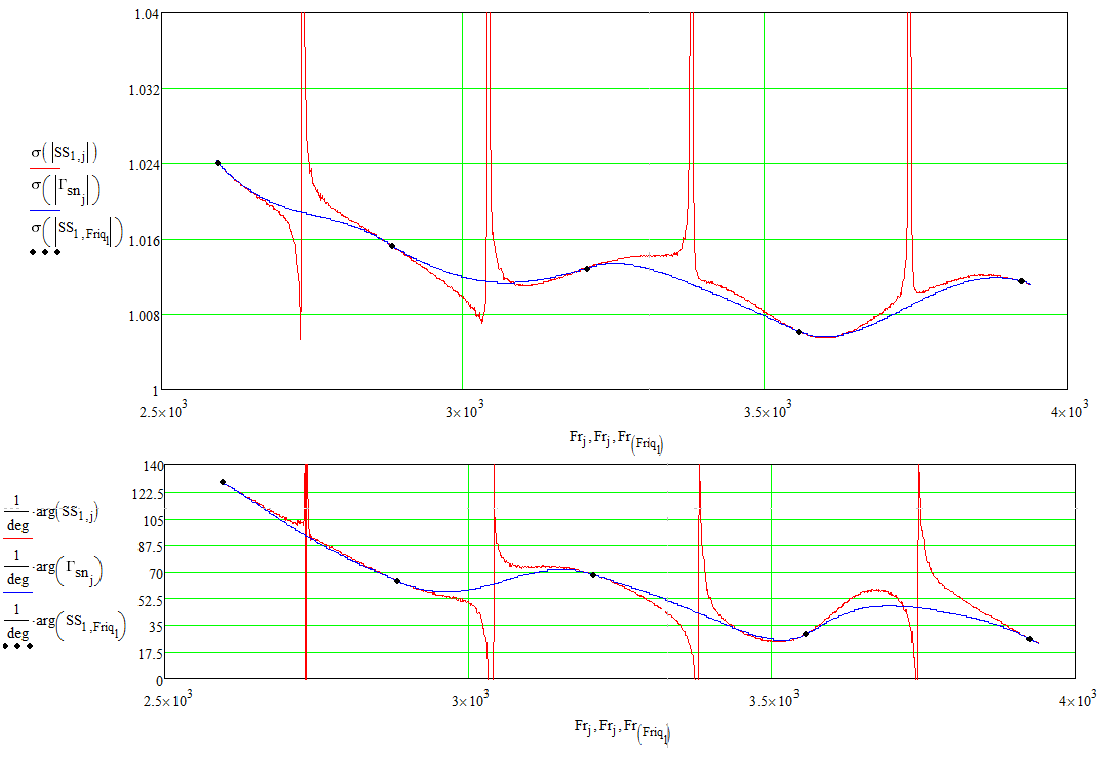
Рисунок 18 – Расчетах методом калибровки частотного параметра
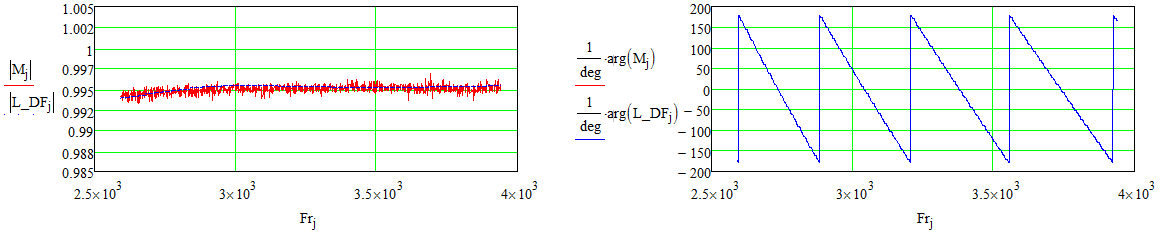
Рисунок 19 – Расчетах методом калибровки частотного параметра
При этом остаточные параметры порта имеют частотную зависимость представленную на рисунке 20.
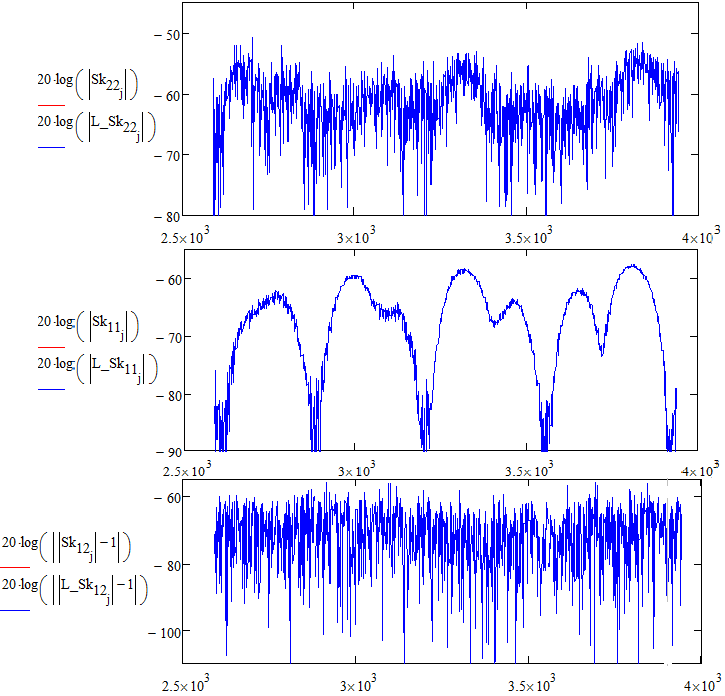
Рисунок 20 – Остаточные параметры порта
Естественно, что реальные значения частотных зависимостей – это аппроксимирующая функция по максимальным значениям.
Для удобства возьмем -58 дБ – как наихудший вариант в частотном диапазоне и -56 дБ, -51 дБ аналогично. Такие хорошие результаты объясняются хорошими параметрами МВС, а так же достаточно стабильной работы аппаратуры в этом диапазоне частот (малым джитером).
Таким образом, по формуле (34) получаем зависимость погрешности вносимой остаточными параметрами порта в зависимости от измеряемой величины Гx.
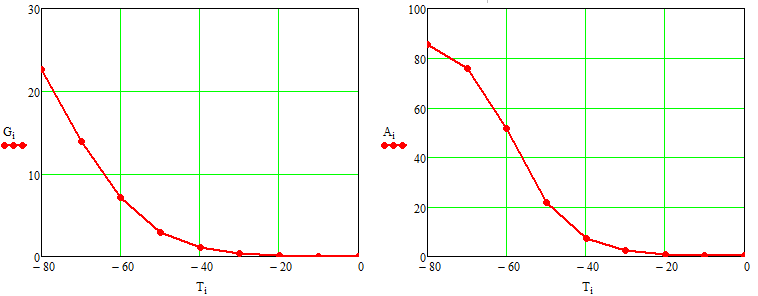
Рисунок 21 – Зависимость погрешности вносимой остаточными параметрами порта в зависимости от измеряемой величины Гx
Тем не менее джитер присутствует и его можно заметить при многократном повторении калибровки и накладывании графиков, к примеру, параметров порта друг на друга. Результирующий график представлен на рисунке 22.
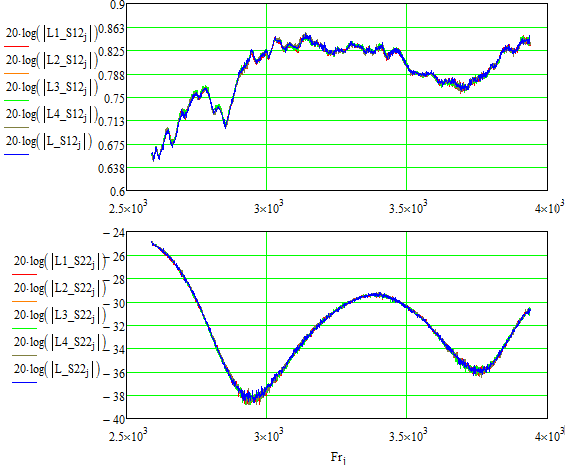
Рисунок 22 – Джитер присутствует при многократном повторении калибровки и накладывании графиков
Исследование погрешности джитера целесообразно проводить для n=5 измерений, тогда для доверительной вероятности коэффициент стьюдента при расчетах составит 4,6004.
Проведя измерения и рассчитав (по формуле трех) получим макс отклонение собственных параметров порта .
К примеру, для выше указанных модулей параметров порта и в частотной зависимости это будет выглядеть, как представлено на рисунке Х.
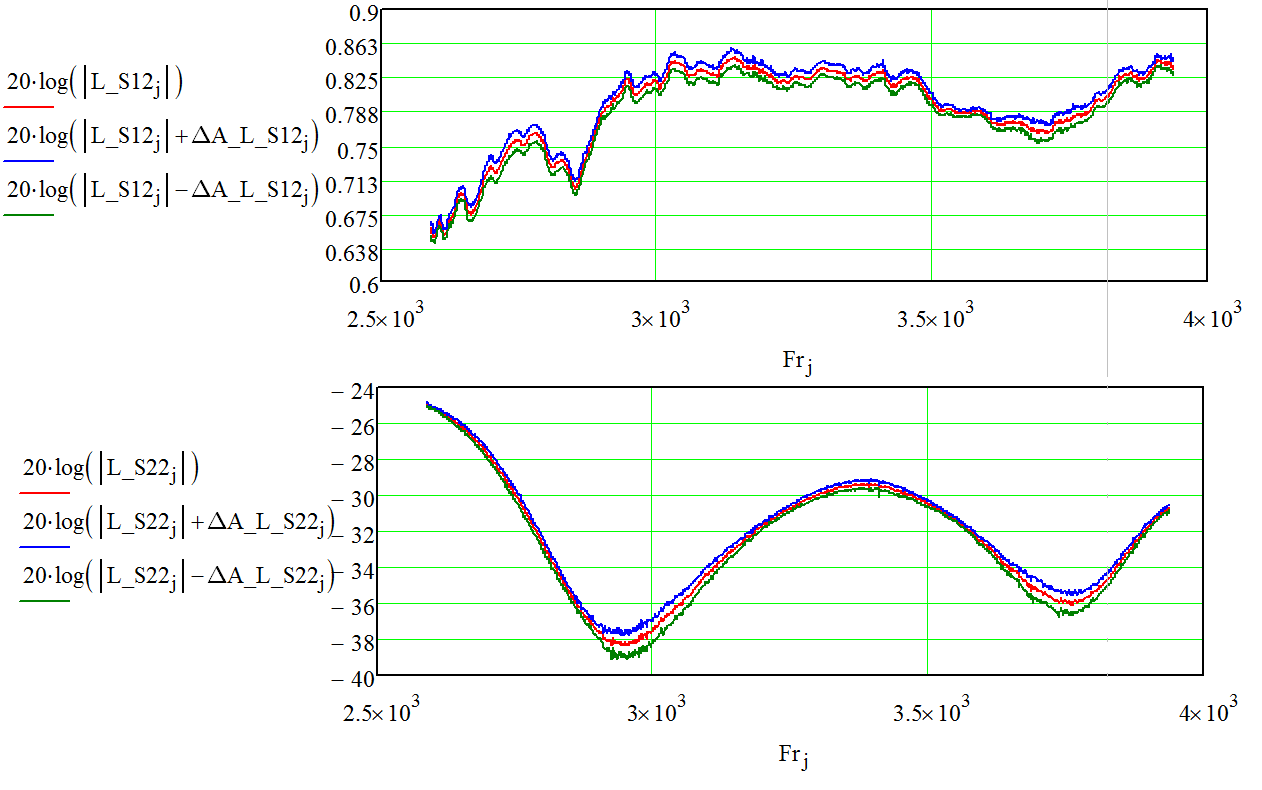
Рисунок 23 – Максимальное отклонение собственных параметров порта
Таким образом результирующая погрешность джитера U может быть представлена графиками: рисунок 24
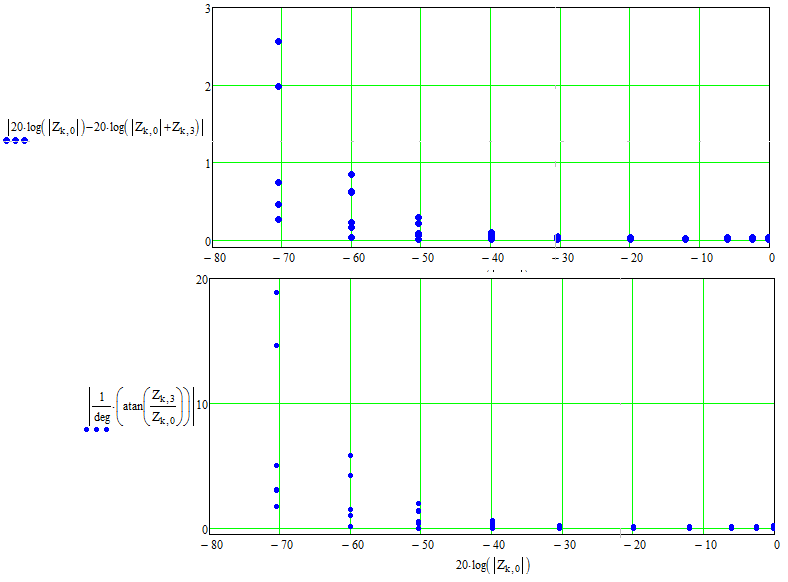
Рисунок 24 – Результирующая погрешность джитера
Так как измерения проводились для полого волновода с КЗ в виде плоского короткозамыкателя, то коэффициент отражения КЗ считается известным на этих частотах без погрешности так как поверхность имеет изгиб не более шероховатости гальванического покрытия золотом.
Таким образом, полная погрешность складывается из двух и и имеет вид, показанный на рисунке 25.
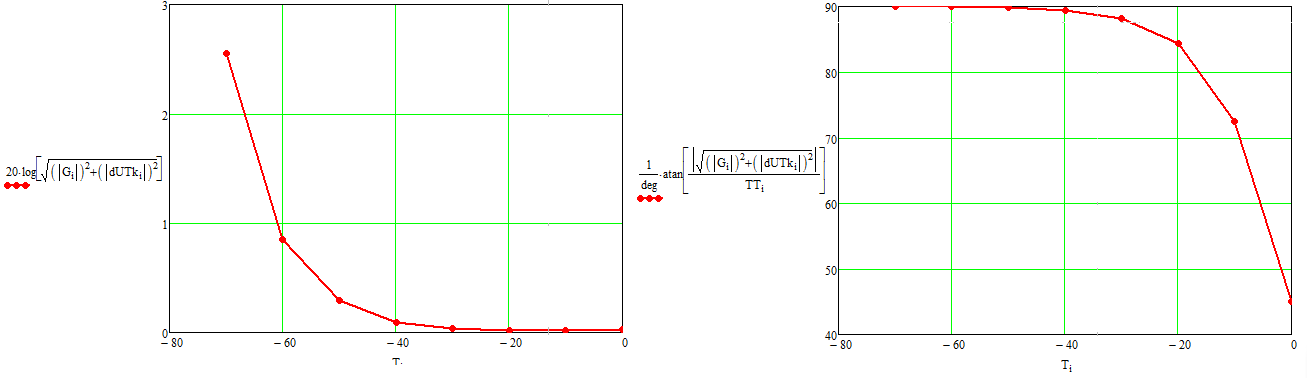
Рисунок 25 – Полная погрешность и
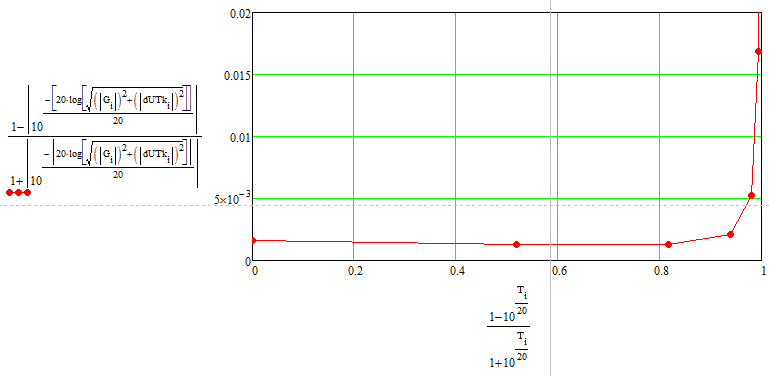
Рисунок 26 – Полная погрешность и в КСВН
Экспериментальная часть. Коаксиал
Исследуем влияние схем калибровки и измерений на погрешность определения характеристик четырехполюсников СВЧ (в данном случае коэффициентов отражения) в широком диапазоне частот 10Мгц – 18ГГц векторными анализаторами цепей (РК4-74) для коаксиального тракта 7/3,04.
При этом, параметры КЗ, ХХ и СН известны из результатов калибровки «32 государственного научно-исследовательского института», и согласно сертификату калибровки их метрологические характеристики представлены в таблице 8
Таблица 8 – Результы калибровки «32 государственного научно-исследовательского института»
|
Тип нагрузки |
Частота, ГГц |
|||||||||
|
1.0 |
2.0 |
3.0 |
4.0 |
5.0 |
6.0 |
7.0 |
8.0 |
9.0 |
||
|
НСВ |
k |
1.009 |
1.014 |
1.017 |
1.020 |
1.017 |
1.011 |
1.008 |
1.018 |
1.029 |
|
|
– |
– |
– |
– |
– |
– |
– |
– |
– |
|
|
НХХВ |
|
0.989 |
0.991 |
0.991 |
0.987 |
0.989 |
0.989 |
0.986 |
0.988 |
0.983 |
|
|
–15.60 |
–30.99 |
–47.21 |
–63.60 |
–80.47 |
–96.33 |
–112.08 |
–127.85 |
–145.03 |
|
|
НКЗВ |
|
0.999 |
1.000 |
1.000 |
1.000 |
0.994 |
0.994 |
1.000 |
1.000 |
1.000 |
|
|
163.03 |
146.07 |
129.34 |
112.71 |
95.47 |
79.49 |
63.32 |
45.99 |
29.27 |
Пределы относительной погрешности калибровки по КСВН 3%, пределы абсолютной погрешности калибровки по модулю КО 0.0175 и по фазе КО, град 1.
Стоит отметить странные значения НК3В, на частоте 5ГГц резко изменяется на 0.006, хотя с погрешностью в 0.0175 – это и понятно. Тем не менее, исходя из фазы НК3В – плоскость смещена от разъемного соединения на величину =6,97 мм, что может быть определено по зависимости описанной следующей формулой:
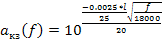
, (47)
где
– амплитудная зависимость от частоты коэффициента отражения КЗ
– фазо-частотная зависимость от частоты коэффициента отражения КЗ
Отсюда следует, что с такой погрешностью для КЗ можно было бы принять равной единице, так как ее изменения должны приходиться экспоненциально с увеличением частоты до величины 0.99992 на частоте 18 ГГц. Поэтому факт провала на частоте порядка 5 ГГц объясним, как «сильный» дефект разъемного соединения при подсоединении КЗ. Сам фак провала значения КЗ зафиксирован оборудованием «32-ГНИИИ» на приборе, который имеет относительную погрешность много меньше, чем абсолютную, поэтому факт резкого скачка КЗ в районе 4 – 7 ГГц будем считать имеющим место, что непременно приведет к завышению погрешностей калибровки самого РК4-74. Именно от качества нагрузок и точности изготовления разъемных соединений зависит погрешность исследуемого метода калибровки.
Кроме того, в таблице данные для КЗ приведены до частоты 9 ГГц, поэтому до частоты 18 ГГц достроим эти данные исходя из геометрического расположения плоскости КЗ:
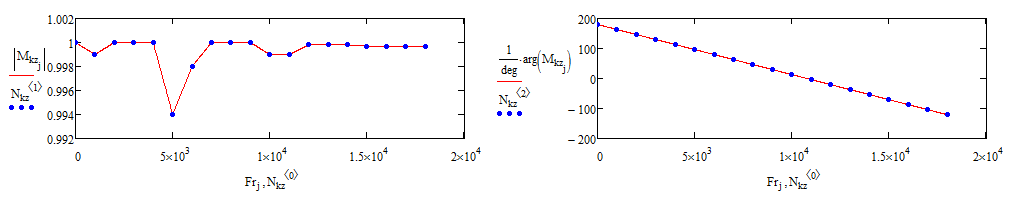
Рисунок 27 – Достроение данных до 18 ГГц исходя из геометрического расположения плоскости КЗ
Исследование будем проводить аналогично исследованиям для волновода. То есть, по пять измерений при прикручивании КЗ, ХХ, СН напрямую к порту измерителя и так же по пять через МВС. Длина МВС 75 мм (если быть точным, то 74,98, а вносимый фазовый сдвиг в градусах).
При применении исследуемого метода калибровки со средними измеряемыми величинами для каждых пяти измерений КЗ, ХХ и СН и через МВС: частотные параметры Гхх, Гсн и Мvs получились такими, как представленного на рисунке 28:
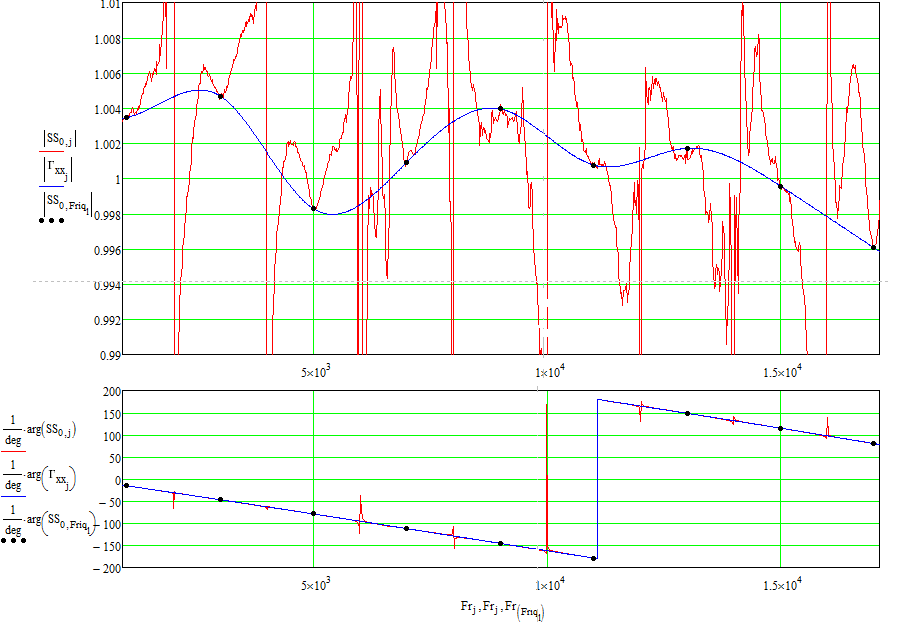
Рисунок 28 – Частотный параметр Гхх
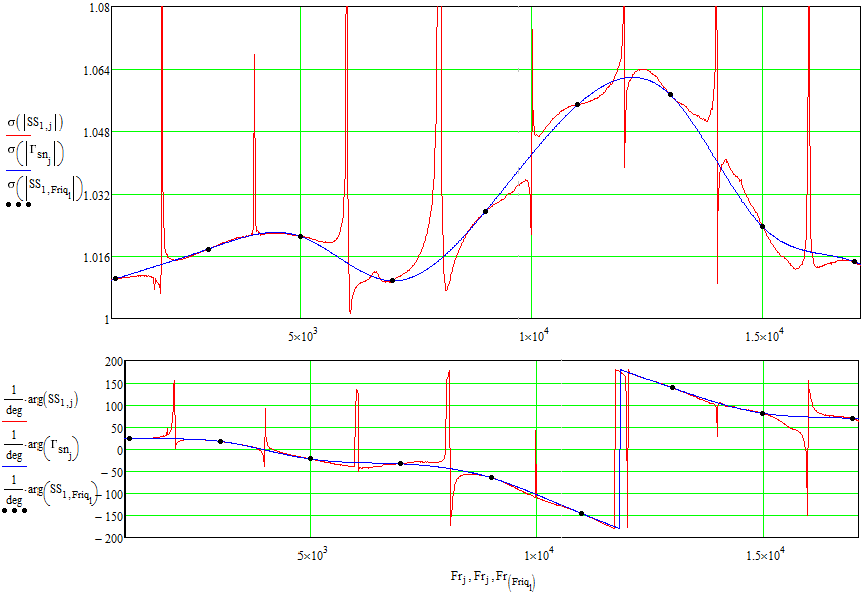
Рисунок 29 – Частотный параметр Гсн
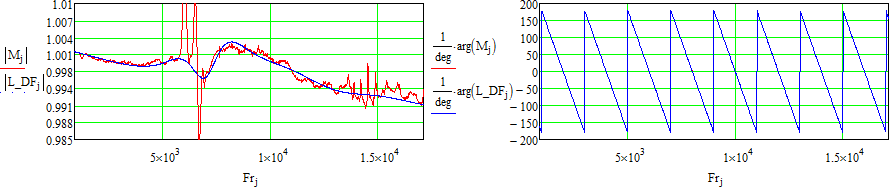
Рисунок 30 – Частотный параметр Мvs
Проанализируем эти графики. Как видно амплитуда Гхх получилась более 1, что теоретически не может быть. Однако, значения амплитуды КЗ заданы с погрешностью во втором знаке 0,0175, а Гхх получилось больше единицы-максимум в третьем (0,005). К примеру, если модуль коэффициента отражения КЗ взять на значение погрешности меньше от единицы 0,9825 то Гхх получиться следующим:
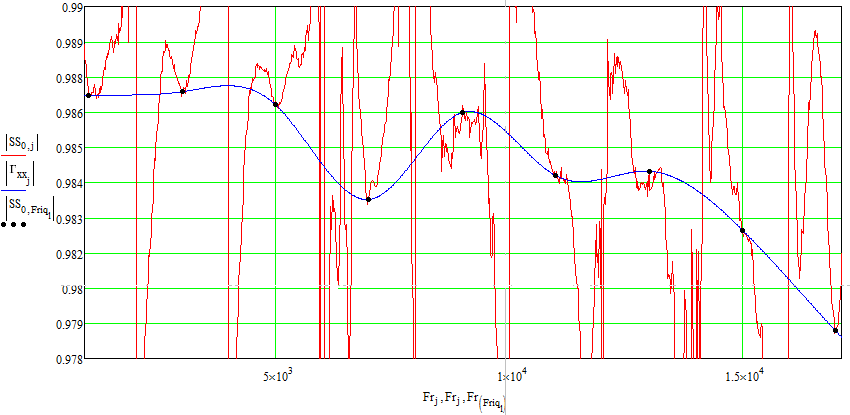
Рисунок 31 – Частотный параметр Гхх с учетом погрешности
Как видно, получившиеся значения модуля коэффициента отражения КЗ меньше табличных.
Поэтому, как уже указывалось, математическая погрешность из-за точности значения КЗ должны быть обязательно учтена в дальнейшем.
Вид изменения КСВн Гсн совпадает с видом изменения ее значений в таблице метрологических характеристик; а значения в опорных частотах с точностью до погрешностей результатов калибровки согласно сертификату укладывается в отведенные 3% (на самом деле даже меньше 0,5).
По параметрам МВС видны две проблемы при калибровке: одна в районе от 5.5 ГГц до 7 ГГц, другая начинается после 13 ГГц.
Первая проблема была ожидаема и описана ранее, вот вторая вызвана использованием разъемных соединений N-типа они изначально рассчитывались на использование до частот 12 ГГц. Однако, после усовершенствований Юлиуса Ботка из HP их использование расширили до частот 18 ГГц. Как видно, вторая проблема хоть и присутствует, но при этом менее выражена (для полых волноводов с точными геометрическими размерами такой проблемы не возникает, из-за работы в узком диапазоне частот гармоники H10).
При применении метода, остаточные параметры порта усредненных 5 измерений каждого сочленения представлены на рисунке 32
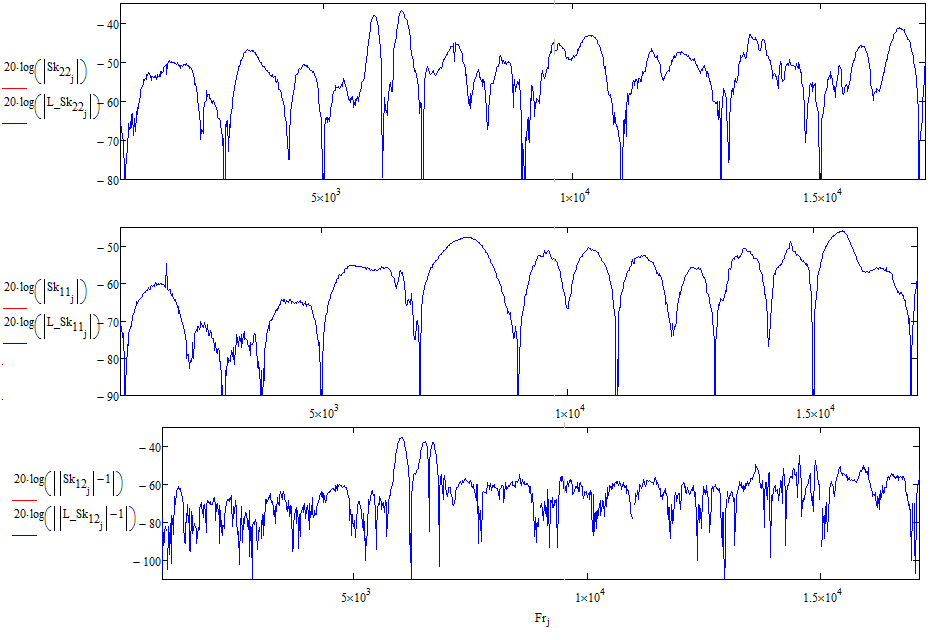
Рисунок 32 – Остаточные параметры порта усредненных 5 измерений каждого сочленения
Как видно, в районе 5,8 – 6,8 ГГц остаточные параметры порта и , как и ожидалось, сильно завышены. Поэтому расчет погрешностей будем проводить в дальнейшем раздельно для трех областей частот: от 10 МГц до 5ГГц, от 5ГГц до 7ГГц, 7 ГГц до 18 ГГц. Естесственно, что вторая область будет иметь завышенные параметры погрешностей.
Таким образом:
- От 10 МГц до 5 ГГц: =–60 дБ; =–47 дБ; =–60 дБ;
- От 5 ГГц до 7 ГГц: =–55 дБ; =–37 дБ; =–35 дБ;
- От 10 МГц до 5 ГГц: =–47 дБ; =–43 дБ; =–50 дБ;
По формуле *** получаем зависимости погрешностей вносимыми остаточными параметрами порта в зависимости от измеряемой величины Гх
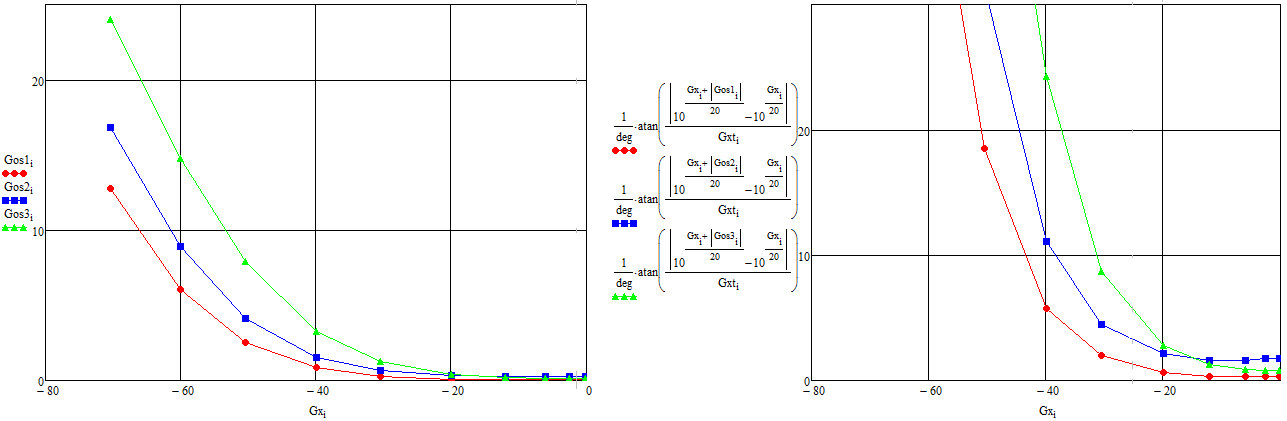
Рисунок 33 – Зависимости погрешностей вносимыми остаточными параметрами порта в зависимости от измеряемой величины Гх
Результирующая погрешность максимального джитера для количества экспериментов n=5, доверительной вероятности (достоверности) и коэффициента стьюдента 4.6004 согласно описанной в теоретической части исследований представлены на рисунке 34
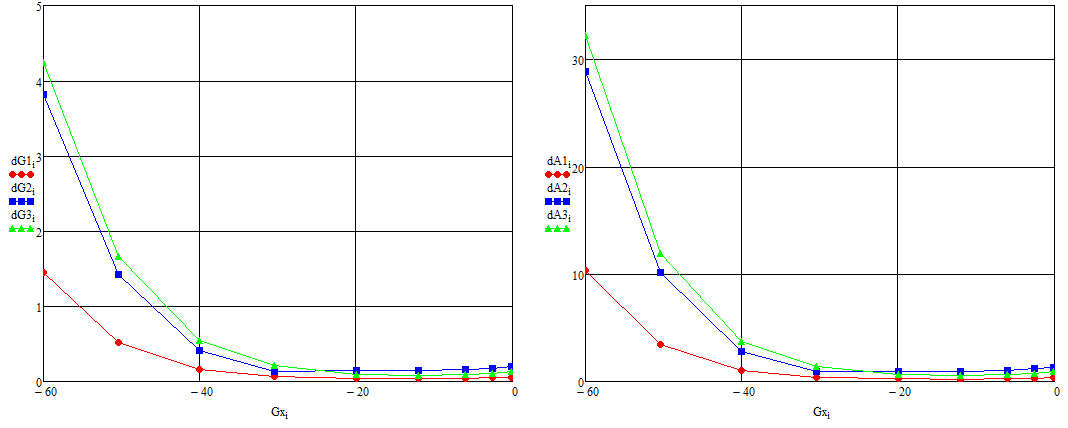
Рисунок 34 – Результирующая погрешность максимального джитера для количества экспериментов n=5
Как видно, чем выше частота работы векторного анализатора цепей, тем более нестабильны его характеристики.
Осталось определить величину третьей составлявшей погрешности: зависимость от точности знания параметров КЗ.
Как видно, именно точность знания параметров КЗ добавляет весомый вклад в общую погрешность.
Полная погрешность будет складываться из трех составляющих , и и иметь вид:
(48)
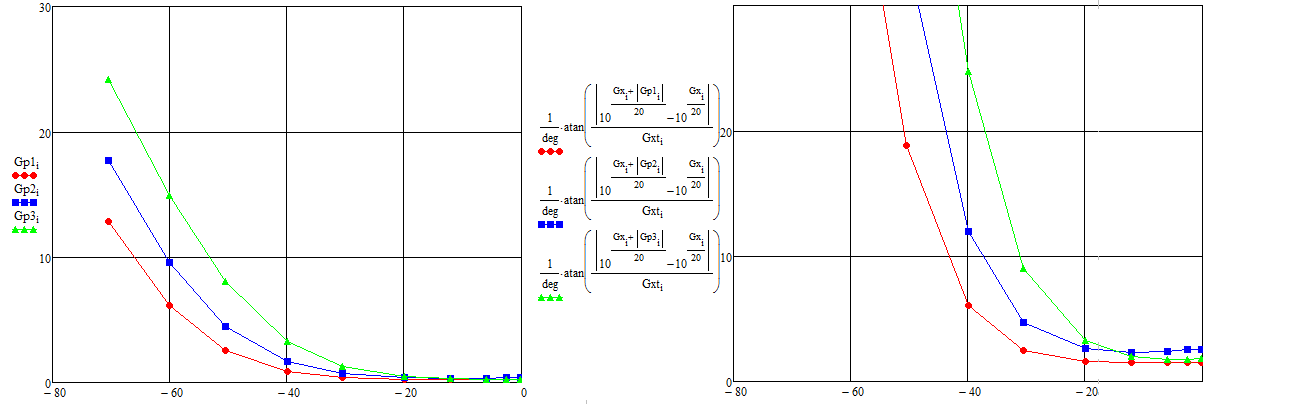
Рисунок 35 – Полная погрешность из трех составляющих , и
Как видно, при измерении больших коэффициентов отражения, в общую погрешность весомы вклад вносит джитер. На значениях коэффициента отражения минус 20 дБ, погрешности джетера и неточности знания КЗ суммарно вносят минимальный вклад, чем остаточные параметры порта. Что, во первых, говорит о стабильности работы оборудования РК4-74 и, во вторых, достаточную точность знания КЗ, которая вызывает погрешность математического расчета намного меньше, чем погрешности калибровки. Основной вклад погрешности (как волноводных КЗ, так и коаксиальных) вносит погрешность сомой калибровки, то есть знания остаточных параметров порта. Поэтому чем лучше набор мер, тем ближе параметры откалиброванного оборудования к предельным параметрам, определяемым погрешностью джитера совместно с погрешностью знания коэффициента отражения эталонной КЗ.
Теперь сравним табличные значения нагрузок и их погрешности:
Таблица 9 – Табличные значения нагрузок и их погрешности
|
НСВ |
||||
|
Частота |
Табличные значения |
Табличная погрешность (3%) |
Расчетная погрешность (<1%) |
Расчетные |
|
1 ГГц |
1.009 |
0.030 |
0.0023 |
1.0102 |
|
2 ГГц |
1.014 |
0.030 |
0.0024 |
1.0140 |
|
3 ГГц |
1.017 |
0.031 |
0.00186 |
1.0178 |
|
4 ГГц |
1.020 |
0.031 |
0.00224 |
1.0215 |
|
5 ГГц |
1.017 |
0.03051 |
0.00219 |
1.021 |
|
6 ГГц |
1.011 |
0.03033 |
0.00493 |
1.0142 |
|
7 ГГц |
1.008 |
0.03024 |
0.00438 |
1.0096 |
|
8 ГГц |
1.018 |
0.03054 |
0.00891 |
1.015 |
|
9 ГГц |
1.029 |
0.03087 |
0.00934 |
1.0276 |
Таблица 10 – Табличные значения нагрузок и их погрешности
|
НХХВ, |
НХХ, |
|||||||||
|
Частота |
Табл. знач. |
Табл. погр. |
Погр. изм. |
Измер. знач. |
Табл. знач. |
Табл. погр. |
Погр. изм. |
Измер. знач. |
||
|
1 ГГц |
0.989 |
±0.0175 |
±0.023 |
1.0035 |
-15.60 |
±1° |
±1.5° |
-15.798 |
||
|
2 ГГц |
0.991 |
±0.0175 |
±0.023 |
1.0047 |
-30.99 |
±1° |
±1.5° |
-28.956 |
||
|
3 ГГц |
0.991 |
±0.0175 |
±0.023 |
1.0046 |
-47.21 |
±1° |
±1.5° |
-47.196 |
||
|
4 ГГц |
0.987 |
±0.0175 |
±0.023 |
1.0014 |
-63.60 |
±1° |
±1.5° |
-61.408 |
||
|
5 ГГц |
0.989 |
±0.0175 |
±0.032 |
0.99826 |
-80.47 |
±1° |
±1.5° |
-79.175 |
||
|
6 ГГц |
0.989 |
±0.0175 |
±0.032 |
0.99862 |
-96.33 |
±1° |
±1.5° |
-95.895 |
||
|
7 ГГц |
0.986 |
±0.0175 |
±0.032 |
1.0007 |
-112.08 |
±1° |
±1.5° |
-112.33 |
||
|
8 ГГц |
0.988 |
±0.0175 |
±0.032 |
1.0033 |
-127.85 |
±1° |
±1.5° |
-129.33 |
||
|
9 ГГц |
0.983 |
±0.0175 |
±0.032 |
1.004 |
-145.03 |
±1° |
±1.5° |
-145.8 |
Как видно из таблицы 9, значение из метрологического паспорта СН и полученные в процессе калибровки коррелируются между собой в пределах погрешности калибровки 1%, кроме частотной точки на 5 ГГц. Однако, так как погрешность из метрологического паспорта больше, чем полученная при калибровки прибора новым методом и составляет 3%, то уж в эту погрешность попадает и точка на 5 ГГц.
Если сравнивать значения погрешностей в таблице 10, то во первых, видно, что измеряемые значения НХХ в некоторых случаях получаются больше единицы. В основном, это вызвано тем, что заданное значение КЗ используемое при расчетах, естественно, берется из метрологического паспорта КЗ, соответствующее численному значению, указанному в паспорте, изначально не учитывающее его погрешности. Если взять коэффициент отражения КЗ немного меньше, чем указанно в метрологическом паспорте, но в пределах абсолютной погрешности, то при вычислениях модуль отражения от нагрузки ХХ станет чуть меньше единицы. Во вторых, полученная при калибровке погрешность перекрывает значения полученные в метрологическом паспорте. Однако, они немного больше, чем в используемом паспорте. Вид же характеристики нагрузки ХХ, то есть относительное ее изменение вдоль параметров частоты, имеет аналогичную динамику изменений, что и в метрологическом паспорте. Для того, чтобы эта динамика была видна, мы оставили пятый знак после запятой. Если эту таблицу рассматривать относительно фазы ХХ, то полученные в ходе калибровки прибора значения с точностью до погрешности совпадают со значениями в метрологическом паспорте. При этом полученные погрешности составляют полтора градуса, против одного градуса из метрологического паспорта.
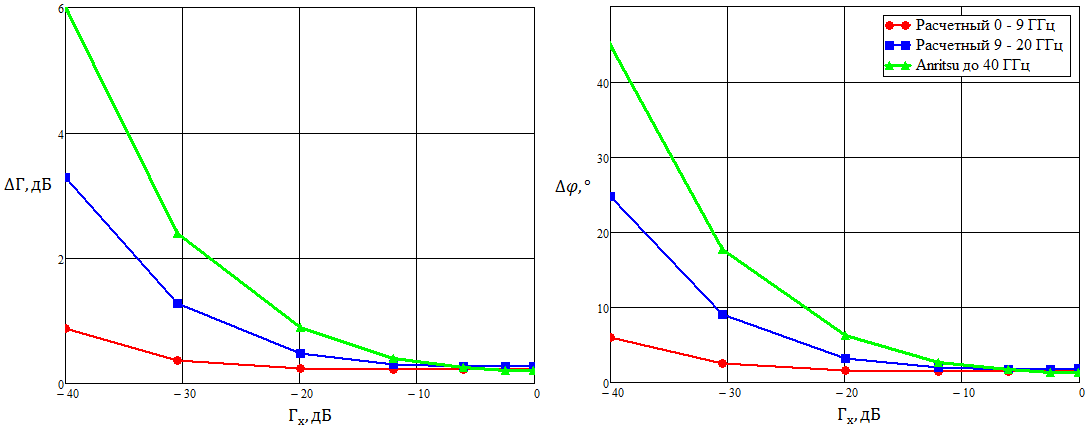
Рисунок 36 – Сравнение погрешностей измерения нового метода с известными погрешностями Anritsu
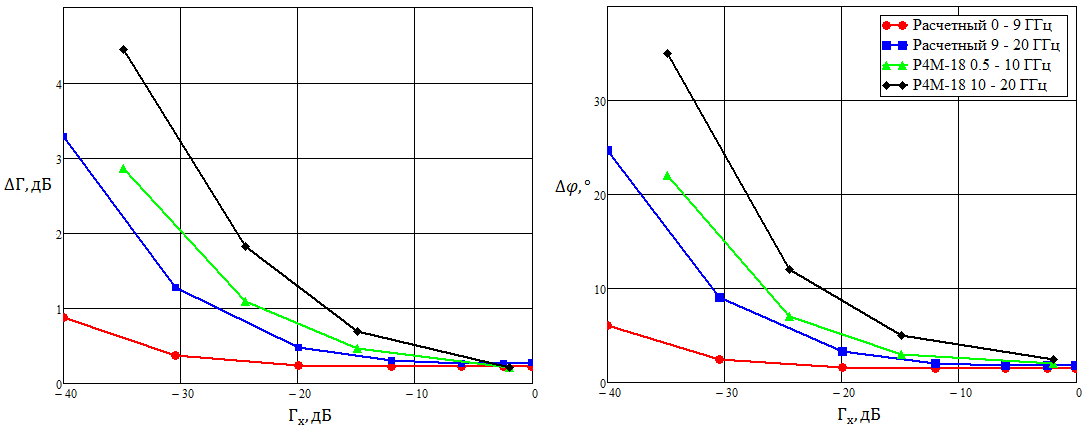
Рисунок 37 – Сравнение погрешностей измерения нового метода с известными погрешностями Anritsu
Сравнивая абсолютную погрешность полученную для прибора РК4-74, откалиброванного по новому методу, с абсолютной погрешностью аналогичных приборов Микран и Antritsu, видно, что в области от 0 до –10 дБ, погрешности по модулю и фазе примерно у всех приборов лежат на одном и том же уровне. Однако уже с –20 дБ калибровка обеспечивает прибору РК4-74 погрешности измерения фазы вдвое лучше, чем у сравниваемого оборудования. Если сравнивать РК4-74 и 37000D по модулю, то от 0 до –15 дБ параметры оборудования на одном и том же. Однако, при значениях нагрузок –20 дБ и более в выигрыше в два раза по абсолютной погрешности оказывается РК4-74. Если же сравнивать РК4-74 и Р4М-18 относительно модуля, то ситуация состоит в том, что Р4М-18 проигрывает 37000D настолько, насколько 37000D проигрывает откалиброванному РК4-74.
Заключение
В результате выполнения дипломной работы были проведены статистические измерения на волноводном и коаксиальном векторных анализаторах цепей РК4-74, проведены математические исследования согласно новому методу калибровки векторных анализаторов цепей.
Вычислена абсолютная погрешность векторного анализатора цепей РК4-74, включающая в себя: погрешность калибровки новым методом; погрешность джитера внутренних схем прибора определена статистически; погрешности возникающие из-за неточности знания коэффициента отражения КЗ в применяемом математическом аппарате. Основные выводы изложены в самой работе.
Проведено сравнение полученных погрешностей прибора с аналогичными векторными анализаторами Р4М-18 производства «Микран» и 37000D производства «Antritsu».
Сравнение показало, что при значениях модуля коэффициента отражения нагрузок менее –20 дБ новый вид калибровки обеспечивает прибору РК4-74 погрешности измерения модуля коэффициента отражения и фазы вдвое лучше, чем у сравниваемого оборудования.
Список использованных источников
1 Харари Ф. Теория графов / Пер. с англ. и предисл. В. П. Козырева. Под ред. Г. П. Гаврилова. Изд. 2-е. – М.: Едиториал УРСС, 2003. – 296 с.
2 Силаев М. А. Приложение матриц и графов к анализу СВЧ-устройств / М. А. Силаев, С. В. Брянцев. М.: Советское радио, 1970.248 с.
3 Робишо А. Направленные графы и их применение к электрическим цепям и машинам / А. Робишо, М. Буавер, Ж. Робер. М.: Энергия, 1964.317 с.
4 Пат. 2482504 Россия, МПК G01R27/28. Способ аттестации собственных S-параметров устройств для измерения комплексных коэффициентов передачи и отражения четырехполюсников СВЧ/ К.С. Коротков, А.С. Левченко, Д.Н. Мильченко, И.Н. Шевченко // ОАО «Научно-производственная компания «Ритм» (Россия). 2011119094/28 Заявл. 12.05.2011, Опубл. 20.05.2013.
5 А.А. Дубанов, Д.В. Базархандаев, Ц.Ц. Цыдыпов, Б.Б. Будажапова Методическое пособие по решению задач геометрического моделирования в системе MathCAD. ВСГТУ, 2002 – 64 с.
6 Метрологическое обеспечение измерейий параметров оконечных элементов в коаксиальных волноводах / А.Л. Берхоер, Э.М. Гутина, Б.А. Хворостов и др. // Измерительная техника/ – 1981. № 5. – С. 44–45.
7 Современное состояние метрологического обеспечения измерения параметров радиоцепей на СВЧ / А.Л. Берхоер, В.И. Евграфов, Э.М. Шейнин. и др. // М., ВНИИКИ. 1977. – 63 с.
8 Высокоточные измерения параметров передачи и отражения в диапазоне по 36 ГГц / В.И. Евграфов, В.А. Никонеко, Б.А. Хворостов и др. // Тр. межд. НТК. "Актуальные проблемы электронного приборостроения АПЭП-92. Измерения в радиоэлектронике". – Новосибирск, 1992. – т. 5. – С. 3–4.
9 Механиков А.И., Фрумкин В.Д., Чуйко В.Г. Развитие эталонной базы в области радиотехнических измерений // Изм. техн. – 1976. –№8 – С. 52.
10 Абубакиров Б.А., Львов А.Е. Образцовые меры для калибровки автоматизированных анализаторов цепей // Техника средств связи. Серия Радиоизмерительная техника. – 1983. – Вып. 7(46). – С. 72–80.
11 Пути повышения точности панорамных измерителей комплексных параметров волноводных СВЧ-узлов / С.А. Баканов, Б.В. Кожевников, И.В. Сидоренко и др. II Докл. Всесоюз. симпозиума "Современные методы и аппаратура для измерения параметров радиоцепей". – Новосибирск, 1974. – С. 178–180.
a
b
S21
S12
a`
b`
S11
S22
S21
S11
S22
S12
Гх
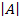
ИССЛЕДОВАНИЕ ВЛИЯНИЯ СХЕМ КАЛИБРОВКИ И ИЗМЕРЕНИЙ НА ПОГРЕШНОСТИ ОПРЕДЕЛЕНИЯ ХАРАКТЕРИСТИК ЧЕТЫРЕХПОЛЮСНИКОВ СВЧ ВЕКТОРНЫМ АНАЛИЗАТОРОМ ЦЕПЕЙ