Исследование квантово-размерных структур

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «КубГУ»)

Физико-технический факультет

Кафедра оптоэлектроники

Допустить к защите в ГАК

_____ . ____ . 2013 г.

Заведующий кафедрой

д-р техн. наук, профессор

_______________Н. А. Яковенко

ДИПЛОМНАЯ РАБОТА

Исследование квантово-размерных структур

Работу выполнил _________________________ Потапов Д.И.

Направление 2100700.62 Инфокоммуникационные технологии и системы связи

Научный руководитель

канд. физ.-мат. наук, доцент __________________________ Л.Р. Григорьян

Нормоконтролер инженер __________________________ И. А. Прохорова

Краснодар 2013

РЕФЕРАТ

Дипломная работа: 84 с., 37 рис., 19 ист.

ОПТИКА, НАНОЭЛЕКТРОНИКА, НАНОСТРУКТУРА, ГЕТЕРОСТРУКТУРА, КВАНТОВО-РАЗМЕРНЫЕ СТРУКТУРЫ, КВАНТОВЫЕ ТОЧКИ, КВАНТОВЫЕ ПРОВОЛОКИ, КВАНТОВЫЕ ЯМЫ, МОЛЕКУЛЯРНО-ЛУЧЕВАЯ ЭПИТАКСИЯ, ГАЗОФАЗНАЯ ЭПИТАКСИЯ, НАНОЛИТОГРАФИЯ, ЛАЗЕР.

Объектом исследования данной дипломной работы являются квантово-размерные структуры, их типы, методы получения и их оптические свойства.

Целью работы является исследование квантово-размерных структур и проведение сравнительного анализа вертикальных лазеров на квантовых точках.

В результате выполнения данной работы было проведено исследование квантово-размерных структур, их свойств, способов получения, областей применения; был проведен сравнительный анализ вертикальных лазеров на квантовых точках.

СОДЕРЖАНИЕ

Введение…………………………………………………………………....…...4

1 Квантово-размерные структуры……………………………………….……6

1.2 Методы исследования квантово-размерных структур……………...……6

1.3 Типы квантово-размерных структур………………………………...……9

1.4 Методы получения квантово-размерных структур………………..……15

2 Оптические свойства квантовых ям…………………..…………………...31

2.1 Классификация гетероструктур…………………….………………31

2.2 Электронные подзоны в квантовых ямах……….…………………35

3 Оптические свойства квантовых нитей …………………...………………37

3.1 Методы изготовления квантовых нитей …….…………….………37

3.2 Плотность электронных состояний ……………..…………………38

4 Оптические свойства квантовых точек ……………………….……......…42

4.1 Оптические методы исследования квантовых точек ……..………42

4.2 Однофотонное поглощение квантовыми точками …………......…45

4.3 Лазеры на квантовых точках для волоконной связи………………50

4.4 Сравнительный анализ вертикальных лазеров на КТ……………..61

5 Создание приборов на системах с размерным квантованием……………77

Заключение……………………………………………………………………82

Список использованных источников….……………………………………..83
ВВЕДЕНИЕ

Наноэлектроника-область науки и техники, связанная с разработкой архитектур и технологий производства функциональных устройств электроники с топологическими размерами элементов, не превышающими 100 нм, а также с изучением физических основ функционирования таких устройств.

Для создания наноэлектронных приборов и устройств, построенных на эффектах размерного квантования, в настоящее время используются достаточно хорошо разработанные в рамках технологии микроэлектроники процессы, такие как молекулярно-лучевая эпитаксия, осаждение из газовой фазы, а так же в самое последнее время ионный синтез. При этом во всех указанных направлениях рассматриваются процессы самоорганизации с формированием наноразмерных элементов, включая пространственно упорядоченные. Это направление представляется одним их наиболее перспективных, однако степень разработки, как технологических подходов, так и теоретического понимания для конкретных условий является в настоящее время недостаточной.

Технология наноэлектроники включает средства и методы не только ранее неизвестные для микроэлектроники, например, использование нанотрубок и фуллеренов, но в некоторых случаях привлекает новые методические разработки, служащие как для измерения и анализа параметров наноструктурных объектов, так, собственно, и средством для их создания. Наиболее ярким примером в этом направлении могут служить различные ветви зондовой микроскопии (туннельная микроскопия и атомно-силовая микроскопия), с помощью которых объекты наноэлектроники могут, как исследоваться, так и создаваться.

Интерес к созданию структур с размерами элементов в области нанометров и большой плотностью таких элементов проявился в 90-х годах прошлого столетия в связи с обнаружением в таких системах квантово-размерных эффектов, которые к настоящему времени позволяют разделить эти структуры на следующие типы:

- квантовые точки (КТ) - структуры, у которых во всех трех направлениях размеры составляют несколько межатомных расстояний (в зависимости от масштаба рассмотрения структура считается нульмерной или трехмерной);

- квантовые проволоки (КП) - структуры, у которых в двух направлениях размеры составляют несколько межатомных расстояний, а в третьем направлении представляют собой макроскопическую величину;

- квантовые ямы - структуры, у которых в одном направлении размер составляет несколько межатомных расстояний, а в двух других направлениях представляет собой макроскопическую величину.

Усилия разработчиков в последнее время заключаются в создании систем с квантовыми точками, являющимися предельным случаем систем с пониженными размерностями ("нульмерные" системы). Практическая направленность исследования свойств КТ сосредоточена главным образом на изучении их оптических свойств, которые определяются рядом преимуществ таких объектов по сравнению с двумерными квантовыми объектами.

1 Квантово-размерные структуры

1.1 Методы исследования квантово-размерных структур.

Для исследования квантово-размерных структур применяется ряд методов:

- Сканирующая туннельная микроскопия (СТМ);

- Атомно-силовая микроскопия (ACM);

- Просвечивающая электронная микроскопия (ПЭМ);

- Сверхвысоковакуумная отражательная электронная микроскопия (СВВ ОЭМ).

В основе метода CTM лежит эффект квантового туннелирования, т. е. переноса электронов сквозь потенциальный барьер между двумя проводящими поверхностями, разделенными вакуумным или диэлектрическим зазором шириной в несколько нанометров. Сканирование обычно производится двух режимах: или режиме постоянного тока, или в режиме постоянного уровня кантилевера. В первом случае предполагается, что постоянный ток соответствует постоянному зазору между поверхностью и кантилевером, и при сканировании снимается положение кантилевера, что фактически соответствует рельефу поверхности. Во втором случае снимаются токовые зависимости.

Метод АСМ основан на использовании сил взаимодействия кантилевера и поверхности образца. Природа этих сил может быть различна: взаимодействие электронных оболочек атомов, электростатическая, магнитная и т. д. Режимы движения кантилевера аналогичны СТМ, только вместо силы тока используется силы взаимодействия кантилевера и поверхности.

При исследовании методом ПЭМ получают картины дифракции электронов на исследуемом образце с малым углами рассеяния (~ 1°). Контрастные, пригодные для анализа картины формируются при направлении пучка вблизи кристаллографических направлений с малыми индексами[1].

Поскольку обратная задача дифракции - восстановление исходной структуры по полученной дифракционной картине - до сих пор не решена, используют следующий подход. Берут несколько наиболее вероятных структур, для них получают теоретические дифракционные картины и полагают истинной ту структуру, для которой теоретическая дифракционная картина наиболее близка к экспериментальной. Для большей достоверности используют сразу несколько дифракционных картин, полученных в различных рефлексах.

В методе СВВ ОЭМ пучок высокоэнергетических электронов (100 кэВ) падает под малым углом к поверхности, что обуславливает высокую чувствительность получаемых ОЭМ-изображений к структурному совершенству исследуемой поверхности. Следует однако отметить, что из-за малого угла падения пучка электронов к исследуемой поверхности реальные масштабы изображений в ОЭМ искажены: отношение продольного масштаба к поперечному на изображениях определяется углом падения пучка электронов и составляет 30-50.

Серьезной проблемой при формировании гетероструктур, включая квантовые структуры, является несоответствие параметров решеток подложки и эпитаксиальных структур. Для компенсации этого несоответствия могут возникать различные дефекты структуры на межфазной границе, например, дислокации несоответствия. Эти дефекты возникают, когда толщина пленки или высота островков превышают некоторую критическую величину, зависящую от температуры роста.

Вышеперечисленные методики дают достаточно полную информацию о структурных особенностях наноразмерных структур. Они достаточно эффективны, однако являются уникальными и дорогостоящими, что не дает возможности применять их в массовых, рутинных измерениях, которые бывают необходимы для получения достоверной информации, особенно при изменении условий проведения эксперимента. В этом направлении очень хорошо в последние годы зарекомендовали себя методы сканирующей микроскопии: туннельный и атомно-силовой. Полученные в данной работе экспериментальные результаты базируются именно на таких методах.

Структурные методы не дают возможности однозначного доказательства проявления эффектов размерного квантования. Для этой цели, как показала мировая практика, наиболее эффективными являются оптические и фотоэлектрические методы исследования, такие как комбинационное рассеяние света (рамановское рассеяние), а также люминесценция (прежде всего фотолюминесценция). Эти методы максимально были использованы в наших исследованиях. Именно с их помощью были получены однозначные доказательства проявления эффектов размерного квантования в исследуемых нами материалах.

Анализ полученных в мировой практике результатов показал, что наиболее важные параметры приборов наноэлектроники и нанофотоэлектроники зависят от упорядоченности структур с квантово- размерными элементами и от их параметров, в частности от величины разброса по размерам таких элементов[2].

1.2 Типы квантово-размерных структур

Важнейшим свойством наноструктур является зависимость их свойств от характерного размера неоднородностей. Наиболее широко известное проявление этого свойства – так называемый «эффект размерного квантования». Он обусловлен тем, что пространственное ограничение движения элементарных возбуждений в такой системе в области неоднородности приводит к сильной перестройке их энергетического спектра. Как и в любом объекте конечного размера (рисунок 1) в «объемных» однородных кристаллических материалах их собственные возбуждения - электроны, дырки, экситоны, колебания решетки и другие волны и частицы, вообще говоря, обладают дискретным энергетическим спектром.

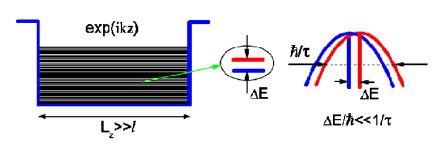
Рисунок 1 - Схематическое изображение энергетического спектра электронной подсистемы объемного материала

Однако характерный масштаб этой дискретности, т.е. энергетическое расстояние между соседними состояниями E, мал по сравнению со спектральной шириной этих состояний, определяемой обратным временем их жизни . В этом смысле можно говорить о непрерывном энергетическом спектре собственных возбуждений объемного материала. Можно также определить объемный материал как такой, размер которого Lz больше, чем длина свободного пробега l его собственных возбуждений. Введение здесь длины свободного пробега в качестве характерного масштаба вполне адекватно, поскольку собственные возбуждения могут описываться бегущими волнами exp(ikz). Если размер материала уменьшается и становится меньше длины свободного пробега (рисунок 2), или более точно, энергетический зазор между соседними состояниями превышает обратное время их жизни, то энергетический спектр элементарных возбуждений должен считаться дискретным. Это и есть эффект размерного квантования, а соответствующие структуры называются квантово-размерными. В этом случае крайне существенным является отражение элементарного возбуждения, представляющего собой стоячую волну, от границ материала.

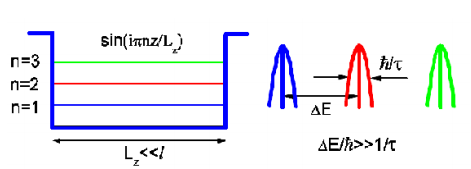
Рисунок 2 - Схематическое изображение энергетического спектра электронной подсистемы наноструктуры

На первый взгляд может показаться, что различие между объемными и квантово-размерными материалами чисто количественное. Однако такое заключение будет абсолютно неверным. Действительно, физические свойства объемных материалов практически не зависят от их размера и формы. В частности дискретность энергетического спектра их собственных возбуждений никак экспериментально не проявляется. Совершенно иначе обстоит дело с квантово-размерными структурами, в которых не только энергетические спектры, но взаимодействие элементарных возбуждений друг с другом и с внешними полями зависит от размера и формы структуры.

Среди низкоразмерных структур можно выделить три элементарные структуры. Это квантовые ямы, квантовые нити и квантовые точки (рисунок 3). Эти элементарные структуры представляют собой кристаллический материал, пространственно ограниченный в одном, двух и трех измерениях. Для изготовления наноструктур используют всевозможные полупроводниковые соединения, а также полупроводники четвертой группы Si и Ge.

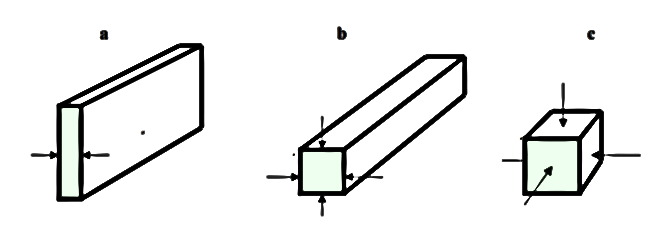
Рисунок 3 - Квантовые ямы (a), квантовые нити (b), квантовые точки (c)

Пространственное ограничение или конфайнмент приводит к тому, что энергетический спектр объемного материала трансформируется.

Зонные спектры расщепляются на подзоны размерного квантования для квантовых ям и нитей и на дискретные уровни для квантовых точек (рисунок 4). В результате, в плотности состояний низкоразмерных систем возникают характерные особенности (рисунок 5).

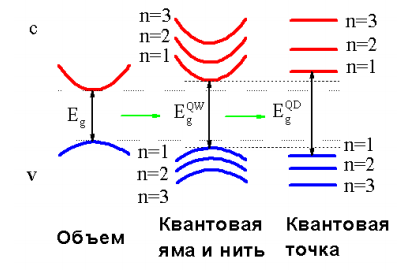
Рисунок 4 - Трансформация энергетического спектра элементарных наноструктур

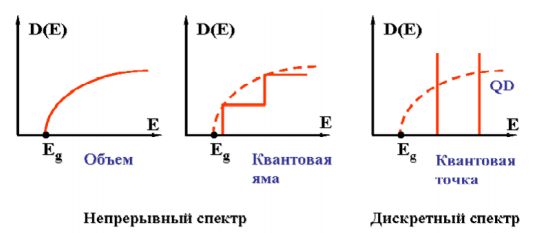
Рисунок 5 - Плотность состояний элементарных наноструктур

На рисунке 6 представлены изображения реальных элементарных наноструктур, полученные с помощью электронного микроскопа.

Рисунок 6 - Изображения (слева направо) квантовой нити, квантовой точки CdS в SiO2, квантовой точки InAs в GaAs, полученные с помощью просвечивающего электронного микроскопа

Из элементарных наноструктур можно построить сложные наноструктуры, например, многослойные квантовые ямы и сверхрешетки (рис. 7), одномерные и двумерные массивы квантовых нитей или двумерные и трехмерные массивы квантовых точек (рис. 8).

Рисунок 7 - Изображение многослойной структуры из квантовых ям, полученное с помощью просвечивающего электронного микроскопа

Рисунок 8 - Изображения (слева направо) двумерного и трехмерного массива квантовых точек, полученные с помощью просвечивающего электронного микроскопа

Наличие размерных зависимостей параметров наноструктур неоднократно подтверждалось экспериментально и, прежде всего, оптическими методами. Еще в 1962 году Сандомирский предсказал, что край фундаментального поглощения света в тонких пленках кристаллов должен смещаться в синюю область спектра при уменьшении их толщины Lz в соответствии с формулой

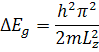
Вопрос о первом экспериментальном наблюдении эффекта размерного квантования остается открытым. Вероятно, что такие наблюдения были сделаны довольно давно, но целенаправленное изучение этого эффекта начинается именно в 60 годы[8,9].

1.3 Методы получения квантово-размерных структур

Молекулярно-лучевая эпитаксия

Молекулярно-пучковая эпитаксия или молекулярно-лучевая эпитаксия (MBE – Molecular Beam Epitaxy) представляет собой усовершенствованную разновидность метода термического напыления материалов в условиях сверхвысокого вакуума. Метод MBE позволяет выращивать гетероструктуры заданной толщины с моноатомно гладкими гетерограницами и с заданным профилем легирования. В установках MBE имеется возможность исследовать качество плёнок «in situ» (то есть прямо в ростовой камере во время роста). Для процесса эпитаксии необходимы специальные хорошо очищенные подложки с атомарногладкой поверхностью.

Идею метода MBE можно пояснить с помощью блок-схемы технологической установки, изображенной на рисунке 10. Потоки атомов или молекул создаются в зоне генерации (I) за счет испарения жидких или сублимации твердых материалов, помещенных в эффузионные ячейки (источники). Эффузионная ячейка – это цилиндрический либо конический тигель, на выходе которого имеется круглое отверстие (диафрагма). Для изготовления тиглей часто используют пиролитический графит высокой чистоты или нитрид бора BN. Потоки атомов (молекул) направляются на подложку, проходя зону смешивания (II), и осаждаются на ней в зоне роста (III), образуя пленку из вещества требуемого состава. Зону роста можно разделить на три области, первая из которых представляет собой подложку или очередной выросший моноатомный слой материала. Вторая область – газовая смесь компонентов гетероструктуры в приповерхностной области. Третья область – переходной слой, геометрия которого и протекающие в нем процессы сильно зависят от выбора условий роста. Составом выращиваемой пленки и наличием легирующих примесей определяется количество эффузионных ячеек, используемых в MBE установке. Так для выращивания чистых элементарных полупроводников кремния Si и германия Ge, требуется лишь одна ячейка. Если необходим легированный элементарный полупроводник, то нужно добавить, по крайней мере, еще одну ячейку. Очевидно, что для получения пленок сложных полупроводников, например, двойных и тройных соединений требуется ячейка для каждого компонента пленки. Температура эффузионной ячейки определяет величину потока частиц, поступающих на подложку, и поэтому тщательно контролируется.

1 – подложка, 2 – растущая пленка, 3 – заслонки, 4 – эффузионные ячейки основных компонентов, 5 - эффузионные ячейки легирующих примесей

Рисунок 10 - Схема MBE установки; I – зона генерации молекулярных пучков, II – зона смешивания пучков, III – зона кристаллизации на подложке (зона роста)

Управление составом выращиваемого материала и концентрацией легирующих примесей осуществляется с помощью заслонок, которые перекрывают тот или иной поток частиц. Если при выращивании структуры нужно резко менять концентрацию одной и той же примеси, то используют несколько эффузионных ячеек с легирующим веществом, нагретых до различных температур. Однородность состава пленки по площади и ее кристаллическая структура определяется однородностью молекулярных пучков. Для повышения однородности, во многих случаях, подложка с растущей пленкой постоянно вращается. MBE включает в себя следующие элементарные процессы, протекающие в зоне роста (рис. 11):

• Адсорбция (прилипание) падающих на подложку атомов или молекул, составляющих выращиваемое соединение.
• Миграция (поверхностная диффузия) адсорбированных атомов по поверхности подложки, которая может предваряться диссоциацией (распадом) молекул выращиваемого соединения.
• Встраивание атомов, составляющих гетероструктуру, в кристаллическую решетку подложки или растущий моноатомный слой.
• Термическая десорбция (отрыв) атомов, не встроившихся в кристаллическую решетку.
• Образование и дальнейший рост двумерных зародышей кристалла на подложке или поверхности растущего слоя.
• Взаимная диффузия атомов, встроившихся в кристаллическую решетку.

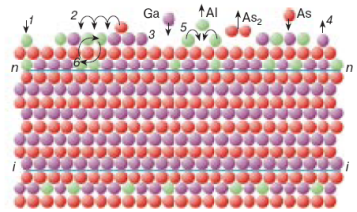
1 – адсорбция атомов из зоны смешивания на поверхности, 2 – миграция адсорбированных атомов по поверхности, 3 – встраивание адсорбированных атомов в кристаллическую решетку, 4 – термическая десорбция, 5 – образование поверхностных зародышей, 6 – взаимная диффузия

Рисунок 11 - Элементарные процессы в зоне роста

Над растущей поверхностью показаны атомы газовой смеси компонентов в приповерхностной области. Буквами n-n и i-i показаны нормальная и инвертированная поверхности раздела растущей гетероструктуры.

В результате адсорбции и миграции по поверхности атомы занимают вполне определенные положения в кристаллической решетке. За время роста одного моноатомного слоя, которое обычно составляет одну секунду, атом совершает несколько тысяч диффузионных прыжков, пока не займет свое окончательное положение в решетке. Таким образом, имеет место своего рода самоорганизация растущей структуры.

Каждый твердотельный материал может быть выращен послойно при фиксированной скорости роста. Температура подложки обеспечивает оптимальную для данного соединения скорость поверхностной диффузии. Так как химические связи в различных материалах разные, то различаются и энергии активации поверхностной диффузии атомов, входящих в состав этих соединений. В связи с этим качество гетерограниц может существенно отличаться в зависимости от того, какое из соединений при выбранном температурном режиме растет первым. Границы называют нормальными, если компонент с более низкой температурой плавления растет первым. Если последовательность роста обратная, то такие границы называют «инвертированными». На рисунке 11 на примере структуры AlxGa1-xAs/GaAs дается иллюстрация границ этих типов, обозначенных индексами n и i. Для получения гладких и совершенных гетерограниц часто используют методику прерывания роста или методику осаждения пульсирующим пучком, которые реализуются с помощью механического перекрывания эффузионных ячеек заслонками.

Сглаживание поверхности за время перекрывания пучков обусловлено поверхностной миграцией и сублимацией атомов, адсорбированных на поверхности выращиваемого монослоя. Температура подложки регулирует соотношение между потоками адсорбции и десорбции атомов, входящих в состав растущей структуры.

Для характеризации этого соотношения используют коэффициент прилипания атома данного сорта к поверхности, на которой происходит эпитаксиальный рост. Этот коэффициент определяет долю падающего потока атомов, адсорбируемую на поверхности. Температура подложки задает скорость поверхностной диффузии, предшествующей встраиванию атомов в кристаллическую решетку. Для обеспечения необходимого числа 104 диффузионных прыжков атома по поверхности, температура должна быть достаточно высокой. Среднее перемещение атома по поверхности за время t равно:

, (1)

где

(2)

- коэффициент поверхностной диффузии, Ds0=a2v , a – длина диффузионного прыжка, т.е. расстояние между эквивалентными положениями атома на поверхности роста, T – температура в энергетических единицах, 1012 с-1– частота колебаний атома на поверхности, Esd – энергия активации поверхностной диффузии, которая для полупроводников обычно составляет 1–1.5 эВ.

Слишком высокие температуры подложки не желательны, поскольку в этом случае уменьшается коэффициент прилипания и активизируется взаимная диффузия атомов между слоями. В связи с тем, что гетероструктуры представляют собой резко неоднородные по химическому составу системы, то из-за процессов взаимной диффузии с течением времени эти системы должны либо переходить в термодинамически равновесное состояние с однородным распределением концентраций всех компонентов, либо расслаиваться на фазы определенного состава. Однако, поскольку энергия активации взаимной диффузии, например, в полупроводниках обычно составляет 4–5 эВ, то в интервале температур от 600 до 800оС этот эффект пренебрежимо мал. Действительно, элементарная оценка показывает, что среднее смещение атома за несколько десятков часов за счет взаимной диффузии оказывается заметно меньше межатомного расстояния. Таким образом, ясно, что выбор и поддержание оптимальной температуры роста является одним из важнейших условий реализации MBE.

Технология молекулярно-пучковой эпитаксии была создана в конце 1960-х годов Дж. Р. Артуром и Альфредом Чо. Несмотря на достаточно простую идею, реализация данной технологии требует чрезвычайно сложных технических решений. Основные требования к установке эпитаксии следующие:

• В рабочей камере установки необходимо поддерживать сверхвысокий вакуум – давление остаточных газов должно быть ниже 10-8Па (10-10мм рт. ст.).
• Чистота испаряемых материалов должна достигать 99,999999%.
• Необходим молекулярный источник, способный испарять тугоплавкие вещества (такие как металлы) с возможностью регулировки плотности потока вещества.
• Особенностью эпитаксии является медленная скорость роста пленки (обычно менее 1000 нм в минуту)[8].

Газофазная эпитаксия

Эпитаксиальный рост материалов путем осаждения на подложку продуктов термического разложения (пиролиз) молекул органических газов, содержащих необходимые химические элементы, называется методом осаждения металлоорганических соединений из газообразной фазы (MOCVD – Metalorganic Chemical Vapour Deposition). Этот термин был предложен создателем метода Гарольдом Манасевитом в 1968 году. В отличие от MBE при MOCVD рост происходит не в вакууме, а в присутствии газа при умеренных давлениях. При комнатных температурах металлоорганические соединения находятся в жидком или даже твердом состоянии. Поскольку эти вещества, как правило, имеют высокое давление паров, их можно легко доставить в зону химической реакции путем продувки газа носителя через жидкости или над твердыми телами, играющими роль источников. В качестве газа носителя используют водород или инертные газы (гелий, аргон). Идею метода MOCVD можно проиллюстрировать с помощью рисунка 12, схематически изображающего реактор, в котором происходит эпитаксиальный рост структуры.

Кристаллизация материала на нагретой подложке, расположенной в реакторе с холодными стенками, осуществляется при пропускании над ней однородной газовой смеси реагентов с газом-носителем. В результате пиролиза, при котором газообразные соединения разлагаются на компоненты на горячей поверхности, образуется стабильное твердое полупроводниковое соединение.

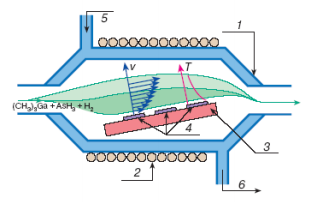
1 – кварцевый корпус, 2 – катушка высокочастотного генератора для нагревания подложки, 3 – блок нагревания, 4 – подложки, 5 – водяное охлаждение (впуск), 6 – водяное охлаждение (выпуск)

Рисунок 12 - Схема горизонтального реактора открытого типа с охлаждаемыми стенками для MOCVD

Схематически показано распределение скоростей v и температуры T в газовом потоке в диффузионном слое вблизи подложки.

Температура пиролиза составляет 600–8000С. Подложка и растущая пленка обычно нагреваются высокочастотным генератором с частотой 450 кГц. Пиролиз происходит в открытом реакторе при атмосферном или пониженном давлении (70 мм рт. ст.). Снижая давление газовой смеси при выращивании соединений можно управлять градиентом изменения состава основных компонент и примесей в гетероструктуре. При пониженных давлениях выращивание ведется при больших, чем при атмосферном давлении скоростях газового потока, что позволяет получать более однородные слои.

Вблизи от поверхности роста располагается переходная область, где параметры газовой смеси плавно меняются от значений, характерных для области конвекции, до значений соответствующих приповерхностному слою. В горизонтальных реакторах толщина переходной области (пограничный слой) равна примерно 4 мм. Температура газовой смеси и ее состав в пограничном слое зависят от расстояния до поверхности роста. В области конвекции температура газа меньше температуры роста и состав газовой фазы не меняется. Во многих случаях электрические и кристаллографические свойства выращиваемых слоев зависят от характеристик пограничного слоя.

В качестве примера рассмотрим реакции, протекающие в процессе MOCVD, при выращивании полупроводниковых соединений GaAs и AlxGa1-xAs. Благодаря относительной простоте приготовления и легкости пиролиза в атмосфере молекулярного водорода для этого чаще всего используются метиловые и этиловые металлоорганики, которые поставляют атомы металлов с побочными продуктами реакции в виде метана или этана. Химическая реакция, приводящая к росту GaAs из триметилгаллия и гидрида мышьяка, имеет вид:

(CH3)3Ga+AsH3GaAs+3CH4

Подобная реакция используется для выращивания других двойных, тройных и четверных соединений. В частности AlxGa1-xAs растет в результате следующей реакции:

(1-x)[(CH3)3Ga]+x[)[(CH3)3Al]+ AsH3AlxGa1-xAs+3CH4

В этом случае атомная концентрация x алюминия в AlxGa1-xAs определяется относительными начальными парциальными давлениями триметилгаллия и триметилалюминия в газовой фазе.

Методом MOCVD могут быть последовательно выращены многослойные, многокомпонентные эпитаксиальные структуры в едином ростовом цикле, поскольку к реактору можно подключить несколько источников различных материалов и изменять состав газовой смеси в реакторе. Скорость, с которой можно обеспечить нужное изменение, зависит от геометрии реактора и величины полного потока газа через реактор. При высоких скоростях потока изменение состава можно осуществлять достаточно быстро и, следовательно, можно получать гетеропереходы с резкой гетерограницей. Методом MOCVD можно выращивать структуры достаточно высокого качества с толщиной отдельных слоев, составляющих всего 5-6 межатомных расстояний[6].

Нанолитография

Нанолитография является естественным развитием методов, используемых на протяжении многих лет в микроэлектронике для производства различных приборов и устройств, в том числе и больших интегральных схем. Традиционно рисунок будущих приборов и схем создается с помощью фотолитографии следующим образом. На первом этапе каким-либо образом изготавливают увеличенное изображение (маску) прибора. Затем это изображение с уменьшением переносится на полупроводниковую пластинку, которая покрыта фоточувствительным слоем (резистом), то есть фотографируется с уменьшением. Схема этого процесса представлена на рисунке 13. Фоторезист это сложная полимерная светочувствительная композиция.

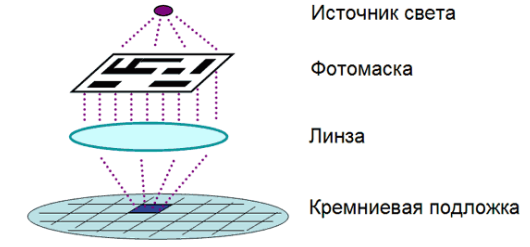
Рисунок 13 - Схематическое изображение проекционной системы для процесса фотолитографии

Фоторезист, у которого растворимость освещенного участка уменьшается, называется негативным, а фоторезист, растворимость которого после облучения возрастает, – позитивным. После обработки освещенного фоторезиста в специальном составе, удаляющем растворимые участки, образуется рельефное изображение, которое должно быть устойчивым к воздействию технологических факторов, в частности кислот, с помощьюкоторых стравливается полупроводниковая структура. Процесс получения рисунка называют литографией, а установки, с помощью которых это делают, – литографами. Последующее изготовление прибора или схемы весьма сложный процесс, включающий большое число циклов травления и осаждения новых слоев различных материалов. Почти перед каждой операцией требуется нанесение фоторезиста и фотографирование маски с каким-то новым рисунком.

Рассмотрим более детально процесс фотолитографии. Очевидно, что наименьшие размеры отдельных деталей, которые требуются для изготовления наноструктур, ограничены предельной разрешающей способностью оптических устройств, которая в свою очередь определяется дифракционным критерием Рэлея. Согласно этому критерию разрешение проекционной системы определяется выражением:

, (3)

где k – коэффициент пропорциональности, равный 0.61 в простейшем случае, – длина волны света, Na – числовая апертура объектива, пропорциональная показателю преломления среды между объектом и объективом. Отсюда следует, что для фотолитографии первостепенное значение имеет длина волны света, с помощью которого осуществляется перенос изображения маски на пластину с фоторезистом. В соответствии с критерием Рэлея (3) минимальная ширина линии, получаемой в изображении, пропорциональна длине волны экспонирующего света. Для видимого света (с длиной волны ~0.4 мкм) минимальная ширина линии составляет – 244 нм, что явно недостаточно для изготовления квантовых структур. Чтобы достигнуть меньших размеров отдельных деталей, в фотолитографии видимый свет заменяют ультрафиолетовым освещением (длина волны 193–365 нм). Еще одним достоинством ультрафиолетовой литографии является большая скорость, так как время освещения меньше, чем для видимого света. В настоящее время в промышленном производстве в качестве источников света используют лазеры ArF с длиной волны 193 нм. Их применение позволило реализовать 90, 65 и даже 45 нм технологические процессы производства микросхем (рис 14). Сейчас для литографических установок разрабатываются источники света, использующие длину волны 13 нм (Extreme Ultra Violet –EUV).

Элементарная оценка с помощью (3) показывает, что для длины волны света 193 нм, числовой апертуры 1 и коэффициента k=0.61 разрешение проекционной системы должно быть 118 нм.

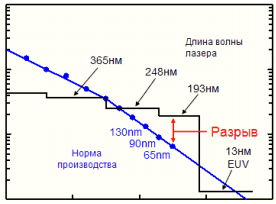
Рисунок 14 - Зависимость технологического процесса изготовления микросхем от длины волны света, используемого для литографии

Возникает вопрос: Каким образом удается реализовать 90, 65 и 45 нм технологические процессы производства микросхем применяя такой источник света? Ответ на него содержится в выражении (3). Действительно, при фиксированном значении для получения меньших величин amin можно попытаться уменьшить k и увеличить числовую апертуру Na. Для того, чтобы понять каким образом удается добиться желаемого результата вернемся к схеме фотолитографической проекционной системы (рис. 14). Видно, что кроме источника света в ее состав входят еще два важных элемента – фотомаска и «линза», которая на самом деле представляет собой сложный объектив, состоящий из большого числа оптических элементов.

Рассмотрим пути повышения разрешающей способности проекционной литографической системы с использованием специальных фотошаблонов, называемых фазосдвигающими масками. Принцип их действия иллюстрируется рисунком 15. В таких масках на одну из двух соседних прозрачных линий накладывается фазовый фильтр, сдвигающий фазу проходящей волны на 180°. В результате интерференции волн в противофазе происходит их взаимное ослабление в области между двумя экспонируемыми линиями, что делает их более различимыми и повышает разрешающую способность, т.е. уменьшает коэффициент k.

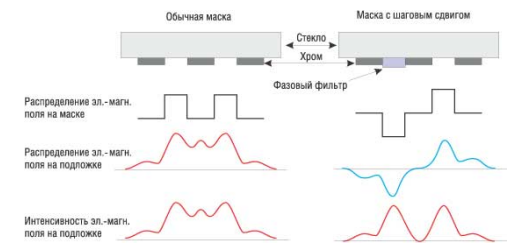
Рисунок 15 - Сравнение пространственного распределения интенсивности световой волны прошедшей через обычную маску и фазосдвигающую маску

Другим способом улучшения разрешающей способности проекционной литографической системы является использование масок с оптической коррекцией создаваемого рисунка (OPC или Optical Proximity Correction), где сложная форма маски используется для исправления последствий естественной дифракции света на краях (рис. 16).

Рисунок 16 - Схема, иллюстрирующая принцип оптической коррекции создаваемого фотолитографического рисунка

Применение этой коррекции уменьшает величину коэффициента k. Применение фазосдвигающих масок с оптической коррекцией создаваемого рисунка является необходимым условием реализации 45 нм технологического процесса производства микросхем.

Наконец существует способ уменьшения коэффициента k, связанный с внеосевым освещением шаблона и использованием сложной апертуры источника света (рис. 16).

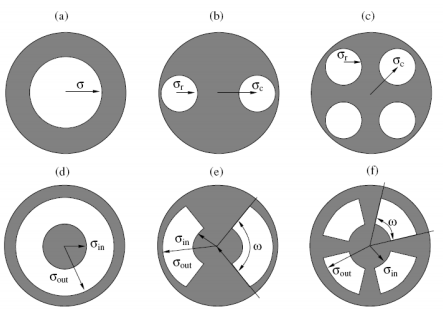
a – простая круглая апертура, b – круглая дипольная апертура, c – круглая квадрупольная апертура, d – простая кольцевая апертура, e – кольцевая дипольная апертура, f – кольцевая квадрупольная апертура

Рисунок 16 - Основные типы апертуры источника света и их параметры

Все апертуры, кроме простой круглой, используются при внеосевом освещении.

Для повышения пространственного разрешения литографического процесса широко используется способ, основанный на увеличении численной апертуры Na. Он заключается в том, что в литографическом процессе применяют иммерсионные объективы. В этом случае между объектом и объективом помещают жидкость с высоким показателем преломления, например, сверхчистую воду (рис. 17)[8].

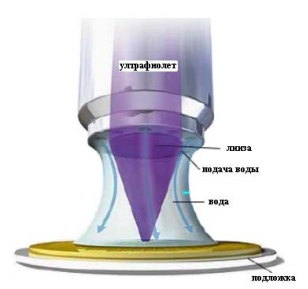
Рисунок 17 - Иммерсионный объектив, применяемый в литографии

2 Оптические свойства квантовых ям

2.1 Классификация гетероструктур

В настоящее время сложилась устойчивая терминология низкоразмерной физики полупроводников. Перечислим и кратко охарактеризуем различные гетероструктуры и сверхрешетки, указывая в скобках соответствующий термин и сокращение на английском языке.

Систематику удобно начать с одиночного гетероперехода между двумя композиционными материалами – полупроводниками A и B. Один или оба композиционных материала могут быть твердыми растворами, например, Al1-xGaxAs или Cd1-xMnxTe. Приведем примеры гетеропар A/B: GaAs/Al1-xGaxAs, In1-xAlxAs/Ga1-yAlyAs, InAs/AlSb, Ga1-xInxAs/InP, CdTe/Cd1-xMnxTe, Zn1-xCdxSe/ZnSySe1-y, ZnSe/BeTe, ZnSe/GaAs, Si1-xGex/Si и т.д. Здесь индексы x,1-x или y,1-y означают долю атомов определенного сорта в узлах кристаллической решетки или какой-либо из подрешеток. По определению, в гетеропереходах типа I запрещенная зона Eg одного из композиционных материалов лежит внутри запрещенной зоны другого материала. В этом случае потенциальные ямы для электронов или дырок расположены в одном и том же слое, например, внутри слоя GaAs в гетероструктуре GaAs/Al1-xGaxAs с x < 0.4. Пусть материал A характеризуется меньшей запрещенной зоной, т.е. EAg < EBg. Тогда высота потенциального барьера на интерфейсе A/B составляет Vc = EcB – EcA для электронов и Vh = EvA - EvBдля дырок, где Ecj, Evj - энергетическое положение дна зоны проводимости c и потолка валентной зоны v в материале j =A, B. Сумма Vc + Vh равна разности EBg - EAg. В широко применяемой гетеросистеме GaAs/Al1-xGaxAs отношение потенциальных барьеров Vc/Vh составляет 1.5.

В структурах типа II дно зоны проводимости Ec ниже в одном, а потолок валентной зоны Ev выше в другом материале, как в случае GaAs/Al1-xGaxAs с x>0.4, InAs/AlSb или ZnSe/BeTe. Для указанных гетеропар запрещенные зоны EAg и EBg перекрываются. Имеются также гетеропереходы типа II (например, InAs/GaSb), у которых запрещенные зоны не перекрываются и дно зоны проводимости в одном материале лежит ниже потолка валентной зоны в другом материале. К типу III относят гетеропереходы, в которых один из слоев является бесщелевым, как в случае пары HgTe/CdTe.

Двойной гетеропереход B/A/B типа I представляет собой структуру с одиночной квантовой ямой, если EAg < EBg, или структуру с одиночным барьером, если EAg > EBg. В широком смысле квантовой ямой называют систему, в которой движение свободного носителя, электрона или дырки, ограничено в одном из направлений.

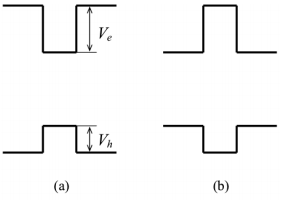
Рисунок 18 - Зонная схема структуры с одиночной квантовой ямой (a) и одиночным барьером (b). Ve,h – высота потенциального барьера (или разрыв зон) на интерфейсе в зоне проводимости и валентной зоне соответственно

В результате возникает пространственное квантование и энергетический спектр по одному из квантовых чисел из непрерывного становится дискретным. Ясно, что двойная гетероструктура типа II является структурой с одиночной квантовой ямой для одного сорта частиц, скажем, для электронов, и структурой с одиночным барьером для носителя заряда противоположного знака. Наряду с прямоугольными квантовыми ямами, представленными на рисунке 18, можно выращивать ямы другого профиля, в частности параболического или треугольного.

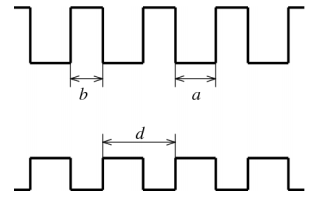
Рисунок 19 - Зонная схема периодической структуры с квантовыми ямами (если барьеры широкие) или сверхрешетки (если барьеры тонкие)

Естественным развитием однобарьерной структуры являются двух- и трехбарьерные структуры. Аналогично от одиночной квантовой ямы естественно перейти к структуре с двумя или тремя квантовыми ямами и структурам с целым набором изолированных квантовых ям (рис. 19). Даже если в такой структуре барьеры практически непроницаемы, двухчастичные электронные возбуждения, экситоны, в различных ямах могут быть связаны через электромагнитное поле, и присутствие многих ям существенно влияет на оптические свойства структуры. По мере того как барьеры становятся тоньше, туннелирование носителей из одной ямы в другую становится заметнее. Таким образом, с уменьшением толщины b квазидвумерные состояния (2D состояния), или состояния в подзонах (subband) размерного квантования изолированных ям, трансформируются в трехмерные минизонные состояния. В результате периодическая структура изолированных квантовых ям, или толстобарьерная сверхрешетка, превращается в тонкобарьерную сверхрешетку, или просто сверхрешетку.

Формирование минизон становится актуальным, когда период сверхрешетки d = a + b становится меньше длины свободного пробега носителя заряда в направлении оси роста структуры (в дальнейшем ось z). Эта длина может зависеть от сорта носителя, в частности, из-за различия эффективных масс электрона и дырки. Поэтому одна и та же периодическая структура с квантовыми ямами может быть одновременно как сверхрешеткой для более легких носителей, обычно это электроны, так и структурой с набором изолированных ям для другого сорта носителей, например тяжелых дырок. Последние также могут перемещаться вдоль оси роста, однако это движение носит не когерентный характер, а представляет собой цепочку некогерентных туннельных прыжков между соседними ямами[12].

Строго говоря, по определению сверхрешетки толщины слоев a и b должны существенно превышать постоянную кристаллической решетки a0. В этом случае для описания электронных состояний можно использовать метод эффективной массы или, в более широком смысле, метод плавных огибающих. Тем не менее, полезно в поле зрения физики низкоразмерных систем в качестве предельного случая включить «ультратонкую» сверхрешетку AmBn, например (GaAs)m(AlAs)n с m,n = 2 - 4 и даже полупроводниковое соединение типа (GaAs)1(AlAs)1, т.е. GaAlAs2.

Аналогично приведенной выше классификации гетероструктур по взаимному выстраиванию запрещенных зон EAg и EВg каждая сверхрешетка принадлежит к одному из трех типов, соответственно типу I, II и III. Сверхрешетки, состоящие из чередующихся слоев различных материалов, называются композиционными. Первоначально для создания квантовых ям и сверхрешеток подбирались гетеропары с практически одинаковыми постоянными решетки, например пара GaAs/AlGaAs. Структуры с рассогласованием постоянной решетки a0/a0, не превышающим 0.01, называются согласованными, или ненапряженными. Совершенствование технологии роста позволило получить бездислокационные сверхрешетки и при заметном рассогласовании постоянных решетки. В таких многослойных структурах, по крайней мере, один из слоев, A или B, должен быть достаточно тонким, чтобы согласование кристаллических решеток происходило за счет внутреннего напряжения, сжатия одного из слоев и, возможно, растяжения другого. Структуры сквантовыми ямами и сверхрешетки с a0/a00.01 называются напряженными. В композиционных спиновых сверхрешетках один или оба слоя A и B содержат магнитные примеси или ионы. Примером служит гетероструктура CdTe/CdMnTe.

Наряду с композиционными сверхрешетками, образованными периодическим изменением состава, сверхрешетки могут создаваться модулированным легированием донорной и/или акцепторной примесью. Такие сверхрешетки, в частности сверхрешетка n-GaAs/p-GaAs или nipi-структура, называются легированными[13].

2.2 Электронные подзоны в квантовых ямах

Расчеты электронных состояний в полупроводниковых наноструктурах, выполняемые в методе эффективной массы, выглядят часто как практические занятия по квантовой механике. Мы начнем с простейшей структуры с одиночной квантовой ямой A с толщиной a, заключенной между полубесконечными барьерами B. В случае простой зоны проводимости, изотропной и параболической, огибающая записывается в виде:

(4)

Здесь z - главная ось структуры, k|| - двумерный волновой вектор с компонентами kx и ky, он описывает движение электрона в плоскости интерфейсов (x,y), S - площадь образца в этой плоскости. Зависящая от z огибающая (z) удовлетворяет следующему уравнению Шредингера:

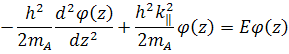
, (5)

где mA,B - эффективная масса электрона в материале A или B.

При конечной высоте барьера Ve имеются два вида решений уравнения (5). Если величина положительна, решения в пределах каждого слоя являются линейными комбинациями двух плоских волн и энергетический спектр в этой области энергий непрерывен даже при фиксированной величине 2D-волнового вектора k||. В области энергий с отрицательными значениями , которая рассматривается в дальнейшем, внутри ямы функция (z) есть линейная комбинация плоских волн exp(±ikz), а в левом и правом барьерах она экспоненциально спадает как exp(±z) соответственно. Здесь:

(6)

В этом случае возникают размерно-квантованные электронные состояния, которые нумеруются дискретным индексом ( = 1, 2,...), и для электронов в зоне проводимости обозначаются составным индексом e. Энергетический спектр этих состояний представляет собой набор ветвей Eek||, называемых подзонами, которые сдвинуты вертикально относительно друг друга. Полная энергия электрона складывается из энергии размерного квантования Ez = Ee0 и кинетической энергии Exyk|| = Eek|| - Ee0 при свободном движении электрона в плоскости (x,y)[14].

3 Оптические свойства квантовых нитей

3.1 Методы изготовления квантовых нитей

Большинство способов изготовления квантовых нитей основывается на том, что в системе с двумерным электронным газом (квантовая яма) тем или иным способом ограничивается движение носителей заряда в еще одном направлении. Для этого есть несколько способов. Наиболее очевидный из них – это непосредственное «вырезание» узкой полоски с помощью литографической техники (рис. 20 а).

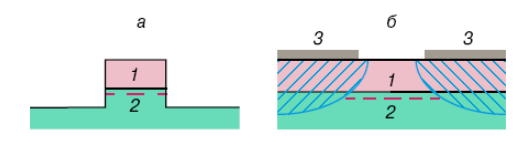
1 – полупроводник с широкой запрещенной зоной (например, AlGaAs),

2 – полупроводник с узкой запрещенной зоной (например, GaAs),

3 – металлический затвор

Рисунок 20 - Полупроводниковые гетероструктуры с квантовыми нитями, полученные с помощью субмикронной литографии за счет вытравливания узкой полоски из самой структуры (а) или щели в затворе Шотки (б), образующийся вблизи гетерограницы узкий электронный канал показан штриховой линией. Заштрихованы области обеднения электронами

При этом для получения электронных нитей шириной в сотни ангстрем, где квантование энергий электронов будет заметным, необязательно делать полоски именно такой ширины, что требует литографической техники сверхвысокого разрешения. Дело в том, что на боковых гранях вытравленной полоски, как и на свободной поверхности полупроводника, образуются поверхностные состояния, создающие, как правило, слой обеднения. Этот слой вызывает сужение проводящего канала, в результате чего квантовые эффекты можно наблюдать и в полосках большей ширины – порядка десятой доли микрона.

Можно поступить иначе. Поверхность полупроводниковой структуры покрывают металлическим слоем, создающим с полупроводником контакт Шотки и имеющим узкую щель (рис. 20 б). Если гетерограница находится достаточно близко от поверхности, в слое обеднения, то двумерные электроны на границе будут отсутствовать всюду, кроме узкой области под щелью. Такой тип одномерной структуры обладает дополнительным преимуществом: меняя напряжение на затворе, мы можем управлять эффективной шириной квантовой нити и концентрацией носителей в ней[18].

3.2 Плотность электронных состояний

Все основные свойства квантовых нитей, в том числе и оптические, определяются законом дисперсии, т.е. зависимостью энергии электронных состояний от импульса:

(7)

где m* – эффективная масса электронов (дырок), Ei – дискретные значения энергии (i=1,2,…), связанные с эффектом размерного квантования, pz – импульс носителя заряда в направлении его свободного движения. Выражение Ei(pz) описывает i-тую подзону размерного квантования. В связи с этим интересно сравнить между собой объемные материалы с законом дисперсии:

(8)

и квантовые нити (7). Несмотря на внешнюю похожесть приведенных формул, разное число измерений, по которым электроны (дырки) могут свободно двигаться, вызовет качественную разницу почти во всех свойствах.

Важнейшей характеристикой электронной системы наряду с ее законом дисперсии является плотность состояний, т.е. число состояний в единичном интервале энергии. Поскольку электроны подчиняются принципу Паули, то плотность состояний определит то максимальное число электронов, которое может разместиться в данном интервале энергий, а распределение электронов по энергиям определит все их остальные свойства.

Основной вопрос здесь заключается в следующем: насколько должны отличаться импульсы двух электронов, чтобы они могли считаться принадлежащими к различным квантовым состояниям и не подчиняться принципу Паули? Пусть размер образца вдоль оси z равен Lz. Из соотношений неопределенности квантовой механики следует, что при этом неопределенность импульса pz будет равна 2h/ Lz и, следовательно, различными могут считаться состояния со значениями импульса, различающимися на 2h/ Lz . Аналогичные рассуждения относятся и к другим направлениям, в которых электроны двигаются как свободные.

Теперь мы можем вычислить важную промежуточную характеристику системы G(E) – полное число состояний, имеющих энергию, меньшую, чем E. В трехмерном случае:

(9)

где V – объем образца, Vp(E) – объем импульсного пространства, т.е. области в осях px, py, pz, для которой энергия меньше, чем E. Легко понять, что эта область представляет собой шар радиусом и объемом (4 /3)( 2m*E)3/2, так что окончательно в трехмерном случае:

(10)

Очевидно, что G(E) образовалось суммированием всех состояний с энергиями от 0 до E. При этом интересующая нас плотность состояний вблизи заданной энергии будет определяться производной G(E) по энергии. Кроме того, обычно интересуются плотностью состояний не на весь образец, а на единицу объема и учитывают то, что в каждом состоянии могут находиться два электрона с противоположными спинами. Это дает окончательную формулу для трехмерной плотности состояний:

(11)

Аналогичный расчет для квантовой нити приводит к следующему выражению:

(12)

Здесь суммирование проводиться по подзонам размерного квантования.

Рисунок 21 - Плотность состояний в объемном полупроводнике (левая панель) и в квантовой нити (правая панель)

На рисунке 21 схематично показаны плотности состояний для объемного материала и квантовой нити. Видно, что они качественно различаются. В объемном полупроводнике плотность состояний монотонно растет с увеличением энергии, а в квантовых нитях в плотности состояний возникают сингулярности каждый раз, когда мы приближаемся к экстремуму очередной подзоны размерного квантования. На рисунке 22 представлены экспериментальные спектры поглощения и дифференциального пропускания света квантовыми нитями, изготовленными путем внедрения GaAs в асбестовые нанотрубки. Спектральные особенности связаны с сингулярностями плотности состояний. Из-за разброса размеров квантовых нитей в образце спектры оказываются неоднородно уширенными. В связи с этим не удается наблюдать всю возможную энергетическую структуру квантовых нитей. Для исследования этой структуры необходимо использовать размерно-селективные методы оптической спектроскопии.

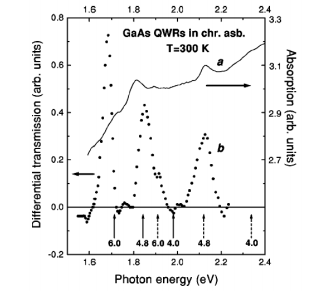
Рисунок 22 - Спектры линейного поглощения (а) и дифференциального пропускания (b) GaAs квантовых нитей

Сплошными и штриховыми стрелками показаны теоретические значения межзонных переходов из подзоны тяжелых (hh) и легких (lh) дырок для квантовых нитей с диаметром 4 нм, 4.8 нм и 6 нм[17].

4 Оптические свойства квантовых точек

4.1 Оптические методы исследования квантовых точек

Оптические методы являются самыми мощными и универсальными методами исследования полупроводниковых квантовых точек. Это связано с тем, что они позволяют резонансно возбуждать и селективно исследовать те или иные состояния различных наноструктур. В ряде случаев только оптические методы применимы для исследования квантовых точек. Такая ситуация имеет место для нанокристаллов, выращенных в диэлектрических матрицах, а также помещенных в жидкости или полимеры. Линейные и нелинейные оптические методы открывают возможность изучения широкого круга параметров, эффектов и процессов в квантовых точках в стационарном и нестационарном режимах. С их помощью может быть получена информация об энергетической структуре элементарных возбуждений, например энергетические спектры электронной и колебательной подсистем, о взаимодействии элементарных возбуждений между собой и с внешними полями, о перенормировке энергетических спектров и возникновении коллективных возбуждений, а также о динамике элементарных возбуждений и релаксационных процессах. Кроме того, оптические методы позволяют осуществлять характеризацию и контроль качества квантовых точек, т. е. определять их химический состав и размеры, а также качество границ раздела и наличие дефектов.

Взаимодействие электромагнитного излучения с электронами и дырками главным образом определяется выражением:

(12)

где m – масса свободного электрона, A=eA0 – векторный потенциал световой волны с поляризацией e, p=ih – оператор импульса заряженной частицы. Взаимодействие (12) приводит к межзонным и внутризонным переходам электронной подсистемы квантовой точки, в результате которых поглощаются или испускаются фотоны. Такими переходами обусловлено большинство оптических процессов, включая поглощение и рассеяние света, а также люминесценцию (рис. 23).

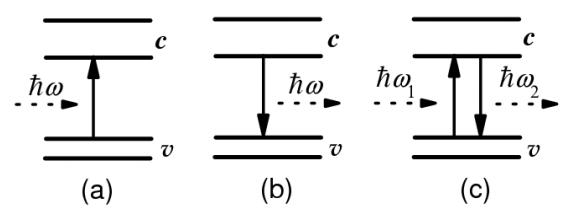
h – энергия поглощенных или излученных фотонов,

h1 и h2 – энергии падающих и рассеянных фотонов

Рисунок 23 - Схема межзонных электронных переходов в квантовой точке, иллюстрирующая процессы поглощения (a), люминесценции (b) и рассеяния света (c)

Для того чтобы выяснить, каким образом трехмерное пространственное ограничение модифицирует электронфотонное взаимодействие, рассмотрим матричный элемент (12). Для простоты будем использовать двухзонную модель полупроводника (зона проводимости с и валентная зона v) и предполагать, что в сферической квантовой точке, находящейся в режиме сильного конфайнмента, потенциальная яма для электронов и дырок имеет бесконечно высокие стенки. Необходимо различать два качественно различных типа оптических переходов. Первый из них, называемый внутризонным, имеет место, когда начальное и конечное электронные состояния принадлежат одной и той же зоне, например зоне проводимости. В этом случае матричный элемент взаимодействия (12) имеет вид:

, (13)

где символами 1и 0 обозначены наборы из трех квантовых чисел n1,l1,m1 и n0,l0,m0, характеризующие конечное и начальное состояния соответственно. В дипольном приближении (13) упрощается:

, (14)

где mc - эффективная масса электрона в зоне проводимости.

Важной особенностью электрон-фотонного взаимодействия при внутризонных переходах является зависимость его матричных элементов от размера квантовой точки. Для режима сильного конфайнмента эта зависимость достаточно простая – матричный элемент пропорционален обратной величине характерного размера квантовой точки. Можно показать, что эта закономерность справедлива для квантовых точек любой формы[5].

Рассмотрим теперь в режиме сильного конфайнмента межзонные переходы, в результате которых образуется электрондырочная пара, т. е. электрон из валентной зоны переходит в зону проводимости. Матричный элемент взаимодействия (7), описывающий такой переход, может быть представлен следующим образом:

(15)

В дипольном приближении выражение (15) упрощается:

(16)

4.2 Однофотонное поглощение квантовыми точками

Предположим, что образец представляет собой квантовые точки из полупроводника с кубической симметрией, внедренные в диэлектрическую матрицу, например, стекло. Тогда нанокристаллы в этой матрице имеют почти сферическую форму, и для описания их электронной подсистемы можно воспользоваться моделью квантовой точки с бесконечно высокими потенциальными барьерами для электронов, дырок и экситонов. Пусть на образец падает электромагнитная волна, энергия фотонов которой h попадает в область межзонных переходов в нанокристаллах (рис. 24), а ее интенсивность (I) не слишком высока.

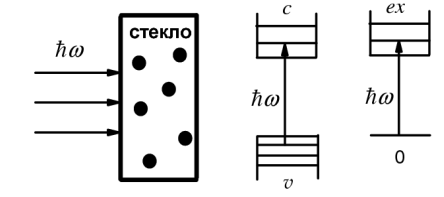
Рисунок 24 - Схема межзонных электронных переходов в квантовой точке в режиме сильного и слабого конфайнмента, иллюстрирующая процесс однофотонного поглощения.

, (17)

где – матричный элемент электронфотонного взаимодействия, вычисленный с использованием полных волновых функций.

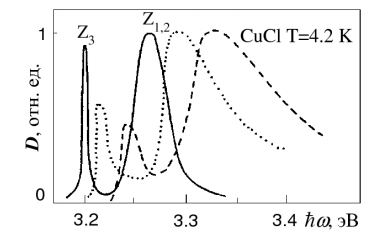
Рисунок 25 - Спектры однофотонного поглощения нанокристаллов CuCl с различными средними радиусами R0=3.1 (1), R0=2.9 (2) и R0=2.0 нм (3)

На рисунке 25 приведены спектры однофотонного поглощения нанокристаллов в стеклянной матрице, изготовленных из кубического полупроводника CuCl. Измерения проводились при температуре T=4.2 К для образцов, содержащих ансамбли квантовых точек со средними радиусами 3.1, 2.9 и 2.0 нм. Поскольку боровский радиус экситона Rex в CuCl равен 0.7 нм, то можно считать, что нанокристаллы во всех трех образцах находятся в режиме слабого конфайнмента.

Из рисунке 25 видно, что при уменьшении среднего радиуса нанокристаллов их спектры поглощения смещаются в высокоэнергетическую область. Этот сдвиг достаточно хорошо описывается выражением h22/2MR2 в соответствии с предсказанием простой теории межзонного поглощения квантовыми точками в режиме слабого конфайнмента. В то же время каждый спектр на рисунке 25 состоит из двух линий, достаточно близких по амплитуде. Энергетическое расстояние между этими линиями не согласуется с величиной 3h22/2MR2 , равной энергетическому зазору между двумя нижайшими экситонными уровнями размерного квантования, однофотонный переход в которые разрешен правилами отбора. Таким образом, интерпретировать вторую (высокоэнергетическую) линию спектра поглощения не удается в рамках двухзонной модели полупроводника. Чтобы объяснить наличие высокоэнергетической линии, необходимо вспомнить, что валентная зона полупроводников с кубической симметрией обладает сложной структурой (рис. 26).

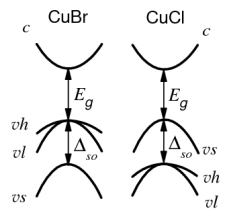
Eg – ширина запрещенной зоны,

so – спин-орбитальное расщепление,

vh, vl и vs - подзоны тяжелых, легких и спино-рбитально отщепленных дырок соответственно

Рисунок 26 - Энергетическая зонная структура кубических полупроводников

Она состоит из подзон тяжелых и легких дырок, вырожденных в центре зоны Бриллюэна, и подзоны спин-орбитально отщепленных дырок, отделенной от двух первых энергетическим зазором so. Трехмерное пространственное ограничение приводит к размерному квантованию всех трех подзон валентной зоны. В случае нанокристаллов CuCl верхней является подзона спин-орбитально отщепленных дырок. Отсюда следует, что низкоэнергетическая линия спектров поглощения, представленных на рисунке 25, соответствует генерации экситонов, образованных электроном зоны проводимости и дыркой из этой подзоны валентной зоны. Вторая же высокоэнергетическая линия связана с возбуждением экситонов, в которые включены дырки из подзон легких и тяжелых дырок. Энергетическое расстояние между парой линий можно приближенно описать выражением:

(18)

где mvs и mvh – эффективные массы спин-орбитально отщепленных и тяжелых дырок.

Учет сложной структуры валентной зоны в простейшем варианте может быть выполнен в рамках модели, в которой подзоны валентной зоны считаются независимыми друг от друга. При этом полный энергетический спектр электронных, дырочных и экситонных состояний квантовых точек будет суперпозицией спектров изолированных зон. Данная модель позволяет выполнить тривиальное обобщение теории однофотонного поглощения. Действительно, полный спектр поглощения является простой суперпозицией спектров, сформированных оптическими переходами между изолированными подзонами валентной зоны и зоной проводимости.

Следует отметить, что интерпретировать спектры однофотонного поглощения квантовых точек в режиме сильного конфайнмента значительно труднее, чем в режиме слабого конфайнмента. На рисунке 27 представлен коэффициент поглощения нанокристаллов со средним радиусом 3 нм в воде, изготовленных из кубической модификации CdSe. Поскольку боровский радиус экситона в CdSe равен 5.7 нм, можно считать, что квантовые точки находятся в режиме сильного конфайнмента. Трудность интерпретации таких спектров обусловлена тем, что спектральные особенности коэффициента поглощения, например на рисунке 27 в области 2.25 и 2.8 эВ, связанные с переходами из подзон тяжелых/легких дырок и спин-орбитально отщепленных дырок соответственно, являются полосами.

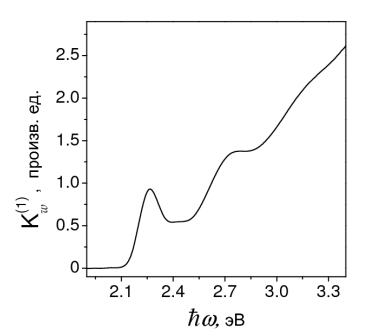
Рисунок 27 - Коэффициент однофотонного поглощения квантовых точек из CdSe в воде (средний радиус нанокристаллов 3 нм)

Они сформированы не одной неоднородно уширенной линией, а целыми сериями линий одиночного нанокристалла , которые соответствуют оптическим переходам с различными угловыми моментами (v,l=0c, l=0; v,l=1c,l=1; v,l=2c,l=2; ...). Из-за достаточно большого неоднородного уширения линии с различными угловыми моментами спектрально не разрешаются и не удается определить квантовые числа перехода, которому соответствуют максимумы спектральных особенностей коэффициента поглощения[6].

4.3 Лазеры на квантовых точках для волоконной связи

Развитие оптоволоконных телекоммуникаций привело к необходимости создания эффективных полупроводниковых лазеров и оптических усилителей, работающих в спектральной области минимальных потерь волноводов (1.25-1.65мкм). Наибольшая длина волны, достигнутая лазерами на квантовых ямах InGaAs/GaAs, составляет 1230 нм - для устройств, генерирующих с торца, и 1260 нм для лазеров с вертикальным резонатором. Достаточно большие пороговые токи, низкая рабочая температура и невысокая температурная стабильность таких лазеров не всегда удовлетворяют требованиям, предъявляемым к высокоскоростным телекоммуникационным устройствам.

Прогресс в изготовлении многослойных структур самоорганизованных квантовых точек соединений A3B5, достаточно однородных по размеру и форме при большой поверхностной плотности, привел к созданию полупроводниковых лазеров с квантовыми точками в качестве активной среды. В результате спектральная область 1.0–1.7 мкм стала доступной для генерации как для лазеров традиционной конструкции, так и для лазеров с вертикальным резонатором, использующих квантовые точки InGaAs и подложки GaAs. В частности, оба типа лазеров могут генерировать излучение с длиной волны 1.3 мкм с чрезвычайно низкими пороговыми токами и высокой выходной мощностью. Недавно был продемонстрирован широкополосный лазер на квантовых точках, излучающий на 1.5 мкм с плотностью тока всего в 70 А/см2

на один слой квантовых точек при комнатной температуре. Оптические усилители на основе квантово-точечных структур представляют интерес для высокоскоростной обработки сигналов со скоростью свыше 40 Гбит/с. Существенно, что развитые GaAs-технологии позволяют изготавливать достаточно дешевые монолитные лазеры на квантовых точках с вертикальным резонатором c распределенными брэгговскими зеркалами на основе пар AlAs/GaAs и AlOx/GaAs.

Следует отметить, что благодаря неоднородному уширению электронных переходов в квантовых точках возникает возможность расширения области непрерывной перестройки длины волны генерации. При некотором увеличении пороговых токов она может достигать 200 нм (1.033-1.234 мкм). Лазеры, использующие InAs-квантовые точки и InP-подложки, также представляют интерес, поскольку они позволяют получать генерацию в более длинноволновом диапазоне (1.8–2.3 мкм), важном для применений в молекулярной спектроскопии и дистанционном контроле газовых атмосфер с помощью лидаров. В то же время, генерация излучения с длиной волны 1.9 и 2 мкм лазера с активной средой из такой гетероструктуры была получена пока только при низкой (77 К) температуре. Интересно, что генерация на длинах волн 1.6 и 1.78 мкм была также продемонстрирована для лазеров на InAs квантовых проволоках – одномерных квантовых структурах на (001)InP-подложке. И наконец, непрерывная генерация в области 2 мкм получена при комнатной температуре при использовании в качестве активной среды лазера квантовых точек на основе InAsSb, выращенных на (001)InP-подложке. Интенсивное развитие этого направления привело к тому, что в настоящее время некоторые типы полупроводниковых лазеров с активной средой на основе квантовых точек стали коммерчески доступны.

Преимущества лазера на квантовых точках по сравнению с лазером на квантовых ямах можно условно разделить на физические и технологические. Физические преимущества обусловлены в основном -образным спектром плотности состояний и гигантской силой осциллятора оптических переходов на единицу объема КТ, обусловленную эффективным перекрытием волновых функций электрона и дырки из-за их пространственной локализации. К таким преимуществам относят сверхвысокую температурную стабильность пороговой плотности тока [4], гигантские коэффициенты максимального удельного усиления материала (material gain) и максимального дифференциального усиления материала (differential gain), на два-три порядка превышающие аналогичные значения для лазера на квантовых ямах. К преимуществам лазеров на КТ можно также отнести малое время заселения основного состояния и, соответственно, высокие рабочие частоты. К технологическим преимуществам можно отнести отсутствие или подавление диффузии неравновесных носителей, что приводит к уменьшенному растеканию неравновесных носителей из области полоска, подавлению безызлучательной рекомбинации на точечных и протяженных дефектах и, соответственно, подавлению эффекта роста дислокаций, а также подавлению эффекта перегрева зеркал за счет поверхностной рекомбинации. Кроме того, упорядоченный массив квантовых точек, расположенный в оптическом волноводе, может приводить к распределенной обратной связи и одномодовой генерации. В случае вертикально излучающих лазеров имеется принципиальная возможность создания лазера на одной квантовой точке, что позволяет избежать неоднородного уширения, характерного для ансамбля квантовых точек, и полностью реализовать преимущества трехмерного квантования. Рабочие характеристики лазеров на КТ, полученных различными методами, исследовались в работах [5].

При низких температурах лазерная генерация начинается при энергиях, близких к максимуму пика фотолюминесценции, указывая на то, что за лазерную генерацию ответственны переходы через основное состояние квантовых точек. С повышением температуры пороговая плотность тока практически не изменялась, сохраняя свое значение 80 А/см2 до температур порядка 180 K. Если аппроксимировать температурную зависимость пороговой плотности тока выражением вида J = J0 exp(T /T0), то в этом температурном диапазоне T0 = 380 K, что выше теоретического предела для лазеров на квантовых ямах. При этом длина волны генерации находится вблизи максимума пика ФЛ и ЭЛ при слабом уровне возбуждения. При повышении температуры свыше 180 K пороговая плотность тока начинала расти, что совпадает с уменьшением интегральной интенсивности фотолюминесценции с энергией активации 8090 мэВ. Данная величина хорошо согласуется с энергией локализации дырок в квантовых точках и указывает на то, что причиной роста пороговой плотности тока является недостаток усиления, связанный с термическим выбросом носителей из квантовых точек. Эффект насыщения усиления сопровождается сдвигом длины волны генерации в коротковолновую сторону, соответствующую области излучения возбужденных состояний квантовых точек и смачивающего слоя InGaAs.

Таким образом, инжекционные лазеры на квантовых точках демонстрируют низкие значения пороговой плотности тока и рекордную температурную стабильность при низких температурах в соответствии с теоретическими предсказаниями. Однако недостаточная энергия локализации носителей приводит к сильной температурной зависимости пороговой плотности тока при температурах вблизи комнатной.

Возможность реализации инжекционного лазера на квантовых точках в существенной степени зависит от соотношения между усилением излучения из квантовых точек и оптическими потерями в структуре. В случае инжекционного лазера на квантовой яме, типичная ширина которой составляет 100 A , фактор оптического ограничения (пропорциональный интегралу перекрытия между волновой функцией электрона и световой волной) составляет порядка 0.03. В случае уменьшения толщины ямы до 10–30 A данный коэффициент существенно не уменьшается из-за проникновения волновой функции в барьеры. Следует отметить, что усиление в лазерах на квантовых ямах мало, и низкие пороговые плотности тока могут быть реализованы только для больших длин резонатора, когда удается в существенной степени уменьшить влияние потерь на вывод излучения, или в четырехсколотых образцах. В случае массива квантовых точек волновая функция основного состояния полностью локализована внутри квантовой точки. Даже в случае плотного массива островков только примерно 2 монослоя InAs преобразуются в квантовые точки, что соответствует усредненному по площади поверхности экситонному объему, вследствие чего фактор оптического ограничения очень мал [5]. Тем не менее реализация инжекционного лазера на квантовых точках оказалась возможной вследствие гигантского возрастания ”удельного усиления” в соответствии с теоретическими оценками.

Удельное усиление было непосредственно определено из условия равенства усиления и потерь на пороге генерации. Внутренние потери измерялись из зависимостей пороговой плотности тока от длины резонатора и дифференциальной эффективности от потерь на выход. Фактор оптического ограничения оценивался исходя из известных данных электронной микроскопии геометрических размеров точек. Полученное значение максимального ”удельного усиления” составляет 1.5 105 см1 [7], что более чем на порядок превосходит значение для лазеров на квантовых ямах. Вследствие линейной зависимости между усилением и током, дифференциальное усиление в лазерах на квантовых точках возрастает также более чем на 3 порядка [101] по отношению к лазерам на квантовых ямах и достигает величин порядка 1012 см2.

Возрастание усиления является прямым следствием размерного квантования в квантовых точках. Последнее уменьшает число состояний, которое необходимо заполнить для достижения определенного усиления. Основными факторами, снижающими усиление при определенной плотности тока, являются тепловой выброс носителей из квантовых точек и утечки через безызлучательную рекомбинацию в материале барьера.

Ухудшение характеристик лазера на квантовых точках при температурах выше 150180 K обусловлено недостаточным усилением. Для увеличения усиления необходимо либо повысить однородность массива квантовых точек, что в принципе может быть достигнуто путем оптимизации режимов выращивания, либо путем увеличения концентрации точек, что достигается путем использования вертикально связанных квантовых точек (ВСКТ) [71–74]. Преимущество вертикально связанных КТ это — наряду с большим коэффициентом оптического ограничения, возможность более быстрой релаксации носителей в основное состояние, меньшее время излучательной рекомбинации [7] и возможность эффективного туннелирования электронов и дырок между точками в соседних рядах, которая отсутствует в случае рядов изолированных КТ.

Лазеры на вертикально связанных квантовых точках демонстрируют гораздо большее оптическое усиление, а насыщение усиления в них отстутствует вплоть до коротких длин резонатора. Они демонстрируют генерацию через основное состояние квантовых точек до комнатной температуры, и длина волны генерации следует за температурной зависимостью ширины запрещенной зоны GaAs. Пороговая плотность тока резко уменьшается до величин порядка 90 А/см2 (300 K) при увеличении числа циклов складирования до 10 (рис. 16). Данный эффект обусловлен увеличением усиления вследствие роста фактора оптического ограничения. Дифференциальная эффективность также возрастает с увеличением N, достигая 50% при N = 10. Невысокие значения дифференциальной эффективности обусловлены низкой величиной внутренней квантовой эффективности (0.5), что означает, что существенная часть носителей рекомбинирует безызлучательно, наиболее вероятно в GaAs, покрывающем квантовые точки, который осаждается при низкой температуре 480C.

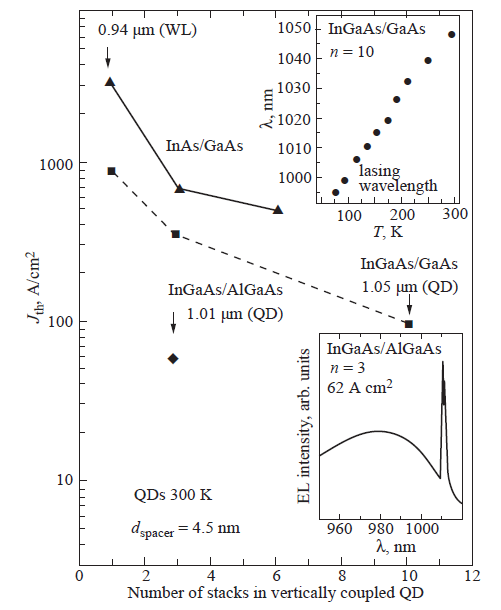
Рисунок 28. Зависимость плотности порогового тока от циклов осаждения InAs или InGaAs для инжекционного лазера на вертикально связанных квантовых точках.

Длина волны лазерного излучения в зависимости от температуры приведена на вставке справа вверху (рис 28). Спектр излучения представлен на вставке справа внизу.

Хорошие динамические характеристики лазера на КТ следуют из малых времен релаксации носителей в основное состояние и больших коэффициентов дифференциального усиления. Прямые измерения частоты отсечки лазера на КТ дают величину порядка 10 ГГц [4].

Другой важный аспект, характеризующий работу лазера при высоких частотах, — это фактор спектрального уширения линии генерации. Всякий пик поглощения или усиления обусловливает модуляцию коэффициента преломления вблизи энергии соответствующего резонанса согласно соотношениям Крамерса–Кронига. Таким образом, длина волны фотона в кристалле может изменяться за время импульса тока накачки. Этот эффект описывается фактором спектрального уширения линии (). В случае структур с квантовыми ямами форма спектра поглощения или усиления является сильно асимметричной, что обусловливает большую величину (от единицы до двух). Напротив, в случае структур с квантовыми точками спектр поглощения и усиления более симметричени имеет гауссову форму. Таким образом, производная по энергии и, соответственно, изменение коэффициента преломления в области максимума поглощения или усиления равны нулю. Экспериментально измеренные величины составляют 0.5, что связано с конечным вкладом возбужденных состояний КТ в спектр усиления вблизи порога генерации, обусловливающим некоторую асимметричность профиля коэффициента усиления [4].

Условие прозрачности в КТ реализуется тогда, когда КТ захватывает один экситон. В этом случае вероятности излучить или поглотить квант света с образованием биэкситона равны. Следует, однако, отметить, что, в общем случае, энергии экситонного и биэкситонного состояния в КТ различны, и заселение КТ одним экситоном может приводить одновременно к появлению линии экситонного усиления и линии биэкситонного поглощения. Если неоднородное уширение линий меньше, чем энергетическая разность между энергиями экситона и биэкситона в КТ, то возможен чисто экситонный механизм усиления. Следует также отметить важность вклада заряженных экситонов в спектр усиления [10].

Если возможность транспорта носителей между соседними КТ отсутствует (что типично при низких температурах), тогда вероятность захвата экситонов и носителей в КТ не зависит от температуры. При высоких температурах термический выброс носителей из более мелких КТ может приводить к преимущественному заселению более глубоких КТ. Поведение спектров усиления различно в этих двух случаях: в первом случае максимум усиления не изменяет своего положения при увеличении тока накачки, во втором случае он смещается в сторону больших энергий [11].

Поверхностно излучающие лазеры на КТ, работающие при оптическом возбуждении при низких температурах через основное состояние КТ, были получены в работе. Инжекционные лазеры на вертикально складированных изолированных КТ были реализованы в работе. Пороговая плотность тока при комнатной температуре составила 500 А/см2, а генерация осуществлялась через возбужденные состояния КТ. При использовании структур с 7-микронной апертурой в окисле AlO для уменьшения областей токовой инжекции в работе был реализован режим генерации через основное состояние КТ при комнатной температуре (300 K), плотности тока 1000 А/см2 и пороговом токе 0.5 мА[4].

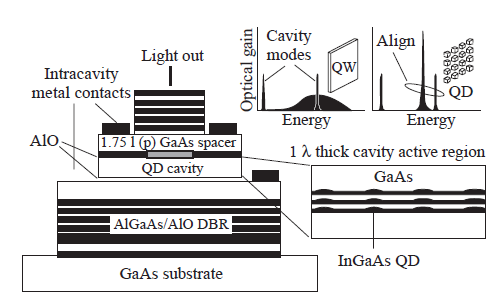
Рисунок 29 Схема лазера, излучающего с поверхности, на вертикально связанных квантовых точках InGaAs в матрице GaAs.

На рис. 29 приведены для сравнения спектры оптического усиления для структуры с квантовыми ямами и для структуры с квантовыми точками. На рис. 30 приведено поперечное сечение активной области лазера.

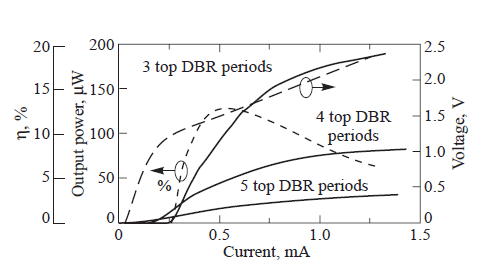
Рисунок 30. Зависимости выходной мощности и кпд лазера на вертикально связанных квантовых точках InGaAs в матрице GaAs от тока инжекции. Сплошные линии — мощность лазера; короткий пунктир — кпд лазера, длинный пунктир — вольтамперная характеристика.

4.4 Сравнительный анализ вертикальных лазеров на квантовых точках.

Условием начала лазерной генерации является баланс между оптическим усилением и суммарными оптическими потерями, включающими потери на вывод излучения и внутренние потери в лазерной структуре. В общем случае для каждой оптической моды это условие можно представить в следующей форме:

, (19)

где gth — оптическое усиление активного материала на пороге генерации, (i) — внутренние оптические потери для данной моды, m — потери на вывод оптического излучения через зеркала, — трехмерный фактор оптического ограничения световой волны, характеризующий взаимодействие электромагнитного поля рассматриваемой моды с активной (усиливающей) средой. Произведение gth определяет величину модового оптического усиления на пороге генерации.

В традиционных полосковых лазерах зеркала ограничивающие оптический резонатор Фабри–Перо, образованы торцевыми гранями структуры, а сам резонатор, как правило, имеет большую длину по сравнению с периодом стоячей волны оптического поля (рис. 31, a). При этом оптическая волна распространяется в плоскости активного слоя и длина активной (усиливающей) области обычно совпадает с длиной резонатора Lc, равной в данном случае геометрическому расстоянию между сколотыми зеркалами. Трехмерный фактор оптического ограничения можно представить в виде произведения фактора оптического ограничения в направлении z, совпадающем с направлением роста эпитаксиальной структуры, (z) и фактора оптического ограничения в плоскости xy, параллельной поверхности структуры, (xy) [4]. Для традиционного лазера при ширине полоска в несколько десятков мкм и длине в сотни мкм xy 1. В этом случае условие (1) принято записывать в форме:

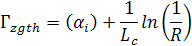
, (20)

где R1, R2 — коэффициенты отражения переднего (выводного) и заднего зеркал.

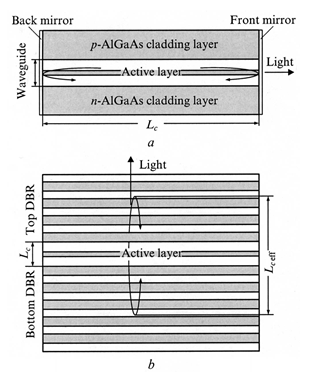
a — традиционный полосковый лазер

b — вертикально-излучающий лазер

Рисунок 31. Схематическое изображение лазерных структур

Если активный слой очень тонкий (как в случае КЯ или КТ) и расположен в центре волноводного слоя с симметричными эмиттерными слоями, фактор оптического ограничения для нулевой моды приближенно можно вычислить по формуле:

(3)

Здесь E — амплитуда оптической волны, Emax — ее максимальное значение в середине волноводного слоя, Lact — толщина активного слоя, nact — показатель преломления активного слоя, neff — эффективный показатель преломления для рассматриваемой моды. Индексы «tot» и «act» означают интегрирование по всей структуре или только в пределах активной области соответственно.

По сравнению с традиционными торцевыми лазерами структуры ВИЛ имеют существенные особенности (рис. 1, b):

• использование распределенных брэгговских отражателей (РБО) в качестве верхнего и нижнего зеркал;
• относительно малая длина оптического резонатора (реализуется режим микрорезонатора, соответствующий существенно неоднородному пространственному распределению амплитуды стоячей волны оптического излучения);
• направление распространения световой волны перпендикулярно плоскости активного слоя;
• для ВИЛ на основе КЯ или КТ толщина активного слоя намного меньше длины резонатора.

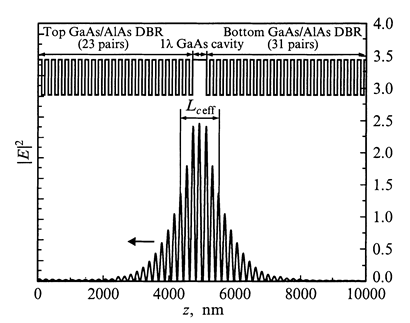
Рисунок 32. Распределение квадрата амплитуды оптического поля |E|2 и профиль показателя преломления для типичной структуры ВИЛ на подложке арсенида галлия.

При записи условия (19) для ВИЛ в первую очередь следует учесть, что оптическая волна проникает в РБО на некоторую глубину, т. е. эффективная длина резонатора Lceff отличается от геометрического расстояния между зеркалами (рис. 32). Кроме того, для тонких активных слоев следует принять во внимание положение активной области относительно пространственного распределения амплитуды стоячей волны оптического поля в микрорезонаторе, для чего вводится фактор стоячей волны . Если активная область толщиной Lact лежит между двумя зеркалами резонатора, то для вычисления фактора стоячей волны можно использовать выражение [4]

, (21)

где = 2neff/c — постоянная распространения для рассматриваемой моды оптического излучения, c —резонансная длина волны, Zs — сдвиг между положением активного слоя и максимумом стоячей волны. Очевидно, что для тонкой активной области (Lact«1) фактор стоячей волны может принимать значения в диапазоне от 0 (Zs = c /4neff) до 2 (Zs = 0). Для приборов с относительно большими латеральными размерами (диаметр оптической апертуры больше 3–5 мкм) xy 1, поскольку можно пренебречь рассеянием световой волны на краях и считать распределение интенсивности излучения по площади прибора однородным. Тогда, с учетом выражения (21), соотношение (19) принимает вид [6]:

(22)

Оценку принципиальной возможности реализации ВИЛ с тем или иным оптическим резонатором можно сделать на основе экспериментальных характеристик для полосковых лазеров с такой же активной областью. Из соотношений (20) и (21) получаем выражение для расчета материального усиления полоскового лазера на пороге генерации:

, (23)

где gmod — измеренное модовое усиление.

Если толщина активного материала ВИЛ по сравнению с полосковым лазером не изменилась, то для оценки принципиальной возможности генерации можно преобразовать соотношение (22). В результате имеем

(24)

Следует отметить, что толщина активного слоя Lact не входит в соотношение (24). Это особенно важно при анализе структур с КТ, где не вполне ясно, что принимать в качестве толщины активной области. Измерив пороговое модовое усиление для полоскового лазера и рассчитав значение K, распределение амплитуды оптического поля и соответствующие коэффициенты отражения верхнего и нижнего зеркал для конкретного резонатора, можно оценить возможность достижения лазерной генерации при определенном уровне внутренних потерь.

Ранее мной было показано, что оптимизация условий МПЭ позволяет формировать структуры с несколькими слоями КТ InAs/InGaAs, имеющие высокую поверхностную плотность массива и проявляющие яркую фотолюминесценцию (ФЛ) в диапазоне длин волн вблизи = 1.3 мкм без увеличения полуширины линии по сравнению со структурами, содержащими только один слой КТ [6]. В полосковых лазерах с такой активной областью достигаются низкопороговая лазерная генерация (<80 А/см2) и высокая выходная мощность в непрерывном режиме (> 2.5 Вт) [13]. Однако для структур на основе КТ InGaAs наблюдается насыщение усиления при увеличении тока инжекции, обусловленное конечным значением поверхностной плотности КТ [7]. Измеренное значение модового оптического усиления для длинноволновых торцевых лазеров на основе КТ InAs/InGaAs составляет 10–12 см1 (рис. 33) при внутренних оптических потерях (1.5 ± 0.3) см1 (лазерные структуры с тремя слоями КТ, Al0.8Ga0.2As-эмиттерами и GaAs-волноводом толщиной 0.4 мкм, при эффективной толщине активного слоя 5 нм имеют z = 0.017 и K = 3.4 · 104см1).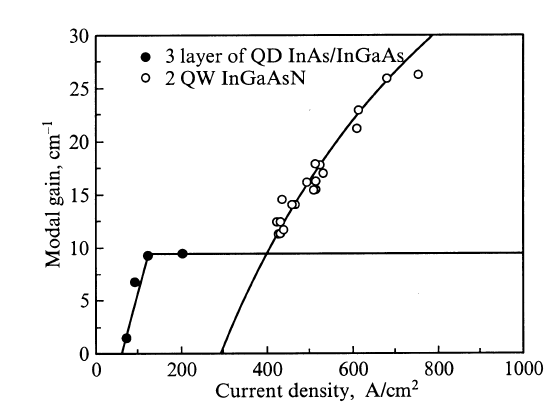

Рисунок 33. Зависимость модового оптического усиления от плотности тока для полосковых лазеров с активной областью на основе 3 слоев квантовых точек (QD) InAs/InGaAs [14] и 2 квантовых ям (QW) InGaAsN [16].

По сравнению со структурами на основе КТ InAs/InGaAs, в структурах с КЯ InGaAsN достигаются большие значения оптического усиления [6] (рис. 33). Зависимость величины модового оптического усиления gmod от плотности тока инжекции J для структур с КЯ можно аппроксимировать выражением:

, (25)

где Jtr — плотность тока прозрачности, g0 — численный параметр.

Для лазерных структур с двумя КЯ InGaAsN (n- и p-эмиттеры Al0.3Ga0.7As, GaAs-волновод толщиной 0.4 мкм, толщина КЯ 6.5 нм, z0.014 и K = 2.15 · 104 см1) измеренные значения составляют g0 = 30 см1 и Jtr = 290 А/см2 при внутренних оптических потерях (7.0 ± 0.5) см1 [16].

Рассмотрим стандартную конструкцию ВИЛ с верхним и нижним РБО AlAs/GaAs и GaAs-резонатором толщиной Lc GaAs = c/nGaAs, точно в центре которого помещен тонкий активный слой (здесь nGaAs —коэффициент преломления GaAs на резонансной длине волны c = 1300 нм). Расчетное распределение квадрата амплитуды оптического поля для такой структуры представлено на рис. 32. При вычислении эффективной длины резонатора воспользуемся приближенным соотношением для глубины проникновения оптического поля в РБО [4]

, (26)

где nhigh, nlow — показатели оптического преломления слоев образующих РБО; hhigh = cnhigh, hlow = c /nlow. В случае РБО AlAs/GaAs (nnigh = nGaAs = 3.44, nlow = nAlAs = 2.91 для c = 1300 нм) эффективная длина резонатора

Lc eff = Lc GaAs +2Lpen = 377,6 + 2 · 617,31600 нм

Используя соотношение (24) и предполагая нулевые внутренние потери, получаем, что в случае активной области на основе трех слоев КТ InAs/InGaAs ( 1.85, максимальное модовое усиление 12 см1 при K = 3.4 · 104 см1) для начала лазерной генерации необходимо иметь R > 0.9994. При величине внутренних потерь 2 см1 требуется уже значение R > 0.9997, что соответствует коэффициентам отражения зеркал (при симметричных верхнем и нижнем РБО) не менее 0.9998. Оценка для активного слоя на основе двух КЯ InGaAsN дает требуемые значения R > 0.994 (нулевые внутренние потери) и R > 0.995 (при внутренних потерях 2 см1). Здесь при расчетах усиления предполагалась пороговая плотность тока 3 кА/см2. Таким образом, более высокое оптическое усиление для структур с КЯ InGaAsN позволяет несколько снизить требования к качеству микрорезонатора. Тем не менее в обоих случаях для получения лазерной генерации требуются очень высокие коэффициенты отражения зеркал.

Возможность использования традиционной конструкции ВИЛ с верхним и нижним контактами к легированным зеркалам n- и p-типа проводимости. Один из основных механизмов потерь для зеркал на основе AlGaAs/GaAs обусловлен поглощением в слоях p-GaAs (как на свободных носителях, так и в результате межподзонных переходов в валентной зоне). Максимально возможный коэффициент отражения РБО можно вычислить по формуле [15]

, (27)

где — коэффициент поглощения на свободных носителях. Расчеты и экспериментальные исследования показывают, что для РБО p-GaAs/p-AlAs при среднем уровне легирования (12) · 1018 см3 максимальный уровень отражения ограничен значением 0.995. Меньшие уровни легирования ведут к резкому возрастанию последовательного сопротивления прибора из-за дополнительного падения напряжения на гетерограницах [4]. Недавние исследования показали, что и для РБО n-AlAs/n-GaAs при уровнях легирования 1018см3 максимальное значение коэффициента отражения не превышает 0.997 [18].

Таким образом, экспериментальная реализация длинноволновых ВИЛ на подложках GaAs в традиционной конструкции представляется проблематичной. Анализ показал, что наиболее оптимальной для реализации длинноволновых ВИЛ на подложках GaAs является конструкция с верхним и нижним нелегированными РБО AlAs/GaAs или AlxOy/GaAs. Зеркала второго типа можно получить селективным оксидированием слоев AlGaAs в атмосфере, насыщенной парами воды [19]. Большое различие в величинах показателей преломления слоев для оксидированных зеркал (nGaAs = 3.44, nAlx Oy = 1.61 для = 1300 нм) обеспечивает широкую спектральную область с высокими значениями коэффициента оптического отражения и в результате снижает чувствительность к погрешностям калибровки. В то же время использование непроводящих зеркал приводит к некоторому усложнению технологии изготовления приборов из-за необходимости формирования p- и n-контактов к легированным слоям, расположенным внутри резонатора, а также из-за возможного возрастания последовательного сопротивления. В своих исследованиях я использовал РБО AlAs/GaAs для приборов с активной областью на основе КЯ InGaAsN и оксидированные зеркала для создания ВИЛ на основе КТ InAs/InGaAs.

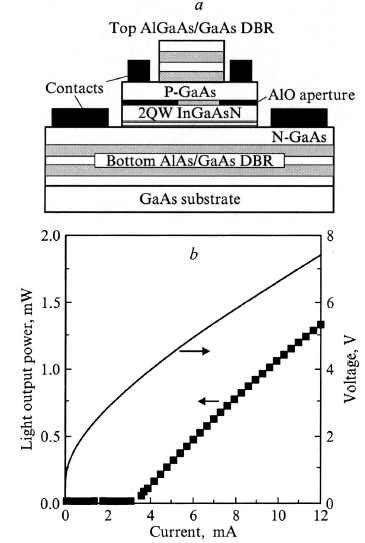
Рисунок 34. Схематическое изображение поперечного сечения (a) и характеристики ВИЛ с активной областью на основе двух квантовых ям (QW) INGaAsN (b), = 1.29 мкм, импульсный режим.

На рис. 34 представлены конструкция и основные характеристики ВИЛ с активной областью на основе двух КЯ InGaAsN. Приборы с размером оксидированной апертуры 3 7 мкм2 имеют пороговый ток 3.3 мА при внешней квантовой эффективности d = 18% (вывод излучения через верхнее зеркало) [4]. Максимальная выходная мощность в непрерывном режиме при температуре 10C превышает 1 мВт, что является лучшим опубликованным результатом для длинноволновых ВИЛ на подложках GaAs.

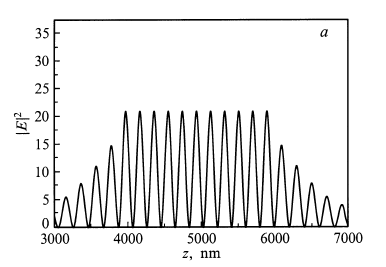
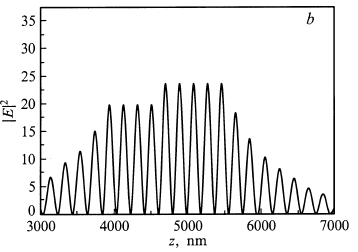
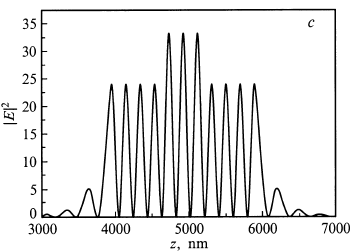
a — РБО AlAs/GaAs, GaAs-резонатор толщиной 5c/nGaAs; b — РБО AlAs/GaAs, GaAs-резонатор толщиной 4c /nGaAs с одной оксидированной апертурой; c — РБО AlGaO/GaAs, GaAs-резонатор толщиной 5c /nGaAs с двумя оксидированными апертурами.

Рисунок 35. Нормированные пространственные распределения квадрата амплитуды оптического поля для трех микрорезонаторов.

При исследовании конструкции оптического резонатора учитывалась необходимость относительно толстого контактного p-слоя из-за сравнительно низкой подвижности дырок в GaAs. Для снижения внутренних оптических потерь, в первую очередь обусловленных поглощением на свободных носителях в p-слое, используется относительно толстый апертурный слой AlGaAs, который позволяет частично перераспределить оптическое поле в резонаторе по сравнению со структурой без апертуры (рис. 35, a и b). При номинальной толщине резонатора Lc GaAs = 4c /nGaAs имеем Lc eff 2750 нм.

Расчетные значения коэффициентов отражения для обоих зеркал на резонансной длине волны составляют 0.9977, что дает оценку потерь на вывод оптического излучения 8 см1. Предполагая, что ток равномерно распределен по сечению активной области (апертуры) и справедливо соотношение (25), получаем, что пороговой плотности тока 15 кА/см2 соответствует модовое оптическое усиление полоскового лазера 140 см1. Из соотношения (24) следует, что условию начала генерации соответствуют внутренние потери 35 см1. Такое значение внутренних потерь при заданном уровне потерь на вывод излучения позволяет оценить величину внутренней квантовой эффективности: i 1. Таким образом, полученные результаты подтверждают высокое качество активного материала и позволяют рассчитывать на существенное улучшение характеристик прибора при дальнейшей оптимизации конструкции микрорезонатора.

Поскольку уровень оптического усиления структур с КТ ограничен, при реализации ВИЛ на основе КТ InAs/InGaAs был изучен оптический микрорезонатор с РБО AlxOy/GaAs, предварительно оптимизированный для снижения оптических потерь. Схематическое изображение сечения и основные характеристики ВИЛ представлены на рис. 36. Для приборов с размером оксидированной апертуры 8 8 мкм2 пороговый ток составляет 1.8 мА при внешней квантовой эффективности 41% (при выводе излучения через верхнее зеркало), что является наилучшими опубликованными значениями для ВИЛ диапазона = 1.3 мкм на подложках GaAs. В непрерывном режиме при комнатной температуре максимальная выходная мощность превышает 0.6 мВт при внешней квантовой эффективности 39%. Пороговые плотности тока ВИЛ превосходят характерные значения, при которых достигается насыщение усиления основного состояния КТ. Возможно, это связано с неоднородным распределением плотности тока по площади апертуры.

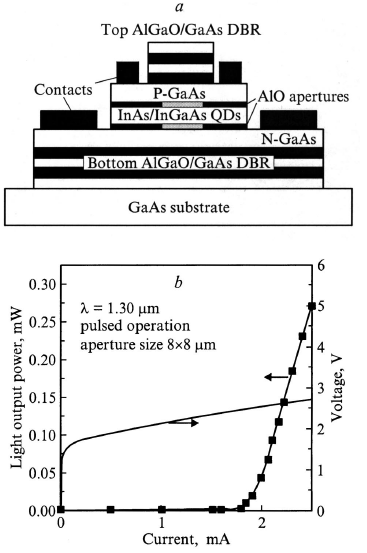
Рисунок 36. Схематическое изображение поперечного сечения (a) и характеристики ВИЛ с активной областью на основе 3 слоев квантовых точек (QD) InAs/InGaAs (b), = 1.30 мкм, импульсный режим.

Две AlxOy-апертуры, полученные частичным оксидированием слоев AlGaAs, обеспечивают не только ограничение тока, но и дополнительное перераспределение оптического поля в резонаторе. По сравнению с полупроводниковыми резонаторами амплитуда оптического поля в активной области существенно возрастает, а глубина проникновения оптического поля в зеркала уменьшается (рис. 35, c). Расчетные значения Lc eff 2300 нм и R = 0.9996 дают потери на вывод оптического излучения 1.5 см1. Используя изложенную выше методику, получил, что уровень внутренних оптических потерь, при которых возможно выполнение условия начала генерации, не должен превышать 1.5 см1. С другой стороны, для оценки внутренних оптических потерь можно воспользоваться соотношениями, связывающими внешнюю и внутреннюю квантовые эффективности ВИЛ с неодинаковыми коэффициентами отражения зеркал [11]:

,

,

Здесь — внешняя квантовая эффективность для излучения, выводимого через верхнее зеркало с коэффициентом отражения R1. Можно показать, что при измеренной внешней квантовой эффективности 41% уровень внутренних оптических потерь в структуре не должен превышать 2.6 см1 (для внутренней квантовой эффективности i = 1) и 1.6 см1 (при величине i = 0.7, характерной для полосковых лазеров с аналогичной активной областью [11]). Таким образом, наблюдается хорошее совпадение значений внутренних оптических потерь, рассчитанных на основе результатов измерений для торцевых лазеров и непосредственно из измеренных характеристик ВИЛ. Достигнутый уровень оптических потерь (i)Lc eff = 0.040.05% на один проход фотона соответствует лучшим опубликованным значениям для ВИЛ всех типов [4]. Следует отметить, что уровень внутренних потерь для ВИЛ диапазона = 1.3 мкм существенно меньше, чем для ВИЛ аналогичной конструкции с активной областью на основе вертикально-связанных КТ InGaAs, излучающего в диапазоне = 1 мкм. В последнем случае потери, измеренные по методике, предложенной в работе, составляют 8 см1. Интересно, что и для полосковых лазеров с КТ InAs/InGaAs закономерно наблюдаются меньшие оптические потери по сравнению с полосковыми лазерами на вертикально -связанных КТ InGaAs.

Обобщая результаты исследования и сравнения ВИЛ на основе КТ InAs/InGaAs и КЯ InGaAsN можно сделать следующие выводы:

• высокий уровень оптического усиления, достигаемый в структурах на основе КЯ InGaAsN, позволяет реализовать ВИЛ на основе полупроводниковых микрорезонаторов с относительно высокими внутренними потерями;
• для реализации ВИЛ на основе массивов КТ целесообразно использовать резонаторы с AlxOy-зеркалами, которые по своим оптическим характеристикам, как правило, существенно превосходят резонаторы с полупроводниковыми зеркалами.

5 Создание приборов на системах с размерным квантованием

Проявление эффектов размерного квантования собственно в электронных приборах наиболее показательно для системы приборов, в которых проявляется эффект одноэлектронного туннелирования в присутствии квантовой точки.

При использовании двух и более переходных систем между двумя электродами находятся малые объекты, которые при определенных условиях (геометрические размеры и температура) могут рассматриваться как квантовые точки, т.е. нульмерные объекты, в которых энергетический спектр представляет собой набор дискретных уровней.

Для полупроводниковых точек необходимая температура будет выше из-за более низкой плотности состояний.

Конструкции одноэлектронных приборов весьма различны, однако их можно классифицировать по нескольким признакам:

- по направлению протекания тока конструкции делятся на горизонтальные (латеральные) и вертикальные. В горизонтальных приборах направление протекания тока параллельно плоскости поверхности структуры, в вертикальных - перпендикулярно к плоскости поверхности.

- по способу формирования квантовых точек бывают приборы на постоянных и временных квантовых точках.

Термин «квантовая точка» по отношению к малому объекту не всегда корректен, так как квантования энергетического спектра может и не наблюдаться. Однако этот термин широко используется в силу того, что для квантования спектра достаточно понизить температуру. В дальнейшем мы будем придерживаться такой терминологии.

Постоянная квантовая точка существует все время и представляет собой чаще всего какой-либо кластер (металлический или полупроводниковый). Временная квантовая точка создается в двумерном электронном газе путем приложения обедняющих напряжений, т. е. существует лишь во время работы прибора. Кроме того, приборы на временных квантовых точках можно разделить по способу формирования двумерного электронного газа на инверсные и гетероструктурные. В инверсных приборах двумерный электронный газ формируется в инверсных приповерхностных каналах путем приложения соответствующего напряжения. В гетероструктурных приборах двумерный электронный газ сосредоточен на гетерогранице.

По количеству квантовых точек приборы делятся на нульмерные (одноточечные), одномерные (цепочка точек) и двумерные (массив точек).

По управляемости параметрами квантовых точек приборы делятся на неуправляемые (двухэлектродные) и управляемые (многоэлектродные, с одним или несколькими затворами).

При рассмотрении общего состояния проблемы по созданию, исследованию и применению квантово-размерных структур в качестве отдельной проблемы следует выделить и особо подчеркнуть, что пути и методы создания таких структур до сих пор являются главным сдерживающим фактором в развитии и широком применении данного приборного направления. Рассмотренные выше технологические подходы хотя и позволяют реализовать электронные наноструктуры, однако не дают возможности надеется на массовое производство поскольку являются уникальными и дорогостоящими. Поиск принципиально новых путей технологической реализации заставляет обратиться к физическим явлениям, интенсивно исследуемым в последнее время и позволяющим надеется на технологический прорыв при их использовании. К таким направлениям следует отнести явления самоорганизации в разупорядоченных твердотельных структурах. Наиболее перспективным ответвлением этого направления является самоорганизация в кристаллах, подвергнутых радиационным воздействиям.

Все квантовые объекты являются гетерофазными, т. е., как правило, имеют разные параметры решетки. Это, в свою очередь, приводит к возникновению деформаций сопряжения. С ними связанные напряжения меняют полную энергию системы. Кроме того, разность параметров решетки влияет на адсорбционные свойства, уже варьирующиеся из-за различных химических потенциалов.

Прогресс в экспериментальном изучении физических свойств квантово-размерных структур тесно связан с развитием технологии их получения и в значительной мере им и определяется. Изготовление квантово-размерных структур в большинстве случаев требует создания полупроводниковых гетеропереходов с необходимыми свойствами. Для этого, прежде всего, необходимо подобрать подходящую пару полупроводниковых материалов. Выбор этих материалов зависит от типа структуры, которую необходимо получить. Для создания структур с двумерным электронным газом на основе гетеропереходов основным условием является требование равенства постоянных решетки у обоих полупроводников. Нарушение этого условия может привести к образованию высокой плотности дислокаций несоответствия вблизи гетерограницы, что резко ухудшает свойства переходов и делает невозможным наблюдение эффектов размерного квантования.

Гетеропереход GaAs-AlxGa1-xAs наиболее часто используют для изготовления квантово-размерных структур. Эти материалы обладают хорошим согласием решеток при любом составе твердого раствора и потому позволяют создавать гетеропереходы с различными разрывами зон на границе. Среди полупроводников класса A3B5 есть еще несколько идеальных гетеропар, например InP-In0.53Ga0.47As, но они обладают согласием решеток лишь при одном фиксированном составе и потому не позволяют варьировать ЕС и ЕV. Другие классы полупроводников реже используются для изготовления квантовых гетероструктур. Одно из главных требований к технологии изготовления квантовых гетероструктур связано с необходимостью получения очень резких гетеропереходов с переходным слоем промежуточного состава, имеющим толщину всего в несколько постоянных решетки. Как видно из рис. 37, для плавного перехода образуется потенциальная яма большой ширины, что уменьшает расстояние между уровнями Еn и затрудняет наблюдение квантовых размерных эффектов.

Рисунок 37. Потенциальный профиль края зоны проводимости для резкого (а) и плавного (б) гетеропереходов.

Другим важным требованием к технологии является возможность получения сложных профилей состава и легирования. При изготовлении сверхрешеток необходимо строго периодически менять состав растущего слоя, причем период изменения может составлять лишь несколько десятков ангстрем. При выращивании -слоев и структур с модулированным легированием необходимо со столь же высокой точностью менять концентрацию легирующих примесей.

Далеко не всякая эпитаксиальная технология удовлетворяет приведенным требованиям. Плохо пригодными, в частности, оказываются наиболее распространенные методики газотранспортной и жидкостной эпитаксии. Получение сложного профиля состава и легирования наталкивается на ряд технических трудностей, а сравнительно высокая температура роста вызывает диффузионное размывание гетерограницы, не позволяя получать очень резкие границы.

В настоящее время наиболее часто для изготовления качественных гетероструктур применяют метод молекулярно лучевой эпитаксии. Другим возможным способом изготовления гетероструктур является газовая эпитаксия из металлоорганических соединений. Она не требует столь сложного и дорогого оборудования, обладает меньшими возможностями контроля и управления, но, тем не менее, позволяет растить гетеропереходы требуемой резкости и структуры достаточно сложного профиля, включая сверхрешетки, квантовые нити и точки.

Получение одно- и нульмерных структур возможно путем выделения их с помощью литографии. Однако это требует применения особых методов литографии – нанолитографии, поскольку столь малые структуры трудно приготовить при помощи стандартных методов.

Значительные успехи были достигнуты в изготовлении квантовых точек и квантовых нитей с использованием эффектов самоорганизации упорядоченных наноструктур на полупроводниковых подложках. Этот метод предъявляет специфические требования к материалам гетеропары[1,3,8].

ЗАКЛЮЧЕНИЕ

В настоящей работе проанализированы особенности создания длинноволновых ВИЛ на подложках GaAs и проведено сравнительное исследование характеристик приборов с активными областями на основе КТ InAs/InGaAs и КЯ InGaAsN. Анализ показывает, что уровень электрических и внутренних оптических потерь для структур второго типа значительно выше, что связано с неоптимальной конструкцией вертикального полупроводникового микрорезонатора. Тем не менее, благодаря высокому оптическому усилению активной области, ВИЛ на основе КЯ InGaAsN имеют рекордную выходную мощность для всех ВИЛ на подложках арсенида галлия (> 1 мВт в непрерывном режиме). Оптимизация конструкции должна существенно улучшить их характеристики. Что касается ВИЛ на основе КТ, для них целесообразно использовать микрорезонаторы с РБО AlxOy/GaAs, которые обеспечивают минимальный уровень внутренних оптических потерь (0.04–0.05% на один проход фотона), низкие пороговые токи (<2 мА) и высокую дифференциальную эффективность ( 40%). Представляется, что ВИЛ на основе КТ будут иметь преимущества при создании приборов с малыми (менее 12 мкм) размерами излучающей области из-за подавления латеральной диффузии носителей.

Обобщая результаты исследования и сравнения ВИЛ на основе КТ InAs/InGaAs и КЯ InGaAsN можно сделать следующие выводы:

• высокий уровень оптического усиления, достигаемый в структурах на основе КЯ InGaAsN, позволяет реализовать ВИЛ на основе полупроводниковых микрорезонаторов с относительно высокими внутренними потерями;
• для реализации ВИЛ на основе массивов КТ целесообразно использовать резонаторы с AlxOy-зеркалами, которые по своим оптическим характеристикам, как правило, существенно превосходят резонаторы с полупроводниковыми зеркалами.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ

1 Гуртов В. А. Оптоэлектроника и волоконная оптика: Учебное пособие. - Петрозаводск: Изд-во ПетрГУ, 2005.

2 Никоноров Н. В. Материалы и технологии волоконной оптики: специальные оптические волокна: Учебное пособие/ Н. В. Никоноров, А.И. Сидоров. СПб.: СПбГУ ИТМО, 2009.

3 Скляров О. К. Современные ВОСП. Аппаратура и элементы. – М.; Солон, 2001.

4 Леденцов H. H. Гетероструктуры с квантовыми точками: получение, свойства, лазеры / H. H. Леденцов, В. М. Устинов, В. А. Щукин и др. ФТП. 1998. - Т.32. -№ 4.

5 Пчеляков О. П. Кремний-германиевые наноструктуры с квантовыми точками: механизмы образования и электрические свойства / О. П. Пчеляков, Ю. Б. Болховитянов, A. B. Двуреченский. ФТП. 2000. - Т. 34.

6 Двуреченский A. B. Квантовые точки в системе Ge/Si, / A. B. Двуреченский, А. И. Якимов Изв. ВУЗов. Материалы электронной техники. 1999. - № 4.

7 Шик А. Я. Физика низкоразмерных систем/ А. Я. Шик, Л. Г. Бакуева, С. Ф. Мусихин, С. А. Рыков. СПб.: Наука, 2001.

8 Гусев А. И. Наноматериалы, наноструктуры, нанотехнологии. М.: Физматлит, 2005.

9 Оптика наноструктур/ Под ред. А. В. Федорова. Спб.: Недра, 2005.

10 Воробьев Л. Е. Оптические явления в полупроводниковых квантово-размерных структурах/ Л. Е. Воробьев, Л. Г. Голуб, С. Н. Данилов и др. Спб.: Изд-во СПбГТУ, 2000.

11 Гайнутдинов И. С. Свойства и методы получения интерференционных покрытий для оптического приборостроения/ И. С. Гайнутдинов, Е. А. Несмелов, А. В. Михайлов, В. П. Иванов, Г. И. Абзалова. Казань: Фэн, 2003.

12 Федоров А. В. Физика и технология гетероструктур, оптика квантовых наноструктур: Учебное пособие. Спб.: Изд-во ИТМО, 2009.

13 Щука А. А. Наноэлектроника. М.:Физматкнига, 2007. 

14. Носов Ю. Р. Оптоэлектроника. М.: Радио и связь, 1989.

15 Ильин В. И. Варизонные полупроводники и гетероструктуры. В. И. Ильин, С. Ф. Мусихин, А.Я. Шик. Спб.: Наука, 2000.

16 Бонч-Бруевич В. Л. Физика полупроводников, В. Л. Бонч-Бруевич, С.Г. Калашников. Спб.: Изд-во ИТМО, 2000.

17 Кардон М. Основы физики полупроводников / Пер. с англ. И.И. Решиной. Под ред. Б.П. Захарчени. 3-е изд. М.: ФИЗМАТЛИТ, 2002.

18 Милнс А. Гетеропереходы металл – полупроводник / А. Милнс, Д. Фойхт; пер. с англ. Л.В. Шаронова. M.: Мир, 1975.

19 Шарма Б. Л. Полупроводниковые гетеропереходы/ Б. Л. Шарма, P. К. Пурохит; пер. с англ. Ж. И. Алферов, С. А. Гуревич. М.: Mир, 1979.

Исследование квантово-размерных структур