Определения теории графов

Содержание:

1. Введение
2. Теория. Основные понятия
3. Постановка задачи
4. Реализация
5. Тестовый пример

Введение

Бурное развитие дискретной математики обусловлено прогрессом компьютерной техники, необходимостью создания средств обработки и передачи информации, а также представления различных моделей на компьютерах, являющихся по своей природе конечными структурами.

Нахождение кратчайшего пути на сегодняшний день является жизненно необходимой задачей и используется практически везде, начиная от нахождения оптимального маршрута между двумя объектами на местности (например, кратчайший путь от дома до университета), в системах автопилота, для нахождения оптимального маршрута при перевозках, коммутации информационного пакета в сетях и т.п.

Кратчайший путь рассматривается при помощи некоторого математического объекта, называемого графом. Поиск кратчайшего пути ведется между двумя заданными вершинами в графе. Результатом является путь, то есть последовательность вершин и ребер ,инцидентных двум соседним вершинам, и его длина.

Теория и основные понятия

Первая работа по теории графов принадлежит Леонарду Эйлеру (1736 год), хотя термин «граф» впервые ввел в 1936 году венгерский математик Денеш Кениг. Графами были названы схемы, состоящие из точек и соединяющих эти точки отрезков прямых или кривых.

С помощью графов часто упрощалось решение задач, сформулированных в различных областях знаний: в автоматике, электронике, физике, химии и др. С помощью графов изображаются схемы дорог, газопроводов, тепло- и электросети. Помогают графы в решении математических и экономических задач.

Определения теории графов

Простым графом G называется пара (V, E), где V - непустое конечное множество, элементы которого называются вершинами графа, а E - конечное множество неупорядоченных пар различных элементов из V, элементы множества E называются ребрами.

В дальнейшем будем рассматривать только простые графы, опуская при этом слово простые.

Если (u,v) - некоторое ребро графа G, то вершины u и v называются смежными, а вершины u и ребро (u,v), также как вершина v и ребро (u,v), называютсяинцидентными друг другу. Степенью вершины v в графе G называется число ребер графа G, инцидентных вершине v.

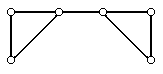
Пример графа

В данном примере
V = {v1, v2, v3, v4, v5, v6},
E = {(v1, v2), (v2, v3), (v1, v3), (v3, v4), (v4, v5), (v4, v6), (v5, v6)}

Пусть G = (V, E) - некоторый граф, u и v - его вершины. Маршрутом в графе G, соединяющим вершины  u и v, называется конечная чередующаяся последовательность вершин и ребер вида v1, e1, v2, e2,...,ek-1, vk, где v1,...,vk из V, а e1,...,ek-1 из E. Маршрут называют цепью, если все его ребра различны. Цепь называют путем (или простой цепью), если все ее вершины кроме, быть может, концевых различны. Если начальная и конечная вершина пути совпадают, то его называют замкнутым путем или циклом.

Граф называется связным графом, если для любых двух его вершин существует соединяющий их маршрут.

Теперь мы можем определить особый класс графов - деревья. Деревом называется связный граф без циклов.

Ориентированным графом D называется пара (V, A), где V - непустое конечное множество, элементы которого называются вершинами графа, а A - конечное множество упорядоченных пар различных элементов из V, элементы множества A называются дугами.

Подобно графам для ориентированных графов вводятся понятие смежности вершин, понятие инцидентности и так далее.

Основанием ориентированного графа D = (V, A), называется граф G = (V, E), где E = A, то есть упорядоченные пары вершин заменяются на неупорядоченнные.

^ Транспортной сетью называется конечный Связный орграф G(V, E) без петель, каждой дуге которого поставлено в соответствие некоторое неотрицательное число c(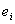), называемое пропускной способностью дуги, и существует:

1)   ровно одна вершина 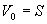, в которую не заходит ни одна дуга, называемая источником или началом сети;

2)   ровно одна вершина 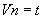, из которой не выходит ни одной дуги; эта вершина называется стоком или концом сети.

^ Потоком сети называется неотрицательная функция f(1) такая, что f(e) меньше или равно c(e). (Поток не может превышать пропускную способность дуги.)

Дуга 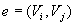называется насыщенной потоком f, если 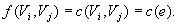(Поток называется полным, если содержит насыщенную дугу f(e)=c(e).)

     Разрезом L сети G(V,E) называется множество насыщенных дуг, отделяющих источник s от стока t.

Алгоритм Дейкстры

Данный алгоритм является алгоритмом на графах, который изобретен нидерландским ученым Э. Дейкстрой в 1959 году. Алгоритмнаходит кратчайшее расстояние от одной из вершин графа до всех остальных и работает только для графов без ребер отрицательного веса.

Каждой вершине приписывается вес – это вес пути от начальной вершины до данной. Также каждая вершина может быть выделена. Если вершина выделена, то путь от нее до начальной вершины кратчайший, если нет – то временный. Обходя граф, алгоритм считает для каждой вершины маршрут, и, если он оказывается кратчайшим, выделяет вершину. Весом данной вершины становитсявес пути. Для всех соседей данной вершины алгоритм также рассчитывает вес, при этом ни при каких условиях не выделяя их.Алгоритм заканчивает свою работу, дойдя до конечной вершины, и весом кратчайшего пути становится вес конечной вершины.

Алгоритм Дейкстры

Шаг 1. Всем вершинам, за исключением первой, присваивается вес равный бесконечности, а первой вершине – 0.

Шаг 2. Все вершины не выделены.

Шаг 3. Первая вершина объявляется текущей.

Шаг 4. Вес всех невыделенных вершин пересчитывается по формуле: вес невыделенной вершины есть минимальное число из старого веса данной вершины, суммы веса текущей вершины и веса ребра, соединяющего текущую вершину с невыделенной.

Шаг 5. Среди невыделенных вершин ищется вершина с минимальным весом. Если таковая не найдена, то есть вес всех вершин равен бесконечности, то маршрут не существует. Следовательно, выход. Иначе, текущей становится найденная вершина. Она же выделяется.

Шаг 6. Если текущей вершиной оказывается конечная, то путь найден, и его вес есть вес конечной вершины.

Шаг 7. Переход на шаг 4.

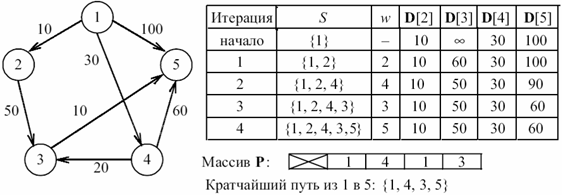
В программной реализации алгоритма Дейкстры построим множество S вершин, для которых кратчайшие пути от начальной вершины уже известны. На каждом шаге к множеству S добавляется та из оставшихся вершин, расстояние до которой от начальной вершины меньше, чем для других оставшихся вершин. При этом будем использовать массив D, в который записываются длины кратчайших путей для каждой вершины. Когда множество S будет содержать все вершины графа, тогда массив D будет содержать длины кратчайших путей от начальной вершины к каждой вершине.

Помимо указанных массивов будем использовать матрицу длин C, где элемент C[i,j] –длина ребра (i,j), если ребра нет, то ее длина полагается равной бесконечности, то есть больше любой фактической длины ребер. Фактически матрица C представляет собой матрицу смежности, в которой все нулевые элементы заменены на бесконечность.

Для определения самого кратчайшего пути введем массив P вершин, где P[v] будет содержать вершину, непосредственно предшествующую вершине v в кратчайшем пути .

Постановка задачи

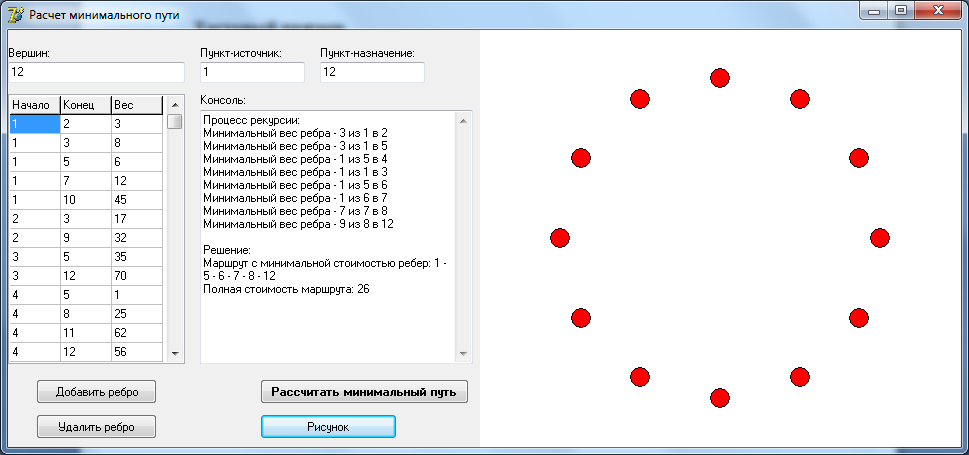
Основной задачей моей курсовой является запрограммировать алгоритм, Дейкстры, по решению задачи о нахождение кратчайшего пути в сети. Для написания программы мною был выбран язык программирования Delphi.

Реализация

Программа написана на языке Delphi и откомпилирована в Borland Delphi7.

unit Unit1;

interface

uses

Windows, SysUtils, Classes, Graphics, Controls, Forms, StdCtrls, Grids, Types,

ExtCtrls, XPMan;

type

TForm1 = class(TForm)

cmdAdd: TButton;

cmdComp: TButton;

cmdDel: TButton;

Grid: TStringGrid;

Label1: TLabel;

Memo1: TMemo;

txtDest: TLabeledEdit;

txtSrc: TLabeledEdit;

txtVertex: TLabeledEdit;

Image1: TImage;

Button1: TButton;

procedure cmdAddClick(Sender: TObject);

procedure cmdCompClick(Sender: TObject);

procedure cmdDelClick(Sender: TObject);

procedure FormCreate(Sender: TObject);

procedure txtDestChange(Sender: TObject);

procedure txtHandlerKeyPress(Sender: TObject; var Key: Char);

procedure txtSrcChange(Sender: TObject);

procedure txtVertexChange(Sender: TObject);

procedure Button1Click(Sender: TObject);

end;

THackGrid = class(TStringGrid);

var

Form1: TForm1;

type TElement = record

_start, _end, _weight, _initial:Integer;

_checked:boolean;

end;

TVertex = record

_vertex:integer;

_data:integer;

end;

TVertexArray = array of TVertex;

implementation

uses Math;

{$R *.dfm}

var VertexCount:Integer = 12;

VertexSrc:Integer = 1;

VertexDest:Integer = 12;

const EdgesCount = 25;

Edges:array[1..EdgesCount, 1..3] of Integer =

(( 1, 2, 3), (1, 3, 8), (1, 5, 6), (1, 7, 12), (1, 10, 45), ( 2, 3, 17),

( 2, 9, 32), (3, 5, 35), (3, 12, 70), (4, 5, 1), (4, 8, 25), ( 4, 11, 62),

( 4, 12, 56), (5, 6, 3), (5, 11, 90), (6, 7, 1), (6, 9, 21), ( 7, 8, 7),

( 7, 11, 64), (8, 12, 9), (9, 10, 1), (9, 11, 8), (9, 12, 3), (10, 11, 14),

(11, 12, 23));

function InArr(const Arr:TVertexArray; const Num:Integer):Boolean;

var I:Integer;

begin

Result:=False;

for I:=0 to High(Arr) do

if Arr[I]._vertex = Num then

begin

Result:=True;

Exit;

end;

procedure TForm1.cmdAddClick(Sender: TObject);

var I:Integer;

begin

Grid.RowCount:=Grid.RowCount + 1;

for I:=0 to 2 do Grid.Cells[I, Grid.RowCount - 1]:='0';

end;

procedure TForm1.FormCreate(Sender: TObject);

var I, J:Integer;

begin

txtVertex.OnKeyPress:=txtHandlerKeyPress;

txtSrc.OnKeyPress:=txtHandlerKeyPress;

txtDest.OnKeyPress:=txtHandlerKeyPress;

Grid.RowCount:=EdgesCount + 1;

txtVertex.Text:=IntToStr(VertexCount);

txtSrc.Text:=IntToStr(VertexSrc);

txtDest.Text:=IntToStr(VertexDest);

Grid.Cells[0, 0]:='Начало';

Grid.Cells[1, 0]:='Конец';

Grid.Cells[2, 0]:='Вес';

for I:=1 to EdgesCount do

for J:=1 to 3 do Grid.Cells[J-1, I]:=IntToStr(Edges[I, J]);

end;

procedure TForm1.cmdCompClick(Sender: TObject);

var I, _from, _to:Integer;

Vertex, VertArr:TVertexArray;

Bool:Boolean;

Massiv:array of TElement;

procedure Process;

var I, Min, MinPos:Integer;

begin

if InArr(VertArr, VertexDest) then Exit;

Min:=MaxInt;

// ищем ребро с минимальным весом в оба направления

for I:=0 to High(Massiv) do

if (Massiv[I]._weight < Min) and not (Massiv[I]._checked) then

begin

if InArr(VertArr, Massiv[I]._start) and (Vertex[Massiv[I]._end - 1]._vertex = -1) then

begin

Min:=Massiv[I]._weight;

MinPos:=I;

Bool:=False;

end

else if InArr(VertArr, Massiv[I]._end) and (Vertex[Massiv[I]._start - 1]._vertex = -1) then

begin

Min:=Massiv[I]._weight;

MinPos:=I;

Bool:=True;

end;

// -------------------------

if not Bool then

begin

_from:=Massiv[MinPos]._start;

_to:=Massiv[MinPos]._end;

end

else

begin

_to:=Massiv[MinPos]._start;

_from:=Massiv[MinPos]._end;

end;

Memo1.Lines.Add('Нашли минимальный вес ребра - ' + IntToStr(Min) + ' из ' + IntToStr(_from) + ' в ' + IntToStr(_to));

// вычитаем из стоимости всех проверенных ребер стоимость наименьшего

for I:=0 to High(Massiv) do

if (not Massiv[I]._checked) and (InArr(VertArr, Massiv[I]._start) or InArr(VertArr, Massiv[I]._end)) then

begin

Massiv[I]._weight:=Massiv[I]._weight - Min;

if Massiv[I]._weight = 0 then

begin

Vertex[_to - 1]._vertex:=_from;

Vertex[_to - 1]._data:=Massiv[MinPos]._initial;

end;

// ------------------------------------

// заносим в список вершин очередную, к которой ведет ребро с минимальным весои

SetLength(VertArr, Length(VertArr) + 1);

if not Bool then VertArr[High(VertArr)]._vertex:=Massiv[MinPos]._end

else VertArr[High(VertArr)]._vertex:=Massiv[MinPos]._start;

// и отмечаем ребро с мин. стоимостью

Massiv[MinPos]._checked:=True;

Application.ProcessMessages;

// звем рекурсию для добавленной в список вершины

Process;

end;

var Res:string;

Sum:Integer;

begin

if VertexSrc = VertexDest then

begin

MessageBox(Handle, 'Исходный и конечный пункты совпадают', '', MB_ICONEXCLAMATION);

Exit;

end;

if (VertexCount < VertexSrc) or (VertexCount < VertexDest) then

begin

MessageBox(Handle, 'Неверное значение источника или назначения', '', MB_ICONEXCLAMATION);

Exit;

end;

Memo1.Clear;

SetLength(Massiv, Grid.RowCount - 1);

for I:=0 to High(Massiv) do

begin

Massiv[I]._start:=StrToInt(Grid.Cells[0, I+1]);

Massiv[I]._end:=StrToInt(Grid.Cells[1, I+1]);

Massiv[I]._weight:=StrToInt(Grid.Cells[2, I+1]);

Massiv[I]._initial:=Massiv[I]._weight;

Massiv[I]._checked:=False;

end;

SetLength(Vertex, VertexCount);

for I:=0 to High(Vertex) do Vertex[I]._vertex:=-1;

Vertex[VertexSrc-1]._vertex:=0;

SetLength(VertArr, 1);

VertArr[0]._vertex:=VertexSrc; // задаем начальный узел

Memo1.Lines.Add('Процесс рекурсии:');

Process;

I:=VertexDest - 1; // считаем стоимость маршрута

Res:=IntToStr(VertexDest);

Sum:=0;

while Vertex[I]._vertex > 0 do

begin

Res:=IntToStr(Vertex[I]._vertex) + ' - ' + Res;

Sum:=Sum + Vertex[I]._data;

I:=Vertex[I]._vertex - 1;

end; // ---------------

Memo1.Lines.Add(#13#10 + 'Решение:' +

#13#10 + 'Маршрут с минимальной стоимостью ребер: ' + Res +

#13#10 + 'Полная стоимость маршрута: ' + IntToStr(Sum));

end;

procedure TForm1.cmdDelClick(Sender: TObject);

var I:Integer;

begin

THackGrid(Grid).DeleteRow(Grid.Selection.Top);

if Grid.RowCount = 1 then

begin

Grid.RowCount:=2;

Grid.FixedRows:=1;

for I:=0 to 2 do Grid.Cells[I, Grid.RowCount - 1]:='0';

end;

procedure TForm1.txtVertexChange(Sender: TObject);

begin

TryStrToInt(txtVertex.Text, VertexCount);

end;

procedure TForm1.txtSrcChange(Sender: TObject);

begin

TryStrToInt(txtSrc.Text, VertexSrc);

end;

procedure TForm1.txtDestChange(Sender: TObject);

begin

TryStrToInt(txtDest.Text, VertexDest);

end;

procedure TForm1.txtHandlerKeyPress(Sender: TObject; var Key: Char);

begin

if not ((Key in ['0'..'9']) or (Key = #8)) then

begin

Key:=#0;

Beep;

end;

procedure TForm1.Button1Click(Sender: TObject);

var

cntrx,cntry : integer;

R,rm : integer;

n,m,i : integer;

x,y : integer;

begin

Image1.Canvas.Brush.color := clWhite;

Image1.Canvas.FillRect(Canvas.ClipRect);

cntrx := round(Image1.Width/2);

cntry := round(Image1.Height/2);

R := round(cntrx/1.5);

rm := 10;

for i:=1 to VertexCount do

begin

Image1.Canvas.Brush.color := clRed;

x := round(cntrx+R*cos(i*2*pi/VertexCount));

y := round(cntry+R*sin(i*2*pi/VertexCount));

Image1.Canvas.Ellipse(x-rm,y-rm,x+rm,y+rm);

end;

end.

Тестовый пример

Определения теории графов