ГАЗООБМЕН ПОМЕЩЕНИИ И ТЕПЛОФИЗИЧЕСКИЕ ФУНКЦИИ, НЕОБХОДИМЫЕ ДЛЯ ОПИСАНИЯ ЗАМКНУТОГО ПОЖАРА
ЛЕКЦИЯ
по дисциплине "Прогнозирование опасных факторов пожара"
Тема №3. «ГАЗООБМЕН ПОМЕЩЕНИИ И ТЕПЛОФИЗИЧЕСКИЕ ФУНКЦИИ, НЕОБХОДИМЫЕ ДЛЯ ОПИСАНИЯ
ЗАМКНУТОГО ПОЖАРА»
План лекции:
Лекция 1,2. ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ ИНТЕГРАЛЬНОЙ МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПОЖАРА ДЛЯ РАСЧЕТА РАСХОДОВ УХОДЯЩИХ ГАЗОВ И ПОСТУПАЮЩЕГО ЧЕРЕЗ ПРОЕМЫ ВОЗДУХА
1.1. Введение
1.2. Распределение давлений по высоте помещения
1.3 Плоскость равных давлений и режимы работы проема
1.4. Распределение перепадов давлений по высоте помещения
1.5. Формулы для расчета расхода газа, выбрасываемого через прямоугольный проем
1.6. Формулы для расчета расхода воздуха, поступающего через прямоугольный проем
1.7. Влияние ветра на газообмен
Лекция 3,4. УРАВНЕНИЯ ИНТЕГРАЛЬНОЙ МОДЕЛИ ПОЖАРА ДЛЯ РАСЧЕТА ТЕПЛОВОГО ПОТОКА В ОГРАЖДЕНИЯ И СКОРОСТИ ВЫГОРАНИЯ ГОРЮЧИХ МАТЕРИАЛОВ
2.1 Приближенная оценка величины теплового потока в ограждения
2.2 Эмпирические методы расчета теплового потока в ограждения
2.3 Полуэмпирические методы расчета теплового потока в ограждения
2.4 Методы расчета скорости выгорания горючих материалов и скорости тепловыделения
Цели лекции:
- Учебные
В результате прослушивания материала слушатели должны знать:
- интегральные уравнения для расчета параметров газообмена
- уравнения интегральной модели для определения тепловых потоков к конструкциям помещения при пожаре
- влияний внешних условий на тепло и газообмен при пожаре
Уметь: прогнозировать обстановку на пожаре с учетом теплогазообмена
- Развивающие: выделять самое главное, самостоятельность и гибкости мышления, развитие познавательного мышления.
Литература
- Д.М. Рожков Прогнозирование опасных факторов пожара в помещении. – Иркутск 2007. С.89
- Ю.А.Кошмаров, М.П. Башкирцев Термодинамика и теплопередача в пожарном деле. ВИПТШ МВД СССР, М., 1987 г.
- Ю.А.Кошмаров Прогнозирование опасных факторов пожара в помещении. – Москва 2000. С.118
- Ю.А.Кошмаров, В.В. Рубцов, Процессы нарастания опасных факторов пожара в производственных помещениях и расчет критической продолжительности пожара. МИПБ МВД России, М., 1999 г.
1. ДОПОЛНИТЕЛЬНЫЕ УРАВНЕНИЯ ИНТЕГРАЛЬНОЙ
МАТЕМАТИЧЕСКОЙ МОДЕЛИ ПОЖАРА ДЛЯ РАСЧЕТА
РАСХОДОВ УХОДЯЩИХ ГАЗОВ И ПОСТУПАЮЩЕГО
ЧЕРЕЗ ПРОЕМЫ ВОЗДУХА
1.1. Введение
При пожаре происходит газообмен помещения с окружающей средой через проемы различного назначения (окна, двери, технологические отверстия и т.д.).
Побудителем движения газа через проемы является перепад давлений, т.е. разность между давлением внутри помещения и давлением в окружающей атмосфере. Перепад давлений обусловлен тем, что при пожаре плотность газовой среды внутри помещения существенно отличается от плотности наружного воздуха. Кроме того, необходимо учитывать влияние ветра на величину этого перепада. Дело в том, что наружное давление на наветренной стороне здания выше, чем наружное давление на подветренной стороне. Рассмотрим условия, когда ветер отсутствует.
1.2. Распределение давлений по высоте помещения
Чтобы определить перепады давлений в проеме, прежде всего необходимо установить законы распределения давлений по вертикали (по высоте) снаружи и внутри помещения. Будем использовать в математических выкладках обозначения, которые указаны на рис. 1.
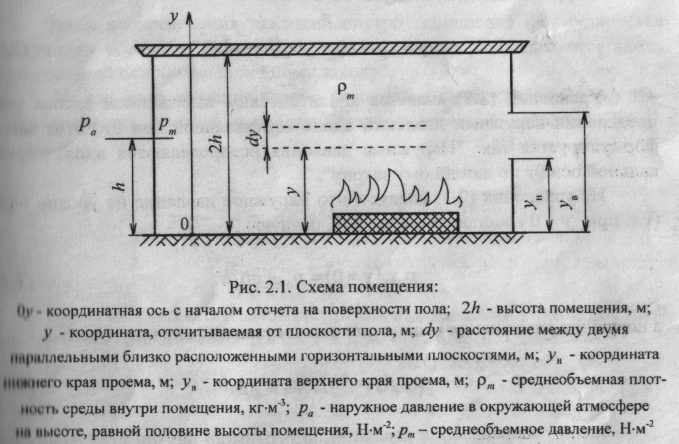
Отметим, что во всех точках снаружи помещения, т.е. в области 0 < у < 2h, плотность наружного воздуха практически одинакова и равна а. Изменение давления с высотой в наружном воздухе описывается дифференциальным уравнением гидростатики, которое при указанном условии имеет следующий вид:
(3.1)
где g - ускорение свободного падения, мс-2; рнар - абсолютное давление во внешней атмосфере, Нм-2. Обозначим давление снаружи на высоте, равной половине высоты помещения (т.е. при у = h), символом ра.
Для того чтобы установить закон распределения давлений снаружи помещения, проинтегрируем дифференциальное уравнение (3.1). При этом правую часть этого уравнения проинтегрируем в пределах от у = h до текущего значения координаты у, а левую часть соответственно в пределах от ра до рнар. В результате интегрирования получим следующее уравнение:
(3.2)
Из уравнения (3.2) следует
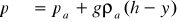(3.3)
Уравнение (3.3) является аналитическим выражением закона распределения наружных давлений вдоль вертикальной оси 0у. Этот закон формулируется так: "Наружные давления распределяются вдоль вертикальной оси 0у по линейному закону".
Из уравнения (3.3) следует, что наружное давление на уровне пола (т.е. при у = О) составляет величину, равную
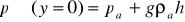(3.4)
а наружное давление на уровне потолка составляет величину, равную:
(3.5)
Закон распределения давлений по вертикали внутри помещения устанавливается аналогичным образом. При этом делается одно допущение. Суть его в том, что плотность газовой среды в помещении во всех точках т.е. в области 0 < у < 2h, принимается одинаковой и равной среднеобъемному значению m. Изменение давления с высотой внутри помещения описывается дифференциальным уравнением гидростатики, которое с учетом указанного допущения имеет следующий вид:
(3.6)
где рвн - давление внутри помещения, Нм2; m - среднеобъемная плотность газовой среды в помещении, кгм-3.
Для того чтобы установить закон распределения давлений вдоль оси Оу внутри помещения, проинтегрируем уравнение (3.6). При этом правую часть этого уравнения проинтегрируем в пределах от y = h до текущего значения координаты у, а левую часть соответственно в пределах от рвн(h) до рвн, где рвн(h) - давление внутри помещения на высоте у = h. В результате получим следующее аналитическое выражение закона распределения давлений внутри помещения:
(3.7)
Закон распределения давлений внутри помещения формулируется следующим образом: "Давление внутри помещения распределяется вдоль вертикальной оси Оу по линейному закону".
Так как распределение внутри помещения является линейным, давление на высоте у = h равно среднеобъемному значению давлений. Действительно:
где V = Fnoл 2h; dV = Fnoлdy; Fпол - площадь пола.
С учетом сказанного закон распределения давлений внутри помещения окончательно записывается следующим образом:
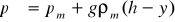(3.8)
1.3 Плоскость равных давлений и режимы работы проема
Установленные законы распределения давлений внутри и снаружи помещения позволяют найти положение горизонтальной плоскости, на которой наружное давление равно давлению внутри помещения. Эту плоскость называют плоскостью равных давлений (ПРД). Положение этой плоскости определяется координатой, которую обозначают символом у*,
Чтобы найти значение координаты ПРД, воспользуемся уравнениями (3.3) и (3.8). Обозначив в этих уравнениях значение координаты равным у*, и приравняв правые части этих уравнений, получим следующее выражение:
(3.9)
После несложных преобразований из уравнения (3.9) получается следующая формула для определения координаты ПРД:
(3.10)
Из формулы (3.10) следует, что положение ПРД зависит от параметров состояния газовой среды в помещении. В процессе развития пожара параметры состояния среды внутри помещения изменяются. Следовательно, в процессе развития пожара изменяется положение ПРД, т.е. изменяется значение координаты у*.
В зависимости от расположения проемов относительно ПРД возможны три разных режима "работы" этих проемов. Если проем целиком расположен выше ПРД, то через этот проем будут только выбрасываться газы из помещения. Этот режим называется режимом "выталкивания". Если проем целиком расположен ниже ПРД, то через этот проем будет только поступать воздух из окружающей среды. Этот режим называется режимом "всасывания" воздуха. Наконец, если ПРД проходит через проем, разделяя его на две части, то в этом случае через верхнюю часть проема выталкиваются газы из помещения, а через нижнюю часть всасывается свежий воздух. Этот режим называется "смешанным". В процессе развития пожара может происходить смена режимов работы всех проемов, так как положение ПРД в течение времени изменяется.
Вышесказанное можно пояснить с помощью рис. 2.2. На этом рисунке дана схема помещения с тремя проемами, расположенными в трех уровнях. Рядом со схемой помещения представлена эпюра давлений, которая соответствует условиям в некоторый момент процесса развития пожара. Распределения давлений внутри и снаружи помещения изображаются отрезками прямых линий в соответствии с вышеустановленными законами (3.3) и (3.8). Угол наклона линии, изображающей распределение наружных давлений, больше, чем угол наклона линии, изображающей распределение давлений внутри помещения, потому что при пожаре плотность среды внутри помещения меньше плотности наружного воздуха, т.е. т < а. В точке, где эти линии пересекаются, расположена ПРД. Этому расположению ПРД соответствует координата у*. На всех уровнях, расположенных выше ПРД, внутреннее давление больше наружного. Разность этих давлений на эпюре изображена стрелками, направленными "из помещения". На всех уровнях, расположенных ниже ПРД, внутреннее давление меньше наружного. Разность этих давлений изображена на эпюре стрелками, направленными "в помещение".
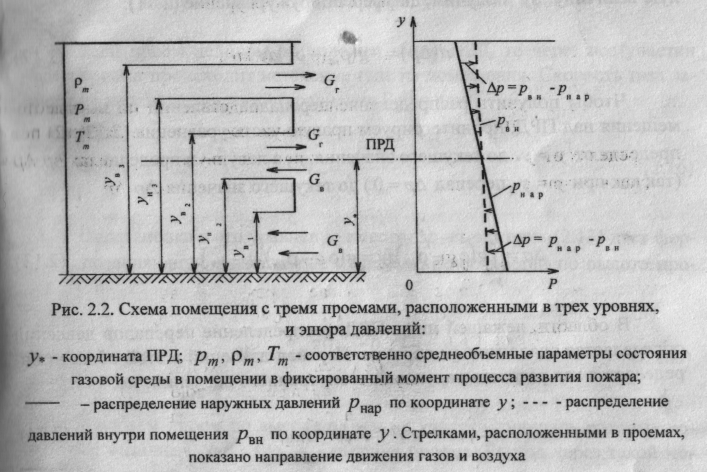
При указанном на рис. 2 расположении ПРД через весь проем, находящийся выше ПРД, будет иметь место только выброс газов из помещения. В то же время через проем, целиком расположенный ниже ПРД, будет иметь место только поступление свежего воздуха в помещение. Средний проем при этом будет работать в смешанном режиме.
1.4. Распределение перепадов давлений по высоте помещения
Разность между наружным и внутренним давлениями на разной высоте может быть различна. Другими словами, перепад давлений изменяется с высотой. Установление перепадов (разности) давлений по высоте помещения относительно ПРД необходимо для определения основных параметров газообмена, осуществляемого через наружные проемы.
Рассмотрим сначала область, лежащую выше ПРД. На высоте, соответствующей координате у (см. рис. 2), разность давлений определим с помощью уравнений (3.3) и (3.8). Из этих уравнений следует:
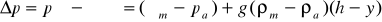(3.11)
где р - перепад давлений в области у > у*
Изменение этой разности давлений при увеличении высоты на малую величину dy получим, дифференцируя уравнение (3.11):
(3.12)
Чтобы получить распределение перепадов давлений по высоте помещения над ПРД, проинтегрируем правую часть уравнения (3.12) по у в пределах от у = у* до текущего значения у, а левую - в пределах от р = 0 (так как при у = у* перепад р = 0) до текущего значения р:
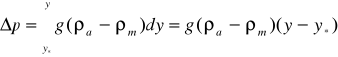(3.13)
В области, лежащей ниже ПРД, распределение перепадов давлений определяется аналогичным образом. Перепад давлений в этой области определяется как разность наружного и внутреннего давлений, т.е.:
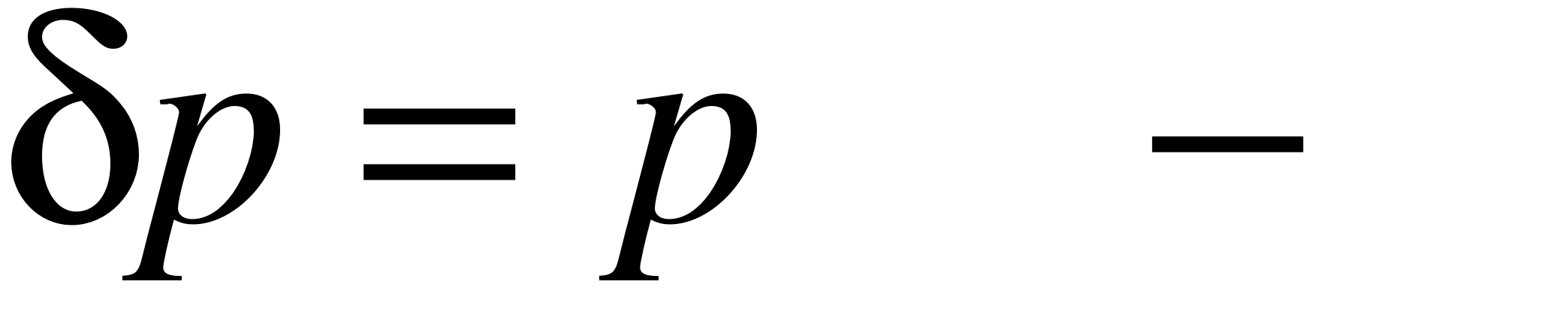(3.14)
где р - перепад давлений в области у< у*.
После математических операций, аналогичных использованным выше, получается следующая формула, описывающая распределение перепадов давлений по высоте помещения под ПРД (т.е. в области у< у*):
(3.15)
Знак "минус" перед правой частью в уравнении (3.15) означает, что перепад давлений р действует в направлении, противоположном перепаду давлений р.
Абсолютное значение перепада давлений ниже ПРД определяется по формуле:
(3.15а)
1.5 Формулы для расчета расхода газа, выбрасываемого через прямоугольный проем
Если проем целиком расположен выше ПРД, то через все участки этого проема происходит истечение газа из помещения. Скорость газа зависит от перепада давлений (уравнение Бернулли):
(3.16)
Подстановка в это уравнение вместо р выражения (3.13) дает формулу, позволяющую рассчитать распределение скоростей по высоте проема:
(3.16а)
Разобьем проем по высоте на малые участки, площадь которых составляет величину bdy, где b - ширина проема. Расход через такой малый участок проема равен произведению площади этого участка проема на скорость истечения и на плотность истекающего газа:
(3.17)
Расход газа через весь проем получим, интегрируя правую часть уравнения (3.17) по высоте проема:
(3.18)
где ун - координата нижнего края проема, м; ув - координата верхнего края проема, м.
После подстановки в уравнение (3.18) выражения (3.16а) получим следующий результат:
(3.19)
В результате после интегрирования получается следующая формула для расчета расхода газа через проем при условии, когда ун > у*:
(3.20)
В том случае, когда плоскость равных давлений пересекает проем и распределяет его на две части, количество газа, выбрасываемого из проема, вычисляется также путем интегрирования выражения (3.17). Однако в этом случае интегрирование правой части уравнения (3.17) производится в пределах от у* до ув:
(3.21)
Формула для расчета расхода уходящих газов через проем при смешанном режиме его работы, которая получается после интегрирования, имеет следующий вид:
(3.22)
1.6 Формулы для расчета расхода воздуха, поступающего через прямоугольный проем
Если проем целиком расположен ниже ПРД, то через все участки такого проема происходит поступление свежего воздуха в помещение. Скорость втекающего воздуха зависит от перепада давлений:
(3.23)
Подстановка вместо р выражения (3.15а) дала формулу, позволяющую рассчитать распределение скоростей воздуха по высоте проема. Расход воздуха через малый участок проема, площадь которого равна (bdy), составляет величину
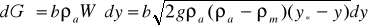(3.24)
Расход воздуха через весь проем, который лежит ниже ПРД, вычисляется путем интегрирования правой части уравнения (3.24) в пределах от у = ув до у = ун:
(3.25)
В случае, когда проем работает в смешанном режиме, формула для расчета воздуха получается путем интегрирования правой части уравнения (3.24) в пределах от у = у*: до у = ун:
(3.26)
При выводе формул для расчетов расходов уходящих газов и поступающего воздуха влияние вязкости не учитывалось. Учет вязкости делается путем введения в правую часть всех формул множителя, называемого коэффициентом сопротивления.
Формулы для расчета GB и GГ, которые были получены выше, применимы к любому прямоугольному проему рассматриваемого помещения. Газообмен через круглые проемы подробно рассмотрен в книге Ю.А. Кошмарова, Термодинамика пожаров в помещении. Сройиздат, 1988.-448 с..
Полные расходы уходящих газов и поступающего воздуха в случае, когда помещение имеет несколько разных (по размерам и расположению) проемов, определяются путем суммирования расходов через каждый взятый в отдельности проем:
где z - число проемов; GBi - расход воздуха через i-й проем; GГi расход газа через i-й проем.
Вышеизложенное позволяет сделать следующий вывод. Значения расходов поступающего воздуха и уходящих газов при пожаре однозначно определяются значениями среднеобъемных параметров состояния газовой среды в помещении и геометрическими характеристиками проемов, т.е.
где
При пожаре параметры состояния среды в помещении изменяются во времени. Следовательно, изменяются во времени расходы поступающего воздуха и уходящих газов. Кроме того, в процессе развития пожара могут вскрываться в определенные моменты времени те или иные проемы, которые в начале пожара были закрыты. Например, когда среднеобъемная температура достигает значения 300 - 400 °С, разрушается остекление оконных проемов. Это обстоятельство необходимо учитывать при расчетах процесса развития пожара.
1.7 Влияние ветра на газообмен
Влияние ветра особенно заметно, если одна часть проемов расположена на наветренной стороне здания, а другая на подветренной. Дело в том, что из-за торможения потока воздуха на наветренной поверхности здания давление значительно повышается. В то же время на подветренной стороне здания в аэродинамической тени возникает область пониженного давления.
Вдали от здания распределение давлений вдоль вертикали Оу описывается формулой (3.3):
В непосредственной близости от наружной наветренной стороны здания распределение давлений описывается формулой следующего вида:
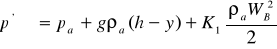(3.27)
где К1 - первый аэродинамический коэффициент (эмпирическая величина); WB - скорость ветра.
Распределение давлений около наружной подветренной стороны здания описывается формулой следующего вида:
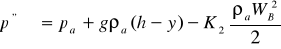(3.28)
где К2 - второй аэродинамический коэффициент (эмпирическая величина).
Распределение давлений внутри здания описывает формула (3.7).
Располагая формулами, которые описывают распределение давлений во внешней среде с учетом влияния ветра, нетрудно вычислить расходы уходящих из помещения газов и поступающего в помещение воздуха. При этом соблюдается та же самая последовательность математических выкладок (операций), которые использовались в случае, когда влияние ветра отсутствует.
2. УРАВНЕНИЯ ИНТЕГРАЛЬНОЙ МОДЕЛИ ПОЖАРА ДЛЯ РАСЧЕТА ТЕПЛОВОГО ПОТОКА В ОГРАЖДЕНИЯ И СКОРОСТИ ВЫГОРАНИЯ ГОРЮЧИХ МАТЕРИАЛОВ
2.1 Приближенная оценка величины теплового потока в ограждения
Ограждающие конструкции поглощают лишь часть той тепловой энергии, которая выделяется внутри помещения в результате горения горючих материалов. Исходя из этого очевидного факта, можно написать следующую формулу для суммарного теплового потока в ограждения:
(3.29)
где Qпож = - выделяющаяся в пламенной зоне в единицу времени тепловая энергия (скорость тепловыделения), Вт; - коэффициент, представляющий собой долю поглощенного тепла от выделившегося (коэффициент теплопоглощения). В ГОСТ 12.1.004-91 "Пожарная безопасность. Общие требования" этот коэффициент называется коэффициентом теплопотерь; QW - суммарный тепловой поток в ограждения (стены, потолок, пол), Вт:
Исследования пожаров показали, что доля поглощенного тепла, т.е. коэффициент , не является "универсальной" константой. Значение этого коэффициента зависит от большого числа параметров (размеров помещения, количества горючего материала, свойств ограждений и др.), и, кроме того, изменяется во времени по мере развития пожара, т.е. этот коэффициент является функцией времени т. Для того чтобы установить вид этой функции, необходимо знать зависимости от времени развития пожара теплового потока QW и скорости тепловыделения Qпож. Эти зависимости можно установить, обращаясь к теории теплообмена и горения.
Экспериментальные исследования разных пожаров и их различных стадий развития показали, что доля поглощенного конструкциями тепла от выделяемого может составлять от 0,2 до 0,75 ("Термогазодинамика пожаров в помещении" / Под ред. Ю.А. Кошмарова, - М, Стройиздат, 1988, 121 с). При приближенных оценках опасных факторов пожара в некоторых случаях используют допущения о постоянстве величины . Такое допущение приемлемо, если рассматривается достаточно малый интервал времени развития пожара. Например, в рекомендациях "Расчет необходимого времени эвакуации людей из помещений при пожаре" (М., ВНИИПО МВД СССР, 1989) принималось, что = 0,6.
Методы расчета тепловых потоков в ограждающие конструкции основываются на результатах экспериментальных исследований. Эти методы можно разделить на две группы - эмпирические и полуэмпирические.
2.2 Эмпирические методы расчета теплового потока в ограждения
Эти методы целиком и полностью базируются на эмпирических формулах, которые представляют собой зависимость теплового потока от средней температуры газовой среды в помещении или от времени.
Применение эмпирических формул ограничивается условиями, при которых велись исследования теплообмена при пожаре (к этим условиям относятся вид и количество горючего материала, число и размеры проемов, свойства материала ограждений, размеры помещений и др.).
Первую группу таких формул представляют зависимости, полученные на основании результатов исследований М.П. Башкирцева:
при То < Тт < 333 К
(3.30)
при Тт>333 К
(3.31)
где а = 0,8 К-1; 1=4,07 Вт/м2; 2=11,6 Вт/м2; b1 = 0,00065 К-1; n = 0,0023 К-1 ;S = SCT + Sпот + Sпол - суммарная площадь поверхностей ограждений (стен потолка, пола), м2; Тт - средняя температура газовой среды; Tо - температура среды перед пожаром; Qw - суммарный тепловой поток в ограждения, Вт.
Эти формулы были получены на основе исследования пожаров в помещениях объемом от 2,5 до 6000 м3 с ограждающими конструкциями из кирпича и бетона. В опытах сжигались горючие жидкости (дизельное топливо, бензин, спирты).
Позднее под руководством проф. Ю.А. Кошмарова адъюнктами СИ. Зерновым, B.C. Козловым и B.C. Агаповым были проведены исследования пожаров в помещении объемом V = 200 м3 с ограждениями из кирпича и бетона. В опытах сжигались древесина и органическое стекло. Полученная при этом зависимость, для определения потоков тепла Qw дает результаты, близкие к тем, которые следуют из вышеприведенных формул.
Вторая группа эмпирических формул для расчета тепловых потоков в ограждения была получена И.С. Молчадским. Эти формулы позволяют вычислить тепловые потоки отдельно в вертикальные стены, потолок (перекрытие) и пол. Суммарный тепловой поток есть сумма потоков тепла в стены, потолок и пол:
(3.32)
где
(3.33)
где ст, пот, пол - средние коэффициенты теплоотдачи соответственно для стен, потолка и пола, кВт·м-2·К-1; Тт - среднеобъемная температура среды, К; Т0 - начальная температура, К.
Значения приведенных коэффициентов теплоотдачи вычисляются по эмпирическим формулам:
где
G - количество (масса) горючего материала, приходящегося на 1 м2 суммарной площади поверхностей всех ограждающих конструкций (удельная горючая нагрузка), кг·м-2; М - масса горючего материала, находящегося в помещении, кг.
Приведенные здесь формулы были установлены на основе данных, полученных при исследовании пожаров в помещениях объемом от 60 до 200 м3 с ограждениями из бетона и кирпича. В опытах сжигалась древесина (G = 0,811 кгм-2).
Третью группу эмпирических формул представляют зависимости тепловых потоков в стены, потолок и пол от времени:
где Sст, Sпот, Sпол - площади стен, потолка и пола соответственно, м2.
Значения величин q и зависят от удельной горючей нагрузки G:
где
2.3 Полуэмпирические методы расчета теплового потока в ограждения
При пожаре имеет место сложный радиационно-конвективный теплообмен на поверхностях ограждений. Полуэмпирические формулы получены с помощью теории пограничного слоя. Для развитой стадии пожара они были получены д-ром техн. наук Молчадским И. С. методом, который основывается на использовании интегральных уравнений пограничного слоя. Формулы для расчета средних коэффициентов теплоотдачи (подробности даны в книге "Термодинамика пожаров в помещении" под ред. Ю.А. Кошмарова) имеют следующий вид:
для вертикальных поверхностей высотой Н:
(3.45)
для горизонтальных поверхностей (потолок, пол)
где - число Грасгофа; - число Прандтля;
N = f(Tw) - аналог числа Кирпичева, характеризующего соотношение радиационного и кондуктивного тепловых потоков; Вu - аналог числа Бугера, характеризующего оптическую плотность среды; Re - число Рейнольдса; Тw - температура поверхности ограждения.
Для того чтобы определить с помощью формул (3.45 - 3.47) тепловой поток в ограждающую конструкцию, необходимо знать температуру поверхности ограждающей конструкции Tw. Температуру Tw можно определить путем решения дифференциального уравнения теплопроводности. Температура поверхности Tw зависит не только от условий теплоотдачи (т. е. от величины коэффициента теплоотдачи), но и от толщины конструкции, а также от теплофизических свойств материала конструкции.
Математически задача об определении Tw формулируется так:
(3.48)
начальное условие: t = t0 при = 0
граничные условия: (3.49)
где tw - температура на внутренней поверхности ограждений, tw =TW - 273, К; tw - температура ограждений на внешней стороне; а, - коэффициенты температуропроводности и теплопроводности материала ограждения; - толщина ограждения; - время; х - координата, отсчитываемая от внутренней поверхности ограждения.
После того как вычислены коэффициент теплоотдачи для ограждающей конструкции и температура внутренней поверхности ограждения Tw, определяем тепловой поток в это ограждение по формуле:
Суммарный поток тепла Qw получают суммированием потоков во все конструкции.
Следует отметить, что температура среды в помещении заранее неизвестна. Следовательно, задача о нагревании ограждения (об отыскании Tw) должна решаться совместно с основной системой дифференциальных уравнений интегральной математической модели пожара (ИММП).
2.4 Методы расчета скорости выгорания горючих материалов и скорости тепловыделения
Скорость выгорания твёрдых и жидких материалов есть скорость поступления летучих веществ с поверхности горючих материалов (ГМ) в пламенную зону (в пламя). Следует отметить, что летучие вещества есть горючие газы, которые образуются в результате термического разложения твердых ГМ (этот процесс называют пиролизом) или в результате испарения жидких ГМ. Следовательно, скорость выгорания твёрдых и жидких материалов есть величина, равная расходу горючих газов, поток которых с поверхности ГМ возникает в результате процессов термического разложения или испарения. Скорость выгорания обозначается буквой , имеет размерность кгс-1. Скорость выгорания на единицу поверхности воспламенившихся твёрдых и жидких ГМ называют массовой скоростью выгорания (иногда удельной массовой скоростью выгорания). Эту величину обозначают уд, её размерность кгм -2·с-1.
Очевидно, что = удSг, где Sг - площадь поверхности ГМ, охваченной пламенем (В. Т. Монахов, 1963 г.).
Следует отметить, что и пиролиз, и испарение являются процессами, сопровождающимися затратами (поглощением) тепловой энергии. Энергетическими характеристиками этих процессов являются теплота испарения и теплота газификации (пиролиза) . Примеры: теплота испарения =490 кДжкг-1; =1000 кДжкг-1; теплота пиролиза =1800 кДжкг-1. Значения и зависят от природы горючего вещества, т.е. для разных веществ они различны.
Из сказанного следует, что величина массовой скорости выгорания, т.е. уд, зависит от природы ГМ. Это утверждение относится только к твёрдым и жидким ГМ. Если ГМ представляет собой газообразное вещество (метан, пропан и т.д.), поступающее в помещение из отверстий в стенках трубопроводов или аппаратов, то скорость выгорания этого газа равна его расходу из отверстий и не зависит от природы этого газа.
Массовая скорость выгорания зависит не только от свойств горючего материала. Скорость выгорания вещества в помещении может отличаться от его скорости выгорания и тепловыделения на открытом пространстве. Возможны два предельных режима горения материала в помещении.
Первый режим выгорания горючих материалов характеризуется наличием достаточного количества кислорода (воздуха). При таком режиме горение материала в помещении аналогично горению его на открытом воздухе. Режим пожара в этом случае называют пожаром, регулируемым нагрузкой (ПРН).
Второй предельно возможный режим выгорания горючего материала характеризуется тем, что кислорода в помещении недостаточно и скорость тепловыделения лимитируется количеством поступающего извне кислорода (воздуха). Режим пожара в этом случае называют пожаром, регулируемым вентиляцией (ПРВ).
В реальных условиях в процессе развития пожара один режим выгорания может переходить в другой, т.е. вслед за ПРН наступает ПРВ и наоборот. Между ПРН и ПРВ имеют место промежуточные режимы.
Следует отметить, что скорость выгорания материала в определенной степени зависит от температуры газовой среды в помещении.
Скорость выгорания при ПРН вычисляется по формуле следующего вида:
(3.50)
где - удельная скорость выгорания на открытом воздухе, кгм -2·с-1; SГ – площадь поверхности горения, м2.
Если горючим веществом является жидкость, площадь горения полагается равной площади ее зеркала.
Площадь горения ТГМ вычисляется на основе экспериментальных данных о линейной скорости распространения пламени. В частности, при круговом распространении используется следующая формула:
(3.51)
где - время, с; vл - линейная скорость распространения пламени по поверхности пожарной нагрузки, мс-1.
Формула (3.51) применима лишь до момента времени, вычисляемого по формуле:
(3.52)
где тS - масса ТГМ, приходящаяся на единицу поверхности пола (или массовая пожарная нагрузка).
После этого момента времени в центре круга окажется площадка, где горение прекратилось из-за отсутствия горючего материала. Тогда площадь горения вычисляется по формуле:
(3.53)
В случае, когда горючий материал расположен на прямоугольной площадке, а горение начинается в центре этой площадки, формулы (3.51) и (3.53) применимы лишь при условии:
(3.54)
где lmin - меньшая сторона прямоугольника.
Если r превышает , lmin то из площади круга, равной r2, вычитаются площади соответствующих сегментов (рис. 3). Входящие в формулы (3.50 - 3.54) величины и Vл, определяются в основном свойствами горючей нагрузки. Для многих видов горючей нагрузки уже имеются экспериментальные сведения об этих величинах.
При расчетах процесса выгорания твердых материалов принимается допущение о том, что при ПРН величина остается неизменной вплоть до полного выгорания пожарной нагрузки. Однако в действительности может иметь место уменьшение скорости выгорания из-за образования на горящей поверхности материала слоя золы и угля.
Рис. 3. Схема кругового распространения пламени
по поверхности слоя горючего материала:
r1, - радиус зоны горения в момент 1; r2 - радиус зоны горения
в момент 2 > 1; l1, l2 - стороны прямоугольника
По мере развития пожара может наступить такой режим, когда количество кислорода О2, поступающего в помещение с наружным воздухом через проемы, становится равным количеству, необходимому для полного сгорания (окисления) летучих веществ, поступающих с поверхности ГМ. Весь поступающий кислород расходуется для окисления выделяющихся летучих веществ (продуктов пиролиза или испарения). При таком режиме скорость выгорания считают по формуле:
(3.55)
где GB - расход воздуха, поступающего в помещение через проемы, кгс-1; х1В - концентрация кислорода в поступающем воздухе; L - стехиометрический коэффициент, т.е. количество кислорода, необходимое для сгорания 1 кг горючего материала. Эта формула, строго говоря, позволяет определить количество прореагировавших в помещении продуктов пиролиза или испарения. Некоторая часть летучих веществ может догорать (сгорать) за проемами вне помещения. Два режима, рассмотренные выше, являются предельными. В реальных условиях наблюдаются промежуточные режимы, приближающиеся в той или иной степени к одному из предельных. Формула, которая позволяет рассчитать скорость выгорания при любом режиме, имеет следующий вид:
(3.56)
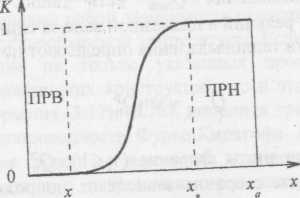
где К - функция, зависящая от среднеобъемной концентрации кислорода в помещении. На рис. 4 представлено графическое изображение этой функции.
Рис. 4. Функция режима пожара:
х*- начало перехода от режима ПРН к режиму ПРВ; х** - конец перехода от режима ПРН к режиму ПРВ; ха - концентрация кислорода во внешней атмосфере.
Когда концентрация кислорода снизится и достигнет значения х**, наступает режим ПРВ. При х = х*,. функция К должна удовлетворять следующим условиям:
a) K=1;
Всем этим условиям удовлетворяет совокупность функций следующего вида:
(3.58)
где (3.59)
В заключение следует отметить, что продолжающиеся теоретические и экспериментальные исследования процессов выгорания ГМ рано или поздно приведут к более полному пониманию сложных взаимосвязанных процессов, определяющих пиролиз ТГМ и испарение ЖГМ при пожаре в помещениях. Скорость тепловыделения Qпож есть тепло, выделяющееся в результате химических реакций в пламенной зоне за единицу времени. Значение скорости тепловыделения определяют по формуле
(3.60)
где - коэффициент полноты сгорания (<1); - теплота сгорания, Джкг-1. Значения теплоты сгорания зависят от природы ГМ (например, = 13,8 ·106 Джкг-1- для древесины; = 41,8 · 106 Джкг-1 - для бензина).
Значение вычисляется по эмпирическим формулам, полученным в результате исследований пожаров в помещениях.
PAGE 25
ГАЗООБМЕН ПОМЕЩЕНИИ И ТЕПЛОФИЗИЧЕСКИЕ ФУНКЦИИ, НЕОБХОДИМЫЕ ДЛЯ ОПИСАНИЯ ЗАМКНУТОГО ПОЖАРА