ЗОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОЖАРА В ПОМЕЩЕНИИ. ЧИСЛЕННАЯ РЕАЛИЗАЦИИ ЗОННОЙ МОДЕЛИ

ЛЕКЦИЯ

по дисциплине "Прогнозирование опасных факторов пожара"

Тема №6. «ЗОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОЖАРА В ПОМЕЩЕНИИ. ЧИСЛЕННАЯ РЕАЛИЗАЦИИ ЗОННОЙ МОДЕЛИ»

План лекции:

Введение

Постановка задачи о зонном моделировании.
Конвективная колонка
Припотолочный слой

Выводы по лекции

Цели лекции:

Учебные

В результате прослушивания материала слушатели должны знать:

опасные факторы пожара, воздействующие на людей, на конструкции и оборудование
предельно допустимые значения ОФП
методы прогнозирования ОФП

Уметь: прогнозировать обстановку на пожаре.

Развивающие:

выделять самое главное
самостоятельность и гибкости мышления
развитие познавательного мышления

Литература

Д.М. Рожков. Прогнозирование опасных факторов пожара в помещении. – Иркутск 2007 С.89
Ю.А.Кошмаров, М.П. Башкирцев Термодинамика и теплопередача в пожарном деле. ВИПТШ МВД СССР, М., 1987 г.
Лабораторный практикум «Прогнозирование опасных факторов пожара». Ю.А.Кошмаров, Ю.С.Зотов. 1997 г.
Ю.А.Кошмаров, В.В. Рубцов, Процессы нарастания опасных факторов пожара в производственных помещениях и расчет критической продолжительности пожара. МИПБ МВД России, М., 1999 г.

Введение

Зонные математические модели в основном используются для исследования динамики опасных факторов пожара в начальной стадии пожара. В начальной стадии распределение параметров состояния газовой среды по объему помещения характеризуется большой неоднородностью (неравномерностью). В этот период (отрезок) времени пространство внутри помещения можно условно поделить на ряд характерных зон с существенно различающимися температурами и составами газовых сред. Границы этих зон по мере развития пожара не остаются неизменными и неподвижными. В течение времени геометрическая конфигурация зон меняется и сглаживается контрастное различие параметров состояния газа в этих зонах. В принципе, пространство внутри помещения можно разбить на любое число зон. В этой лекции рассмотрим простейшую зонную модель пожара, которая применима при условиях, когда размеры очага горения значительно меньше размеров помещения.

Процесс развития пожара можно представить следующим образом. После воспламенения горючих веществ образующиеся газообразные продукты устремляются вверх, образуя над очагом горения конвективную струю. Достигнув потолка помещения, эта струя растекается, образуя припотолочный слой задымленного газа. В течение времени толщина этого слоя увеличивается.

1. Постановка задачи о зонном моделировании.

В соответствии с вышесказанным в объеме помещения можно выделить три характерные зоны: конвективную колонку над очагом пожара, припотолочный слой нагретого газа и воздушную зону с практически неизменными параметрами состояния, равными своим начальным значениям. Математическая модель пожара, базирующаяся на разбиении пространства на характерные области, получила название трехзонной модели. Схема этой модели показана на рис. 6.1. На этой схеме использованы следующие обозначения: ук - координата нижней границы припотолочного слоя, отсчитываемая от поверхности горения; уДВ - высота дверного проема; dэ - эквивалентный диаметр очага горения; 2h - высота помещения; GK - поток газа, поступающего в припотолочный слой из конвективной колонки, кг·с-1; GB - поток воздуха, поступающий в колонку из зоны III, кг·с-1;. GГ - поток вытесняемого газа из помещения, кг·с-1; - скорость выгорания, кг·с-1; - расстояние от пола до поверхности горения, м.

В дальнейшем ограничимся рассмотрением первой фазы начальной стадии пожара. Под понятием "первая фаза начальной стадии пожара" подразумевается отрезок времени, в течение которого нижняя граница припотолочного слоя, непрерывно опускаясь, достигает верхнего края дверного проема. При первой фазе начальной стадии пожара нагретые газы лишь накапливаются в припотолочной зоне.

При второй фазе нижняя граница II зоны расположена ниже верхнего края дверного проема. С наступлением второй фазы начинается процесс истечения нагретых газов из помещения через дверной проем. До наступления этой фазы имеет место лишь вытеснение (через дверной проем) холодного воздуха из III зоны.

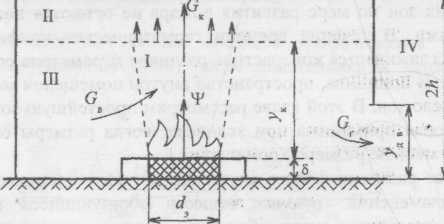
Рис. 6.1. Схема трехзонной модели пожара:

I — зона конвективной струи (конвективная колонка);

II - зона припотолочного нагретого газа; III - зона холодного

воздуха; IV - зона наружного воздуха (наружная атмосфера)

2. Конвективная колонка

Рассмотрим прежде всего I зону. Теория свободной конвективной струи к настоящему времени весьма детально разработана. Эта теория является одним из разделов вязкой аэродинамики газов. Она позволяет рассчитывать поля температур, плотностей и скоростей в конвективной колонке. Для определения температур и массовых расходов в сечениях конвективной колонки можно использовать формулы:

(6.1)

(6.2)

где Qпож - скорость тепловыделения, Вт; QpH – низшая теплота сгорания, Дж·кг-1; уд - удельная скорость выгорания, кг·м-2·с-1; g -ускорение свободного падения, м·с-2; То и 0 - температура и плотность холодного (окружающего) воздуха; G - расход газов через сечение струи, отстоящее от поверхности горения на расстояние у, кг·с-1; ср - изобарная теплоемкость газа, Дж·кг-1·К-1; - доля, приходящаяся на поступающую в ограждение теплоту от выделившейся в очаге горения; у - координата сечения колонки, отсчитываемая от поверхности горения, м; у0 - расстояние от фиктивного источника тепла до поверхности горения, м.

С помощью формул (6.1) и (6.2) можно рассчитать расход газа из I зоны, поступающего во II зону, и его температуру. Для этого нужно положить координату у в формулах (6.1) и (6.2) равной координате нижней границы припотолочного слоя ук.

Расстояние от фиктивного источника тепла до поверхности горения вычисляется по формуле:

(6.3)

где FГ - площадь пожара, м2.

3. Припотолочный слой

Рассмотрим теперь II зону (припотолочный слой нагретых газов). Объем этой зоны в момент времени равен

где FП0T - площадь потолка; ук - координата нижнего края припотолочного слоя газов. Масса газа, заключенная во II зоне, составляет величину т2 = р2V2 Давление в зоне II практически не меняется и остается равным начальному значению, т.е. Р0. Внутренняя (тепловая) энергия II зоны составляет:

Запишем уравнения материального баланса и энергии для II зоны применительно к первой фазе начальной стадии пожара:

(6.4)

(6.5)

где 2 - средняя плотность во II зоне; Т2 - средняя температура во II зоне; Qw2 - тепловой поток от припотолочного слоя газа в ограждения, кВт.

Параметры состояния Т2 и 2 связаны между собой следующим уравнением:

(6.6)

Уравнение (6.6) следует из условия равенства давлений во всех зонах. Это условие является приближенным, но применимым для реальных пожаров.

Преобразуем уравнение энергии (6.5), используя уравнение (6.6):

или

и окончательно (6.7)

Из уравнения (6.1) следует:

(6.8)

Подставляя формулу (6.8) в уравнение (6.7), получим:

Примем, что (для начальной стадии = 0,66).

После дальнейших преобразований получим следующее уравнение:

(6.8а)

Подставим в это уравнение выражение для Gk (6.2):

(6.9)

Отметим, что в этом уравнении

Введем обозначения:

Функции () и () при горении твердых ГМ в момент времени = 0 равны нулю, так как FГ 0. Уравнение (6.9) принимает вид:

(6.10)

Начальное условие .

Решение уравнения (6.10) при заданном начальном условии будем искать для интервала времени от = 0 до *, где * - момент окончания первой фазы начальной стадии пожара. После того как найдена функция ук(), находим Gk =f1(); V2 =f2().

Преобразуем уравнение материального баланса (6.4). Интегрируя его, получаем:

(6.11)

После преобразований из формулы (6.11) получаем:

(6.12)

После вычислений плотности 2 определяется средняя температура в припотолочном слое газа:

(6.13)

Уравнение баланса для токсичного газа (продукт горения) во II зоне имеет вид:

(6.14)

где n - парциальная плотность токсичного газа; L - количество (масса) токсичного газа, образующаяся при сгорании 1 кг горючего материала. Из формулы (6.14) следует формула:

(6.15)

где М - количество (масса) ГМ, выгоревшего к моменту времени .

Уравнение дыма для припотолочного слоя имеет вид:

и, следовательно:

Исходя из выше изложенного, имеем уравнение с разделяющимися переменными, с помощью которого рассчитывается изменение координаты границы припотолочного слоя в течение времени:

где:

при условии: y0 =const;

Выводы по лекции: зонная модель представляет собой опять же частный случай интегральной модели для припотолочного слоя, и с применением известных теорий, в частности - теории конвективной колонки.

PAGE 6

ЗОННАЯ МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПОЖАРА В ПОМЕЩЕНИИ. ЧИСЛЕННАЯ РЕАЛИЗАЦИИ ЗОННОЙ МОДЕЛИ