Основные понятия и уравнения интегральной математической модели пожара в помещении

ЛЕКЦИЯ

по дисциплине "Прогнозирование опасных факторов пожара"

Тема №2. «Основные понятия и уравнения интегральной математической модели пожара в помещении»

План лекции:

Лекция 1. Основные понятия математической модели пожара в помещении

1.1 Допущения интегрального метода термодинамического анализа пожара

1.2 Среднеобъемная плотность газовой среды

1.3 Среднеобъемная парциальная плотность

1.4 Среднеобъемная (удельная) внутренняя энергия

1.5 Дым и его влияние на термодинамические параметры среды

Лекция 2. Дифференциальные уравнения пожара

Цели лекции:

Учебные

В результате прослушивания материала слушатели должны знать:

опасные факторы пожара, воздействующие на людей, на конструкции и оборудование
предельно допустимые значения ОФП
методы прогнозирования ОФП

Уметь: прогнозировать обстановку на пожаре.

Развивающие:

выделять самое главное
самостоятельность и гибкости мышления
развитие познавательного мышления

Литература

Д.М. Рожков Прогнозирование опасных факторов пожара в помещении. – Иркутск 2007. С.89
Ю.А.Кошмаров, М.П. Башкирцев Термодинамика и теплопередача в пожарном деле. ВИПТШ МВД СССР, М., 1987 г.
Ю.А.Кошмаров Прогнозирование опасных факторов пожара в помещении. – Москва 2000. С.118
Ю.А.Кошмаров, В.В. Рубцов, Процессы нарастания опасных факторов пожара в производственных помещениях и расчет критической продолжительности пожара. МИПБ МВД России, М., 1999 г.

Лекция 1. Основные понятия математической модели пожара в помещении

1.1 Допущения интегрального метода термодинамического анализа пожара

Интегральная математическая модель пожара описывает в самом общем виде процесс изменения во времени состояния газовой среды в помещении.

1) С позиций термодинамики газовая среда, заполняющая помещение с проемами (окна, двери и т.п.), как объект исследования есть открытая термодинамическая система (рис. 1.1).

2)Ограждающие конструкции (пол, потолок, стены) и наружный воздух (атмосфера) являются внешней средой по отношению к этой термодинамической системе. Граница между термодинамической системой и внешней средой (контрольная поверхность) показана условно на рис. 1.1 пунктирной линией. Эта система взаимодействует с внешней средой путем тепло- и массообмена. В процессе развития пожара через одни проемы выталкиваются из помещения нагретые газы, а через другие поступает холодный воздух.

3) Количество вещества, т.е. масса газа в рассматриваемой открытой термодинамической системе, в течение времени изменяется. Поступление холодного воздуха обусловлено работой проталкивания, которую совершает внешняя среда.

4) Термодинамическая система в свою очередь совершает работу, выталкивая нагретые газы во внешнюю атмосферу. Эта термодинамическая система взаимодействует также с ограждающими конструкциями путем теплообмена. Кроме того, в эту систему с поверхности горящего материала (т.е. из пламенной зоны) поступает вещество в виде газообразных продуктов горения.

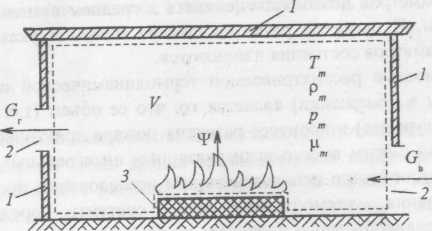
Рис. 1.1. Схема пожара в помещении:

---- контрольная поверхность;1 - ограждения; 2 - проемы (окна, двери); 3 – горящий материал; Gг - расход уходящих газов; Gв - расход поступающего холодного воздуха; - скорость выгорания материала

Состояние рассматриваемой термодинамической системы изменяется в результате взаимодействия с окружающей средой. Приступая к изложению сути интегрального метода описания процесса изменения состояния рассматриваемой термодинамической системы, отметим прежде всего следующие два факта.

5) Всегда с большой точностью можно считать, что газовая среда внутри помещения при пожаре есть смесь идеальных газов.

6) В каждой точке пространства внутри помещения в любой момент времени реализуется локальное равновесие. Это означает, что локальные значения основных термодинамических параметров состояния (плотность, давление, температура) связаны между собой уравнением Клапейрона, т.е.

(2.1)

где р - локальное давление, Н·м-2; - локальная плотность, кг·м-3; R -газовая постоянная, Дж·кг-1 К-1; Т - локальная температура, К.

При пожаре поля локальных термодинамических параметров состояния являются нестационарными и неоднородными. Расчет этих полей представляет собой чрезвычайно сложную математическую задачу. Интегральный метод описания состояния среды в помещении позволяет не рассматривать эту задачу.

7) Особенностью рассматриваемой термодинамической системы (т.е. газовой среды в помещении) является то, что ее объем (т.е. пространственная конфигурация) в процессе развития пожара практически не изменяется. В связи с этим в интегральном методе описания состояния термодинамической системы, коей является газовая среда в помещении, используются "интегральные" параметры состояния термодинамической системы среднеобъемные параметры - среднеобъемную плотность газовой среды и среднеобъемную (удельную) внутреннюю энергию.

Отношение этих двух интегральных параметров позволяет оценивать в среднем степень нагретости газовой среды. В процессе развития пожара значения указанных интегральных параметров состояния изменяются.

1.2 Среднеобъемная плотность газовой среды в помещении представляет собой отношение массы газа, заполняющего помещение, к объему помещения, т.е.

(2.2)

где М - масса газа, заполняющего помещение, кг; V - свободный объем помещения, м3. Нижний индекс т, используемый здесь и далее, представляет собой первую букву в немецком слове mittel (средний). Следует отметить, что

(2.3)

С формальных позиций среднеобъемная плотность газовой среды есть результат осреднения по объему помещения всех значений локальной плотности, т.е.

(2.4)

Газовая среда в помещении представляет собой смесь кислорода, азота и продуктов горения. В процессе развития пожара количественное соотношение между компонентами смеси изменяется. В интегральном методе описания процесса изменения массы i-го компонента смеси в течение времени используется параметр, называемый среднеобъемной парциальной плотностью i-го компонента смеси.

1.3 Среднеобъемная парциальная плотность i-го компонента представляет собой отношение массы i-го компонента смеси (например О2), содержащейся в объеме помещения, к объему помещения, т.е.

(1.5)

(2.5)

где М, - масса i-го компонента, находящегося в помещении, кг. Отметим, что с формальной точки зрения среднеобъемная парциальная плотность i -го компонента есть результат осреднения по объему помещения всех значений локальной парциальной плотности этого компонента, т.е.

(2.6)

где i, - локальное значение парциальной плотности i-го компонента, кг·м-3.

1.4 Среднеобъемная (удельная) внутренняя энергия представляет собой отношение внутренней тепловой энергии всего газа, заполняющего помещение, к объему помещения, т.е.

(2.7)

где и - внутренняя энергия всей газовой среды, заполняющей помещение, Дж. С формальных позиций среднеобъемная внутренняя энергия газовой среды есть результат осреднения по объему всех значений локальной удельной (объемной) внутренней энергии, т.е.

(2.8)

где UV - локальное значение удельной (объемной) внутренней энергии, Дж·м -3. Локальные значения удельной объемной внутренней энергии и удельной массовой внутренней энергии связаны между собой простым соотношением, которое имеет следующий вид:

(2.9)

где и - локальное значение удельной массовой внутренней энергии газа, Дж·кг. Отметим здесь, что между локальным значением удельной массовой внутренней энергии и локальной температурой идеального газа существует простая взаимосвязь, а именно

(2.10)

где cv - изохорная теплоемкость газа, Дж·кг·К.

В интегральном методе описания процесса изменения состояния термодинамической системы (т.е. газовой среды в помещении) вместо среднеобъемной внутренней энергии используется параметр состояния, называемый среднеобъемным давлением. Эти два параметра в формальном отношении являются взаимозаменяемыми. Покажем это. Формулу (2.8) можно преобразовать с помощью выражений (2.9) и (2.10)

(2.11)

Если теперь воспользоваться уравнением Клапейрона (2.1), то формулу (2.11) можно преобразовать и получить следующее выражение:

(2.12)

где p - локальное давление, Н·м -2;

к = Cp / CV - отношение изобарной и изохорной теплоемкостей идеального газа (показатель адиабаты). С достаточной для практики точностью можно считать, что показатель адиабаты во всех точках внутри помещения есть одна и та же постоянная величина. С учетом этого замечания формулу (2.12) можно преобразовать:

(2.13)

Выражение в прямоугольных скобках представляет собой операцию осреднения всех локальных значений давления по объему помещения. Результат этого осреднения называют среднеобъемным давлением, т.е.

(2.14)

где рт - среднеобъемное давление, Н·м -2

Сравнивая выражения (2.13) и (2.14), получим следующее соотношение между среднеобъемной внутренней энергией и среднеобъемным давлением:

(2.15)

Из последней формулы следует, что среднеобъемное давление прямо пропорционально среднеобъемной внутренней энергии. Среднеобъемное давление необходимо знать при расчетах газообмена помещения с внешней атмосферой, что будет показано в дальнейшем.

Степень нагретости газовой среды характеризуется в среднем отношением внутренней энергии этой среды к ее массе. Отношение этих физических величин можно представить с помощью формул (2.2), (2.7) и (2.15) в следующем виде:

(2.16)

Если правую и левую части равенства (2.16) поделить на изохорную теплоемкость, то получится следующее выражение:

(2.17)

Комплекс в левой части выражения (2.17) имеет размерность "Кельвин". Этот комплекс представляет собой параметр состояния рассматриваемой термодинамической системы, который называется среднемассовой температурой газовой среды, т.е.

(2.18)

С помощью выражения (2.18) можно преобразовать формулу (2. ] 7) и в результате получить следующее уравнение:

(2.19)

Вывод: Уравнение 2.19 является основным и связывает между собой три важных параметра состояния газовой среды в помещении при пожаре. По внешнему виду это уравнение такое же, как уравнение Клапейрона для локальных параметров состояния. В дальнейшем уравнение (2.19) для краткости будем называть усредненным уравнением состояния газовой среды, заполняющей помещение.

1.5 Дым и его влияние на термодинамические параметры среды

Газовая среда, заполняющая помещение при пожаре, содержит в себе мельчайшие твердые частицы. Следует отметить, что доля тепловой энергии, приходящейся на эти частицы, пренебрежимо мала по сравнению с внутренней энергией газовой среды, находящейся в помещении. Не существенным является также вклад этих частиц в суммарную массу среды, заполняющей помещение при пожаре. Поэтому можно не учитывать присутствие этих частиц при вычислениях таких параметров состояния среды, как среднеобъемная плотность, среднеобъемное давление и среднемассовая температура. Однако присутствие этих частиц сильно изменяет оптические свойства среды в помещении. В результате рассеяния энергии световых волн из-за многократного диффузного отражения от этих мельчайших частиц (их диаметр приблизительно равен 0,2-4 мкм) ухудшается видимость. Оптические свойства среды, находящейся в помещении, характеризуются среднеобъемной оптической плотностью дыма.

Среднеобъемная плотность (концентрация) дыма представляет собой отношение оптического количества дыма, находящегося в помещении, к объему помещения, т.е.

(2.20)

где S - оптическое количество дыма, Нп·м2; µm - среднеобъемная оптическая плотность дыма, Нп·м-1. Здесь сокращением «Нп» обозначено слово "Непер". Оптическое количество дыма в помещении есть произведение средней концентрации твердых частиц на объем помещения и эффективное сечение экстинкции, т.е.

S = NVx, (2.21)

где N - средняя концентрация частиц, т.е. число частиц, приходящееся на единицу объема, м -3; - эффективное сечение экстинкции, м2. Чем выше оптическая плотность (концентрация) дыма, тем хуже видимость в помещении. Оптическая плотность дыма и дальность видимости связаны между собой следующим приближенным соотношением:

(2.22)

где lвид - дальность видимости, м.

К числу важнейших понятий, используемых в дальнейшем, относятся упомянутые ранее теплота сгорания, стехиометрические коэффициенты и дымообразующая способность горючих материалов. Последнее понятие требует некоторых пояснений.

Дымообразующая способность горючего материала есть оптическое количество дыма, образующегося при сгорании единицы массы горючего материала, т.е.

D = J , (2.23)

где D - дымообразующая способность ГМ, Нп·м2·кг-1; J - число частиц, образующихся при сгорании единицы массы горючего материала, кг-1; - эффективное сечение экстинкции частиц, м2.

Лекция 2. Дифференциальные уравнения пожара

Уравнения пожара описывают в самом общем виде изменение среднеобъемных параметров состояния газовой среды в помещении в течение времени (в процессе развития пожара). Эти уравнения были сформулированы в 1976г. проф. Ю.А. Кошмаровым (статья "Развитие пожара в помещении" в научном сборнике ВНИИПО МВД СССР "Горение и проблемы тушения пожаров". М.: ВНИИПО МВД СССР, 1977).

Уравнения пожара являются обыкновенными дифференциальными уравнениями. Они вытекают, как и большинство уравнений математической физики, из фундаментальных законов природы - первого закона термодинамики для открытой термодинамической системы и закона сохранения массы. Подробный вывод этих уравнений приведен в учебнике Ю.А. Кошмарова и М.П. Башкирцева "Термодинамика и теплопередача в пожарном деле" (М., ВИПТШ МВД СССР, 1987). Ограничимся здесь кратким изложением рассуждений, используемых при выводе уравнений пожара.

Первое уравнение - уравнение материального баланса пожара в помещении - вытекает из закона сохранения массы. Применительно к газовой среде, заполняющей помещение, этот закон можно сформулировать так: изменение массы газовой среды в помещении за единицу времени равно алгебраической сумме потоков массы через границы рассматриваемой термодинамической системы. Под границей системы здесь подразумевается воображаемая контрольная поверхность, ограничивающая пространство, внутри которого заключена рассматриваемая газовая среда. На рис. 1.1 эта поверхность условно показана пунктирной линией. Часть этой поверхности совпадает с поверхностью ограждений (стены, пол, потолок). Там, где находятся проемы, эта поверхность является воображаемой. Объем пространства, заключенный внутри этой поверхности, называется свободным объемом помещения и обозначается буквой V. Введем следующие обозначения:

а) GB - расход поступающего воздуха из окружающей атмосферы в помещение, который имеет место в рассматриваемый момент времени процесса развития пожара, кгс-1;

б) GГ - расход газов, покидающих помещение через проемы в рассматриваемый момент времени, кгс-1;

в) - скорость выгорания (скорость газификации) горючего материала в рассматриваемый момент времени, кгс-1;

г) mV - масса газовой среды, заполняющей помещение в рассматриваемый момент времени, кг.

За малый промежуток времени, равный dx, будет иметь место малое изменение массы газовой среды. В то же время можно считать, что значения GГ, GB и в течение этого малого промежутка времени остаются практически неизменными. С учетом вышесказанного уравнение материального баланса для газовой среды в помещении записывается следующим образом:

(2.24)

где левая часть уравнения есть изменение массы газовой среды за единицу времени в интервале, равном d. Правая часть есть алгебраическая сумма потоков массы.

Уравнение (2.24) называется уравнением материального баланса пожара.

Аналогичные рассуждения позволяют получить дифференциальные уравнения баланса массы кислорода, баланса продуктов горения и баланса оптического количества дыма. Уравнение баланса массы кислорода:

(2.25)

Уравнение баланса токсичного продукта горения:

(2.26)

Уравнение баланса оптического количества дыма:

(2.27)

В этих уравнениях использованы следующие обозначения: 1, - среднеобъемная парциальная плотность кислорода, кг·м-3; 2 - среднеобъемная парциальная плотность токсичного продукта горения, кг·м-3; м - объемная оптическая концентрация дыма, Нп·м-1.

В правой части уравнения (2.25) - уравнения баланса массы кислорода - использованы, кроме ранее указанных, следующие обозначения: х1в - массовая доля кислорода в поступающем воздухе; средняя массовая доля кислорода в помещении; L1 - стехиометрический коэффициент для кислорода (количество кислорода, необходимое для сгорания единицы массы горючего материала), кгкг-1; - коэффициент полноты сгорания; n3, - коэффициент, учитывающий отличие концентрации кислорода в уходящих газах от среднеобъемной концентрации кислорода.

В правой части уравнения (2.26) - уравнения баланса токсичного продукта горения - использованы, кроме ранее указанных, следующие обозначения: L2 - стехиометрический коэффициент для продукта горения (количество продукта горения, образующегося при сгорании единицы массы горючего материала), кгкг-1; средняя массовая доля токсичного газа в помещении; п2 - коэффициент, учитывающий отличие концентрации токсичного газа в уходящих газах от среднеобъемной концентрации этого газа.

В правой части уравнения (1.36) - уравнения баланса оптического количества дыма - использованы, кроме ранее указанных, следующие обозначения: n3- коэффициент, учитывающий отличие оптической концентрации дыма в уходящих газах от среднеобъемного значения оптической концентрации дыма; Fw - площадь поверхности ограждений (потолка, пола, стен), м2; кс - коэффициент седиментации частиц дыма на поверхностях ограждающих конструкций, Нп·с-1. Коэффициент седиментации по физическому смыслу есть скорость осаждения частиц дыма.

На основе первого закона термодинамики выводится уравнение энергии пожара. Рассматриваемая термодинамическая система, т.е. газовая среда внутри контрольной поверхности, характеризуется тем, что она не совершает работы расширения. Кинетическая энергия видимого движения газовой среды в помещении пренебрежимо мала по сравнению с ее внутренней энергией. Потоки массы через некоторые участки контрольной поверхности (проемы) характеризуются тем, что в них удельная кинетическая энергия газа пренебрежимо мала по сравнению с удельной энтальпией.

С учетом всего сказанного получается следующее уравнение энергии пожара:

(2.28)

Левая часть этого уравнения есть скорость изменения внутренней тепловой энергии газовой среды в помещении за единицу времени в рассматриваемый малый промежуток времени d, т.е.

(2.29)

В правой части уравнения (2.28) первый член представляет собой количество тепла, поступающего за единицу времени в газовую среду в результате горения (скорость тепловыделения). Второй член есть поток энергии в помещение, поступающий вместе с продуктами газификации (пиролиз, испарение) горючего материала. Здесь величина ir - энтальпия этих продуктов. Третий член представляет собой сумму внутренней тепловой энергии поступающего за единицу времени воздуха и работы проталкивания, которую совершает внешняя атмосфера. Четвертый член есть сумма внутренней тепловой энергии, которую уносят за единицу времени уходящие газы, и работы выталкивания, которую совершает рассматриваемая термодинамическая система. Пятый член представляет собой тепловой поток, поглощаемый ограничивающими конструкциями и излучаемый через проемы.

Представленные выше пять дифференциальных уравнений содержат шесть неизвестных функций – pm(), pm(), Тm(), р1(), р2() и m (). Эту систему уравнений дополняет алгебраическое уравнение - усредненное уравнение состояния (2.19).

Начальные значения для этих функций задаются условиями, которые имеют место в помещении перед началом пожара, т.е.

(2.30)

Представленная здесь система уравнений описывает свободное развитие пожара. Развитие пожара называют свободным, если не осуществляется тушение, т.е. если помещение не подаются огнетушащие вещества. Эффекты, обусловленные подачей огнетушащих веществ в объем помещения, можно учесть путем введения в дифференциальные уравнения дополнительных членов. Например, при тушении инертными газами (аргон, азот, диоксид углерода) уравнение материального баланса пожара записывается следующим образом:

(2.31)

где Goв - массовый расход подачи огнетушащего вещества, кгс-1. Соответствующим образом изменяются в этом случае и остальные дифференциальные уравнения пожара.

Как уже говорилось, в уравнениях пожара искомыми (неизвестными) функциями являются среднеобъемные параметры газовой среды, а независимой переменной является время. Кроме этих переменных величин, уравнения содержат целый ряд других физических величин, которые можно разделить на две группы. К первой группе относятся величины, заданные условиями однозначности, которые представляют собой сведения о размерах помещения (объем V и поверхность ограждений Fw) и свойствах горючего материала (теплота сгорания Qрн, стехиометрические коэффициенты L1, L2, дымообразующая способность D, энтальпия продуктов горения in. Ко второй группе относятся те величины, которые зависят, помимо всего прочего, от параметров состояния среды в помещении. К этим величинам относятся массовые расходы поступающего через проемы воздуха GB и уходящих через проемы газов GГ, тепловой поток, поглощаемый ограждающими конструкциями и излучаемый через проемы Qw, коэффициент полноты сгорания , скорость тепловыделения Qpн. Для вычисления значений физических величин, относящихся ко второй группе, необходимо располагать дополнительными уравнениями.

Конкретный вид дополнительных уравнений установлен путем привлечения сведений из теории конвективного и лучистого теплообмена, теории газообмена помещения с окружающей атмосферой через проемы из-за различия плотностей наружного воздуха и газовой среды внутри помещения, теории горения.

В заключение необходимо сделать некоторые замечания по поводу общих положений, касающихся сущности описания пожара на уровне осредненных параметров состояния.

В интегральной математической модели мы оперируем с интегральными характеристиками термодинамической системы. Этот подход не требует каких-либо допущений и оговорок о том, как распределены локальные значения термодинамических параметров состояния по объему помещения. Здесь не уместны оговорки такого, например, типа: "предположим, что температурное поле является однородным", или часто используемое выражение о "размазанности" того или иного параметра состояния газовой среды.

Естественным является вопрос о том, как определить значение того или иного термодинамического параметра состояния в заданной точке объема помещения, если будет известно среднеобъемное значение. К этому вопросу мы вернемся в параграфах, посвященных интегральной математической модели пожара.

Здесь лишь отметим, что процесс развития пожара в помещении можно расчленить на ряд характерных временных этапов. Каждому этапу присущи характерные законы распределения локальных термодинамических параметров состояния внутри помещения. Это обстоятельство используется для ответа на поставленный здесь вопрос.

PAGE 3

Основные понятия и уравнения интегральной математической модели пожара в помещении