Основные статистические характеристики многомерного регрессионного анализа в моделировании массовой оценки недвижимости

Лекция № 10

ОСНОВНЫЕ ТИПЫ МАТЕМАТИЧЕСКИХ СВЯЗЕЙ

Количественная зависимость одних показателей от других характеризуется формой связи. В экономическом анализе встречаются два типа связи между результативными показателями и факторами производства: функциональная и корреляционная.

Функциональная (полная) - классическая, например. Законы механики, физики. Первый тип — функциональная (или детерминированная) связь - выражается в виде формульной зависимости. В этом случае одна из переменных полагается независимой, а другая - зависимой. Зная точное значение независимой переменной и подставляя его в связующую формулу, получим единственное значение зависимой переменной.

При функциональной связи за изменением одного признака (независимой переменной, фактора, аргумента) всегда следует строго определенное изменение другого (зависимой переменной, результата, функции). Такая связь возможна, если вторая величина зависит только от первой и ни от чего более. Функциональная связь может быть выражена математическим уравнением, действительным для любого значения аргумента.

Определению функциональной связи препятствует метеорологические, психологические, объективные моменты. Поэтому в практике имеем дело с корреляционной связью. При статистической связи наряду с изучаемым фактором на результат действуют многие случайные причины. Это приводит к тому, что разным значениям фактора соответствуют разные вероятностные распределения. При одной и той же величине аргумента можно иметь каждый раз новые значения функции. Потому при корреляционной связи говорят не о точных, а о средних изменениях, их соотношениях.

Статистическая, корреляционная (неполная) - тип связи, который проявляется как тенденция, т.е. в общем при массовых наблюдениях. При корреляционной связи изменение независимой переменной влияет на изменение среднею значения зависимой переменной.

О практической ценности построенных производственных функций можно судить только после оценки полученных результатов.

Эффективное применение оценщиком «оценочных» моделей во многом предопределяется знаниями рынка недвижимости и владением аппарата МРА (линейного и нелинейного). По результатам модельных расчетов стоимости недвижимости необходимо дать квалифицированное заключение: насколько модельная расчетная стоимость недвижимости адекватна объективно сложившейся на рынке стоимости?

Ответ на этот вопрос можно дать с помощью статистических характеристик используемой «оценочной» модели относительно ее адекватности объективной реальности.

К ним относят корреляционное отношение (R), коэффициент определенности (детерминации) (D2), среднеквадратическую ошибку () и коэффициент вариации (Cy). Каждая из этих характеристик отражает степень адекватности используемых в модели статистических уравнений.

Вторая группа статистических характеристик определяет статистическую значимость отдельных переменных модели: коэффициент корреляции (r), критерии Стьюдента и Фишера и бета-коэффициент.

Практика применения корреляционного анализа. Корреляционно-регрессионный анализ может быть представлен двумя методами: методом парной корреляции и методом множественной корреляции (многофакторным анализом).

Парная корреляция подразумевает выявление наличия и формы корреляционной зависимости между результативным показателем (ценой) и одним из анализируемых факторных признаков (характеристикой). При этом обычно предполагается условное равенство всех прочих характеристик в сравниваемых объектах, а результативный показатель есть функция от значения анализируемой ценообразующей характеристики аналогичных объектов.

Y=f(х)

Коэффициент корреляции (r) является одной из статистических характеристик, относящихся к анализу значимости отдельных переменных регрессионной модели. Коэффициент корреляции показывает, насколько зависимость от , выраженная выборкой, близка к линейной. (Указывает на степень тесноты связи между фактором и результатом производства.). Он служит мерой линейной зависимости между двумя переменными, принимая значения в интервале от -1 до +1. При этом необходимо иметь в виду, что нулевое или близкое к нулю значение (r) не означает «отсутствие» зависимости (между двумя переменными), а лишь указывает на «отсутствие» линейной зависимости (может быть еще и нелинейная зависимость). Величина коэффициента корреляции отражает не тесноту связи и вообще, а близость связи к линейной. Существуют примеры, когда коэффициент корреляции по абсолютной величине мал (линейная связь слабая), а реальная связь результата производства с производственными факторами тесная. Если =0-0,15 – связь отсутствует; если =0,3-0,4 – умеренная; =0,4-0,6 – средняя; =0,7-0,8 – связь хорошая; >0,8 – связь очень хорошая, зависимость близка к линейной и производственную функцию можно представить в форме линейной регрессии.

По общему направлению корреляционная связь может быть прямой или обратной. При прямой связи увеличение факторного признака приводит к повышению результативного, и наоборот, если при повышении факторного признака результативный уменьшается, это говорит о наличии обратной связи.

При - связь обратная, т. е. с увеличение фактора значение результата уменьшается (рис. 1).

Если - связь прямая (рис. 2), если - связь функциональная.

Одним из главных статистических показателей, знак, при котором указывает направление корреляционной связи, является коэффициент корреляции (знак «+» говорит о наличии прямой связи, «-» - обратной). Коэффициент корреляции является мерой тесноты связи между ценой и анализируемой характеристикой.

Чем ближе его значение по модулю к 1, тем теснее связь. В силу того, что сравниваемые объекты имеют, как правило, несколько ценообразующих характеристик, линейный коэффициент корреляции может использоваться для выделения какой-либо одной из них, оказывающей максимальное влияние на формирование цен выбранных объектов-аналогов.

Линейный коэффициент корреляции рассчитывается следующим образом:

Для парной (однофакторной) зависимости (К=1) выборочное значение коэффициента парной корреляции вычисляется по формуле:

Будем обозначать Х независимую переменную (факторный показатель), У - зависимую переменную (результативный показатель). Для корреляционной связи значению факторного показателя Х ставится в соответствие не единственной значение результативного показателя У, как при функциональной связи, а некоторое распределение значений У.

Корреляционно-регрессионный анализ заключается в установлении степени тесноты связи (корреляционный анализ) и ее формы, т.е. аналитического выражения, связывающего выражения, связывающего переменные (регрессионный анализ).

Первым шагом в проведении исследования является построение специального графика, называемого корреляционным полем, или диаграммой рассеяния. На координатной плоскости по оси абсцисс откладывается значение факторного показателя, а но оси ординат- соответствующее значение результативного показателя. На плоскости отмечается точка, для которой отложенные по осям значения являются координатами. Каждой паре наблюдений (X, У) будет соответствовать точка корреляционною ноля. Чем теснее связь между переменными, тем более плотно точки должны располагаться вокруг некоторой лини. Эта линия будет графиком аналитической зависимости между переменными. Если точки корреляционного поля, беспорядочно разбросаны на координатной плоскости, то это означает отсутствие тесной взаимосвязи между переменными.

Пример 1

Рассмотрим взаимосвязь между площадью (х) и стоимостью земельных участков. На основании представленных наблюдений построить корреляционное поле зависимости. Соответствующее корреляционное поле представлено на рисунке.Визуальный анализ графика показывает, что зависимость между переменными вполне реальна. В данном случае в качестве ее аналитического выражения может выступать, например, прямая с положительным угловым коэффициентом.

В общем случае если с увеличением или уменьшением факторного показателя наблюдается концентрация значений результативною показателя около прямой с положительным наклоном, то говорят, что имеет место линейная положительная корреляционная связь, или положительная корреляция. Если факторный показатель изменяется в одном направлении, а соответствующие значения результативною показателя располагаются достаточно тесно около прямой, имеющей отрицательный угловой коэффициент, то такая связь называется линейной отрицательной корреляционной связью, или просто отрицательной корреляцией.

Пример отрицательной корреляции

Х- удаленность земельного участка от центра

У- стоимость земельного участка

На рисунке 2 представлен график корреляционного поля для пар наблюдений:

Х— удаленность земельного участка от центра, У- стоимость земельного участка. Отрицательная корреляция здесь очевидна.

Корреляция может быть необязательно линейной (рис.З).

Нелинейная корреляция

Х - удаленность земельного участка от железнодорожной

станции

У - стоимость земельного участка

Когда имеем дело с множественной зависимостью (К>1) можно ввести коэффициент множественной корреляции для пар отдельных факторов: и так далее, которые отражают коррелированность соответствующих факторов (но только в смысле линейной связи).

В случае зависимости результата производства от двух факторов совокупный коэффициент равен:

где ryx1,x2 коэффициент парной корреляции между соответствующими факторами и результатом.

Cсуществующее программное обеспечение позволяет рассчитать корреляционную матрицу коэффициентов корреляции между всеми парами переменных. При анализе корреляции той или иной независимой переменной с зависимой переменной следует иметь в виду, что коэффициент корреляции является безразмерной величиной или процентным отношением, отражающим наличие только линейной зависимости между двумя переменными.

Например, рассчитаны два коэффициента корреляции, отражающие тесноту связи: между ценой и площадью объекта недвижимости ryx1 = 0,92 и ценой и местоположением ryx2 = 0,62. Это позволяет лишь утверждать, что для рассматриваемых двух пар существует линейная зависимость и для первой пары (стоимость объекта недвижимости от его площади) эта зависимость более существенна для данного регионального рынка недвижимости.

Существующее программное обеспечение позволяет рассчитать корреляционную матрицу коэффициентов корреляции между всеми парами переменных. При анализе корреляции той или иной независимой переменной с зависимой переменной следует иметь в виду, что коэффициент корреляции является безразмерной величиной или процентным отношением, отражающим наличие только линейной зависимости между двумя переменными. Например, рассчитаны два коэффициента корреляции, отражающие тесноту связи: между ценой и площадью объекта недвижимости ryx1 = 0,92 и ценой и местоположением ryx2 = 0,62. Это позволяет лишь утверждать, что для рассматриваемых двух пар существует линейная зависимость и для первой пары (стоимость объекта недвижимости от его площади) эта зависимость более существенна для данного регионального рынка недвижимости.

Тесноту нелинейных связей можно характеризовать выборочным корреляционным отношением:

;

где сглажен. - значение полученное по уравнению регрессионной зависимости; - среднее арифметическое значение;

уj – фактическое значение результативного показателя из выборки.

Область значения корреляционного отношения .

Корреляционное отношение показывает насколько принятая регрессионная зависимость, не обязательно линейных функций соответствует реальной статистической картине. Для линейной регрессии:

- случай множественной связи

- случай парной связи., .

Если связь с () тесна и близка к линейной, то как , так и будут близки 1, т. е. в случае линейной регрессии значения коэффициентов R и ry,x1... xk совпадают, но характеризуют различные аспекты статистической информации, полезно использовать их совместно.

Оценка погрешностей определения коэффициентов корреляции.

Коэффициенты корреляции рассчитываются по выборкам, они имеют статический характер. В связи с чем правомерен вопрос о достаточности расчета коэффициентов.

Оценку достоверности расчета коэффициента по приведенным формулам можно получить при помощи стандартной (среднеквадратической) ошибки определения коэффициента парной корреляции при достаточно большой выборке (n>50)

при малых выборках (n<30)

Стандартные ошибки определения коэффициента множественной корреляции и корреляционного отношения (R) могут быть оценены по формулам:

случай n>50

случай n<30

n- объем выборки;

К- число факторов.

Знание стандартной ошибки позволяет оценить достоверность расчета коэффициента корреляции при помощи правила трех сигм: если , то выборочная оценка коэффициента корреляции приемлема.

Для более полной оценки погрешности необходима оценка закона распределения коэффициентов корреляции. Используя критерий достоверности р, определяют погрешность коэффициента корреляции и корреляционного отношения: .

При n>50, допускаем, что распределение значений случайных величин подчиняется нормальному закону распределения. Расчетное значение критерия достоверности сравнивают с фиксированными значениями р - распределения Стьюдента, - вероятность ожидаемых выводов (0,95, 0,99, 0,999), - число степеней свободы по таблице Стьюдента.

Если табличного, то коэффициент корреляции является достоверным. Для оценки коэффициента корреляции в генеральной совокупности, рассчитывают его доверительные границы:

Когда закон распределения коэффициента корреляции отличается от нормального(случай , ):, в этом случае используется статистика Фишера. Доверительный интервал для коэффициента r0 в генеральной совокупности определится соотношением

где ;

tp – находится с помощью таблиц значений функции Лапласа по уровню доверительной вероятности р= 95%.

Критерий Стьюдента ( t - статистика) показывает меру значимости (или весомости) переменной регрессии на изменения зависимой переменной (цены сделки) и вычисляется как отношение соответствующего коэффициента регрессии (а) к его среднеквадратической ошибке (а):

. (15.13)

По определению из любой регрессионной модели можно определить параметры (а0, а1,…,аm) при соответствующих независимых переменных. Величина а характеризует среднеквадратическое отклонение коэффициента регрессии а и отражает погрешность при использовании этого коэффициента в качестве статистической характеристики связи независимой переменной Xi, и зависимой переменной У. Ошибка коэффициента регрессии рассчитывается по формуле, где

- средние квадратические отклонения;

- средние значения квадратов;

- квадраты средних значений, тогда ошибка коэффициента регрессии позволит определить доверительный интервал для коэффициентов регрессии по формуле:

где - коэффициент регрессии;

величина находится с помощью таблиц значений функции Лапласа, - уровень доверительной вероятности 95%.

В том случае, если значение t достаточно велико, то есть основание считать, что Xj, является значимой переменной при расчете У (цены продажи). Наоборот, если значение t мало, то можно предположить нулевое значение соответствующего коэффициента регрессии а1 , а также и несущественную значимость независимой переменной Xi, для моделируемой цены продажи У. Для данного критерия имеется специальная таблица, по которой можно определить его значение, исходя из числа степеней свободы (п - k - 1), где п - число переменных; k - количество независимых переменных. В общем случае, при достаточно большой статистической выборке (не менее 50 объектов недвижимости) значение t-статистики более ±2,00 свидетельствует о существенной значимости соответствующей независимой переменной, так как при таком табличном значении t-распределения Стьюдента нулевая гипотеза о равенстве нулю коэффициента регрессии отвергается (считается значимым). Предположим, что для 60 сделок с недвижимостью (число степеней свободы равно 58) t-статистика для независимой переменной - площадь объекта - определена на уровне 8,3. Табличное значение t-распределения Стьюдента для числа степеней свободы 58 равно ± 2,001, при котором с вероятностью 95% можно утверждать, что коэффициент регрессии не равен нулю. Следовательно, в данном случае при моделировании стоимости недвижимости площадь является существенной независимой переменной.

Критерий Фишера (F-статистика) связан с критерием Стьюдента и также используется для определения значимости независимых переменных регрессионной модели. В МРА математическая зависимость критериев Стьюдента и Фишера определяется уравнением

F = t2 (15.14)

Для определения этого критерия также имеются таблицы, как в специальной литературе, так и в учебниках по математической статистике В общем случае при достаточно большой выборке табличное значение F-статистики, превышающее 4,0, указывает на то, что соответствующая независимая переменная значима при моделировании У (стоимости недвижимости) с вероятностью 95%.

Бета-коэффициенты представляют собой «нормированные» коэффициенты регрессии, являющиеся мерой значимости отдельных переменных относительно друг друга. Бета-коэффициенты и коэффициенты регрессии связаны между собой следующим уравнением ,

где х - среднеквадратическое отклонение X;

sу - среднеквадратическое отклонение У.

Бета-коэффициенты эффективны, если необходимо сравнить относительную значимость независимых переменных. Допустим, например, что оценщику нужно определить; какая из двух переменных - площадь или эффективный возраст недвижимости - более значима для стоимости объекта недвижимости. Поскольку площадь измеряется в квадратных метрах, а эффективный возраст - в годах, коэффициенты регрессии нельзя сравнить непосредственно. Если обе переменные нормировать, то можно осуществить такое сравнение. Допустим, что бета-коэффициент для площади равен 0,3, а для эффективного возраста - (-0,45). Это означает, что при постоянных значениях остальных независимых переменных регрессионной модели увеличение площади, например на 10%, вызовет увеличение стоимости недвижимости на 3%. Аналогично, увеличение эффективного возраста на 10% снизит стоимость недвижимости на 4,5%. В данном случае, эффективный возраст в большей степени влияет на изменение стоимости недвижимости, чем ее площадь.

Кроме коэффициента корреляции в корреляционно-регрессионном анализе используются и другие статистические показатели: среднеквадратическое отклонение, среднеквадратическая ошибка, коэффициент вариации, достоверность и т.д.

Коэффициент определенности (детерминации) (D2).

Для количественной оценки степени тесноты связи вычисляют коэффициент детерминации. В случае линейной регрессии коэффициент детерминации равен квадрату корреляционного отношения.

Величина D2 соответствует доле (проценту) цен, «объяснимых» регрессионной моделью. Этот коэффициент может принимать значения в интервале от 0 до 1. Когда D2 =0, никакая вариация (отклонение от средней цены) цен «не объясняется» моделью. Наоборот, когда D2 = 1, все отклонения от средней цены У «объясняются» уравнениями регрессии.

Коэффициент детерминации характеризует: какая доля изменений величины у обусловлена изменением факторов (). Он показывает сколько % (какой удельный вес) занимает фактор в формировании результата, если D=0.9 , то говорят, что ~90% изменений величины (у) вызвано изменением производственных факторов - влиянием неучтенных факторов, если то D=25%.

По определению из любой регрессионной модели можно определить остаточную дисперсию (отклонения). Последняя отражает вариацию переменных от их средних значений («остатки») «не объяснимых» данной регрессионной моделью.

Степень влияния производственного фактора j на результат производства уj определим на основе дисперсий отклонений сглаженных значений от среднего наблюдаемого и отклонений наблюдаемых величин уj от сглаженных значений , т.е. от линии регрессии (Дост).

Дисперсии вычисляются по формулам:

; .

Помимо указанных дисперсий вводится их сумма:

; .Для линейной регрессии:

; .

Коэффициент детерминации D характеризует какая доля изменений величины у обусловлена изменением фактора х.

, тогда .

Величина (1-D) – характеризует долю изменений величины у от влияния неучтённых факторов. Коэффициент детерминации D=0,94 показывает, что 94% изменений величины у вызвано изменением производственного фактора х, а (1-D)=1-0,94=0,06, т.е. 6% обусловлены влиянием неучтённых факторов. В случае линейной регрессии ; ; .

Среднеквадратическая ошибка модели () измеряет величину отклонения расчетных, (прогнозных) цен продаж, получаемых из регрессионной модели, от фактически сложившихся цен продаж на рынке. Величина представляет собой меру среднеквадратической ошибки или дисперсию регрессионной модели. В отличие от коэффициента D2, который выражается в долях (в процентах), измеряет отклонения (погрешность) в стоимостном выражении. Существующее программное обеспечение регрессионного анализа позволяет вычислить не только значение ; но и соответствующие доверительные интервалы для расчетной (модельной) стоимости по отдельным объектам недвижимости. Эта стоимость является функцией от и индивидуальных (количественных и качественных) параметров конкретных объектов недвижимости. Чем ближе параметры объекта недвижимости к параметрам типового объекта (их значения ближе к средним значениям), тем меньше среднеквадратическая ошибка и доверительный интервал расчетной (модельной) стоимости.

=- стандартное отклонение уj от поверхности регрессии.

Выборочная оценка дисперсии отклонения случайной величины уj от линии регрессии равна

;

Несмещённая выборочная оценка стандартного отклонения величины уj от линии регрессии составляет 0,4.

Можно найти % отклонения уj от . . Допустим, что изменяется от 9,22 до 14,28, тогда из пропорции находим, что % отклонения уj от . . составляет от 2,8% до 4,3%.

9,22 – 100 % 14,28 – 100%

0,4 – х 0,4 –х

х=4,3% х=2,8%.

Коэффициент вариации (Сy) в регрессионном анализе определяется как отношение к средней цене продажи (сделки):

Сy = Коэффициент Сy аналогичен показателю коэффициента вариации, используемого при анализе вариационного ряда и определяемого как отношение среднеквадратического отклонения цен продаж к средней цене.. Если предположить, что рассчитанная среднеквадратическая ошибка по регрессионной модели составила, например, 5000 у.е., а средняя цена сделок с недвижимостью определена на уровне 50 000 у.е., то коэффициент вариации будет равен (5000/50000 • 100%== 10%). Это означает, что при нормальном распределении случайных величин (цен продаж на рынке недвижимости) примерно 2/3 расчетных (модельных) цен из регрессионной модели находятся в пределах 10%-ных отклонений от средних цен. Такой результат моделирования стоимости недвижимости можно рассматривать как, безусловно, хороший.

Приведенные выше статистические характеристики в МРА можно рассматривать не только как оценочные параметры адекватности модели объективным реалиям, но и как инструмент калибровки модели посредством введения соответствующих корректировок.

Существующее программное обеспечение позволяет квалифицированному оценщику проводить такого рода «настройку» модели, работая в диалоговом режиме с компьютером.

Оценка меры достоверности анализируемого уравнения регрессии. Оценка меры достоверности (D) анализируемого уравнения регрессии производится с помощью процентного соотношения среднеквадратической ошибки уравнения (Sе) и математического ожидания по результативному признаку (У): Среднеквадратическая ошибка рассчитывается по формуле:

где Yj - фактическое значение цены 1 -го объекта-аналога;

Урасчетное - расчетное значение цены 1-го объекта-аналога по выбранному уравнению регрессии;

п - количество объектов в выборке;

1 - число параметров уравнения регрессии (Ао…Аn).

В случае, если максимальное значение D не превышает 15%, анализируемое уравнение регрессии достаточно корректно отображает корреляционную связь и может быть использовано для расчета стоимости оцениваемой недвижимости.

Пример. Рассмотрим применение некоторых указанных выше статистических характеристик в МРА. Предположим, что с помощью компьютерной программы проведен регрессионный анализ рыночных данных по сделкам с жилой недвижимостью. Результаты этого анализа на л-м этапе моделирования распечатаны (или представлены на дисплее компьютера) в следующем виде (табл. 15.6).

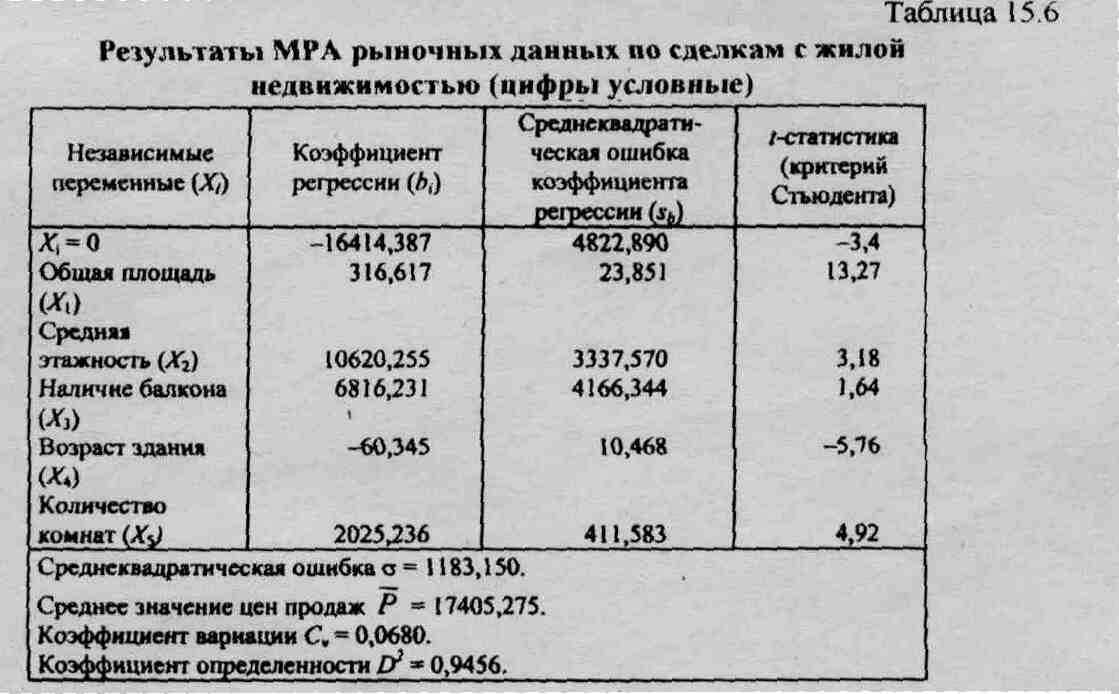
Критерий D2 равен 0,9456, что означает 94,5% вариаций (отклонений) цен продаж квартир от средней цены «объясняются» регрессионной моделью; абсолютная вариация цен продаж от средней составляет 1183,150 у.е. (Среднеквадратическая ошибка ), а коэффициент вариации Сy, равный 0,0680, свидетельствует о том, что две трети расчетных (модельных) цен из регрессионной модели находятся в пределах 6,8% вариаций (отклонений) от средних цен (при нормальном распределении случайных величин на рынке - цен продаж). Все это позволяет сделать вывод о высокой согласованности модели объективно сложившейся на рынке жилья конъюнктуры относительно рассматриваемых пяти факторов (независимых переменных).

Используя расчетные значения t-статистик (критерия Стьюдента), можно проранжировать независимые переменные по степени значимости их влияния на стоимость квартиры; 1) общая площадь, 2) возраст здания, 3) количество комнат, 4) средняя этажность квартиры, 5) наличие балкона. Как видно, наиболее существенно влияет на стоимость квартиры ее общая площадь (t = 13,27), а наименее существенно - наличие балкона (t = 1,64).

Уравнение (модель) стоимости квартиры (V) можно сформулировать в аналитической форме, используя полученные из регрессионной модели коэффициенты регрессии:

V = -16414,387 + 316,617 •X1 + 10620,255 • Х2 + 6816,231 •Хз - 60,345 • Х4 + 2025,236•X5.

Имея соответствующие параметры той или иной квартиры, расположенной в рассматриваемом районе, можно рассчитать ее стоимость. Например, необходимо оценить стоимость квартиры для целей налогообложения, которая характеризуется следующими параметрами: общая площадь - 53,4 м2 находится на среднем этаже (не первый и не последний этажи), имеет балкон, ее возраст - 15 лет, состоит из двух комнат. Качественные характеристики квартиры (средняя этажность и наличие балкона) в модели закодированы бинарными переменными. Подставив эти значения независимых переменных в уравнение стоимости квартиры, получим:

V = -16414,387 + 316,617 • 53,4 + 10620,255 • 1 + 6816,231 • 1- 60,345 • 15 +

+2025,236•2 = 21074,743 у.е.

Таким образом, стоимость оцениваемой двухкомнатной квартиры составит 21000 у.е.

Рассмотрим применение корреляционно-регрессионного анализа для расчета стоимости оцениваемой недвижимости методом парной корреляции на следующем примере.

Пример. Необходимо оценить стоимость 1 сотки загородного земельного участка, расположенного в 85 км от города, используя информацию о продажах аналогичных земельных участков (табл. 8.9). При этом предполагается условное равенство всех прочих (кроме отдаленности от города) ценообразующих характеристик сравниваемых объектов. Таблица8.9

Аналоги	Расстояние до города, (Хia),км	Цена продажи (Yia), у.е./сотка	Линейная (Yi расч.)	Логарифмическая (Yi расч.)	Экспоненциальная (Yi расч.)	Степенная (Yi расч.)	Полиномиальная (Yi расч.)
1	25	400	379,03	416,01	455,69	542,59	405,25
2	35	340	331,53	325,92	338,57	315,65	332,63
3	45	270	284,03	258,63	251,55	210,61	261,41
4	60	18	212,78	181,598	161,09	132,54	183,45
5	90	65	70,28	73,03	66,07	68,996	65,49
6	100	45	22,78	44,82	49,09	58,23	40,97
математическое ожидание	59,17	216,67	-	-	-	-	-

Для расчета необходимых статистических показателей, а также коэффициентов регрессии можно использовать калькулятор или компьютер, имеющий стандартную программу статистических расчетов. Результаты расчетов по 5 видам регрессионной модели показаны в табл. 8.9 и 8.10.

Вид регрессионной зависимости	Коэффициент корреляции	Среднеквадратическая ошибка модели	Достоверность Коэффициент детерминации
Линейная У= -4,75х +497,78
Логарифмическая У=- 267,76lnX+1277.9
Экспоненциальная Y=957.7E-0.0297[
Степенная У=

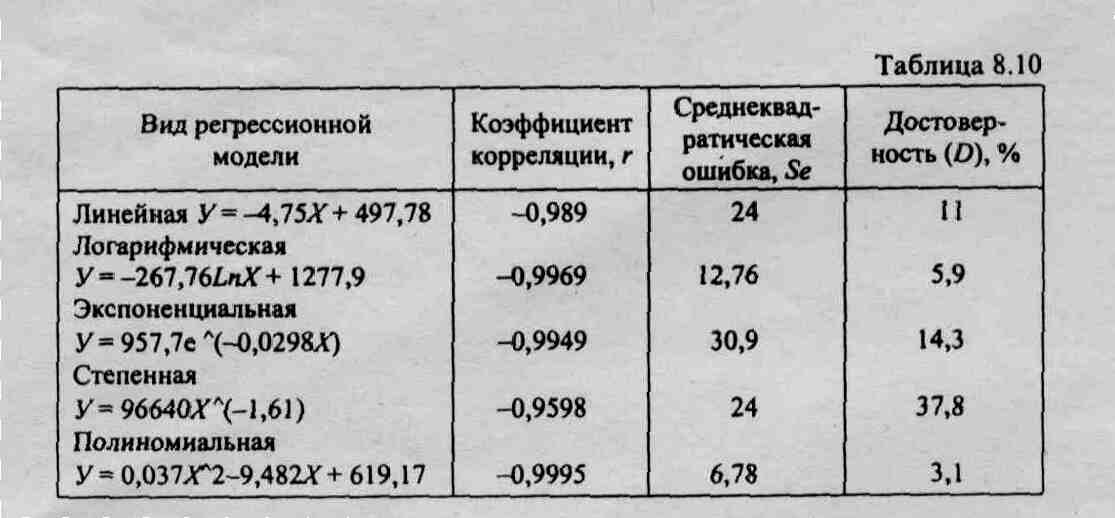
По полученным результатам можно судить о возможности использования каждого анализируемого вида регрессионной модели для расчета стоимости оцениваемого объекта. Наименьшее значение достоверности 3,1% и максимальная близость по модулю коэффициента корреляции к 1 свидетельствует о корректности применения именно полиномиальной модели, а следовательно, и наиболее высокой точности расчета стоимости оцениваемого объекта. Знак «-» при коэффициенте корреляции указывает на наличие обратной корреляционной связи между расстоянием от города и ценой на земельные участки.

Стоимость одной сотки оцениваемого земельного участка, рассчитанная на основе полиномиальной регрессионной модели, равна 80,53 у.е.

На рис. 8.2 представлена графическая интерпретация вышерассмотренных видов регрессионных моделей.

y=96640x-1,6097 …………Степенная модель (1ряд)

R2=0,9212

y=-4,7511x+497,78 -------Линейная модель (1 ряд)

R2=0,9782

y=-267,76Ln(x)+1277,9 ______Логарифмическая модель (1 ряд)

R2=0,9938

y=957,7e-0,0298x -.-.-.-.-.-.Экспоненциальная модель (1 ряд)

R2=0,9899

y=0,0372x2-9,4823x+619,17 ________Полиномиальная модель (1 ряд)

R2=0,999

Рис. 8.2. Зависимость цены продажи земельных участков от расстояния до города