Анализ данных

PAGE 22

Курс лекций для заочного отделения по дисциплине

«Анализ данных»


Содержание

[0.0.1] Этапы исследования данных с помощью методов Data Mining

[0.0.2] Методы Data Mining

[0.0.2.1] 3) Деревья решений

[0.0.2.2] 5) Нейронные сети

[0.0.2.3] 7) Генетические алгоритмы

[0.0.2.4] 8) Эволюционное программирование

[0.0.2.5] 9) Визуализация (когнитивная графика)


ТЕМА 1: Статистика выводов

Основные компоненты статистики выводов являются:

  • Доверительные интервалы;
  • Критерии проверки гипотез.

1.1. Доверительные интервалы

Доверительные интервалы помогают определить точность оценки истинного среднего на основе выборочного среднего.

Основные свойства распределения и выборки при определении доверительного интервала:

  1. выборочное среднее приблизительно удовлетворяет нормальному распределению со средним распределением и стандартным отклонением , где n – размер выборки;
  2. в нормальном распределении около 95% значений попадают в диапазон двух стандартных отклонений от среднего. Пример: если = 10, а n = 25, то выборочное среднее удовлетворяет нормальному распределению со средним и стандартным отклонением 2. Т.е. с вероятностью 95% выборочное среднее попадает в диапазон отклонения на 4 единицы от . Это значит, что если выборочное среднее равно 20, то с вероятность 95% находится в диапазоне от 16 до 24. Этот диапазон называется доверительным интервалом. Для уменьшения доверительного интервала нужно увеличить размер выборки.

Нужно вычесть среднее распределение из выборочного среднего и разделить частное на стандартную ошибку. Полученное значение удовлетворяет стандартному нормальному распределению и называется z-статистикой: .

Для случайной переменной Z должно выполняться условие:

(1.1)

Формула расчета доверительного интервала с учетом z-статистики:

(1.2)

где - среднее отклонение;

- стандартное отклонение;

n – размер выборки;

P – вероятность попадания в центр распределения;

- вероятность попадания в один из хвостов распределения (которая равна 1-P);

Z – случайная переменная. При P=0,95 и =0.05

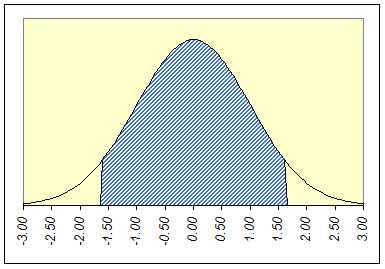Рис. 1.1. Двустороннее z-значение

Т.о. верхняя и нижняя границы доверительного интервала для равны .

1.2. Проверка гипотез.

Метод проверки гипотез основан на создании теории изучаемого явления и проверке ее обоснованности с помощью статистических параметров. В статистике сначала формулируется теория, затем собираются данные, и выполняется проверка.

Алгоритм создания и проверки теории (рис. 1.2):

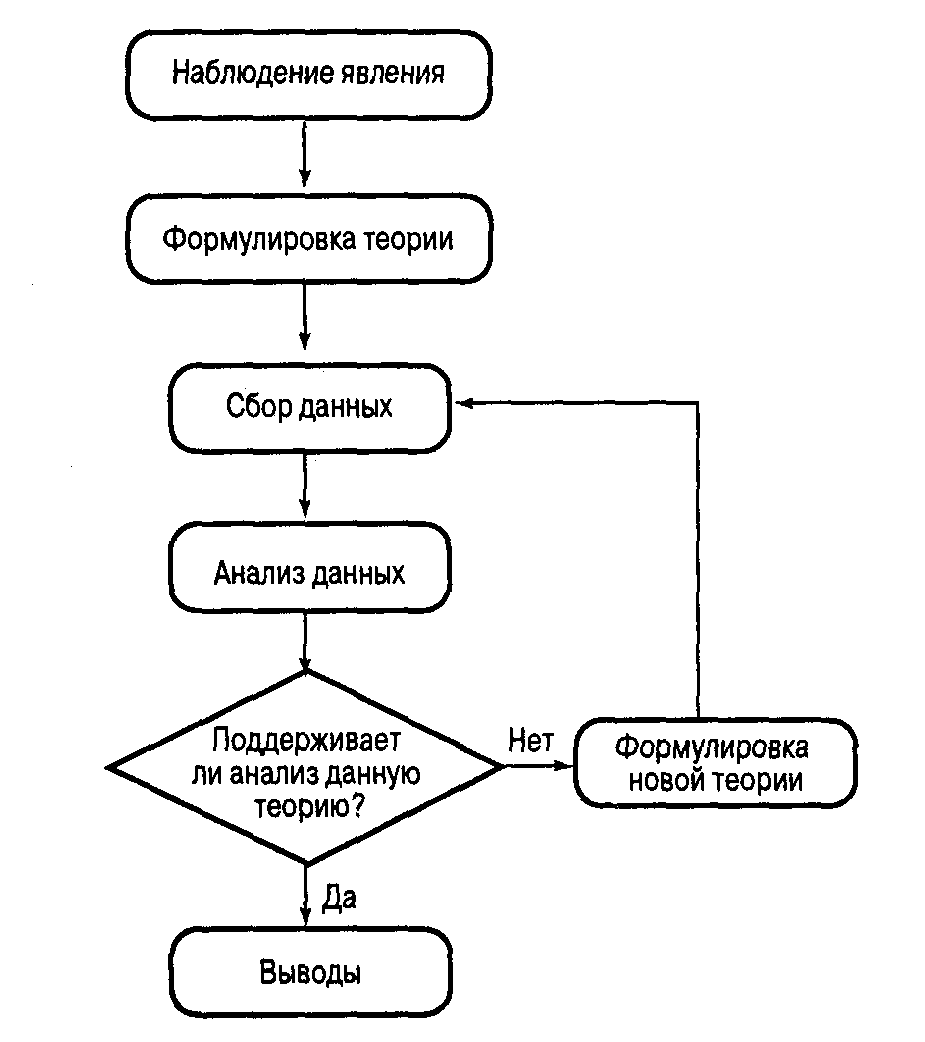
Рис. 1.2. Создание и проверка теории

Проверка гипотезы включает четыре основных элемента:

  1. Формулировка нулевой гипотезы .
  2. Формулировка альтернативной гипотезы .
  3. Вычисление статистики теста.
  4. Определение области непринятия гипотезы.

Нулевая гипотеза, или нуль-гипотеза представляет используемую по умолчанию или общепринятую теорию изучаемых явлений. Нулевая гипотеза считается истинной, если только нет убедительных контраргументов.

Альтернативная гипотеза представляет альтернативную теорию, которая автоматически считается истинной, если отвергается нулевая гипотеза.

Статистика теста — это статистика, вычисленная после анализа данных, которые используются для принятия или непринятия нулевой гипотезы.

Область (или диапазон) непринятия гипотезы — это набор значений статистики теста, для которых нулевая гипотеза отвергается (или принимается).

Типы ошибок

1. Ошибка первого типа заключается в отказе от нулевой гипотезы, которая на самом деле является истинной. Обозначение: .

2. Ошибка второго типа заключается в принятии нулевой гипотезы, тогда как на самом деле истинной является альтернативная гипотеза. Обозначение: .

В статистике используется предельное значение, которое называется уровнем значимости и является самым высоким значением, допускающим вероятность возникновения ошибки первого типа. Чаще всего для уровня значимости используется величина 0,05; т.е. если нулевая гипотеза верна, то данные попадают в этот диапазон непринятия с вероятностью 0,05, причем в таком случае нулевая гипотеза отвергается.

Области принятия и непринятия

Область непринятия гипотезы. Наоборот, значения внутри данного диапазона образуют область принятия гипотезы, т.е. при попадании значений выборочного среднего в эту область нулевая гипотеза принимается. Верхняя и нижняя границы области принятия гипотезы называются критическими значениями, так как занимают критически важное положение при определении приемлемости или неприемлемости нулевой гипотезы.

Попробуем применить эту формулу в данном примере, где 0 = 50, = 15, n = 25, = 0,05, т.е. вероятность возникновения ошибки первого типа равна 5%. Поэтому область принятия гипотезы вычисляется так:

граница области принятия = .

Любое значение меньше 44,12 или больше 55,88 дает основание для отказа от нулевой гипотезы. Поскольку 45 попадает в область принятия гипотезы, то следует принять нулевую гипотезу и не считать, что внедрение нового технологического процесса снижает количество дефектных резисторов в партии.

Вероятность того, что некое значение так же экстремально, как и наблюдаемое заданное значение, называется p-значением и вычисляется при помощи z-значения: . p-значение для одностороннего теста вычисляется как:

р-зачение=НОРМСТРАСП(z).

Если р меньше, чем =0,05 (при 95% доверительном интервале), то нулевая гипотеза отвергается с уровнем значимости , иначе нулевая гипотеза принимается.


ТЕМА 2: Регрессия и корреляция

2.1. Регрессия

В регрессионном анализе рассматривается связь между одной переменной, называемой зависимой переменной, и несколькими другими, называемыми независимыми переменными. Эта связь представляется с помощью математической модели, т.е. уравнения, которое связывает зависимую переменную с независимыми с учетом множества соответствующих предположений. Независимые переменные связаны с зависимой посредством функции регрессии, зависящей также от набора неизвестных параметров. Если функция линейна относительно параметров (но необязательно линейна относительно независимых переменных), то говорят о линейной модели регрессии. В противном случае модель называется нелинейной.

Статистическими проблемами регрессионного анализа являются:

  1. получение наилучших точечных и интервальных оценок неизвестных параметров регрессии;
  2. проверка гипотез относительно этих параметров;
  3. проверка адекватности предполагаемой модели;
  4. проверка множества соответствующих предположений.

Две причины использования регрессионного анализа:

  1. Описание зависимости между переменными помогает установить наличие возможной причинной связи.
  2. Для получения предиктора для зависимой переменной, т.к. уравнение регрессии позволяет предсказывать значения зависимой переменной по значениям независимых переменным.

Величина линейной зависимости между двумя переменными измеряется посредством простого коэффициента корреляции, величина линейной зависимости одной переменной от нескольких измеряется множественным коэффициентом корреляции.

Простая линейная взаимосвязь

При выполнении анализа линейной регрессии пытаются найти такую линию, которая наилучшим образом оценивает взаимосвязь между двумя переменными (зависимой переменной y и независимой переменной x). Такая линия называется подогнанной линией регрессии, а описывающее ее уравнение – уравнением регрессии.

Уравнение регрессии

Для подгонки линии регрессии используется уравнение вида: , где y – зависимая переменная, значения которой нужно предсказать; х — независимая переменная, или предиктор, на основе которой нужно сделать предсказание; а и b — коэффициенты.

На рис. 2.1 показана линия с коэффициентами а = 10 и b = 2. Короткие вертикальные отрезки представляют собой ошибки или остатки, т.е. промежутки между подогнанной линией и точками. Остаток — это разность между наблюдаемыми и предсказываемыми значениями.

Если линия направлена вниз так, что при возрастании значений переменной х уменьшаются значения переменной у, то линия регрессии имеет отрицательный наклон. Например, если переменная х обозначает возраст автомобиля в годах, а переменная у — его цену, то в таком случае наклон обозначает ежегодное снижение цены. В этом примере пересечение регрессии обозначает цену нового автомобиля, а остатки представляют разницу между фактической и предсказанной ценой. Если при прочих равных условиях линия регрессии правильно моделирует ситуацию, то положительный остаток означает завышенную цену данного автомобиля, а отрицательный — заниженную (т.е. выгодное предложение).

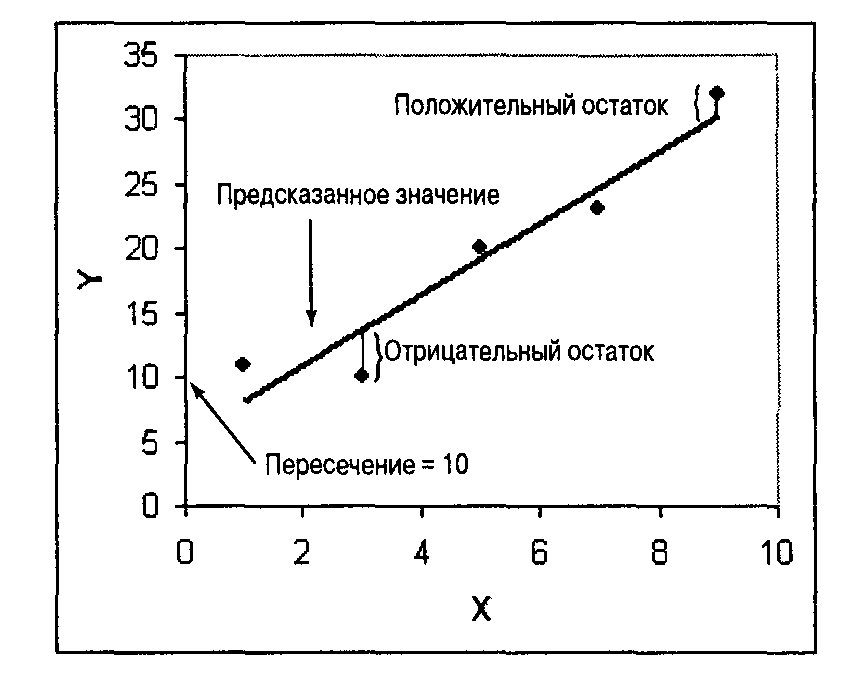
Рис. 2.1. Подогнанная линия регрессии

В Excel предусмотрено несколько функций для оценки регрессии на основе метода наименьших квадратов. В табл. 2.1 описаны две такие функции:

Табл. 2.1. Функции Excel для оценки регрессии на основе метода наименьших квадратов

Например, если значения переменной у находятся в ячейках диапазона А2:А11, а значения переменной x — в ячейках диапазона В2:В11, то функция ОТРЕЗОК (А2:А11, В2:В11) вернет значение коэффициента а, а функция НАКЛОН(А2:А11, В2:В11) — значение коэффициента b.

Для создания диаграммы для анализа регрессии необходимо выбрать меню Вставка Диаграмма Точечная диаграмма Выбрать необходимый диапазон для анализа, состоящий из зависимой и независимой переменных Добавить линию регрессии

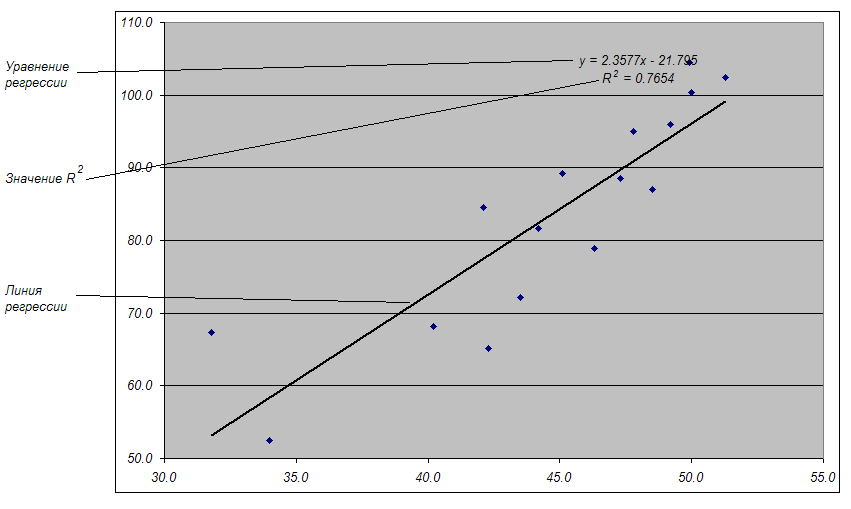Рис. 2.2. Подогнанная линия регрессии

Величина R2 – величина достоверности аппроксимации, которая измеряет процентную долю изменчивости значений зависимой переменной, которая может объясняться изменениями независимой переменной. Величина R2 может изменяться от 0 до 1. В данном случае значение 0,7654 говорит о том, что изменчивость, составляющая 76,54% может объясняться изменениями от независимой переменной. Оставшаяся доля (23,46%) изменчивости может объясняться случайной изменчивостью.

Для анализа регрессии используется инструменты модуля Пакет анализа (Analysis ToolPak) Регрессия.

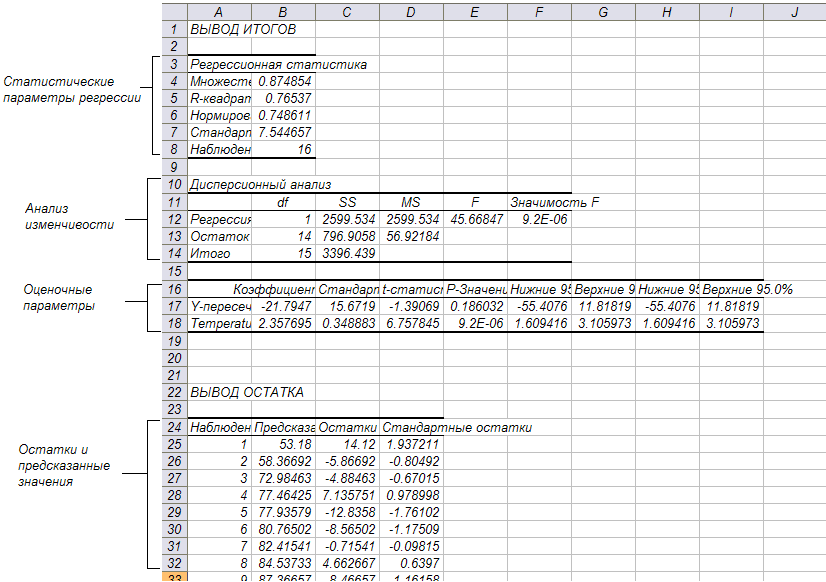
Рис. 2.3. Результат выполнения команды Регрессия из пакета анализа данных

Интерпретация параметров регрессии

- статистические параметры регрессии

Регрессионная статистика

Множественный R

(Коэффициент множественной корреляции) описывает корреляцию между предсказываемой переменной и линейной комбинацией предикторов

R-квадрат

Величина достоверности аппроксимации

Нормированный R-квадрат

Для анализа регрессии с несколькими предикторами

Стандартная ошибка

Типичное отклонение (x,y) от линии регрессии

Наблюдения

Размер выборки

- результат анализа изменчивости

Дисперсионный анализ

 

df

SS

MS

F

Значимость F

Регрессия

1

2599.534

2599.534

45.66847

9.20184E-06

Остаток

14

796.9058

56.92184

Итого

15

3396.439

 

 

 

df – количество степеней свободы

SS – значения суммы квадратов. Общая сумма квадратов в ячейке на пересечении со строкой Итого содержит сумму квадратов отклонений уровня зависимой переменной от среднего. Общая сумма квадратов складывается из двух частей: одна определяется изменениями линии регрессии, а другая связана с хаотичными изменениями и указана в ячейке на пересечении со строкой Остаток.

MS – результат деления суммы квадратичных отклонений на количество степеней свободы (для определения стандартной ошибки).

F – результат отношения среднеквадратического значения для регрессии и среднеквадратического значения для остатков. Большая величина F - отношения означает большую статистическую значимость регрессии.

- оценка статистических параметров

(см. предыдущую тему)

- остатки и предсказываемые значения

Наблюдение

Предсказанное

Остатки

Стандартные остатки

1

53.17999556

14.12000444

1.937211191

…

…

…

…

16

99.15503896

3.344961035

0.458916

Остаток – разность между наблюдаемыми значениями и линией регрессии (предсказываемыми значениями).

Стандартные остатки – нормированные остатки, которые не зависят от исходной единицы измерения.

,

где n – количество наблюдений в наборе данных

2.2. Корреляция

Корреляция выражает силу взаимосвязи по безразмерной шкале от -1 до 1 (величина наклона в уравнении регрессии, зависящая от единицы измерения данных).

Положительная корреляция означает сильную положительную взаимосвязь, т.е. увёличение одной переменной вызывает увеличение другой переменной (рис. 2.4). Например, такая корреляция наблюдается между ростом и весом человека. Отрицательная корреляция означает сильную отрицательную взаимосвязь, т.е. увеличение одной переменной вызывает уменьшение другой переменной (см. рис. 2.4). Например, увеличение цены товара может сопровождаться уменьшением объема продаж. Близкая к нулю корреляция означает, что между двумя переменными нет никакой взаимосвязи. Кроме того, между переменными может существовать нелинейная взаимосвязь, которая характеризуется нулевой корреляцией.

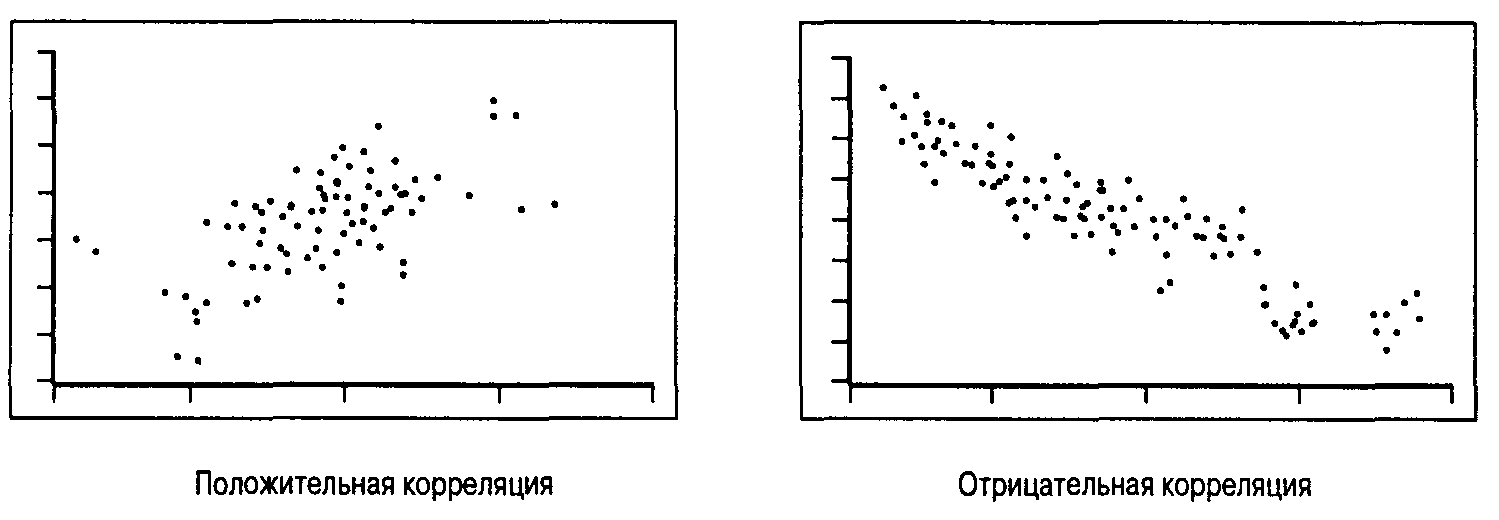
Рис. 2.4. Примеры корреляции

Наклон корреляции может выражаться любым действительным числом, но корреляция всегда должна быть в промежутке от — 1 до +1. Корреляция + 1 означает, что все точки данных падают точно на одну линию с положительным наклоном. В таком случае все остатки равны нулю, а подогнанная линия регрессии точно проходит через все точки.

Для вычисления корреляции в Ехсеl предусмотрено несколько функций, некоторые из них перечислены в табл. 2.2.

Табл.2.2. Функции вычисления корреляции

Матрица корреляции

При наличии нескольких переменных полезно вычислить корреляцию между переменными. Таким образом, можно сразу же получить представление о взаимосвязи между переменными, определяя пары переменных с сильной и слабой связью. Один из способов анализа таких данных заключается в создании матрицы корреляции, в которой значения корреляции (и соответствующие р-значения) располагаются в квадратной решетке.

Для создания матрицы корреляции используется меню StatPlus Multivariate Analysis Correlation Matrix (StatPlus Многовариантный анализ Матрица корреляции).

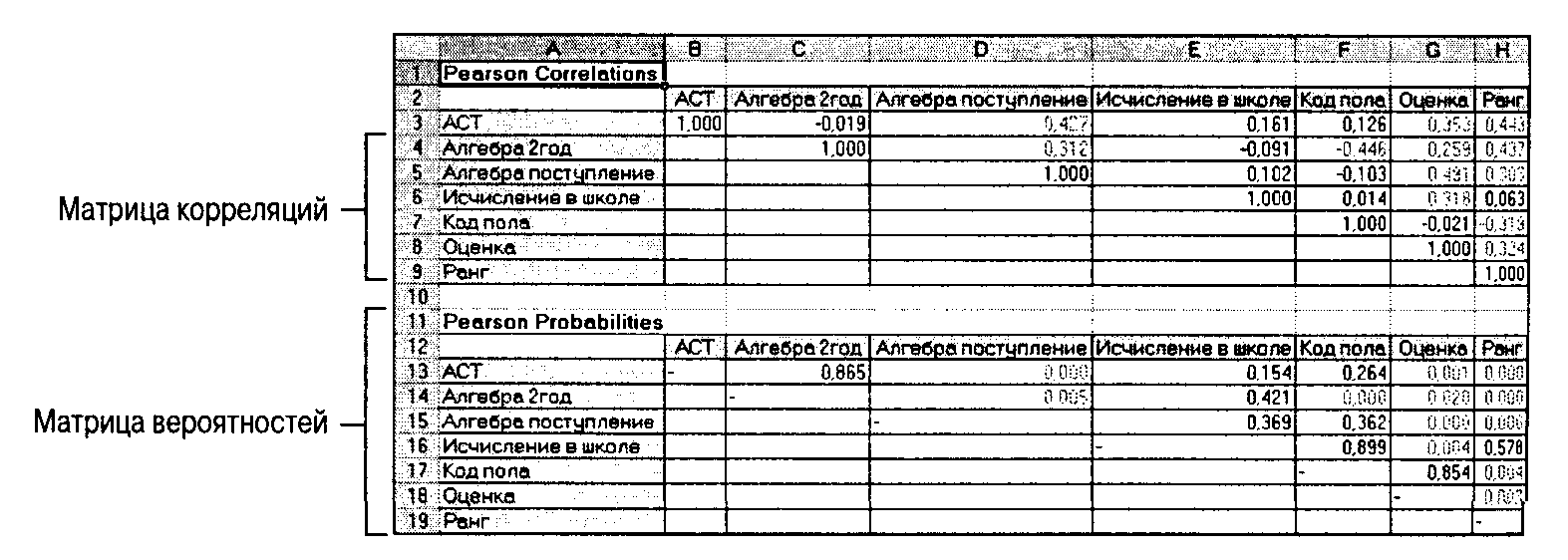
Рис. 2.5. Матрица корреляции

2.3. Множественная регрессия

Множественная регрессия позволяет оценивать статистические отношения между двумя и более переменными. Множественная регрессия также позволяет составлять уравнения, в которых значение одной из переменных (зависимой переменной) может быть предсказано на основе значений одной или нескольких независимых переменных. Метод множественной регрессии используется для прогнозирования значений любых числовых показателей (например, цен, объемов продаж) на основе значений других числовых показателей.

Уравнение множественной регрессии записывается следующим образом:

где Y – зависимая переменная, значение которой может быть предсказано на основе значений независимых переменных .

Для четырех независимых переменных уравнение множественной регрессии записывается следующим образом:

Где коэффициенты - неизвестные параметры,

- случайная ошибка с нормальным распределением со средним 0 и дисперсией .

Учтите, что предикторы могут быть функциями переменных, как в показанных ниже примерах моделей множественной регрессии.

Полиномиальная:

Тригонометрическая:

Логарифмическая:

Обратите внимание: все эти уравнения являются примерами линейных моделей, даже несмотря на использование в них тригонометрических и логарифмических функций. Слово “линейный” в определении линейная модель относится к коэффициентам и случайной ошибке , т.е. данные уравнения линейны по отношению к этим значениям. Например, можно создать новые переменные l=sin(x) и k=cos(x), а затем еще одну модель на основе линейного уравнения у=b0+b1l+b2k+.

После вычисления оценок для коэффициентов придется вставить их в уравнение для предсказания значений переменной y. Тогда оценочная модель регрессии выражается следующей формулой:

где — оценки коэффициентов , а остаток соответствует случайной ошибке .

Одной из задач анализа регрессии является предсказание значений.

  1. Нелинейная регрессия

Любая модель, вид которой не совпадает с уравнением линейной регрессии , называется моделью нелинейной регрессии и может быть представлена в виде

, i=1,…, n,

Где f( ) – нелинейная функция параметров ,

- некоррелированная ошибка.

Пример нелинейной функции и др.

ТЕМА 3: Временные ряды

Временной ряд — это последовательность наблюдений, зафиксированных в последовательные моменты времени, (например ежедневная температура, ежемесячные показатели стоимости ценных бумаг, ежеквартальные доходы или ежегодное потребление энергии). Анализ временных рядов включает поиск закономерности, которая помогла бы понять характер изменения данных и предсказать будущие наблюдения. Для некоторых временных рядов наблюдаются так называемые сезонные изменения, например, ежемесячные колебания объема продаж. Учет сезонных изменений имеет большое значение для точности предсказания.

Обычно наилучший способ анализа временных рядов — это создание диаграммы зависимости данных от времени для отображения тренда, сезонных изменений и выбросов.

Перед началом любых вычислений с временным рядом рекомендуется исследовать его графическими средствами:

команда меню Вставка – Диаграмма.

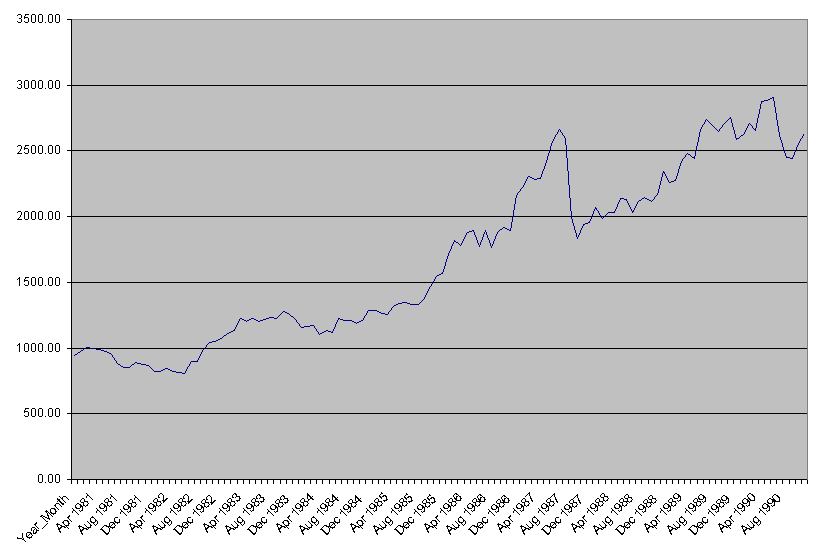Рис. 3.1. Диаграмма временного ряда

Для вычисления статистических параметров средних значений (ежемесячных) необходимо:

Меню StatPlus – Descriptive Statistics – Univariate Statistics – .

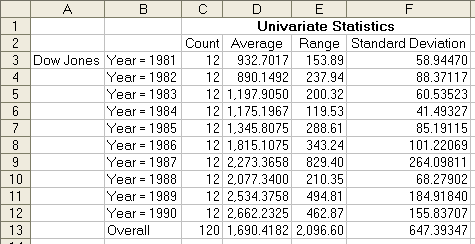
Рис. 3.2. Статистические параметры для средних значений (ежемесячных) в течение 1980-х годов.

Автокорреляционная функция

Если для временного ряда характерна повторяющаяся закономерность изменений, это может пригодиться для предсказания будущих наблюдений. Например, падение фактора ниже среднего значения в одном месяце может сопровождаться его ростом в следующем месяце. Или наоборот: падение фактора среднего значения в одном месяце может продолжиться в следующем месяце.

Для поиска таких закономерностей предназначена автокорреляционная функция, или АКФ, которая позволяет вычислять корреляцию значений временного ряда с его запаздывающими значениями. АКФ для интервала 1 (обозначается как r1) вычисляет степень взаимосвязи между значениями временного ряда с его запаздывающими значениями следующим образом:

.

Здесь – первое наблюдение,

– второе наблюдение и т.д.

– последнее наблюдение временного ряда.

АКФ для интервала 2 (обозначается как r2) вычисляется по формуле:

,

Общая формула АКФ для интервала k (обозначается как rk) имеет вид

Пример:

Среднее значение  = 5, =6, =4, =8,…, =7.

АКФ для интервала 1:

.

АКФ для интервала 2:

.

Полученные отрицательные значения соответствуют отрицательной корреляции между текущими и запаздывающими значениями (т.е. двумя предыдущими значениями). Это значит, что низкое значение в один момент времени говорит о наличии более высоких значений в следующие моменты времени. После аналогичных вычислений можно получить значение АКФ для интервала 3, равное 0,275. Эта положительная величина указывает на положительную взаимосвязь между значениями временного ряда, которые расположены с интервалом 3 пункта.

Для вычисления АКФ необходимо:

Меню StatPlus – Time Series – ACF Plot (StatPlus – Временной ряд – Диаграмма АКФ).

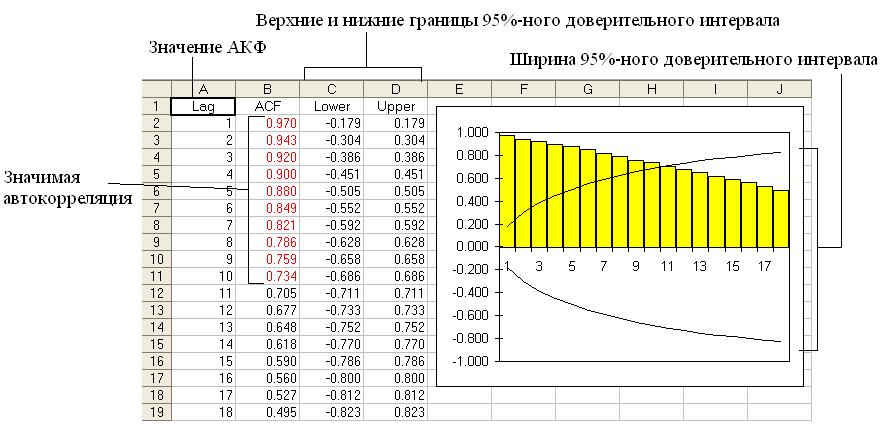
Рис. 3.4. Автокорреляционная функция для средних значений

Закономерности АКФ

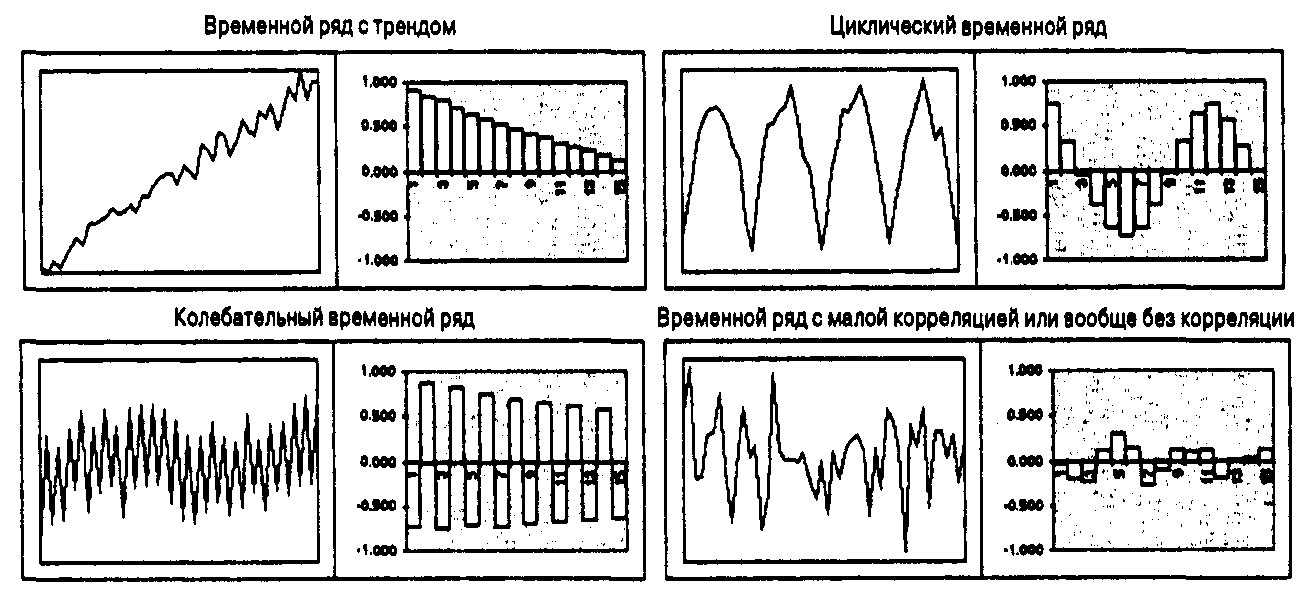
Рис. 3.5. Четыре примера временных рядов с разными закономерностями

Линейная фильтрация

Данные временного ряда могут непредсказуемо флуктуировать с течением времени. Для сглаживания непредсказуемых взлетов и падений значений временного ряда можно использовать средние значения для близких друг к другу значений. Например, можно вычислить среднее значение для недавних наблюдений и использовать его для сравнения с текущим значением.

Вычисленное среднее значение для каждых шести последовательно расположенных временных факторов (месяцев) называется скользящим средним для шести месяцев. (Вся процедура такого вычисления называется линейной фильтрацией.) Для вычисления скользящего среднего yсс(6) для шести значений временного ряда, которые располагаются перед значением уn, используется следующая формула:

,

где 6 – это период.

Период – количество наблюдений, используемое для вычисления скользящего среднего.

Для вычисления скользящего среднего необходимо создать линию тренда для точечной диаграммы. Тип линии – линейная фильтрация.

3.1. Простое экспоненциальное сглаживание

Экспоненциальное сглаживание часто используется для предсказания значения следующего наблюдения на основе текущего и предыдущего значений. В такой ситуации известно значение уn и нужно предсказать следующее значение — уn+1. Формула для предсказанного значения Sn называется экспоненциальным сглаживанием или однопараметрическим экспоненциальным сглаживанием:

,

Или

где w – фактор сглаживания (константа сглаживания).

После определения значения S0 можно вычислить следующие экспоненциально сглаженные значения:

Здесь Sn дает предсказанное значение для следующего наблюдения временного ряда.

3.2. Двухпараметрическое экспоненциальное сглаживание

Двойное экспоненциальное сглаживание сильнее сглаживает колебания в прогнозе и быстрее выявляет изменение тенденции развития (тренда), чем метод единичного экспоненциального сглаживания. В уравнении тренда кроме константы сглаживания w вводится дополнительная константа сглаживания T (параметр тренда).

Формулы двухпараметрического сглаживания подобны формулам однопараметрического сглаживания. Пусть Sn — это значение параметра размещения для n -го наблюдения, а Tn — параметр тренда. Для этих двух параметров нужно задать две константы сглаживания: w для параметра размещения Sn и t для параметра тренда Tn.

Тогда:

,

Аналогично, формула для предсказываемого значения уn-1 будет иметь следующий вид:

Метод декомпозиции

Временные ряды можно определить как хронологически упорядоченные данные, которые могут содержать один или более компонентов исследуемого показателя – тренд, сезонные, циклические и случайные компоненты. Декомпозиция временного ряда означает идентификацию и выделение этих компонентов из данных временного ряда. Относительно легко можно выделить тренд и сезонные компоненты.

Два типа сезонных колебаний:

  • Аддитивные сезонные колебания;
  • Мультипликативные сезонные колебания.

Аддитивные сезонные колебания учитываются как постоянная сезонная компонент, значение которой не зависит от тренда.

Прогноз, включающий тренд и сезонную компоненту (FIST) вычисляется по формуле:

FIST = Тренд + Сезонная компонента

Мультипликативные сезонные колебания учитываются путем умножения тренда на сезонный фактор, причем сезонные колебания зависят от тренда, который вычисляется по формуле:

FIST = Тренд * Сезонный фактор

ТЕМА 4: Когнитивный анализ. Графы.

Когнитивная карта ситуации – известные субъекту основные законы и закономерности наблюдаемой ситуации в виде ориентированного знакового графа, в котором вершины графа – это факторы (признаки, характеристики ситуации), а дуги между факторами – причинно-следственные связи между факторами.

Пример когнитивной карты некоторой экономической ситуации приведен на рис. 4.1.

Рис.4.1 Пример когнитивной карты

Для отображения детального характера влияний или динамику изменения влияния в зависимости от изменения ситуации требуется перехода на следующий уровень структуризации информации, отображенной в когнитивной карте, т.е. к когнитивной модели.

На этом уровне каждая связь между факторами когнитивной карты раскрывается до соответствующего уравнения, которое может содержать как количественные (измеряемые) переменные, так и качественные (не измеряемые) переменные.

В когнитивной модели выделяют два типа причинно-следственных связей: положительные и отрицательные.

Формально когнитивная модель ситуации может быть, как и когнитивная карта, представлена графом, однако каждая дуга в этом графе представляет уже некую функциональную зависимость между соответствующими базисными факторами, т. е. когнитивная модель ситуации представляется функциональным графом.

При анализе конкретной ситуации пользователь обычно знает или предполагает, какие изменения базисных факторов являются для него желательными. Факторы, представляющие наибольший интерес для пользователя, называются целевыми. Это – выходные факторы когнитивной модели. Задача выработки решений по управлению процессами в ситуации состоит в том, чтобы обеспечить желательные изменения целевых факторов.

Методика когнитивного анализа сложных ситуаций

Когнитивный анализ сложной ситуации

  1. Формулировка задачи и цели исследования;
  2. Изучение процесса с позиций поставленной цели;
  3. Сбор, систематизация, анализ существующей статистической и качественной информации по проблеме;
  4. Выделение основных характеристических признаков изучаемого процесса и взаимосвязей, определение действия основных объективных законов – это позволит выделить объективные зависимости, тенденции в процессах;
  5. Определение присущих исследуемой ситуации требований, условий и ограничений;
  6. Определение путей, механизмов действия – это позволит в дальнейшем определить стратегии поведения и предотвращения нежелательных последствий развития ситуации.

Моделирование

Моделирование – это средство получения теоретических и практических знаний о проблеме и формулирования на этой основе практических выводов.

Моделирование представляет собой циклический процесс. Знания об исследуемой проблеме расширяются и уточняются, а исходная модель постоянно совершенствуется.

Цель когнитивного моделирования заключается в генерации и проверке гипотез о функциональной структуре наблюдаемой ситуации до получения функциональной структуры, способной объяснить поведение наблюдаемой ситуации.

Основные требования к компьютерным системам когнитивного моделирования – это открытость к любым возможным изменениям множества факторов ситуации, причинно-следственных связей, получение и объяснение качественных прогнозов развития ситуации (решение прямой задачи «Что будет, если …»), получение советов и рекомендаций по управлению ситуацией (решение обратной задачи «Что нужно, чтобы …»).

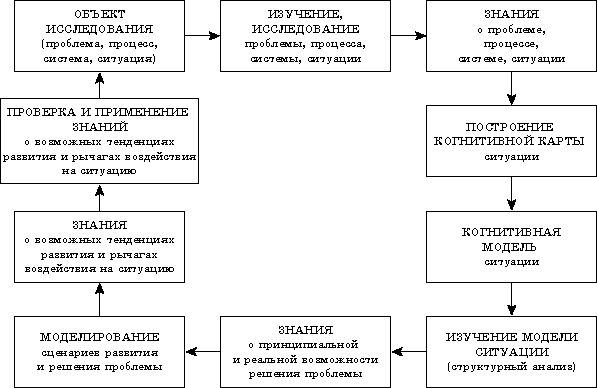
Рис. 4.2. Процесс моделирования

Этапы моделирования:

  • определение начальных условий, тенденций, характеризующих развитие ситуации на данном этапе. Это необходимо для придания адекватности модельного сценария реальной ситуации, что усиливает доверие к результатам моделирования;
  • задание целевых, желаемых направлений (увеличение, уменьшение) и силы (слабо, сильно) изменения тенденций процессов в ситуации;
  • выбор комплекса мероприятий (совокупности управляющих факторов), определение их возможной и желаемой силы и направленности воздействия на ситуацию;
  • выбор комплекса возможных воздействий (мероприятий, факторов) на ситуацию, силу и направленность которых необходимо определить;
  • выбор наблюдаемых факторов (индикаторов), характеризующих развитие ситуации, осуществляется в зависимости от целей анализа и желания пользователя.

ТЕМА 5: Системы аналитической обработки данных

  1. OLAP – технология (Оперативная система аналитической обработки данных)

OLAP – это сводные отчеты в разнообразных разрезах, создаваемых за считанные секунды самим пользователем по мере надобности и имеющие наглядную форму (таблицы, графики, диаграммы и т.д.). Например, если руководитель телекоммуникационной компании хочет увидеть динамику подключений к сети по времени года, то система покажет ему все данные о подключении по месяцам и сезонам, а также зависимость изменения объемов подключений от времени года или месяца и соответствие уровня подключений планам компании.

Гиперкуб – это некая фигура в многомерном пространстве, число измерений (осей) которого определяется факторами, важными для деятельности предприятия. OLAP-системы позволяют накапливать в гиперкубе всю информацию, которая может заинтересовать руководителя или аналитика. При этом в качестве осей могут использоваться, например, категории услуг, тарифы, география и объемы подключений, классы абонентов, время и т.д.

На сегодняшний день в состав мощных СУБД, например, в состав СУБД Oracle Database, входят специальные компоненты технологии многомерного анализа OLAP [33]. Они позволяют хранить и обрабатывать многомерную информацию на том же сервере баз данных, где находится реляционное хранилище. По функциональным возможностям эта подсистема сравнима с многомерной СУБД. Средства OLAP поддерживают в полном объеме основной язык сервера Express (или DML – язык обработки многомерных данных).

Технология OLAP дает возможность быстро менять взгляд на данные в зависимости от выбранных параметров и обеспечивает лицу, принимающему решения, полный обзор ситуации в бизнесе с его собственной стратегической точки зрения. Она принципиально отличается от традиционных технологий поддержки принятия решений, чаще всего базируется на анализе большого числа жестко структурированных отчетов. OLAP-системы позволяют консолидировать информацию из различных баз данных и представить ее в единых сводных таблицах. Также OLAP-системы обеспечивают непротиворечивость данных между отчетами: при детализации некоего итога независимо от настроек аналитических разрезов итоговая сумма всегда сходится.

  1. CRM – технология (Customer Relationship Management)

CRM – это направленная на построение устойчивого бизнеса концепция и бизнес стратегия, ядром которой является «клиенто - ориентированный» подход. Эта стратегия основана на использовании передовых управленческих и информационных технологий, с помощью которых компания собирает информацию о своих клиентах на всех стадиях его жизненного цикла (привлечение, удержание, лояльность), извлекает из нее знания и использует эти знания в интересах своего бизнеса путем выстраивания взаимовыгодных отношений с ними.

Каждый контакт должен работать на привлечение покупателя.

CRM-приложения позволяют компании отслеживать историю развития взаимоотношений с заказчиками, координировать многосторонние связи с постоянными клиентами и централизованно управлять продажами и клиент - ориентированным маркетингом, в том числе через Internet.

В зависимости от цели можно выделить три вида использования стандартных CRM-систем:

  • Системы оперативного использования. Применяются для повседневных управленческих целей.
  • Аналитические системы. Используются маркетологами для обработки больших объёмов данных (как правило, о клиентах) с целью получения новых знаний.
  • Коллаборационные системы. Позволяют клиенту влиять на деятельность фирмы в целом тем или иным образом (в том числе на процессы разработки, производства, доставки и обслуживания товара).

Следует отметить один из главных тезисов концепции CRM, который также можно отнести и к телекоммуникационным операторам: «наиболее желанный и прибыльный клиент имеет право на первоочередное и эксклюзивное обслуживание. Соль в том, чтобы учиться у своего клиента, иметь обратную связь и работать так, как клиент хочет. Сейчас мало сказать клиенту: «Мы здесь». Надо сказать: «Мы здесь для тебя, и работаем здесь для тебя, и даем тебе то, что ценно для тебя, предугадывая то, что ты хочешь».

  1. Интеллектуальный анализ данных (Data Mining)

Термин «Data Mining» переводится как «извлечение информации» или «добыча данных». Цель Data Mining состоит в выявлении скрытых правил и закономерностей в наборах данных. Результатом такого метода обработки данных являются эмпирические модели, классификационные правила, выделенные кластеры и т.д.

Этапы исследования данных с помощью методов Data Mining

  1. Приведение данные к форме, пригодной для применения конкретных реализаций систем Data Mining.
  2. Предварительная обработка данных с одинаковыми значениями для всех колонок.
  3. Применение методов Data Mining.
  4. Верификация и проверка получившихся результатов.
  5. Интерпретация.

Методы Data Mining

1) Кластеризация

Позволяет разделить изучаемую совокупность объектов на группы «схожих» объектов, разнести записи в различные группы, или сегменты.

К недостаткам кластеризации следует отнести зависимость результатов от выбранного метода кластеризации и методы кластерного анализа не дают какого-либо способа для проверки достоверности разбиения на кластеры.

(Предметно-ориентированные аналитические системы, к.п., $300 – $1000).

2) Ассоциация

Ассоциация, или метод «корзины покупателя», является одним из вариантов кластеризации, используемым для поиска групп характеристик, наблюдаемых одновременно. Анализ ассоциации имеет смысл в том случае, если несколько событий связаны друг с другом.

имеют форму:

если {условие}, то {результат}.

Примером такого правила, служит утверждение, что абонент, использующий услугу А, будет использовать услугу Б.

система WizWhy (WizSoft) (стоимость системы около $4000).

3) Деревья решений

При данном методе правила представляются в виде последовательной иерархической структуры, называемой деревом решений, при которой каждый уровень дерева включает проверку (test) определённой независимой переменной.

Иерархические структуры деревьев решений весьма наглядны. Их выразительная мощность в значительной степени определяется множеством, в котором ищутся критерии расщепления узлов.

Самыми известными являются See5/C5.0 (Австралия), Clementine (Integral Solutions,Великобритания), SIPINA (University of Lyon, Франция), IDIS (Information Discovery, США), Knowledge SEEKER (ANGOSS, Канада). Стоимость этих систем варьируется от $1000 до $10000.

4) Метод «ближайших соседей»

Цель данного метода заключается в том, чтобы предсказать значение зависимой переменной для некоторой записи из определенного массива, для которого известны значения как зависимой, так и независимой переменных. Для этого в этом массиве записей, выбирается запись, наиболее «близкая» к той, для которой необходимо сделать предсказание, и она интерпретируется как искомая зависимая переменная.

Примеры систем, использующих данный метод, – КАТЕ tools (Acknosoft, Франция), Pattern Recognition Workbench (Unica, США).

5) Нейронные сети

Нейронная сеть представляет из себя структуру, состоящую из узлов и связей между ними. Причем, для того чтобы данную сеть можно было бы применять в дальнейшем, её прежде надо «настроить» с использованием полученных ранее данных, содержащих значения входных и выходных параметров (правильные ответы). Настройка состоит в подборе весов межнейронных связей, обеспечивающих наибольшую близость ответов сети к известным правильным ответам.

Основной недостаток, сдерживающий использование нейронных сетей для извлечения знаний – их «непрозрачность». Построенная модель, как правило, не имеет четкой интерпретации (концепции «черного ящика»).

Примеры нейросетевых систем – BrainMaker (CSS), NeuroShell (Ward Systems Group), OWL (HyperLogic). Стоимость их довольно значительна: $1500 – $8000.

6) Нечеткая логика

Нечеткая логика] применяется для анализа таких наборов данных, когда невозможно причислить данные к какой-либо группе и возникает необходимость манипулировать категорией «может быть» в дополнении к «да» и «нет».

7) Генетические алгоритмы

Генетические алгоритмы обладают ярко выраженным свойством создания нового знания. Интуитивный анализ генетического алгоритма помогает выявить аналогии между искусственной генетической системой и свойственными человеческому интеллекту процессами, обычно называемыми творческими и инновационными (направленными на создание новшеств).

Одним из недостатком данного метода заключается в том, что критерий отбора хромосом и используемые процедуры являются эвристическими и далеко не гарантируют нахождения «лучшего» решения. Это становится особенно заметным при решении высокоразмерных задач со сложными внутренними связями.

Примером может служить система GeneHunter (Ward Systems Group). Её стоимость – около $1000.

8) Эволюционное программирование

Основная идея этого метода состоит в формировании гипотез о зависимости целевой переменной от других переменных в виде автоматически синтезируемых программ, выраженных на внутреннем языке программирования. Использование универсального языка программирования позволяет выразить практически любую зависимость или алгоритм.

PolyAnalyst [20], Стоимость системы около $10000.

NeuroShell. Стоимость системы до $5000.

9) Визуализация (когнитивная графика)

Графическое представление результатов работы систем Data Mining может значительно облегчить процесс восприятия и интерпретации нового знания человеком.

Визуализация позволяет рассматривать многомерные данные с разных точек зрения, непосредственно видеть, что происходит с моделью при добавлении новых переменных или, наоборот, при удалении одной или нескольких переменных. Визуализация позволяет уменьшать или, наоборот, увеличивать степень детальности модели, наблюдать естественные изменения, происходящие, например, с классификационным деревом решений при изменении порога отсечения малозначимых ветвей.

DataMiner 3D (Dimension5), стоимость которой может достигать нескольких сотен долларов.

Анализ данных