Физическая химия

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ РФ

Дальневосточный государственный университет

Кафедра физической химии и физико-химических проблем экологии

Физическая химия

Методические указания

для студентов нехимических специальностей ДВФУ

Владивосток

Издательство Дальневосточного федерального университета

2013

СОДЕРЖАНИЕ

Введение 2

Программа курса «Физическая химия» 3

1. Краткая характеристика газов 3

2. Основы химической термодинамики и термохимии 4

3. Химическое равновесие. Фазовое равновесие 9

4. Свойства разбавленных растворов 12

5. Химическая кинетика и катализ 16

6. Электрохимия 20

Рекомендуемая литература 23

Введение

«Физическая и коллоидная химия» – дисциплины, изучением которых завершается химическая подготовка специалистов биологов и биохимиков. Физическая химия является основой для дальнейшего изучения специальных дисциплин, поскольку предусматривает изучение связи между физическими процессами и химическими превращениями, протекающими при производстве, транспортировке, хранении, а также и в реализации полиграфической продукции.

Физическая химия – наука, которая, основываясь на законах физики, изучает химические превращения, происходящие в сложных физико-химических системах. Наиболее полезно изучение таких разделов физической химии, как термодинамика, фазовые равновесия, кинетика, свойства растворов электролитов и неэлектролитов, электрохимия.

Физическая химия обеспечивает преемственность и связь с неорганической, органической, аналитической химией, а также некоторыми разделами физики, т. е. обеспечивает целостную систему физико-химической подготовки специалиста.

Цель дисциплины – дать будущим специалистам знания, необходимые для профессионального решения вопросов производства, транспортировки, хранения и реализации полиграфической продукции.

В результате изучения дисциплины студент должен:

знать основные законы физической и коллоидной химии, методику расчета термодинамических и кинетических величин для определения направленности и условий протекания химических процессов, методы экспериментального определения основных физических и химических параметров процесса;
уметь применять полученные знания в профессиональной деятельности.

ПРОГРАММА КУРСА

«Физическая химия»

Краткая характеристика газов

Энергетическое взаимодействие между частицами вещества (атомами, молекулами, ионами) определяет существование его в твердом, жидком или газообразном состояниях (агрегатное состояние вещества). Взаимодействия между частицами у вещества в газообразном состоянии очень слабые, они усиливаются, когда вещество переходит в жидкое или твердое состояние. Если силы межчастичного притяжения больше энергии тепловых колебаний – вещества находятся в твердом состоянии. Твердое кристаллическое состояние характеризуется упорядоченной структурой (геометрически правильное расположение частиц в пространстве).

Если силы взаимодействий между частицами уже не способны преодолевать тепловые колебания, существующие связи между частицами рвутся и образуются новые, частицы смещаются относительно друг друга, и хотя контакт между ними сохраняется, нарушается геометрически правильная структура – это жидкое состояние. Таким образом, частицы в жидкости взаимосвязаны, но структура ее не определена, хотя на близком расстоянии от определенной частицы расположение других частиц может быть упорядоченным. Твердое и жидкое состояния называют конденсированным состоянием.

Если же частицы вещества не связаны друг с другом – это газообразное состояние.

Идеальный газ – это идеализированное состояние реальных газов при бесконечно малом давлении (концентрации). Принимается, что между частицами идеального газа нет никаких взаимодействий – ни притяжения, ни отталкивания. Частицы свободны и перемещаются беспрепятственно (неупорядоченное состояние), причем собственный объем молекул газа настолько мал по сравнению с объемом, в котором эти молекулы располагаются, что его можно не учитывать. Понятие идеальное состояние принято для упрощения первичного математического описания систем, а переход к реальному состоянию осуществляется путем введения в уравнения для идеального газа необходимых поправок (учитывая межчастичные взаимодействия и объем частиц).

В твердом состоянии вещество с трудом изменяет объем и форму (слабо сжимается и ничтожно мало деформируется), в жидком – с трудом изменяет объем, но легко может менять форму (чрезвычайно слабо сжимается, но свободно деформируется), а в газообразном – легко изменяет как объем, так и форму.

При очень высокой температуре (сотни тысяч градусов) энергия столкновений между частицами газа настолько велика, что молекулы разрушаются, а атомы теряют электроны, в результате чего образуется плазма, состоящая из ядер и электронов. Плазма рассматривается как четвертое – плазменное состояние материи (например, вещества внутри Солнца).

Газовые системы являются наиболее наглядными моделями при изучении законов термодинамики и кинетики. От свойств идеальных газов легко перейти к свойствам идеальных жидких растворов, а затем и к свойствам реальных растворов.

Уравнение состояния идеального газа определяет соотношение между давлением, температурой и объемом газа. Так, для случая переменных параметров состояния P, V и T они связаны между собой следующим образом:

(1.1)

где n – число моль идеального газа в объеме V, т.е., здесь m – масса газа, г;

M – молярная масса газа, г/моль;

R – универсальная газовая постоянная (коэффициент пропорциональности), которую для 1 моль идеального газа (из уравнения 1.1) можно выразить:

. (1.2)

В численном выражении (в системе СИ) универсальная газовая постоянная равна 8,31 Дж/моль.К, а учитывая, что 1 кал = 4,18 Дж, R = 1,987 кал/моль·К. Во внесистемных единицах R = 0,082 л·атм/моль·К.

Если в объеме V смешано несколько идеальных газов, то каждый из них будет оказывать на стенки сосуда свое собственное (парциальное) давление – такое, как если бы только один газ занимал весь объем. Тогда наблюдаемое полное давление будет равно сумме парциальных давлений каждого газа (закон Дальтона), и уравнение состояния для смеси газов А, В и С в объеме V при температуре Т примет вид:

PV = (PА + РВ + РС)V = (nА + nВ + nC)RT, (1.3)

где РА, РВ и РС – парциальное давление индивидуальных газов А, В и С, Па;

nA, nB и nC – количество моль отдельных газов А, В и С.

Отметим, что для реальных газов (с более высокими, т.е. реальными, концентрациями молекул) должны учитываться взаимные притяжения газовых молекул и их собственный объем, который будет занимать уже заметную долю от всего объема. Тогда объем, в котором движутся молекулы реального газа, будет не V, а V – b, где константа b – учет суммарного собственного объема молекул и их взаимного отталкивания (на малых расстояниях). Кроме того, вследствие наличия в реальном газе сил межмолекулярного притяжения, давление реального газа должно быть ниже давления идеального газа, что также необходимо учитывать, т.е. вводить еще один дополнительный коэффициент а, относящийся к свойству молекул конкретного реального газа. Тогда уравнение состояния (1.4) для реального газа принимает вид (Ван-дер-Ваальс):

, (1.4)

где a и b – константы, характеризующие свойства молекул данного реального газа; находятся экспериментальным путем.

2. Основы химической термодинамики и термохимии

Химическая термодинамика. Позволяет ответить на вопросы: возможно или невозможно протекание в системе желательных или нежелательных процессов, в каких условиях возможна или невозможна та или иная реакция? Это достигается путем установления связи между превращениями веществ (например, изменение их химического или фазового состава) и превращениями химической энергии в теплоту, работу или другие формы энергии.

Таким образом, химическая термодинамика описывает химические процессы, сопровождаемые выделением или поглощением теплоты и производством работы, посредством исследования изменений энергетического состояния компонентов (т.е. изменения количества теплоты и работы) в процессе перехода из одного состояния (1) в другое (2). Она рассматривает, в частности, переход энергии от одних веществ к другим, энергетические эффекты химических процессов, а в итоге устанавливает критерии направления и предела протекания любых химических процессов.

Химическая термодинамика позволяет рассчитать конечный результат – равновесный состав реакционной смеси, оценить максимально возможный выход продуктов реакции и подобрать оптимальные условия ее проведения. Для биологических систем термодинамика позволяет оценить вероятность протекания процесса по тому или иному механизму, отбросив те из них, которые противоречат ее законам. Это способствует лучшему пониманию биологических процессов, протекающих, например, в продуктах питания.

Объектами исследования химической термодинамики являются тепловые балансы физико-химических процессов, фазовые (плавление, испарение, возгонка и др.) и химические равновесия. Поэтому определение тепловых эффектов реакций – одна из основных задач химической термодинамики. В то же время механизм и скорость протекания процессов термодинамикой не рассматриваются, важны только свойства системы в исходном (1) и конечном (2) состояниях. Основана термодинамика на фундаментальных законах природы (постулатах), выведенных логическим путем.

Термодинамика оперирует понятиями со строго определенным смыслом. Так, если выделить из окружающей среды (с помощью реально существующих или воображаемых границ) вещество или совокупность взаимодействующих химических веществ и продуктов их взаимодействия, то вместе с конкретными параметрами в этом пространстве (концентрация веществ, температура, давление) выделенный объем будет называться химической системой. Вещества, образующие данную химическую систему, называются ее химическими компонентами.

Всякое изменение, происходящее в системе, и связанное с ним изменение хотя бы одного из свойств системы, будет называться термодинамическим процессом. Любая термодинамическая величина, которая может характеризовать процесс, называется термодинамическим параметром процесса. Например, при переходе системы из состояния 1 в состояние 2 процесс может быть охарактеризован величиной изменения давления DР = Р2 – Р1, температуры DТ = Т2 – Т1, объема DV = V2 – V1 и т.д. (здесь и далее в тексте знак дельта означает изменение величины).

Изолированные системы от окружающей среды изолированы полностью, не обмениваются ни веществом, ни энергией. Закрытые от окружающей среды системы не обмениваются с окружающей средой веществом, но возможны другие виды взаимодействия (обмен энергией). В открытых системах может происходить обмен с окружающей средой веществом и энергией (например, живой организм).

Количественный обмен энергией между системой и окружающей средой рассматривается с помощью понятий теплота и работа. Эти понятия применимы только для характеристики протекающих процессов, но не конкретного состояния системы. Теплота и работа являются возможными формами передачи энергии от одной системы к другой, т.е. имеющими место лишь при взаимодействии системы с внешней средой или с другой системой.

Теплота (Q) (или тепловой эффект процесса) – это количественная характеристика энергии, которую система в ходе данного процесса получает (отдает) из окружающей среды. Теплота является формой передачи энергии, реализуемой путем изменения кинетической энергии теплового (хаотического) движения частиц (атомов, молекул и др.). Если процесс сопровождается переходом энергии из окружающей среды к системе, он называется эндотермическим, в обратном направлении – экзотермическим.

Работа (А), совершаемая системой, обусловлена взаимодействием системы с внешней средой, в результате которого преодолеваются внешние силы, нарушившие равновесие в системе. Например, система может отдавать энергию в форме произведенной работы.

Сумма всех видов энергии, присущих данной изолированной системе (включая энергии движения и взаимодействия составляющих систему частиц – молекул, атомов, ядер, электронов), называется внутренней энергией системы (U). Абсолютное значение внутренней энергии определить невозможно, поэтому для расчетов используется значение изменения DU при переходе системы из одного конкретного состояния в другое. Она характеризует изменения в системе в процессе перехода ее от состояния 1 к состоянию 2 – при постоянном объеме DU = U2 – U1.

В основе термодинамики лежат первый и второй законы термодинамики (или первое и второе начала термодинамики).

Первый закон термодинамики применим к процессам, связанным с превращением теплоты и работы.

В соответствии с первым законом термодинамики (по-другому – законом сохранения энергии), энергия не возникает из ничего и не исчезает бесследно, но энергия одного вида может переходить в энергию другого вида. Отсюда следует, что невозможно создать машину – вечный двигатель первого рода – без сообщения ей энергии.

Энергия, полученная системой в форме теплоты, может превращаться в работу, и наоборот, энергия, полученная в форме работы – в теплоту.

Первый закон термодинамики утверждает, что энергия изолированной системы постоянна. В неизолированной системе энергия может изменяться за счет: а) совершения работы над окружающей средой; б) теплообмена с окружающей средой.

Первый закон термодинамики может быть сформулирован так: в любом процессе приращение внутренней энергии системы DU (в исходном состоянии система обладала внутренней энергией U1, а в конечном U2) равно количеству сообщаемой системе теплоты Q минус количество работы А, совершаемой системой, т.е.

DU = U2 – U1 = Q – A. (2.1)

Изменение внутренней энергии не зависит от пути проведения процесса, а определяется только начальным и конечным состояниями системы. Это означает, что внутренняя энергия является функцией состояния, и ее значение определяется только параметрами данного конкретного состояния, а не путями и самим процессом его достижения. Если система завершила круговой (циклический) процесс и вернулась в исходное состояние, то изменение ее внутренней энергии равно нулю, а значит и сумма балансов теплоты и работы равна нулю. Теплота и работа (имеется в виду любой вид работ: расширение газа, поднятие груза, перенос заряда, изменение поверхностного натяжения и др.), представляющие собой формы передачи энергии, не являются функциями состояния системы, а зависят от пути проведения процесса. По этой причине первый закон записывается в виде дифференциального уравнения:

dU = dQ – dA, (2.2)

где d означает, что dQ и dA не являются полными дифференциалами. Например, для процесса, в котором совершается только механическая работа расширения газа, т.е. dА = P · dV,

dU = dQ – PdV (закрытая система). (2.3)

Для изохорного процесса, т.е. при V = const, откуда dV = 0, следует, что DUV = QV, т.е. вся теплота, подведенная к системе, идет на увеличение U (здесь и далее по тексту нижние индексы V, P или T при параметре означают значение данного параметра соответственно при постоянном объеме, давлении или температуре в системе).

Для изобарного процесса, т.е. когда Р = const, следует:

DUP = QP – P(V2 – V1),

или

QP = U2 – U1 + PV2 – PV1 = (U2 + PV2) – (U1 + PV1). (2.4)

В этом случае не вся теплота, подведенная к системе, идет на увеличение внутренней энергии, часть ее расходуется, например, на работу расширения газа.

В термодинамике для удобства сумма U + PV обозначена буквой Н и названа энтальпией. Тогда можно сказать, что

QP = H2 – H1 = DH, т.е. теплота изобарного процесса равна изменению энтальпии.

Из определения энтальпии также следует, что для процесса при постоянном давлении

Qp = DH = DU + PDV, (2.5)

а при постоянном объеме

QV = DU. (2.6)

Связь Qр и QV.

Qp = QV + nRT

Энтальпия оказывается весьма удобной для анализа тепловых эффектов химических реакций.

Термохимия. Все химические реакции протекают с выделением или поглощением тепла; изучением тепловых эффектов реакций занимается одним из разделов физической химии – термохимия. Проявление тепловых эффектов при химических реакциях связано с разрывом одних химических связей и возникновением других. Разница в энергиях образующихся связей и тех, которые претерпели разрыв, проявляется в виде результирующего теплового эффекта данного химического процесса. Тепловой эффект реакции обычно относят к 1 моль конечного продукта.

Основой термохимии является закон Гесса: тепловой эффект химической реакции определяется только природой, составом и агрегатным состоянием исходных веществ и продуктов реакции и не зависит от возможных промежуточных химических стадий, т.е. от способа перехода от исходного состояния к конечному (при Р = const или V = const).

Неизвестные тепловые эффекты Qр (где Qp = DH) произвольных химических реакций можно рассчитать при помощи так называемых термохимических уравнений. Последние представляют собой обычные стехиометрические уравнения химических реакций, дополненные указанием агрегатного состояния всех веществ и численным значением теплового эффекта для данной реакции. Термохимическими уравнениями можно оперировать как уравнениями алгебраическими, т.е. складывать их, вычитать, умножать на постоянный множитель и др. Тогда для нахождения неизвестной теплоты какой-либо заданной реакции обычно производят операции комбинирования термохимических уравнений с уравнениями других подходящих реакций, для которых уже известны численные данные по тепловым эффектам (берутся из таблиц). Результатом такой процедуры является получение конечного уравнения искомой реакции с уже найденным (при комбинировании с привлеченными дополнительными уравнениями) численным значением ее теплового эффекта.

Тепловой эффект процесса зависит от температуры. В соответствии с законом Кирхгофа, изменение теплового эффекта с температурой равно разности теплоемкости продуктов реакции и теплоемкости исходных веществ.

Теплоемкостью (Ср) называется отношение количества сообщенной системе теплоты к наблюдаемому при этом повышению температуры. Для нахождения теплового эффекта H2 при температуре Т2 надо знать H1 при температуре Т1 и иметь данные по температурной зависимости теплоемкостей веществ, участвующих в реакции, в интервале температур от Т1 до Т2. Последние находятся обычно экспериментальным путем и описываются уравнениями в форме степенного ряда.

Так, если разность теплоемкостей продуктов реакции и исходных веществ = const, то

(2.9)

где – линейная функция температуры.

Второй закон термодинамики. Этот эмпирический закон не имеет единой формулировки, некоторые приведены ниже:

1. Невозможен самопроизвольный (естественный, спонтанный) переход энергии (в форме теплоты) от менее нагретого тела к более нагретому.

Перенос теплоты от холодного тела к горячему связан с компенсацией, т.е. с необходимостью дополнительной затраты работы, которая переходит в конечном счете в теплоту, поглощаемую горячим телом (так, в домашнем холодильнике происходит перенос теплоты от предметов к деталям прибора, а затем и в воздух; этот перенос требует затраты электроэнергии). Процессы, реализация которых связана с компенсацией, называются необратимыми.

2. Невозможно создать вечный двигатель 2-го рода. Тепло океана, например, может быть превращено в работу (согласно первому закону термодинамики), однако только при наличии соответствующего холодильника (согласно второму закону термодинамики).

3. Даже при обратимом течении реакции в работу может перейти только часть теплоты процесса. Другая часть, не превращенная в работу, передается при этом от более нагретых к более холодным частям системы.

Применительно к химическим реакциям (при Р = const, Т = const) этот закон можно выразить математически:

H = G + TS или G = H – TS, (2.10)

где DH2 – тепловой эффект реакции, наблюдаемый при ее необратимом течении;

DG2 – изменение свободной энергии Гиббса, или изменение изобарно-изотермического потенциала, т.е. это та максимальная часть энергии системы, которая в данных условиях может превратиться в полезную работу. При DG 0 реакция протекает самопроизвольно.

DS – энтропия. Энтропия является функцией каждого конкретного состояния системы и не зависит от пути (например, какие промежуточные стадии проходит система при переходе из состояния 1 в состояние 2 для достижения нового состояния).

Произведением TDS определяется переносимое Q, которое не может быть превращено в работу даже при обратимом ходе реакции (величина «связанной энергии»). Это произведение показывает количество внутренней энергии, теряемой системой в форме теплоты:

TDS = Q или DS = Q / T, (2.11)

где DS = S2 – S1 – изменение энтропии системы при реакции, равное сообщенному системе теплу, деленному на абсолютную температуру, при которой система эту теплоту получает (отдает).

Кроме термодинамического потенциала – свободной энергии Гиббса (G), в термодинамике в качестве вспомогательной функции для описания процессов большое значение имеет и другой введенный термодинамический потенциал – свободная энергия Гельмгольца (F), или изохорно-изотермический потенциал,

DF = DUG – TDS (2.12)

В результате самопроизвольных процессов совершается работа, и когда эта возможность исчерпывается наступает равновесие. Поскольку самопроизвольным процессам соответствуют отрицательные изменения F и G, то знак изменения функции G (при P = const, Т = const) или функции F (при V = const, Т = const) и будет показывать возможность или невозможность самопроизвольного протекания реакции. Если изменения этих функций для состояний системы 1 и 2 равны нулю, то система находится в равновесии. Изобарно-изотермический потенциал реакции рассчитывается так же, как и тепловой эффект реакции – по стандартным теплотам образования веществ:

. (2.13)

Для расчета любой реакции надо из суммы энтропий образования продуктов вычесть сумму энтропий образования исходных веществ (с учетом стехиометрических коэффициентов). Так, для стандартных условий:

. (2.14)

4. Самопроизвольно (следовательно, необратимо) в изолированной системе могут протекать только те процессы, которые связаны с увеличением энтропии, т.е. система из менее вероятного состояния переходит в наиболее вероятное и достигает такого макроскопического состояния, которому соответствует наибольшее число микроскопических состояний. Другими словами, процессы бывают самопроизвольными, когда конечное состояние может быть реализовано большим числом микросостояний и энтропия является мерой стремления системы к равновесию. Такие процессы должны сопровождаться увеличением энтропии.

Если для изолированных систем найденное значение S положительное (S 0), то это является признаком самопроизвольности процесса, т.е. осуществление процесса возможно.

При S 0 самопроизвольное (без внешних воздействий) осуществление процесса невозможно, т.е. невозможен переход тепла от одного тела к другому телу с более высокой температурой.

Для равновесного процесса S = 0 энтропия отличается от других параметров состояния системы (Р, Т, V) тем, что ее численное значение и значения ее изменения не поддаются непосредственному измерению и могут быть получены только косвенным, расчетным путем.

Можно сказать (принцип Больцмана), что энтропия – это мера вероятности пребывания системы в данном состоянии, а само содержание второго закона термодинамики обусловлено молекулярной природой и структурой вещества. Поскольку для неупорядоченного состояния термодинамическая вероятность всегда больше, чем для упорядоченного, то и энтропию, связанную с этой вероятностью, часто рассматривают как количественную меру хаотичности атомно-молекулярной структуры вещества. Так, найдено, что значение энтропии увеличивается: с ростом молекулярной массы в ряду веществ-аналогов; при реакциях, протекающих с увеличением числа молекул; при фазовых переходах от твердого к жидкому и от жидкого к газообразному состоянию и др.

Для неизолированной системы критерии возможности протекания процесса остаются теми же, но требуется знание общего изменения энтропии уже для новой термически изолированной системы (т.е. с учетом источника тепла).

Таким образом, критериями возможности самопроизвольного протекания процесса являются:

DS > 0 (изолированная система);
DF < 0 (V = const, T = const);
DG < 0 (Р = const, Т = const).

Если термодинамика дает отрицательный ответ на вопрос о возможности самопроизвольного протекания процесса, это означает, что без внешнего подвода энергии процесс невозможен (например, фотосинтез возможен только под воздействием солнечной энергии).

DG и DH имеют размерность Дж (кДж)/моль (для продуктов питания кДж/кг); DS – Дж/К·моль (энтропийная единица, э.е.); теплоемкость – Дж/К·моль.

Расчет DGо и DНо производится с использованием имеющихся в справочниках значений:

D So298, D Go298 и D Но298 – образования химических соединений.

Таблица 1.1. Стандартные термодинамические величины некоторых веществ и энергии связи

3. Химическое равновесие. Фазовое равновесие

В соответствии с законом действующих масс для произвольной реакции

а A + b B = c C + d D (3.1)

уравнение скорости прямой реакции можно записать:

, (3.2)

а для скорости обратной реакции

. (3.3)

По мере протекания реакции (3.1) слева направо концентрации веществ А и В будут уменьшаться и скорость прямой реакции будет падать. С другой стороны, по мере накопления продуктов реакции C и D скорость реакции справа налево будет расти. Наступает момент, когда скорости 1 и 2 становятся одинаковыми, концентрации всех веществ остаются неизменными, следовательно,

, (3.4)

откуда . (3.5)

Постоянная величина Кс, равная отношению констант скоростей прямой и обратной реакций, количественно описывает состояние равновесия через равновесные концентрации исходных веществ и продуктов их взаимодействия (в степени их стехиометрических коэффициентов) и называется константой равновесия. Константа равновесия является постоянной только для данной температуры, т.е.

Кс = f (Т). Константу равновесия химической реакции принято выражать отношением, в числителе которого стоит произведение равновесных молярных концентраций продуктов реакции, а в знаменателе – произведение концентраций исходных веществ.

Если компоненты реакции (3.1) представляют собой смесь идеальных газов, то константа равновесия (Кр) выражается через парциальные давления компонентов:

. (3.6)

Соотношения (3.4) и (3.5) выражают закон действующих масс. Для перехода от Кр к Кс воспользуемся уравнением состояния P · V = n·R·T (см. уравнение 1.1). Поскольку

, то P = CRT.

Тогда . (3.7)

Из уравнения (3.7) следует, что Кр = Кс при условии, если реакция идет без изменения числа моль в газовой фазе, т.е. когда (с + d) = (a + b).

Если реакция (3.1) протекает самопроизвольно при постоянных Р и Т или V и Т, то значения G и F этой реакции можно получить из уравнений:

, (3.8)

где С А, С В, С С, С D – неравновесные концентрации исходных веществ и продуктов реакции.

, (3.9)

где Р А, Р В, Р С, Р D – парциальные давления исходных веществ и продуктов реакции.

Уравнения (3.8), (3.9) называются уравнениями изотермы химической реакции Вант-Гоффа. Это соотношение позволяет рассчитать значения G и F реакции, определить ее направление при различных концентрациях исходных веществ.

Необходимо отметить, что как для газовых систем, так и для растворов, при участии в реакции твердых тел (т.е. для гетерогенных систем) концентрация твердой фазы не входит в выражение для константы равновесия, поскольку эта концентрация практически постоянна. Так, для реакции

2СО (г) = СО2 (г) + С(тв)

константа равновесия записывается в виде

Зависимость константы равновесия от температуры (для температуры Т2 относительно температуры Т1) выражается следующим уравнением Вант-Гоффа:

, (3.10)

где Н – тепловой эффект реакции.

Для эндотермической реакции (реакция идет с поглощением тепла) константа равновесия увеличивается с повышением температуры, система как бы сопротивляется нагреванию. Качественно направление этого изменения определяется принципом (правилом) Ле-Шателье: при повышении температуры равновесное состояние сдвигается в сторону эндотермического процесса (происходит поглощение энергии); при понижении температуры происходит сдвиг равновесия в обратную сторону – реакция пойдет справа налево (по отношению к установившемуся соотношению исходного и конечного количества реагентов в равновесной системе), т.е. в сторону экзотермического процесса (идет выделение энергии за счет обратной реакции).

Влияние других факторов на химическое равновесие, кроме температуры, также обусловлено правилом Ле-Шателье:

если на систему, находящуюся в термодинамическом равновесии, воздействовать путем изменения каких-либо условий, при которых это равновесие существует, то в системе возникнет реакция, ослабляющая эффект произведенного воздействия.

На увеличение концентрации одного из реагентов равновесная система отреагирует таким образом, чтобы уменьшилось это изменение, то есть реакция пойдет в направлении уменьшения концентрации этого компонента. В частности, для газовых систем, если число молей реагентов равно числу молей продуктов реакции (в соответствии со стехиометрическим уравнением), то константа равновесия не будет зависеть от увеличения или уменьшения давления, т.е. смещения положения равновесия при изменении давления не произойдет. Однако, если в результате реакции происходит изменение числа моль исходных веществ относительно числа моль продуктов реакции, то увеличение давления смещает равновесие в направлении той реакции, которая приведет к уменьшению полного числа моль. При понижении давления эта реакция пойдет в сторону увеличения числа моль, и система в итоге придет к новому состоянию равновесия (численное значение константы равновесия в новом равновесном состоянии системы будет тем же самым). Таким образом, принцип смещения равновесия – это принцип уменьшения системой эффективности воздействующих на нее сил.

Химическая система является гомогенной (однофазной), если она физически однородна (смесь газов в воздухе). Если система состоит более чем из одной фазы, то она называется гетерогенной, например, лед вместе с водой. Фаза – это гомогенная часть гетерогенной системы, ограниченная поверхностью раздела (фаза льда в водной фазе) и обладающая одинаковыми химическим составом и термодинамическими свойствами. Характерным является то, что по обе стороны от границы раздела фаз параметры каждой фазы имеют резкие различия. Так, в системе Н2О(кр) – Н2О(ж) – Н2О(г) могут одновременно сосуществовать три фазы – твердая, жидкая и газообразная (в точке таяния льда). Число фаз обозначают (Ф).

Для гетерогенных систем важным понятием является число степеней свободы (C), или вариантность. Степень свободы – это число термодинамических параметров состояния (Р, Т, концентрация), которые можно изменять, и при этом не изменится число сосуществующих в системе фаз, находящихся в состоянии равновесия.

Системы могут быть однокомпонентными или многокомпонентными. Число компонентов (К) определяется минимальным количеством веществ, посредством которых можно выразить состав любой фазы. Например, из водного раствора нитрата цинка можно выделить воду, Zn(NO3) 2 и ряд кристаллогидратов. Но эта система является двухкомпонентой, поскольку любые фазы можно получить из Н2О и Zn(NO3) 2.

В соответствии с правилом фаз Гиббса для равновесной гетерогенной системы число фаз плюс число степеней свободы равно числу компонентов плюс два:

Ф + С = К + 2. (1.43)

Так, для однокомпонентой системы имеем: С = К + 2 – Ф = 3 – Ф. Тогда при наличии только одной фазы число степеней свободы равно 2, и система будет бивариантна, т.е. гомогенность системы будет сохраняться при независимом изменении двух параметров – давления и температуры. Примерами таких систем являются вода или водяной пар. При равновесии в однокомпонентной, но двухфазной системе число степеней свободы С = 3 – 2 = 1, т.е. данная система уже моновариантна, и фазовое равновесие в ней будет сохраняться при независимом изменении только одного из параметров, например температуры. В качестве примеров таких систем могут служить системы вода пар или лед пар. Наконец, если система не имеет ни одной степени свободы, то она будет называться нонвариантной, например система, в которой сосуществуют лед, вода и пар.

Для наглядного изображения фазовых равновесий в конкретных системах используется графический метод, например прямоугольная система координат: на оси абсцисс откладывается абсолютная температура, а на оси ординат – давление, строится диаграмма. Такое изображение фазовых равновесий называют фазовой диаграммой или диаграммой состояния.

Рассмотрим диаграмму состояния воды. Внутри диаграммы наносятся точки, отвечающие экспериментально найденным значениям Р и Т, характеризующим фазовые равновесия между, например, двумя фазами. Тогда каждой фазе в однокомпонентной системе будет отвечать определенное поле на диаграмме, а различные состояния межфазного равновесия будут расположены на кривой Р = f (Т). По одну сторону от этой кривой система находится только в виде одной фазы, по другую сторону располагается рассматриваемый компонент в виде второй фазы. Каждая точка на этой линии характеризует, например, для системы жидкость – пар, конкретное значение температуры, которой отвечает только одно равновесное значение давления насыщенного пара жидкости. Тогда можно утверждать, что на этой линии число С = 1, следовательно, в соответствии с правилом фаз, независимо можно изменять лишь один параметр. Отсюда, если изменить Т, то межфазное равновесие сохранится при условии, что Р самопроизвольно изменится строго определенным образом. Для данной однокомпонентной системы аналогично можно рассмотреть равновесия между жидкостью и твердым телом, между твердым телом и паром. В итоге получим совокупность кривых, которые и образуют диаграмму состояния данного вещества.

Диаграммы состояния двухкомпонентных систем имеют более сложное строение, для получения представления о них необходимо обратиться к рекомендуемой литературе.

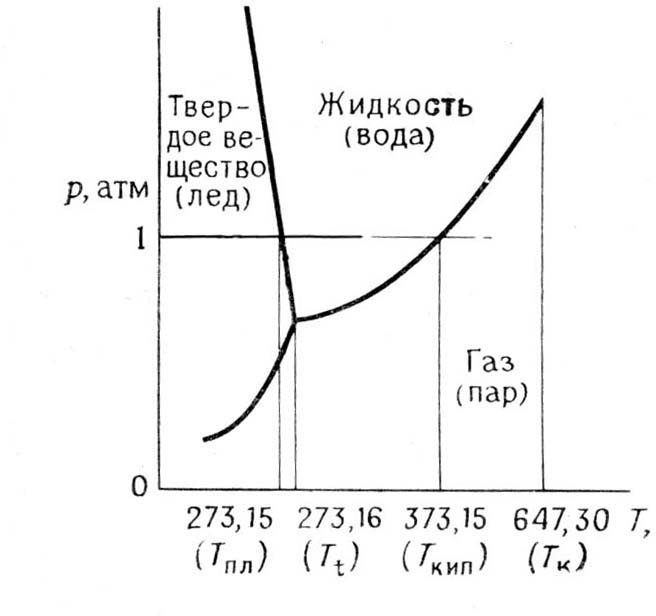
Диаграмма состояния позволяет решать ряд практических вопросов. В частности, с ее помощью можно проследить, как при изменении общего давления (при Т = const) изменяются равновесные составы жидкости и пара, а также и соотношение их масс. С помощью диаграммы состояния легко решается вопрос, в каком состоянии – жидком, газообразном или гетерогенном – будет находиться данная, например бинарная, система при заданных температуре, давлении и общем составе.

4. Свойства разбавленных Растворов

Раствором называют гомогенную систему, состоящую из нескольких компонентов, т.е. образованную из двух или более индивидуальных веществ. По определению Гиббса: раствор - это фаза переменного состава. Условно состав раствора подразделяют на растворитель (компонент, присутствующий в системе в относительно большем количестве) и растворенное вещество (другие компоненты). Раствор будет идеальным, если образование его не сопровождается уменьшением или увеличением его объема, а также выделением или поглощением тепла. Идеальные растворы подчиняются закону Рауля (см. ниже) при всех концентрациях и всех температурах. Реальные растворы в связи с явлениями ассоциации, диссоциации, сольватации и др. не обладают упомянутыми выше свойствами. Но в состоянии сильного разбавления, а также, если они образованы сходными по химическому составу и физическим свойствам веществами, приближаются к идеальным, поэтому, к ним можно с некоторым приближением применять количественные закономерности, описывающие состояние идеальных растворов.

Здесь рассматриваются только растворы, в которых растворителем является жидкость (чаще всего вода), а растворенными веществами – газы, жидкости или твердые вещества. Состав раствора характеризуется количеством растворенного вещества (веществ) в единице количества раствора или растворителя.

Осмос – самопроизвольное движение молекул растворителя через полупроницаемую мембрану, разделяющую растворы разной концентрации, из раствора меньшей концентрации в раствор с более высокой концентрацией, что приводит к разбавлению последнего. В качестве полупроницаемой мембраны, через маленькие отверстия которой могут селективно проходить только небольшие по объему молекулы растворителя и задерживаются крупные или сольватированные молекулы или ионы, часто служит целлофановая пленка – для высокомолекулярных веществ, а для низкомолекулярных – пленка из ферроцианида меди. Процесс переноса растворителя (осмос) можно предотвратить, если на раствор с большей концентрацией оказать внешнее гидростатическое давление (в условиях равновесия это будет так называемое осмотическое давление, обозначаемое буквой ). Для расчета значения в растворах неэлектролитов используется эмпирическое уравнение Вант-Гоффа:

= C R T, (4.1)

где С – молярная концентрация вещества, моль/кг;

R – универсальная газовая постоянная, Дж/моль · К.

Величина осмотического давления пропорциональна числу молекул (в общем случае числу частиц) одного или нескольких веществ, растворенных в данном объеме раствора, и не зависит от их природы и природы растворителя. В растворах сильных или слабых электролитов общее число индивидуальных частиц увеличивается вследствие диссоциации молекул, поэтому в уравнение для расчета осмотического давления необходимо вводить соответствующий коэффициент пропорциональности, называемый изотоническим коэффициентом.

= i C R T, (4.2)

где i – изотонический коэффициент, рассчитываемый как отношение суммы чисел ионов и непродиссоциировавших молекул электролита к начальному числу молекул этого вещества.

Так, если степень диссоциации электролита, т.е. отношение числа молекул, распавшихся на ионы, к общему числу молекул растворенного вещества, равна и молекула электролита распадается при этом на n ионов, то изотонический коэффициент рассчитывается следующим образом:

i = 1 + (n – 1), (i > 1). (4.3)

Для сильных электролитов можно принять = 1, тогда i = n, и коэффициент i (также больше 1) носит название осмотического коэффициента.

Явление осмоса имеет большое значение для растительных и животных организмов, поскольку оболочки их клеток по отношению к растворам многих веществ обладают свойствами полупроницаемой мембраны. В чистой воде клетка сильно набухает, в ряде случаев вплоть до разрыва оболочки, а в растворах с высокой концентрацией солей, наоборот, уменьшается в размерах и сморщивается из-за большой потери воды. Поэтому при консервировании пищевых продуктов к ним добавляется большое количество соли или сахара. Клетки микроорганизмов в таких условиях теряют значительное количество воды и гибнут.

Осмотическое давление обеспечивает движение воды в растениях за счет различия осмотических давлений между клеточным соком корней растений (5-20 бар) и почвенным раствором, дополнительно разбавляемом при поливе. Осмотическое давление обусловливает в растении подъем воды от корней до вершины. Таким образом, клетки листьев, теряя воду, осмотически всасывают ее из клеток стебля, а последние берут ее из клеток корня.

Растворимость газов в жидкостях изменяется в широких пределах и зависит не только от природы газа и растворителя, но и от давления и температуры. Количество растворенного газа пропорционально давлению его паров над раствором (закон Генри). Растворимость газов уменьшается при увеличении температуры и присутствии в растворе других веществ.

Равновесие между жидкостью и паром является динамическим – между ними происходит непрерывный обмен молекулами (частицами), причем количество этих молекул, проходящих через единицу поверхности раздела обеих фаз в условиях равновесия, одинаково (в обоих направлениях).

Согласно закону Рауля относительное понижение давления пара растворителя (А) над раствором зависит только от мольной доли растворенного в жидкости вещества (В), то есть определяется числом частиц вещества В в единице объема, но не зависит от свойств растворенного вещества:

, (4.4)

где N В – мольная доля вещества В в растворе, определяемая по формуле

, (4.5)

где n – количество моль вещества;

– давление насыщенного пара над чистым растворителем;

РА – давление пара растворителя над раствором (при той же температуре).

Закон Рауля выполняется для идеальных и сильно разбавленных растворов.

РА = (при Т = const), (4.6)

где NA – мольная доля вещества А в растворе, определяемая по формуле

. (4.7)

Приведенное уравнение (4.6) показывает, что давление пара растворителя над реальным раствором прямо пропорционально мольной доле растворителя в этом растворе.

При решении задач, связанных с испарением конденсированной фазы чистого вещества, можно использовать следующее уравнение:

(4.8)

где Р1 и Р2 – давление паров при абсолютных температурах Т1 и Т2 соответственно;

– мольная теплота испарения (парообразования), считающаяся постоянной в данном температурном интервале;

R – универсальная газовая постоянная.

Жидкость кипит при той температуре, при которой давление насыщенного пара над ней достигает внешнего давления. С ростом в ней концентрации растворенного нелетучего вещества давление пара растворителя над раствором понижается и раствор кипит при более высокой температуре, чем чистый растворитель. Повышение (изменение) температуры кипения от Т0 для чистого растворителя до Т для разбавленных растворов рассчитывают с помощью следующего уравнения:

Ткип = Т – То = Кэ·Сm,в, (4.9)

где Ткип – повышение температуры кипения раствора, К;

Кэ – эбулиоскопический коэффициент, К · кг · моль– 1;

Сm, В – моляльная концентрация вещества В, моль/кг.

Из уравнения (4.9) видно, что Кэ = Ткип. при Сm, В= 1 моль/ кг. Повышение температуры кипения зависит от концентрации раствора, т.е. от числа частиц в единице объема, но не зависит от типа и свойств этих частиц.

Эбулиоскопический коэффициент зависит только от природы растворителя и определяется следующим образом:

, (4.10)

где МА – молярная масса растворителя; г/моль;

Нисп – мольная теплота испарения чистого растворителя.

Поскольку , (4.11)

где m B – масса растворенного вещества В, г;

М В – молярная масса растворенного вещества В, г/моль;

m A – масса растворителя, г,

то уравнение (4.9) с учетом уравнения (4.11) можно записать:

. (4.12)

Полученное уравнение (4.12) можно использовать для определения неизвестной молярной массы растворенного вещества В по экспериментально найденному значению Ткип.

Для расчетов повышения температуры кипения растворов слабых или сильных электролитов необходимо использовать понятие об изотоническом коэффициенте i, приведенном в разделе об осмотическом давлении (см. уравнение 4.3). Тогда уравнение (4.9) принимает следующий вид:

Ткип = КЭ · i · Сm, В. (4.13)

Растворы замерзают при более низкой температуре, чем чистый растворитель, что является следствием понижения давления пара растворителя над раствором. Для разбавленных растворов понижение температуры замерзания от Т0 для чистого растворителя до Т для раствора зависит от количественного состава раствора:

Тзам = Т0 – Т = Кк · Сm, В, (4.14)

где Тзам – понижение температуры замерзания раствора, К;

Кк – криоскопический коэффициент, К · кг · моль– 1;

Сm, В – моляльная концентрация вещества В, моль/кг.

Из уравнения (4.14) следует, что Тзам = Кк при Сm, В = 1 моль/кг и понижение температуры замерзания раствора определяется только числом частиц в единице его объема, но не зависит от природы этих частиц.

Значение Кк можно рассчитать по формуле:

, (4.15)

где МА – молярная масса растворителя А, г/моль;

Н пл – мольная теплота плавления чистого растворителя.

Если в массе растворителя m А находится масса растворенного вещества В, то

, (4.16)

где m B – масса растворенного вещества В, г;

М В – молярная масса растворенного вещества В, г/моль;

m A – масса растворителя, г.

Тогда уравнение (4.14) можно записать:

(4.17)

Уравнение (4.17) можно использовать при экспериментальном определении и расчете молярной массы неизвестного вещества по понижению температуры замерзания его раствора в известном растворителе.

Если растворенное вещество распадается в растворе на ионы, то увеличение числа частиц за счет диссоциации его молекул учитывается через введение изотонического коэффициента i (см. уравнение 4.3):

Т зам = Кк · i · Сm, В. (4.18)

Пример

Водный раствор спирта, содержащий 0,17 г спирта и 20 г воды, замерзает при температуре – 0,354 0С. Рассчитать молярную массу спирта, если криоскопический коэффициент для воды равен 1,86 о С · кг · моль–1.

Решение

Для решения воспользуемся уравнением (1.60):

г/моль.

Ответ. М сп = 46 г/моль.

Первый закон Коновалова (применим как для идеальных, так и для отклоняющихся от закона Рауля растворов): насыщенный пар над равновесным ему раствором из двух жидкостей относительно богаче тем компонентом, добавление которого к системе повышает общее давление пара (или снижает температуру кипения). Поэтому при испарении раствора пар обогащен более летучим компонентом, а жидкость – менее летучим. На различиях в составах раствора и равновесного с ним пара основан метод разделения смесей (в основном органических жидкостей) путем ректификации. Повторяя операции испарения – конденсации, можно получить чистые компоненты. На практике это реализуется в ректификационных колонках.

Для растворов, значительно отклоняющихся от закона Рауля, на кривых зависимости давления пара над раствором от состава раствора часто имеется точка максимума или минимума. В экстремальных точках состав пара совпадает с составом жидкости (второй закон Коновалова). Такие смеси называются азеотропными, разделить их перегонкой (ректификацией) нельзя.

Для сильно различающихся по своей природе и по этой причине практически не смешивающихся жидкостей давление пара каждого компонента над смесью равно давлению пара чистого компонента. Тогда полное давление пара равно сумме давлений насыщенного пара обоих компонентов в чистом состоянии (при этой же температуре):

Р = РА + РВ. (4.19)

Однако температура кипения такой смеси ниже температур кипения каждой из индивидуальных жидкостей. Это свойство используется для перегонки с водяным паром путем барботирования его через не смешивающуюся с водой жидкость с последующей конденсацией выходящих паров. Перегонка с водяным паром позволяет отгонять высококипящие жидкости при температуре ниже 100 оС.

5. Химическая кинетика и катализ

Учение о скоростях химических реакций называется химической кинетикой.

Скорость химической реакции характеризует развитие реакции во времени и определяется изменением концентрации любого из реагирующих веществ (или продуктов реакции) в единицу времени. От скорости химической реакции зависит время достижения в системе равновесного состояния. Поскольку количества взаимодействующих исходных веществ и продуктов связаны уравнением химической реакции, то изменения концентраций всех участвующих в реакции веществ пропорциональны друг другу (с учетом стехиометрических коэффициентов в уравнении реакции). Скорость реакции зависит от концентрации реагирующих веществ, температуры, давления, наличия катализатора, воздействия излучений и др. Для биологических систем характерным является протекание реакций с незначительными скоростями (например гидролиз нуклеиновых кислот, полисахаридов, белков).

Скорость реакции, измеренная по изменению концентрации вещества за некоторый промежуток времени, называется средней скоростью (). Средняя скорость реакции неодинакова в интервале времени . Чем меньше рассматриваемый интервал времени, тем ближе определяемая скорость к скорости истинной (при 0 истинная скорость равна производной концентрации по времени: , т.е. это мгновенная скорость, или скорость в данный момент). Скорость химической реакции в зависимости от концентрации выражается законом действующих масс (Гульберг и Вааге): скорость гомогенной реакции при постоянной температуре пропорциональна произведению мольных концентраций реагирующих веществ, причем концентрация каждого данного вещества берется в степени, равной его стехиометрическому коэффициенту в уравнении реакции.

Так, для произвольной реакции

а A + b B = c C + d D

уравнением для расчета скорости прямой реакции будет:

(5.1)

где k – постоянный для каждой реакции и данной температуры коэффициент пропорциональности между скоростью и концентрациями, называемый константой скорости реакции, причем, как следует из уравнения (5.1), = k при = 1. Константа скорости реакции не зависит от концентрации реагирующих веществ, но зависит от их природы, температуры процесса и наличия катализатора. Для гетерогенной реакционной системы, например

С(т) + Н2О(г) = СО(г) + Н2 (г),

скорость реакции будет зависеть от степени развития поверхности (измельчения) твердого угля, что учитывается константой скорости реакции, и для данной степени развития поверхности скорость будет определяться только концентрацией паров воды: = k · С (Н2О).

Скорость газовых реакций будет зависеть от давления. Так, при увеличении давления в два раза для системы Н2 + I2 = 2НI концентрации водорода и паров йода также увеличатся в два раза, следовательно, скорость реакции возрастет в четыре раза.

Сумма всех показателей степеней при концентрациях в уравнении для скорости реакции (5.1), т.е. a + b = n, называется порядком реакции.

Для характеристики простейших реакций, протекающих в одну стадию, введено понятие об их молекулярности. Молекулярность реакции определяется минимальным числом молекул, одновременно участвующих в элементарном акте данной реакции. Молекулярность и порядок реакции численно совпадают только для простейших реакций. Для сложных процессов эти характеристики реакции будут отличаться (порядок реакции меньше ее молекулярности). Следовательно, формальное понятие о порядке реакции в большинстве случаев не отражает ее сложного механизма, т.е. наличия нескольких промежуточных элементарных реакций (стадий). Однако знание экспериментального порядка реакции позволяет судить о ее предполагаемом механизме путем сопоставления расчетных и экспериментально наблюдаемых значений величины n. Когда порядок реакции, найденный экспериментально, не соответствует числу моль реагентов, участвующих в реакции, то это говорит о том, что реакция не является элементарным процессом, а протекает по сложному механизму. Для сложного механизма скорость суммарной реакции определяется скоростью наиболее медленной (лимитирующей) стадии многоступенчатого процесса. Таким образом, если реакция протекает в одну стадию, то порядок ее равен молекулярности; если реакция протекает в несколько стадий, то порядок каждой из стадий реакции равен молекулярности только этой стадии. Следовательно, экспериментальное определение порядка реакции может служить методом изучения ее механизма.

Если для осуществления элементарного акта необходима всего одна частица (молекула) А, то такая реакция называется мономолекулярной, и для нее = kCА. Для элементарного процесса с одновременным участием двух частиц реакция будет называться бимолекулярной ( = k·CA·CB, или (при СА = СВ =Ci) = k) и т.д.

Хотя скорость реакций пропорциональна частоте столкновений между молекулами, к реакциям приводят только столкновения между активными молекулами, средняя энергия которых превышает среднюю энергию участников реакции. При сообщении молекулам некоторой энергии активации Е (избыточная энергия над средней) уменьшается потенциальная энергия взаимодействия атомов в молекулах, связи внутри молекул ослабевают, молекулы становятся реакционноспособными. Энергия активации не обязательно подводится извне, она может быть сообщена некоторой части молекул путем перераспределения энергии при их столкновениях. По Больцману, среди N молекул находится следующее число активных молекул N обладающих повышенной энергией:

, (5.2)

где Е – энергия активации, показывающая тот необходимый избыток энергии, по сравнению со средним уровнем, которым должны обладать молекулы, чтобы реакция стала возможной; остальные обозначения общеизвестны.

При термической активации для двух температур T1 и T2 отношение констант скоростей будет:

, (5.3)

откуда , (5.4)

что позволяет определять энергию активации по измерению скорости реакции при двух различных температурах Т1 и Т2.

Расчеты с использованием теоретического уравнения (5.3) подтвердили найденное ранее эмпирическим путем правило о том, что повышение температуры на 100 увеличивает скорость реакции в 2 – 4 раза (приближенное правило Вант-Гоффа). Число, показывающее, во сколько раз увеличивается скорость реакции (следовательно, и константа скорости) при увеличении температуры на 100 называется температурным коэффициентом реакции:

. (5.5)

или . (5.6)

Это означает, например, что при увеличении температуры на 1000 для условно принятого увеличения средней скорости в 2 раза ( = 2) скорость реакции возрастает в 210, т.е. приблизительно в 1000 раз, а при = 4 –в 410, т.е. в 1000000 раз. Правило Вант-Гоффа применимо для реакций, протекающих при сравнительно невысоких температурах в узком их интервале. Резкое возрастание скорости реакции при повышении температуры объясняется тем, что число активных молекул при этом возрастает в геометрической прогрессии.

Можно показать, что между lg k и имеется линейная зависимость:

(уравнение Аррениуса), (5.7)

где А = const, В = const.

Величина А определяется соотношением: . (5.8)

Величина В определяется по числу столкновений между молекулами (С):

В = lg С. (5.9)

Уравнение Аррениуса справедливо для более широкого интервала температур, чем температурный интервал, определяемый правилом Вант-Гоффа.

Постоянные А и В в уравнении (5.7) можно найти используя графическую зависимость константы скорости реакции от температуры (тангенс угла наклона прямой есть величина А, а отсекаемый ею на оси lg k отрезок позволяет найти величину В). Таким путем можно определять энергию активации Е изучаемой реакции.

Катализ – это изменение скорости реакции под действием веществ, которые, участвуя в процессе, к концу его остаются химически неизменными. Такие вещества называются катализаторами. Катализатор только ускоряет наступление равновесия, но не смещает его, и поэтому в присутствии катализатора нельзя получить в равновесной смеси больше продуктов реакции, чем без него. Различают два типа катализа: гомогенный (катализатор и реакционная смесь образуют гомогенную фазу) и гетерогенный (катализатор находится в виде самостоятельной фазы, и реакция протекает на его поверхности). Скорость реакции изменяется путем уменьшения энергии активации данной реакции. Механизм действия катализаторов многообразен, но часто он заключается в образовании с одним из участвующих в реакции веществ промежуточного соединения, которое затем реагирует с другим веществом с образованием конечного продукта и свободного катализатора. При этом энергия активации каждой из стадий меньше энергии активации реакции, идущей в отсутствие катализатора.

Скорость гомогенных каталитических реакций (в качестве катализаторов здесь часто выступают растворы активных веществ в воде или органических растворителях) пропорциональна концентрации добавленного катализатора, хотя количество последнего обычно невелико. Во многих случаях гомогенный катализ может быть вызван ионами водорода или гидроксила (кислотно-основной катализ). Так, при инверсии тростникового сахара (расщепление его на глюкозу и фруктозу) по реакции

С12Н22О11(сахар) + Н2О = С6Н12О6 (глюкоза) + С6Н12О6 (фруктоза),

энергия активации ее составляет 133,76 кДж/моль, тогда как в присутствии катализаторов (ионов водорода) она снижается до 107,01 кДж/моль и даже до 39,29 кДж/моль – в присутствии фермента сахаразы.

В гетерогенном катализе катализатор обычно представляет собой твердое вещество, а вещества, участвующие в реакции, – жидкости или газы. Реакция протекает на поверхности катализатора, адсорбирующего одно или несколько реагирующих веществ, которые образуют с поверхностью нестойкие промежуточные соединения (химическая адсорбция). Затем молекулы адсорбированных веществ вступают в целевую реакцию, что сопровождается уменьшением энергии активации. Свойства молекулы адсорбированного вещества в энергетическом смысле заметно изменяются и при простой физической адсорбции, т.е. протекающей без образования промежуточного комплекса. В этом случае происходит «разрыхление», ослабление связей у реагирующих веществ, что также приводит к снижению энергии активации. При гетерогенном (поверхностном) катализе важную роль (для активности катализатора) играют свойства поверхности – удельная поверхность, химический состав поверхностного слоя, его структура (неоднородность, существование активных центров) и др. С этими факторами часто бывает связана и значительная избирательность действия гетерогенных катализаторов.

Дополнительные вещества, повышающие активность катализатора, называются активаторами или промоторами. Вещества, понижающие активность катализаторов, называются каталитическими ядами.

Ферментативный катализ (биокатализ), играющий исключительную роль в жизнедеятельности животных и растений, реализуется в природе с помощью ферментов – полимерных веществ белковой природы. Ферменты состоят в основном(иногда полностью) из белков, т.е. они образованы из аминокислот с определенной пространственной структурой полипептидных цепей. В состав небелковой части фермента могут входить ионы металлов и некоторые органические вещества. При этом каталитической активностью обладает только определенный участок молекулы фермента – ее активный центр, образующий с молекулой реагирующего вещества промежуточное соединение, способное к дальнейшим превращениям. Отличительной чертой ферментов-катализаторов, наряду с их высокой эффективностью, является и резко выраженное дифференцированное каталитическое действие, что проявляется в ускорении только очень узкого круга реакций. Так, время «полупревращения» для реакции разложения мочевины водой при 25оС составляет 109c, а в присутствии фермента – уреазы 10-4c. Активность ферментов зависит в значительной мере от рН среды, концентрации фермента и температуры.

Комплексное соединение кобальта (витамин В12) необходимо для процессов кроветворения. Металлопорфирины железа входят в состав гемоглобина, а также ферментов каталазы, пероксидазы. Энзимы, гормоны, витамины являются активными биокатализаторами в биохимических процессах и участвуют в процессах пищеварения, различном биологическом окислении, спиртовом и уксуснокислом брожении и др.

6. Электрохимия

Электропроводность (способность проводить ток под действием постоянного электрического поля) растворов электролитов обусловлена переносом вещества (направленным движением ионов) и его химическими превращениями. В этом случае раствор называется проводником второго рода. Электропроводность такого раствора зависит, прежде всего, от природы электролита (от подвижности ионов), его концентрации в растворе, вязкости и температуры самого раствора и др. В проводниках первого рода (к ним относятся преимущественно металлы) переноса вещества не происходит.

Согласно теории Аррениуса, электролиты в водном растворе диссоциируют на заряженные частицы – ионы, которые и являются переносчиками электричества. Не все электролиты диссоциируют в одинаковой степени: одни – сильные электролиты, диссоциируют в растворе полностью; другие – слабые электролиты – лишь частично. В последнем случае доля распавшихся молекул, называемая степенью диссоциации (), зависит от концентрации электролита и температуры.

В растворе слабого электролита между недиссоциированными молекулами и ионами устанавливается равновесие:

KnAm nKm+ + mAn-

Для бинарного электролита: КА К+ + А-

Константа равновесия процесса электролитической диссоциации называется константой диссоциации (Кд).

Положим, что степень диссоциации равна . Если концентрация кислоты в растворе равна С (моль/л), то концентрации катиона и аниона равны С, а концентрация недиссоциированной части (1-)С. Поэтому

, (6.1)

Вычисленная практическая константа Кд зависит от концентрации. Независимой от концентрации является термодинамическая константа диссоциации, выраженная через активность ионов и молекул:

, (6.1/)

где- активность ионов К+, - активность ионов А-, , - коэффициенты активности соответствующих ионов, с – концентрация электролита.

Ионы в растворе электролита находятся в непрерывном беспорядочном движении. При наложении внешнего электрического поля на хаотичное движение ионов накладывается ориентированное поступательное движение к поверхности электродов: катионов – к отрицательному, а анионов – к положительному электроду. В результате возникает электрический ток.

Величина, характеризующая способность веществ проводить электрический ток под действием внешнего электрического поля, называется электрической проводимостью.

Электрическая проводимость (L) – величина, обратная электрическому сопротивлению проводника (R). Измеряется в сименсах (См): См=Ом-1.

Так как

то

, (6.2)

где - удельное сопротивление; - удельная электрическая проводимость; S – площадь сечения проводника; l – длина проводника.

Электрическая проводимость в растворах электролита зависит от числа ионов в объеме раствора между электродами и скорости их движения.

Для оценки проводимости растворов и влияния на нее различных факторов применяют две величины: удельную () и молярную () электрическую проводимость.

Удельной электрической проводимостью () называют электропроводность раствора, находящегося между параллельными электродами площадью 1 см2, расположенными на расстоянии 1 см.

Удельная электрическая проводимость измеряется в Смсм-1 или Смм-1.

Молярная электрическая проводимость – мера электрической проводимости всех ионов, образующихся при диссоциации 1 моля электролита при данной концентрации.

Молярная электрическая проводимость равна электрической проводимости такого объема (V, см3) раствора, в котором содержится 1 моль растворенного вещества, причем электроды находятся на расстоянии 1 см друг от друга.

Удельная и молярная электрические проводимости связаны соотношением:

, (6.3)

где С – концентрация, мольдм-3; - молярная электрическая проводимость, Смсм2моль-1; - удельная электрическая проводимость, Смсм-1.

Поскольку электрическая проводимость объема раствора электролита определяется количеством в этом объеме ионов, переносящих электричество, и скоростью их миграции, для молярной проводимости справедливо соотношение:

, (6.4)

где U+, U- - абсолютные скорости движения ионов (т.е. скорости их передвижения в поле с напряженностью 1 В·см-1); - степень диссоциации электролита; F – число Фарадея, т.е. количество электричества, которое несет 1 моль однозарядных катионов или анионов.

где NA = 61023 – число Авогадро, е – 1,610-19 Кл – заряд электрона.

При разбавлении раствора молярная электрическая проводимость как сильных, так и слабых электролитов возрастает: для слабых электролитов – вследствие увеличения степени диссоциации (), для сильных – в результате повышения абсолютной скорости движения ионов (U+, U-).

Предельное значение 0, отвечающее молярной электрической проводимости гипотетического бесконечно разбавленного раствора, характеризующегося полной диссоциацией электролита и отсутствием сил электростатического взаимодействия между ионами, в соответствии с (6.4) может быть выражено соотношением:

(6.5)

Произведения и называются предельными молярными проводимостями, или предельными подвижностями катионов и анионов. Уравнение (6.5) можно записать в виде:

. (6.6)

Молярная электрическая проводимость электролита при бесконечном разбавлении (0) равна сумме предельных подвижностей анионов и катионов.

Соотношение (6) установлено Кольраушем и называется законом независимого движения ионов.

Предельная подвижность ионов зависит только от природы растворителя и температуры; для многих ионов эта величина экспериментально определена и приведена в справочниках.

Молярная электрическая проводимость растворов слабых электролитов меньше, чем сильных. Это связано с тем, что даже при низких концентрациях степень диссоциации слабых электролитов мала (1), следовательно, несмотря на то, что в объеме раствора, заключенного между электродами, содержится 1 моль электролита, ионов-переносчиков электрического тока в этом объеме меньше, чем в растворе сильного электролита. Повышение молярной электрической проводимости слабых электролитов при разбавлении растворов связано именно с увеличением степени диссоциации.

Из уравнений (6.4) и (6.5) следует:

(6.7)

- коэффициент электрической проводимости, характеризующийся степенью торможения ионов.

Абсолютные скорости движения ионов в разбавленных растворах электролитов (U+, U-) и в бесконечно разбавленных (U0+, U0-) близки между собой (), поэтому

(6.8)

Таким образом, степень диссоциации электролита в растворе заданной концентрации можно рассчитать, если измерить молярную электрическую проводимость этого раствора и знать 0, которую можно рассчитать по формуле (6.5).

Электродными процессами называют химические превращения, происходящие в растворе на электродах из проводников первого рода.

Гальванический элемент – прибор, преобразующий энергию химической реакции в электрическую. Он состоит из двух электродов, погруженных в растворы своих солей. Между каждым электродом и раствором возникает разность потенциалов. Если растворы соединить мостиковым контактом через насыщенный раствор, например, хлористого калия, то это обеспечит возможность электрической проводимости между ними при отсутствии их взаимодиффузии. Если эти электроды соединить, например, медной проволокой, то на одном из электродов пойдет реакция окисления, а на другом – реакция восстановления. Возникающая при этом разность потенциалов между электродами называется электродвижущей силой (ЭДС) элемента. ЭДС гальванического элемента равна разности электродных потенциалов:

= E1 – E2. (6.9)

где – электродвижущая сила гальванического элемента, В;

E – электродный потенциал, В.

Величина электродного потенциала зависит от природы электролита, концентрации раствора и температуры (формула Нернста):

, (6.10)

где Ео – стандартный электродный потенциал, т.е. потенциал при активности (а) образующих потенциал ионов, равной единице, В;

n – заряд иона или число электронов;

F – число Фарадея, Кл · моль–1;

nF – перенесенное количество электричества;

a i – активность иона, которая для сильноразбавленных растворов может быть заменена его концентрацией.

Для расчета величины ЭДС используется уравнение Нернста, которое для гальванического элемента, где протекает окислительно-восстановительная реакция, записанная в общем виде:

a A + b B = c C + d D,

в условиях равновесия будет выглядеть так:

, (6.11)

где о – стандартное значение ЭДС, В;

– активности веществ, участвующих в участников реакции.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

Основная

Эткинс П. Физическая химия. – М.: Мир, 1980. Т. 2, гл. 26, 27. (Atkins P. Physical Chemistry. 5th edition. – Oxford Univ. Press, 1994, ch. 25 – 27).
Горшков В.И., Кузнецов И.А. Основы физической химии. – М., Изд-во Моск. ун-та, 1993.
Чанг Р. Физическая химия с приложениями к биологическим системам. – М., Мир, 1980.
Киселева Е.В., Каретников Г.С., Кудряшов И.В. Сборник примеров и задач по физической химии. – М., Высшая школа, 1976.

Дополнительная

Горшков В.И., Кузнецов В.В. Основы физической химии, М. : БИНОМ. Лаборатория знаний, 2011. – 407 с. ISBN 978-5-9963-0546-9
Беляев А.П., Кучук В.И., Евстратова К.И., Купина М.А., Малахова Е.Е. Физическая и коллоидная химия. – М. : ГЭОТАР-Медиа, 2008. – 704 с. ISBN 978-5-9704-0595-6

- 21 -

Физическая химия