Интерполирование функций полиномами
Министерство образования и науки Украины
Севастопольский национальный технический университет
Кафедра технической кибернетики
ОТЧЁТ
По лабораторной работе №2
“Интерполирование функций полиномами.”
Выполнил: студент гр. А-22д
Литус И.В.
Проверил: старший преподаватель
Захаров В.В.
Севастополь
2011
1 ЦЕЛЬ РАБОТЫ
- Освоить методы алгоритмизации и программирования формы представления интерполяционного полинома Ньютона с равномерным расположением узлов.
- Изучить свойства интерполяционного полинома Ньютона.
- Исследовать зависимость ошибки интерполирования функции от количества и расположения узлов для интерполяционного полинома Ньютона.
2 ВАРИАНТ ЗАДАНИЯ
|
№ варианта
|
С1
|
С2
|
С3
|
С4
|
С5
|
Форма
Fm(x)
|
|
9
|
0
|
0,5
|
4,6
|
-1,87
|
0,65
|
Ньютон
|
3 КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
Интерполирование - это приближённое определение значений функции f(x) в промежуточных точках заданного замкнутого интервала xB x xE изменения её аргумента x по известным значениям f(x1), f(x2),…, f(xm). Значения аргумента xi[xB, xE] , i=1,2…,m интерполируемой функции f(x) называются узлами интерполяции.
Интерполирование функции f(x) полиномом означает построение такого полинома минимальной степени Fm(x), который в m узлах интерполяции удовлетворяет условиям:
f(k)(xi) = Fm(k)(xi) , i = 1,2,…,m , k = 0,1,…,mi-1 . (1)
Здесь f(k)(xi) – известные значения функции f(x) и её производных k- ого порядка f(k)(x) в узлах интерполяции, а mi – кратность i- ого узла. Если mi=1, i-тый узел называется простым.
Интерполирование функций f(x) полиномом с простыми узлами (mi=1, i =1,2,…,m) означает построение такого полинома минимальной степени Fm(x), который в m узлах интерполяции удовлетворяет условиям:
f(xi) = Fm(xi) , i = 1,2,…,m .
Функция
, (2)
для которой необходимо построить интерполяционный полином Fm(x) в форме Ньютона на интервале 0 x 1 изменения аргумента x, задана аналитически. Это даёт возможность при любом значении x[0,1] вычислить величину абсолютной ошибки интерполирования
(3)
и, таким образом, провести полное исследование зависимости точности интерполирования от количества узлов интерполирования m и расположения точки x относительно узлов интерполирования xi. Значения коэффициентов c1, c2, c3, c4, c5 и форма представления интерполяционного полинома определены вариантом задания. Таблица вариантов приведена в разделе «Приложение».
В работе предполагается, что узлы xi - простые и расположены равномерно на интервале [0,1]. При этом первый x1 и последний xm узлы находятся на концах интервала (x1=0, xm=1), так что шаг интерполирования h (расстояние между двумя соседними узлами) является величиной постоянной на интервале [0,1] и определяется формулой
h = 1/(m1) ,
а узлы - формулой
xi = (i1) h , i=1,2,…,m . (4)
Интерполяционный полином Лагранжа [1,2] может быть представлен в виде
Fm (x) = , (5)
где
, i (x,0) = 1 . (6)
Коэффициенты аi интерполяционного полинома Ньютона определяются как решение системы линейных алгебраических уравнений с нижней треугольной матрицей коэффициентов, которая получается при подстановке (5) в (1). В случае равномерного расположения узлов коэффициенты аi определяются аналитически через конечные разности значений функции f(x) в узлах интерполирования (4) формулой
. (7)
Ошибка интерполирования функции f(x) на интервале обычно оценивается как максимальное значение на этом интервале абсолютной величины ошибки . Поскольку вычислить E(x) во всех точках интервала невозможно, то в работе предлагается вычислить её значение в точках
zi = (i-1)·0,01 , i = 1,2,…,101 (8)
и определить оценку ошибки интерполирования функции на заданном интервале [0,1], как
e = |E(zi)| . (9)
4 СХЕМА ПРОГРАММЫ
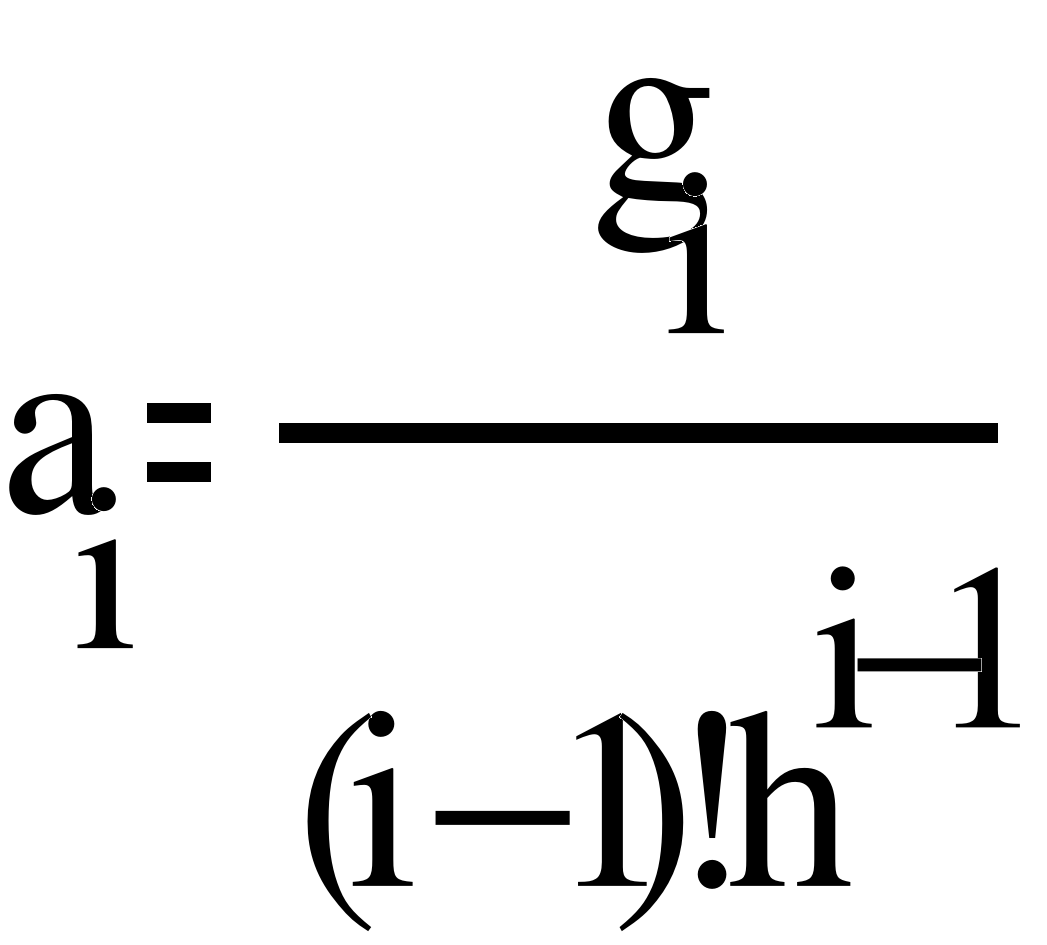
I
Fm (z) =
emax = |e(zk)|
5 ЛИСТИНГ ПРОГРАММЫ
#include <stdio.h>
#include <math.h>
#include <stdlib.h>
double tochnoe (double x, double *c);
int main ()
{
int l,k,i,j,m;
double x,e,a,z,h,emax,tt;
double c[5],t[100],g[100];
printf ("Vvedite kol-vo uzlov:");
scanf("%d",&m);
printf ("vvedite coefficieti:\n");
emax=0;
for (i=0;i<5;i++)
scanf("%lf",&c[i]);
h=1/double(m-1);
t[0]=0;
g[0]=tochnoe(t[0],c);
for (i=1;i<=m;i++)
{
t[i]=t[i-1]+h;
g[i]=tochnoe(t[i],c);
}
for (i=2;i<=m;i++)
for (j=m;j>=i;j--)
g[j]=g[j]-g[j-1];
tt=1;
for (k=2;k<m;k++)
{
tt=tt*h*(k-1);
g[k]=g[k]/tt;
}
for (l=0;l<101;l++)
{
z=l*0.01;
x=g[m];
for (i=m-1;i>0;i--)
{
x=g[i]+(z-t[i])*x;
}
e=tochnoe(z,c)-x;
if (emax<fabs(e))
emax=e;
if (l%10==0)
printf("N=%lf f(z)=%lf Fm(z)=%lf E=%lf\n",z,tochnoe(z,c),x,e);
}
printf("shag %lf\n",h);
printf("osibka %e\n",emax);
system("pause");
return 0;
}
double tochnoe (double x, double *c)
{
double f;
int i;
f=(c[0]*x+c[1])/(x*x*x+c[2]*x*x+c[3]*x+c[4]);
return f;
}
6 PЕЗУЛЬТАТЫ РАБОТЫ ПРОГРАММЫ
При m=3

При m=10

При m=20
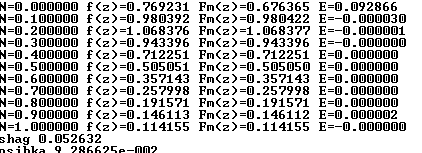

Рисунок 6.1-графики зависимости значения точного и приближенного значения функции
от узлов интерполирования.
Из рисунка 6.1 видно что при увеличении узлов интерполирования, решение с помощью полинома Ньютона становится практически равным точному решению.
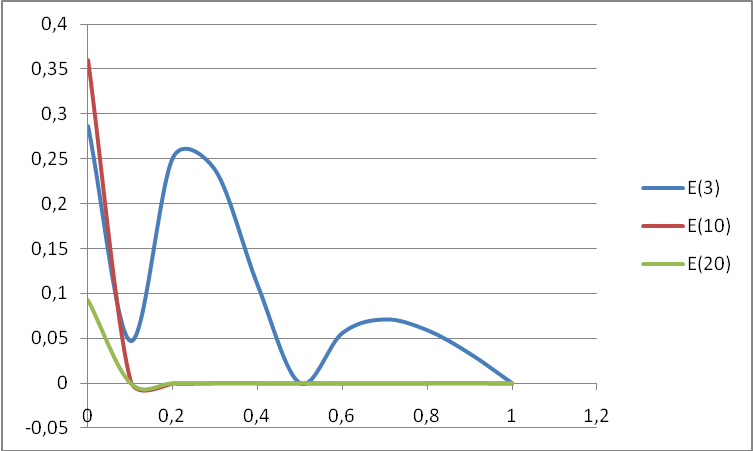
Рисунок 6.2-графики зависимости ошибки от узлов интерполирования.
Из рисунка 6.2 видно что при увеличении количества узлов интерполирования ошибка стремится к 0.
ВЫВОД
В ходе лабораторной работы были освоены методы алгоритмизации и программирования формы представления интерполяционного полинома Ньютона с равномерным расположением узлов, а также изучены свойства интерполяционного полинома Ньютона и исследована зависимость ошибки интерполирования функции от количества и расположения узлов для интерполяционного полинома Ньютона.
Из рисунка 6.1 видно что при увеличении узлов интерполирования, решение с помощью полинома Ньютона становится практически равным точному решению.
Из рисунка 6.2 видно что при увеличении количества узлов интерполирования ошибка стремится к 0.
Интерполирование функций полиномами