Модель инвестиций в условиях ожидания кризиса

Ващенко Михаил Петрович

ВЦ РАН

г. Москва

Модель инвестиций в условиях ожидания кризиса1

В докладе обсуждается проблема оценки доходности инвестионных проектов в ситуации, когда момент завершения инвестиционной деятельности заранее не известен и связан с кризисным явлением, точного момента наступления которого инвестор не знает. Для оценки исследуется уравнение Беллмана в модифицированной модели Кантора –Липмана ([1]). Обсуждаются эффективность осторожной стратегии инвестирования, гарантирующей неразорение инвестора, оценки доходности инвестиционных проектов для осторожного инвестора.

Описание модели

Финансовое состояние инвестора описывается вектором , -ая компонента которого равна денежным остаткам в момент времени при условии, что начиная с момента времени , новые проекты не начинались. Если обозначить через – интенсивность реализации проекта в момент времени , то динамика финансовых состояний будет описываться уравнением:

(1)

где

Предполагается, что инвестиционная деятельность ведется в условиях самофинансирования. Это означает, что денежные остатки у инвестора должны быть неотрицательны в любой момент времени: .

В каждый момент времени возможны два события: проект либо остается по-прежнему доступным для инвестиций, либо проект «закрывается» (исчезает спрос на инвестиции) и тогда инвестор должен завершить все уже начатые инвестиционные проекты, не начиная новые. При этом делается предположение, что вероятность наступления второго события постоянна и и равна .

Обозначим через компоненту вектора с номером , считая, что нумерация начинается с нуля. Тогда можно записать задачу инвестора:

(2)

Обозначим через функцию Беллмана, которая будет оценивать наилучший результат инвестирования в описанных условиях при начальном финансовом состоянии . Тогда

Этому уравнению соответствует оператор Беллмана:

Стратегию, соответствующую решению уравнения Беллмана,

назовем оптимальной стратегией инвестирования.

Теорема 1 ([2]). Обозначим: . Если , то осторожная стратегия будет оптимальной, т.е.:

(3)

Теорема 1 подтверждает гипотезу о том, что если риск превышает некую оценку эффективности проекта, то инвестор будет вести себя осторожно. В нашем случае характеристикой риска является вероятность наступления кризиса , а оценкой доходности проекта - выражение , где – минимальные необходимые для реализации проекта вложения, – максимальные чистые поступления от проекта за все время его реализации .

Оценка темпа роста капитала

Будем далее рассматривать систему (1) при . Как было показано (Теорема 1), при таком условии оптимальной стратегией инвестирования является . Таким образом мы приходим к динамической системе:

(4)

Т.е. на каждом шаге применяется один из операторов

(5)

Каждый из операторов задается матрицей

Оценки сверху на темп роста капитала

Определение 1. Совместным спектральным радиусом операторов называется число

где максимум берется по всевозможным функциям , где . A

В системе (4) оценкой сверху на максимальный темп роста капитала будет совместный спектральный радиус операторов (5). Далее будем рассматривать матрицы , соответствующие операторам (9).

Вычисление совместного спектрального радиуса – достаточно сложная процедура. В [3] показано, что вычисление совместного спектрального радиуса с произвольной точностью – NP полная задача. Следующие факты позволяют реализовать достаточно затратную (с точки зрения времени) процедуру расчета совместного спектрального радиуса с заданной точностью.

Теорема 2 ([4]). Пусть , и - матрица линейного оператора , где - симметрическая матрица. Тогда

где - спектральный радиус опреатора.

На основе последней теоремы в среде MatLab был реализованы расчеты совместного спектрального радиуса, произведено сравнение оценки Кантора–Липмана и совместного спектрального радиуса.

Пример 1.

Был взят инвестиционный проект, заданный следующим вектором

Для него вектор выглядит следующим образом:

Пример 2.

Был взят инвестиционный проект, заданный следующим вектором

Для него вектор выглядит следующим образом:

На рисунках (1), (2) показаны совместный спектральный радиус операторов (5), доходность проектов к моменту времени – () и оценка Кантора–Липмана для проектов. Из примеров видно, что возможны ситуации, когда более качественную оценку сверху на темп роста капитала в системе (4) дает IRR, возможны ситуации, когда наблюдается обратная картина. Также следует заметить, что ожидание кризиса существенным образом влияет на оценку доходности проекта: в примерах традиционная оценка Кантора–Липмана оказывается выше фактической доходности более чем в два раза.

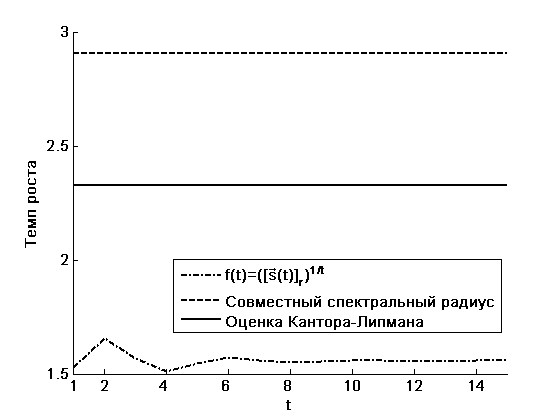
Рис. 1: Оценки на темп роста капитала в примере 1

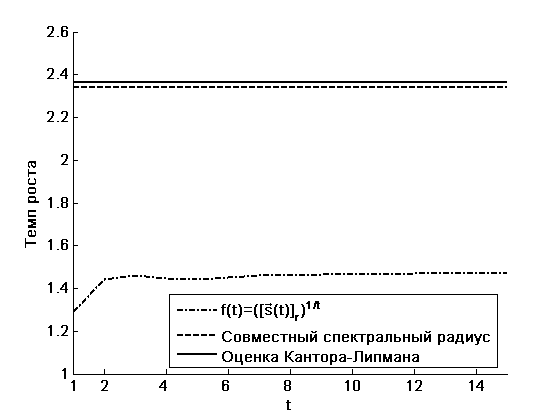
Рис. 2: Оценки на темп роста капитала в примере 2

Оценки снизу на темп роста капитала

При расчетах для сравнения верхних оценок оказалось, что на практике траектория системы (4), как правило, оказывается периодической в смысле применяемых операторов из набора (5). Т.е. , : , .

Поэтому имеет смысл брать в качестве оценки снизу темп роста капитала, который реализуется на такой периодической в смысле применяемого в силу системы набора операторов траектории.

Определение 2. Будем говорить, что у системы (4) существует траектория сбалансированного роста с темпом на периоде длины , задаваемая операторами , , ..., , если

Теорема 3 ([5]). Система (4) имеет траекторию сбалансированного роста с темпом на периоде длины , тогда и только тогда, когда имеет решение следующая система:

(6)

где

Утверждение теоремы 3 сводит проблему поиска траекторий сбалансированного роста к решению системы (6). Это позволяет эффективно решать поставленную задачу проверки существования у системы (4) траектории сбалансированного роста на периоде длины , задаваемой некоторым заданной функцией . Для этого достаточно решить задачу на поиск собственных чисел и собственных векторов оператора (последнее равенство системы (6)), после чего проверить, удовлетворяет ли хотя бы она пара , неравенствам системы (6). Среди тех пар, которые будут удовлетворять этому условию, можно взять пару с максимальным значением . Это и будет оценка снизу на темп роста капитала в системе (4).

Пример 3.

Возьмем инвестиционный проект, заданный следующим вектором . Для него вектор выглядит следующим образом: , а система (8):

(7)

В силу Теоремы 3 у системы (7) существует траектория сбалансированного роста с темпом на периоде длины , где , , . Матрицы из системы (6) выглядят следующим образом:

Можно сравнить темп роста, реализующийся на траектории, IRR и оценку Кантора–Липмана для этого проекта . Оценка Кантора–Липмана и IRR имеют смысл годовой доходности проекта, а показатель , который мы рассчитали, имеет смысл доходности проекта за период, соответствующий длине траектории, на которой реализуется рост, – два года. Поэтому, для сравнения показателей, их необходимо привести к одинаковой размерности, например, извлечь соответствующий корень из показателя , т.е. рассматривать .

На рисунке 3 показаны средняя доходность проекта за период в годовом выражении – , годовая доходность проекта, реализующаяся на траектории сбалансированного роста – , и оценка Кантора–Липамана.

Рис. 3: Оценки на темп роста капитала в примере 3

Литература

Л.И. Биккинина, Шананин А.А. К теории доходности инвестиционных проектов в условиях несовершенного финансового рынка // Сб. трудов XLVI конф. МФТИ. Москва–Долгопрудный: МФТИ, 2003. C.136–137.
Ващенко М.П. Исследование уравнения Беллмана в одной задаче оптимального инвестирования // Сб. статей молодых ученых факультета ВМиК МГУ. М.: Изд. отдел ф-та ВМиК МГУ, 2006. Вып. №3. C.32–43.
Tsitsiklisy J., Blondel V. The Lyapunov exponent and joint spectral radius of pairs of matrices are hard – when not impossible – to compute and to approximate)// Mathematics of Control, Signals, and Systems, 10, 1997. P.31–40.
Blondel V., Nesterov Y. Computationally efficient approximations of the joint spectral radius// SIAM Journal of Matrix Analysis, 27:1, 2005. P.256–272.
Ващенко М.П. Оценка доходности инвестиционных проектов условиях неопределенности // Математическое моделирование, 2009. Т 21. №3. с.18–30.
Ващенко М.П. Оценка доходности инвестиционных проектов в модифицированной модели Кантора-Липмана // Вест. Моск. Ун-та Сер. 15 Вычисл. матем. и киберн., 2009. №2. с.29–37.

1 Работа поддержана грантами РФФИ (08-07-00158, 09-01-13534 офи-ц), РГНФ N 08-02-00347, программой поддержки ведущих научных школ НШ 2982.2008.01, ПФИ ОМН РАН N3, ПФИ президиума РАН N2, ФЦП "Научные и научно-педагогические кадры инновационной России" на 2009-2013 годы (проект П949).

PAGE 1

Модель инвестиций в условиях ожидания кризиса