Измерение фазового сдвига

Контрольная работа

Содержание

1. Общие положения.

2. Осциллографические методы измерения угла сдвига фаз

2.1. Измерение угла сдвига фаз методом линейной развертки

2.2. Измерение угла сдвига фаз методом синусоидальной развертки

3 Измерение фазового сдвига путём преобразования во временной интервал.

4 Цифровые фазометры

4.1 Цифровые фазометры с преобразованием фазового сдвига в постоянное напряжение.

4.2 Цифровой фазометр с время-импульсным преобразованием за 1 период.

4.3 Цифровой фазометр с время-импульсным преобразованием за несколько периодов

Литература

1. Общие положения

Фазовым сдвигом называют модуль разности аргументов двух гармонических сигналов одинаковой частоты: и , т.е. разности начальных фаз 1–2.

Фазовый сдвиг является постоянной величиной и не зависит от момента отсчёта. Обозначим Т интервал времени между моментами, когда сигналы находятся в одинаковых фазах, например при переходах через нуль от отрицательных к положительным значениям. Тогда фазовый сдвиг = T = 2T/T, или

(1)

где Т – период гармонических сигналов (рис. 1).

Рисунок 1.

Фазовый сдвиг проявляется, когда электрический сигнал проходит через цепь, в которой он задерживается. Колебательные контуры, фильтры, фазовращатели и другие четырёхполюсники вносят фазовый сдвиг между входным и выходным напряжением = t3 , где t3 – длительность задержки в секундах. Усилительный каскад обычного типа вносит фазовый сдвиг, равный . Многие радиотехнические устройства – радиолокационные, радионавигационные, телевизионные, широкополосные усилители всех назначений, фильтры – характеризуются наряду с другими параметрами фазочастотной характеристикой (), т.е. зависимостью фазового сдвига от частоты.

Если напряжения с одинаковыми частотами имеют несинусоидальную форму, то фазовый сдвиг рассматривается между их первыми гармониками. При измерении напряжение высших гармоник отфильтровываются с помощью фильтров нижних частот.

2. Осциллографические методы измерения угла сдвига фаз

1. Измерение угла сдвига фаз методом синусоидальной развертки производится во втором режиме работы осциллографа. На входы Y и X подаются гармонические сигналы со сдвигом фазы . Формируется осциллограмма в виде эллипса, для которой определяются расстояние между точками пересечения с осью X и проекция L эллипса на ось X (рис.2).

Рисунок 2

Измеряемый сдвиг фазы вычисляется из соотношения

Характерные положения осциллограммы для различных значений угла сдвига фаз показаны на рис.3.

Рисунок 3

В этом случае на экране формируется временная развертка напряжений поданных на входы Y1 и Y2 осциллографа. На полученной осциллограмме определяют расстояние , соответствующее фазовому сдвигу, и расстояние L, соответствующее периоду сигнала. Измеряемый угол сдвига фаз вычисляется из соотношения

(2)

2. Измерение угла сдвига фаз методом линейной развертки производится с помощью двухканального (двух лучевого) осциллографа (рис.8.9)

Рисунок 4

3. Измерение фазового сдвига путём преобразования во временной интервал.

Суть метода заключается в преобразовании двух синусоидальных напряжений u1 и u2, фазовый сдвиг которых требуется измерить, в периодические последовательности коротких импульсов, соответствующих моментам переходов этих напряжений через нуль с производными одинакового знака. Пояснения даны на рис. 5. Исходные синусоидальные напряжения известными методами (усиление, ограничение, дифференцирование) превращаются в последовательность остроконечных импульсов. Импульсы uимп1 соответствуют моменту t1 – переходу синусоидального напряжения u1 через ноль. Соответственно uимп2 соответствуют моменту t2 напряжения u2. Ясно, что интервал T между импульсами uимп1 и uимп2 пропорционален фазовому сдвигу.

Рисунок 5

После описанных преобразований измеряется отношение интервала Т к периоду Т. Смысл измерения указанного отношения легко выясняется из следующих известных соотношений = T и 2/T. Произведя подстановку получим

(4)

Изложенный метод получил широкое распространение. Он встречается в различных фазометрах, отличающихся друг от друга главным образом способом измерения относительного интервала времени. Структурная схема аналогового измерителя фаз такого типа представлена на рис. 6.

Рисунок 6

На данном рисунке представлено двухканальное формирующее устройство, каждый канал которого состоит из входного блока и формирователя. Устройство преобразует два синусоидальных напряжения в серии коротких импульсов положительной полярности, как это показано на рис. 5.

Из соседних пар импульсов с помощью триггера формируются прямоугольные импульсы длительностью Т, как показано на последней осциллограмме рис. 4. До начала измерений триггер находится в исходном состоянии. После подачи на оба входа фазометра двух синусоидальных напряжений на выходах каналов появляются две периодические последовательности положительных импульсов. Первый импульс последовательности перебрасывает триггер в новое состояние и на его выходе повышается напряжение, второй импульс приводит триггер в исходное состояние. Через период Т процесс повторяется. Триггер формирует прямоугольные импульсы длительностью Т.

Магнитоэлектрический измерительный прибор показывает среднее значение напряжения

. (5)

Сравнение 4 и 5 приводит к формуле

(6)

из которой видно, что зависимость между величинами и Uср линейна. Шкалу индикаторного прибора можно проградуировать непосредственно в градусах (это возможно, так как Um на выходе триггера постоянно). В этом варианте построения прибор является аналоговым. Если напряжение измерить цифровым вольтметром, то прибор становится аналого-цифровым. Основное преимущество заключается в возможности цифрового отсчёта и представление результата измерения в цифровом коде, что удобно при формировании автоматизированных измерительных систем.

4. Цифровые фазометры

В основу работы цифровых фазометров (ЦФ) положено уравнение (1), по способу реализации которого ЦФ делят на две группы:

с промежуточным преобразованием фазового сдвига в постоянное напряжение;
с время-импульсным преобразованием:
- с измерением за один период;
- с измерением среднего значения за несколько периодов (интегрирующие).

4.1. Цифровой фазометр с преобразованием фазового сдвига в постоянное напряжение

Метод реализуют с помощью следующей структурной схемы:

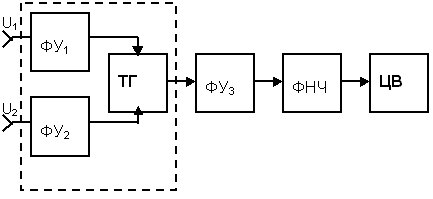
Рисунок 7

ФУ1,2 – формирующие устройства, которые формируют из гармонического сигнала сигнал с крутыми фронтами.

ФУ3 – формирующее устройство для формирования сигнала с калиброванным пиковым значением UР.

ФНЧ – фильтр нижних частот для выделения постоянной составляющей сигнала UСР.

ЦВ – цифровой вольтметр постоянного напряжения.

БФ – блок формирования временного интервала t.

На рисунке 8 показаны временные диаграммы сигналов в разных точках структурной схемы:

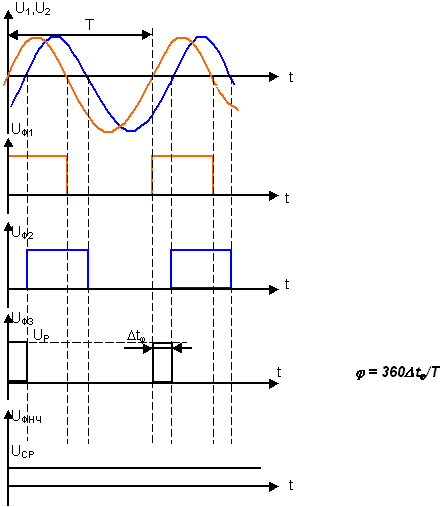
Рисунок 8

Среднее значение напряжения на выходе ФНЧ определяется выражением:

(7)

Следовательно, показание ЦВ будет пропорционально фазовому сдвигу

Источники погрешности измерения:

1) погрешность формирования временного интервала t

2) нестабильность напряжения Up

3) погрешность ЦВ

4.2. Цифровой фазометр с время-импульсным преобразованием за 1 период.

Структурная схема такого фазометра имеет вид:

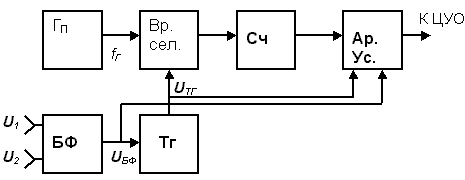
Рисунок 9

ГП – генератор коротких импульсов с частотой следования fГ;

Вр. сел. – временной селектор (электронный ключ, электронный коммутатор);

Сч – счетчик импульсов;

Тг – триггер;

Ар.Ус. – арифметическое устройство;

БФ – блок формирования интервала t (см. предыдущую схему).

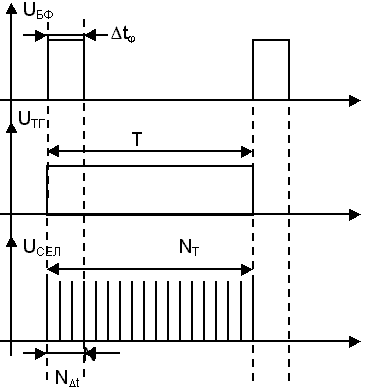
Рисунок 10

Выразим фазовый сдвиг через показания счетчика:

(8)

здесь k – коэффициент пропорциональности.

Источники погрешности:

- погрешность, вносимая БФ;

- погрешность дискретизации (квантования)

(9)

Из формул видно, что с ростом частоты исследуемого сигнала f погрешность дискретизации увеличивается и на высоких частотах становится недопустимо большой.

4.3. Цифровой фазометр с время-импульсным преобразованием за несколько периодов (с постоянным временем измерения)

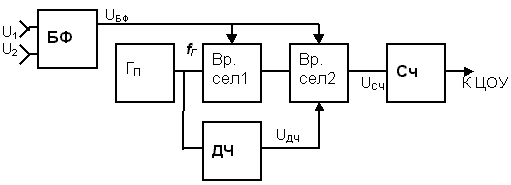
Рисунок 11 Структурная схема цифрового фазометра средних значений

ДЧ – делитель частоты в n раз – формирует временной интервал TИЗМ, в течение которого происходит измерение;

ЦОУ – цифровое отсчетное (отображающее) устройство;

остальные обозначения соответствуют предыдущей схеме.

Работа схемы проиллюстрирована временными диаграммами (рис.12):

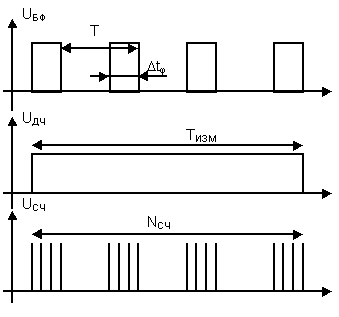
Рисунок 12

Количество пачек импульсов на выходе Вр.сел2 m:

(10)

Количество импульсов в пачке Nпач: Nпач = t fГ

Тогда общее количество импульсов, накопленное в счетчике за время измерения TИЗМ :

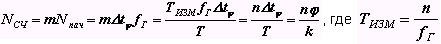(11)

Если коэффициент деления частоты fГ n=360, то 1 импульс счетчика будет соответствовать 1 градусу фазового сдвига и показания счетчика будут равны фазовому сдвигу. Для повышения точности измерения достаточно увеличить коэффициент деления частоты до 3600 или 36000 и погрешность индикации уменьшится до 0,1 или 0,01 соответственно.

Погрешность дискретизации определяется двумя факторами: случайным временным положением интервалов t относительно счетных импульсов д1 и случайным положением интервала TИЗМ относительно интервалов

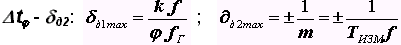
Суммарная погрешность дискретизации равна:

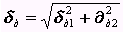
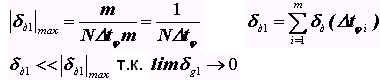
Источники погрешности:
- погрешность дискретизации;
- погрешность формирования интервала t (БФ).

Литература

1. Аполлонский, С.М. Теоретические основы электротехники. Электромагнитное поле: Учебное пособие / С.М. Аполлонский. - СПб.: Лань, 2012. - 592 c.

2. Башарин, С.А. Теоретические основы электротехники: Теория электрических цепей и электромагнитного поля: Учебное пособие для студ. высш. учеб. заведений / С.А. Башарин, В.В. Федоров. - М.: ИЦ Академия, 2010. - 368 c.

3. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: Учебник для бакалавров / Л.А. Бессонов. - М.: Юрайт, 2013. - 701 c.

4. Буртаев, Ю.В. Теоретические основы электротехники: Учебник / Ю.В. Буртаев, П.Н. Овсянников; Под ред. М.Ю. Зайчик. - М.: ЛИБРОКОМ, 2013. - 552 c.

5. Лоторейчук, Е.А. Теоретические основы электротехники.: Учебник / Е.А. Лоторейчук. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2013. - 320 c.

6. Лоторейчук, Е.А. Теоретические основы электротехники.: Учебник / Е.А. Лоторейчук. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2013. - 320 c.

7. Прянишников, В.А. Теоретические основы электротехники: Курс лекций / В.А. Прянишников. - СПб.: КОРОНА-принт, 2012. - 368 c.

8. Ярочкина, Г.В. Основы электротехники: Учебное пособие для учреждений нач. проф. образования / Г.В. Ярочкина. - М.: ИЦ Академия, 2013. - 240 c.

u1(t)

u2(t)

u1(t)

u2(t)

Y Z X

Измерение фазового сдвига