Измерение частоты и временных интервалов электрических сигналов

Контрольная работа

Содержание

1 Методы измерения частоты

2. Осциллографические методы измерения частоты

2.1. Измерение частоты методом линейной калиброванной развертки

2.2. Измерение частоты методом линейной развертки с внешним генератором образцовой частоты

2.3. Измерение частоты методом синусоидальной развертки

2.4. Измерение частоты методом круговой развертки

3 Резонансный и гетеродинный методы измерения частоты

4. Цифровые частотомеры и измерители временных интервалов

Литература

1. Методы измерения частоты.

В связи используется широкий диапазон частот: от нескольких сот килогерц до десятков гигагерц. Низкочастотное оборудование охватывает полосы частот от 20 Гц до 120 кГц. В зависимости от частотного диапазона на практике применяются различные методы измерения. Частота f и время Т являются обратными величинами: , где f измерено в герцах а Т в секундах. Кроме того частота связана с длиной волны известным выражением: f = c/ , где с= 3·108 м/с – скорость света в свободном пространстве; - длина волны в метрах. Следовательно измерение частоты, периода или длины волны равноценны. Аппаратура для измерения частотно – временных параметров представляет собой единый комплекс приборов, обеспечивающих измерение с привязкой к Государственному первичному эталону времени и частоты.

Частоту можно измерять методом сравнения, резонансным методом и методом дискретного счёта. Каждый из методов имеет свои преимущества и недостатки и область применения. Все приборы для измерения частоты образуют подгруппу Ч, внутри которой выделяют стандарты частоты и времени Ч1, частотомеры резонансные (Ч2), электронно-счётные (Ч3) и гетеродинные (Ч4).

Основой всех частотно-временных измерений в России является группа стандартов – высокоточных мер частоты и времени, в которую входит водородный, рубидиевый, цезиевый и кварцевый стандарты.

2. Осциллографические методы измерения частоты

2.1. Измерение частоты методом линейной калиброванной развертки

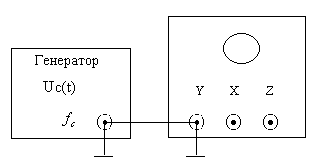
Схема подключения источника сигнала к осциллографу приведена на рис. 1, а.

(1)

Рисунок 1, а

Измеряемый сигнал uc(t) подается на вход Y осциллографа. На пластины X ЭЛТ поступает сигнал ГР uГР(t). Порядок функционирования блоков осциллографа определяется структурной схемой на рис. 1, б. На экране наблюдается осциллограмма, которая для синусоидального сигнала будет иметь вид, приведенный на рис. 2.

Рисунок 1, б

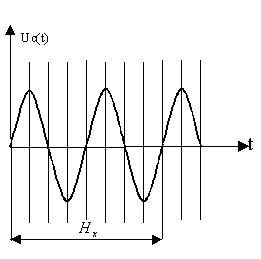
Рисунок 2

Определяем геометрический размер [дел], соответствующий целому числу периодов сигнала. Период и частота исследуемого сигнала определяются из соотношений

(2)

(3)

где n – целое число периодов сигнала

- коэффициент отклонения по горизонтали (цена деления по оси X) []. Его численное значение определяется положением дискретного переключателя скорости развертки (калиброванная величина).

Погрешность измерения периода по аналогии с разделом 3 определяется из соотношений:

систематическая абсолютная составляющая

(4)

СКО случайной составляющей

(5)

Где- абсолютная погрешность измерения геометрического размера [дел];

- абсолютная погрешность задания коэффициента

- СКО погрешность измерения величины [дел]

- СКО погрешности задания коэффициента .

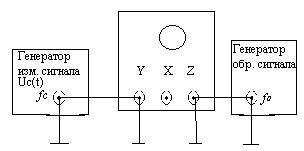
2.2. Измерение частоты методом линейной развертки с внешним генератором образцовой частоты

Рисунок 3 5.9

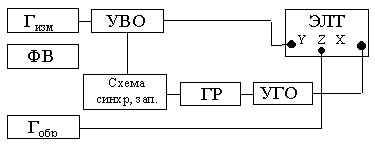
Рисунок 4

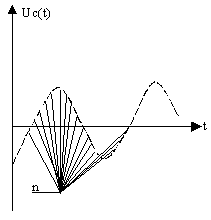
Рисунок 5

(6)

Измеряемый сигнал uc(t) подается на вход Y осциллографа. На пластины X ЭЛТ поступает сигнал ГР uГР(t). Источник образцовой частоты подключается к входу Z осциллографа (рис.3). Порядок функционирования блоков осциллографа определяет структурная схема, представленная на рис.4. На осциллограмме возникают яркостные метки. Подсчитывается их число “n” в одном периоде сигнала рис. 5. Измеряемая частота определяется из соотношения , при условии, что .

2.3. Измерение частоты методом синусоидальной развертки - производится во втором основном режиме работы осциллографа (П1 в положении 2). Гармонические сигналы подаются на входы Y и X осциллографа.

Схема подключения источников сигнала приведена на рис. 6.

Порядок функционирования блоков осциллогафа определяет структурная схема, представленная на рис. 7. На экране наблюдаем фигуру Лиссажу, вид которой зависит от частотных и фазовых соотношений поданных сигналов. Полученная фигура мысленно пересекается двумя взаимно перпендикулярными осями. (Оси не должны проходить через узлы фигуры). Подсчитывается количество точек пересечения с осью X - и осью Y - (рис. 8). В этом случае выполняется соотношение

Рисунок 6

Рисунок 7

Рисунок 8

Откуда неизвестная частота определится как

(7)

Где - известная частота [Гц].

2.4. Измерение частоты методом круговой развертки производится во втором режиме работы осциллографа (переключатель П1 переводится в положение 2).

Рисунок 9. Схема подключения источников сигналов

Рисунок 10

Рисунок 11

(8)

На входы Y и X подаются гармонические сигналы неизвестной частоты. Фазовращатель обеспечивает сдвиг фазы между ними . На вход Z поступает образцовая частота от дополнительного источника. Порядок функционирования блоков осциллографа определяет структурная схема, представленная на рис. Подсчитывается число “n” яркостных меток на круговой развертке (рис.11). Измеряемая частота определяется из соотношения , при условии, что

3. Резонансные и гетеродинные методы измерения частоты

При резонансном методе измерения частоты используется явление резонанса в колебательном контуре. Поэтому принцип действия резонансного частотомера основан на сравнении измеряемой частоты f0 с собственной резонансной частотой fр градуированного колебательного контура или резонатора. Измерительные приборы, работающие на основе этого метода, называются резонансными частотомерами; их обобщенная структурная схема приведена на рис. 12.

Рисунок 12 Обобщенная структурная схема резонансного частотомера

Перестраиваемая колебательная система через входное устройство возбуждается сигналом измеряемой частоты u(fx). Интенсивность колебаний в колебательной системе резко увеличивается в момент резонанса, т. е. при fx = fp. Этот момент фиксируется индикатором резонанса, связанным с колебательной системой, и значение измеряемой частоты fx считывается с градуированной шкалы механизма настройки.

Из самого принципа измерения частоты fx сравнением ее с резонансной частотой колебательного контура следует, что резонансная кривая колебательного контура должна иметь достаточно четко выраженный максимум. Как известно, резонансная кривая тем острее, чем выше добротность Q контура. В зависимости от типа колебательного контура добротность составляет от нескольких сотен единиц у контуров с сосредоточенными постоянными до 10 000 - 30 000 у контуров, выполненных в виде объемных резонаторов.

В качестве колебательной системы на частотах до сотен мегагерц используют колебательные контуры; на частотах до 1 ГГц — контуры с распределенными параметрами (отрезки коаксиальной линии); на частотах свыше 1 ГГц — объемные резонаторы.

На рис. 6.5 приведена структурная схема резонансного частотомера (это прибор на СВЧ называют волномером) с объемным резонатором.

Рисунок 13. Структурная схема резонансного частотомера.

1 – волновод; 2 – петля связи; 3 – детектор (диод); 4 – объемный резонатор;

5 – плунжер; И – индикатор резонанса

Линейный размер объемного резонатора l в момент настройки в резонанс однозначно связан с длиной волны X возбуждаемых в нем электромагнитных колебаний. Резонанс наступает при длине резонатора l = п/2, где п = 1, 2, 3 и т. д. Поэтому, перемещая плунжер 5 до момента получения первого резонанса, а затем следующего и оценивая по отсчетной шкале разность l = l1- l2 = /2, можно определить длину волны , где l1и l2 — линейные показания отсчетной шкалы в момент 1-го и 2-го резонансов. Измеренную частоту fx вычисляют по формуле fx = с/, где с — скорость распространения света в вакууме.

Резонансные частотомеры имеют сравнительно простое устройство и достаточно удобны в эксплуатации. Наиболее точные из таких приборов обеспечивают измерение частоты с относительной погрешностью 10-3 – 10-4. Основными источниками погрешностей измерения частоты являются погрешность настройки в резонанс резонатора, погрешность отсчетной шкалы и погрешность считывания данных.

Гетеродинный метод является одной из разновидностей методов сравнения измеряемой частоты fx с частотой эталонного генератора — гетеродина. Этот метод использует принцип построения измерительных схем с нулевыми биениями. Упрощенная структурная схема гетеродинного частотомера представлена на рис. 14. Она содержит: входное устройство, кварцевый генератор, смеситель, гетеродин, усилитель низкой частоты и индикатор (нулевых биений). Действие гетеродинного частотомера сводится к простому принципу: при переводе ключа К в положение 1 производят калибровку шкалы гетеродина; при положении 2 — измерение частоты fx, подаваемой на входное устройство.

Рисунок 14. Упрощенная структурная схема гетеродинного частотомера

Калибровку шкалы гетеродина осуществляют непосредственно перед измерением с помощью дополнительного кварцевого генератора. Сигнал, поступающий с кварцевого генератора, имеет сложную форму и содержит ряд гармонических составляющих с кратными частотами: f кв1, fкв, ..., fквi...,f кв n, где п — номер гармоники. Эти частоты называют кварцевыми точками. Отсчетный лимб гетеродина устанавливают в положение, соответствующее ближайшей к измеряемой частоте fx кварцевой точке (примерное значение измеряемой частоты должно быть известно, иначе процесс измерения очень усложняется).

Сигналы с кварцевого генератора fкв i, и гетеродина fг поступают на смеситель, поэтому на его выходе возникают колебания с суммарными, разностными и комбинационными частотами. Индикатор фиксирует наличие сигнала биений на минимальной разностной частоте Fб =|fкв i – fг|, проходящего через усилитель низкой частоты (высокочастотные составляющие, получающиеся в результате смешения частот кварцевого генератора и гетеродина, через усилитель низкой частоты не проходят). Меняя емкость конденсатора в контуре гетеродина, получают нулевые биения, следовательно, частота гетеродина становится равной частоте кварцевой гармоники fг fкв i. Затем приступают к измерению неизвестной частоты fx, переводя ключ К в положение 2. Вращая отсчетный лимб гетеродина, добиваются нулевых биений и по откорректированной шкале гетеродина определяют значение измеряемой частоты fx fг.

Гетеродинные частотомеры являются достаточно точными измерительными приборами. Их относительная погрешность измерения лежит в пределах 10-3 - 10-5. Однако в диапазоне средних частот (до 300 МГц и ниже) их вытесняют электронно-счетные частотомеры, которые обеспечивают ту же высокую точность, но значительно проще в эксплуатации.

В диапазоне СВЧ-колебаний гетеродинный метод измерения частоты применяется совместно с цифровыми методами. Расширение предела измерения до .. 12 ГГц достигается за счет переноса (преобразования) измеряемой частоты в область более низких частот. Такой перенос осуществляют с помощью дискретного гетеродинного преобразователя частоты, структурная схема которого вместе с низкочастотным цифровым частотомером приведена на рис. 15.

Рисунок 15. Структурная схема дискретного гетеродинного преобразователя

В состав цифрового частотомера гетеродинного преобразователя входит генератор опорной (образцовой) частоты f0, (на схеме для упрощения не показан). Эта частота поступает на генератор гармоник (нелинейный элемент), который формирует сетку гармонических составляющих fn, = пf0, где п = 1,2, ... – целые числа. С помощью перестраиваемого фильтра (объемного резонатора с отсчетной шкалой) Добиваются выделения из них гармоники fn, ближайшей к измеряемой частоте fx. При этом на выходе смесителя появляется сигнал с разностной частотой f = |fx - nf0|. Усилитель промежуточной частоты УПЧ имеет полосу пропускания, соизмеримую с разностной частотой f.

Результат измерения неизвестной частоты fx колебаний автоматически вычисляется по формуле fx = |nf0 ± f|, в которой номер гармоники п считывается со шкалы перестраиваемого фильтра. Поскольку последнее выражение неоднозначно, то для получения наиболее точного результата проводят второе измерение, выбирая с помощью перестраиваемого фильтра гармонику (n ± 1)f0, соседнюю с гармоникой nf0. Если результаты вычисления частоты fх совпали при двух измерениях, то они считаются верными.

4. Цифровые частотомеры и измерители временных интервалов.

Для измерения частоты fх периодического сигнала достаточно сосчитать число N его периодов за известный интервал времени t0. Результат измерения определяется отношением . С другой стороны, при измерении неизвестного интервала времени tх достаточно подсчитать число периодов T0 сигнала известной частоты f0 за измеряемый интервал tх. Результат измерения представляется выражением . Период сигнала известной частоты Т определяет в данном случае, по сути дела цену деления "электронной линейки", с помощью которой измеряют неизвестный временной интервал. Аппаратурное выполнение электронно-счётного частотомера и измерителя временных интервалов весьма схожее, поэтому часто измерение временного интервала и частоты осуществляется одним прибором.

Упрощенная структурная схема цифрового (электронно-счётного) частотомера изображена на рис. 16.

Рисунок 16

Исследуемый сигнал поступает на входное устройство, где осуществляется необходимое усиление (или ослабление) и фильтрация сигнала. Формирующее устройство преобразует исследуемый сигнал в последовательность импульсов uфу , частота которых равна частоте исследуемого сигнала. Селектор представляет собой управляемый электронный ключ, который пропускает на электронный счётчик сформированные импульсы неизвестной частоты только при наличии на управляющем входе стробирующего импульса uуу, длительность которого определяет время измерения t0. Стробирующий импульс вырабатывает устройство управления с помощью делителей частоты из сигнала высокостабильного опорного генератора, и его длительность выбирается кратной 10k с, где k – целое число. Число импульсов N, отсчитываемое электронным счётчиком на выходе селектора и фиксируемое цифровым отсчётным устройством (ЦОУ), пропорционально частоте входного сигнала. Так как t0 =10k с, частота fx = N = 10-k Гц. Значение множителя 10-k учитывается положением десятичной запятой на ЦОУ с указанием размерности получаемого результата (Гц, кГц).

Составляющие погрешности измерения могут быть определены с помощью диаграмм, показанных на рис. 17. Как видно из рисунка количество импульсов стробированных с помощью временного селектора зависит от величины калиброванного интервала времени t0. Эта погрешность определяется неточностью начальной установки и нестабильностью частоты опорного кварцевого генератора. Обычно в цифровых частотомерах применяются термостатированные кварцевые генераторы с f = 0,1…1 МГц, максимальная относительная погрешность частоты которых составляет 10-7…10-9. Это достаточно малая величина, которой во многих практических случаях можно пренебречь по сравнению с другой составляющей – погрешностью дискретности. Действительно, зафиксировать изменение частоты с помощью счётчика возможно только в случае, когда это приведёт к появлению (или пропаданию) хотя бы одного импульса. Если учесть, что стробирующий импульс и исследуемый сигнал между собой не связаны, возможная погрешность подсчёта составляет +1 импульс. Таким образом абсолютная погрешность составляет +1 (единицы счёта). Для определения относительной погрешности эту величину следует разделить на N – общее количество подсчитанных импульсов. В результате для максимальной относительной величины погрешности дискретности при измерении частоты, получаем выражение:

(9)

Как видно из приведенных формул, погрешность дискретности уменьшается с увеличением измеряемой частоты fх и времени измерения t0. Подбором этих величин погрешность дискретности может быть снижена до приемлемой величины.

Рисунок 17.

Расширение частотного диапазона в сторону высоких частот ограниченно быстродействием элементной базы, в частности элементов схемы временного селектора и счётчика. При измерении высоких частот относительное значение погрешности дискретности снижается и становится соизмеримым с погрешностью опорного кварцевого генератора. Поэтому в этом случае необходимо применять генераторы чрезвычайно большой стабильности. Для работы на частотах 1 ГГц и выше используют гетеродинное преобразование частоты и измеряют цифровым методом разность частот исследуемого сигнала и сигнала перестраиваемого высокочастотного гетеродина.

С уменьшением измеряемой частоты относительное значение погрешности дискретности увеличивается. В некоторых пределах это увеличение можно скомпенсировать увеличением времени измерения. Однако наиболее радикальным является переход на измерение периода исследуемого сигнала.

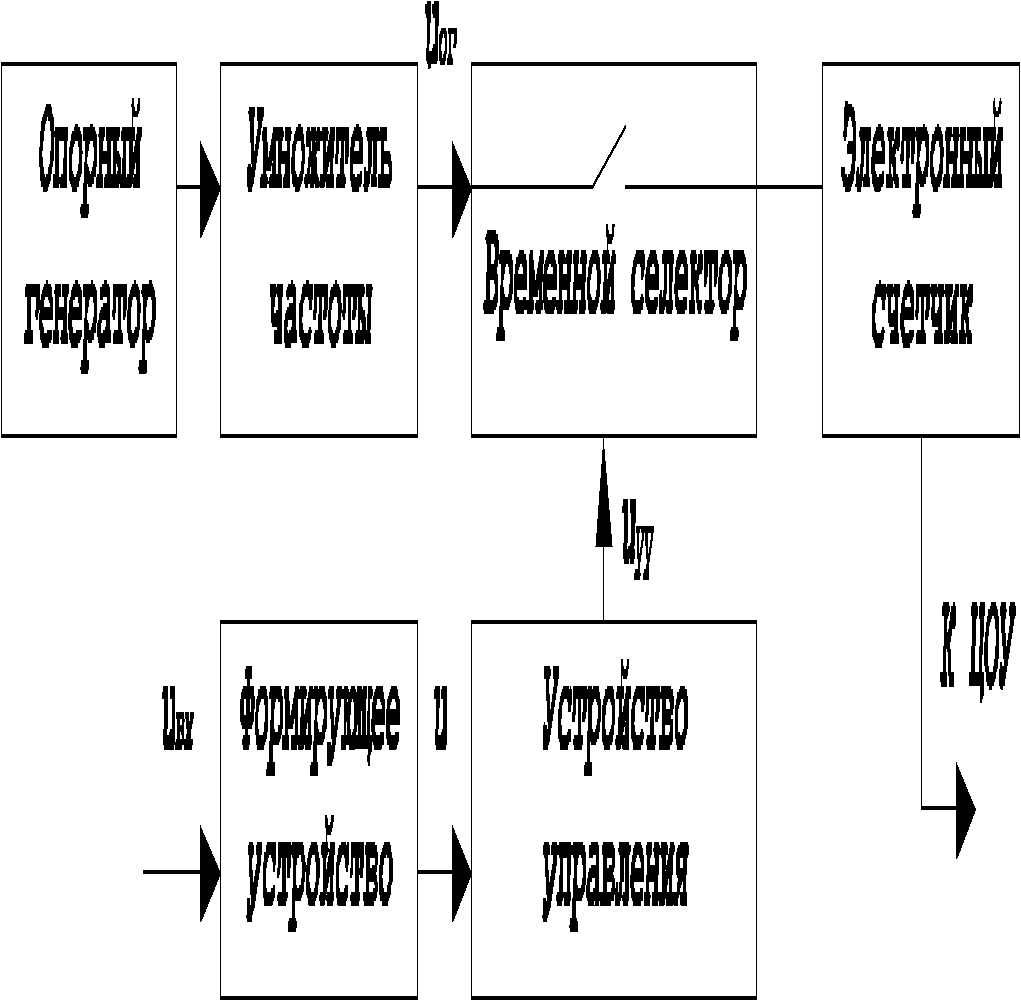
Рисунок 18

Измерение периода сигнала является частным случаем измерения временных интервалов. Ранее отмечалось, что с аппаратурной точки зрения измерители временных интервалов и цифровые частотомеры весьма схожи. На рис. 18 представлена структурная схема измерителя временных интервалов построенного на принципе дискретного счёта.

Как видно из рисунка основные элементы измерителя временных интервалов и электронно-счётного частотомера одни и те же, однако включены в другом порядке. Это позволяет перевести цифровой частотомер путём несложных переключений в режим измерения временного интервала (периода). Задача формирующего устройства и устройства управления – сформировать из исследуемого сигнала импульс uуу с крутыми фронтами, длительность которого определяет время открытого состояния временного селектора. За это время через селектор на электронный счётчик проходят импульсы uвс, период которых задаётся высокостабильным опорным генератором. Относительная нестабильность частоты этого генератора определяет одну из составляющих погрешности измерения временного интервала. Поэтому в качестве опорного генератора и в этом случае следует применять высокостабильные кварцевые генераторы.

Рисунок 19

Последовательность формирования сигналов в измерителе интервалов времени показана на рис.19. Из исходного синусоидального сигнала, период которого измеряется, формируется с помощью усилителя-ограничителя управляющий импульс uуу. Длительность этого импульса равна периоду исходного сигнала. Импульсы, поступающие от опорного генератора u поступают на временной селектор, который выделяет из них "пакет" с числом Nх. Количество импульсов в пакете связано с измеряемым периодом Тх и периодом опорного сигнала Т0 следующим соотношением: Nх= Тх/Т0. Откуда измеряемая величина может быть определена как .

Минимально возможное значение периода меток времени Т определяет абсолютную погрешность дискретности. Как и в случае измерения частоты погрешность дискретности определяется погрешностью счёта в ± один импульс. Т.е. абсолютная погрешность равна +Т , а относительная .

Рассмотренные цифровые методы являются не единственными. Существуют приборы с более сложными вариантами обработки сигналов, которые обеспечивают большие функциональные возможности и более высокую точность.

Литература

1. Аполлонский, С.М. Теоретические основы электротехники. Электромагнитное поле: Учебное пособие / С.М. Аполлонский. - СПб.: Лань, 2012. - 592 c.

2. Башарин, С.А. Теоретические основы электротехники: Теория электрических цепей и электромагнитного поля: Учебное пособие для студ. высш. учеб. заведений / С.А. Башарин, В.В. Федоров. - М.: ИЦ Академия, 2010. - 368 c.

3. Бессонов, Л.А. Теоретические основы электротехники. Электрические цепи: Учебник для бакалавров / Л.А. Бессонов. - М.: Юрайт, 2013. - 701 c.

4. Буртаев, Ю.В. Теоретические основы электротехники: Учебник / Ю.В. Буртаев, П.Н. Овсянников; Под ред. М.Ю. Зайчик. - М.: ЛИБРОКОМ, 2013. - 552 c.

5. Лоторейчук, Е.А. Теоретические основы электротехники.: Учебник / Е.А. Лоторейчук. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2013. - 320 c.

6. Лоторейчук, Е.А. Теоретические основы электротехники.: Учебник / Е.А. Лоторейчук. - М.: ИД ФОРУМ, НИЦ ИНФРА-М, 2013. - 320 c.

7. Прянишников, В.А. Теоретические основы электротехники: Курс лекций / В.А. Прянишников. - СПб.: КОРОНА-принт, 2012. - 368 c.

8. Ярочкина, Г.В. Основы электротехники: Учебное пособие для учреждений нач. проф. образования / Г.В. Ярочкина. - М.: ИЦ Академия, 2013. - 240 c.

Гизм

Гобр

УВО

ГР

Схема синхр, зап.

ФВ

УГО

ЭЛТ

Y Z X

Гизм

Гобр

УВО

ГР

Схема синхр, зап.

УГО

ЭЛТ

Y Z X

ФВ

Измерение частоты и временных интервалов электрических сигналов