Анализ спектра и измерение нелинейных искажений
Контрольная работа
Анализ спектра и измерение нелинейных искажений
Содержание
1. Общие положения
2. Методы анализа спектра сигналов
3. Цифровые методы анализаторов спектра сигналов
4. Анализаторы спектра сигналов на цифровых фильтрах
5. Измерение нелинейных искажений
Литература
1. Общие положения
В теории сигналов широкое применение нашли два способа матема�тического и физического представления электрических сигналов: временной и спектральный.
При временном способе анализа электрический сигнал отра�жается непрерывной функцией времени или совокупностью эле�ментарных импульсов, следующих друг за другом через опреде�ленные интервалы времени.
Спектральный способ основан на представлении (аппроксимации) сигнала в виде суммы гармонических составляющих разных, обычно кратных друг другу частот. Процессы в электрических це�пях получаются тем сложнее, чем более сложной является форма сигналов. В этих случаях часто становится эффективным и полез�ным спектральное представление сигналов.
Для оценки степени искажений, претерпеваемых гармониче�скими сигналами при прохождении их через нелинейные цепи, ис�пользуют измерение нелинейных искажений.
Для периодических сигналов Фурье ввел разложение по различ�ным видам математических рядов — тригонометрическим, гармони�ческим, комплексным и т. д. Фурье также доказал, что непериодические (импульсные) сигналы можно описать с помощью двух его ин�тегральных преобразований — прямого и обратного.
Анализ спектра включает определение как амплитуд гармоник (спектра амплитуд), так и их начальных фаз (спектра фаз). Однако для многих практических задач достаточно знать лишь спектр амплитуд. Поэтому под анализом спектра принято понимать определение ампли�туд гармоник исследуемого сигнала.
Автоматическое определение амплитуд гармоник исследуемого сигнала осуществляют специальными приборами — анализаторами спектра. Анализаторы спектра сигналов классифицируют:
• по способу анализа — последовательные, параллельные (одновре�менные) и смешанные;
• по диапазону частот — низкочастотные, высокочастотные, сверхвы�сокочастотные, широкодиапазонные.
Основные характеристики анализаторов — разрешающая способ�ность, время анализа и погрешности измерения частоты и амплитуды.
При спектральном анализе непериодических (импульсных) сиг�налов чрезвычайно удобна известная в математике формула прямого преобразования Фурье, характеризующая спектральную плотность исследуемого сигнала:
(1.)
С аналитической точки зрения имеет место одно об�стоятельство, общее для всех схем анализаторов, ограничивающее точность анализа спектра сигнала: преобразование Фурье применимо при исследованиях процессов, если для них выполняются условия Дирихле и абсолютной интегрируемости. Для реальных процессов эти условия обычно выполняются. Преобразования Фурье предпола�гают, что сигнал u(t) задан на всей оси времени от - до + и спектр (1) определяется всем закончившимся процессом. Однако при практических измерениях анализируют процессы на конечном интервале времени Та (времени анализа, наблюдения), т. е. не закон�чившиеся во времени. Это несоответствие позволяет установить мо�дель текущего частотного спектра, определяемого соотношением:
(2)
Текущая спектральная плотность зависит от в�ремени анализа, и форма текущего спектра в общем случае отличается от истинного тем больше, чем меньше Та. Отличие текущего спектра от спектра закончившегося процесса зависит от того, проявились ли за время анализа ТЛ все характерные особенности сигнала. Если ис�следуемый анализатором сигнал — периодический с периодом сле�дования Т, то необходимо лишь выполнение условия: Та >> Т.
При анализе спектра сигналов нижний предел времени анализа является конечным, т. е. интегрирование (усреднение) проводится в интервале от 0 до Тa. За счет этого возникает методическая погреш�ность определения составляющих спектра, связанная с методом из�мерений. Эта погрешность для ряда технических применений ана�лизаторов не играет особой роли, но в некоторых случаях ее необ�ходимо учитывать.
Как и все измерительные приборы, анализаторы спектров сигналов делят на аналоговые и цифровые. Несмотря на многие достоинства цифровых анализаторов, аналоговые анализаторы еще широко исполь�зуют, особенно в верхней части высокочастотного и СВЧ-диапазонов, где цифровые преобразователи имеют определенные частотные огра�ничения. Современные аналоговые анализаторы спектров содержат и цифровые устройства. Цифровые анализаторы спектра кроме спек�тральных характеристик обычно вычисляют статистические характери�стики сигналов.
Практически во всех аналоговых анализаторах выделение гармо�ник сигнала производится узкополосными фильтрами. Основным элементом таких анализаторов является полосовой фильтр (высоко�добротный резонатор) с узкой полосой пропускания, который выделяет отдельные составляющие или узкие диапазоны частот исследуемого спектра. Используется также и группы фильтров, каждый из которых на�строен на индивидуальную полосу частот, или одну гармонику
2. Методы анализа спектра сигналов
Практически все анализаторы спектра реализуют по двум схе�мам: параллельного и последовательного действия.
Метод параллельного анализа спектра
Метод параллельного анализа чаще применяют для исследования спектров одиночных импульсных сигналов. Структурная схема анали�затора параллельного типа содержит п полосовых фильтров Ф, каждый из которых настроен на определенную частоту (рис. 1, а).
Рисунок 1. Метод параллельного анализа спектра
а – структурная схема анализатора; б – исследуемый спектр; в - АЧХ фильтров;
г – спектр на выходе анализатора
Исследуемый сигнал u(t), спектр которого расположен в полосе частот u(t) (рис. 1, б), подают на все фильтры одновременно. Фильтры имеют похожие АЧХ с одинаковыми полосами пропускания n и на�строены на определенные частоты (рис. 1, в). Сигналы на выходе фильтров определяют составляющие спектра анализируемого про�цесса (рис. 1, г). После детектирования в детекторах Д спектраль�ные составляющие поступают на регистрирующие устройства РУ.
Метод последовательного анализа спектра.
Метод последовательного анализа чаще всего применяют для исследования спектров многократно или периодически повторяю�щихся временных процессов.
На рис. 2 показана упрощенная структурная схема анализатора спектра последовательного типа, которая содержит супергетеродинный приемник, индикаторное (чаще осциллографическое) устройство и ка�либратор. Основной блок супергетеродинного приемника — преобра�зователь частоты, состоящий из смесителя, генератора качающейся частоты ГКЧ и усилителя промежуточной частоты. К приемнику также относятся входное устройство, детектор (в данном случае амплитуд�ный) и выходной усилитель.
Рисунок 2. Структурная схема анализатора спектра последовательного типа
В супергетеродинном приемнике спектр анализируемого сигнала u(t) с помощью преобразователя частоты переносится с несущей час�тоты/) на (как правило, более низкую) промежуточную (на которой работает усилитель промежуточной частоты):
(3)
где г — центральная частота ГКЧ.
На один вход смесителя через входное устройство подается вход�ной сигнал u{t), а на другой его вход поступает напряжение с ГКЧ. Настройку приемника на разные частоты производят напряжением, поступающим на ГКЧ с выхода генератора развертки. С помощью индикаторного устройства наблюдают спектр исследуемого процесса. Калибратор используют для измерения характерных параметров спек�тра: частот, соответствующих максимумам или нулевым значениям огибающей спектра и т. д.
Основные характеристики анализаторов спектра.
Основные характеристики анализаторов — чувствительность, рабочий диапазон частот, разрешающая способность и время анализа.
Чувствительность отражает отношение изменения сигнала на выходе анализатора к вызвавшему его изменению анализируемой ве�личины. Наличие в анализаторах спектра преобразователей частоты с УПЧ ставит их в ряд приборов с высокой чувствительностью, и по�этому они могут применяться для анализа слабых сигналов. В диапазоне радиочастот чувствительность обычно выражается в милливоль�тах или микровольтах. В диапазоне СВЧ чувствительность выражает�ся в ваттах и составляет обычно от 10-7до 10-14 Вт.
Рабочий диапазон частот — диапазон, в пределах которого по�грешность анализатора, полученная при изменении частоты сигнала, не превышает допускаемого предела. Он определяется максимальной и минимальной частотами настройки узлов анализатора и вспомога�тельных устройств (генератора частотных меток, частотомера). Важ�ной частотной характеристикой анализатора спектра является также максимальная полоса частот, в которой можно одновременно наблю�дать составляющие спектра на экране анализатора. Эта величина оп�ределяется максимальной полосой качания частоты ГКЧ.
Время анализа — интервал времени Та, в течение которого полу�чают полное изображение исследуемого спектра на экране анализа�тора. За это время происходит изменение частоты напряжения ГКЧ от минимального до максимального значений.
Разрешающая способность характеризует минимальное рас�стояние по частоте между двумя соседними составляющими в спек�тре сигнала с равными амплитудами, при котором соответствующие им выбросы на экране анализатора спектра наблюдаются раздельно.
Анализаторы спектра характеризуются статической и динамиче�ской разрешающими способностями. Первая соответствует случаю, когда переходные процессы в УПЧ не искажают формы выбросов на экране анализатора, вторую определяют с учетом переходных про�цессов в избирательном устройстве анализатора.
Статическая разрешающая способность зависит только от ши�рины полосы пропускания УПЧ fУПЧ. Для анализатора спектра по�следовательного типа статическая разрешающая способность
(4)
Динамическая разрешающая способность анализатора спектра зависит от скорости перестройки частоты ГКЧ. Дело в том, что при увеличении скорости изменения частоты ГКЧ напряжение на выходе УПЧ не успевает изменяться в соответствии с изменением напряже�ния на его входе, так как энергия, запасенная в колебательной систе�ме этого усилителя, не может измениться мгновенно. В результате и появляются динамические искажения АЧХ УПЧ и соответственно искажения формы эпюр на экране анализатора спектра. Подобное явление возникает в том случае, если время переходного процесса в УПЧ соизмеримо с временем изменения частоты колебаний на входе УПЧ в пределах его полосы пропускания. Отсюда время анализа опре�деляется неравенством (для упрощения формула приведена без вывода):
(5.)
где fГКЧ f max — fmin;
A — коэффициент, определяемый схемой УПЧ и допустимыми динамическими погрешностями.
Из отмеченного следует, что время анализа спектра обратно про�порционально квадрату разрешающей способности анализатора. Чем выше разрешающая способность (меньше fp), тем больше должно быть время анализа. Для повышения разрешающей способности (уменьшения fp) применяют схемы с двойным или тройным преоб�разованием частоты, которые здесь не рассматриваются.
Между разрешающей способностью и временем анализа анали�затора спектра существует определенная связь. Время анализа обрат�но пропорционально квадрату разрешающей способности. Чем выше разрешающая способность, тем больше должно быть время анализа.
Необходимое время анализа для достаточно точного воспроизве�дения спектра сигнала при параллельном исследовании может быть принято равным у — времени установления неизменного уровня на�пряжения на выходе фильтра с прямоугольной АЧХ и рабочей поло�сой f (от уровня 0,1 до уровня 0,9 от установившегося значения). Из теории электрических фильтров известно, что время установления у 0,86 (f), следовательно, Та у = 1/(f). Тогда скорость парал�лельного анализа
(6)
В параллельных анализаторах при сужении полосы пропускания фильтра скорость анализа снижается. На погрешность при параллель�ном анализе влияют: конечность времени установления колебаний на выходе фильтра и зависимость ее от полосы пропускания, различие ха�рактеристик фильтров, настроенных на разные частоты.
Измеряют параметры составляющих спектра вспомогательными устройствами. Положение на оси частот отдельных спектральных со�ставляющих и характерных участков спектра определяют с помощью частотных меток. Одну частотную метку создают подачей на анализа�тор спектра вместе с исследуемым сигналом напряжения от измери�тельного генератора гармонических колебаний. При этом на экране анализатора спектра появится частотная метка — риска, соответст�вующая частоте сигнала измерительного генератора. Изменяя частоту этого генератора, добиваются совпадения метки с определяемой точ�кой спектра. Частоту спектральной составляющей анализируемого сигнала затем считывают со шкалы измерительного генератора.
Чтобы создать набор равноотстоящих друг от друга меток, в ана�лизаторах спектра применяют специальные генераторы (например, ге�нераторы частотно-модулированного сигнала). Из радиотехники из�вестно, что спектр частотно-модулированного сигнала состоит из ряда гармонических составляющих, отстоящих друг от друга на частоту мо�дуляции Fм. Предусматривают возможность изменять среднюю часто�ту колебаний fср и частоту модуляции Fм. При изменении частоты мо�дуляции меняют интервал между метками; при изменении средней частоты колебаний все метки сдвигают по оси частот. Напряжение от генератора частотно-модулированных колебаний вместе с исследуемым сигналом подают на вход анализатора спектра. При этом на эк�ране наблюдают картину наложения двух спектров. Изменяя парамет�ры напряжения калибровки (среднюю частоту и частоту модуляции), совмещают метки с характерными точками исследуемого спектра.
Современные анализаторы спектра могут обеспечить работу в диапазоне частот от 10 Гц до 40 ГГц с полосой пропускания 0,001...300 кГц и разрешающей способностью 1 кГц на высоких час�тотах. Погрешность измерения уровней напряжений достигает 5 %.
3. Цифровые методы анализа спектра сигналов
При цифровом анализе спектра исследуемый сигнал преобразуют в цифровой код и вычисляют составляющие спектра с помощью спе�циализированных микропроцессоров. Цифровые анализаторы спек�тра по совокупности дискретных отсчетов (выборок) аналогового сигнала вычисляют спектральную плотность (9.1) путем замены ин�теграла на конечную сумму из некоторого числа выборок. Такие вы�числения осуществляют с помощью алгоритмов дискретного и быст�рого преобразований Фурье.
Алгоритмы дискретного и быстрого преобразований Фурье. Ес�ли исследуемый сигнал u(t), являющийся непрерывной функцией времени на интервале 0 – Ти, представлен своими -ми отсчетами ам�плитуды {u(kt)} = {uk}= uk, взятыми через отрезки времени t, то его можно представить в виде дискретного преобразования Фурье (ДПФ):
(7)
где N = Tи/t — число отсчетов;
Сn — комплексные гармоники иссле�дуемого спектра;
п = 0, 1, 2,..., (N/2 – 1) — номер спектральной со�ставляющей.
Многократно сократить число вычислительных операций позволя�ет быстрое преобразование Фурье (БПФ). В основу алгоритма БПФ положен принцип разбиения (прореживания во времени или децима�ции) заданной последовательности {uk} из N = 2r элементов, где r — целое число (если это условие не выполняется, то последовательность искусственно дополняют нулями до требуемого значения N) отсчетов дискретного сигнала на ряд промежуточных подпоследовательностей. При этом входную последовательность представляют в виде двух подпоследовательностей с четными и нечетными номерами и половинным числом членов в каждой:
uчт = u2k; uнч = u2k+1 ; k = 0, 1, 2, …, N/2-1 (8)
Коэффициенты ДПФ для подпоследовательностей с четными и нечетными номерами записывают отдельно как Сn чт и Сn нч. Оказыва�ется, что коэффициенты Сn, результирующего ДПФ входной последо�вательности в диапазоне номеров отсчетов от 0 до (N/2 - 1) определя�ются соотношением
Cn = Cn чт + е-j2n/N Cn нч ; n = 0, 1, 2, …, N/2-1 (9)
а коэффициенты Сn ДПФ входной последовательности для отсчетов с номерами от N/2 до N-1:
CN/2 + n = Cn чт – е-j2n/N Cn нч ; n = 0, 1, 2, …, N/2-1 (10)
Формулы (9) и (10) представляют собой алгоритмы БПФ. В этих алгоритмах экспоненциальные фазовые множители exp(-j2nk/N) учитывают влияние сдвига нечетной подпоследовательности отсче�тов сигнала относительно четной. Чтобы уменьшить число вычисле�ний, четную и нечетную подпоследовательности также разбивают на две промежуточные части. Разбиение продолжают вплоть до получе�ния простейших двухэлементных последовательностей. При объеди�нении ДПФ четной и нечетной подпоследовательностей используют алгоритмы (9) и (10), подставляя в них соответствующие значения номеров N и n.
Структурная схема цифрового анализатора спектра, реализующая один из алгоритмов БПФ, показана на рис.3.
Рисунок 3. Структурная схема анализатора спектра с реализацией БПФ
В схеме используются: процессоры БПФ с каскадной структурой организации параллельной работы; q – log2 N арифметических уст�ройств АУ; (q – 1) блоков памяти БП емкостью 2i комплексных слов каждый. В режиме реального времени все N отсчетов обрабатываемой группы через устройство ввода-вывода информации УВВ поступают в ОЗУ. Последним тактом ввода группы отсчетов к ОЗУ последова�тельно подключают блоки АУ, осуществляющие обработку информа�ции в соответствии с заданным алгоритмом БПФ. Служебная инфор�мация о комплексных весовых коэффициентах exp(-j2nk/N) автома�тически вводится в схемы АУ из ПЗУ. Вывод результатов обработки осуществляют непосредственно из АУ. Синхронизация работы всех устройств цифрового анализатора спектра выполняют командами, вырабатываемыми устройством управления УУ.
Цифровые анализаторы спектра.
Современный цифровой анализатор представляет собой качест�венно новый тип аппаратуры, в которой специфические функции многочисленных приборов моделируют с помощью набора компью�терных программ: для изменения характера функционирования дос�таточно вызвать соответствующую программу обработки без аппара�турной перестройки устройств. Комплекс программ цифрового ана�лизатора спектра позволяет сочетать в одном приборе практически все функциональные возможности, необходимые для всестороннего исследования параметров различных сигналов и процессов.
Принцип действия цифрового анализатора спектра основан на вычислительных процедурах определения параметров и характери�стик различных процессов. В функциональные возможности совре�менного цифрового анализатора заложены алгоритмы:
восстановление сигнала по его спектру, т. е. вычисление обратно�го преобразования Фурье;
анализ и синтез характеристик электрических цепей: определе�ние импульсных, передаточных и фазовых характеристик цепей; ана�лиз известных диаграмм Вольперта (характеристики и параметры це�пей с распределенными постоянными); устойчивость цепей со звень�ями обратных связей — анализ критерия устойчивости Найквиста;
корреляционный анализ сигналов: вычисление корреляционных и взаимокорреляционных функций (ВКФ); определение фазовых соот�ношений сигналов (идентификация сигналов);
• измерение параметров сигналов (амплитуды, частоты, фазы, ин�декса модуляции, девиации частоты), определение параметров им�пульсных сигналов (амплитуды, длительности, длительностей фрон�тов, периода следования и т. д.);
спектральный анализ периодических, импульсных и случайных сигналов: анализ квадратурных составляющих — модуля спектра, фа�зового спектра, комплексного спектра; определение спектра мощности случайного процесса и его функции когерентности; вычисление взаим�ного спектра; усреднение спектра по полосе частот; определение кеп-стра мультипликативных сигналов;
цифровая обработка и фильтрация сигналов и вычисление произ�ведения спектров (операция, обратная свертке);
анализ статистических характеристик случайных процессов; по�строение гистограмм мгновенных значений сигналов; определение одномерной плотности вероятности и интегральной функции распре�деления случайных процессов.
Структурная схема цифрового анализатора спектра приведена на рис.4. Исследуемые сигналы по одному (А) или двум (А, Б) каналам подают на соответствующие усилители с переменным коэффициен�том усиления, которые приводят различные уровни входных сигналов (от 0,01 до 10 В) к значению, необходимому для нормальной работы последующих трактов. Затем сигналы поступают на ФНЧ, который выделяет подлежащую анализу полосу частот.
Рисунок 4. Цифровой анализатор спектра
Исследователь может включать и выключать фильтры. С выхода фильтров сигналы поступают на АЦП, где они преобразуются в па�раллельный 10-разрядный двоичный код. Может работать как один, так и оба канала одновременно. В последнем случае выборки сигнала проходят параллельно по обоим каналам, что позволяет сохранить в цифровом коде информацию о фазовых соотношениях сигналов, не�обходимую для измерения взаимных характеристик. Частота выборки задается встроенным кварцевым генератором и может изменяться ис�следователем в пределах 0,2... 100 кГц. Эта частота определяет отсчетный масштаб анализатора спектра сигналов во временной и час�тотной областях.
Тракты прохождения исследуемых сигналов от входов усилите�лей до выхода АЦП имеет калиброванные значения коэффициента передачи во всем диапазоне частот и уровней напряжений. Информа�ция о значении коэффициента передачи и частота выборки АЦП вво�дятся в вычислительное устройство (микропроцессор) и учитывается при формировании конечного результата исследований. Микропро�цессор работает в соответствии с заложенной в его память програм�мой. Программа состоит из ряда подпрограмм, организующих ту или иную вычислительную операцию (вычисление спектра или корреля�ционной функции, определение вероятностных характеристик, по�строение гистограммы и т. д.). Вызов необходимой подпрограммы осуществляют с помощью устройства управления. Результаты вычис�лений выводят на индикаторное или регистрирующее устройство, в качестве которого могут быть использованы цифровой графопострои�тель, принтер, цифровой магнитофон, дисковый накопитель, осцилло�граф или самописец. Последние два подключают через ЦАП. Все ре�зультаты сопровождают масштабным коэффициентом для перевода их в физические единицы.
При анализе сигналов, представленных в цифровом виде, данные вводятся непосредственно в вычислительное устройство с помощью устройства ввода цифровых данных с наборного табло пульта управ�ления в десятичном коде. Основные режимы работы цифрового ана�лизатора спектра: спектральный, цифровая фильтрация, статистиче�ский и корреляционный анализ; измерение спектра мощности, взаим�ного спектра двух сигналов.
4. Анализаторы спектра сигналов на цифровых фильтрах
Внедрение цифровых методов обработки сигналов в измерительной технике привело к созданию эффективных и высокоскоростных анализа�торов спектра на цифровых фильтрах. Цифровой фильтр имеет стабиль�ную частотную характеристику, не нуждается в подстройке, компенси�рующей неточности из-за старения элементов, и его универсальность намного выше аналогового фильтра. При перестройке цифрового фильт�ра не надо менять элементы, а достаточно его перепрограммировать. Од�нако главное преимущество цифровой фильтрации в измерительной тех�нике — применение высокоточных цифровых детекторов и устройств усреднения (цифровых интеграторов). Цифровой детектор измеряет практически истинное среднее квадратическое значение анализируемого сигнала без ограничений, связанных с его амплитудным значением.
Цифровое устройство усреднения, усредняющее анализируемый сигнал по линейному и экспоненциальному (или показательному) за�конам, отличается универсальностью и эффективностью, которые не�достижимы для аналоговых усредняющих устройств.
Важной операцией цифровой обработки сигналов в измеритель�ной технике является цифровая фильтрация. Она заключается в циф�ровом преобразовании последовательности числовых отсчетов вход�ного сигнала {u(kt)} = {uk} в последовательность числовых отсчетов {y(kt)} = {уk} выходного сигнала.
Структурные схемы цифровых фильтров. Цифровые фильтры де�лятся на два больших класса: нерекурсивные и рекурсивные. Термин «рекурсивный» связан с известным математическим приемом «рекур�сией» — циклическим обращением к вычисленным данным, получен�ным на предыдущих этапах математических операций.
В нерекурсивных фильтрах отклик зависит только от значений входной последовательности, и для формирования k-го выходного отсчета используют лишь предыдущие значения входных отсчетов. Такие фильтры обрабатывают входной дискретный сигнал {uk} в со�ответствии с алгоритмом
(11)
где yk – выходной сигнал;
а0, а1, а2, …, аm – действующие постоянные (весовые) коэффициенты;
m – порядок нерекурсивного фильтра, т.е. максимальное число запоминаемых чисел.
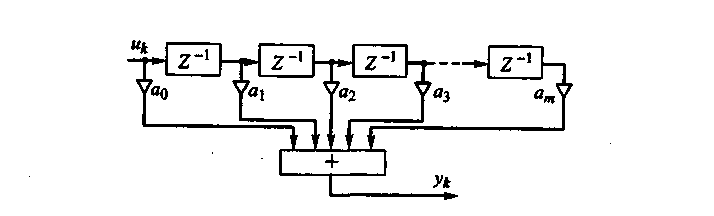
Рис.5. Структурная схема нерекурсивного цифрового фильтра
Аналитическую сторону алгоритма обработки (11) характери�зует структурная схема цифрового фильтра, показанная на рис.5.
Основой любого цифрового фильтра являются элементы задерж�ки входной цифровой последовательности {uk} на интервал дискрети�зации Z-1 (задержка сигнала на интервал t в общепринятых симво�лах известного в математике z-преобразования), а также масштабные (весовые) блоки аm, выполняющие в цифровой форме операции ум�ножения на соответствующие коэффициенты. По существу элементы задержки являются ячейками памяти. Сигналы с масштабных блоков поступают в сумматор (+), на выходе которого образуется последова�тельность отсчетов выходного сигнала {уk}.
Не проводя подробного анализа, отметим, что коэффициенты a0, a1, а2,,... ,аm совпадают с соответствующими отсчетами импульсной характеристики цифрового фильтра h0, h1 , h2,..., hm.
Рекурсивные цифровые фильтры. Возможности нерекурсивного цифрового фильтра существенно расширяются при введении в его схе�му обратных связей, формирующих k-й выходной отсчет уk путем ис�пользования предыдущих значений как входного, так и выходного дис�кретных (выраженных в цифровой форме) значений сигналов:
(12)
Здесь постоянные коэффициенты a0, a1, а2,,... ,аm как и в алгоритме обработки (11), характеризуют нерекурсивную часть, а коэффици�енты b0, b1, b2, ... ,bn — рекурсивную часть алгоритма цифровой фильт�рации, причем последние не равны нулю одновременно. Порядок та�кого цифрового фильтра определяется коэффициентом т нерекурсив�ной части алгоритма обработки.
Структурная схема цифрового рекурсивного фильтра представ�лена на рис. 6.
Рис.6. Структурная схема рекурсивного цифрового фильтра
На цифровых фильтрах создают различные схемы анализаторов спектра сигналов, в том числе анализаторы последовательного и па�раллельного типов.
5 Измерение нелинейных искажений.
Измерение ряда физических величин, отражающих параметры и характеристики сигналов или электрических цепей, осуществляют с помощью приборов, аналогичных по структуре анализаторам спек�тра. К таким параметрам и характеристикам относят нелинейные ис�кажения и связанные с ними изменения формы и спектра сигналов, которые возникают в цепях с нелинейной амплитудной характеристи�кой. При прохождении по нелинейным цепям полезные колебания теряют синусоидальную форму (искажаются) и в их спектре появля�ются высшие гармоники.
Возникающие при нелинейных искажениях гармоники можно исследовать и измерить с помощью анализаторов спектра. Известны несколько количественных показателей уровня нелинейных искаже�ний. Наибольшее распространение получил такой показатель, как коэффициент нелинейных искажений (коэффициент гармоник), представляющий собой отношение среднего квадратического значе�ния всех высших гармоник напряжения (или тока)
(13)
к среднему квадратическому значению его первой гармоники
Kг =Uг /U1 (14)
Для измерения относительного значения напряжения гармоник можно использовать анализатор спектра, если его разрешающая спо�собность позволяет наблюдать раздельно спектральные составляю�щие. Если детектор анализатора линейный, то в формулу (13) вме�сто напряжений U1, U2, …, Un можно подставить значения их ампли�туд, измеренных на экране анализатора в единицах длины.
Существуют специальные приборы, измеряющие коэффици�ент нелинейных искажений, — измерители нелинейных искаже�ний. Упрощенная структурная схема аналого-цифрового измерите�ля нелинейных искажений показана на рис. 11.
Рисунок 11. Упрощенная структурная схема аналого-цифрового
измерителя нелинейных искажений
В основе измерительной методики таких приборов лежит ме�тод подавления основной частоты исследуемого сигнала. Входное устройство служит для согласования измерительного прибора с ис�точником исследуемого сигнала. Перед измерением переключатель Кл ставят в положение Калибровка. Затем с помощью усилителя уровень исследуемого сигнала повышают до такого фиксированного значения, при котором электронный цифровой вольтметр среднего квадратического значения будет проградуирован в значениях коэф�фициента нелинейных искажений. При этом измеряется среднее квадратическое значение напряжения всего исследуемого сигнала
. (15)
Затем переключатель Кл прибора ставят в положение Измерение. Настраивая заграждающий фильтр, подавляют напряжение основной частоты (первой гармоники U1). Полное подавление гармоники U1 будет при минимальном показании прибора. В этом случае цифровой вольтметр показывает среднее квадратическое значение суммы выс�ших гармонических составляющих сигнала Ur (13). Сравнивая по�казания во втором и первом случаях, находят коэффициент гармоник
Kг =Uг /U (16)
При положении переключателя Кл Измерение измеряют коэффициент Kг1. При этом коэффициент гармоник вычисляют по формуле
(17)
При небольших нелинейных искажениях исследуемого сигнала (Кг < 0,1) коэффициенты Кг и Кг1 отличаются меньше чем на 1 %. Обычно измерители нелинейных искажений применяют для измере�ния коэффициента гармоник Кг в пределах 0,1...30%. При этом диапазон рабочих частот составляет полосу от 0,01 кГц до 25 МГц.
Литература
1. Барыбин, А.А. Электроника и микроэлектроника. Физико-технологические основы / А.А. Барыбин. - М.: ФИЗМАТЛИТ, 2006. - 424 c.
2. Белов, Н.В. Электротехника и основы электроники: Учебное пособие / Н.В. Белов, Ю.С. Волков. - СПб.: Лань, 2012. - 432 c.
3. Белоусов, В.В. Судовая электроника и электроавтоматика: Учебник / В.В. Белоусов, В.А. Волкогон. - М.: Колос, 2008. - 645 c.
4. Борисенко, В.Е. Наноэлектроника: теория и практика: Учебник / В.Е. Борисенко, А.И. Воробьева, А.Л. Данилюк, Е.А. Уткина. - М.: БИНОМ. ЛЗ, 2013. - 366 c.
5. Вайнштейн, Л.А. Теория дифракции. Электроника СВЧ / Л.А. Вайнштейн. - М.: Радио и связь, 1995. - 600 c.
6. Велстистов, Е. Все о приключениях Электроника: Повести / Е. Велстистов. - СПб.: Азбука-Аттикус, 2013. - 592 c.
7. Велтистов, Е.С. Победитель невозможного: третья книга из цикла о приключениях Электроника / Е.С. Велтистов. - М.: Дет. лит., 2010. - 235 c.
8. Воронков, Э.Н. Твердотельная электроника. Практикум: Учебное пособие для студ. высш. учеб. заведений / Э.Н. Воронков. - М.: ИЦ Академия, 2010. - 128 c.
9. Воронков, Э.Н. Твердотельная электроника: Учебное пособие для студ. высш. учеб. заведений / Э.Н. Воронков, А.М. Гуляев, И.Н. Мирошникова. - М.: ИЦ Академия, 2009. - 320 c.
10. Гальперин, М.В. Электротехника и электроника: Учебник / М.В. Гальперин. - М.: Форум, НИЦ ИНФРА-М, 2013. - 480 c.
11. Голубева, Н.С. Основы радиоэлектроники сверхвысоких частот: Учебное пособие / Н.С. Голубева, В.Н. Митрохин; Под общ. ред. проф. д.т.н. И.Б. Федоров. - М.: МГТУ им. Баумана, 2008. - 488 c.
12. Горохов, П.К. Толковый словарь по радиоэлектронике / П.К. Горохов. - М.: Русский язык, 1993.
13. Гусев, В.Г. Электроника и микропроцессорная техника: Учебник / В.Г. Гусев, Ю.М. Гусев. - М.: КноРус, 2013. - 800 c.
14. Джонс, М.Х. Электроника - практический курс / М.Х. Джонс. - М.: Техносфера, 2013. - 512 c.
15. Евстратов, В.А. Радиоэлектроника прогулочных судов / В.А. Евстратов. - М.: ТрансЛит, 2008. - 128 c.
16. Ермуратский, П.В. Электротехника и электроника / П.В. Ермуратский, Г.П. Лычкина, Ю.Б. Минкин. - М.: ДМК Пресс, 2013. - 416 c.
17. Ефимов, И.Е. Основы микроэлектроники / И.Е. Ефимов, И.Я. Козырь. - М.: Высшая школа, 1983.
Анализ спектра и измерение нелинейных искажений