МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ В ОСНОВНОЙ ШКОЛЕ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФГБОУ ВПО «АРМАВИРСКАЯ ГОСУДАРСТВЕННАЯ ПЕДАГОГИЧЕСКАЯ
АКАДЕМИЯ»

ИНСТИТУТ ПРИКЛАДНОЙ ИНФОРМАТИКИ, МАТЕМАТИКИ И ФИЗИКИ

Кафедра математики, физики и МП

ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА

НА ТЕМУ:

МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ В ОСНОВНОЙ ШКОЛЕ

Выполнила: студентка 4 курса ИПИМиФ,

направления «Педагогическое образование»; профиль «Математическое образование»

ХАЧАТРЯН Лариса Сергеевна

Научный руководитель:

к. п. н., доцент

ПАЛАДЯН Каринэ Анатольевна

Армавир, 2015

Содержание

ВВЕДЕНИЕ……..………..……………………….…………….….………….

ГЛАВА 1. ТЕОРЕТИЧЕСКИЕ ОСНОВЫ ОБУЧЕНИЯ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ В ШКОЛЬНОМ КУРСЕ МАТЕМАТИКИ.…….

1.1. Определение задачи, решение задач………………………….....

1.2. Виды задач в математике……………………………..…….……..

1.3. Введение понятия процент……………..………..……………….

1.4. Краткий анализ современного состояния процентов в школьном курсе математике………………………………………………….

ГЛАВА 2. МЕТОДИЧЕСКИЕ ОСОБЕННОСТИ ИЗУЧЕНИЯ ПРОЦЕНТОВ В ОСНОВНОЙ ШКОЛЕ.......................………...……………

2.1. Методика введения процентов в учебнике «Математика 5» (под редакцией Н. Я. Виленкин, А. С. Чесноков и другие)…..…...……..

2.2. Методика введения процентов в учебнике «Математика 5» (под редакцией Л. Н. Шеврин, А. Г. Гейн, И.О. Коряков и другие).…...…

2.3. Методика изучения процентов в учебниках для V – IX классов (под редакцией Г.В. Дорофеева)……………..………………………….…...

2.4. Методика нахождения нескольких процентов от числа.…...…..

2.5. Методика нахождения числа по его процентам….…....………..

2.6. Методика нахождения процентного отношения….……………

2.7. Задачи на проценты для младших классов…...……..…………..

2.8. Задачи на сложные проценты…………….……...………………

2.9. Задачи на концентрацию, смеси и сплавы…….………..………

ГЛАВА 3. Методика обучения учащихся решению задач на проценты в рамках элективного курса «Проценты на все случаи жизни» для предпрофильной подготовки учащихся 9 классов………….………………………….…………….

3.1. Содержание обучения на элективном курсе…..….…….……..…

3.2. Примерное тематическое планирование….……………...…..…

3.3. Методические разработки для апробации элективного курса.....

ЗАКЛЮЧЕНИЕ…...…………………………………………………………...

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ..……………………………

ВВЕДЕНИЕ

В настоящее время уделяется большое внимание школьному образованию как одному из уровней образовательного процесса. Одна из важнейших его задач – обеспечить школьникам глубокие и прочные знания, а также умение рационально применять их в учебной и практической деятельности.

Большое практическое значение имеет умение решать задачи на проценты, потому что понятие процента широко используется и в реальной жизни, и в различных областях науки.

В школьном курсе эта тема изучается в V – VI классе, но ей отводится очень мало времени и места, в результате учащиеся не умеют решать задачи на проценты. Наблюдения действительно показывают, что многие школьники испытывают трудности, когда встречаются с понятием процента. Школьники не разбираются в вопросах инфляции, ценообразования, банковских вкладах и кредитах. Поэтому желательно уделять внимание этой теме постоянно, учитывая, что проценты тесно связаны с повседневной жизнью, что с ними постоянно приходится иметь дело.

Кроме того, при поступлении в различные техникумы, колледжи, институты и университеты требуются знания, связанные с процентами. А сейчас при сдаче ЕГЭ нужны знания о процентах, так как задачи на проценты включены в его состав. При подготовке к экзамену по математике учителю предстоит повторить со школьниками процентные вычисления, а что-то придётся объяснить заново. Это очень важная работа, так как учащиеся впервые с процентами знакомились в V классе, а среди заданий экзамена есть задачи на процентные вычисления.

Задачи на проценты становятся прерогативой химии, которая внедряет свой взгляд на проценты, а в математике их место только в рамках задач на повторение, задач повышенной трудности. Таким образом, школьниками забываются проблемы общезначимости процентов, разнообразия сфер их применения.

Проценты в мире появились из практической необходимости, при решении определенных задач, в основном это экономические потребности. И поэтому надо отметить важность процентов в нашей жизни. Так как проценты проникли практически во все отрасли знаний. Мы часто видим, что проценты применяют даже там, где на первый взгляд не применимы. Например, человек на вопрос: «Как у Вас здоровье?», – может ответить, что здоров процентов на восемьдесят. Отсюда и видно, что проценты можно применять при измерении не только точных величин, таких как килограммы, рубли и.т.д. Таким образом, проценты являются универсальной величиной измерения разных величин и объектов.

Проценты появились в древности, когда появилось понятие долга, так как они необходимы были для выплаты по закладным и займам и т. д. И поэтому в математике стала развиваться новая область – проценты. Первая потребность в процентах была экономическая. Затем проценты стали широко применятся в различных отраслях и науках (математика, химия и т д.). И только в наше время проценты приобрели широкое распространение. И именно поэтому в работе рассмотрим как ведется изучение процентов в школе.

Цель данной работы состоит в разработке методических рекомендаций по изучению темы «Проценты» по учебникам под редакцией Н. Я. Виленкин, А. С. Чесноков и другие «Математика 5»[13], под редакцией Л. Н. Шеврин, А. Г. Гейн, И.О. Коряков и другие «Математика 5»[16], под редакцией Г.В. Дорофеева для V–IX классов [10], [11], [12],[14], [15].

Объектом исследования является процесс обучения математике в V - IX классов.

Предмет исследования – обучение школьников решению задач на проценты в курсе алгебры VII-IX классов.

В данной работе выдвинута следующая гипотеза: обучение решению задач на проценты будет более эффективным, если:

1. Формирование понятия процента начать в V-VI классе.

2. Рассматривать различные типы задач на проценты в течение всего курса алгебры VII - IX класса.

3. Использовать символическую наглядность, как при формировании понятия процента, так и при изучении основных типов задач.

Задачами работы является изучение методики обучения процентов в школьном курсе, рассмотрение особенностей обучения в пятых классах, анализ особенностей изложения данной темы в разных учебниках. Разработка собственной методики преподавания процентов, которая заключается в том, чтобы взять все самое лучшее из разных источников и объединить это для улучшения методики изучения процентов. Также в работе предполагается рассмотреть методику решения задач связанных с такими понятиями как «концентрация» и «процентное содержание», это задачи связанные с составлением смесей и сплавов. Надо отметить, что задачи связанные с такими понятиями как «концентрация» и «процентное содержание» решаются в старших классах и это, как правило, задачи на составление уравнений.

Для достижения поставленных целей, проверки гипотезы и решения сформулированных выше задач были использованы следующие методы исследования:

1. Изучение учебно-методической и математической литературы.

2. Анализ школьных учебников.

3. Опытное преподавание.

4. Наблюдение во время проведения занятий с учащимися.

Выпускная квалификационная работа состоит из введения, трех глав, заключения и списка используемых источников.

Во введении обоснована актуальность исследования, даны его основные характеристики.

Глава 1 посвящена теоретическим основам обучения математики, рассматриваются определения понятий «задача», «процент», отражаются основные виды задач, а также проводится краткий анализ современного состояния процентов в школьном курсе.

В главе 2 рассматриваются методические аспекты изучения процентов в основной школе, отражается авторский подход изучения проблемы (анализ учебников под редакцией Н.Я. Виленкина и др., Л.Н. Шеврина и др., Г.В. Дорофеева). Достаточно внимания уделяется следующим проблемам: методика нахождения нескольких процентов от числа, числа по его процентам, процентного соотношения; задачи на проценты для младших классов, на сложные проценты, на концентрацию, смеси и сплавы.

Глава 3 посвящается методике обучения учащихся решения задач на проценты в рамках элективного курса «Проценты на все случаи жизни» для предпрофильной подготовки учащихся 9 классов.

В заключении приведены основные выводы исследования, результат апробации.

Список используемых источников содержит 31 наименование.

ГЛАВА 1. Теоретические основыобучения решению задач на проценты в школьном курсе математики

1.1. Определение задачи, решение задач

Задача — это проблемная ситуация с явно заданной целью, которую необходимо достичь; в более узком смысле задачей также называют саму эту цель, данную в рамках проблемной ситуации, то есть то, что требуется сделать.

В задаче выделяют:

Элементы ситуации;
Правила преобразования ситуации;
Требуемое решение (цель).

Требуемое решение может быть задано по-разному:

как конечное состояние ситуации (например, то, как должна выглядеть собранная головоломка);
как получение нового знания (например, 2 + 2 = ?);
как установление неких связей (отношений) между элементами ситуации (например, когда требуется определить, какой из двух предметов тяжелее) и т. д.

Решение задач — это процесс выполнения действий или мыслительных операций, направленный на достижение цели, заданной в рамках проблемной ситуации — задачи; является составной частью мышления. С точки зрения когнитивного подхода процесс решения задач является наиболее сложной из всех функций интеллекта и определяется как когнитивный процесс более высокого порядка, требующий согласования и управления более элементарными или фундаментальными навыками.

Процесс решения задачи состоит из таких основных подпроцессов, как:

обнаружение проблемной ситуации;
постановка задачи: выявление и более или менее строгое определение исходного (данного) — его элементов и отношений между ними — и требуемого (цели);
нахождение решения задачи[31].

1.2. Виды задач в математике

Существует несколько классификаций видов задач в математике.

1) Виды задач классифицируют по содержанию, сюда входят следующие виды задач: вычислительные, задачи на доказательство, задачи на построение, комбинированные задачи.

Особое место при изучении задач занимает такой вид, как текстовые задачи, которые можно подразделить на традиционные и нетрадиционные (проблемные). Традиционные текстовые задачи – это задачи на движение, работу, сплавы и смеси. Проблемные текстовые задачи – это и есть нестандартные задачи.

2) Виды задач классифицируют по функциям: дидактические, развивающие, познавательные и контролирующие задачи.

Дидактические задачи опережающего характера могут быть и познавательными, и развивающими. Функции задач можно определить как глобально, так и локально. Вышеперечисленные функции являются глобальными. Локальные функции учитываются при подготовке к конкретному уроку. Дидактические задачи предусматривают и используют на этапе закрепления. Познавательные задачи несут в себе то новое, что предусматривается в целях обучения на данном этапе. Развивающие задачи – это новые незнакомые проблемные задачи.

3) Виды задач классифицируют по обучающей роли в изучении школьного курса: задачи на усвоение, задачи на овладение математической символикой, задачи на обучение доказательству, задачи на формирование математических умений и навыков, задачи развивающего характера.

Любую дидактическую или обучающую задачу можно преобразовать, усилив развивающую функцию, этого можно достичь различными путями: частичным изменением условия задач, рассмотрение ее частных или предельных случаев, постановкой дополнительных вопросов, решение задачи более рациональным способом.

4) В зависимости от числа известных ученику компонентов выделяют следующие виды задач:

тренировочные упражнения (шаблонные задачи), в них известны и цель, и способ решения, и ответ. К первому виду задач относят учебные задачи, где известны цель и условие задачи, они занимают наибольшее содержание учебника;
нестандартные задачи – в таких задачах известно только условие;
задачи-проблемы – известна только цель. Данные задачи встречаются в быту и производстве, где четко определена только цель, необходимые условия пути и средства решения ученик должен определить самостоятельно [31].

1.3. Введение понятия процент

Слово «процент» происходит от латинского «procentum», что буквально означает «на сотню», «со ста» или «за сотню». В популярной литературе возникновение этого термина связывается с внедрением в Европе десятичной системы счисления в XV веке. Но идея выражения частей целого постоянно в одних и тех же величинах, которая вызвана практическими соображениями, родилась еще в древности у вавилонян. Ряд задач клинописных табличек посвящен исчислению процентов, но вавилонские ростовщики считали не «со ста», а «с шестидесяти». Проценты были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. От римлян проценты перешли к другим народам Европы [22].

Процент, по-видимому, возник в Европе вместе с ростовщичеством. Существует мнение, что понятие процент ввел бельгийский ученый Симон Стевин. Он опубликовал таблицы процентов в 1584 г. В России употребление термина «процент» начинается в конце XVIII в. Долгое время под процентами понималось исключительно прибыль или убыток на каждые 100 рублей. Проценты применялись только в торговых и денежных сделках. Затем область применения процентов расширилась, они встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике.

Интересно происхождение обозначения процента. Есть версия, будто бы знак % происходит от итальянского procento (сто), которое в процентных расчетах часто сокращенно писалось cto. Отсюда, путем дальнейшего сокращения в скорописи буква t превратилась в наклонную черту (/), возник современный знак процента (см. схему 1.1).

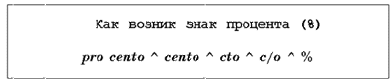
Схема 1.1. Возникновение знака процента

Также, в учебнике Н.Я. Виленкина, В.И. Жохова, А.С. Чеснокова и С.И. Шварцбурда «Математика 5» [13] в рубрике «История математики» дана еще одна достаточно любопытная версия возникновения знака %. Существует предположение, что знак % возник в результате опечатки. В Париже в 1685 г. была напечатана книга Матьёде ла Порта «Руководство по коммерческой арифметике», где по ошибке наборщик вместо cto напечатал знак %.

В данном учебнике также содержатся достаточно полезные, с точки зрения общего развития, дополнительные сведения, которые касаются промилле (от латинского «с тысячи») – десятой части процента. Сказать учащимся об этом обязательно нужно, указав при этом его обозначение ‰.

1.4. Краткий анализ современного состояния процентов в школьном курсе математике

Исторически сложились две стороны назначения математической науки: практическая, которая связана с созданием и применением инструментария, необходимого человеку в его продуктивной деятельности, и духовная, которая связана с мышлением человека и с овладением определенным методом познания. Исходя из этого, определяются методы обучения математике. Математическая подготовка нужна для понимания принципов устройства, использования современной техники и восприятия научных и технических понятий. Математика– язык современной науки. Значения математического образования для формирования духовной сферы человека вызвано тем громадным запасом общечеловеческих, общекультурных ценностей, которые накопила математическая наука в ходе своего развития [8].

В процессе обучения в запас приемов и методов человеческого мышления естественным образом включается индукция и дедукция; общение и конкретизация; анализ и синтез; классификация и систематизация; абстрагирование; аналогия. Объекты математических умозаключений, правила их конструирования вскрывают механизм логических построений, вырабатывают умение формулировать, обосновывать и доказывать суждения, тем самым развивать логическое мышление. В ходе решение задач, которые представляют собой основной вид учебной деятельности на уроках математики, развиваются творческая и прикладная стороны мышления.

Принципиальным положением организации школьного математического образования должна стать технология уровневой дифференциации обучения математике в основной школе. Это означает, что при освоении общего курса, одни школьники в своих результатах ограничиваются обязательным уровнем подготовки, а другие, в соответствии со своими склонностями и способностями, достигают более высоких результатов. При этом, достижения обязательного уровня должны стать непременной обязанностью учащихся в их учебной деятельности. При этом, каждый имеет право самостоятельно решить: ограничится ли этим уровнем, или продвинуться дальше. Именно на этом пути осуществляется гуманистические начала в обучение математике.

У практического интеллекта, кроме связанной с этим названием способности решать практические задачи, есть и другие атрибуты: здравый смысл, смекалка, « золотые руки », интуиция. Долгое время, развитием этих сторон интеллекта ребенка школа пренебрегала, или сводила их главным образом к приобретению учащимися элементарных трудовых умений и навыков, которые относились к малоквалифицированной работе. В условиях перехода к рыночным отношениям и самостоятельной экономической деятельности людей, значение практического интеллекта особенно возросло, так как каждому человеку теперь нужно вести расчетливый и продуманный образ жизни.

В структуру практического интеллекта входят следующие качества ума: предприимчивость, экономичность, расчетливость, умение быстро и оперативно решать возникающие задачи.

Предприимчивость проявляется в том, что в сложной жизненной ситуации человек способен находить несколько решений возникшей проблемы, а главное – том, что какая бы проблема перед ним ни возникла, он всегда готов и в состоянии отыскать ее оптимальное решение в практическом плане. Предприимчивый человек из любой ситуации сможет найти выход [17].

Сами проценты не дают экономического развития, однако их знание помогает в развитии практических способностей, а также умение решать экономические задачи. Обдуманное изучение процентов может способствовать развитию таких навыков как экономичность и расчетливость.

Экономичность, как качество практического ума заключается в том, что обладающий этим качеством человек в состоянии найти такой способ действия, который в любой сложившейся ситуации с наименьшими затратами и издержками приведет к нужному результату.

Расчетливость – умение заглядывать далеко вперед, и, предвидя последствия тех или иных решений и действий, точно определять их результат, оценивать то, чего он может стоить.

Наконец, умение оперативно решать поставленные задачи – это динамическая характеристика практического интеллекта, которая проявляется в количестве времени, которое проходит с момента возникновения задачи до ее практического решения.

Развитое мышление – это такое практическое мышление, которое обладает всеми указанными свойствами. Экономичность сформировать у детей проще, чем другие качества практического ума, но делать это надо систематически, пробуждая детей в школе и дома самостоятельно производить расчеты материальных затрат на интересующие их дела.

Тему «Проценты» невозможно отнести к темам, которые поддаются легкому усвоению. Ее традиционное изучение сосредоточено в строгих временных рамках курса V – VI классов, что не позволяет расширить спектр практических приложений и полноценно учитывать возрастные возможности учащихся в формировании ряда практических умений в работе с процентами.

Вопросы, связанные с процентами, позволяют сделать курс практико-ориентированным, показать учащимся, что приобретаемые ими математические знания применяются в повседневной жизни. Интерес в значительной степени поддерживается также и содержанием задач, основы которые приближены к современной тематике и к жизненному опыту детей, а затем и подростков. Это служит достаточно сильным мотивом для решения предлагаемых задач.

Введение процентов опирается на предметно – практическую деятельность школьников, на геометрическую наглядность, геометрическое моделирование. С самого начала освоения понятия школьники выполняют много заданий, в которых требуется заштриховать, закрасить, начертить, вырезать часть фигуры. Широко используются рисунки и чертежи, помогающие разобраться в задаче и увидеть путь решения.

Как и во всех остальных разделах курса, при рассмотрении этой темы использованы широкие возможности для дифференцированного обучения школьников. Задачи даются разной сложности – от самых простых, базовых, до достаточно трудных. Учитель может подобрать материал, соответствующий возможностям школьников.

При обучении решению задач на проценты школьники знакомятся с разными способами решения задач, причем спектр примеров шире, чем это бывает обычно. Ученик овладевает разнообразными способами рассуждения, обогащая свой запас приемов и методов. Но при этом также важно, что он имеет возможность выбора и может пользоваться тем приемом, который ему кажется более удобным [30, c. 33-40].

ГЛАВА 2. Методика изучения процентов в младших классах

2.1 Методика введения процентов в учебнике «Математика 5» (под редакцией Н. Я. Виленкин, А. С. Чесноков и другие)

Процентные расчеты довольно плохо знают учащиеся школы. Тому есть несколько причин:

Во-первых: в настоящее время проценты изучаются без всякой связи с соответствующими задачами на дроби. Первое знакомство с процентами происходит по учебнику Н.Я. Виленкина и др. в конце 5 класса. К этому моменту школьники умеют в задачах практического характера находить дробь числа, число по его дроби, и какую часть одна величина составляет от другой. Указанные умения если и обобщаются учителем в виде правил, то сами правила никак не помогают перенести уже освоенное умение в новую ситуацию, так как при решении конкретных задач на проценты речь ведут не про числитель и знаменатель дроби, а про количество процентов, которые содержатся в целом и его части.

Во-вторых: и это влияет на умении школьников решать более сложные задачи на проценты, после изучения в VI классе правил нахождения дроби числа умножением на дробь и нахождения числа по его дроби делением на дробь, эти приемы не переносятся на задачи на проценты.

В-третьих: в решении задач на проценты довольно скоро начинают применять пропорции – тем самым процесс решения задач «механизируется», что мешает учащимся понимать смысл своих действий.

Сотую часть рубля называют копейкой, сотую часть метра – сантиметром, сотую часть гектара – аром или соткой. Принято называть сотую часть величины или числа процентом. Значит одна копейка – от одного рубля, а один сантиметр – от одного метра, один ар – гектара, две сотых – от числа два.

Процентом называют одну сотую часть числа [13].

Для краткости слов «процент» после числа заменяют знаком.

Предложение «На слет направили пионеров нашей школы» читают так: «На слет направили два с половиной процента пионеров нашей школы», а предложение «В этом месяце завод перевыполнил план на » читают так: «В этом месяце завод перевыполнил план на двенадцать процентов».

Так как равен сотой части величины, то вся величина ровна .

Задача 2.1: Швейная фабрика выпустила 1200 платьев. Из них 32% платьев нового фасона. Сколько платьев нового фасона выпустила фабрика?

Решение:

Так как 1200 платьев – это выпуска, то, чтобы найти выпуска, надо разделить на . Получим, что , значит, выпуска равен платьям. Чтобы найти, чему равны выпуска, надо умножить на . Так как , то фабрика выпустила платья нового фасона.

Задача 2.2: За самостоятельную работу по математике 12 учеников получили отметку «4», что составляет всех учеников. Сколько учеников в классе?

Решение:

Сначала узнаем, чему равен всех учеников. Для этого разделим на . Так как , то равен . Чтобы узнать, чему равны надо умножить на . Так как , то в классе учеников.

Задача 2.3: Из га колхозного поля га засажено свеклой. Какой процент поля засажен свеклой?

Решение:

Свеклой засажено всего поля. Обратим дробь в десятичную. Для этого разделим на . Получим . Значит, свеклой засажена сотая всего поля. Каждая сотая равна поля, поэтому свеклой засажен всего поля.

2.2 Методика введения процентов в учебнике «Математика 5» (под редакцией Л. Н. Шеврин, А. Г. Гейн, И.О. Коряков и другие)

Сотая часть метра – это сантиметр, сотая часть рубля – копейка, сотая часть центнера– килограмм. Люди давно заметили, что сотые доли величин удобны в тактической деятельности. Потому для них было придумано специальное название – процент (от латинского “по-центум” – на сто). Значит одна копейка – от одного рубля, а один сантиметр – от одного метра.

Один процент – это одна сотая доля числа [16].

Математическими знаками один процент записывается так: . Записи , читают: три процента, пять процентов.

Прочитайте предложение:

«К маю вспахано пахотных земель»;

(К шестнадцатому маю вспахано восемьдесят девять процентов пахотных земель).

«Производительность труда повысилась на »;

(Производительность труда повысилась на шесть процентов).

«Цены снижены на ».

(Цены снижены на двадцать пять процентов»).

Определение одного процента можно записать равенством:

Каждый быстро сообразит, что ; ; и т. д.

Подумаем, как найти от числа. Раз это одна сотая часть, надо число разделить на . Мы уже сделали вывод, что деление на можно заменить умножением на . Поэтому, чтобы найти от данного числа, нужно умножить его на . А если нужно найти от числа, то умножаем данное число на и т.д.

Получилось правило:

Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь.

Пример решения задачи на проценты:

Задача 2.4: Токарь вытачивал за час деталей. Применив резец из сверхпрочной стали, он стал вытачивать на деталей в час больше. На сколько процентов повысилась производительность труда токаря?

Решение:

Чтобы решить эту задачу, надо узнать, сколько, процентов составляют деталей от . Для этого найдем сначала, какую часть составляет число от числа .

Мы знаем, что нужно разделить на . Получится . А теперь запишем в процентах – . Получаем ответ: производительность труда токаря повысилась на.

Итак, чтобы найти, сколько процентов одно число составляет от другого, нужно разделить первое число на второе и полученную дробь записать в виде процентов.

Задача 2.5: Тракторист вспахал кв. км поля. Это составило всей площади, которую должен вспахать. Какова вся площадь, которую ему нужно вспахать?

Решение:

Давайте рассуждать. Вся площадь нам не известна. Обозначим ее буквой . Мы знаем, что от числа составляет .

Значит сначала нужно заменить десятичной дробью, а затем записать уравнение . Решая его, получаем, что Х (кв. км).

Как же мы нашли ? Во-первых, заменили проценты десятичной дробью, во-вторых, разделили данное нам число на получившуюся десятичную дробь.

Конечно, площадь и число процентов в этой задаче могли быть другими. Но путь решения останется прежним. Значит можно сформулировать правило: если дано, сколько процентов от искомого числа составляет данное число, то чтобы найти искомое число, нужно заменить проценты десятичной дробью и разделить на эту дробь данное число.

2.3 Методика изучения процентов в учебниках для V-IX классов (под редакцией Г.В. Дорофеева)

Впервые о процентах учащиеся узнают в VI классе. Проценты предлагается рассматривать дважды: в начале учебного года, т.е. еще до изучения десятичных дробей (при повторении и систематизации материала, связанного с обыкновенными дробями), а затем в середине учебного года после изучения десятичных дробей.

Первый этап: нужно сформировать понимание процента как специального способа выражения доли величины, выработать умение выражать процент соответствующей обыкновенной дробью. Процент определяется как одна сотая часть некоторой величины. Причем перед введением определения следует рассмотреть примеры употребления процентов [21].

Не стоит торопиться приступать к решению задач на нахождение процента от некоторой величины. Нужно дать учащимся возможность привыкнуть к введенному понятию, освоить фактически другую терминологию. Через систему упражнений учебника ребята учатся употреблению нового термина, «переводу» задач с языка долей и дробей на язык процентов и обратно. В результате еще до решения основных задач на проценты, учащиеся прочно овладевают достаточно большим набором фактов, которые помогают им в дальнейшем. Так, они усваивают некоторые «эквиваленты»:

величины – это этой величины;
половина некоторой величины – это ее ;
величины втрое больше, чем ее и т.п. [5].

Ребята учатся сравнивать доли величины, заданные разными способами:

больше, чем ;
некоторой величины больше этой величины;
меньше четверти; вся величина - это . И т. д.

Выработке навыков помогает специальная работа учащихся в тетради, по специальному материалу, подобранному специально по учебник. Предлагаемая серия практических заданий способствует усвоению учащимися понятия процента. Приведем несколько примеров для рабочей тетради.

Пример: Заштрихуйте на рисунки указную часть круга:

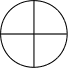
Выберите для каждого процента в левом столбце соответствующую ему дробь:

Среди упражнений, направленных на сознательное усвоение материала, могут предлагаться такие задачи:

Примеры:

1. Для каждой фразы из левого столбца подберите соответствующую фразу правом:

учащихся школы

а) половина всех учащихся школы

б) все учащихся школы

в) четверть всех учащихся школы

г) десятая часть всех учащихся школы.

2. Туристы проехали пути на поезде и пути на автобусе. Весь ли путь они проехали?

3. В классе девочек. Кого в классе больше – мальчиков или девочек?

4. Что больше:

а) всего класса или половина класса?

б) зарплаты или четверть зарплаты?

в) половина или всего населения страны?

Теперь, когда школьники достаточно свободно и осознано, владеют понятием процента, можно перейти к задаче на нахождение процентов некоторой величины. Методически целесообразно сначала находить один процент величины, а потом – несколько процентов этой величины (желательно чтобы у педагога уже были сформированы основные алгоритмы по методике нахождению процентов). Что касается второго приема решения (путем умножения на обыкновенную дробь), то здесь он, конечно, рассматривается, однако его обязательное условие отнесено на более поздние сроки. Опыт показывает, что соответствующий навык вырабатывается в процессе многократного применение первого приема, как результат «свернутого» действия. Поэтому на данном этапе, второй прием в обязательные требования не включается.

Формулировки некоторых задач предлагаются в развернутом виде, то есть к рассматриваемому в условии сюжету поставлены не один, а несколько последовательных вопросов. Тем самым привлекается внимание школьников к тому, какую информацию можно извлечь из ситуации с процентами.

Пример:

1. В магазине было 800 кг свеклы. Продали свеклы.

Сколько килограммов свеклы продано?
1. Сколько % всей свеклы осталось в магазине?
2. Сколько килограммов свеклы осталось в магазине?

2. В кассе организации было руб. На оплату командировочных израсходовали этой суммы. Какие вопросы можно поставить к задаче? Ответьте на них.

Специальная серия задач, посвященная трудному вопросу об увеличении на , и т.д. Нужно постепенно подводить учащихся к пониманию того, что, например, увеличение на – это то же самое, что увеличение в раза и т.д. Приведем примеры:

Задача 2.6: Фирма в первый месяц выпустила игрушечных автомобилей, в следующем месяце она увеличила выпуск игрушек на . Сколько игрушечных автомобилей стала выпускать фирма? Во сколько раз увеличился выпуск игрушечных автомобилей?

Задача 2.7: В первом квартале года квартплата в Москве в домах с лифтом была на выше квартплаты в домах без лифта (рис. 2.1). Во сколько раз квартплата в домах с лифтом была выше квартплаты в домах без лифта?

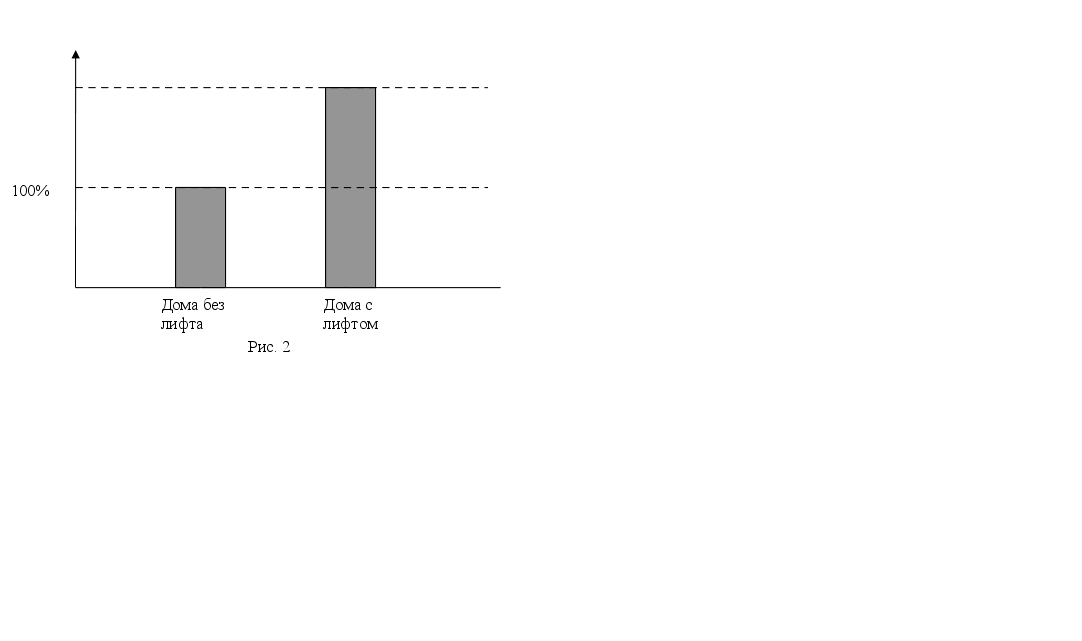
Рис. 2.1. Квартплата домов в Москве

Задача 2.8:В связи с инфляцией стоимость проезда в троллейбусах за полгода возросла на. Во сколько раз повысилась стоимость проезда?

Учащиеся также знакомятся с формой неявного использования процентов, типичной для средств массовой информации, например: «Из каждых новорожденных - девочки».

Второй этап в изучении процентов связывается с десятичными дробями. После изучения десятичных дробей и операций над ними нужно снова возвратиться к понятию процента. Здесь предлагается два специальных пункта. В пункте «Главная задача на проценты» школьники учатся находить процент величины умножением на десятичную дробь. Прежде чем приступить к решению задач, нужно рассмотреть с учащимися правило и упражнения на перевод процентов в десятичную дробь.

«Чтобы выразить проценты десятичной дробью, нужно число, стоящее перед знаком %, разделить на 100 или, что-то же самое, умножить на 0,01».

Приведем пример задачи и ее решения разными способами.

Пример:

Задача 2.9: Оптовая цена товара на складе руб. Торговая надбавка в магазине составляет . Сколько стоит товар в магазине?

I способ: – это ; от руб. составляет (руб.), поэтому товар в магазине стоит (руб.).

II способ: оптовая цена составляет , а цена товара в магазине на больше, то есть она составляет ; – это ; от руб. составляет (руб.).

В пункте «Выражение долей в процентах» центральной является задача об определение того, сколько процентов одна величина составляет от другой. Здесь принят подход, в соответствии с которым сначала находят, какую часть одна величина составляет от другой, выражают ее при необходимости десятичной дробью, а затем – в процентах.

Одна из особенностей вычислительной линии курса состоит в формировании умений выполнять прикидку или оценку результата вычисления. При изучении процентов эта работа, естественно, продолжается. Школьникам предлагаются задачи из повседневной практики, в которых требуется найти приближенно с помощью прикидки процент от заданной величины, для этого достаточно заменить данные другими числами, близкими к ним и удобными для расчетов. Так, если требуется прикинуть, чему равны от какой – либо величины, то находят этой величины, то есть ее пятую часть.

Примеры:

Задача 2.10: Перед новым годам магазин снизил цены на товары на . На сколько примерно рублей понизилась цена товара, если до снижения она составляла руб.? руб.? руб.? руб.?

Выполните прикидку и вычислите примерно:

а) от кг;

б) от руб.;

в) от м;

г) от руб.;

д) от км;

е) от г.

Третий этап в изучении процентов отнесен к VII классу. В силу возрастных возможностей семиклассников и уже накопленного ими опыта работы с процентами, школьникам становятся доступными многие вопросы из тех, что традиционно не рассматривались со всем классом, а изучались лишь в качестве дополнительных в работе с сильными учениками. Учащиеся уже знакомы со всеми основными видами задач, теперь они осваивают другие способы их решения, которые были им неизвестны.

В первой главе учебника выделен пункт «Решение задач на проценты», в котором помещен материал, позволяющий вспомнить сведения из шестого класса и продвинуться в решении задач. Теперь есть возможность рассмотреть более сложные в техническом отношении задачи. Они требуют достаточно прочного навыка представления процентов дробью и наоборот, умение находить процент от величины, понимание того, какая из величин, участвующих в задаче, принимается за 100%. Поэтому в начале теоретической части пункта рассматриваются приемы, с помощью которых десятичная дробь выражается в процентах и наоборот; здесь специально выделяется вопрос о «маленьких» (меньше 1%) и «больших» (больше 100%) процентах, как наиболее трудный для усвоения.

Пример:

Задача 2.11: Летом цена товара была повышена на , а зимой – еще на . Сколько стал стоить товар, если его стоимость была руб.?

Решение:

Для начала найдем стоимость после первого повышения:

или отсюда рублей.

рублей.

Найдем стоимость после второго повышения.

или рубля отсюда рублей

рублей.

Ответ: рублей.

Предлагаемые в системе упражнения задачи, как правило, допускают разные способы рассуждений, и школьники самостоятельно выбирают более удобный, понятный для себя.

Кроме задач на нахождение процента от величины, рассматриваются задачи на нахождение величины по известному проценту.

Отметим еще один методический подход, используемый в изучение процентов. Первую главу заключает раздел «Для тех, кому интересно», в котором учащиеся еще раз встречаются с задачами на проценты. Здесь рассматриваются восемь, если можно так сказать, «классических олимпиадных» задач. Обычно они не включаются в учебники, так как являются трудными, но будет жаль, если учащиеся уйдут из школы, не увидев эти красивые и изящные задачи. Приведем пример одной из задач.

Пример:

Задача 2.12: Книга дороже альбома на . На сколько процентов альбом дешевле книги?

Решение:

Цена альбома – . Изобразим ее каким-либо отрезком (рис. 2.2). Увеличим этот отрезок на , то есть на его часть; получим отрезок соответствующий цене книги.

Рис. 2.2

Теперь цена книги составляет . Она изображена большим отрезком. Цена альбома меньше цены книги на этого отрезка. Так как составляет , то альбом дешевле книги на .

Вся методика обучения решению задач, принятая в учебнике, позволяет показать учащимся наглядный способ их решения с помощью рисунков (хотя, конечно, эти задачи можно решить арифметически).

При изучении следующей главы «Отношения и пропорции» школьники активно пользуются опытом работы с процентами и приобретают новые знания. В систему упражнений включены новые задачные ситуации, проиллюстрированные ниже.

Пример:

1. В сплав входит медь, олово и сурьма в отношении 4:15:6. Сколько процентов сплава составляет каждый металл?

2. На облицовку подъезда в строящемся доме ушло 18 дней. За сколько дней можно было бы выполнить эту же работу, если повысить производительность на 20 %?

По мере овладения новым математическим аппаратом при изучении алгебры, школьники осваивают стратегию решения расчетных задач на проценты – с помощью составления уравнения.

В VIII классе в теме «Алгебраические дроби» школьники снова обращаются к задачам на проценты. Задачи на «концентрацию», «сплавы», «банковские расчеты» – это хорошие примеры практических задач, позволяющих продемонстрировать, как формальные алгебраические знания применяются в реальных жизненных ситуациях. Для того, чтобы помочь школьникам осознать на новом уровне подход к решению задач с процентами, стоит обратить их внимание на то, что в учебнике приводятся образцы решения ряда задач. К разобранному образцу учащиеся при желании может вернуться вновь и использовать его в качестве опоры при решении подобной задачи.

Задача 2.13: Клиент открыл счет в банке на некоторую сумму денег. Годовой доход по этому вкладу составляет . Если бы он добавил руб., то через год получил бы доход руб. Какая сумма была внесена им в банк?

Решение:

Пусть руб. – сумма, которую клиент внес в банк. Тогда руб. было бы на вкладе, если бы клиент добавил руб.;

руб. – доход в , который мог бы получить клиент с этой суммы.

Так как доход равен руб., то имеем равенство: .

, отсюда , следовательно, ответ: клиент внес в банк рублей.

В IX классе в главе «Дробные уравнения» также можно предложить задачи на проценты, решение которых основано на составлении дробных рациональных уравнений.

Пример:

На первые и вторые премии в конкурсе студенческих работ было выделено тыс. р., причем этих денег пошло на первые премии. Вторых было выдано на больше, чем первых. Сколько студентов получили первые премии и сколько вторые, если известно, что вторая премия составляла первой?

Завершается линия процентных вычислений в IX классе темой «Простые и сложные проценты», включенной в изучение главы «Арифметическая и геометрическая прогрессии». Сведения о простых и сложных процентах, которые сами по себе имеют большую практическую значимость, являются достаточно хорошим материалом для применения знаний, полученных на уроках математики. Возможность опереться на сформированные навыки в работе с процентами, на умение воспользоваться калькулятором, табличным и графическим представлением информации позволило расширить диапазон решаемых задач на проценты.

В учебнике не вводятся формулы простых и сложных процентов. Учащиеся должны решать задачи, опираясь не на формулы, а на понимание на смысл понятия «процент», на умение находить процент от числа. В теме широко используется калькулятор, который позволяет рассматривать самые разнообразные задачи.

В ходе решения предлагаемых авторами задач учащиеся видят, что понятия арифметической и геометрической прогрессии, а также формулы их сумм – это не просто абстрактное отвлеченное понятие, а конкретное математическое знание, необходимое для жизни.

В данном курсе в русле новой содержательной линии «Анализ данных» формулируются приемы сбора, представления и анализа информации, так или иначе связанной с процентами.

Проценты также используются в VI – VII классах для представления информации в виде таблиц и диаграмм, а VIII – IX классах – при изучении вероятно-статистического материала.

Таким образом, авторы данного курса уделяют большое внимание понятию процента. С помощью богатого задачного материала учащиеся могут увидеть все разнообразие применения данного математического термина.

Можно заметить, что понятие процента, как математически тривиального, вводится уже в младших классах среднего звена. В силу их возрастных особенностей и невысокой математической грамотности учащиеся не могут ознакомиться со всем спектром задач на проценты. В VII – IX классах данный термин забывается, и простейшие задачи шестого класса становятся для школьников сложными. Поэтому целесообразным уделять процентам больше внимания, как это сделано в учебном комплекте под редакцией Г. В. Дорофеева.

2.4 Методика нахождения нескольких процентов от числа

В данном разделе рассмотрим методику нахождения нескольких процентов от числа, так как эта тема является одной из трех важнейших тем, которые должны понять учащиеся при изучении такой темы, как «Проценты». А главное они должны понять алгоритм нахождения одного или нескольких процентов от числа, и применять эти способности на практике, при решении различных задач на проценты.

Главное чтобы школьники поняли, что для того, чтобы находить проценты от числа нужно понять, что один процент является одной сотой от данного числа. Из этого следует, для определения одного процента (а это главное, так как чтобы найти несколько процентов от числа нужно найти сначала один процент) можно записать равенством:

, а от сюда любой учащийся быстро поймет, что ; ; и т. д.

Как найти от числа? Раз это одна сотая часть, надо число разделить на . Мы уже сделали вывод, что деление наможно заменить умножением на . Поэтому, чтобы найти от данного числа, нужно умножить его на .

Так что отсюда можно вывести алгоритм нахождения одного или нескольких процентов от числа:

Чтобы найти данное число процентов от числа, нужно проценты записать десятичной дробью, а затем число умножить на эту десятичную дробь [15].

2.5 Методика нахождения числа по его процентам

Дальше рассматривается общая методика нахождения числа от одного или нескольких процентов. Это также является важной частью в изучение процентов, так как встречаются не только задачи на нахождение процентов от числа, но числа по процентам, это особенно хорошо видно в задачах связочных с экономикой (на пример когда в банк ложится сумма под проценты, а через какое-то время забирается на с набежавшими процентами и нужно найти данную сумму). Так что школьникам нужно так же раскрыть алгоритм нахождения числа от нескольких процентов.

Учащиеся уже знают, что один процент можно записать десятичной дробью: .

Так вот возникает вопрос, как найти искомое число, если известно лишь, сколько процентов составляет другое число от искомого? Для этого нужно сначала проценты записать десятичной дробью, после чего нужно данное нам число разделить на эту десятичную дробь в результате получим число от нескольких процентов.

Если дано, сколько процентов от искомого числа составляет данное число, то, чтобы найти искомое число, нужно заменить проценты десятичной дробью и разделить на эту дробь данное число [15].

2.6 Методика нахождения процентного отношения

Так же рассмотрим последнее, но не менее важное для нахождения процентов при решение задач – это нахождение процентного отношения. В этом разделе рассмотрим алгоритм нахождения процентного отношения.

Встречаются задачи, в которых даны два числа и нужно найти их процентное отношение, для этого нужно взять первое число назовем его и разделим его на второе число, назовем его число , а затем результат умножим на, то мы получим процентное отношение первого числа на второе:

Чтобы найти процентное отношение двух чисел и , надо отношение этих чисел умножить на сто процентов, тоесть получить формулу[15].

2.7 Задачи на проценты для младших классов

Надо сразу отметить, что такие задачи очень важны в курсе изучения не только процентов, но и всей математике, так как здесь, как и числа, так и процентное содержание, а это, как правило, пугает детей, так как их приучили работать с чем-то одним при решении задач.

Задача 2.14: Винни-Пух очень любил мед и стал разводить пчел.В первый год пчелы дали кг меда, но Винни-Пуху этого было мало, во второй год пчелы увеличили производства меда на , но и этого было мало Винни-Пуху. Он подсчитал, что ему надо примерно кг меда. Вопрос: сколько лет должен ждать Винни-Пух, чтобы удовлетворить свои потребности при условии, что пчелы каждый год будут увеличивать производство меда на .

Решение:

Для того чтобы узнать, сколько надо ждать Вини-Пуху надо узнать, сколько у него будет меда через год, а будет ; кг, через два года кг, и только на третий год он удовлетворит свои потребности.

Ответ: года.

Задача 2.15: Когда Том Сойер нашел клад, он решил часть денег отдать тетушке, а часть оставить себе, так, чтобы, положив их в банк пригодовых каждый год получать эти проценты на личные расходы, он даже подсчитал что ему примерно надо в год долларов. Сколько он должен положить в банк?

Решение:

Если это долларов, то будет равно долларов.

Ответ: долларов.

2.8. Задачи на сложные проценты

Тема «Проценты», связана с повседневной жизнью. Мы часто сталкиваемся с банковскими операциями: различные вклады, ссуды. Между тем, многие ребята, да и взрослые, при столкновении с этими задачами боятся их, потому что не умеют их решать. В учебниках не вводятся формулы простых и сложных процентов. Школьники должны решать задачи, опираясь не на формулы, а на понимание, на смысл понятия «процент», на умение находить процент от числа, число по его проценту. Вообще, данный вид задач применяется во многих областях хозяйственной деятельности, бухгалтерского учёта, а также в различных статистических расчётах, где используются формулы простых и сложных процентов.

Для нахождения простых процентов пользуются формулой простых процентов: если с величины нарастает за год (или другой период), то через лет, полученную сумму можно получить по формуле :

При этом предполагается, что по истечении каждого года доход за этот год исчисляется с первоначальной величины.

Если же доход причисляют к первоначальной величине и, следовательно, доход за новый год исчисляется с наращенной суммы, то говорят о сложных процентах; в этом случае величина, в которую превращаетсячерез лет вычисляется по формуле сложных процентов :

Примеры [2]:

Задача 2.16: Клиент положил в банк на год рублей. Какая сумма у него будет через год, если банк выплачивает годовых?

Решение:

Данную задачу можно решить двумя способами.

1 способ: Сначала находим, сколько рублей приходится на:

1) ( р.) – на .

Далее находим, сколько рублей будет составлять :

2) (р.) – на .

А теперь найдём, какая сумма получится в конце года:

3) (р.) – получилась сумма к концу года.

2 способ: Сначала находим, сколько процентов будет в конце года:

1) - к концу года.

Находим, сколько приходится на:

2) (р.) – на 1%.

А теперь найдём нужную нам сумму:

3) (р.) – сумма в конце года.

Ответ: рублей.

Задача 2.17:Владелец садового участка взял в банке ссуду рублей для постройки дома на участке. Он должен был вернуть эти деньги через год с надбавкой , какую сумму он должен был вернуть?

Решение:

1) - должен вернуть в банк владелец.

(р.) – должен вернуть.

Ответ: рублей.

Задача 2.18:Ирина внесла в январе рублей на счёт, по которому ежемесячно начисляется . И затем каждый месяц в течение года она вносила ещё по рублей, не снимая с него никаких сумм. Сколько рублей на её счете будет в конце декабря?

Решение:

Выразим процент десятичной дробью: . Вклад ежемесячно увеличивается в раза и идёт последовательное накопление вклада:

январь – р.;

февраль – р.;

март – р.;

декабрь –

(р.)

Ответ: 1341 рубль.

В ходе решения подобных задач школьники видят, что формула суммы геометрической прогрессии – это не просто абстракция, отвлечённая формула, а конкретные математическое знание, необходимое в жизни.

Задача 2.20: Вклад, положенный в банк года назад, достиг р. Каков был первоначальный вклад при годовых?

Решение:

Пусть (р.) – первоначальный размер вклада. В конце первого года вклад составит:

1).(р.)

2). (р.) – настолько увеличился вклад к концу второго года по сравнению с первым;

(р.) – таким станет вклад к концу второго года, то есть составит по условию р. Имеем:, откуда . Значит (р.) – первоначальный вклад.

Ответ: рублей.

2.9 Задачи на концентрацию, смеси и сплавы

Данный вид задач представляет собой сложный вид, так как эти задачи учащиеся решают очень плохо. После объяснения решения таких задач целесообразно прорешать аналогичные, как индивидуально, так и со всеми вместе.

Для решения задач на смеси и сплавы, на концентрации нужно уметь рассуждать и решать задачи на дроби и проценты, на составление уравнений и их систем. Эти задачи решаются арифметически, применением линейного уравнения и их систем. Рассмотрим задачи, решаемые арифметическим способом.

Приступая к решению задач, связанных с понятиями «концентрация» и «процентное содержание», необходимо объяснить школьникам, что обычно в условиях таких задач речь идет о составлении сплавов, растворов, смесей из двух или нескольких веществ. При решении таких задач принимаются следующие основные допущения:

Все получающиеся сплавы или смеси однородны;
При слиянии двух растворов, имеющих объемы и, получается смесь, объемом ;
При слиянии двух растворов масса смеси равняется сумме масс, составляющих ее компонентов.

Объемной концентрацией компонента называется отношение объема чистого компонента в растворе ко всему объему смеси :

; .

Объемным процентным содержанием компонента называется величина, то есть концентрация этого вещества, выраженная в процентах.

Аналогично определяются массовая концентрация и процентное содержание: отношение массы чистого вещества в сплаве к массе всего сплава. Под процентным содержанием вещества понимается часть, которую составляет вес этого вещества от веса всего соединения.

Примеры [2]:

Задача 2.21:Для проведения опыта научный сотрудник химической лаборатории смешал раствор некоторого химического вещества и раствора этого же вещества и получил мл.раствора. Сколько мл раствора и сколько раствора было взято.

Решение:

Обозначим через – количество раствора, а через – количество раствора. Запишем первое уравнение системы, так как должно получится мл. раствора:

Второе уравнение системы связывает количество соли в , и получившимся растворах:

Решим получившуюся систему уравнений:

; .

Значит: мл взяли раствора и мл раствора.

Ответ: мл; мл.

Задача 2.22: Кусок сплава золота и серебра весом кг содержит золота. Сколько кг чистого золота нужно прибавить к этому куску, чтобы получившийся новый сплав содержал золота?

Решение:

Пусть добавили кг чистого золота.

(кг) – чистого золота было в сплаве.

Всего чистого золота стало кг, а сплав массой (кг) – чистого золота.

Составим и решим уравнение: , , то есть(кг) – надо добавить чистого золота.

Ответ: кг.

ГЛАВА 3. Методика обучения учащихся решению задач на проценты в рамках элективного курса «Проценты на все случаи жизни» для предпрофильной подготовки учащихся 9 классов

3.1 Содержание обучения на элективном курсе

«Брать ссуду в банке или купить в кредит? Может быть выгоднее накопить денег для покупки дорогостоящей вещи?» Чтобы ответить на эти вопросы, требуется умение решать задачи по теме «Проценты».

«Вы умеете рационально тратить деньги? Вы можете купить товар, на приобретение которого у вас недостаточно средств? Вы знаете, какие для этого существуют возможности?» Данный курс позволит ответить и на эти поставленные вопросы. А может быть вы будущий бизнесмен, экономист, банковский работник или химик, то вам просто необходимо «дружить» с процентами.

Курс предполагает, что учащиеся смогут свободно решать задачи, предлагаемые самой жизнью, сумеют просчитать различные предложения магазинов, кредитных отделов и различных банков, и выбрать наиболее выгодные. Практические задачи повседневной жизни человека в современном обществе, требуют для своего решения не только первичных знаний о процентах, но и более глубоких знаний (простые и сложные проценты, арифметическая и геометрическая прогрессия).

Математика, давно став языком науки и техники, в настоящее время все шире проникает в повседневную жизнь и обиходный язык, все более внедряется в традиционно далекие от нее области. Интенсивная математизация различных областей человеческой деятельности особенно усилилась с внедрением современных информационных технологий, требующих математической грамотности человека буквально на каждом рабочем месте. Это предполагает и конкретные математические знания, и определенный стиль мышления, вырабатываемый математикой. Проценты – одно из математических понятий, которые часто встречаются в повседневной жизни. Понимание процентов и умение производить процентные расчеты в настоящее время необходимо каждому человеку, это способствует «вхождению» в современную информационно-экономическую среду и, в конечном счете, облегчает социализацию.

Одним из направлений модернизации школьного образования является профилизация старшей ступени общеобразовательной школы. Начальной составляющей реализации профильного обучении является предпрофильная подготовка школьников. Курс «Проценты на все случаи жизни» является предметно-ориентированным курсом по выбору в рамках предпрофильной подготовки.

Курс по выбору «Проценты на все случаи жизни» рассчитан на 1 час в неделю, всего 34 часа, в течение всего учебного года. Группа формируется из учащихся 9-х классов, желающих заниматься математикой. Состав группы постоянный, количество учащихся до человек. Реализация программы осуществляется за счет часов, отводимых на выполнение школьного компонента.

Тема «Проценты» является универсальной в том смысле, что она связывает между собой многие точные и естественные науки, бытовые и производственные сферы жизни. Учащиеся встречаются с процентами на уроках физики, химии, чтении газет, просмотре телепередач. Умением грамотно и экономно проводить элементарные процентные вычисления обладают далеко не все учащиеся, хотя многие из них ориентированы на поступление в высшие учебные заведения. Практика показывает, что очень многие окончившие школу не только не имеют прочных навыков обращения с процентами в повседневной жизни, но даже не понимают смысла процентов, как доли от некоторой заданной величины. Происходит это потому, что проценты изучаются на первом этапе основной школы, в 5-6 классах, когда учащиеся в силу возрастных особенностей еще не могут получить полноценные представления о процентах, об их роли в повседневной жизни.

В последнее время экзамен по математике проводится в форме ЕГЭ, и в контрольно-измерительных материалах ЕГЭ присутствует задача на проценты. Специфика темы такова, что значительное позитивное влияние на знания и умения учащихся оказывает последующее обучение, причем не математике, а химии, где процентные расчеты являются существенным элементом содержания обучения, об этом свидетельствуют и приемы решения задач, и способы записи их решения.

Содержание программы курса включает углубление базовой общеобразовательной программы, а так же расширение по отдельным темам. Каждое занятие включает теоретический материал (30%) и практические задания.

Этот курс ориентирован на выбор профиля обучения в старшей школе. Данный курс имеет прикладное и общеобразовательное значение, использует целый ряд межпредметных связей, прежде всего с химией.

Условия реализации программы:

наличие часов, отводимых на выполнение школьного компонента;
наличие квалифицированного преподавателя;
предварительное разъяснение учащимся целей, задач и содержания данного курса.

Цели программы данного курса следующие:

Обеспечить условия:

для получения полноценного представления о процентах, об их роли в повседневной жизни;
для развития мыслительной деятельности учащихся, умения сравнивать, обобщать и делать выводы, умения анализировать и устанавливать причинно-следственные связи;
формирования способности к осознанному выбору профиля обучения в старшей школе и к выбору перспектив дальнейшего обучения.

Задачи курса:

формировать умение грамотно и экономно проводить элементарные процентные вычисления;
формировать культуру решения задач, культуру поиска способа решения задач;
помочь учащимся в освоении методов и способов решения нестандартных заданий и заданий повышенной сложности на уровне, превышающим уровень государственных образовательных стандартов;
развивать способности учащихся к исследовательской и проектной деятельности;
повысить информационную и коммуникативную компетентность учащихся.

3.2 Примерное тематическое планирование

Таблица 3.1

№ п/п	Тема	Кол-во часов
Модуль №1 (теоретический)
1	Дроби и проценты. Простейшие виды задач.	2
2	Экзаменационные задачи по теме «Проценты».	4
3	Систематизация стандартных знаний. Способы решения задач.	2
4	Решение экзаменационных задач на проценты.	2
5	Текстовые задачи с практическим содержанием.	2
6	Процентное содержание, процентный раствор. Концентрация. Смеси и сплавы.	2
7	Старинный способ решения.	2
8	Занимательные задачи, олимпиадные задачи.	4
9	Решение расчетных задач с прагматической ориентацией.	1
10	Практическая работа: составление плана конспекта по изученному материалу; оформление работы.	4
Модуль №2 (создание проекта)
11	Постановка целей. Формулирование задач для достижения целей. Определение плана дальнейшей работы. Информация о вариантах оформления результатов работы. Первичный сбор материалов	1
12	Практическая работа над проектом: изучение, собранных материалов, поиск и сбор дополнительной информации по теме проекта, уточнение способа оформления проекта.	4
13	Представление учащимися самостоятельно выполненных проектов. Мониторинг.	2
14	Заключительное занятие. Подведение итогов работы.	2
Итого	34

Методический комментарий к проведению элективного курса:

При изучении курса учащиеся систематизируют знания и умения по теме «Проценты», полученные в 5 и 6 классах (переводить проценты в десятичную дробь, десятичную дробь обращать в проценты, преобразовывать десятичные и обыкновенные дроби, решать задачи простейших видов), и углубят их, познакомившись с различными способами решения задач, не входящих в школьную программу.

Учащиеся развивают и углубляют общеучебные навыки и умения за счет: решения дополнительных задач (на процентное содержание, процентный раствор и концентрацию); новых способов их решения (уравнение, система уравнений, геометрически, старинный способ); решения задач с практической ориентацией; решения олимпиадных задач и из материалов ЕГЭ.

Обучение учащихся осуществляется через практическую, самостоятельную или групповую деятельность учащихся, через выявление, актуализацию и обогащение их собственного опыта в сотрудничестве с другими учащимися и учителем. В конце изучения курса учащиеся представляют свой проект по выбранной ими теме. Они самостоятельно определяют для себя, его цели и задачи. Одни из них собирают предложения магазинов и банков, просчитывают реальные суммы, выраженные в рублях, а затем, анализируя результаты, выбирают наиболее для них выгодные. Другие рассматривают конкретные задачи, которые предлагаются на уроках химии, физики или экономики. В проекте должны быть

теоретическая часть, в которой отражены основные знания и умения по теме «Проценты»;
различные материалы по теме проекта «Кредит, ссуда или сберегательный вклад?», «Проценты на уроках»: выполненные расчеты по предложениям магазинов и банков, анализ полученных результатов, выбор наиболее выгодных предложений и т.д.

Школьники оформляют проекты, представляют их, учатся при этом обоснованно и рационально излагать свои мысли, вырабатывают умение слушать товарищей, дополнять и комментировать их ответы. Решение практических задач позволит учащимся применить в новых ситуациях известные приемы, установить связь между изученным материалом и окружающей реальностью. При этом в будущем, любой ученик свободно сможет воспользоваться, полученными знаниями и навыками, подобных расчетов, что, безусловно, будет полезно в его дальнейшей жизни. Проект может быть использован при самоподготовке к экзаменам (например, за 9 класс), а так же учащийся сможет дать консультацию по теме своего проекта одноклассникам, друзьям, родственникам или знакомым.

Таким образом, создаются условия для активизации познавательного интереса, и учащиеся становятся активными участниками происходящих вокруг них жизненных событий, осмысливают материал курса и целенаправленно смогут применить полученные знания, умения и навыки в практической деятельности. Изучение курса поможет учащимся соотнести свои индивидуальные возможности, интересы с особенностями, современными требованиями предмета математики и, далее, определиться в выборе профиля обучения.

Внутрипредметные связи, при изучении содержания курса, находят свое воплощение в построении и исследовании математических моделей (уравнений и их систем, графиков функций и т.п.) и служат обобщению и приведению знаний в систему по ходу обучения.

Организация работы группы:

Группа формируется из учащихся 9-х классов школы.
Часы для проведения занятий выделяются из школьного компонента БУП по заявлениям учащихся.
Состав группы постоянный на год.
Занятия проводятся в дневное время (в классных кабинетах и работа в компьютерном классе).
Содержание рассматриваемого материала предлагается учащимся в двух вариантах: на электронных и бумажных носителях.
На занятиях применяется работа в группах, парах, индивидуальная работа с учащимися.
При изучении тем курса используются метод эвристической беседы, проблемный и исследовательский методы, метод проектов.
Формы проведения занятий: семинары и практикумы, частично - лекции учителя с использованием ИКТ.

Требования к уровню усвоения курса:

по окончанию изучения курса учащиеся должны

знать / понимать:

смысл идеализации, позволяющей решать задачи реальной действительности математическими методами;
построения и исследования математических моделей для описания и решения прикладных задач;
понятие процента;

иметь представление: о применении процентов в повседневной жизни;

уметь:

представлять проценты — в виде дроби и дробь – в виде процентов;
находить проценты от величины, величину по ее проценту;
выражать отношения в процентах;
применять полученные математические знания в решении жизненных задач;
уметь использовать дополнительную математическую литературу.

использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

анализа реальных числовых данных, представленных в виде диаграмм, графиков;
решения прикладных задач, в том числе социально-экономических и химических;
самостоятельной работы с источниками информации, обобщения и систематизации полученной информации, интегрирования ее в личный опыт;
выполнения расчетов практического характера;

Критерии и способы отслеживания результатов:

отслеживаются:

знания и практические навыки учащихся;
рефлексивные способности;
самостоятельность, креативность, инициативность.

способы отслеживания результатов:

самоанализ учащимися собственных умений, навыков;
наблюдение за процессом деятельности;
анализ самостоятельных работ учащихся;
оценка проектов.

3.3. Методические разработки для апробации элективного курса

Контроль знаний

Вариант 1

1 уровень

Нарисуйте квадрат со стороной 10 клеток. Заштрихуйте любые 20 клеток. Какой процент квадрата заштрихован?

А.; Б.; В. ;Г..

Часть величины, заданную в процентах, соотнесите с соответствующей обыкновенной дробью:

На круговой диаграмме показано, какой транспорт предпочитают жители города. Используя диаграмму, ответьте на вопрос: какой процент жителей города предпочитает трамвай?

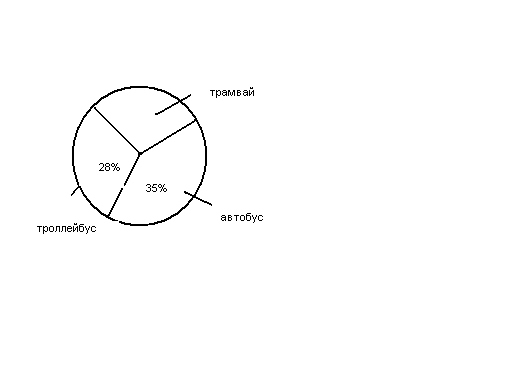
Сравните всех учащихся школы и всех учащихся этой школы

А. меньше всех учащихся школы;

Б. больше всех учащихся школы;

В. равны всех учащихся школы;

Г. Сравнить нельзя.

5. Найдите от рублей.

А. р.; Б. р.; В. р.; Г. р.

6. Укажите верные утверждения:

I. см составляет от м;

II. дм составляет от м;

III. м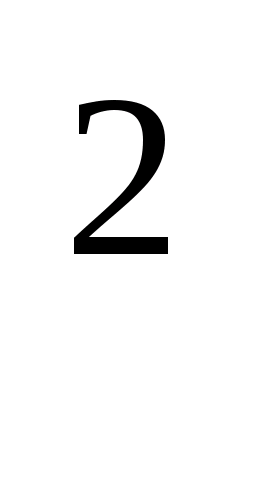 составляет от км;

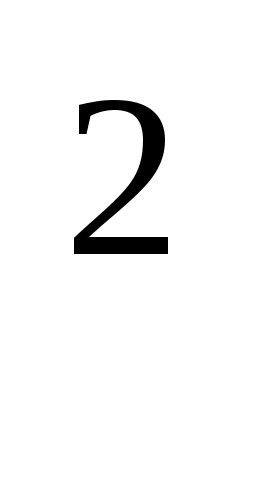IV. мм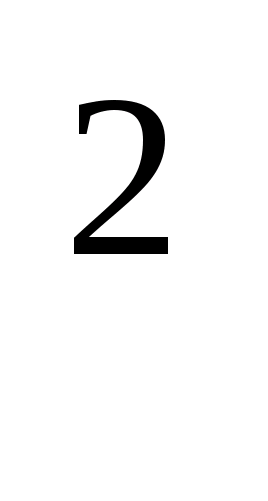 составляет от см.

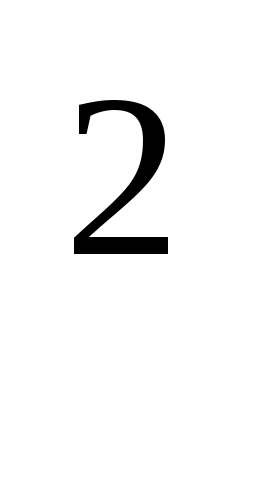А. I и II; Б. II и IV; В. II и III; Г. I и IV.

7. Из учащихся класса занимаются в спортивных секциях. Какая часть класса занимается спортом? Ответ выразите в процентах.

8. Кресло стоило р. После снижения цен оно стало стоить р. На сколько процентов снижена цена этого кресла?

А. на ; Б. На ; В. На ; Г. На .

9. Что больше: от р. или от р.?

А. от р.; Б. от р.; В. Сравнить нельзя; Г. Одинаковые.

10. В книжном магазинеучебников, что составляет всех книг. Сколько книг в библиотеке?

2 уровень

11. В книжный магазин привезли журналов и газет. До обеда продали всех журналов и всех газет. Чего продано больше: газет или журналов? Во сколько раз?

12. В книжный магазин привезли книг. До обеда продали всех книг, а после обеда – . На сколько больше продано книг после обеда?

А. ; Б. ; В. ; Г..

13. Укажите ту часть массы, которая больше других.

А. от кг; Б. от кг; В.от кг; Г. от кг.

14. Цены на зимние спортивные товары летом снижены на . Во сколько раз летние цены ниже по сравнению с зимними?

А. В раза; Б. В раза; В. В раза; Г. В раз.

Вариант 2

1 уровень

1. Нарисуйте квадрат со стороной 10 клеток. Заштрихуйте любые 25 клеток. Какой процент площади квадрата заштрихован?

А. ; Б. ; В. ; Г. .

2. Часть величины, заданную в процентах, соотнесите с соответствующей обыкновенной дробью:

На круговой диаграмме показано, какой вид транспорта выбирают жители города для поездки за город. Используя диаграмму, ответьте на вопрос: какой процент жителей города предпочитают трамвай?

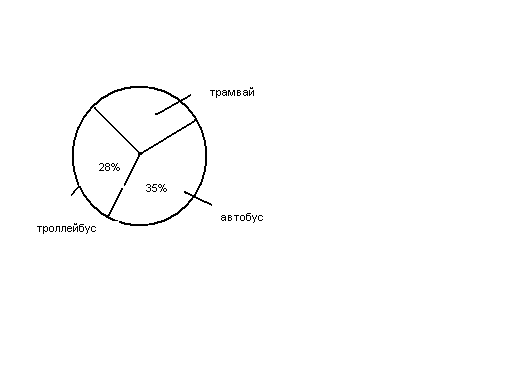
Сравните всех учащихся школы и всех учащихся этой школы.

А. больше всех учащихся школы;

Б. меньше всех учащихся школы;

В. равны всех учащихся школы;

Г. Сравнить нельзя.

5. Найдите от рублей.

А. р.; Б.р.; В. р.; Г. р.

6. Укажите верные утверждения:

I. г составляет от кг;

II. кг составляет от т;

III.кг составляет от ц;

IV. ц составляет от т.

А. I и II; Б. II и IV; В. II и III; Г. III и IV.

7. Из учащихся класса человек занимаются в спортивных кружках. Какая часть класса занимается спортом? Ответ выразите в процентах.

8. Газонокосилка стоила р. После снижения цен она стала стоить р. На сколько процентов снижена цена этой газонокосилки?

А. на ; Б. на ; В. на ; Г. на .

9. Что больше: от р. или от р.?

А. от р.; Б. от р.; В. Сравнить нельзя; Г. Одинаковые.

10. В библиотеке учебников, что составляет всех книг. Сколько книг в библиотеке?

2 уровень

11. В книжный магазин привезли журналов. До обеда продали всех журналов, а после обеда - всех журналов. На сколько больше продано журналов после обеда?

А. ; Б. ; В.; Г..

12. В книжный магазин привезли газет и книг. До обеда продали всех газет и всех книг. Чего продано меньше: газет или книг? Во сколько раз?

13. Укажите ту часть массы, которая меньше других.

А. от кг; Б. от кг; В. от кг; Г. от кг.

14. Цены на зимние спортивные товары летом снижены на . Во сколько раз летние цены ниже по сравнению с зимними?

Тренировочный тест №1 по теме «Проценты»

Запишите 1% в виде десятичной дроби

а) ; б) ; в); г).

2. Сколько процентов сахара содержит сироп, приготовленный из г сахара и гводы?

а) ; б) ; в) ; г) .

3. Мотоциклист ехал из города А в город В. Проехав пути, он оказался в км от города В. Каково расстояние между А и В?

а) км; б) другой ответ; в) км; г)км.

4. Из 200 квартир нового дома -двухкомнатные, а остальные –трехкомнатные. Сколько трехкомнатных квартир в этом доме?

а) ; б) ; в) ; г) .

5. Сумма двух чисел составляет первого слагаемого. На сколько первое слагаемое больше второго?

а) на ; б) на ; в) на ; г) другой ответ.

6. Найдите число, которого равны.

а); б) ; в) ; г) другой ответ.

7. Первое число , а второе . Какой составляет первое число от разности этих чисел?

а) ; б) ; в) ; г) другой ответ.

Проверочная работа

Вариант 1.

1.Вкладчик открыл счет в банке, внеся р. на вклад, годовой доход по которому составляет . Какая сумма будет лежать на его счете через год? Через два года? Через 6 лет?

(Ответ: р.; р. к.; р. к.)

2. Цена товара после двух последовательных снижений на один и тот же процент уменьшилась со до руб. на сколько процентов снижалась цена каждый раз?

(Ответ: )

3. Цена некоторого товара поднялась на , а потом еще на . Другой товар поднялся в цене на и стал по цене равен первому товару. Какова первоначальная цена первого товара, если второй до повышения цены стоил тыс.руб.?

(Ответ: тыс. руб.)

4. К л - ного раствора соли добавили -ный раствор соли и получили ный раствор. Сколько литров -ного раствора добавили?

5. В сплаве содержится кг цинка, кг олова и кг меди. Каково процентное содержание составных частей сплава?

Вариант 2

1. Вкладчик открыл счет в банке, внеся р. на вклад, годовой доход по которому составляет . Какая сумма будет лежать на его счете через год? Через два года? Через лет?

(Ответ: р.; р. к.; р. к.)

(Ответ: )

(Ответ: тыс. руб.)

4. К л -ного раствора соли добавили -ный раствор соли и получили -ный раствор. Сколько литров -ного раствора добавили?

5. В сплаве содержится кг цинка, кг олова и кг меди. Каково процентное содержание составных частей сплава?

Контрольный тест № 2

Вариант 1

Уровень 1

1. Выразите десятичной дробью

А. ; Б. ; В. ; Г..

2. Найдите от мг.

А. 40 мг; Б. 4мг; В. 0,4 мг; Г. 0,04 мг.

3. Какое из утверждений неверное?

А. урожая больше этого урожая;

Б. урожая составляет этого урожая;

В. урожая больше этого урожая;

Г. урожая меньше этого урожая.

4. В декабре сотрудникам фирмы была выплачена премия в размере ежемесячной зарплаты. Какую премию получил сотрудник, зарплата которого была р.?

5. Июньский тираж нового ежемесячного журнала составил экземпляров. В июле его тираж увеличился на , а в августе – еще на . Каким стал тираж журнала в августе?

А. экз.; Б. экз.; В. экз.; Г. экз.

6. В начале года в хоре занимались ребят. К концу года их число увеличилось на. Во сколько раз увеличилось число ребят, занимающихся в хоре?

А. В раза; Б. В раза; В. В раза; Г. Определить нельзя.

7. При оформлении витрины магазина использовались зеленых и оранжевых ламп. Сколько % всех ламп составляют лампы оранжевого цвета?

А.; Б.; В. ; Г..

8. Из 40 учащихся класса занимаются в спортивных кружках, причем из них – в шахматной. Сколько учащихся в шахматной секции?

А. уч.; Б. уч.; В. уч.; Г. уч.

Уровень 2

9. Определите, на сколько примерно процентов снижены цены при распродаже мебели?

Цена	Стол	Стул	кресло
Старая	р.	р.	р.
Новая	р.	р.	р.

А. На ; Б. На ; В. На ; Г.Определить нельзя.

10. В январе тариф на электроэнергию составлял р. за кВт/ч. В середине года он увеличился на , а в конце года – еще на . Какое утверждение верно?

А. Тариф увеличился на;

Б. Тариф увеличился меньше, чем на;

В. Тариф увеличился больше, чем на.

11. Когда 60 пассажиров заняли в автобусе свои места, остались свободными всех мест. Сколько сидячих мест в автобусе?

А. ; Б.; В. ; Г. .

Вариант 2

Уровень 1

1. Выразите десятичной дробью.

А.; Б. ; В. ; Г. .

2. Найдите от мг.

А. мг; Б. мг; В. мг; Г. мг.

3. Какое из утверждений неверное?

А. урожая меньше этого урожая;

Б. урожая меньше этого урожая;

В. урожая больше этого урожая;

Г. урожая больше этого урожая.

5. Февральский тираж нового ежемесячного журнала составил экземпляров. В марте его тираж увеличился на , а в апреле – еще на. Каким стал тираж журнала в апреле?

А. экз.; Б. экз.; В. экз.; Г. экз.

6. В среду на экскурсию записались ребят. В четверг число записавшихся увеличилось на. Во сколько раз увеличилось число ребят, записавшихся на экскурсию?

А. В раза; Б. В раза; В. В раза.; Г. Определить нельзя.

7. При оформлении витрины магазина использовались зеленых и желтых ламп. Сколько всех ламп составляют лампы зеленого цвета?

А. ; Б. ; В. ; Г. .

8. Из учащихся класса занимаются в спортивных кружках, причем из них – в шахматной. Сколько учащихся в шахматной секции?

А. уч.; Б. уч.; В. уч.; Г. уч.

Уровень 2

9. Определите примерно, на сколько процентов снижены цены при распродаже мебели?

Цена	шкаф	кровать	стол
Старая	р.	р.	р.
Новая	р.	р.	р.

А. На ; Б. На ; В. На ; Г. Определить нельзя.

10. Летом портфель стоил р. Осенью цены на портфель снижены на , а зимой еще на . Какое утверждение верно?

А. Цена портфеля снизилась на ;

Б. Цена портфеля снизилась меньше, чем на ;

В. Цена портфеля снизилась больше, чем на .

11. После повышения цен на альбом стал стоить р. Сколько стоил альбом до повышения цен?

ЗАКЛЮЧЕНИЕ

Данная работа посвящена разработке методических рекомендаций для изучения темы «Проценты» в школьном курсе математики. Цель выпускной квалификационной работы достигнута: были разработаны общие методические рекомендации к изучению темы «Проценты».

Основные задачи, которые ставились перед началом исследования, были выполнены

рассмотрены особенности учебного комплекта по математике Г.В Дорофеева;
проведен анализ изложения темы «Проценты» в учебниках под редакцией Шеврина Л.Н. и Виленкина Н.Я.;
изучена история возникновения понятия процент и систематизированы все виды задач на проценты.

Гипотеза, выдвинутая в начале работы, подтвердилась. Действительно, понятие процента, как математически тривиального стоит вводить в V-VI классах, но различные типы задач на проценты следует рассматривать и в курсе алгебры VII-IX класса. Использование символической наглядности делает усвоение понятия процента и умение решать задачи на проценты более эффективным.

При проведении апробации в МБОУ СОШ № 16 города Кропоткин МО Кавказский район по данной теме на специальном курсе по математике в 9 классах было замечено, что учащимся очень нравится данная тема. Они с удовольствие решают задачи на сложные проценты. Так же можно отметить, что особое место у них занимали задачи связанные с экономикой, это задачи на банковские вклады, так как многие очень близко сталкиваются с этим в жизни и хотят об этом знать больше. Надо отметить что, интерес учащихся к этой теме и выбранная методика изучения процентов в школе дали хорошие результаты.

Можно сделать вывод, что эту тему не только можно, но и нужно вводить на спец. курсах по математике. А так же расширить курс изучения процентов в школьном курсе математике.

СПИСОК ИСПОЛЬЗУЕМЫХ ИСТОЧНИКОВ

Актуальные вопросы теории и методики обучения математике в средней школе: сборник научный статей. Вып. 1. – Киров: Изд-во ВятГГУ, 2011. – 111 с.
Алгебра 9 класс. Итоговая аттестация-2014. Предпрофильная подготовка: учебно-методическое пособие / Под ред. Д.А. Мальцева.- Ростов-н/Д : Издатель Мальцев Д.А.; М.: НИИ школьных технологий, 2013.-124 с.
Алгебра: сб. заданий для подготовки к итоговой аттестации в 9 кл./ [Л. В. Бунимович, С. Б. Суворова, Е. А. Бунимович и др.]. – 2-е изд.- М.: Просвещение, 2013. – 191 с.: ил.
Избранные вопросы методики преподавания математики: сборник научно-методических статей / Авторы-сост.: В. Азарова, Е. Артьемьев, А. Нартова и др.; науч. ред. Л. О. Денищева. – М.: МГПУ, 2013. - 76 с.
Изучение процентов в основной школе/Авторы-сост.: Дорофеев Г.В., Кузнецова Л.В., Минаева С.С., Суворова С.Б. //Математика в школе. – 2002. – №1 – с. 19 –24.
Каплан, Б.С., Рузин, Н. К., Столяр, А.А. Методы обучения математике: Некоторые вопросы теории и практики. / Б.С. Каплан, Н.К. Рузин, А.А. Столяр; под ред. А.А. Столяра. – Мн.: Нар. Асвета, 1981. – 191с, ил.
Левитас, Г.Г. Методика преподавания математики в основной школе: учебное пособие / Г.Г. Левитас. – Астрахань: Издательский дом «Астраханский университет», 2009. – 179 с.
Максимова, В.Н. Проблемный подход к обучению в школе: Методическое пособие по спецкурсу/ В.Н. Максимова. - Л.,2003. – 234 с.
Манвелов, С.Г. Конструирование современного урока математики. Кн. для учителя / С.Г. Манвелов. – М.: Просвещение, 2005. – 175 с.: ил.
Математика: Алгебра. Функции. Анализ данных. 8 класс: учеб.для общеобразовательных учреждений / [Г.В. Дорофеев, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение», - 11-е изд. – М.: Просвещение, 2010.
Математика: Алгебра. Функции. 9 класс: учеб.для общеобразовательных учреждений / [Г.В. Дорофеев, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение», - 12-е изд. – М.: Просвещение, 2011.
Математика: Арифметика. Алгебра. Анализ данных. 7 класс: учеб.для общеобразовательных учреждений / [Г.В. Дорофеев, С.Б. Суворова и др.]; под ред. Г.В. Дорофеева; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение», - 11-е изд. – М.: Просвещение, 2011.
Математика. 5 класс: учеб.для учащихся общеобразоват. учреждений/ Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. – 31-е изд., стер. – М.: Мнемозина, 2013. – 280 с.: ил.
Математика. 5 класс: учеб.для общеобразоват. учреждений/ [Г. В. Дорофеев, И. Ф. Шарыгин, С. В. Суворова и др.]; под ред. Г. В. Дорофеева, И. Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение», - 12-е изд. – М.: Просвещение, 2011. – 303 с.: ил.
Математика. 6 класс: учеб.для общеобразоват. учреждений/ [Г. В. Дорофеев, И. Ф. Шарыгин, С. В. Суворова и др.]; под ред. Г. В. Дорофеева, И. Ф. Шарыгина; Рос. акад. наук, Рос. акад. образования, изд-во «Просвещение», - 11-е изд. – М.: Просвещение, 2010. – 303 с.: ил.
Математика. 5 класс:учеб.для учащихся общеобразоват. учреждений/Л.Н. Шеврин, А.Г. Гейн, И.О. Коряков, и др.- М.: Просвещение,2009.
Матюшкин, А.М. Проблемные ситуации в мышлении и обучении. - М.:«Педагогика», 2007. – 198 с.
Методика преподавания математики в средней школе. / В. А. Ованесян и др. – М.: Просвещение, 1980. – 368 с.
Методика преподавания математики в средней школе: Общая методика: Учеб.пособие для студентов физ.-мат. факультетов пед. вузов / Ю.М.Колягин и др. - М.: Просвещение, 1975. — 462с.
Методика преподавания математики в средней школе: Частная методика: Уч. пос. для студ. пед. инст-в по физ-мат. спец-м / А.Я. Блох, В. А. Гусев, Г. В. Дорофеев и др. Сост. В. И. Мишин. – М.: Просвещение, 1987.
Первые уроки по учебному комплекту «Математика 5–8» / Под ред. Дорофеева Г.В. и Шарыгина И.Ф. //Математика. – 1999. – № 27. – с. 9–14
Савин, А.П., Станцо, В.В., Котова, А.Ю. Я познаю мир: Детская энциклопедия: Математика / Под общей ред. О.Г. Хинн – М.: ООО «Фирма «Издательство АСТ», 2006. – 479 с.
Самойлик, Г.А. История математики на уроках. Проценты/ Г.А. Самойлик// Математика. – 2002 – № 36 – с. 3.
Столяр, А.А. Логические проблемы преподавания математики/ А.А. Столяр. – Минск: Высшая школа, 1965. – 255 с.
Столяр, А.А. Методы обучения математике / А.А. Столяр. – Минск: Высшая школа, 1966. – 191 с.
Теория и методика обучения математике в школе: учеб. Пособие / Авторы – сост. Л. О. Денищева, А. Е. Захарова, М. Н. Кочагина и др.; ред. Л. О. Денищева. – М.: БИНОМ, 2013. – 248 с.
Федеральный государственный образовательный стандарт основного общего образования от 17 декабря 2010 г.
Федеральный перечень учебников, рекомендованных Министерством образования и науки Российской Федерации к использованию в образовательном процессе в общеобразовательных учреждениях, на 2013/2014 учебный год.
Шевкин, А.В. Еще раз об изучении процентов / А.В. Шевкин //Математика в школе. – 1993. – №1. – с. 20 – 22.
Шевкин, А.В. От реформы до реформ. Попытка обзора школьных учебников по математике / А.В. Шевкин // Школьное обозрение. – 2002. – №4. – с. 33 – 40.
Сетевые ресурсы
Википедия – свободная энциклопедия / - Режим доступа: https://ru.wikipedia.org. Дата обращения: 23.01.2015.

МЕТОДИКА ОБУЧЕНИЯ УЧАЩИХСЯ РЕШЕНИЮ ЗАДАЧ НА ПРОЦЕНТЫ В ОСНОВНОЙ ШКОЛЕ