Работа с математическим редактором MATLAB
Министерство образования и науки Российской Федерации
Федеральное государственное автономное образовательное учреждение высшего образования
«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ
ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Институт неразрушающего контроля
Направление подготовки (специальность) приборостроение
Кафедра ФМПК
ОТЧЕТ
по лабораторной работе
“Работа с математическим редактором MATLAB”
по дисциплине «Метрологическое обеспечение измерений, контроль и диагностика»
Выполнил студент гр.1БМ53 ____________ Бердыбеков С.Б.
10 сентября 2015г.
Отчет принят:
Должность преподавателя ____________ Старикова Н.С.
Томск 2015 г.
Лабораторная работа 1
Работа с математическим редактором MATLAB
Цель работы
Ознакомление с основными элементами управления MATLAB. Выполнение элементарных вычислений с помощью системы MATLAB. Ознакомление со справочной системой MATLAB.
Практические задания
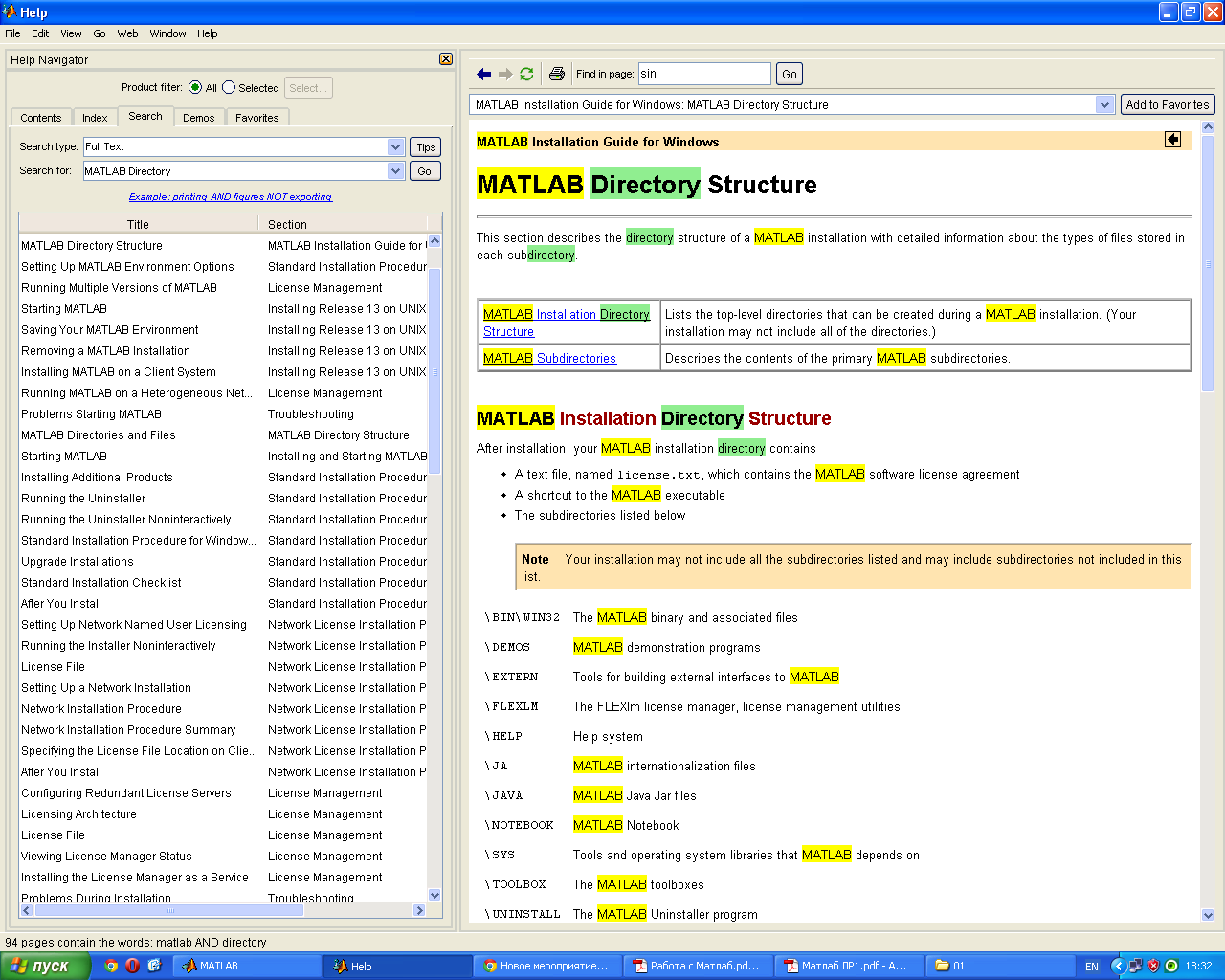
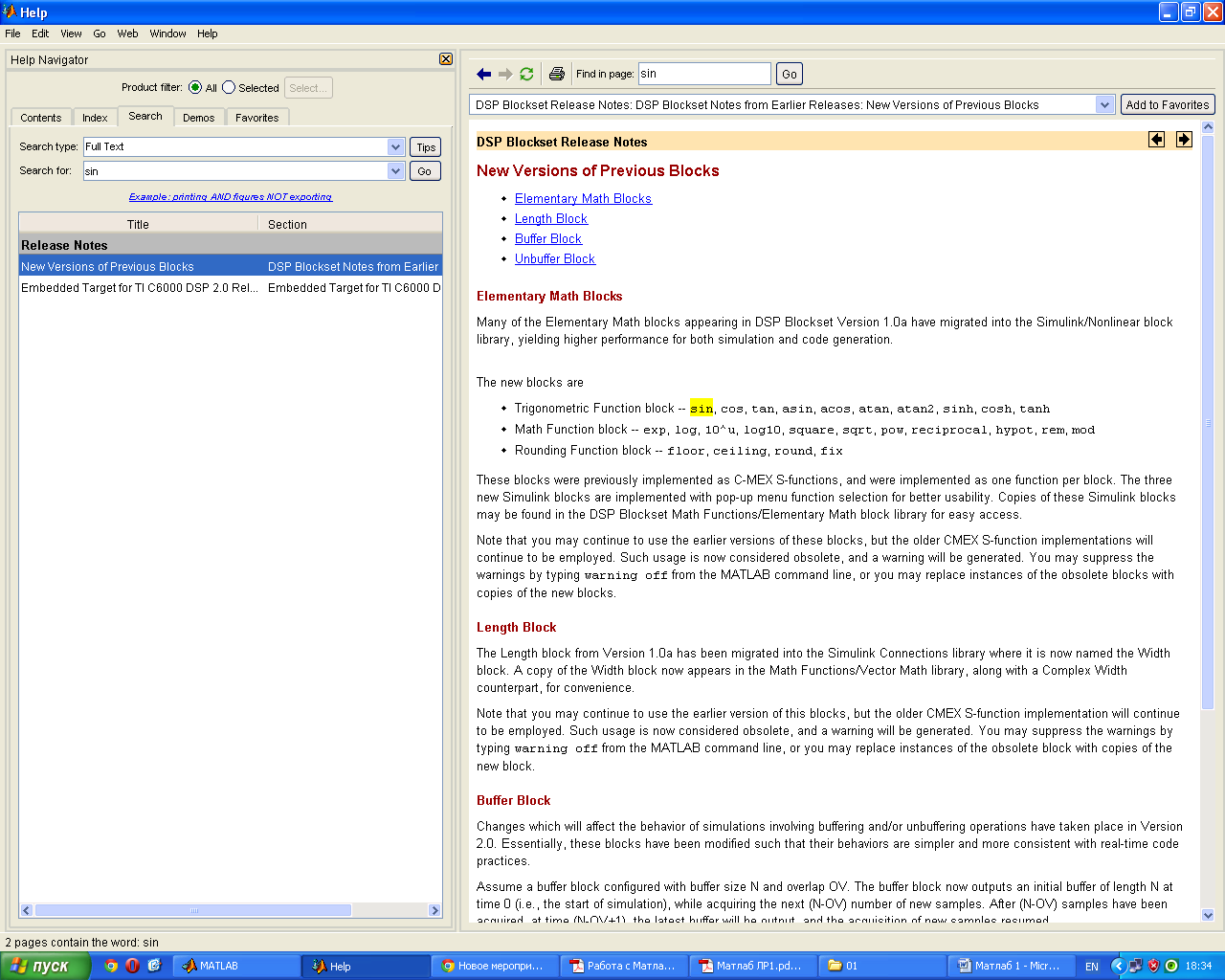
1) Найдите в справочной структуре статью «MATLAB Directory Structure». Добавить эту статью в категорию избранных в справочной системе MATLAB. Найти список всех статей, в которых используется выражение «sin».
2) Наберите в командной строке выражение: help sum. Результатом выполнения этой команды служит справка по функции суммирования элементов для массива. Найдите в директории, в которую установлен MATLAB файл с именем sum.m, откройте его с помощью программы Notepad (Блокнот). По какому алгоритму работает эта функция? Как можно создать справку к своему m файлу? Выполните команду sum ([0 1 2; 3 4 5]), поясните результат.
3) Ввести матрицу: A(:, :, 1) = [1 2 3; 4 5 6]; A(:, :, 2) = [7 8 9; 10 11 12]. Сколько размерностей имеет данная матрица? Вывести значения матрицы на экран. Посчитать сумму всех элементов матрицы используя функцию sum; Посчитать среднее значение всех элементов, используя функцию mean; В матрице B сохранить транспонированную матрицу A(:, :, 1). Вывести матрицу B на экран.
4) Преобразовать 3-х мерную матрицу A( :, :, 1)=[ 1 2 3; 4 5 6]; A( :, :, 2)=[ 7 8 9; 10 11 12]; в 2-х мерную матрицу [ 1 2 3 4 5 6; 7 8 9 10 11 12] размерностью 2х6 используя команду reshape. Преобразовать матрицу А в вектор размерностью 1х12.
5) Посмотрите результат выполнения команды: А = [1 2 3; 4 5 6]; A(:), объясните действия операторов.
6) Что выполняют функции: zeros, ones, eye, fliplr?
7) Решите систему линейных уравнений в матричном виде: Ax = B, где A = [1 2 3; 4 5 6; 7 8 9]; B = [1; 2; 3]
8) Создать двумерную матрицу 5х5, заполнить ее числами, которые заданны в соответствии с равномерным законом распределения, удалить 2 и 4 строки из получившейся матрицы.
9) Создать матрицу размерностью 240х320х10, имитирующую последовательность термограмм. Вывести на экран количество строк, столбцов и количество термограмм, используя команду size.
10) Имеются два вектора A = [1 2 3 4 5] и B = [4 5 6 7 8], вычислить поэлементное произведение векторов.
11) Вычислить произведение чисел 15 2.05*10 и 15 4.1*10 .
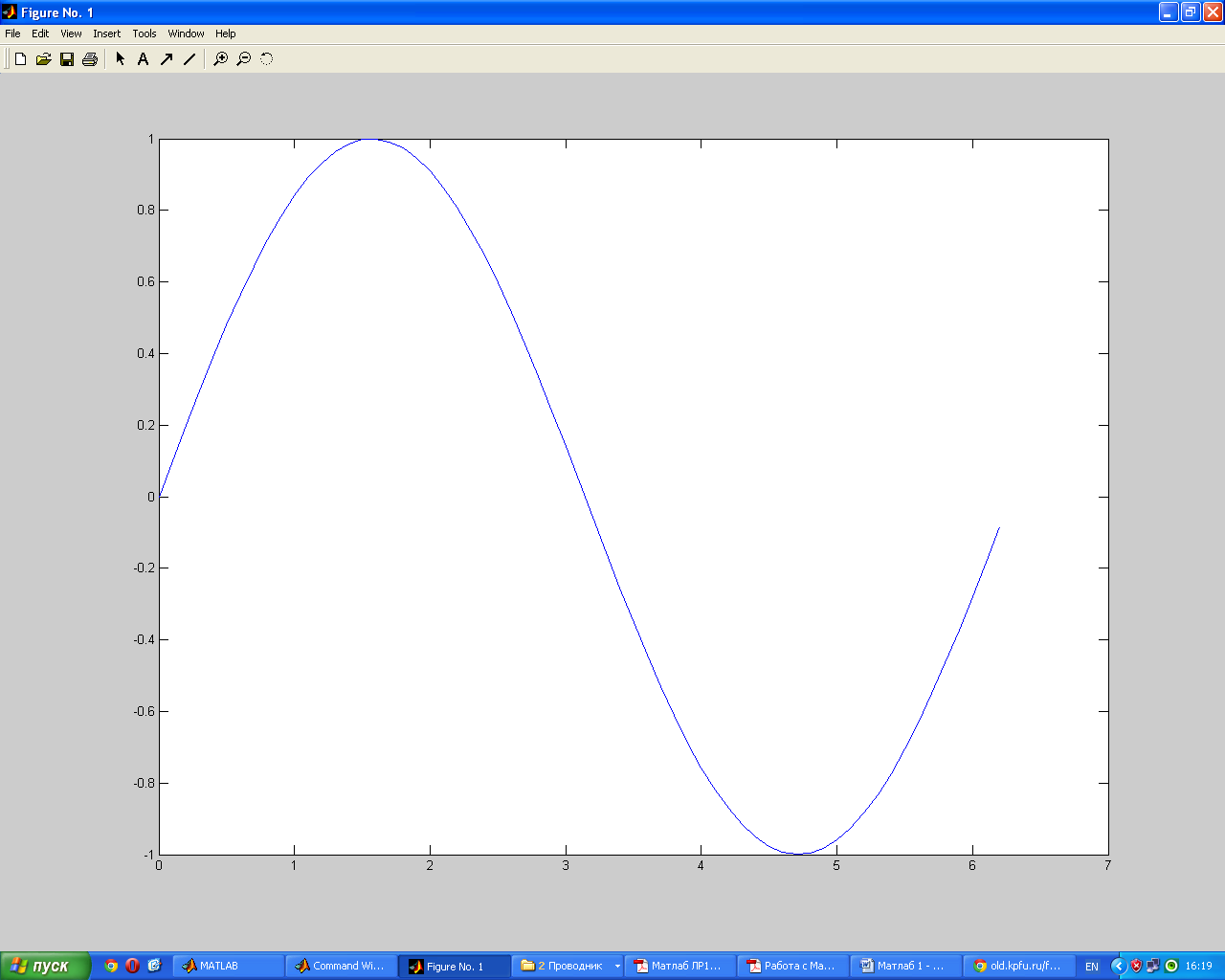
12) Посчитать значение функции sin в диапазоне от 0 до 2 с шагом 0.1 радиан. Построить график функции, использую команду plot.
13) Сравните результат выполнения выражения A = zeros( 500, 500) c введенным символом « ; » и без него.
Выполнение заданий в программе Matlab
1)
2)
>> help sum
SUM Sum of elements.
For vectors, SUM(X) is the sum of the elements of X. For
matrices, SUM(X) is a row vector with the sum over each
column. For N-D arrays, SUM(X) operates along the first
non-singleton dimension.
SUM(X,DIM) sums along the dimension DIM.
Example: If X = [0 1 2
3 4 5]
then sum(X,1) is [3 5 7] and sum(X,2) is [ 3
12];
See also PROD, CUMSUM, DIFF.
Overloaded methods
helpsym/sum.m
ifnargin == 1 & any(size(A) == 1)
s = sym(0);
for k = 1:prod(size(A))
s = s + A(k);
end
elseifnargin == 1 | dim == 1
s = sym(zeros(1,size(A,2)));
fori = 1:size(A,1)
s = s + A(i,:);
end
else
s = sym(zeros(size(A,1),1));
for j = 1:size(A,2);
s = s + A(:,j);
end
end
>>sum([0 1 2; 3 4 5]),
ans =
3 5 7
3)
>>>>A(:, :, 1) = [1 2 3; 4 5 6]; A(:, :, 2) = [7 8 9; 10 11 12]
A(:,:,1) =
1 2 3
4 5 6
A(:,:,2) =
7 8 9
10 11 12
>>>>sum (A(:, :, 1))
ans =
5 7 9
>>sum (A(:, :, 2))
ans =
17 19 21
>> sum(sum(sum(A)))
ans =
78
>> mean (A(:, :, 1))
ans =
2.5000 3.5000 4.5000
>> mean (A(:, :, 2))
ans =
8.5000 9.5000 10.5000
>> mean (mean(mean(A)))
ans =
6.5000
>> A(:, :, 1)'
ans =
1 4
2 5
3 6
>> A(:, :, 2)'
ans =
7 10
8 11
9 12
>> B=A(:, :, 1)'
B =
1 4
2 5
3 6
4)
A(:,:,1) =
1 2 3
4 5 6
A(:,:,2) =
7 8 9
10 11 12
>> b(:,:,1)=A(:,:,1)'
b =
1 4
2 5
3 6
>> b(:,:,2)=A(:,:,2)'
b(:,:,1) =
1 4
2 5
3 6
b(:,:,2) =
7 10
8 11
9 12
>> c=reshape(b,6,2)
c =
1 7
2 8
3 9
4 10
5 11
6 12
>> c'
ans =
1 2 3 4 5 6
7 8 9 10 11 12
>>
c=reshape(b,6,2)
c =
1 7
2 8
3 9
4 10
5 11
6 12
c'
ans =
1 2 3 4 5 6
7 8 9 10 11 12
A=1:12
A =
1 2 3 4 5 6 7 8 9 10 11 12
>> d=reshape(c,1,12)
d =
1 2 3 4 5 6 7 8 9 10 11 12
5)
>> A = [1 2 3; 4 5 6]; A(:),
ans =
1
4
2
5
3
6
Символ « : ». Оператор двоеточие позволяет обозначать колонки, а
также используется для задания диапазонов.
Выражение «A = 1:10» присваивает переменной A значение вектора-
строки, который задается в диапазоне 1..10 с шагом 1. Т.е. в результате
выполнения этого выражения мы задаем вектор A с размерностью 1х10. При
задании диапазонов можно также указывать шаг изменения. Например,
результаты выполнения выражений «А = [1:0.5:2]» и «А = [1.0 1.5 2.0]»
одинаковы.
Выражение «А(2:3)=[]» позволяет исключить из массива А 2-й и 3-й
столбцы. Данный оператор также может использоваться для обозначения
всего диапазона индексов.
6) Функция zeros для предварительного выделения вектора, создаваемого в цикле for. Это позволяет циклу for работать заметно быстрее. zeros (создание массивов с нулевыми элементами)
Функции ones (создание массивов с единичными элементами),
>> A=zeros(4,4)
A =
0 0 0 0
0 0 0 0
0 0 0 0
0 0 0 0
>> zeros(5,1)
ans =
0
0
0
0
0
>> ones(3,3)
ans =
1 1 1
1 1 1
1 1 1
>> eye(3,3)
ans =
1 0 0
0 1 0
0 0 1
>> A=[ 1 2 3; 4 5 6]
A =
1 2 3
4 5 6
>> fliplr(A)
ans =
3 2 1
6 5 4
7)
>> A = [1 2 3; 4 5 6; 7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> B = [1; 2; 3]
B =
1
2
3
>> x=B\A
x =
2.1429 2.5714 3.0000
8)
>> A=[1 2 3 4 5;6 7 8 9 10; 11 12 13 14 15; 16 17 18 19 20;21 22 23 24 25]
A =
1 2 3 4 5
6 7 8 9 10
11 12 13 14 15
16 17 18 19 20
21 22 23 24 25
>> A([2,4],:)=[]
A =
1 2 3 4 5
11 12 13 14 15
21 22 23 24 25
9)
A=rand(240,320,10)
>> size(A)
ans =
240 320 10
10)
>> A = [1 2 3 4 5]
A =
1 2 3 4 5
>> B = [4 5 6 7 8]
B =
4 5 6 7 8
>> A.*B
ans =
4 10 18 28 40
11)
>> 2.05*4.1
ans =
8.4050
>> 2.05*power(10,15)*1.4*power(10,15)
ans =
2.8700e+030
12)
>> x=0:0.1:2*pi
x =
Columns 1 through 17
0 0.1000 0.2000 0.3000 0.4000 0.5000 0.6000 0.7000 0.8000 0.9000 1.0000 1.1000 1.2000 1.3000 1.4000 1.5000 1.6000
Columns 18 through 34
1.7000 1.8000 1.9000 2.0000 2.1000 2.2000 2.3000 2.4000 2.5000 2.6000 2.7000 2.8000 2.9000 3.0000 3.1000 3.2000 3.3000
Columns 35 through 51
3.4000 3.5000 3.6000 3.7000 3.8000 3.9000 4.0000 4.1000 4.2000 4.3000 4.4000 4.5000 4.6000 4.7000 4.8000 4.9000 5.0000
Columns 52 through 63
5.1000 5.2000 5.3000 5.4000 5.5000 5.6000 5.7000 5.8000 5.9000 6.0000 6.1000 6.2000
>> y=sin(x)
y =
Columns 1 through 17
0 0.0998 0.1987 0.2955 0.3894 0.4794 0.5646 0.6442 0.7174 0.7833 0.8415 0.8912 0.9320 0.9636 0.9854 0.9975 0.9996
Columns 18 through 34
0.9917 0.9738 0.9463 0.9093 0.8632 0.8085 0.7457 0.6755 0.5985 0.5155 0.4274 0.3350 0.2392 0.1411 0.0416 -0.0584 -0.1577
Columns 35 through 51
-0.2555 -0.3508 -0.4425 -0.5298 -0.6119 -0.6878 -0.7568 -0.8183 -0.8716 -0.9162 -0.9516 -0.9775 -0.9937 -0.9999 -0.9962 -0.9825 -0.9589
Columns 52 through 63
-0.9258 -0.8835 -0.8323 -0.7728 -0.7055 -0.6313 -0.5507 -0.4646 -0.3739 -0.2794 -0.1822 -0.0831
>> plot(x,y)
13)
A=zeros(500,500)
A=zeros(500,500);
Символ (;) позволяет не выводить на экран значение матрицы А.
Работа с математическим редактором MATLAB