Переходные процессы в линейных цепях

Курсовая работа
«Переходные процессы

в линейных цепях»

Введение

Основными задачами РГР являются:

1. самостоятельный анализ переходных процессов в линейных электрических цепях;
2. расчет электрических цепей с одним и двумя энергоемкими элементами классическим и операторным методами;
3. определение переходной и импульсной характеристик линейных цепей;
4. нахождение реакции цепи на произвольное внешнее воздействие по ее переходной и импульсной характеристикам.

КЛАССИЧЕСКИЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ

Задание:

1. Провести анализ переходного процесса в цепи с одним энергоемким элементом, схема которой представлена на (рис. 1), значения параметров в (табл. 1)

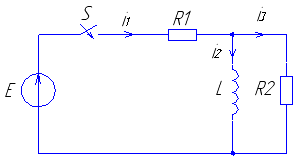
Рис. 1

Таблица 1

Величины параметров элементов цепи	Искомый ток
E, B	L, мГн	R1, Ом	R2, Ом
100	10	20	20	i2(t)

1. Определить заданный ток и напряжения на элементах цепи в переходном режиме.

Решение:

Рассмотрим переходный процесс при замыкании ключа в цепи (рис. 1) с одним энергоемким элементом, используя классический метод анализа.

Анализ цепи до коммутации показывает, что ток индуктивности

i2(0-) =0.

Независимое начальное условие определяется на основании первого закона коммутации и может быть зависимо:

,

т.е. ток индуктивности в первый момент после коммутации равен току индуктивности до коммутации, а затем может плавно изменяться.

Для нахождения заданного тока i2(t) составим дифференциальное уравнение цепи после коммутации. Дифференциальное уравнение цепи получим из системы уравнений электрического равновесия цепи

i1 = i2 + i3; UR1 = i1R1; (1)

UR1 + UL = E; UR2 = i3 R2;

UR2 - UL = 0;

последовательно исключая все неизвестные величины кроме тока i2, запишем выражение

(2)

Используя свойства дифференциала приходим к дифференциальному уравнению цепи

(3)

Решение уравнения (3) будем искать в виде суммы свободной i2св и вынужденной i2вын составляющих тока второй ветви

(4)

Свободную составляющую тока находим, решая однородное дифференциальное уравнение, полученное из дифференциального уравнения цепи (3) (правая часть равна нулю)

(5)

Далее составляем характеристическое уравнение цепи

находим его корень

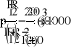
и определяем вид свободной составляющей тока второй ветви

Анализ установившегося процесса в цепи после коммутации позволяет найти вынужденную составляющую тока (частное решение дифференциального уравнения цепи)

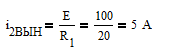
Общий вид реакции цепи соответствует сумме вынужденной и свободной составляющих тока второй ветви

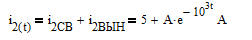
Определим постоянную интегрирования А по зависимым начальным условиям, т.е. по значению тока в начальный момент времени после коммутации t=0+

Т.к. =0, то отсюда

Тогда постоянная интегрирования при подстановки будет равна А=-5

Таким образом ток после замыкания ключа будет записан в виде

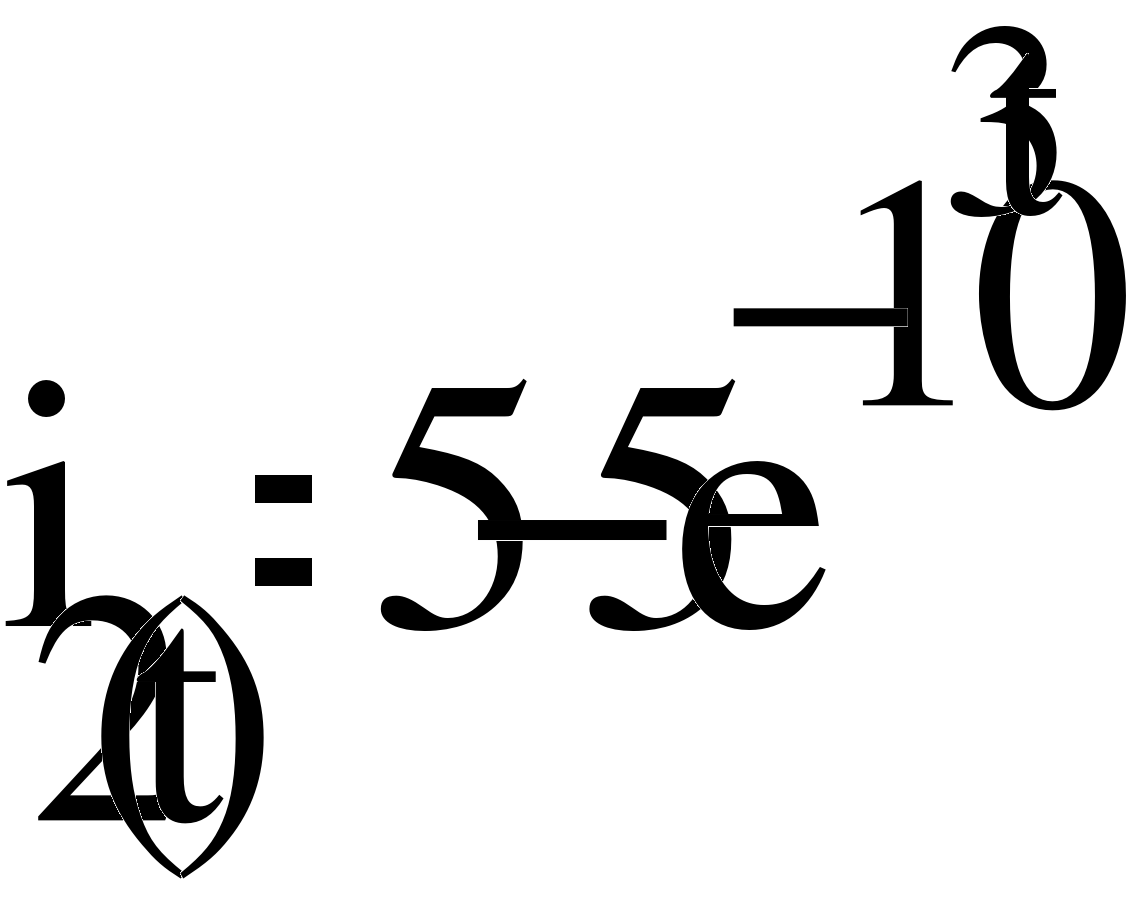
Напряжения на резисторах R1 и R2 можно определить, используя компонентное уравнение

A

В

В

В

1.1.2. Построим график тока второй ветви цепи, рассмотренной в задании 1.1.1.

Данный график (рис. 2) построим при помощи программы Mathcad 15 Portable.

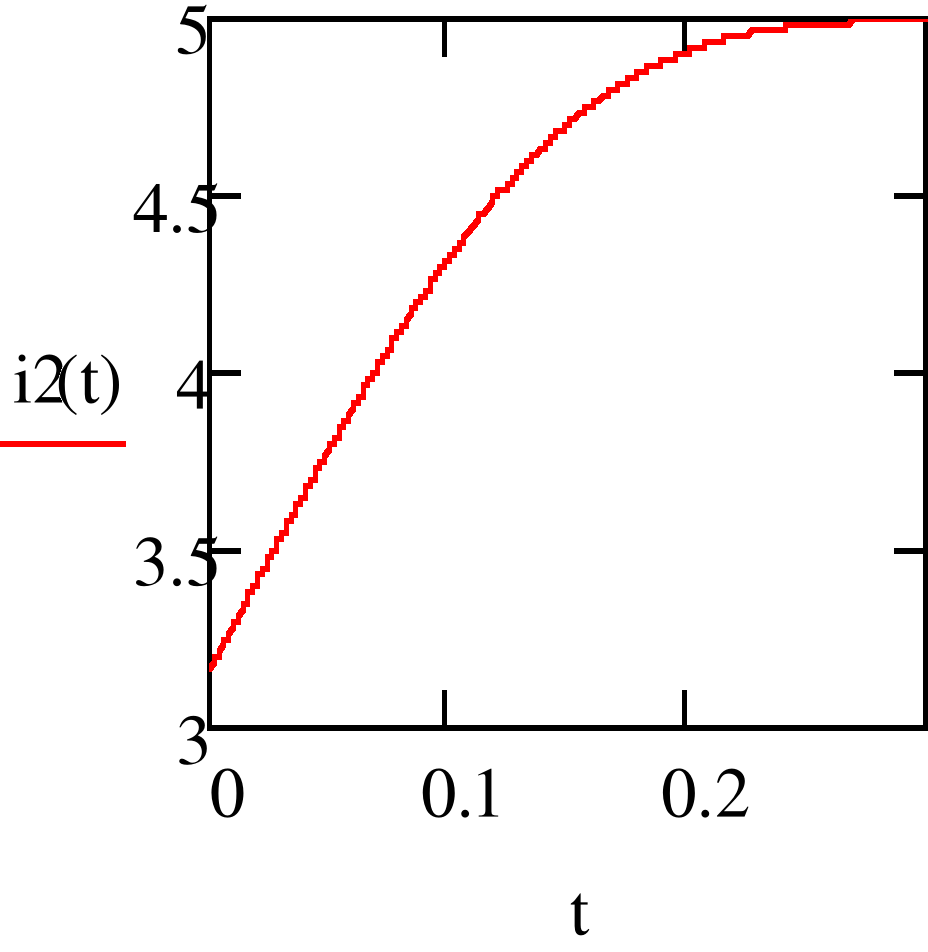
Рис. 2

1.2.Методика анализа переходного процесса классическим методом в цепи с двумя энергоемкими элементами.

Проведем анализ переходного процесса в цепи (рис. 3) при замыкании ключа S. Величины параметров элементов и искомая реакция цепи приведены в (табл. 2).

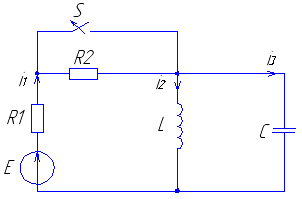
Рис. 3

Таблица 2

Величины параметров элементов цепи	Искомый ток
E, B	R1, Ом	R2, Ом	C, пФ	L,мкГн	i1(t)
10	5000	5000	100	50

Анализ цепи до коммутации показывает, что ток через катушку индуктивности равен нулю, также равно нулю напряжение на конденсаторе .

Независимые начальные условия на основании законов коммутации:

,

.

Составим дифференциальное уравнение цепи после коммутации. Для этого запишем систему уравнений электрического равновесия цепи (рис. 3) относительно неизвестных токов и напряжений ее ветвей:

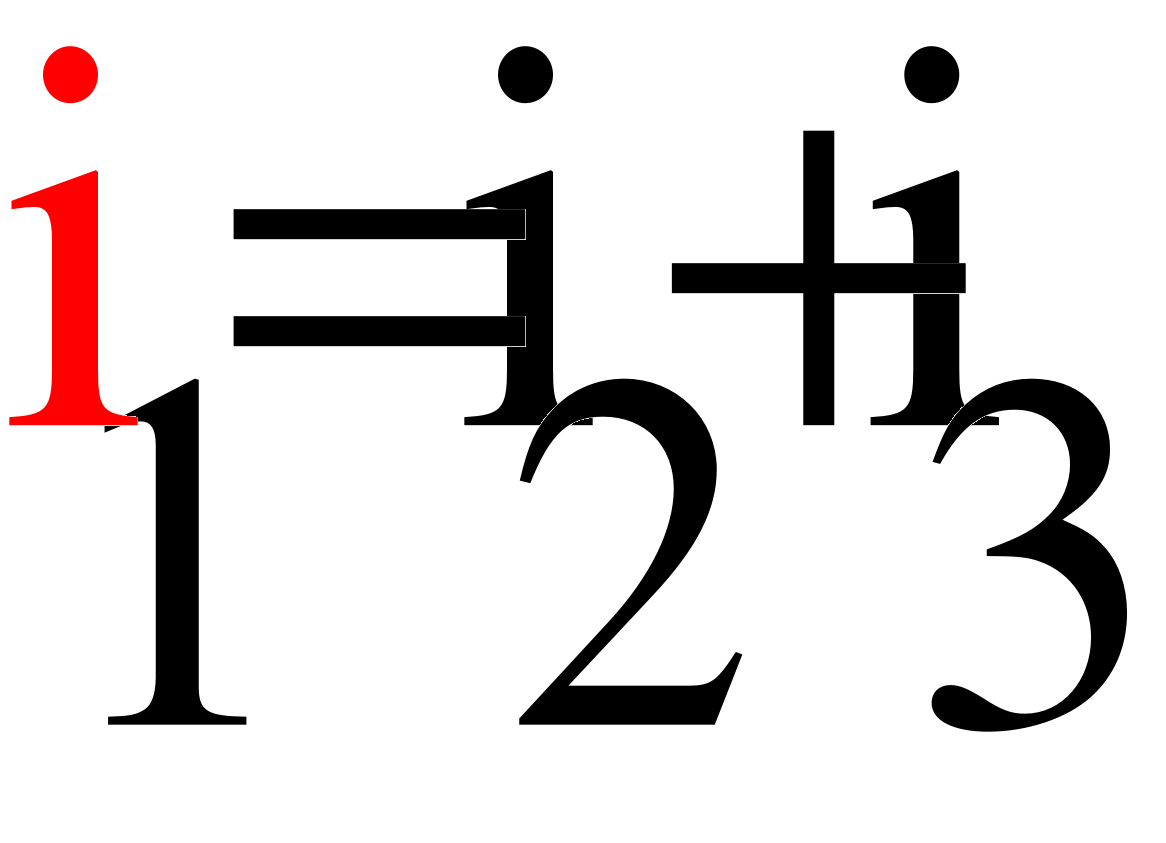
(5)

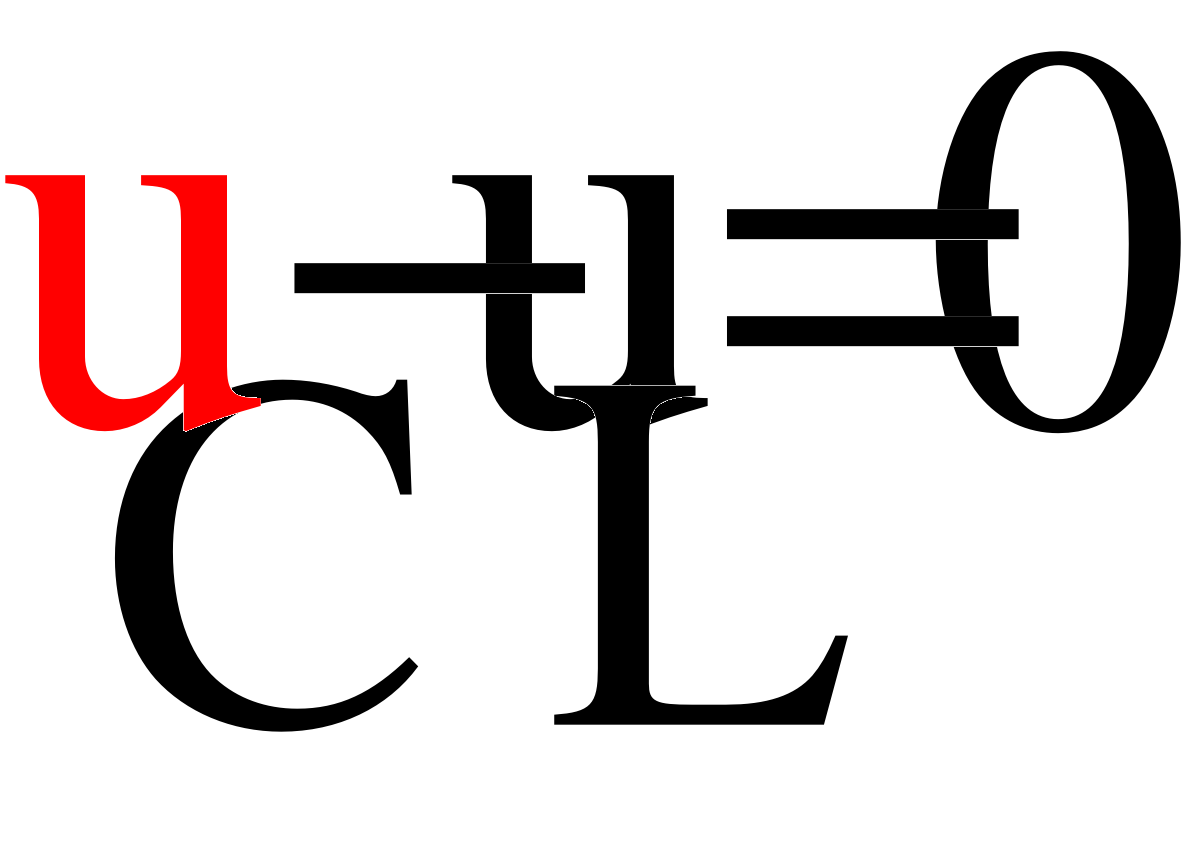
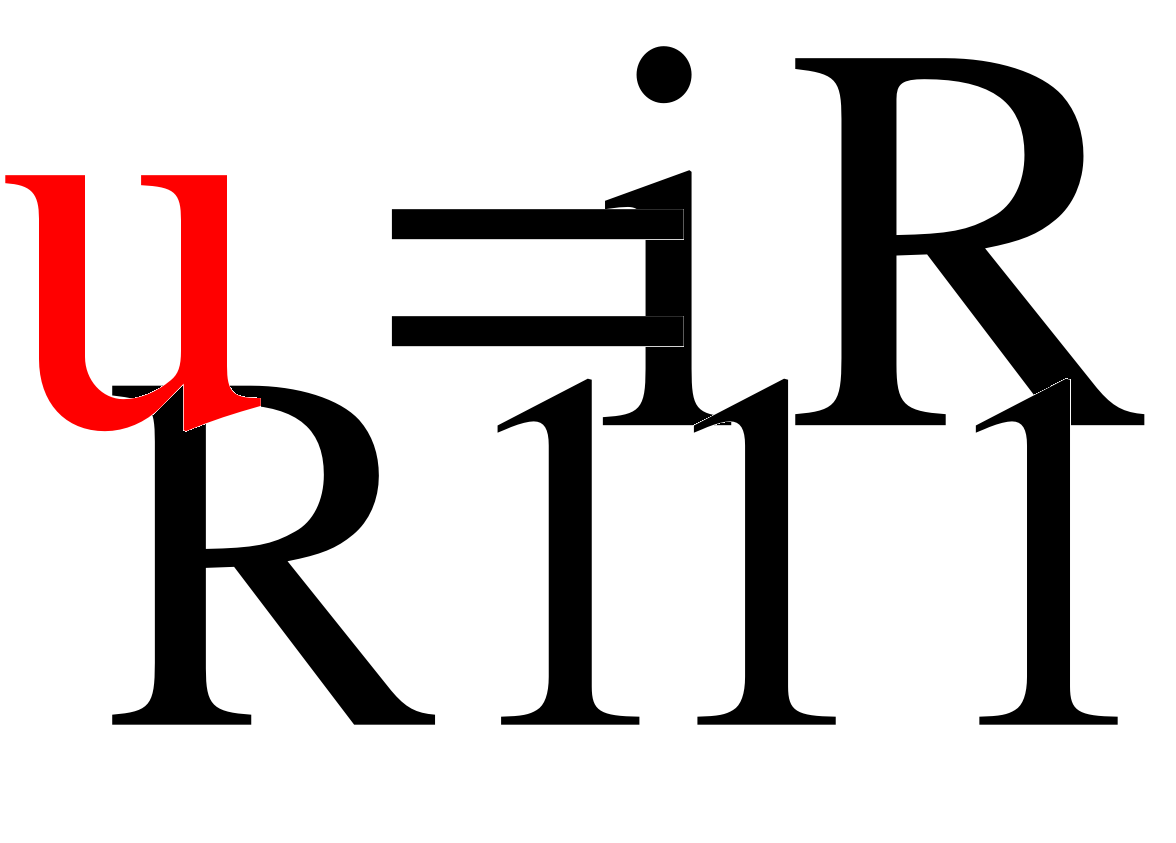
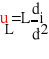
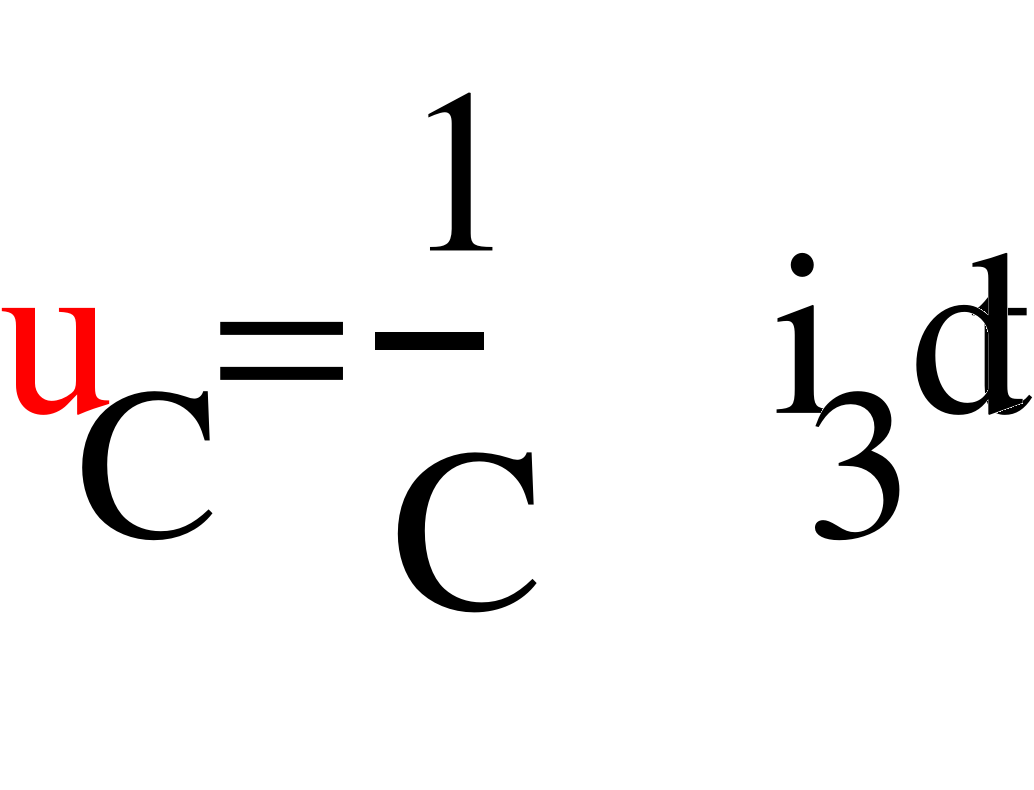
Из полученной системы уравнений (5) исключим все неизвестные кроме одной переменной i1

(6)

Чтобы избавиться от интегралов в последнем уравнении, осуществим дифференцирование его по времени. Преобразуя, получим

(7)

Решение уравнения (7) найдем как сумму свободной i1св и вынужденной i1вын составляющих тока второй ветви.

i1= i1св+ i1вын.

Анализ установившегося процесса после коммутации связан с частным решением дифференциального уравнения цепи (6) и проводится по результатам анализа цепи в установившемся режиме при .

Вынужденная составляющая тока второй ветви будет равна:

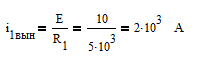
Свободную составляющую тока находим, составляя характеристическое уравнение цепи, решая однородное дифференциальное уравнение цепи:

(7)

Находим его корни

с-1

Таким образом, свободная составляющая тока второй ветви будет равна:

.

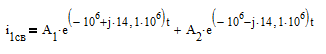Общий вид реакции цепи в переходном режиме равен сумме вынужденной и свободной составляющих тока второй ветви

(8)

Определим постоянные интегрирования. В данном случае их две и для их нахождения необходимо два уравнения. Первое получим из выражения для тока второй ветви в первый момент после коммутации (при )

или . (9)

Второе уравнение получим, определив производную от уравнения тока второй ветви

,

в начальный момент после коммутации

(10)

Однако в уравнениях кроме постоянных интегрирования неизвестны и зависимые начальные условия и , которые необходимо определить из независимых начальных условий и уравнений электрического равновесия цепи в начальный момент после коммутации

;

;

.

На основании законов коммутации и , тогда

Находим постоянные интегрирования

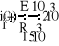
А1=-А2

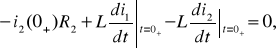
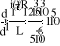
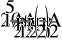
ж

А2 =j0,71 A

Определим реакцию цепи, т.е. ток второй ветви после коммутации. Подставив постоянные интегрирования в уравнение

Выражение тока второй ветви с учетом соотношения

может быть преобразовано к виду А.

1.2.2. Построим график функции тока второй ветви, используя программу MathCad 15 Portable. (рис. 6)

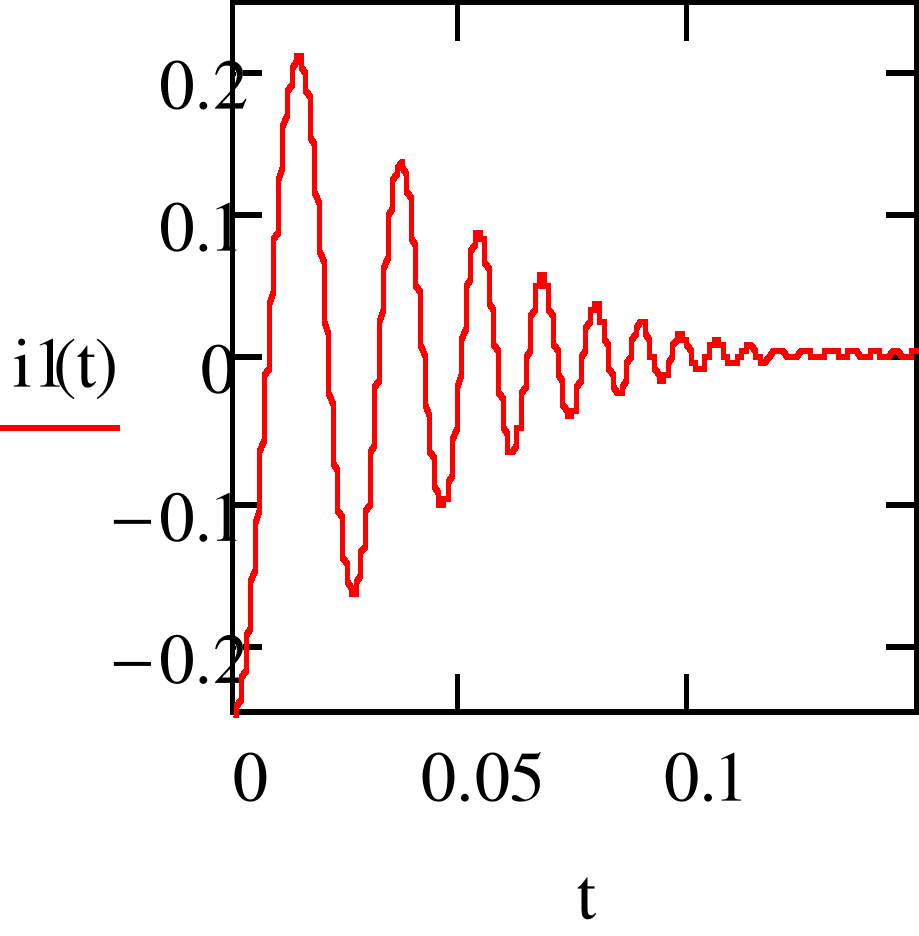
Рис. 4

Как видно из (рис. 4) колебательный процесс носит затухающий характер.

ОПЕРАТОРНЫЙ МЕТОД АНАЛИЗА ПЕРЕХОДНЫХ ПРОЦЕССОВ

ЗАДАНИЯ

1. Провести анализ переходного процесса в цепи с одним энергоемким элементом операторным методом. Варианты схем и величины параметров элементов цепей приведены в табл. 1.
   1. Определить заданный ток и напряжения на элементах цепи операторным методом.
      1. Провести анализ полученных результатов, сравнить их с результатами расчета переходного процесса классическим методом.
   2. Операторным методом провести анализ переходного процесса в цепи с двумя энергоемкими элементами, схема и величины параметров которой заданы в табл. 2.
      1. Операторным методом рассчитать заданный ток в цепи с двумя энергоемкими элементами.
      2. Провести анализ переходного процесса в цепи с двумя энергоемкими элементами и сравнить полученные результаты с результатами анализа классическим методом.

2.1.1. Определим заданный ток и напряжения на элементах в переходном режиме при замыкании ключа S в цепи с одним энергоемким элементом (рис. 1).

Анализируя процессы в цепи до коммутации, определяем начальное значение тока индуктивности:

Независимое начальное значение тока индуктивности на основании первого закона коммутации также равно нулю: .

Составим операторную схему замещения цепи после коммутации (рис. 5).

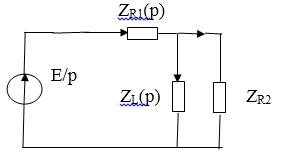
Рис. 5

Для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжения E – операторной ЭДС , мгновенные значения токов и напряжений ветвей – операторными токами и напряжениями соответственно.

Составим уравнения электрического равновесия цепи в операторной форме используя метод контурных токов:

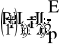
Решение уравнений электрического равновесия цепи с помощью формул Крамера позволяет определить контурные токи:

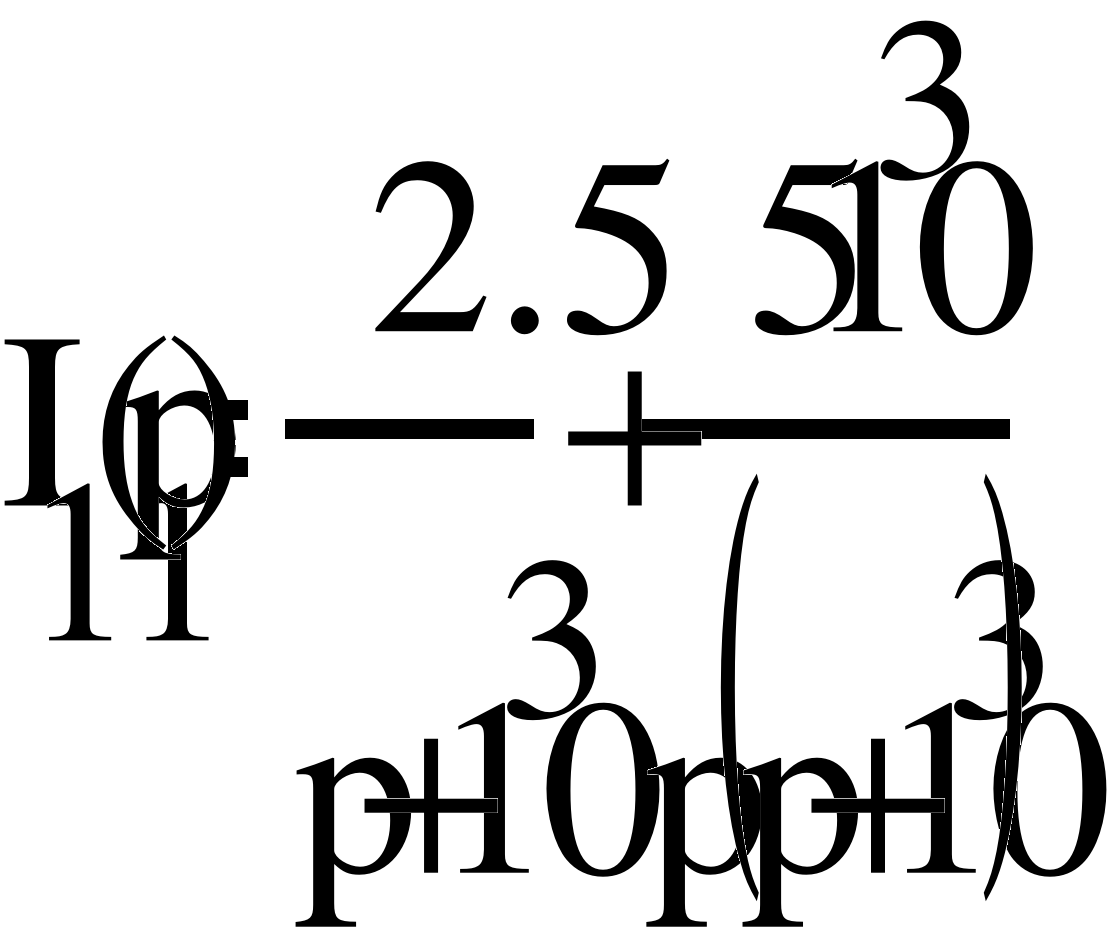
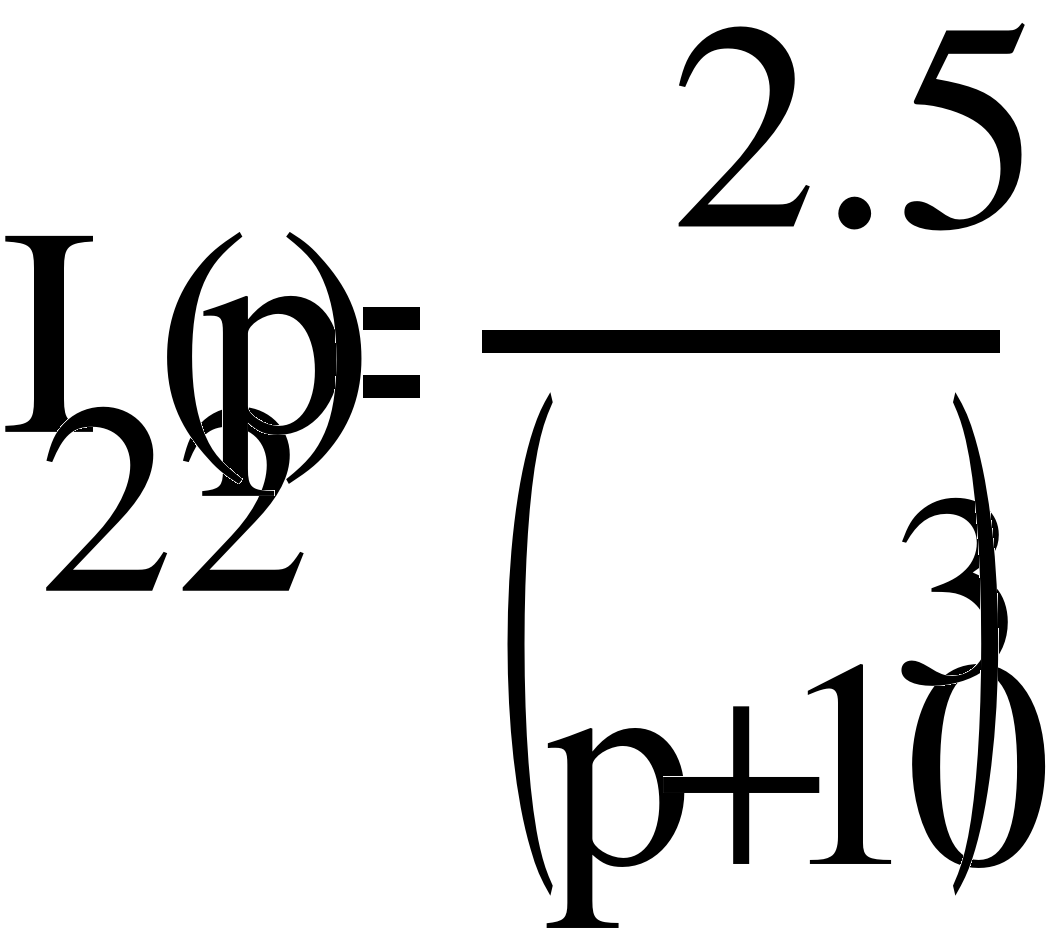
Тогда операторные изображения токов ветвей цепи:

, ,

а искомый ток будет равен разности контурных токов:

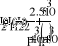
Учитывая, что , находим выражения для искомых тока и напряжений на элементах электрической цепи после замыкания ключа S:

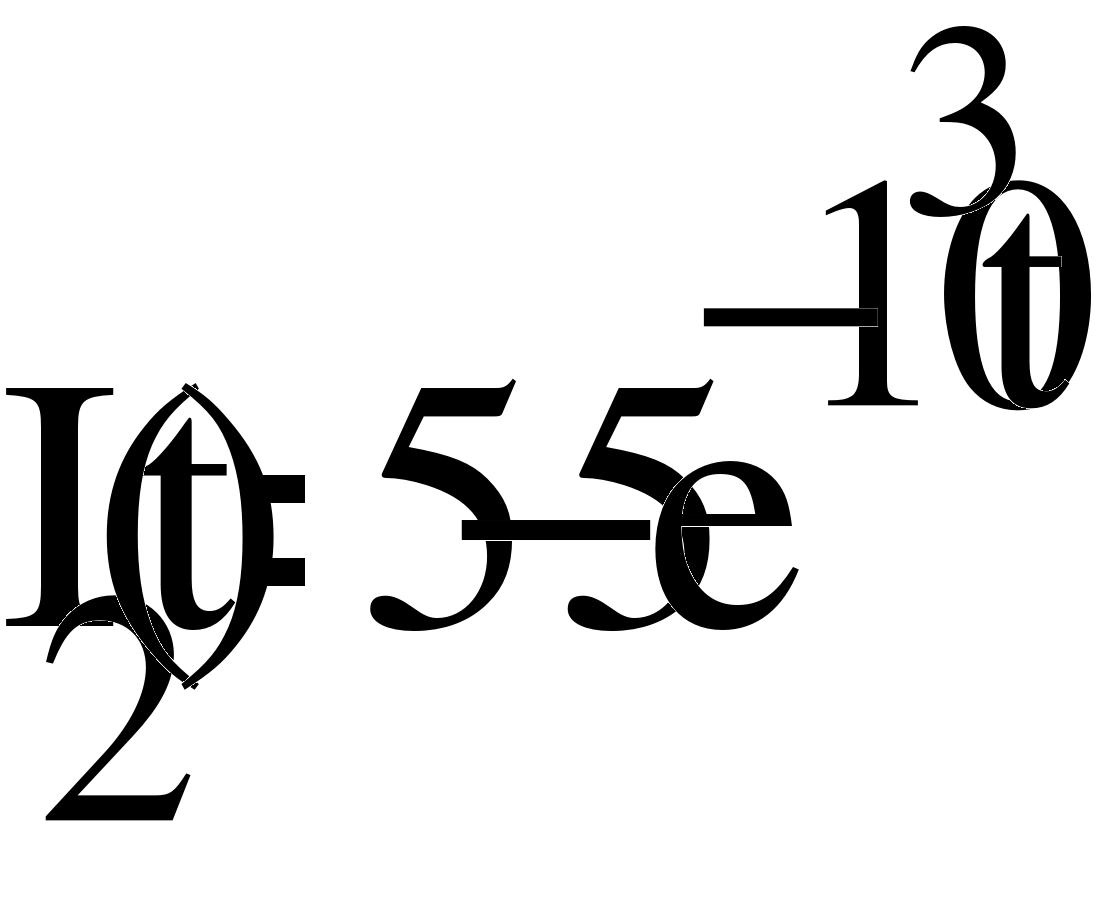
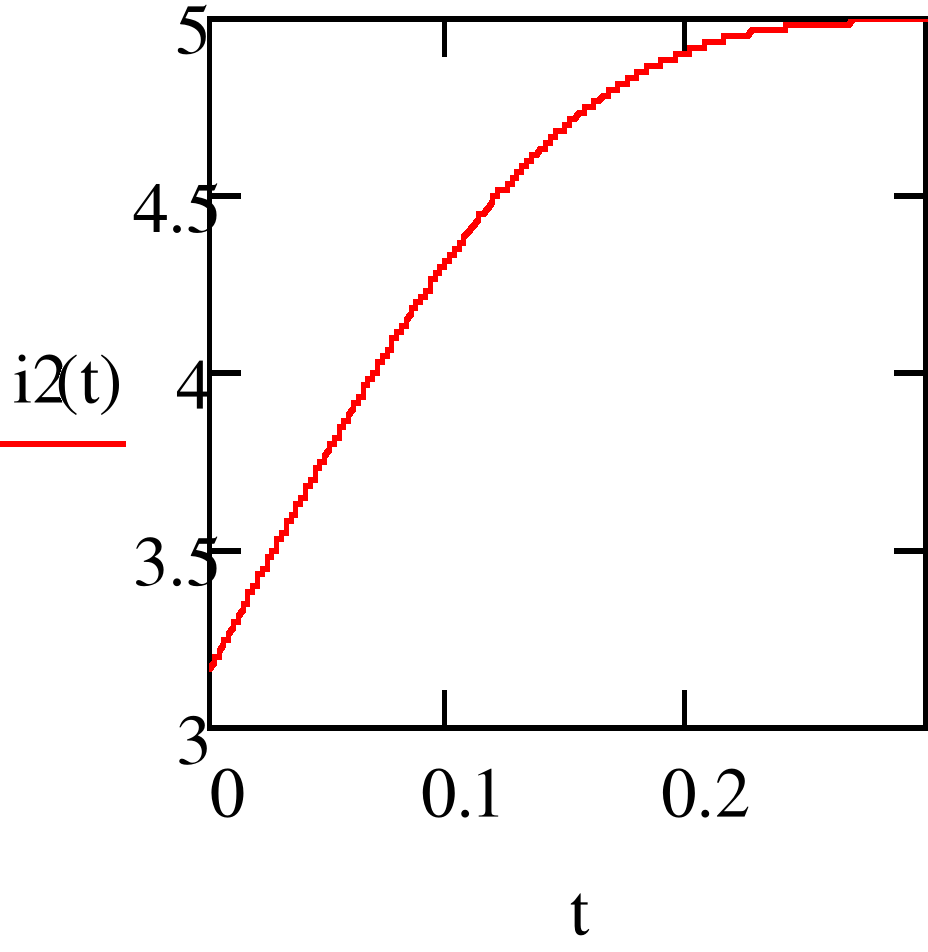
Рис. 6

2.1.2. Ток после замыкания ключа S изменяется скачком. С ростом тока индуктивности, ток начинает увеличиваться, поскольку к резистору параллельно подключается ветвь с резистором . Так как сопротивление резисторов и равны, то в установившемся режиме токи второй и третьей ветвей равны, при этом сопротивление индуктивности постоянному току равно нулю.

Результаты полученные операторным методом полностью совпадают с результатами расчета цепи классическим методом.

2.2. Анализ переходного процесса в цепи с двумя энергоемкими элементами операторным методом

2.2.1. Операторным методом рассчитаем ток второй ветви цепи (рис. 4) при замыкании ключа S. Величины параметров элементов и искомая реакция цепи приведены в (табл. 2).

Проведем анализ цепи до коммутации и определим независимые начальные условия: ток индуктивности и напряжение на конденсаторе .

Изобразим операторную схему замещения цепи после коммутации (рис. 7), для этого заменим идеализированные пассивные элементы их операторными схемами замещения, ЭДС идеализированного источника напряжения - операторной ЭДС , мгновенные значения токов и напряжений ветвей их операторными изображениями и соответственно.

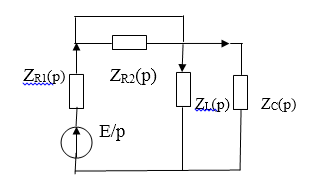
Рис. 7

Составим уравнение электрического равновесия цепи в операторной форме методом двух узлов:

Определим операторный ток первой ветви

(11)

Изображение тока первой ветви можно записать в виде отношения двух полиномов от , не имеющих общих корней

(12)

причем степень полинома выше, чем степень полинома , а уравнение не имеет кратных корней, то для перехода от изображения к оригиналу можно воспользоваться теоремой разложения:

, (13)

где - корни уравнения .

Поскольку знаменатель уравнения (11) имеет один корень равный нулю, т.е. , то для нахождения оригинала тока воспользуемся другой формулой теоремы разложения:

(14)

Подставим численные значения в уравнение (11).

Запишем

и значения функций и при

Найдем корни уравнения

.

Вычислим производную и ее значения при и

Определим при и :

Подставим полученные значения в формулу

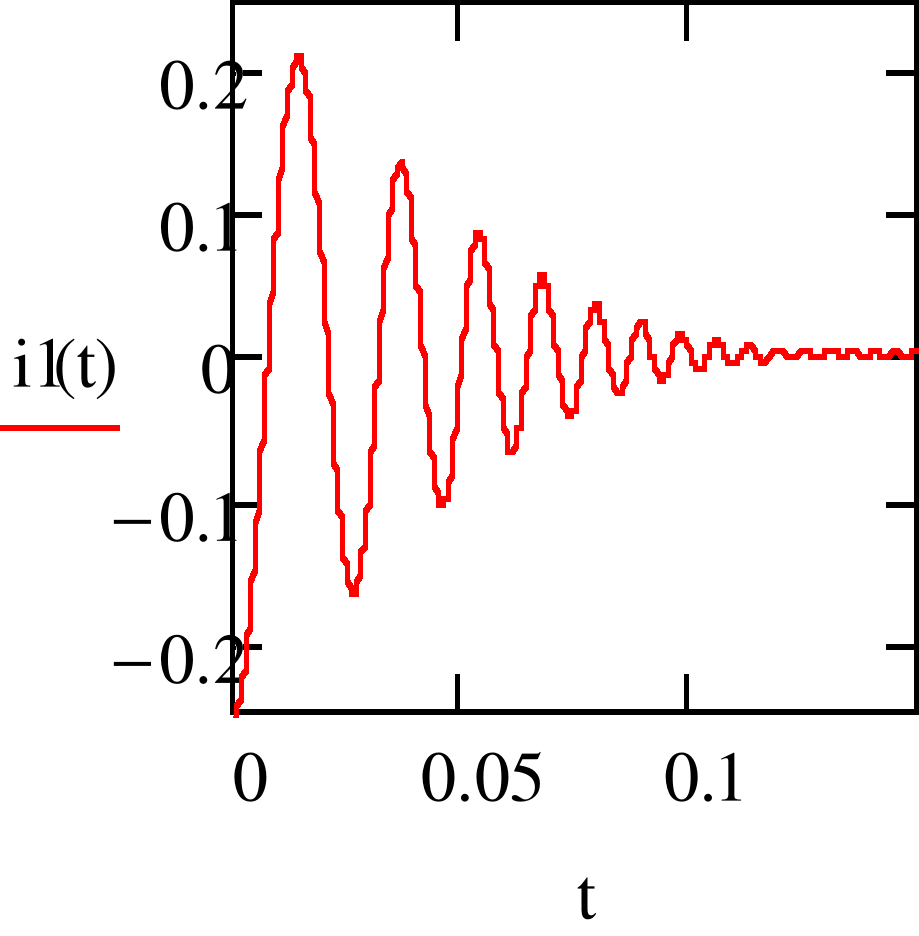
Рис. 8

2.2.2. Анализ переходного процесса в разветвленной цепи с двумя энергоемкими элементами (рис. 4) операторным и классическим методами показал, что переходный процесс в ней носит колебательный характер. Полученные результаты не зависят от метода расчета, однако трудоемкость расчета различными методами не эквивалентна.

Поскольку коэффициент затухания , то колебания затухают достаточно быстро в цепи.

РАСЧЕТ ПЕРЕХОДНЫХ ПРОЦЕССОВ С ПОМОЩЬЮ ИНТЕГРАЛЛА ДЮАМЕЛЯ

ЗАДАНИЯ

3.1. Найти переходную и импульсную характеристики цепи, схема которой представлена на (рис. 9)

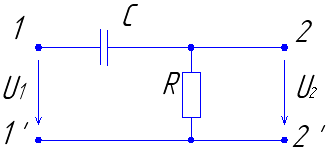
Рис.9

3.2. Определить реакцию цепи на воздействие прямоугольного импульса (рис. 10) по переходной характеристике цепи.

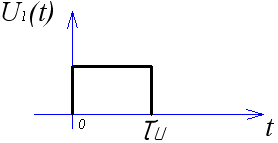
Рис.10

3.3. Определить реакцию цепи для заданного воздействия (задание 3.2.) по ее импульсной характеристике.

3.1. Временные (переходная и импульсная ) характеристики линейной цепи находят используя соотношения связывающие частотные и временные характеристики. Для этого составляют операторную схему замещения электрической цепи при нулевых начальных условиях. Используя полученную схему, определяют операторную характеристику , соответствующую заданному внешнему воздействию на цепь и полученной реакции цепи . По операторной характеристике находят временные характеристики:

(15)

(16)

Рассмотрим методику определения временных характеристик цепи (рис. 9) в режиме холостого хода на режимах 2-2/ . Внешнее воздействие на цепь источник напряжения, подключенный в момент времени =0, реакция цепи – напряжение на зажимах 2-2/ .

Составим операторную схему замещения цепи (рис. 11) при нулевых начальных условиях.

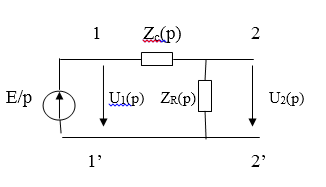
Рис. 11

Определим операторный коэффициент передачи цепи по напряжению в режиме холостого хода ()

Следовательно, операторные изображения переходной и импульсной характеристики цепи имеют вид

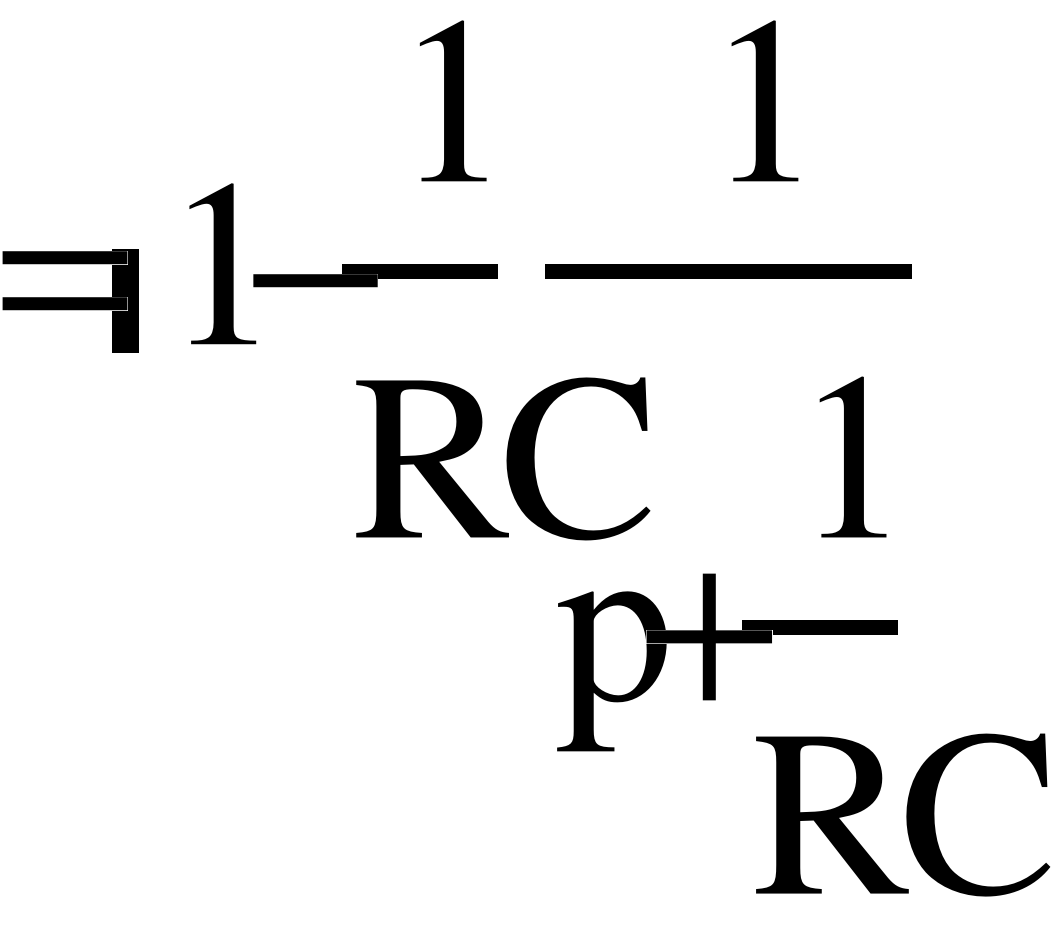
Используя таблицы обратного преобразования Лапласа, переходим от изображений искомых временных характеристик к оригиналам:

(17)

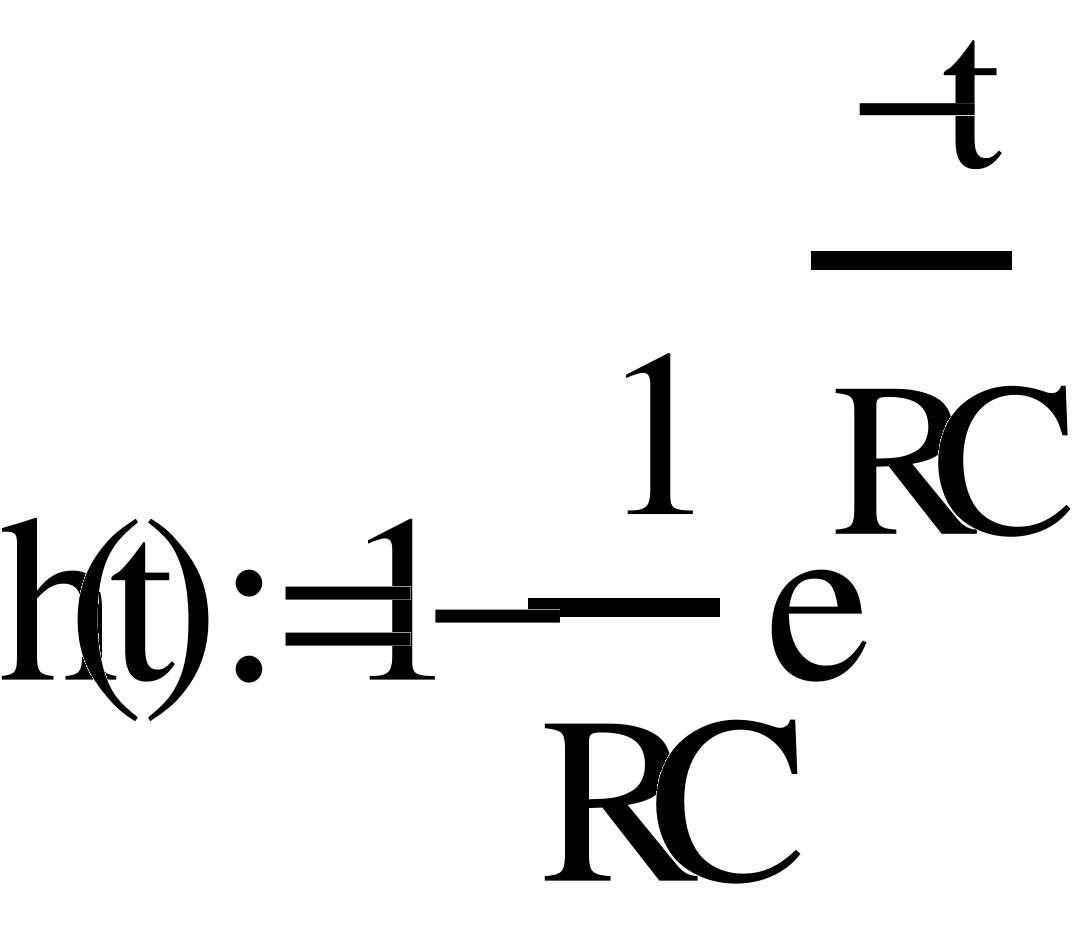
а) б )

Рис. 12

Временные характеристики цепи имеют вид, представленный на (рис. 12): а) переходная; б) импульсная характеристика цепи.

3.2. Определим реакцию цепи (рис.9) на воздействие прямоугольного импульса по ее переходной характеристике с помощью интеграла Дюамеля (интеграл наложения)

(19)

С помощью интеграла Дюамеля можно определить реакцию цепи на заданное воздействие, когда оно описывается кусочно-непрерывной функцией, т.е. функцией, которая имеет конечное число разрывов. В этом случае интервал интегрирования необходимо разбить на несколько промежутков в соответствии с интервалами непрерывности функции и учесть реакцию цепи на конечные скачки функции в точках разрыва.

Внешнее воздействие можно записать:

Разбиваем ось времени на три промежутка в соответствии с интервалами непрерывности функции .

При реакция цепи тождественно равна нулю.

На участке , функция непрерывна, поэтому реакция цепи определяется с помощью интеграла Дюамеля при =0.

.

Выражение переходной характеристики цепи получим при , заменив на в выражении

.

Тогда реакция цепи на рассмотренном участке принимает вид:

.

Поскольку , то реакция цепи .

При интервал интегрирования содержит точку разрыва функции . Для определения реакции цепи интервал интегрирования разобьем на два промежутка и и учтем реакцию цепи на скачки функции в точке . Принимаем во внимание, что при , находим

Графики реакции цепи на воздействие прямоугольного импульса в зависимости то его длительности имеют вид представленный на (рис. 13)

Рис. 13

3.3. Определим реакцию цепи (рис. 10) на воздействие прямоугольного импульса напряжения по ее импульсной характеристике. Как и в предыдущем случае разобьем интервал интегрирования на несколько промежутков в соответствии с интервалами непрерывности функции и на этих интервалах вычислим интеграл Дюамеля

(20)

При напряжение на зажимах 2-2/ цепи тождественно равно нулю (нет воздействия, нет реакции).

На участке функция не имеет разрывов, поэтому напряжение находится непосредственно с помощью выражения (20)

,

где - импульсная характеристика при замене на

.

Реакция цепи на данном участке запишется

При интервал интегрирования содержит точку разрыва функции , разобьем его на два промежутка и и найдем выражение для напряжения на зажимах 2-2/

Как и следовало ожидать, выражения для реакции цепи на воздействие прямоугольного импульса напряжения, найденные с помощью импульсной характеристики цепи совпадают с соответствующими выражениями, полученными с использованием переходной характеристики цепи.

Заключение

В результате проделанной курсовой работы был проведен анализ переходных процессов в линейных электрических цепях, расчет электрических цепей с одним и двумя энергоемкими элементами классическим и операторным методами, определены переходные и импульсные характеристики линейных цепей, найдены реакции цепи на произвольное внешнее воздействие по ее переходной и импульсной характеристикам. Значения токов, рассчитанные с помощью классического и операторного методов, полностью совпадают, что говорит о правильности произведенных вычислений. При расчете переходных процессов с помощью интеграла Дюамеля выражения для реакции цепи на воздействие прямоугольного импульса напряжения, найденные с помощью импульсной характеристики цепи, совпадают с соответствующими выражениями, полученными с использованием переходной характеристики цепи, что также подтверждает правильность расчетов.

Графики в заданиях были построены с использованием программыMathcad 15 Portable.

Список литературы

1. Переходные процессы в линейных цепях: Методические указания к выполнению расчетно-графической работы по дисциплине «Основы теории цепей» для студентов направлений 210300 «Радиотехника» и 210400 «Телекоммуникации» / Сост. Е.Н. Калачев. - Йошкар-Ола: МарГТУ, 2006.

1. Попов В.П. Основы теории цепей: Учеб. для вузов. - 3-е изд., испр. - М: Высш.шк., 2010. - 575 с.
2. Методы формирования уравнений электрического равновесия цепей: Методические указания к выполнению расчетно-графической работы по дисциплине «Основы теории цепей» / Сост. Е.Н. Калачев. – Йошкар-Ола: МарГТУ, 2006. – 32с.
3. Бакалов В.П., Дмитриков В.Ф., Круг Б.Е. Основы теории цепей: Учеб. для вузов / Под ред. В.П.Бакалов. - 2-е изд., перераб. и доп. - М: Радио и связь, 2009 - 592 с.
4. Шебес М.Р., Каблукова М.Р. Задачник по теории линейных электрических цепей: Учеб. пособие для электротехнич., радиотехнич. спец. вузов -4-е изд., перераб. и доп. -М: Высш.шк., 2011. - 544с.

PAGE \* MERGEFORMAT20

EMBED Equation.3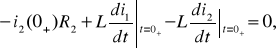

Переходные процессы в линейных цепях