Построение проверяющего теста для логической модели непрерывной системы
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
Кафедра «Автоматика и телемеханика»
Расчётно-пояснительная записка к контрольной работе
по дисциплине «Основы технической диагностики»
студент гр. У-ДТ-АТ-6786
____________ О. А. Липтуга
____.____.________
Руководитель
____________ ____.____.________
Омск 2014
Задание на контрольную работу
Вариант по списку 2
f = {3,5,6,7 (0,1)} a, b, c
Содержание
Введение …………………………………………………………………………………………4
1 Построение проверяющего теста для логической модели непрерывной системы……...5
- Построение диагностического теста ………………………………………………………...7
- Составление тестов для релейно-контактной схемы………………………………………..9
- Построение тестов для релейно-контактной схемы методом цепей и сечений ………….12
- Построение тестов для логических элементов……………………………………………..15
- Проверка комбинационных логических схем……………………………………………...17
Заключение ……………………………………………………………………………………..21
Библиографический список……………………………………………………………………22
Введение
Одной из наиболее важных и актуальных проблем транспорта и машиностроения является повышение качества и надежности деталей, механизмов машин и оборудования. Это вызвано постоянным ростом энерговооруженности оборудования современных предприятий и транспорта, внедрением автоматизированных систем обслуживания и управления [1].
Очевидно, что увеличение эффективности, надежности и ресурса, а также обеспечение безопасной эксплуатации механизмов, машин и оборудования тесно связано с необходимостью оценки их технического состояния. Это и определило формирование нового научного направления - технической диагностики.
Техническая диагностика рассматривает вопросы, связанные с оценкой действительного состояния технических систем. Задачей диагностики является выявление и предотвращение возникающих отказов технических средств с целью повышения их общей надежности.
При эксплуатации устройств железнодорожной автоматики и телемеханики решение проблем технического диагностирования имеет первостепенное значение, поскольку эти устройства являются обслуживаемыми и восстанавливаемыми. При их отказах может произойти задержка поездов и в худшем случае нарушение безопасности движения. Перед эксплуатационным и обслуживающим персоналом (инженерами и электромеханиками) стоят задачи контроля и поддержания исправного состояния устройств ЖАТ, в случае возникновения отказов - быстрого их обнаружения и устранения.
Процесс технической диагностики предусматривает наличие объекта диагностики, средств диагностики и человека-оператора. В процессе диагностики выполняются измерительные, контрольные и логические операции. Эти операции выполняются оператором с использованием средств диагностики с целью определения действительного состояния технического средства. Результаты оценки используются для принятия решения о дальнейшем использовании технического средства [2].
В контрольной работе по дисциплине «Основы технической диагностики» составлены проверяющие и диагностические тесты для различных технических систем.
1 Построение проверяющего теста
Для рассматриваемой логической модели введём некоторые ограничения:
- В модели рассматриваются только одиночные неисправности;
- На входы объекта поступает единственное входное воздействие из области допустимых значений входных сигналов.
Для 2-го варианта функциональная схема имеет вид:
Рисунок 4.1 – Функциональная схема диагностируемого устройства
Исходя из условий и принятых ограничений, можно выделить 9 состояний объекта
– система исправна;
– неисправен 1-ый элемент;
– неисправен 2-ой элемент;
– неисправен 3-ий элемент;
– неисправен 4-ый элемент;
– неисправен 5-ый элемент;
– неисправен 6-ой элемент;
– неисправен 7-ой элемент;
– неисправен 8-ой элемент.
Далее, руководствуясь схемой, построим таблицу функций неисправностей:
Таблица 4.1 – Таблица функций неисправностей
|
Проверка
|
Результат проверки для системы, находящейся в состоянии
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Теперь запишем функцию исправного объекта () и функции неисправностей ().
;
;
;
;
;
;
;
;
.
Далее, для построения теста, необходимо найти проверяющую функцию каждой неисправности:
;
;
;
;
;
;
;
.
Проверяющий тест определяется по формуле
.
Преобразовав полученное выражение по законам алгебры логики, получим
.
Эта проверочная функция показывает, что для определения работоспособности объекта достаточно проверить значение выходной функции .
2 Построение диагностического теста
Далее нам необходимо вычислить различающие функции для всех неисправностей, для этого перемножаем функции неисправностей между собой по модулю 2:
Далее рассмотрим два варианта, вначале примем, что система, априори, неисправна. Тогда диагностический тест находится как произведение всех различающих функций:
Подставив в это выражение наши функции, и упростив его, получим:
Этот тест показывает, на выходе каких блоков необходимо проследить реакцию выходных функций на определённое входное воздействие, для определения неисправного блока. Словарь неисправностей будет иметь вид:
Таблица 4.2 – Словарь неисправностей для
|
Проверка
|
Результат проверки для системы, находящейся в состоянии
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
Во втором случае нам заранее неизвестно, исправен объект или нет. Тогда нам необходимо перемножить проверочный и диагностический тесты, чтобы учесть состояние, когда все блоки исправны:
Тогда тест имеет вид:
Словарь неисправностей будет содержать столбец с исправным состоянием:
Таблица 4.3 – Словарь неисправностей для
|
Проверка
|
Результат проверки для системы, находящейся в состоянии
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1
|
1
|
0
|
0
|
1
|
1
|
1
|
1
|
1
|
|
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
1
|
1
|
|
|
1
|
1
|
0
|
0
|
1
|
0
|
0
|
1
|
1
|
|
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
1
|
1
|
|
|
1
|
0
|
0
|
0
|
1
|
0
|
0
|
0
|
1
|
|
|
1
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
Таким образом, мы выяснили, что при заранее известном состоянии объекта (неисправен), нам придется проверить пять выходных функций для определения неисправного элемента. При заранее неизвестном состоянии объекта, нам придётся делать дополнительно проверку выхода .
3 Составление тестов для релейно-контактной схемы
Для построения теста для релейно-контактной схемы задана функция:
f = {3,4,6,7 (0,1)} a, b, c
Таблица 4 - Таблица истинности для заданной функции алгебры логики
|
|
а
|
b
|
c
|
f
|
|
0
|
0
|
0
|
0
|
~
|
|
1
|
0
|
0
|
1
|
~
|
|
2
|
0
|
1
|
0
|
0
|
|
3
|
0
|
1
|
1
|
1
|
|
4
|
1
|
0
|
0
|
0
|
|
5
|
1
|
0
|
1
|
1
|
|
6
|
1
|
1
|
0
|
1
|
|
7
|
1
|
1
|
1
|
1
|
Для получения минимальной дизъюнктивной нормальной формы используется карта Карно.
Рисунок 2 – Минимизация функции методом Карно
В результате минимизации функция примет вид:
f = a*b + c (2)
По выражению (2) построена схема на релейно-контактных элементах, реализующая заданную функцию.
Рисунок 3 – Схема на релейно–контактных элементах.
По заданию необходимо рассмотреть два вида неисправностей - короткое замыкание и разрыв контактов. В случае короткого замыкания цепь остается замкнутой независимо от состояния реле. При разрыве контакта цепь остается разомкнутой независимо от состояния реле.
Следовательно каждый контакт может находиться в трех состояниях:
исправном а;
короткозамкнутом а1
разорванном а0
Для построения теста для релейно-контактной схемы построим таблицу функций неисправностей.
Таблица 5 - Таблица функций неисправностей для релейно-контактной схемы
|
Входной набор
|
F
|
f1
|
f2
|
f3
|
f4
|
f5
|
f6
|
|
№
|
аbс
|
|
При внесении неисправности
|
|
|
|
|
a1
|
a0
|
b1
|
b0
|
c1
|
c0
|
|
0
|
000
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
1
|
001
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
|
2
|
010
|
0
|
1
|
0
|
0
|
0
|
1
|
0
|
|
3
|
011
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
|
4
|
100
|
0
|
0
|
0
|
1
|
0
|
1
|
0
|
|
5
|
101
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
|
6
|
110
|
1
|
1
|
0
|
1
|
0
|
1
|
1
|
|
7
|
111
|
1
|
1
|
1
|
1
|
1
|
1
|
1
|
Функции неисправностей для исходной функции имеют вид:
f=a*b+c
fl = b + c
f2 = c
f3 = a + c
f4 = c
f5 = 1
f6 = b*a
По таблице неисправностей определены проверяющие функции для каждой неисправности. Причем десятичными цифрам соответствует соответствующий номер набора, на котором различается функция работы исправной схемы и функция неисправности:
1 = 2
2 = 6
3 = 4
4 = 6
5 = 0 + 2 + 4
6 = 1 + 3 +5
Проверяющий тест для заданной релейно-контактной схемы имеет вид:
Тп = 1 • 2 • 3 • 4 • ... • 6 = 2 • 6 • 4 • 6 • (0 + 2 + 4) • (1 + 3 + 5)
Тп = 2 • 4 • 5 • 6
Словарь неисправностей для проверяющего теста имеет следующий вид (таблица 6):
Таблица 6 - Словарь неисправностей для проверяющего теста
|
Входной набор
|
F
|
f1
|
f2, f4
|
f3
|
f5
|
f6
|
|
№
|
аbс
|
|
При внесении неисправности
|
|
|
|
|
a1
|
a0, b0
|
b1
|
c1
|
c0
|
|
2
|
010
|
0
|
1
|
0
|
0
|
1
|
0
|
|
4
|
100
|
0
|
0
|
0
|
1
|
0
|
0
|
|
5
|
101
|
1
|
1
|
1
|
1
|
0
|
0
|
|
6
|
110
|
1
|
1
|
0
|
1
|
1
|
1
|
Для нахождения диагностического теста определим различающие функции i,j:
1,2 = 1,4 = 2 + 6
1,3 = 2+4
1,5 = 0+4
1,6 = 1+2+3+5
2,3 = 3,4 = 4+6
2,4 = полностью совпадают
2,5 = 0+2+4+6
2,6 = 4,6=1+3+5+6
3,5 = 0+2
3,6 = 1+3+4+5
4,5 =0+2+4+6
5,6 =0 1+2+3+4+5
Диагностический тест Тд определяется по формуле:
Тд = 1,2 • 1,3 • 1,4 • 1,5 • 1,6 •..•..•..• 5,6
После подстановки выражения для различающих функций, Тд примет вид:
Тд = (2+6) • (2+4) • (0+4) • (1+2+3+5) • (4+6) • (0+2+4+6) • (1+3+5+6 ) • (0+2) • (1+3+4+5) • • (0+2+4+6) • (0+1+2+3+4+5)
Окончательное выражение для диагностического теста Тд после упрощений примет вид:
Тд=0 • 1 • 2 • 6
Для диагностического теста составлен словарь неисправностей (таблица 7).
Таблица 7 - Словарь неисправностей для диагностического теста Тд
|
Входной набор
|
F
|
f1
|
f2, f4
|
f3
|
f5
|
f6
|
|
№
|
аbс
|
|
При внесении неисправности
|
|
|
|
|
a1
|
a0, b0
|
b1
|
c1
|
c0
|
|
0
|
000
|
0
|
0
|
0
|
0
|
1
|
0
|
|
1
|
001
|
1
|
1
|
1
|
1
|
1
|
0
|
|
2
|
010
|
0
|
1
|
0
|
0
|
1
|
0
|
|
6
|
110
|
1
|
1
|
0
|
1
|
1
|
1
|
Диагностический тест Т'д для релейно-контактной схемы будет иметь вид:
Т'д = Тп • Тд
Т'д = 2 • 4 • 5 • 6 • 0 • 1 • 2 • 6 = 0 • 1 • 2 • 4 • 5 • 6
Таблица 8 - Словарь неисправностей для диагностического теста Тд’
|
Входной набор
|
F
|
f1
|
f2, f4
|
f3
|
f5
|
f6
|
|
№
|
аbс
|
|
При внесении неисправности
|
|
|
|
|
a1
|
a0, b0
|
b1
|
c1
|
c0
|
|
0
|
000
|
0
|
0
|
0
|
0
|
1
|
0
|
|
1
|
001
|
1
|
1
|
1
|
1
|
1
|
0
|
|
2
|
010
|
0
|
1
|
0
|
0
|
1
|
0
|
|
4
|
100
|
0
|
0
|
0
|
1
|
1
|
0
|
|
5
|
101
|
1
|
1
|
1
|
1
|
1
|
0
|
|
6
|
110
|
1
|
1
|
0
|
1
|
1
|
1
|
4 Построение тестов для релейно-контактной схемы методом цепей и сечений
Для схем на релейно-контактных элементах разработан специальный метод для построения проверяющих тестов. Метод цепей и сечений позволяет отказаться от построения таблицы функций неисправностей для нахождения проверяющего теста.
Цепь - набор состояний контактов, которые обеспечивают проводимость между полюсами схемы.
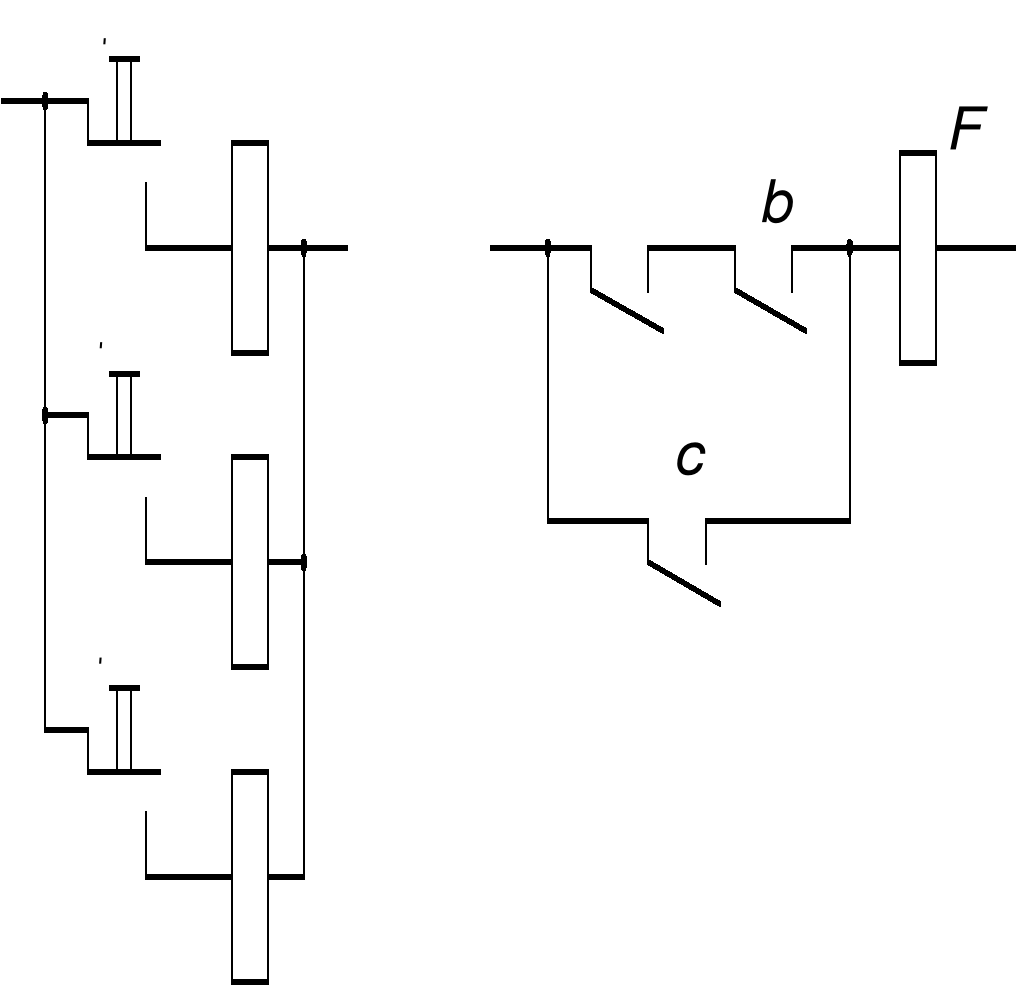
Рисунок 4 - Схема для построения проверяющего теста методом цепей и сечений
Для данной схемы можно выделить две цепи:
G1 = a • b
G2 = c
Сечение - набор состояний контактов, которые обеспечивают разрыв всех цепей схемы.
Схема на рисунке 4 имеет два сечения:
Н1 = • с
Н2 = b • c
Полное перечисление цепей и сечений однозначно задает схему [1]. Цепь урезанная на контакте (а) - набор состояний контактов для данной цепи, из которого исключено состояние контакта (а). Аналогичное определение имеет сечение, урезанное на контакте.
Цепи урезанные на контактах а, b, c соответственно примут вид:
G1/a = b G1/ b = a G3/ c = 1
Сечение, урезанное на контактах а, b, c:
H1/ a = c H1/ c = H2/ c = b H2/ b = c
Для проверки неисправности типа «разрыв» для контакта «а» необходимо создать цепь, в которую входит этот контакт, и разорвать остальные цепи. При разрыве контакта «а» будут разорваны все цепи, и схема будет в разомкнутом состоянии (реле F будет обесточено) вместо замкнутого (реле F под током). Тем самым будет зафиксирована неисправность.
Неисправность типа «разрыв» контакта «а» будет обнаружена, если на входы схемы подается такое воздействие, при котором существует хотя бы одна цепь, содержащая контакт «а» и хотя бы одно сечение, урезанное на контакте «а».
При проверке контакта «а» на неисправность типа «короткое замыкание» необходимо обеспечить разрыва всех цепей схемы и наличие цепи, разорванной на этом контакте. При отсутствии неисправности схема будет разомкнута (реле F обесточено), если есть неисправность, реле F будет под током (замкнутое состояние схемы).
Неисправность типа «короткое замыкание» контакта «а» будет обнаружена, если на входы схемы подается такое воздействие, при котором одновременно существует сечение, содержащее контакт «а» и цепь, урезанная на контакте «а».
Проверяющие функции «разрыв» (ф°) и «короткое замыкание» (ф1) для схемы:
ф°а:
G1 = a • b H1/ a = c
ф°а= a • b • c
ф°b:
G1 = a • b H2/ b = c
ф°b= a • b • c
ф°c:
G2 = c H1/ c =
ф°c= • c
ф1а:
Н1 = • с G1/a = b
ф1а= • b • c
ф1b:
Н2 = b • c G1/ b = a
ф1b= a • b • c
ф1c:
Н1 = • с G2/c = 1
ф1c= • c
Проверяющий тест для релейно-контактной схемы получается путем логического произведения найденных функций.
ф°а= a • b • c
ф°b= a • b • c
ф°c= • c
ф1а= • b • c
ф1b= a • b • c
ф1c= • c
Тп={a • b • c, • c, • b • c,a • b • c, • c}
Проверяющие тесты, найденные при помощи таблицы функций неисправностей и при помощи метода цепей и сечений, совпадают, это говорит об отсутствии ошибок при выполнении задания.
6 Проверка комбинационных логических схем
Для заданной функции схема на логических элементах в базисе И-ИЛИ-НЕ имеет вид: f=b• a+c
Рисунок 6 - Реализация заданной функции в базисе И-ИЛИ-НЕ
На схему наносятся константные неисправности:
Рисунок 7 - Схема в базисе И-ИЛИ-НЕ с нанесенными константными
неисправностями
На рисунке 8 для каждого логического элемента нанесены графы эквивалентных неисправностей и указаны отношения импликаций между неисправностями.
Рисунок 8 - Схема с нанесенными графами неисправностей
На рисунке 9 изображена схема с пронумерованными неисправностями. Неисправности нумеруют следующим образом: среди эквивалентных неисправностей нумеруют только одну, ближе размещенную к выходу. Все неисправности, к которым направлены дуги не нумеруют, если к эквивалентной неисправности направлена дуга, то ее не нумеруют.
Рисунок 9 - Схема с нанесенными графами неисправностей
В результате проведенной операции сокращается список неисправностей, которые необходимо рассмотреть для проверяющего теста.
f=a*b+c
f1=0*b+c=c
f2=0*a+c=c
f3=a*b+0= a*b
f4=1
Таблица 10 – Значения функций неисправностей
|
№
|
Входной набор
|
|
Функция неисправности
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0
|
000
|
0
|
0
|
1
|
0
|
1
|
|
1
|
001
|
1
|
1
|
1
|
0
|
1
|
|
2
|
010
|
0
|
0
|
0
|
0
|
1
|
|
3
|
011
|
1
|
1
|
1
|
0
|
1
|
|
4
|
100
|
0
|
0
|
0
|
0
|
1
|
|
5
|
101
|
1
|
1
|
1
|
0
|
1
|
|
6
|
110
|
1
|
0
|
0
|
1
|
1
|
|
7
|
111
|
1
|
1
|
1
|
1
|
1
|
По ТФН (таблица 10) определены проверяющие функции неисправностей:
1 = 6
2 = 6
3 = 1+3+5
4 = 0+2+4
Проверяющий тест для заданной схемы имеет вид:
Тп = 1 • 2 • 3 • 4
Тп = 6 • 6 • (1+3+5) • (0+2+4)
Тп=6 • 1 • 0
Таблица 11 – Словарь неисправностей для проверяющего теста
|
Входной набор
|
F
|
f1, f2
|
f3
|
f4
|
|
№
|
аbс
|
|
при неисправности
|
|
0
|
000
|
0
|
0
|
0
|
1
|
|
1
|
001
|
1
|
1
|
0
|
1
|
|
6
|
110
|
1
|
0
|
1
|
1
|
При нахождении диагностического теста не учитываются отношения импликации между неисправностями, следовательно, число неисправностей увеличивается.
Рисунок 10 - Схема для построения диагностического теста комбинационной схемы
Таблица 12 - ТФН для построения диагностического теста
|
Входной набор
|
F
|
f1
|
f2
|
f3
|
f4
|
f5
|
f6
|
|
№
|
аbс
|
|
при неисправности
|
|
0
|
000
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
1
|
001
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
|
2
|
010
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
3
|
011
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
|
4
|
100
|
0
|
0
|
0
|
0
|
0
|
1
|
0
|
|
5
|
101
|
1
|
1
|
1
|
0
|
1
|
1
|
0
|
|
6
|
110
|
1
|
0
|
0
|
1
|
0
|
1
|
0
|
|
7
|
111
|
1
|
1
|
1
|
1
|
1
|
1
|
0
|
f=a*b+c
f1=0*b+c=c
f2= a *0 +c=c
f3=a*b+0= a*b
f4=0+c=c
f5=1
f6=0
1 = 6
2 = 6
3 = 1+3+5
4 = 6
5 = 0+2+4
6 = 1+3+5+6+7
Для нахождения диагностического теста определим различающие функции i,j:
1,2 = 1,4 = 2,4 = полностью совпадают
1,3 = 3,4 = 1+3+5+6
1,5 = 2,5 = 4,5 =0+2+4+6
1,6 = 2,6 = 4,6= 1+3+5+7
2,3 = 1+3+5
3,5 = 0+1+2+3+4+5
3,6 = 6+7
5,6 =0 1+2+3+4+5+6+7
После того, как найдены все различающие функции, можно составить диагностический тест для комбинационной схемы на логических элементах.
Тд = 1,2 • 1,3 • 1,4 • 1,5 • 1,6 •..•..•..• 5,6
Тд = (1+3+5+6) • (0+2+4+6) • (1+3+5+7) • (1+3+5) • (0+1+2+3+4+5) •( 6+7) •
• (0 1+2+3+4+5+6+7)
Выражение для диагностического теста содержит минимальный тест:
Тд = 1 • 2 • 7
Таблица 13 - Словарь неисправностей диагностического теста
|
Входной набор
|
F
|
f1,f2,f4
|
f3
|
f5
|
f6
|
|
№
|
аbс
|
|
при неисправности
|
|
1
|
000
|
1
|
1
|
0
|
1
|
0
|
|
2
|
011
|
0
|
0
|
0
|
1
|
0
|
|
7
|
101
|
1
|
1
|
1
|
1
|
0
|
Заключение
В первом разделе контрольной работы исследована работа непрерывной системы и составлен проверяющий тест. Проверяющий тест необходим для того, чтобы определить есть в системе неисправность или нет. Для рассматриваемого варианта проверяющий тест равен 8. То есть, чтобы узнать, исправна система или нет, нет нужды проверять выход каждого элемента, достаточно проверить сигнал на выходе элемента 8.
Во втором разделе контрольной работы составлен диагностический тест для непрерывной системы. Диагностический тест используется для точного отыскания отказавшего элемента. Диагностический тест Тд используется, когда уже известно, что система неисправна, с помощью этого теста находят какой конкретно элемент вышел из стоя. В используемой модели предполагается, что одновременно может выйти из стоя только один элемент. Тд' используется, когда неизвестно, в каком состоянии находится система. То есть при помощи теста Тд' можно во-первых проверить, исправна система или нет, и если система неисправна, то определить какой именно элемент вышел из строя. В рассматриваемом варианте Тд' равен , т.е. необходимо выходы элементов Э2, Э4, Э5, Э6, Э7, Э8.
В третьем разделе контрольной работы составлены проверяющий и диагностический тесты для релейной схемы. Получен проверяющий тест Тп = 2 • 4 • 5 • 6. Данный тест означает, что для того, чтобы проверить, исправна схема или нет, нужно подать на ее входы последовательно наборы 2, 4, 5 и 6, и контролировать состояние реле F. Диагностический тест ( Тд = 0 • 1 • 2 • 6) определяет, какие наборы нужно подать на вход схемы, чтобы определить, какой элемент неисправен (рассмотрены два типа неисправностей - замыкание контактов или обрыв контактов). Диагностический тест Тд используется, если известно, что система неисправна, и необходимо определить конкретное место неисправности.
Метод цепей и сечений рассмотрен в четвертом разделе контрольной работы. Данный метод разработан специально для диагностирования релейных схем. Проверяющий тест, найденный при помощи метода цепей и сечений, и аналитически совпадают.
Шестой раздел контрольной работы посвящены проверке схем на логических элементах. Определены константные неисправности, рассмотрены эквивалентные и импликантные неисправности, составлены проверяющий и диагностический тест для логической схемы.
Библиографический список
1. В.В. Сапожников, Вл. В. Сапожников. Основы технической диагностики. М.: Маршрут, 2004. - 318 с.
2. Пархоменко П.П., Согомонян Е.С. Основы технической диагностики. - М.: Энергоиздат, 1981.
3. Кучер В.Я. Основы технической диагностики и теории надежности. Письменные лекции. СПб. СЗТУ. 2004. 48 с.
4. Сафарбаков А.М. Основы технической диагностики деталей и оборудования. Учебное пособие / А.М.Сафарбаков, А.В.Лукьянов, С.В.Пахомов. - Ч.1. Иркутск: ИрГУПС. 2007. 128 с.
Надежность и эффективность в технике. Справочник. Том 9./ под ред. Клюева.
EMBED Visio.Drawing.11 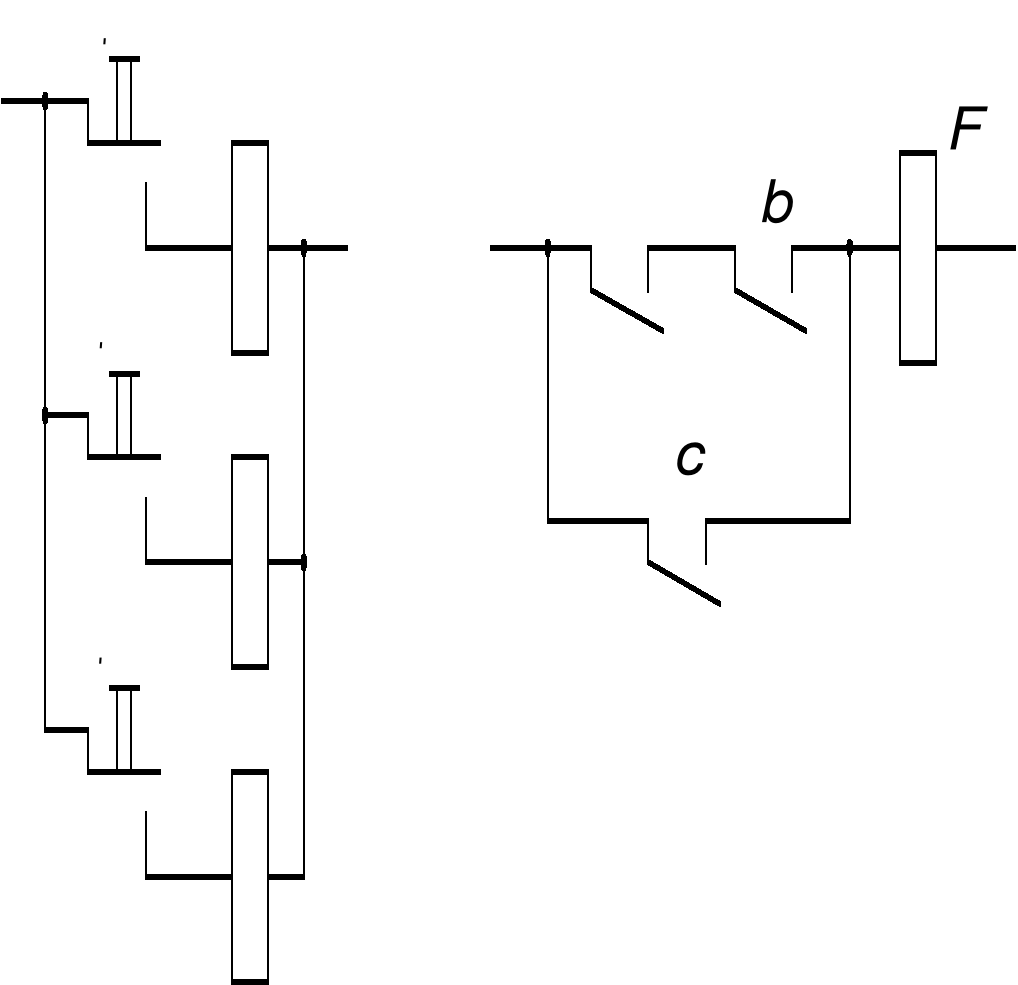
Построение проверяющего теста для логической модели непрерывной системы