Программирование и исследование алгоритмов вычисления определенных интегралов

Пояснительная записка

К курсовой работе:

“Программирование и исследование алгоритмов вычисления определенных интегралов”

Содержание:

Введение

На практике часто возникает необходимость вычислить определённый интеграл. Если интеграл берётся в алгебраических функциях, то всё в порядке и взять его вручную не представляет труда. А если интеграл не берётся в алгебраических функциях или просто их очень много, то приходится прибегать к помощи компьютерной техники. Существуют несколько способов вычисления определённых интегралов на ЭВМ, причем абсолютно все эти способы получают лишь приближённые значения. В этой работе мы рассмотрим два метода вычисления: метод трапеций и метод Симпсона (метод парабол).

Метод трапеций

Пусть Y=, где - интегрируемая функция, непрерывная на отрезке . Для наглядности будем предполагать, что положительна на отрезке . В этом случае Y представляет собой площадь криволинейной трапеции, ограниченной линиями: ,,,. Выберем произвольное натуральное число и разобьём отрезок на равных отрезков при помощи точек: , , , , …, . Прямые разбивают нашу трапецию на полосок. Каждая полоса имеет граничные вертикали: и . Соединим прямой те точки, в которых эти вертикали пересекают интегрируемую функцию . В результате площадь каждой полоски приблизительно стала равна площади обычной прямолинейной трапеции (см. рис. 1).

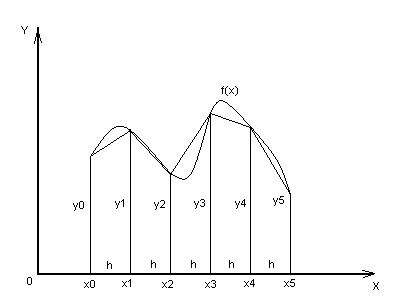
Рис. 1

Площадь самой левой полоски приближённо равна площади самой левой трапеции, а именно: . Из математических соображений и , а высота трапеции . Значит . Площади всех следующих полосок выразятся аналогичным способом и составят: , , , … , . Чтобы найти площадь интересующей нас криволинейной трапеции необходимо сложить площади всех полосок, которые в свою очередь приближённо равны площадям соответствующих прямолинейных трапеций. Следовательно, площадь криволинейной трапеции, а значит и численное значение заданного интеграла , равны

.

Эту формулу можно записать в другом виде, используя математические сокращения и утверждение, что - длина одного из равных отрезков или высота каждой прямолинейной трапеции:

(1).

Данная формула называется формулой трапеций. Её точность зависит от . Чем больше количество разбиений отрезка интегрирования, тем выше точность вычислений.

Теперь перейдём к заданию: нам необходимо найти толщину слоя меди, выделившейся в результате электролиза водного раствора хлорида меди (II) на катоде. Известна зависимость силы тока от времени . Отсюда имеем . Фактически нам надо оформить функцию вычисления заданного определённого интеграла на Visual Basic 6.0 методом трапеций. Назовём функцию metod_trapec. При вызове функции задаваемыми параметрами будут down_predel=0 – нижний предел интегрирования, up_predel – верхний предел интегрирования (время наблюдения), chislo_razb – число разбиений отрезка интегрирования. Программный код функции будет выглядеть так:

__________

Public Function metod_trapec(ByVal a As Single, ByVal b As Single, ByVal n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

h = (b - a) / n

s = (F(a, Io) + F(b, Io)) * h / 2

For i = 1 To n - 1

s = s + F(a + i * h, Io) * h

Next i

metod_trapec = s

End Function

__________

Фактические параметры down_predel, up_predel, chislo_razb соответствуют формальным параметрам a, b, n. В основе лежит формула трапеций (1), записанная по-другому:

.

Накапливаем сумму, результат которой и будет искомым значением определённого интеграла. Далее присваиваем имени функции значение переменной s.

Метод Симпсона (метод парабол)

Пусть Y=, где - интегрируемая функция, непрерывная на отрезке . Для наглядности будем предполагать, что положительна на отрезке . В этом случае Y представляет собой площадь криволинейной трапеции, ограниченной линиями: ,,,. Выберем произвольное натуральное чётное число и разобьём отрезок на равных отрезков при помощи точек: ,,,, … ,. Прямые разбивают нашу трапецию на полосок. Каждая полоса имеет граничные вертикали: и . Отметим точки, в которых эти вертикали пересекают интегрируемую функцию . В результате получились точки: , , , …,. На всём отрезке интегрирования через точки и проведём графики квадратичных функций. В результате получилось, что площадь двух соседних полосок, ограниченных прямыми и приближённо равна площади под параболой, проведённой через точки и (см. рис. 2).

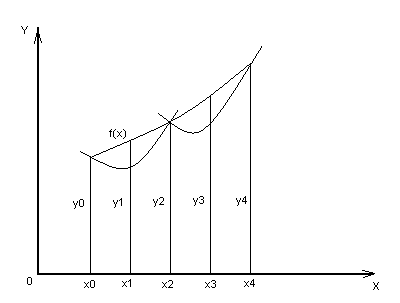
Рис. 2

Вычислим площадь под параболой, проходящей через точки и . Уравнение параболы имеет общий вид . Площадь под параболой:

(2).

Парабола проходит через три точки , и , где . Решая систему из трёх уравнений,

получаем: .

Подставляем в формулу (2). Отсюда следует, что , где . Распространяем на весь отрезок:

. Запишем с применением математических операндов:

(3).

Данная формула называется формулой Симпсона. Её точность зависит от . Чем больше количество разбиений отрезка интегрирования, тем выше точность вычислений.

Фактически нам надо оформить функцию вычисления заданного определённого интеграла на Visual Basic 6.0 методом Симпсона. Назовём функцию metod_Simpson. При вызове функции задаваемыми параметрами будут down_predel – нижний предел интегрирования, up_predel – верхний предел интегрирования, chislo_razb – число разбиений отрезка интегрирования. Программный код функции будет выглядеть так:

__________

Public Function metod_Simpson(ByVal a1 As Single, ByVal b1 As Single, ByVal n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

Dim x As Single

h = (b1 - a1) / n

s = F(a1, Io) + F(b1, Io) + 4 * F(a1 + h, Io)

For i = 1 To Int(n / 2) - 1

x = a1 + 2 * h * i

s = s + 2 * F(x, Io) + 4 * F(x + h, Io)

Next i

metod_Simpson = s * h / 3

End Function

__________

Фактические параметры down_predel, up_predel, chislo_razb соответствуют формальным параметрам a, b, n. В основе лежит формула Симпсона. Сумма первых трёх слагаемых в этой формуле является начальным значением переменной . Далее пробегаем по всему отрезку интегрирования, кроме конечных полосок, и накапливаем сумму. В конце умножаем её на . Результат и будет искомым значением определённого интеграла. Далее присваиваем имени функции значение переменной .

Создание приложения

При запуске Microsoft Visual Basic 6.0 автоматически выскакивает окно с предложением создать новый проект Standard EXE. Нажимаем OK. Начнём создание проекта с титульного листа. Для этого в меню Project выберем команду Add Form. В появившемся диалоговом окне выберем Dialog и нажмем OK. В открывшейся форме расставим объекты: Label1, Label2, ... , Label8, как показано на рисунке (см. рис. 3).

Рис. 3 Титульный лист

Присвоим свойству Caption значение “Титульный лист”. На кнопку Вход напишем следующий программный код:

__________

Private Sub OKButton_Click()

Unload Dialog

Form1.Show

End Sub

__________

При щелчке на кнопке Вход из памяти выгружается форма Dialog и загружается базовая форма, служащая начальной точкой для всех операций с программой, форма Form1. Для того, чтобы создать форму Form1, в меню Project выполним команду Add Form. В появившемся диалоговом окне выберем Form и нажмем OK. Щёлкнем правой кнопкой мыши на панели инструментов, выберем вкладку Components, загрузим нестандартные инструменты, которые понадобятся в будущем: Microsoft Windows Common Controls 6.0. Присвоим свойству Caption формы Form1 значение “Курсовой проект - Тема 7 вариант 9 (нахождение толщины слоя)”. Создадим меню для проекта. Для этого в меню Tools выполним команду Menu Editor. В появившемся диалоговом окне напишем названия пунктов меню и названия процедур, которые будут запускаться при выполнении команд меню. Редактор меню с введёнными именами представлен на рисунке (см. рис. 4).

Рис. 4 Редактор меню

Опишем, какие процедуры выполняются в каждом пункте меню.

1. MnuFileExit – осуществляет выход из приложения.

__________

Private Sub MnuFileExit_Click()

End

End Sub

__________

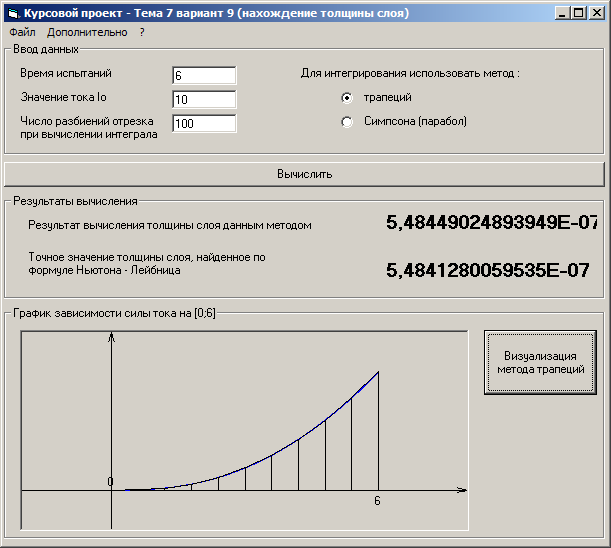
Рис. 5

2. MnuFileSave_rez – осуществляет сохранение результата эксперимента. Результат сохраняется в файле log.txt, куда записывается используемый метод, нижний предел интегрирования, верхний предел интегрирования, количество разбиений отрезка интегрирования, вычисленное значение интеграла, истинное значение интеграла, погрешность вычислений.

__________

Private Sub MnuFileSave_rez_Click()

Dim metod As String

If Option1.Value Then

metod = "Метод трапеций"

Else

metod = "Метод Симпсона"

End If

Open "log.txt" For Output As #1

Print #1, "ОТЧЕТ ПО ВЫПОЛНЕННЫМ ВЫЧИСЛЕНИЯМ"

Print #1, "Используемый метод:", metod

Print #1, "Время наблюдения:", up_predel

Print #1, "Количество разбиений отрезка интегрирования:", chislo_razb

Print #1, "Вычисленное значение интеграла:", znach_integrala

Print #1, "Истинное значение интеграла:", istinnoe_znach_integrala(down_predel, up_predel)

Print #1, "Погрешность вычисления:", Abs(istinnoe_znach_integrala(down_predel, up_predel) - znach_integrala)

Close #1

a = MsgBox("Отчет сохранен успешно!" & Chr(10) & Chr(13) & "для просмотра отчета: Файл>>Просмотр отчета", , "Отчет")

End Sub

__________

3. MnuFileLook_rez – осуществляет вывод на экран ранее сохранённого результата, если предварительно его сохранили.

___________

Private Sub MnuFileOpen_rez_Click()

Form3.Show 1, Form1

End Sub

____________

При выполнении этой процедуры загружается форма Form3, на которой находится объект PictureBox1, в который выводится сохраненный отчет. Для вывода отчета существует кнопка «Загрузить отчет». Программный код Form3:

__________

Dim stroka As String

Private Sub cmdBack_Click()

Unload Form3

End Sub

Private Sub cmdLoadLog_Click()

On Error GoTo Err

Open "log.txt" For Input As #1

For i = 1 To 8

Line Input #1, stroka

Picture1.Print stroka

Next i

Close #1

Err:

If Err.Number = 53 Then

a = MsgBox("Невозможно загрузить результат, ранее не было сохранено результатов!", , "Ошибка")

Unload Form3

End If

End Sub

__________

В процедуре cmdLoadLog_Click(), проверяется существует ли файл с отчетом, если да то происходит открытие указанного файла, построчное считывание из него и вывод в объект Picture1, если такого файла нет, то об этом пользователя об этом уведомляют. Готовая форма Form3 изображена на рисунке (см. рис. 6). При щелчке на кнопке «Назад» (на объекте cmdBack) происходит выгрузка формы Form3 из оперативной памяти.

Рис. 6

4. MnuHelpAbout – выводит на экран информацию о программе. Вывод осуществляется с помощью формы Dialog2.

__________

Private Sub MnuHelpAbout_Click()

Dialog2.Show 1, Form1

End Sub

__________

При щелчке на кнопке «OK» (объект Command1) происходит выгрузка формы Dialog2 из оперативной памяти. Готовая форма Dialog2 изображена на рисунке (см. рис. 7).

Программный код формы Dialog2:

__________

Private Sub OKButton_Click()

Unload Dialog2

End Sub

__________

5. MnuMatemFormula – выводит на экран ручной вывод формулы заданного определённого интеграла. Вывод осуществляется с помощью формы Dialog1.

__________

Private Sub MnuMatemFormula_click()

Dialog1.Show 1, Form1

End Sub

__________

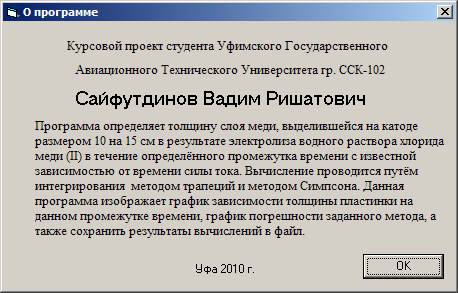
Рис. 7

6. MnuMatemGrafik_Pogreshn – выводит на экран форму Form2. В ней можно построить график зависимости погрешности заданного метода от количества разбиений отрезка интегрирования.

__________

Private Sub MnuMatemGrafik_Pogreshn_click()

Form2.Show 1, Form1

End Sub

__________

Программный код формы Form2:

Dim i As Long

Dim a As Single, b As Single, n As Long

Public Io As Single

Public Function istinnoe_znach_integrala(a As Single, b As Single) As Double

a0 = 0.15: b0 = 0.1: po = 8600: faradey = 96500: M = 64.5 * 10 ^ (-3)

istinnoe_znach_integrala = Io * M / (2 * 2 * faradey * po * a0 * b0) * (b ^ 3 / 3 - 3 / 2 * b ^ 2 + 9 * b - 27 * Log((b + 3) / 3))

End Function

Public Function metod_trapec(ByVal a As Single, ByVal b As Single, ByVal n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

h = (b - a) / n

s = (F(a, Io) + F(b, Io)) * h / 2

For i = 1 To n - 1

s = s + F(a + i * h, Io) * h

Next i

metod_trapec = s

End Function

Public Function metod_Simpson(ByVal a1 As Single, ByVal b1 As Single, ByVal n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

Dim x As Single

h = (b1 - a1) / n

s = F(a1, Io) + F(b1, Io) + 4 * F(a1 + h, Io)

For i = 1 To Int(n / 2) - 1

x = a1 + 2 * h * i

s = s + 2 * F(x, Io) + 4 * F(x + h, Io)

Next i

metod_Simpson = s * h / 3

End Function

Private Sub Command1_Click()

koeff = 2 * 10 ^ 9

Picture1.Cls

Io = Form1.Text2

a = 0

b = Val(Text3.Text)

N1 = Val(Text4.Text)

N2 = Val(Text5.Text)

save = Text1

If Check1.Value = vbChecked Then

Open save For Output As #1

Print #1, "количество разбиений"; " "; "погрешность метода трапеций"; " "; "погрешность метода Симпсона"

Close #1

End If

s = istinnoe_znach_integrala(a, b)

X0 = N1

Y1 = 250 * koeff * Abs(metod_Simpson(a, b, 10) - s)

Y2 = koeff * Abs(metod_trapec(a, b, 10) - s)

Picture1.Scale (-20, 10)-(N2 + 10, -2)

For n = N1 To N2 Step 2

ss = metod_Simpson(a, b, n)

st = metod_trapec(a, b, n)

pogtr = Abs(s - st)

POGss = Abs(s - ss)

If Check1.Value = vbChecked Then

Open save For Append As #1

Print #1, " "; n, " "; pogtr, " "; POGss

Close #1

End If

Picture1.Line (X0, Y1)-(n, 250 * koeff * POGss), RGB(255, 0, 0)

Picture1.Line (X0, Y2)-(n, koeff * pogtr), RGB(0, 0, 255)

Picture1.Line (-50, 0)-((N2 + 50), 0)

Picture1.Line (0, -30)-(0, 20)

X0 = n

Y1 = 250 * koeff * POGss

Y2 = koeff * pogtr

If n <= 30 And n Mod 10 = 0 Then

Picture1.PSet (-16, koeff * pogtr)

Picture1.Print Format(pogtr, "#.##e-#")

Picture1.Line (-20, koeff * pogtr)-(210, koeff * pogtr), RGB(0, 255, 0)

End If

Next n

For i = 10 To N2 + 50 Step 10

Picture1.PSet (i, 0)

Picture1.Print i

Picture1.Line (i, -10)-(i, N2), RGB(0, 255, 0)

Next i

End Sub

Private Sub Command2_Click()

Unload Form2

End Sub

__________

Вычисляем погрешность, отнимая полученное значение интеграла от истинного, вычисляемого функцией istinnoe_znach_integrala, находящейся в форме Form1. Затем строим точку на объекте Picture1. При щелчке на кнопке «Назад» (объект Command2) форма Form2 выгружается из оперативной памяти. Готовая форма Form2 изображена на рисунке (см. рис. 8).

Мы рассмотрели все функции и процедуры, используемые в проекте. Теперь можно рассмотреть работу формы Form1. При щелчке на кнопке «Произвести вычисления» (объект Command1) происходит считывание из текстовых полей заданных параметров: время наблюдения, начальное значение силы тока, число разбиений отрезка интегрирования. Далее следует проверка входных данных. Далее идет вычисление интеграла и вывод результата, а также построение графика интегрируемой зависимости силы тока на заданном участке времени. График строится таким образом, что он всегда выводится в центре объекта Picture1. Это достигается тем, что система координат вводится исходя из максимального и минимального значения функции и из величины концов отрезка интегрирования. Для этого мы и ищем y_max и y_min. Далее ставим подписи на концах отрезка интегрирования.

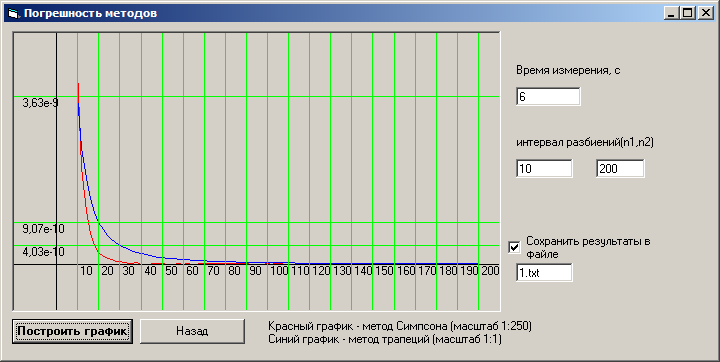
Рис. 8

Программный код формы Form1:

__________

Dim down_predel As Single

Dim up_predel As Single

Dim znach_integrala As Double

Dim chislo_razb As Long

Dim i As Single

'Public Io As Single

Dim y_max As Single

Dim y_min As Single

'Функция вычисления истинного значения интеграла по формуле Ньютона-Лейбница.

Public Function istinnoe_znach_integrala(a As Single, b As Single) As Double

a0 = 0.15: b0 = 0.1: po = 8600: faradey = 96500: M = 64.5 * 10 ^ (-3)

istinnoe_znach_integrala = Io * M / (2 * 2 * faradey * po * a0 * b0) * (b ^ 3 / 3 - 3 / 2 * b ^ 2 + 9 * b - 27 * Log((b + 3) / 3))

End Function

'Функция вычисления интеграла методом трапеций.

Public Function metod_trapec(a As Single, b As Single, n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

h = (b - a) / n

s = (F(a, Io) + F(b, Io)) * h / 2

For i = 1 To n - 1

s = s + F(a + i * h, Io) * h

Next i

metod_trapec = s

End Function

'Функция вычисления интеграла методом Симпсона.

Public Function metod_Simpson(a As Single, b As Single, n As Long) As Double

Dim h As Single

Dim s As Double

Dim i As Long

Dim x As Single

h = (b - a) / n

s = F(a, Io) + F(b, Io) + 4 * F(a + h, Io)

For i = 1 To Int(n / 2) - 1

x = a + 2 * h * i

s = s + 2 * F(x, Io) + 4 * F(x + h, Io)

Next i

metod_Simpson = s * h / 3

End Function

Private Sub Command1_Click()

For i = 0 To 9

Picture3.Line (down_predel + i * (up_predel - down_predel) / 10, 0)-(down_predel + i * (up_predel - down_predel) / 10, F(down_predel + i * (up_predel - down_predel) / 10, Io))

Picture3.Line (down_predel + i * (up_predel - down_predel) / 10, F(down_predel + i * (up_predel - down_predel) / 10, Io))-(down_predel + (i + 1) * (up_predel - down_predel) / 10, F(down_predel + (i + 1) * (up_predel - down_predel) / 10, Io))

Picture3.Line (down_predel + (i + 1) * (up_predel - down_predel) / 10, F(down_predel + (i + 1) * (up_predel - down_predel) / 10, Io))-(down_predel + (i + 1) * (up_predel - down_predel) / 10, 0)

Next i

End Sub

'Функция выхода из программы

Private Sub MnuFileExit_Click()

End

End Sub

Private Sub MnuFileOpen_rez_Click()

Form3.Show 1, Form1

End Sub

'Сохранения результата в файл log.txt

Private Sub MnuFileSave_rez_Click()

Dim metod As String

If Option1.Value Then

metod = "Метод трапеций"

Else

metod = "Метод Симпсона"

End If

Open "log.txt" For Output As #1

Print #1, "ОТЧЕТ ПО ВЫПОЛНЕННЫМ ВЫЧИСЛЕНИЯМ"

Print #1, "Используемый метод:", metod

Print #1, "Время наблюдения:", up_predel

Print #1, "Количество разбиений отрезка интегрирования:", chislo_razb

Print #1, "Вычисленное значение толщины слоя:", znach_integrala

Print #1, "Истинное значение толщины слоя:", istinnoe_znach_integrala(down_predel, up_predel)

Print #1, "Погрешность вычисления:", Abs(istinnoe_znach_integrala(down_predel, up_predel) - znach_integrala)

Close #1

a = MsgBox("Отчет сохранен успешно!" & Chr(10) & Chr(13) & "для просмотра отчета: Файл>>Просмотр отчета", , "Отчет")

End Sub

Private Sub MnuHelpAbout_Click()

Dialog2.Show 1, Form1

End Sub

Private Sub MnuMatemGrafik_Pogreshn_click()

Form2.Show 1, Form1

End Sub

Private Sub cmd_chet_Click()

down_predel = 0

up_predel = Val(Text1.Text)

Io = Val(Text2.Text)

chislo_razb = Val(Text3.Text)

Picture1.Cls

Picture2.Cls

If chislo_razb <= 0 Then

MsgBox "Число разбиений отрезка интегрирования должно быть больше нуля.", vbCritical, "Внимание!"

Exit Sub

End If

If up_predel < 0 Then

MsgBox "Время испытаний не может быть отрицательным", vbCritical, "Внимание!"

Exit Sub

End If

If Option1.Value Then

znach_integrala = metod_trapec(down_predel, up_predel, chislo_razb)

Else

znach_integrala = metod_Simpson(down_predel, up_predel, chislo_razb)

If chislo_razb Mod 2 = 1 Then

MsgBox "Число разбиений отрезка интегрирования при данном методе должно быть четным.", vbCritical, "Внимание!"

Exit Sub

End If

End If

Frame3.Caption = "График зависимости силы тока на [" & down_predel & ";" & up_predel & "]"

Picture1.Print znach_integrala

Picture2.Print istinnoe_znach_integrala(down_predel, up_predel)

y_max = F(down_predel, Io)

y_min = F(down_predel, Io)

For i = down_predel To up_predel Step 0.001

If F(i, Io) < y_min Then

y_min = F(i, Io)

End If

If F(i, Io) > y_max Then

y_max = F(i, Io)

End If

Next i

Picture3.Cls

Picture3.DrawWidth = 1

Picture3.Scale (down_predel - (up_predel - down_predel) / 3, y_max + (y_max - y_min) / 3)-(up_predel + (up_predel - down_predel) / 3, y_min - (y_max - y_min) / 3)

'Рисование осей

Picture3.Line (down_predel - (up_predel - down_predel) / 3, 0)-(up_predel + (up_predel - down_predel) / 3, 0)

Picture3.Line (0, y_max + (y_max - y_min) / 3)-(0, y_min - (y_max - y_min) / 3)

'Стрелка на оси OX

Picture3.Line (up_predel + (up_predel - down_predel) / 3, 0)-(up_predel + (up_predel - down_predel) / 3 - (up_predel - down_predel) / 24, (y_max - y_min) / 50)

Picture3.Line (up_predel + (up_predel - down_predel) / 3, 0)-(up_predel + (up_predel - down_predel) / 3 - (up_predel - down_predel) / 24, -(y_max - y_min) / 50)

'Стрелка на оси OY

Picture3.Line (0, y_max + (y_max - y_min) / 3)-(-(up_predel - down_predel) / 100, y_max + (y_max - y_min) / 3 - (y_max - y_min) / 12)

Picture3.Line (0, y_max + (y_max - y_min) / 3)-((up_predel - down_predel) / 100, y_max + (y_max - y_min) / 3 - (y_max - y_min) / 12)

'Построение графика

Picture3.Line (down_predel, F(down_predel, Io))-(down_predel, 0), RGB(255, 0, 0)

Picture3.Line (up_predel, F(up_predel, Io))-(up_predel, 0), RGB(255, 0, 0)

For i = down_predel To up_predel Step 0.001

Picture3.PSet (i, F(i, Io)), RGB(0, 0, 255)

Next i

'Левая подпись

Picture3.CurrentX = down_predel - (up_predel - down_predel) / 40

If F(down_predel, Io) > 0 Then

Picture3.CurrentY = -(y_max - y_min) / 25

Else

Picture3.CurrentY = (y_max - y_min) / 8

End If

Picture3.Print down_predel

'Правая подпись

Picture3.CurrentX = up_predel - (up_predel - down_predel) / 40

If F(up_predel, Io) > 0 Then

Picture3.CurrentY = -(y_max - y_min) / 25

Else

Picture3.CurrentY = (y_max - y_min) / 8

End If

Picture3.Print up_predel

End Sub

__________

Заключение

Часто возникает необходимость вычислить определённый интеграл. Если интеграл берётся в алгебраических функциях, то всё в порядке и взять его вручную не представляет труда. А если интеграл не берётся в алгебраических функциях или просто их очень много, то приходится прибегать к помощи компьютерной техники. Существуют несколько способов вычисления определённых интегралов на ЭВМ, причем абсолютно все эти способы получают лишь приближённые значения. В этой работе мы рассмотрим два метода вычисления: метод трапеций и метод Симпсона (метод парабол).

Список использованной литературы:

1. Мастер – Самоучитель по Visual Basic 6.0 AlexSoft 2010 г.

2. Информатика. Высшая школа. Острейковский В. А. 2009 г.

Программирование и исследование алгоритмов вычисления определенных интегралов