Двумерные и многомерные случайные величины

Лекция 5. Двумерные и многомерные случайные величины

Двумерная СВ, совместная функция распределения и ее свойства. Дискретная двумерная СВ. Непрерывная двумерная СВ. Независимые случайные величины. Ковариация и коэффициент корреляции СВ, их свойства. Условное математическое ожидание. Регрессия.

ОЛ-1 гл 5, 7, 8.

Определение. Совокупность случайных величин X1 = X1(), .... Хп = Хn(), заданных на одном и той же вероятностном пространстве (, B, Р), называют многомерной (n-мерной) случайной величиной, или n-мерным случайным вектором. При этом сами случайные величины Х1, Х2, ..., Хп называют координатами случайного вектора. В частности, при n = 1 говорят об одномерной, при n = 2 двумерной случайной величине (или двумерном случайном векторе).

Пример. Отклонение точки разрыва снаряда от точки прицеливания при стрельбе по плоской цели можно задать двумерной случайной величиной (X, Y), где X отклонение по дальности, а Y отклонение в боковом направлении.

Определение. Функцией распределения (вероятностей)

(n-мерного) случайного вектора называют функцию, значение которой в точке равно вероятности совместного осуществления (пересечения) событий {X1 < x1}, ..., {Xn < xn}, т.е.

Функцию распределения называют также совместной (n-мерной) функцией распределения случайных величин Х1, Х2, ..., Хп.

Теорема. Двумерная функция распределения удовлетворяет следующим свойствам.

1. 0  F(x1, x2)  1.

2. F(x1, x2) неубывающая функция по каждому из аргументов х1 и х2.

3. .

4. .

5. .

6. F(x1, x2) непрерывная слева в любой точке по каждому из аргументов x1 и x2 функция.

7. , .

Доказательство. Утверждения 1 и 2 доказываются точно так же, как и в одномерном случае. 3. События {Х1 < } и {Х2 < } являются невозможными, а пересечение невозможного события с любым событием, как известно, также невозможное событие, вероятность которого равна нулю. Отсюда с учетом определения вытекает утверждение 3. Аналогично из того, что события {Х1 < +} и {Х2 < +} так же, как и их пересечение, являются достоверными, вероятность которых равна единице, вытекает утверждение 4. 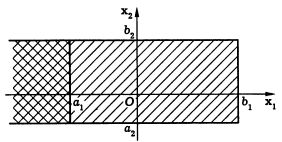Чтобы найти вероятность попадания двумерной случайной величины (Х1, Х2) в прямоугольник (на рис. заштрихован), сначала определим вероятность попадания в полуполосу (отмечена двойной штриховкой). Но эта вероятность представляет собой вероятность попадания в квадрант за вычетом вероятности попадания в квадрант т.е. Теперь осталось заметить, что вероятность попадания в прямоугольник совпадает с вероятностью попадания в полуполосу , из которой вычитается вероятность попадания в полуполосу , равная . Окончательно получим утверждение 5. Подобно одномерному случаю доказывается и утверждение 6. Наконец, событие {Х2 < +} является достоверным, поэтому

Утверждение 7 устанавливает естественную связь между двумерной функцией распределения случайного вектора (Х1, Х2) и функциями и , которые называют одномерными (говорят также частными, или маргинальными) функциями распределения случайных величин X1 и Х2.

Дискретные двумерные случайные величины

Определение. Двумерную случайную величину (X, Y) называют дискретной, если каждая из случайных величин X и Y является дискретной.

Как и в одномерном случае, распределение двумерной дискретной случайной величины естественно описать с помощью перечисления всевозможных пар (xi, yi) значений координат случайного вектора (X, Y) и соответствующих вероятностей, с которыми эти пары значений принимают случайные величины X и Y.

Для простоты ограничимся конечным множеством возможных значений, когда случайная величина X может принимать только значения х1, ..., хп, Y значения y1, ..., yп. Такое перечисление удобно представить в виде таблицы.

Используя табл., нетрудно определить совместную функцию распределения FX,Y(x, y). Ясно, что для этого необходимо просуммировать рij по всем тем значениям i и j, для которых xi < х, yj < у, т.е.

Пример. В соответствии со схемой Бернулли с вероятностью успеха р и вероятностью неудачи q = 1  р проводятся два испытания. Выпишем распределение двумерного случайного вектора (X1, Х2), где Xi, i = 1,2, число успехов в i-м испытании. Каждая из случайных величин Х1 и Х2 может принимать два значения: 0 или 1.

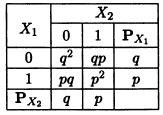
Непрерывные случайные величины

Определение. Непрерывной двумерной случайной величиной (X, Y) называют такую двумерную случайную величину (X, Y), совместную функцию распределения которой можно представить в виде сходящегося несобственного интеграла:

Функцию называют совместной двумерной плотностью распределения случайных величин X и Y, или плотностью распределения случайного вектора (X, Y).

Так же как и в одномерном случае, будем предполагать, что непрерывная (или непрерывная за исключением отдельных точек или линий) функция по обоим аргументам. Тогда в соответствии с определением непрерывной случайной величины и теоремой о дифференцировании интеграла с переменным верхним пределом совместная плотность распределения представляет собой (в точках ее непрерывности) вторую смешанную производную совместной функции распределения:

Теорема. Двумерная плотность распределения обладает следующими свойствами:

l) 2)

3)

4)

5) ; 6)

7) ; 8)

Доказательство. Свойства 15 аналогичны свойствам одномерной плотности распределения. Свойство 6 является обобщением свойства 2. Докажем утверждения 7 и 8. Из свойства 7 двумерной функции распределения и определения двумерной плотности распределения вытекает: откуда, дифференцируя интегралы по переменному верхнему пределу, получаем утверждение 7 для одномерных (частных, маргинальных) плотностей распределения рX(х) и pY(y) случайных величин X и Y.

Определение. Случайные величины X и Y называют независимыми, если совместная функция распределения FX,Y(х, у) является произведением одномерных функций распределения FX(x) и FY(y): FX,Y(х, у) = FX(x)FY(y). В противном случае случайные величины называют зависимыми.

Теорема. Для того чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы для всех х и у pX,Y(х, у) = pX(x)pY(y).

Доказательство. Пусть случайные величины X и Y независимые. Тогда, согласно определению, FX,Y(х, у) = FX(x)FY(y). С учетом свойств совместной плотности распределения имеем Тем самым необходимость утверждения доказана. Для доказательства достаточности следует воспользоваться определением двумерной плотности распределения и определением независимости случайных величин

Теорема. Дискретные случайные величины X и Y являются независимыми тогда и только тогда, когда для всех возможных значений xi и yi:

Определение. Ковариацией (корреляционным моментом) cov(X1, X2) случайных величин X1 и X2 называют математическое ожидание произведения случайных величин и

Для дискретных случайных величин X1 и X2

для непрерывных случайных величин X1 и X2

Полезное равенство для произвольных случайных величин

Теорема. Ковариация имеет следующие свойства.

1. cov(X, X) = DX.

2. cov(X1, X2) = 0 для независимых случайных величин X1 и X2.

3. Если Y1 = a1X1 + b1 и Y2 = a2X2 + b2, то cov(Y1, Y2) = a1a2cov(X1, X2).

4. .

5. Равенство верно тогда и только тогда, когда случайные величины X1 и X2 связаны линейной зависимостью, т.е. существуют такие числа a и b, при которых X2 = aX1 + b.

6. cov(X1, X2) = M(X1X2)  MX1MX2.

Доказательство. 1) Утверждение вытекает из очевидного соотношения cov(X, X) = М(Х  MX)2. 2) Если случайные величины Х1 и Х2 являются независимыми (и имеют математические ожидания), то cov(X1, X2) = M((X1  МХ1)(Х2  МХ2)) = (M(X1  МХ1))(M(Х2  МХ2)), откуда приходим к утверждению 2. 3) Пусть Y = a1X1 + b, Y2 = a2X2 + b2. Тогда 4) Рассмотрим дисперсию случайной величины Yx = xX1  X2, где х произвольное число. В силу свойств дисперсии и свойства 3 ковариации Дисперсия DYx, как функции от х, представляет собой квадратный трехчлен. Но дисперсия любой случайной величины не может быть меньше нуля, а это означает, что дискриминант D = (2cov(X1, X2))2  4DX1DX2 квадратного трехчлена DYx является неположительным. 5) Пусть выполнено равенство . Значит, дискриминант D равен нулю, и уравнение DYx = 0 имеет решение, которое обозначим а. Тогда случайная величина Ya = аХ1  X2 принимает всего одно значение (допустим, b), и, следовательно, Х2 = аХ1  b, т.е. случайные величины X1 и X2 связаны линейной зависимостью. Наоборот, пусть X2 = aX1 + b. Тогда в соответствии со свойством 1 дисперсии DYa = 0, а значит, дискриминант D является неотрицательным. Поскольку при доказательстве утверждения 4 было показано, что этот дискриминант неположителен, то он равен нулю, откуда следует, что 6) Раскрывая скобки в формуле, определяющей ковариацию, и используя свойства математического ожидания, получаем требуемое.

Определение. Случайные величины X и Y называют некоррелированными, если их ковариация равна нулю, т.е. cov(Х, Y) = 0.

Определение. Коэффициентом корреляции случайных величин X и Y называют число  = (X, Y), определяемое равенством (предполагается, что DX > 0 и DY > 0)

Теорема. Коэффициент корреляции имеет следующие свойства.

1. (X, X) = 1.

2. Если случайные величины X и Y являются независимыми (и существуют DX > 0 и DY > 0), то (X, Y) = 0.

3. (a1X1 + b1, a2X2 + b2) = ±(X1, X2) При этом знак плюс нужно брать в том случае, когда а1 и а2 имеют одинаковые знаки, и минус в противном случае.

4. 1  (X, Y)  1.

5. |(X, Y)| = 1 тогда и только тогда, когда случайные величины X и Y связаны линейной зависимостью.

Условные распределения

В случае дискретной СВ закон распределения двумерного случайного вектора (X, Y) удобно задавать набором вероятностей pij = P{X = xi, Y = yj} для всех значений i и j. Зная вероятности pij, нетрудно найти законы распределений каждой из координат по формулам

,

Определение. Для двумерной дискретной случайной величины (X, Y) условной вероятностью ij, i = 1, ..., n, j = 1, ..., m, того, что случайная величина X примет значение xi при условии Y = yj, называют условную вероятность события {X = xi} при условии события {Y = yj} т.е.

При каждом j, j = 1, ..., m, набор вероятностей ij, i = 1, ..., n, определяет, с какими вероятностями случайная величина X принимает различные значения хi, если известно, что случайная величина Y приняла значение yj. Иными словами, набор вероятностей ij, i = 1, ..., n, характеризует условное распределение дискретной случайной величины X при условии Y = уj.

Аналогично определяют условную вероятность того, что случайная величина Y примет значение yj при условии X = хi.

X1	X2
	0	1	PX1
0	q	q	q
1	p	p	p
PX2	q	p

Пример 1. Условное распределение числа Х1 успехов в первом испытании по схеме Бернулли при условии, что число успехов во втором испытании X2 = j, j = 0, 1, задается таблицей. Из этой таблицы следует, что, независимо от числа успехов во втором испытании, 0 или 1 успех в первом испытании происходит с одними и теми же вероятностями р и q. Это очевидно, поскольку испытания по схеме Бернулли являются независимыми.

Пример 2. Условное распределение случайной величины X (числа очков, выпавших на верхней грани игральной кости) при условии Y = yj (числа очков, выпавших на нижней грани игральной кости), j = 1, ..., 6, представлено в таблице. Действительно, если, например, на нижней грани выпало одно очко, то на верхней грани может выпасть только шесть очков (61 = 1).

X	Y
	1	2	3	4	5	6	РX
1	0	0	0	0	0	1	1/6
2	0	0	0	0	1	0	1/6
3	0	0	0	1	0	0	1/6
4	0	0	1	0	0	0	1/6
5	0	1	0	0	0	0	1/6
6	1	0	0	0	0	0	1/6
PY	1/6	1/6	1/6	1/6	1/6	1/6

Перейдем к случаю, когда двумерный случайный вектор (X, Y) имеет непрерывную совместную плотность распределения р(х, у) и непрерывные маргинальные плотности распределения

,

Условная функция распределения

Определение. Условной плотностью распределения случайной величины X (случайной величины Y), являющейся координатой двумерного случайного вектора (X, Y), при условии, что другая его координата приняла некоторое фиксированное значение у (значение x), т.е. Y = y (X = x), называют функцию рX(x|у) (рY(y|x)) определяемую соотношением

Критерий независимости случайных величин X и Y. Случайные величины X и Y являются независимыми тогда и только тогда, когда условное распределение (функция распределения, плотность распределения) случайной величины X при условии Y = у совпадает с безусловным распределением (функцией распределения, плотностью распределения) случайной величины X.

Определение. Для дискретной двумерной случайной величины (X, Y) значением М(Х | Y = yj) условного математического ожидания дискретной случайной величины X при условии Y = yj, называют число

Определение. Условным математическим ожиданием М(Х|Y) дискретной случайной величины X относительно дискретной случайной величины Y называют функцию M(X | Y) = g(Y) от случайной величины Y, где область определения функции g(у) совпадает с множеством значений y1, ..., ym случайной величины Y, а каждому значению yj аргумента у поставлено в соответствие число g(уj) = М(Х | уj).

Подчеркнем еще раз, что условное математическое ожидание М(X|Y) является функцией от случайной величины, т.е. также случайной величиной.

Пример 3. Найдем условное математическое ожидание М(Х|Y) случайной величины X числа очков, выпавших на верхней грани игральной кости, относительно случайной величины Y числа очков, выпавших на нижней грани (см. пример 2). В соответствии с таблицей

Полученный результат в терминах условного математического ожидания можно записать в виде М(Х|Y) = 7  Y.

Теорема. Условное математическое ожидание M(Х|Y) обладает следующими свойствами.

1. М(с|Y) = с.

2. M(aX + b|Y) = aM(X|Y) + b.

3. M(X1 + X2|Y) = M(X1|Y) + M(X2|Y).

4. Пусть случайные величины Х1 и Х2 являются независимыми при условии, что случайная величина Y приняла любое конкретное значение. Тогда M(X1X2|Y) = M(X1|Y)M(X2|Y).

5. MX = M(M(X|Y)).

6. Пусть и(Х) и v(Y) функции от случайных величин X и Y. Тогда M(u(X)v(Y)|Y) = v(Y)M(u(X)|Y).

7. Если X и Y независимые случайные величины, то М(X|Y) = MX.

Определение. Для непрерывной двумерной случайной величины (X, Y) значением М(Х|у) = M(Х|Y = y) условного математического ожидания непрерывной случайной величины X при условии Y = у называют число

Определение. Для непрерывной двумерной случайной величины (X, Y) условным математическим ожиданием M(X|Y) непрерывной случайной величины X относительно случайной величины Y называют функцию g(Y) = М(Х|Y) от случайной величины Y, принимающую значение g(у) = М(X|у) при Y = у.

Определение. Функцию g(у) называют функцией регрессии, или просто регрессией, случайной величины X на случайную величину Y, а ее график линией регрессии случайной величины X на случайную величину Y, или просто X на Y.

Линия регрессии графически изображает зависимость „в среднем" случайной величины X от значения случайной величины Y.

Закон больших чисел и центральная предельная теорема С самого начала изучения курса теории вероятностей мы говорили о том, что практическое применение методов этой математической дисциплины основывается на законе предельного постоянства частоты события. Закон предельного постоянства частоты события установлен эмпирически. В соответствии с этим законом повторение одного и того же опыта приводит к тому, что частота появления конкретного случайного события теряет свойства случайности и приближается к некоторому пределу, который в соответствии со статистическим определением вероятности и называют вероятностью. Однако для того чтобы теория согласовывалась с практикой, при аксиоматическом определении вероятности, которое мы использовали, этот закон предельного постоянства частоты должен быть обоснован теоретически. Иначе говоря, он должен быть сформулирован и доказан в виде одной или нескольких теорем. В теории вероятностей теоремы такого типа обычно называют различными формами закона больших чисел, которые, в частности, поясняют смысл математического ожидания случайной величины, и то, почему его называют также средним значением. Центральная предельная теорема, в свою очередь, объясняет то широкое распространение, которое получило на практике нормальное распределение. Определение. Последовательность Х1, Х2, ..., Xn, ... случайных величин удовлетворяет закону больших чисел (слабому), если для любого  > 0 Иными словами, выполнение закона больших чисел отражает предельную устойчивость средних арифметических случайных величин: при большом числе испытаний они практически перестают быть случайными и совпадают со своими средними значениями. Теорема. Если последовательность Х1, Х2, ..., Xn, ... независимых случайных величин такова, что существуют MXi = mi и DXi = i, причем дисперсии ограничены в совокупности (т.е. ), то для последовательности Х1, Х2, ..., Xn, ... выполнен закон больших чисел. При этом говорят также, что к последовательности Х1, Х2, ..., Xn, ... случайных величин применим закон больших чисел в форме Чебышева. , , Следствие. Если случайные величины Хi, i = 1, 2, ..., в условиях предыдущей теоремы являются также одинаково распределенными (в этом случае mi = m и ), то последовательность Х1, Х2, ..., Xn, ... случайных величин удовлетворяет закону больших чисел в следующей форме: Теорема. (центральная предельная теорема). Пусть X1, X2, ..., Xn, ... последовательность независимых одинаково распределенных случайных величин, MXn = m, DXn = 2. Тогда где Ф(х) функция стандартного нормального распределения.

Двумерные и многомерные случайные величины