Нестационарная теплопроводность
3
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
МАГНИТОГОРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ИМ. Г.И.НОСОВА
КАФЕДРА ТЕПЛОТЕХНИЧЕСКИХ И ЭНЕРГЕТИЧЕСКИХ СИСТЕМ
КУРСОВАЯ РАБОТА
ПО ТЕПЛОМАССООБМЕНУ
|
ВЫПОЛНИЛ:
|
студент спец.140104
гр.ЭТБ-08 Горбунёва Е.С.
|
|
ПРОВЕРИЛ:
|
доцент,
к.т.н. Матвеева Г.Н.
|
МАГНИТОГОРСК
2010
Задача 1. Нестационарная теплопроводность
Металлическая заготовка, имеющая форму пластины (цилиндра), неограниченной длинны, с начальной температурой , нагревается в печи, температура которой поддерживается постоянной до конечной температуры по оси заготовки . Считая длину (и высоту) заготовки большими по сравнению с толщиной, определить:
- Время нагревания заготовки до данной конечной температуры;
- Температуры на оси и на поверхности заготовки для различных моментов времени (с использование монограмм Будрина);
- Распределение температуры по толщине заготовки для четырёх моментов времени (с использованием аналитических формул);
- Количество теплоты, подведённой к телу в течение всего периода нагревания (на 1 поверхности пластины или на 1 длины цилиндра);
- По результатам (2) и (3) построить графики.
Форма тела: ПЛАСТИНА
Материал: СТАЛЬ 40
1._Определение времени нагревания заготовки до конечной температуры
Сначала найдем из справочных таблиц теплофизические параметры пластины (теплоёмкость, коэффициент теплопроводности, коэффициент температуропроводности и плотность) при начальной температуре и конечной температуре центра пластины , и вычислим их средние значения:
|
Параметр
|
|
|
Среднее
|
|
|
0,498
|
0,648
|
0,573
|
|
|
41,4
|
25,4
|
33,4
|
|
|
0,41
|
0,021
|
0,2155
|
|
|
7801
|
7486
|
7643
|
Вычислим число и безразмерную температуру для центра пластины в последний момент времени нагрева:
По номограмме Будрина для центра пластины определим:
Вычислим время нагревания заготовки:
2._Определение температур на оси и на поверхности заготовки для различных моментов времени
Интервал времени нагревания заготовки разобьём на несколько промежутков. Для каждого значения вычислим время (в часах), найдём безразмерные температуры в центре и на поверхности пластины по номограммам Будрина (в зависимости от и ). По безразмерным температурам вычислим температуры в центре и на поверхности пластины в градусах Цельсия.
Для :
- Время нагревания
- Безразмерная температура в центре пластины (определяем по соответствующей диаграмме Будрина в зависимости от и ):
- Безразмерная температура на поверхности пластины (определяем по соответствующей диаграмме Будрина в зависимости от и ):
- Температура на оси пластины:
- Температура на поверхности пластины:
Для остальных значений критерия Фурье вычисления производим по этим же формулам, результаты вычислений заносим в таблицу.
|
|
0,5
|
1
|
1,5
|
2,0
|
2,5
|
3,0
|
3,5
|
4,2
|
|
|
0,169
|
0,336
|
0,5
|
0,673
|
0,84
|
1,009
|
1,17
|
1,31
|
|
|
0,85
|
0,65
|
0,5
|
0,4
|
0,3
|
0,25
|
0,19
|
0,13
|
|
|
0,65
|
0,56
|
0,37
|
0,3
|
0,23
|
0.17
|
0,15
|
0,12
|
|
|
372,5
|
602,5
|
775
|
890
|
1005
|
1062,5
|
1131,5
|
1200
|
|
|
602,5
|
706
|
924,5
|
1005,5
|
1085,5
|
1154,5
|
1177,5
|
1212
|
3._Определение распределения температуры по толщине заготовки для четырёх моментов времени
При определяем из таблиц:
При
При
При
Найдём безразмерные температуры в момент времени
Температура для этой точки:
Для остальных точек и в другие моменты времени вычисления производим аналогичным образом, результаты записываем в таблицу.
|
|
|
|
|
|
|
|
0,843
|
0,5128
|
0,2433
|
0,1340
|
|
|
380
|
760
|
1070
|
1196
|
|
|
0,799
|
0,504
|
0,239
|
0,132
|
|
|
431
|
770
|
1075
|
1198
|
|
|
0,790
|
0,481
|
0,218
|
0,125
|
|
|
442
|
797
|
1099
|
1206
|
|
|
0,727
|
0,442
|
0,209
|
0,115
|
|
|
514
|
842
|
1110
|
1218
|
|
|
0,6939
|
0,4221
|
0,2002
|
0,1103
|
|
|
552
|
864
|
1119
|
1223
|
4._Определение количества теплоты, подведённого к телу за весь период нагревания (в расчёте на 1 метр длинны пластины)
Полное количество теплоты, которое было бы подведено к пластине (на 1 метр её длинны и 1 метр ширины), если бы нагревание длилось до наступления полного теплового равновесия между пластиной и воздухом печи:
Средняя безразмерная температура в последний момент времени нагрева:
Полное количество теплоты, подведённого к пластине (на 1 метр её длинны и 1 метр ширины) за весь период нагрева:
Задача 2. Конвективный теплообмен при вынужденном продольном обтекании плоской поверхности
Плоская пластина м. обтекается продольным потоком жидкости (газа) со скоростью м/с. Температура набегающего потока . Задана температура поверхности пластины . Найти:
- Критическую координату точки перехода ламинарного пограничного слоя в турбулентный;
- Толщины динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности;
- Значения местных коэффициентов теплоотдачи на различных расстояниях от передней кромки пластины;
- Средние коэффициенты теплоотдачи для участков с различными режимами течения;
- Построить графики , .
Жидкость: воздух
1. Вычисление критической координаты точки перехода ламинарного пограничного слоя в турбулентный
Определим теплофизические параметры воздуха при температуре :
Критическое число Рейнольдса:
Вычислим координату точки перехода ламинарного течения в пограничном слое в турбулентное:
2. Вычисление толщин динамического и теплового пограничных слоёв на различных расстояниях от передней кромки поверхности
2.1. Расчёт ламинарного режима течения
2.1.1. Вычисление толщин динамического и теплового пограничных слоёв, а также коэффициентов теплоотдачи для различных точек
Для точек вычислим:
Для других точек ламинарного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.
2.1.2. Вычисление среднего коэффициента теплоотдачи
2.2. Расчёт турбулентного режима течения
2.2.1. Вычисление толщины динамического пограничных слоя, а также коэффициентов теплоотдачи для различных точек
Для точки вычислим:
Для других точек турбулентного режима течения вычисления производим по этим же формулам, результаты записываем в таблицу.
2.2.2. Вычисление среднего коэффициента теплоотдачи и плотности теплового потока
2.3. Результаты вычислений
|
|
Ламинарный участок
|
Турбулентный участок
|
|
|
0,1
|
0,4
|
0,6
|
0,8
|
0,96
|
1
|
1,5
|
2
|
2,5
|
3
|
|
|
10364
|
41458
|
62187
|
82915
|
99499
|
103644
|
155467
|
207289
|
259112
|
310934
|
|
|
0,0045
|
0,0091
|
0,0111
|
0,0128
|
0,0141
|
0,036
|
0,050
|
0,063
|
0,0765
|
0,0885
|
|
|
0,0051
|
0,0103
|
0,0125
|
0,145
|
0,159
|
0,036
|
0,050
|
0,063
|
0,0765
|
0,0885
|
|
|
29,799
|
59,598
|
72,976
|
84,275
|
92,325
|
258,2
|
357,2
|
449,7
|
537,6
|
622
|
|
|
10,6
|
5,3
|
4,3
|
3,7
|
3,4
|
9,2
|
8,48
|
8,0
|
7,65
|
7,39
|
|
|
177,5
|
777,5
|
|
|
6,5
|
8
|
Задача 3. Тепловой расчёт двухходового трубчатого воздухоподогревателя.
В трубчатом двухходовом теплообменнике холодный теплоноситель в количестве должен нагреваться от температуры до . Горячий теплоноситель в количестве движется внутри труб диаметром,воздухоподогревателя со средней скорость Коэфициент теплопроводности материала стенки, из которого изготовлены трубки. Температура горячего теплоносителя на входе в теплообменник на выходе . Холодный теплоноситель движется поперек трубного пучка со средней скоростью Заданы расположение труб в пучке (шахматное или коридорное) и относительные шаги: поперечный и продольный . Потери теплоты составляют .
Определить необходимую поверхность нагрева, длину труб в одном ходе и количество труб, расположенных поперек и вдоль потока холодного теплоносителя.
|
Дымовые газы:
Вода:
|
Коэффициент теплопроводности труб:
Диаметры труб:
Шахматное расположение труб
|
Поперечный относит. шаг:
Продольный относит. шаг:
|
1. определим среднюю температуру воздуха
Определяем количество получаемой теплоты
Определяем физические свойства воздуха
=,
.
2. принимаем температуру дымовых газов на выходе
Средняя температура воды:
При этой температуре выписываем физические свойства дымовых газов из таблице:
3.определение температурного напора
4.определение коэффициентов теплоотдачи
Число Рейнольдса для потока газов
- режим течения воды турбулентный
Для расчета коэффициента теплоотдачи поступают следующим образом.
Определяется эффективная степень черноты поверхности
Коэффициент излучения абсолютно черного тела.
Эффективная толщина излучающего слоя при движении газов внутри труб
по ней определяем по номограммам:
Принимаем
При t=191,5С определяем по графикам
Коэффициент теплоотдачи на стороне дымовых газов
Число Рейнольдса для потока воздуха:
Число Нуссельта и коэффициента теплоотдачи от стенок труб к воздуху при поперечном потоке и шахматном расположении труб
5. определение коэффициента теплоотдачи
- Определение размеров воздухоподогревателя
Общая длина труб:
Поверхность нагрева воздухоподогревателя
Количество труб:
Высота трубы в одном ходе
Живое сечение для прохода воздуха
Число труб, расположенных поперек потока
Число труб, расположенных вдоль потока
Задача 4. Теплообмен излучением между газом и твёрдой ограждающей поверхностью
Вычислить плотность теплового потока, обусловленного излучением дымовых газов к поверхности газохода сечением AxB. Состав газов задан. Общее давление газа . Температура газов на входе в газоход и на выходе . Средняя температура поверхности газохода .
Материал: хром
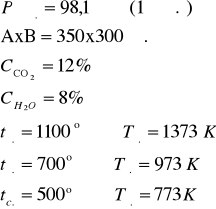
Степень черноты хрома:
Вычислим приведённую степень черноты хром:
Вычислим среднюю температуру газов по тракту:
Эффективная толщина излучающего слоя:
Парциальные давления двуокиси углерода и водяного пара:
объёмная доля и в газе
Первый метод (с использованием диаграмм)
Произведение парциального давления на двуокиси углерода и водяного пара на длину луча:
По графикам определяем степени черноты двуокиси углерода и водяного пара при температуре =900:
По графику определяем поправочный коэффициент учитывающий подчинение поведения водяного пара по закону Бугера-Бера:
Степень черноты газовой смеси:
По графикам определяем степени черноты двуокиси углерода и водяного пара по температуре стенки :
Поглощательная способность газовой смеси:
Плотность теплового потока:
Второй метод (аналитический)
Суммарное парциальное давления водяного пара и двуокиси углерода:
Степень черноты газовой смеси:
Поглощательная способность газовой смеси:
Плотность теплового потока:
Литература
- Е.И. Казанцев. Промышленные печи.
Справочное руководство для расчётов и проектирования.
Москва, «Металлургия», 1975г.
- Ривкин С.Л.,Александров А.А.
Термодинамические своиства воды и водяного пара: Справочник.
Москва, «Энергоатомиздат», 1984г.
- Г.Н.Матвеева. Тепломассообмен.
Методические указания для выполнения курсовой работы
Магнитогорск, МГТУ, 2008г.
Нестационарная теплопроводность