Опыт Штерна и Герлаха

Лекция 8

Среди экспериментов, сыгравших фундаментальную роль в становлении квантовой физики, очень важное место занимает опыт Штерна - Герлаха (1922 г.). Как известно из курса атомной физики, в этом опыте узкий параллельный пучок частиц, обладающих магнитным моментом, пропускался через неоднородное магнитное поле 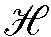. Согласно классической электродинамике в таком поле на частицу действует отклоняющая сила

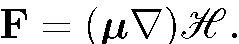(8.1)

Если конфигурация поля такова, что 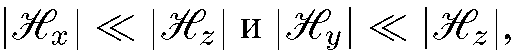то среднее значение вектора магнитного момента частицы ввиду его прецессии вокруг 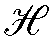направлено по оси 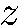. В этом случае

отклоняющая сила F тоже в среднем направлена по :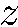

(8.2)

а ее величина пропорциональна 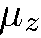— проекции магнитного момента частицы на ось 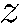. Таким образом, неоднородное магнитное поле действует как анализатор, который сортирует попадающие в прибор Штерна-Герлаха частицы по величине проекции их магнитного момента на характерное для прибора направление — «ось прибора». Историческое значение опыта Штерна - Герлаха заключается в экспериментальном установлении эффекта «пространственного квантования»: пучок, в котором магнитные моменты частиц ориентированы произвольно, расщепляется прибором на несколько отдельных пучков, количество которых строго определяется сортом частиц. Классическая физика не в состоянии объяснить этот результат. Согласно же квантовой механике дело в том, что проекция магнитного момента частицы на любое направление (в том числе на ось прибора) может принимать лишь определенные дискретные значения.

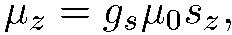(8.3)

где 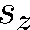проекция спина частицы на ось z:

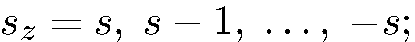(8.4)

отсюда видно, что количество пучков на выходе из прибора Штерна-Герлаха определяется величиной спина частицы и равно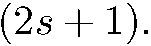

В данном параграфе мы отвлечемся от многих физических вопросов, относящихся к осуществлению опыта Штерна-Герлаха, и сосредоточим внимание лишь на одном пункте — способности прибора сортировать падающие частицы по величине проекции их спина на некоторое направление.

Пусть в прибор с осью, совпадающей с направлением оси 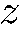, попадают частицы со спином , спиновое состояние которых описывается некоторой заданной волновой функцией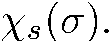

Мы можем разложить ее по полному набору спиноров , описывающих состояния с определенным значением проекции спина на ось .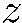

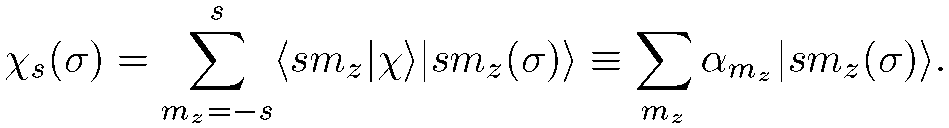(8.5)

В представлении, , это есть разложение по столбцам.

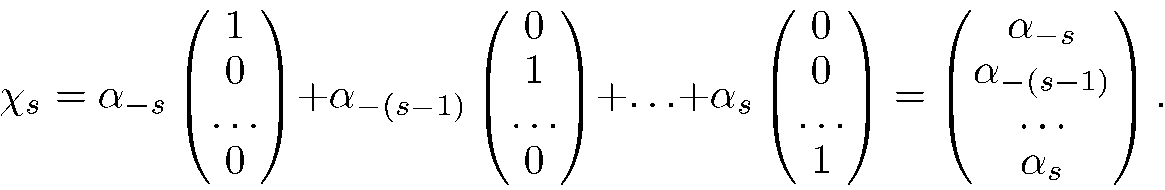(8.6)

Коэффициенты разложения 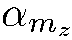определяют вероятности различных значений 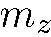и, следовательно, относительные интенсивности пучков на выходе из прибора Штерна-Герлаха:

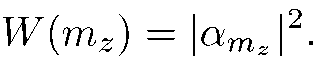(8.7)

Разыграем несколько конкретных вариантов опыта Штерна-Герлаха («мысленный эксперимент»). Для простоты возьмем пучок частиц со спином 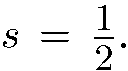В этом случае на выходе из прибора имеется два пучка. В первом (его относительную интенсивность обозначим 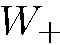) спины всех частиц направлены по оси , во втором (соответствующая интенсивность 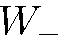) — против оси . Наша задача состоит в том, чтобы найт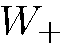и и 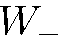в зависимости от свойств падающего пучка.

Вариант 1. Начнем с простейшего случая, когда все частицы входного пучка находятся в состоянии 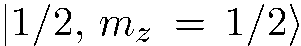, т. е. проекция спина любой частицы на ось с достоверностью

равна 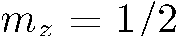. Очевидно, в этом случае на выходе из прибора будет только один пучок: .

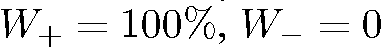Вариант 2. 50% частиц падающего пучка находятся в состоянии 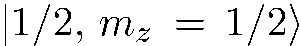и 50% частиц —в состоянии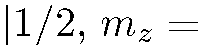 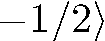). И в этом случае результат очевиден: 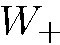= = 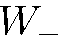50 %.

Вариант 3. Все 100 % частиц падающего пучка находятся в состоянии 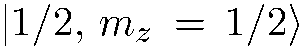, т. е. спины всех частиц направлены по оси 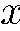. По условию наш прибор «не умеет» различать частицы по тому, как ориентированы их спины относительно оси 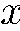; он «знает» только один признак: 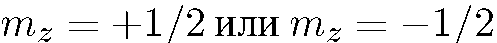. Значит, надо представить волновую функцию 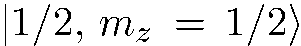в виде суперпозиции соответствующих базисных функци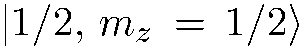й и .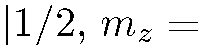

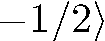Имеем:

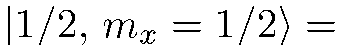
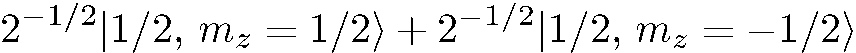(8.8)

Отсюда согласно (8.7) получаем = = 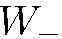50 %.

Вариант 4. Спины всех частиц падающего пучка направлены вдоль вектора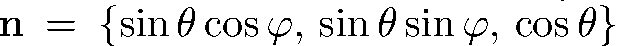

т.е. все частицы находятся в состоянии 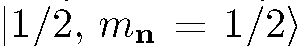, углы 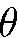и —

любые. Такой вариант есть просто обобщение предыдущего случая, и способ решения здесь тот же: разложим волновую функцию 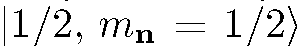по базисным

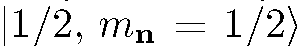
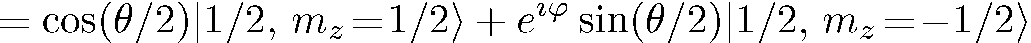(8.9)

и отсюда согласно (8.7) получим

(8.10)

Обратим внимание на то, что результаты нашего мысленного эксперимента в вариантах 2 и 3 совпали. Что это значит? Что совпадают начальные условия 2 и 3, или же что возможности проделанного эксперимента недостаточны для обнаружения различия между этими двумя начальными условиями?

Размышления показывают, что правилен второй ответ, и можно предложить другой эксперимент, чувствительный к различию между начальными условиями 2 и 3. Для этого, не меняя начальных условий, заменим наш прибор Штерна-Герлаха другим, у которого «ось прибора» направлена не по оси , а по оси (образно говоря, повернем прибор на 90° вокруг оси 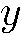). Частицы, попадающие в этот новый прибор, тоже всегда направляются им по одному из двух характерных для него направлений, но здесь сортировка частиц производится уже по другому признаку: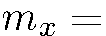 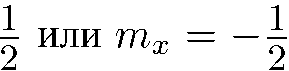. Обозначим соответствующие относительные интенсивност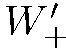и и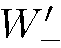. Найдем их значения в вариантах 2 и 3. Сразу видно, что в варианте 3 новый прибор направляет

все частицы по одному направлению: .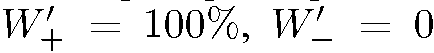

Обратимся к варианту 2. Каждая из частиц падающего пучка, находящаяся в состоянии 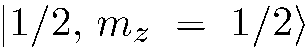, имеет одинаковую вероятность выйти из прибора по направлению, соответствующему 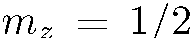, и по направлению, соответствующему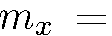 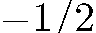. То же справедливо для падающих частиц, находящихся в состоянии 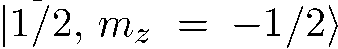. По условию между частицами, находящимися в состоянии 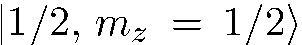и в состоянии 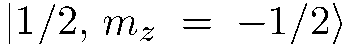нет никакой корреляции. Поэтому получаем 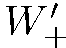= = 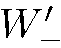50 %. Легко убедиться в том, что результат 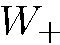= = 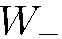50% сохранится в варианте 2 при любой другой ориентации оси прибора. Таким образом, начальные условия 2 характеризуют неполяризованное состояние частиц во входном пучке; мы не можем указать в этом случае никакого выделенного направления в пространстве по отношению к спиновым свойствам рассматриваемой системы.

Итак, использование нескольких приборов Штерна-Герлаха с направленными по-разному осями показывает, что начальные условия в вариантах 2 и 3 различны. Это различие имеет очень глубокий характер. В варианте 3 состояние пучка на входе в прибор характеризуется некоторой определенной волновой функцией. Неважно, что в разных представлениях ее можно записать по-разному; мы подчеркиваем другое: в варианте 3 состояние каждой частицы на входе в прибор характеризуется одним, вполне определенным вектором состояния, здесь это 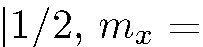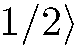. В варианте 2 ситуация другая. Здесь начальные условия заданы так, что невозможно указать никакой одной волновой функции, которая описывала бы состояние всех частиц, попадающих в прибор; какого-либо определенного, единственного вектора начального состояния в варианте 2 нет.

Опыт Штерна и Герлаха