Движение частицы в сферически-симметричном поле (дискретный спектр)

Лекция 5

Движение частицы в сферически-симметричном поле (дискретный спектр).

Найдем стационарные состояния движения частицы в сферически-симметричном поле с потенциальной энергией

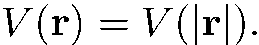
Для этого надо найти решения стационарного уравнения Шредингера

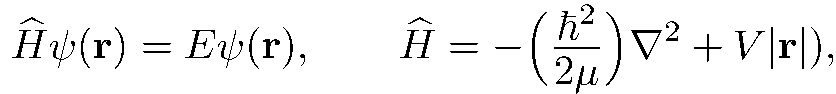(5.1)

удовлетворяющие во всем пространстве требованиям непрерывности, квадратичной интегрируемости и непрерывности градиента.

Ввиду сферической симметрии поля задачу удобно решать в сферической системе координат 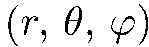, начало которой совпадает с центром симметрии поля, а полярная ось имеет некоторое произвольное направление:

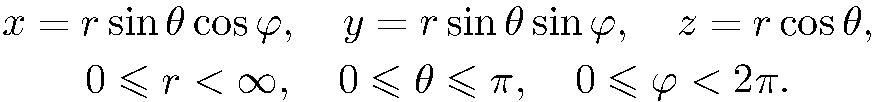(5.2)

В этой системе координат имеем

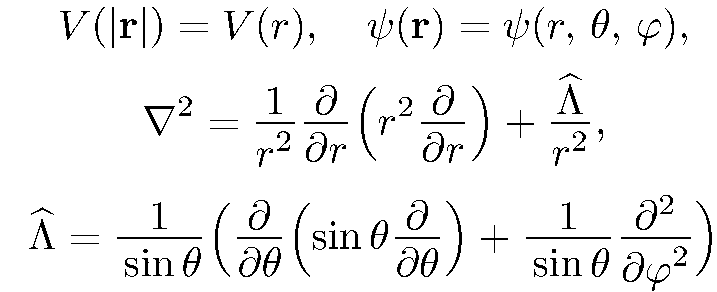(5.3)

знание интегралов движения системы обычно позволяет упростить решение уравнения Шредингера. Поэтому и в данном случае начнем с выявления сохраняющихся физических величин. Легко видеть, что гамильтониан системы (5.1) инвариантен относительно операции 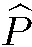инверсии пространства , а поэтому четность есть интеграл движения. Интегралами движения являются также квадрат момента количества движения 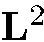и любая его проекция 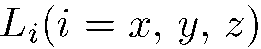. Кроме того, легко проверить , что

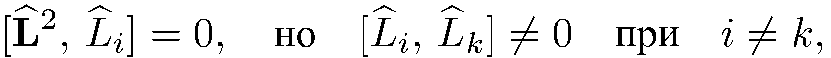
а также

Таким образом, все четыре оператора

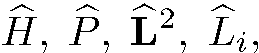(5.4)

где 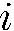имеет какое-нибудь одно из трех возможных значений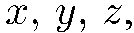, коммутируют друг с другом. Подчеркнем, что в этот набор может быть включена только одна компонента оператора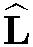 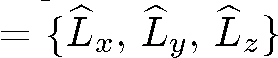, так как различные компоненты этого оператора не коммутируют между собой.

Посколысу все направления в сферически симметричном поле равноправны, то в дальнейшем будем рассматривать следующий набор взаимно коммутирующих операторов:

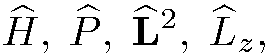(5.5)

т. е. будем искать такие решения {r) уравнения Шредингера, которые являются собственными функциями всех этих операторов. В сферической системе координат соответствующие уравнения имеют вид:

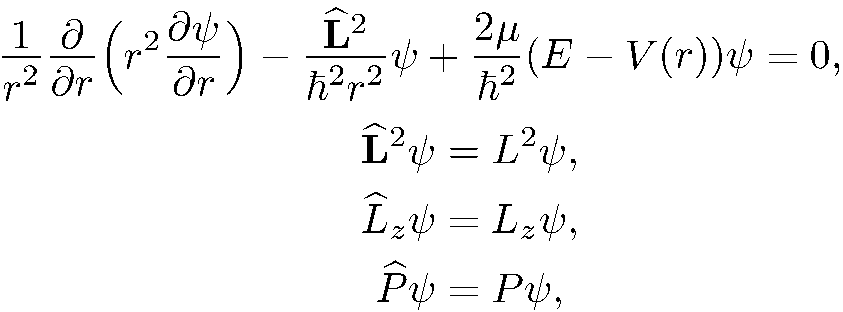
(5.6)

(5.7)

(5.8)

(5.9)

Где

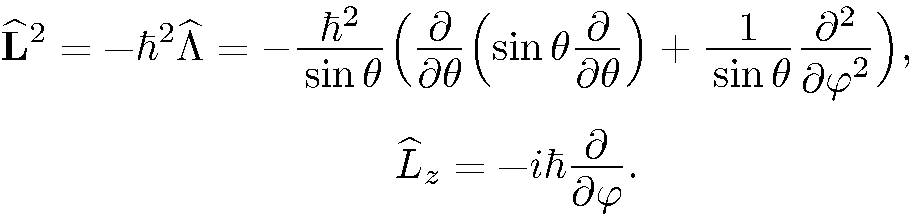
(5.10)

(5.11)

Собственные значения и собственные функции оператора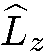

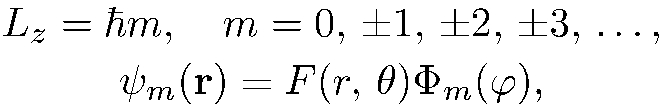
(5.12)

(5.13)

где

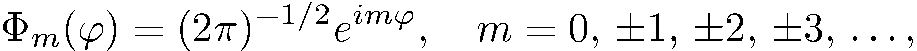
(5.14)

причем

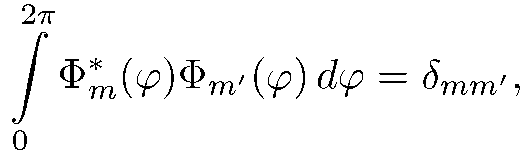
(5.15)

а 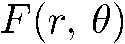есть произвольная квадратично-интегрируемая функция.

Из математики известно, что собственные значения оператора 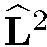даются формулой

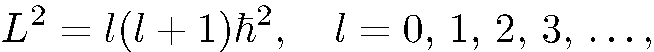(5.16)

а каждому собственному значению соответствуют собственные функции:
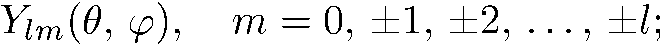(5.17)

это сферические функции , удовлетворяющие условию ортонормированности на сфере

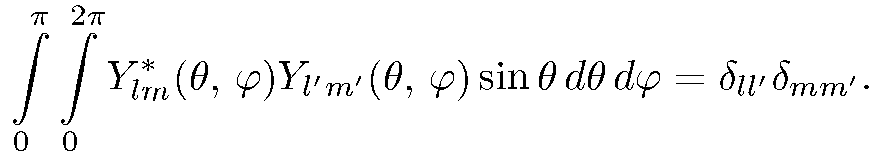(5.18)

Сферические функции всегда могут быть представлены в виде

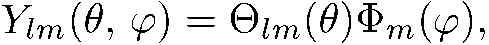(5.19)

Где 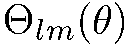некоторые ограниченные функции. Следовательно, каждая функция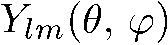

является также собственной функцией оператора 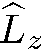, принадлежащей собственному значению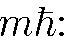

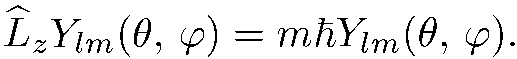(5.20)

Сферические функции при 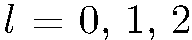имеют следующий явный вид:

(5.21)

В математике показывается, что каждая сферическая функция 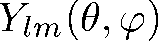удовлетворяет соотношению

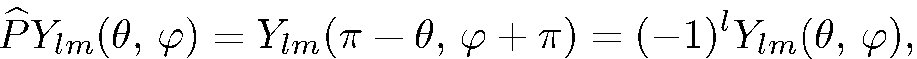(5.22)

т.е. 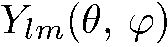есть собственная функция оператора инверсии, принадлежащая собственному значению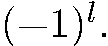

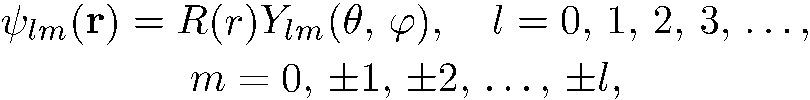(5.23)

где R(r) — некоторая функция г, являются общими собственными функциями операторов 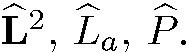Подставляя 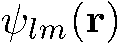в уравнение Шрединга (5.6), получаем

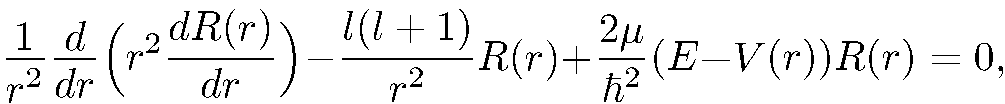
(5.24)

т.е. 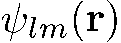есть собственная функция гамильтониана (2.1), если R(r) удовлетворяет уравнению (5.24) и является непрерывной квадратично-интегрируемой функцией с непрерывной первой производной. Уравнение (5.24) иногда называют радиальным уравнением Шредингера. Введем новую функцию

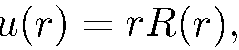(2.25)

для которой из (5.24) получаем уравнение

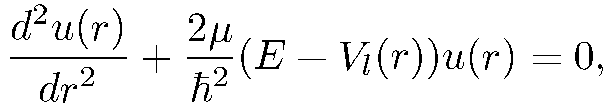(5.26)

где

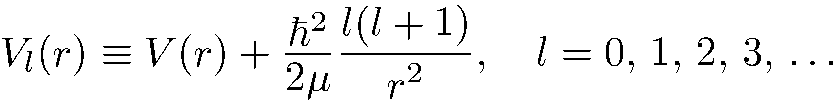(5.27)

Уравнение (5.26) внешне совпадает с уравнением Шредингера для одномерного движения частицы в поле с потенциальной энергией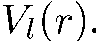

Пусть 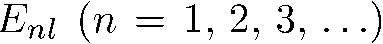есть n-е собственное значение уравнения (5.26) при фиксированном I. Было доказано, что все дискретные энергетические уровни частицы в произвольном одномерном потенциальном поле невырождены, легко показать, что каждому значению 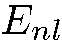соответствует только одно линейно независимое решение уравнения (5.26):

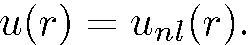
Таким образом, искомые общие собственные функции операторов 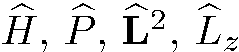имеют вид

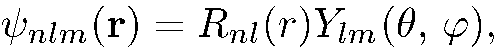(5.28)

где

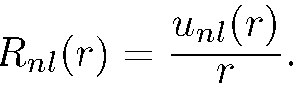
Мы видим, что каждому собственному значению гамильтониана 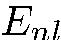соответствует 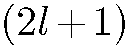линейно независимых собственных функций, отличающихся значениями 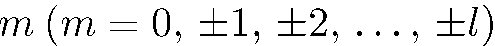. Такое вырождение имеется в любом сферически-симметричном поле. Это «обязательное» вырождение можно было предвидеть еще до решения уравнения Шредингера. Действительно, в сферически-симметричном поле все направления равноправны, а поэтому энергия системы не может зависеть от ориентации в пространстве вектора момента количества движения, в частности от величины его проекции на ось z. Пусть 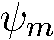и 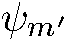— волновые функции двух состояний, отличающихся только значениями т. Тогда любая линейная комбинация этих функций

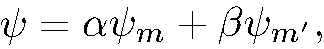
является собственной функцией гамильтониана, принадлежащей тому же энергетическому уровню, которому принадлежат 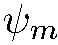и 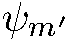, но в отличие от них функция 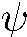не является собственной функцией оператора 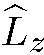. Поэтому в состоянии 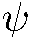проекция момента количества движения на ось z не имеет определенного значения. Таким образом, частица, движущаяся в любом сферически-симметричном поле с некоторым определенным значением энергии, может находиться не только в состояниях с определенным значением проекции момента на некоторое направление, но и в бесчисленном множестве таких состояний, в которых проекция момента не имеет определенного значения (исключением является случай 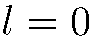, когда проекция момента может иметь только одно значение ).

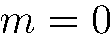В некоторых сферически-симметричных полях одному и тому же значению энергии системы может соответствовать несколько различных значений 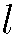, т. е. несколько линейно-независимых функций 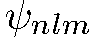. Это вырождение по в отличие от «обязательного» вырождения по 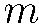иногда называется «случайным». Ниже мы встретимся с примерами такого «случайного» вырождения.

Поскольку собственные функции эрмитова оператора, принадлежащие различным собственным значениям, ортогональны, для всех функций 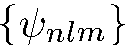имеем

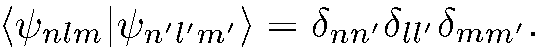(5.29)

Отсюда, в частности, получаем

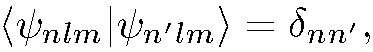
т.е.

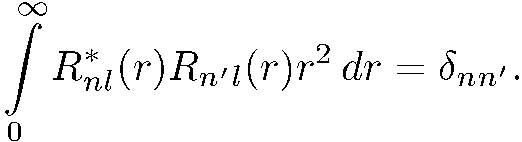(5.30)

Таким образом, функции 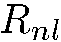удовлетворяют условию нормировки:

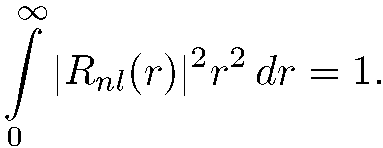(5.31)

Итак, стационарное состояние движения в сферически-симметричном поле однозначно определяется тремя числами n, l, m, для которых приняты следующие названия:

n - главное квантовое число,

l - орбитальное квантовое число,

m - магнитное квантовое число.

Совокупность состояний, отличающихся друг от друга только значениями m, принято объединять в одно состояние и обозначать его символом (иногда вместо n используется какой-либо

другой индекс, характеризующий энергию состояния). При этом вместо значений орбитального квантового числа 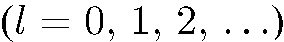обычно используются буквы латинского алфавита со следующим соответствием:

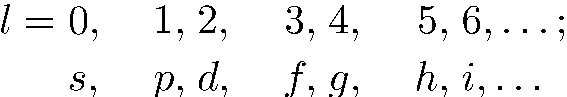(5.32)

Например, символ 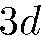обозначает состояние с квантовыми числами 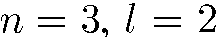(точнее, совокупность состояний с ).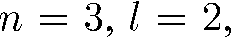

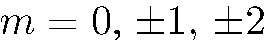Мы видим, что стационарные состояния в сферически-симметричном поле задаются тремя квантовыми числами (n, l, m), хотя мы их искали как собственные функции четырех

коммутирующих операторов (5.5). Очевидно, это «несоответствие» объясняется тем, что не все четыре интеграла движения независимы.

Действительно, из C2.22) следует, что четность состояния однозначно определяется квадратом момента количества движения, т. е. орбитальным квантовым числом

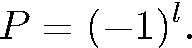(5.33)

В то же время три других интеграла движения 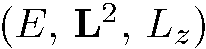образуют полный набор физических величин для данной системы , так как каждой совокупности значений этих величин соответствует одно и только одно линейно независимое состояние. Этот полный набор не является единственным, поскольку наборы 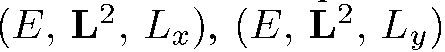тоже являются полными и не сводятся к набору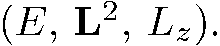

Энергетический спектр системы определяется видом потенциальной энергии V(r). В дальнейшем мы будем в основном рассматривать движение в таких полях, потенциальная энергия в которых ограничена или в начале координат обращается в бесконечность не быстрее, чем 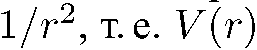удовлетворяет условию

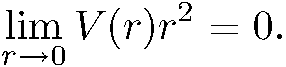(5.34)

Примерами таких полей являются следующие:

1)прямоугольная яма

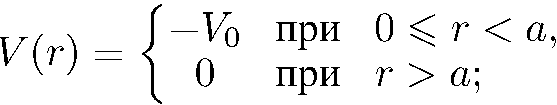
2) гармонический изотропный осциллятор

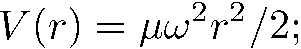
3) кулоновское поле

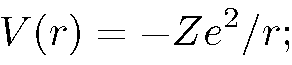
4) экранированное кулоновское поле

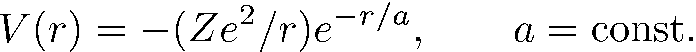
Выясним поведение «радиальной» функции u (г) при г —> 0 для таких систем. Уравнение (5.26) принимает вид

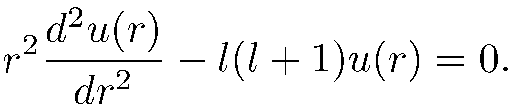
Легко проверить, что его решениями являются функции

Как видно из (5.25) и (5.31), второе решение при не удовлетворяет условию нормировки, так как интеграл расходится на нижнем пределе. Это значит, что соответствующая волновая функция не является квадратично-интегрируемой и не может описывать какое-либо физическое состояние. При 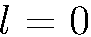функция не приводит к расходимости нормировочного интеграла (5.31), но не удовлетворяет уравнению Шредингера в точке r = 0, так как

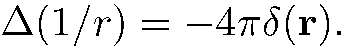
Следовательно, решение при любом должно быть отброшено.

Итак, в окрестности начала координат радиальная функция имеет вид

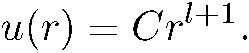(5.35)

Отсюда следует, что она удовлетворяет граничному условию

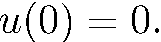(5.36)

Таким образом,

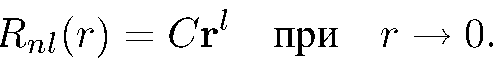(5.37)

При этом плотность вероятности нахождения частицы в окрестности точки г = 0 есть

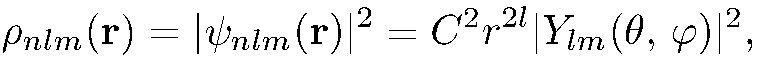(5.38)

т. е. она тем быстрее обращается в нуль в начале координат, чем больше величина момента количества движения в данном состоянии.

В уравнении (5.26) для радиальной функции роль эффективной потенциальной энергии играет величина

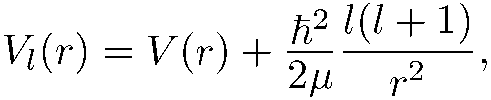( 5.36)

При увеличении I усиливается отталкивание в окрестности центра поля. Именно с этим обстоятельством связано уменьшение вероятности пребывания частицы вблизи центра поля.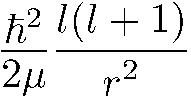

Представление о «квантовых орбитах»

В классической механике орбитой частицы называется траектория ее движения. В квантовой механике термин «орбита» используется для обозначения стационарного состояния 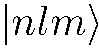движения частицы в сферически-симметричном поле. Каждому энергетическому уровню 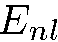соответствуют 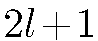«квантовых орбит». Плотность пространственного распределения частицы, находящейся на орбите 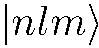, есть

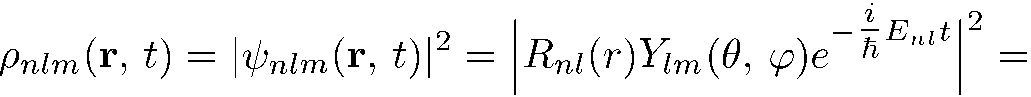
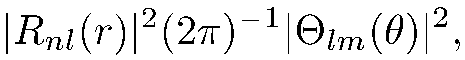(6.1)

т. е. она не зависит от азимутального угла .

Отсюда видно, что 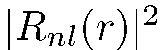есть плотность радиального распределения, a 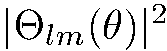- плотность распределения полярного угла частицы, движущейся по орбите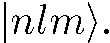

Учитывая (5.22), получаем

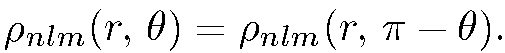(6.2)

Мы видим, что плотность пространственного распределения симметрична относительно плоскости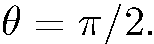

Для наглядного представления угловой зависимости этой величины удобно использовать полярные диаграммы

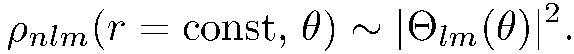(6.3)

Например, в случае l = 0 полярная диаграмма представляет собой окружность, а при I = 1 имеем

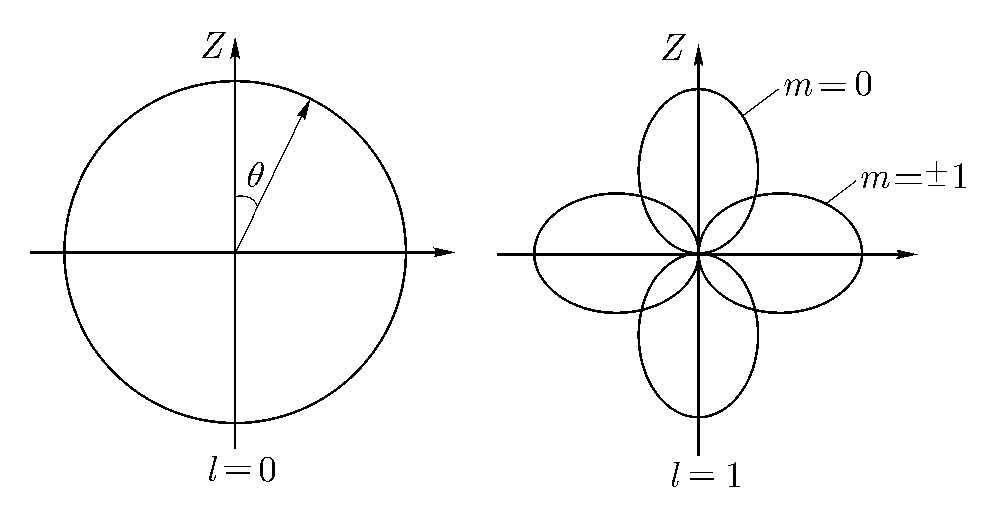Рис. Полярные диаграммы пространственного распределения частицы в s- и р-состояниях

Теперь найдем плотность тока вероятности , соответствующего движению частицы по орбите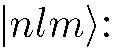

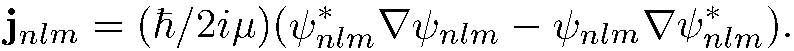
В сферической системе координат оператор градиента есть

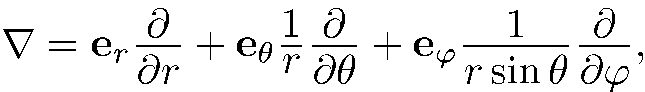
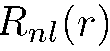Где — соответствующие орты. Поскольку функции и 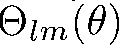вещественны, то

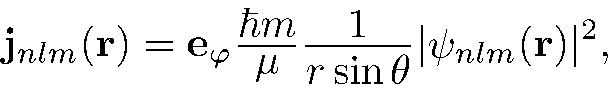
т.е.

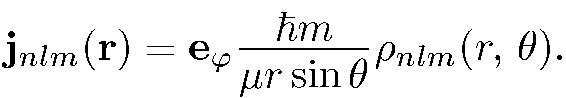(6.4)

Таким образом, плотность тока вероятности не зависит от азимутального угла и всегда имеет направление 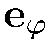.При m=0 имеем j = 0, при 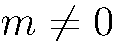абсолютная величина плотности тока не зависит от знака m, а направление тока при изменении знака m изменяется на противоположное:

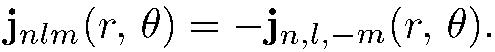(6.5)

Пусть по каждой из 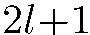орбит, принадлежащих уровню 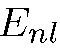, движется по одной частице (взаимодействием частиц друг с другом мы пренебрегаем). Тогда плотность пространственного распределения этих частиц есть

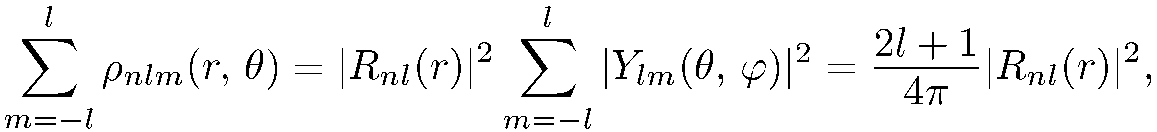(6.6)

т. е. она изотропна.

Используя (6.2), получаем

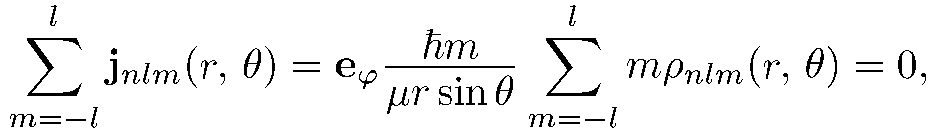(6.7)

т. е. плотность полного тока вероятности в этом случае равна нулю.

Движение частицы в сферически-симметричном поле (дискретный спектр)