Оптимальное управление в электрических схемах
Федеральное агентство по образованию ФГБОУ ВПО
«Саратовский государственный технический университет имени Гагарина Ю.А.»
Кафедра «Техническая кибернетика и информатика»
Пояснительная записка к курсовой работе
по дисциплине
“ Основы теории оптимального управления ”
на тему:
«Оптимальное управление в электрических схемах»
Выполнил:
студент группы УИТ-32
Сырчиков А.В.
Проверила:
Торгашова О. Ю.
Саратов 2012
Задание на курсовую работу
Задача 1
Оптимальное управление в RC-цепи
Для электрической схемы содержащей источник питания e(t), активные сопротивления r, R и емкость C
необходимо:
а) определить оптимальный закон изменения напряжения ис�точника питания e(t), приводящий к изменению напряжения на об�кладках конденсатора от заданного начального значения uC(t0)=uC0 до заданного конечного значения uC(t1)=uC1 , такой, чтобы суммарная энергия активных потерь (затрачиваемая на нагрев) при этом изме�нении была минимальной;
б) определить оптимальный закон изменения напряжения на обкладках конденсатора uC(t) , соответствующий оптимальному за�кону изменения e(t);
в) вычислить энергию активных потерь в схеме при оптималь�ном режиме изменения e(t) и uC(t) и сравнить ее с энергией ак�тивных потерь, затрачиваемой на нагрев при линейном изменении напряжения uC(t) от начального до конечного значения;
г) построить графики оптимальных и линейных изменений ЭДС и напряжения на конденсаторе.
Значения параметров элементов схемы в зависимости от ва�рианта задания приведены в таблице 2.
Таблица 2
|
Номер варианта
|
r
[Ом]
|
R
[Ом]
|
С
[мкФ]
|
uC(t0)
[В]
|
uC(t1)
[В]
|
|
13
|
7,5
|
80
|
5
|
55
|
80
|
Полагать t0=0 , t1=10-3 c .
Задача 2
Для электрической схемы, содержащей источники ЭДС e1(t), e2(t), активные сопротивления R1, R2, r1, r2 индуктивности L1, L2 и емкость С,
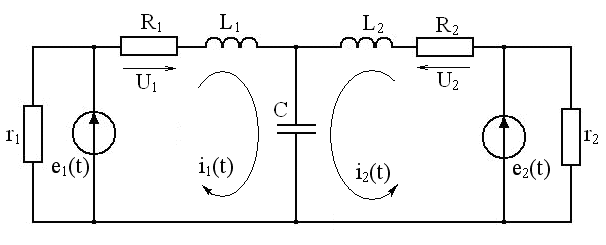
необходимо:
а) определить оптимальные законы изменения напряжений ис�точников питания e01(t), e02(t), приводящих к изменению токов через индуктивности L1, L2 в схеме от заданных начальных значе�ний i10, i20 до заданных конечных значений i11, i21 и изменению напряжения на обкладках конденсатора С в схеме от заданного начального значе�ния uC0 до заданного конечного значения uC1 так, чтобы суммарная энергия активных потерь (затрачиваемая на нагрев) при этом изменении была минимальной;
б) определить оптимальные законы изменения токов i01(t), i02(t) и напряжения на обкладках конденсатора u0C(t), соот�ветствующие оптимальным законам изменения e01(t), e02(t);
в) вычислить энергию активных потерь в схеме при оптималь�ном режиме изменения напряжений источников питания, токов и напряжения на обкладках конденсатора (e01(t), e02(t), i01(t), i02(t), u0C(t)) и сравнить ее с энергией активных потерь, затрачиваемой на нагрев при линейных изменениях токов iЛ1(t) и iЛ2(t) и напряжения на обкладках конденсатора uЛC(t) в схеме от начальных значений до конечных;
г) построить графики оптимальных и линейных изменений ЭДС, токов и напряжения на обкладках конденсатора.
Значения параметров элементов схемы приведены в табл. 3.
Таблица 3
|
№
зад.
|
R1,
Ом
|
R2,
Ом
|
C,
мкФ
|
r1,
Ом
|
r2,
Ом
|
L1,
Гн
|
L2,
Гн
|
i10,
А
|
i11,
А
|
i20,
А
|
i21,
А
|
uC0,
В
|
uC1,
В
|
|
13
|
80
|
45
|
5
|
7,5
|
4,5
|
0,018
|
0,14
|
0,15
|
0,95
|
0,4
|
1
|
55
|
80
|
Полагать t0=0 , t1=10-3 c .
Реферат
Цель работы: систематизация, закрепление и расширение теоретических знаний, и получение практических навыков при расширении конкретных технических задач, развитие навыков самостоятельной работы с технической литературой в ходе расчета.
Объект исследования: в курсовой работе предлагается разработать алгоритмы изменения режима работы электрической схемы, содержащей ак�тивные и реактивные элементы, обеспечивающие минимизацию энергии ак�тивных потерь при переходе от одного режима работы схемы к дру�гому. Необходимо определить вид закона изменения ЭДС источника питания (управляющего воздействия) и проанализировать работу схемы при действии этой ЭДС.
Введение
На протяжении долгих лет очень эффективно используются математические методы моделирования и изучения жизни. Самые различные специалисты вынуждены прибегать к математическим методам оптимального управления. В связи с этим возникает множество проблем и трудностей, которые приходится решать.
Курсовая работа имеет своей целью систематизацию, закрепление и расширение теоретических знаний и практических навыков путем решения конкретных технических задач, развитие навыков само�стоятельной работы с литературой в ходе расчетов.
В процессе выполнения курсовой работы разрабатываются алгоритмы изменения режима работы электрической схемы, содержащей ак�тивные и реактивные элементы, которые обеспечивают минимизацию энергии ак�тивных потерь при переходе от одного режима работы схемы к дру�гому. Также определяется вид закона изменения ЭДС источника питания (управляющего воздействия) и анализируется работа схемы при действии этой ЭДС.
Задача 1
Оптимальное управление в RC – цепи.
1.1. Описание объекта управления.
Математическая модель объекта получается на основе законов Кирхгофа и имеет вид диф�ференциального уравнения
(1)
где x(t)=uc(t) , u(t)=e(t) , p, b – числа, равные p = -1/RC, b = 1/RC
, .
1.2. Конструирование функционала – критерия оптимальности.
Найдем выражение для суммарной энергии активных потерь в схеме за время t1–t0 . Оно представляется в виде
. (2)
Для этого записываем выражение для активной мощности по�терь на сопротивлениях r и R :
или,
Получим, что q =1/R = 0,0125 , n = -2/R = - 0,025, m = 1/r + 1/R = 0,1458.
1.3. Формулировка задачи как вариационной задачи на услов�ный экстремум.
Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).
Таким образом, получаем следующую вариационную задачу:
Определить функции x(t) и u(t), доставляющие экстремум функционалу
,
при граничных условиях ,
и при дополнительном условии (уравнении связи)
накладываемом на функции x(t), u(t) , в классе которых ищется экстремум.
1.4. Синтез оптимального алгоритма управления.
1.4.1. Получение уравнений вариационной задачи.
Уравнения Эйлера – Лагранжа имеют вид
, ,
в которых
(t) – неопределенный множитель Лагранжа, – функция Лагранжа.
В итоге получаем систему уравнений:
(3)
(4)
(5)
Здесь (3), (4) – уравнения Эйлера – Лагранжа. К этим уравнениям добавлено уравнение объекта (5) (уравнение связи).
1.4.2. Отыскание решения уравнений вариационной задачи.
Решим уравнения (3) – (5) в следующем порядке:
1) Выразим из (4) u(t):
Затем подставим его в (3) и (5).
При этом получается система уравнений
,
с коэффициентами
a11 = p – nb/2m = -2285,67,
a12 = b2/2m = 2,1433*107,
a21 = 2q – n2/2m = 0,022,
a22 = nb/2m – p = 2285,67.
Таким образом получим следующую систему:
(6)
2) Запишем систему (6) в матричной форме
, (7)
где
,
.
3) Запишем решение уравнения (7) в виде
, (8)
где
– вектор начальных условий, а матричная экспонента определяется по формуле Лагранжа – Сильвестра
,
где 1 , 2 – собственные числа матрицы А. Е - единичная матрица.
Собственные числа матрицы А определяются из условия. Таким образом получим
,
.
Для определения неизвестного начального значения множителя Лагранжа (t0) , входящего в (8)
а) запишем (8) для момента времени t1
или
,
, (9)
где e11 , е12 , е21 , е22 – элементы матрицы (числа):
б) определим (t0) из первого уравнения системы (9)
Таким образом
Решим уравнение (7):
4). Запишем выражения для оптимальной траектории и оптимального управления:
- оптимальная траектория
- оптимальное управление
1.5. Анализ процессов в системе.
- Анализ процессов при оптимальном режиме
Анализ процессов при оптимальном режиме построим графики x(t) , u(t) на интервале t[t0,t1]. Этот интервал разбивается на 10 частей и вычисляются значения x(t) и u(t) в этих точках.
|
t
|
x(t)
|
u(t)
|
|
0
|
55
|
13,87372
|
|
0,0001
|
47,96211
|
18,06805
|
|
0,0002
|
43,21278
|
23,12452
|
|
0,0003
|
40,52539
|
29,2844
|
|
0,0004
|
39,77171
|
36,84161
|
|
0,0005
|
40,91578
|
46,15676
|
|
0,0006
|
44,01219
|
57,67432
|
|
0,0007
|
49,20869
|
71,94388
|
|
0,0008
|
56,75323
|
89,64631
|
|
0,0009
|
67,0058
|
111,6263
|
|
0,001
|
80,45563
|
138,9327
|
- Анализ процессов при линейном изменении тока i(t)
Полагая, что напряжение изменяется линейно от заданного начального состояния до заданного конечного состояния
xЛ(t) = kt + d ( ucЛ(t) = kt + d),
(величины k , d найдем из условия прохождения iЛ(t) и uЛ(t) через заданные начальное и конечное значения.)
xЛ(0) = 30 , xЛ(0.001) = 0.001k + 55 = 80, k=25000,
xЛ(t) = 25000t + 55.
запишем на основе (1)
выражение для закона управления uЛ(t) , обеспечивающее такое линейное изменение
По полученным данным построим графики процессов xЛ(t), uЛ(t):
|
t
|
xл
|
uл
|
|
0
|
55
|
65
|
|
0,0001
|
57,5
|
67,5
|
|
0,0002
|
60
|
70
|
|
0,0003
|
62,5
|
72,5
|
|
0,0004
|
65
|
75
|
|
0,0005
|
67,5
|
77,5
|
|
0,0006
|
70
|
80
|
|
0,0007
|
72,5
|
82,5
|
|
0,0008
|
75
|
85
|
|
0,0009
|
77,5
|
87,5
|
|
0,001
|
80
|
90
|
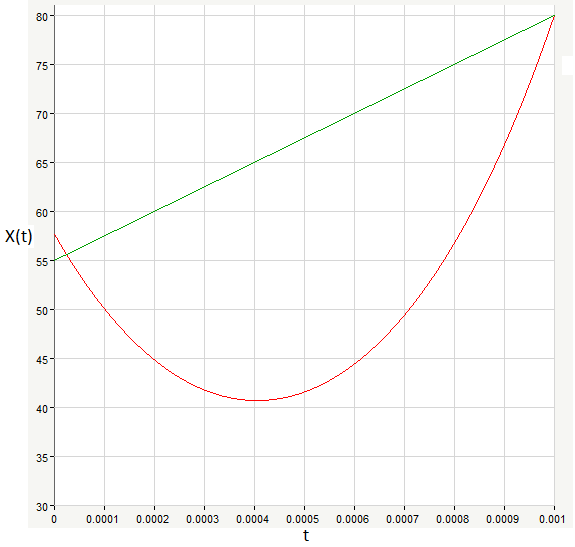
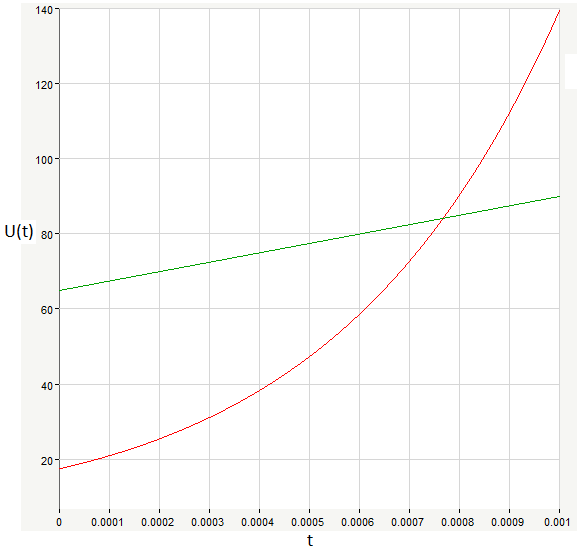
1.6. Сравнительная оценка процессов в схеме при оптимальном и линейном режимах.
1.6.1. Вычислим энергию активных потерь при оптимальном режиме, подставив в (2) x(t) и u(t).
1.6.2. Вычислим энергию активных потерь при линейном режиме путем подстановки в (2) xЛ(t) и uЛ(t).
2.6.3. Сравнивая полученные величины, делаем вывод, что суммарная энергия активных потерь (затрачиваемая на нагрев) при линейном режиме больше, что говорит о целесообразности работы схемы в оптимальном режиме.
Задача 2
2.1 Описание объекта управления
По закону Кирхгофа для узла 1 имеем:
или (1)
Рассмотрим контуры I и II. По закону Кирхгофа для напряжений получаем:
(2)
Введем обозначения:
, , .
Тогда выражения (1), (2) можно записать в виде:
(3)
Уравнения для выходных переменных
, . (4)
Объединяя (3) и (4), получаем математическую модель электрической схемы:
(5)
где
, , ,
, , С=,
Подставляя числовые значения параметров, получим:
, , С=,
Начальное положение объекта:
Конечное положение объекта:
2.2. Конструирование функционала – критерия оптимальности
Критерий оптимальности – квадратичный функционал
(6)
где - симметричная, неотрицательно-определенная матрица чисел, размерами ; - симметричная, положительно-определенная матрица чисел размерами .
Введем обозначения:
,
Запишем выражение для активной мощности по�терь на конденсаторе С, сопротивлениях r1, r2 и R1, R2:
Таким образом,
,
2.3. Формулировка задачи как вариационной задачи на услов�ный экстремум.
Для этого необходимо рассматривать в качестве уравнения связей уравнение системы (1), а в качестве функционала – функционал (2).
Таким образом, получаем следующую вариационную задачу:
Определить функции x(t) и u(t) доставляющие экстремум функционалу
,
при граничных условиях
,
и при дополнительных условиях (уравнениях связи)
накладываемом на функции x(t), u(t) , в классе которых ищется экстремум.
2.4. Синтез оптимального алгоритма управления
Составляем функцию Лагранжа:
Записываем уравнения Эйлера-Лагранжа:
(7)
Вычислим составленные соотношения:
Тогда уравнения Эйлера-Лагранжа принимают вид:
(8)
К последним уравнениям добавляем уравнение связи (уравнение объекта), получаем следующую систему:
(9)
(10)
Найдем U:
и подставим в первые три уравнения (10):
(11)
Введем вектор . Тогда систему (10) с учетом (11) можно представить в виде:
(12)
где Р – блочная матрица, имеющая вид:
(13)
Решение (12) в соответствии с формулой Коши:
(14)
Вычислив , ее можно представить следующим образом:
(15)
где - функциональные матрицы размеров .
Тогда из выражений (14), (15):
(16)
Для определения начального значения множителя Лагранжа запишем следующие соотношения:
(17)
Из первого уравнения (17) можно определить начальное условие множителя Лагранжа:
(18)
Теперь можно записать из выражений (16):
(19)
Оптимальное управление определится выражением:
Таким образом найдены соотношения для оптимальной траектории и оптимального управления:
2.5. Анализ процессов в системе
3.5.1 Анализ процессов при оптимальном режиме
Анализ процессов при оптимальном режиме построим графики X(t) , U(t) на интервале t[t0,t1]. Этот интервал разбивается на 1000 частей и вычисляются значения x(t) и u(t) в этих точках.
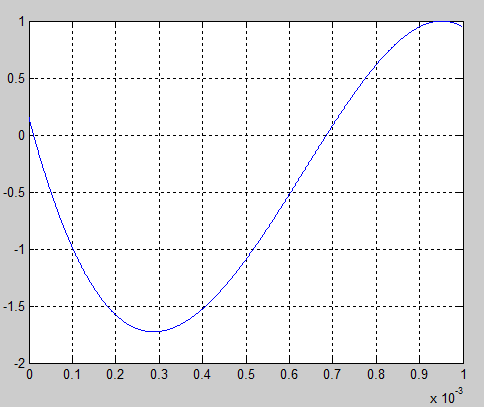
Рис. 1. График оптимального изменения тока i1(t)
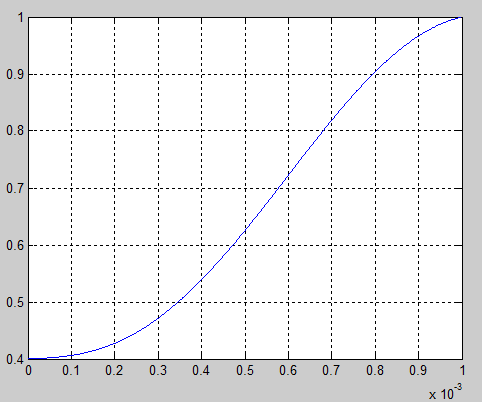
Рис. 2. График оптимального изменения тока i2(t)
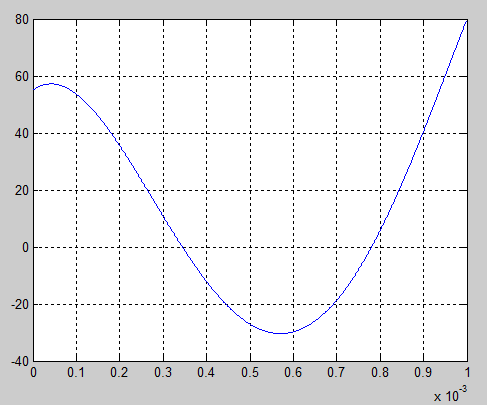
Рис. 3. График оптимального изменения напряжения uC(t)

Рис. 4. График оптимального изменения ЭДС e1(t)
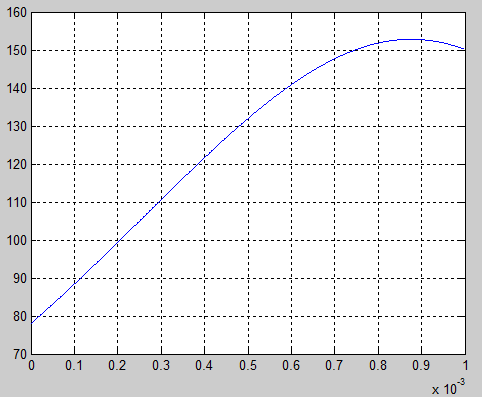
Рис. 5. График оптимального изменения ЭДС e2(t)
2.5.2 Анализ процессов при линейном режиме
Полагая, что ток и напряжения изменяются линейно от заданного начального состояния до заданного конечного состояния
xЛ(t) = kt + d
(величины k , d найдем из условия прохождения iЛ(t) и uЛ(t) через заданные начальное и конечное значения)
xЛ(0) = d=0.15 ,
xЛ1(0.001) = 0.001k + 0.15 = 0.95, k1=800, xЛ1(t) = 800t + 0.15
xЛ2(0.001) = 0.001k + 0.4 = 1, k2=600, xЛ2(t) = 600t + 0.4
xЛ3(0.001) = 0.001k + 55 = 80, k3=25000, xЛ3(t) = 25000t + 55
Запишем на основе (10)
По полученным данным построим графики процессов XЛ(t), UЛ(t).
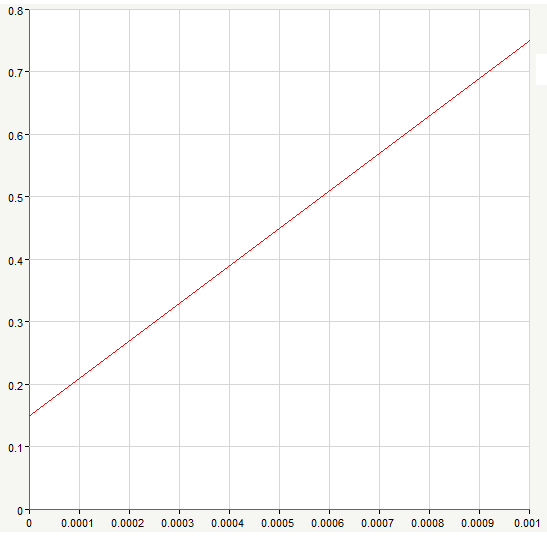
Рис. 6. График линейного изменения тока i1(t)
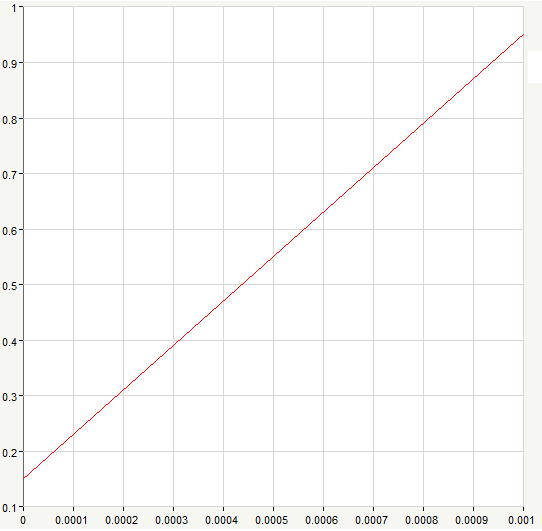
Рис. 7. График линейного изменения тока i2(t)
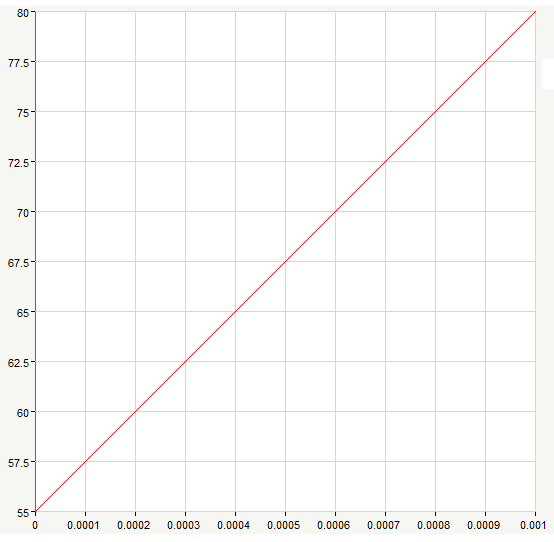
Рис. 8. График линейного изменения напряжения uC(t)
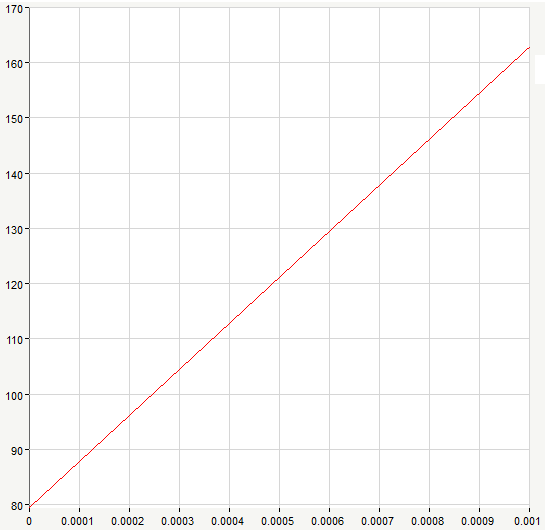
Рис. 9. График линейного изменения ЭДС e1(t)
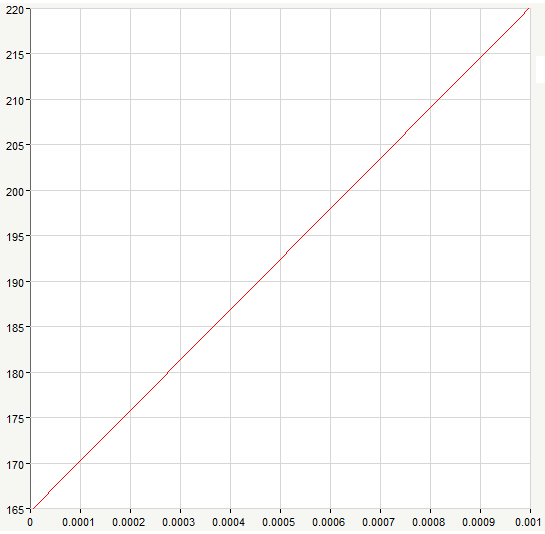
Рис. 10. График линейного изменения ЭДС e2(t)
2.6. Сравнительная оценка процессов в схеме при оптимальном и линейном режимах
2.6.1. Вычислим энергию активных потерь при оптимальном режиме
2.6.2. Вычислим энергию активных потерь при линейном режиме путем подстановки в (2) xЛ(t) и uЛ(t).
1.6.3. Сравнивая полученные величины, делаем вывод, что суммарная энергия активных потерь (затрачиваемая на нагрев) при линейном режиме больше, что говорит о целесообразности работы схемы в оптимальном режиме.
Заключение
В процессе выполнения курсовой работы были разработаны алгоритмы изменения режима работы электрической схемы, содержащей ак�тивные и реактивные элементы, которые обеспечивают минимизацию энергии ак�тивных потерь при переходе от одного режима работы схемы к дру�гому. Также был определен вид закона изменения ЭДС источника питания (управляющего воздействия) и была проанализирована работа схемы при действии этой ЭДС.
r
e(t)
C
R
i(t)
Оптимальное управление в электрических схемах