Экономико-математическое моделирование

Лекция. Экономико - математическое моделирование

1 Основные понятия.

«В мире не происходит ничего, в чем бы не был бы виден смысл какого-нибудь максимума или минимума»

Леонард Эйлер

Математические модели являются инструментальным средством описания задач самого разного класса. Причем задачи из разных областей экономики могут иметь похожие модели и решаться одинаковыми методами. Использование корректно построенной модели какого-либо процесса позволяет формализовать и описать наиболее важные связи между объектами, оценить различные параметры зависимостей, предсказывать поведение объекта, тем самым определять наилучшие решения в той или иной ситуации, оценить количественно эффективность принимаемых решений, прогнозировать их негативные последствия, использовать полученные оценки.

Математическая модель – это условный совокупный образ объекта в виде совокупности уравнений, неравенств, логических соотношений, созданный для получения новых знаний, исследования объекта, анализа и оценки принимаемых решений в конкретных или возможных ситуациях.

Моделирование – это метод исследования объектов, процессов на их моделях, построения и изучения моделей, определения и улучшения их характеристик, рационализирующих способ построения и управления.

Под моделированием понимается конструирование модели и работа с ней, состоящие из ряда последовательных и взаимосвязанных стадий: постановка задачи, построение модели, ее исследование, проверка и оценка полученного на основе модели решения, реализация результатов решения.

В разных науках существуют различные способы классификации моделей. Классификация зависит от признака, лежащего в основе. Экономическая модель - аналог совокупности производственных отношений, определенной общественно - экономической формаций, свойства которых и отношения между которыми описаны математическим методом (аксиомами).

Процесс построения и исследования модели можно представить как последовательность следующих шагов:

1) знакомство с предметной областью, прогноз или анализ процесса. Формулировка целей моделирования, уточнение круга задач. Предварительная оценка целесообразности построения модели;

2) переход от описания предметной области в содержательных терминах к формализованным описаниям: введение переменных, установления связей между объектами в виде формального текста, выбор алгоритма, технологии решения задачи;

3) выбор специального программного и аппаратного обеспечения, реализация разработанной модели программно-аппаратными средствами;

4) анализ построенной модели, оценка адекватности модели, работа с готовой моделью, выдвижение гипотез, альтернативных вариантов, принятие решений, разработка планов действий, контроль над реализацией плана.

Одним из видов математического моделирования экономических задач является линейное программирование – раздел математики, изучающий оптимизационные задачи определенного вида.

2.Линейное программирование.

2.1Введение в линейное программирование

Математические теории и методы играют важную роль во многих науках, начиная с физики и кончая психологией и лингвистикой. В конце XIX и начале XX вв. развитие математики складывалось главным образом под влиянием запросов физики и техники. Математический аппарат преимущественно использовался как инструмент расчета. Однако современная экономическая ситуация потребовала ответов на вопросы: как управлять созданной техникой, расходовать имеющееся сырье, ресурсы. Эти вопросы оказались актуальны и важны. Ясно, что рациональное использование имеющихся ресурсов может дать экономический эффект гораздо выше, чем создание новых. Поэтому развитие экономики поставило задачи оптимального управления производством и планирования. Возникла потребность в новых математических методах и дисциплинах, которые позволили бы разрешать эти важные экономические проблемы. Такие задачи привели к появлению новых математических дисциплин: линейного и нелинейного программирования, теории игр, теории массового обслуживания и т.д. А развитие современной вычислительной техники, персональных компьютеров и информационных технологий дало мощный толчок к применению математических методов и программных продуктов, реализующих эти алгоритмы.

В самых разных областях нашей жизни мы постоянно сталкиваемся по сути дела с одним и тем же классом задач. Нам известна полностью или частично ситуация, в которой мы находимся, и множество возможных альтернативных вариантов нашего дальнейшего поведения. Естественно возникает вопрос: какой из вариантов выбрать, а от каких отказаться. Грубо говоря, в решении этого вопроса и заключается проблема управления. Она с равным основанием может относиться к поведению отдельного человека или группы людей, к развитию тех или иных хозяйственных процессов или экономики в целом, к разработке каких-либо операций и т. п. Итак, необходимо остановиться на одном из допустимых вариантов, отыскать план. Здравый смысл подсказывает нам, что нужно выбрать «наилучший» вариант, который принесет наибольшую выгоду.

Сам по себе вопрос: какой вариант выбрать, ни на йоту не приближает нас к решению задачи управления, он даже не формулирует ее, поскольку абсолютно не ясно, что означают слова «наилучший вариант», «наилучшая выгода». Определение этого и составляет одну из важных проблем, без решения которой невозможны ни постановка, ни решение задачи управления. По существу речь идет о проблеме цели развития управляемой системы.

Цели, вообще говоря, могут быть разными. Применительно к хозяйственному объекту, в качестве цели могут выступать требования обеспечить максимум выпускаемой продукции при известном объеме имеющихся ресурсов, минимум затрат на производство фиксированной продукции, максимум получаемой прибыли, минимум транспортных расходов для оказания каких-либо услуг и т. д. Если цель сформулирована, то понятие «наилучший» становится четко определенным. «Наилучший» или, обычно говорят, оптимальный вариант отвечает двум требованиям: во-первых, он является одним из допустимых (или возможных) и, во-вторых, обеспечивает максимум или минимум (по смыслу) поставленной цели.

Таким образом, общий смысл широкого круга задач управления прост. Постановка задачи управления средствами математического программирования заключается в следующем. Формально записывается совокупность условий деятельности управляемого объекта, которая называется системой ограничений. Например, для производственного предприятия задаются объемы ресурсов, которые можно использовать (не обязательно полностью), возможности производственных мощностей и т. д. Вводятся переменные задачи, которые по своему физическому смыслу неотрицательны. Совокупность условий деятельности объекта записывается в виде системы уравнений и неравенств, которая определяет множество допустимых вариантов. Выбор оптимального варианта осуществляется с помощью, так называемой целевой функции, которая определяет цель развития объекта управления.

Если заданы система ограничений и целевая функция, – это значит, что задача управления поставлена. Те задачи, в которых целевая функция связана с переменными линейной зависимостью и область ограничений задана линейными уравнениями и неравенствами, называются задачами линейного программирования (ЗЛП). Слово «программирование» первоначально отнюдь не означало какую-то связь с ЭВМ, языками программирования и т. д. Оно означало, что в результате решения задачи вы получите некоторую программу действий – оптимальный план для достижения «наилучшего» результата. Хотя сейчас, конечно, все реальные задачи решаются на компьютере и необходимые программы, реализующие известные алгоритмы, написаны

2.2 Общая постановка задачи

Линейное программирование — наука о методах исследования и отыскания экстремальных (наибольших и наименьших) значений линейной функции, на неизвестные которой наложены линейные ограничения.

Эта линейная функция называется целевой, а ограничения, которые математически записываются в виде уравнений или неравенств, называются системой ограничений.

Определение .

Математическое выражение целевой функции и ее ограничений называется математической моделью экономической задачи.

Чтобы составить математическую модель задачи ЛП, необходимо:

— ввести обозначения переменных;

— исходя из цели экономических исследований, составить целевую функцию;

— учитывая ограничения в использовании экономических показателей задачи и их количественные закономерности, записать систему ограничений

В общем виде математическая модель задачи линейного программирования (ЛП) записывается как

Z(x)=C1X1+C2X2 + . . . +СJXJ + . . . +СnXn _ max(min)

при ограничениях:

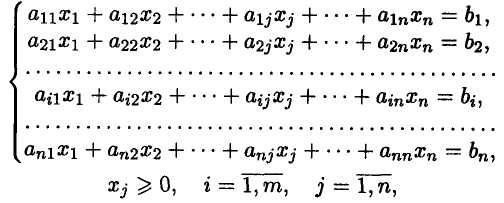
где Xi — неизвестные;a ij , bj , Ci — заданные постоянные величины.

Все или некоторые уравнения системы ограничений могут быть записаны в виде неравенств.

Математическая модель в более краткой записи имеет вид

Z(x) = Ci Xi max(min)

при ограничениях:

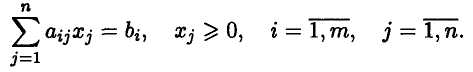
Определение Допустимым решением (планом) задачи линейного программирования называется вектор X = (х1, х2, ,...хn , ) , удовлетворяющий системе ограничений.

Множество допустимых решений образует область допустимых решений (ОДР).

Определение Допустимое решение, при котором целевая функция достигает своего экстремального значения, называется оптимальным решением задачи линейного программирования и обозначается Хопт.

Базисное допустимое решение

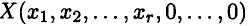
Задача (о составлении плана выпуска при определенной загрузке оборудования).

Некоторому заводу требуется составить оптимальный план выпуска двух видов изделий, которые обрабатываются на четырех видах машин. Известны определенные возможности и производительность оборудования; цена изделий, обеспечивающая прибыль заводу, составляет 4 тыс. руб. за изделие I вида, 6 тыс. руб. за изделие II вида. Составить план выпуска этих изделий так, чтобы от реализации их завод получил наибольшую прибыль. В таблице 2.2 указано время, необходимое для обработки каждого из двух видов изделий на оборудовании всех четырех видов.

Таблица

Изделия	Виды машин
	1	2	3	4
I	1	0,5	1	0
II	1	1	0	1
Возможное время работы машин	18	12	12	9

Построим математическую модель.

В задаче необходимо определить план выпуска изделий, обозначим за количество изделий I вида, за количество изделий II вида. Тогда определим, сколько времени затратит 1-я машина на обработку всех изделий. Она тратит 1 ед. времени на 1 изделие типа I, значит, на штук изделий потратит ед. времени, на обработку изделий типа II затратится ед. времени. Всего резерв времени работы 1-й машины 18 ед. времени. Значит, Аналогичные рассуждения со 2-й машиной, 3-й и 4-й дадут систему ограничений:

Общая прибыль будет выражена целевой функцией.

Задача состоит в нахождении на множестве решений системы такого решения, при котором значение целевой функции было бы максимальным.

2.3Формы записи задачи ЛП

В зависимости от системы ограничения различают в Л.П. три формы модели 1) каноническая 2) стандартная форма 3) общая форма.

Общая форма.

Z= c1x1+c2x2+..+cnxn max( min)

В общей форме линейной математической модели:

Требуется найти максимум или минимум,
Система ограничений содержит и неравенства, и уравнения;
Не все переменные должны быть неотрицательными

Каноническая форма

Z= c1x1+c2x2+..+cnxn max

В канонической форме линейной математической модели:

Требуется найти максимум целевой функции;
Система ограничений состоит только из уравнений;
Все переменные должны быть неотрицательными

Стандартная форма

Z= c1x1+c2x2+..+cnxn max

Z= c1x1+c2x2+..+cnxn min

В стандартной форме линейной математической модели:

Требуется найти максимум или минимум функции;
Все ограничения являются неравенствами;
Все переменные неотрицательные

Эти три формы эквиваленты между собой в том смысле, что от одной формы можно перейти к другой с помощью элементарных преобразований.

Необходимость перехода от одной формы к другой связана с методами решения задач: симплексный метод применяется к задаче, записанной в канонической форме, а графический метод-к стандартной форме матем.модели.

Переход от стандартной или общей формы к канонической форме.

Задачу минимизации z(x) заменяют задачей максимизации функции z1= -z(x).
Неравенства системы ограничений преобразуют в равенства. Для этого в неравенствах вида к их левым частям прибавляют дополнительные переменные хn+I 0, получают уравнение ; а в неравенствах вида вычитают такие переменные, в результате получают уравнения
Если в исходной задаче какая-то переменная хi не удовлетворяет условию неотрицательности, то ее заменяют разностью двух новых неотрицательных переменных: , где

Переход от канонической к стандартной.

Систему уравнений (ограничений) преобразовываем в эквивалентную ей систему неравенств, а целевую функцию записать через переменные полученной системы неравенств.

Приводим к единичному базису методом гауса. Приравняем все свободные переменные к 0, т.е. xm+1=xm+2=0 то получим первоначальное базисное решение.
Выражаем все базисные переменные через свободные.

Х1=b1-a1,m+1xm+1-..-a1,nxn>=0

Xm=bm-am,m+1-…-amnxn>=0

В функция цели вместо базисных переменных подставить их через переменные.

Пример. 1.

Записать в форме основной ЗЛП следующую задачу

Найти максимум функции F= при условиях

ответ

Пример 2.

Записать задачу, состоящую в минимизации функции Z= - при условиях

ответ

Пример.3.

Записать в форме стандартной задачи линейного программирования следующую задачу: найти максимум функции F= при условиях

Решение. Ответ F= x3+2x4 при условиях

2.3Двойственность в задачах линейного программирования

Каждая задача линейного программирования, называемая прямой или исходной, тесно связана с другой задачей, ее называют двойственной.

Математические модели этих задач имеют следующий вид.

прямая задача:

двойственная задача:

Несимметричные задачи	Симметричные задачи
Прямая задача	Двойственная задача	Прямая задача	Двойственная задача

Прямая задача	Двойственная задача	Прямая задача	Двойственная задача

Эти задачи экономически могут быть сформулированы следующим образом.

Прямая задача: сколько и какой продукции хi(i-1, 2, … , n) надо произвести, чтобы при заданных стоимостях единицы продукции Сi, объемом имеющихся ресурсов bj (j=1,2,…, m) и нормах расхода ресурсов аij максимизировать выпуск продукции в стоимостном виде.

Двойственная задача: какова должна быть оценка единицы каждого ресурса yj (j=1, 2,…, m), чтобы при заданных bj, ci и аij минимизировать общую оценку затрат на все ресурсы.

Правила построения двойственной задачи по имеемой прямой задаче:

Если прямая задача решается на максимум, то двойственная задача решается на минимум; если прямая задача решается на минимум то двойственная на максимум;

В задаче на максимум ограничения неравенства имеют вид – , а в задаче на минимум – ;

Каждому ограничению прямой задачи соответствует переменная двойственной задачи, в другой модели ограничению двойственной задачи соответствует переменная прямой задачи;

Матрица системы ограничений двойственной задачей получается из матрицы из матрицы систем ограничений прямой задачи транспонированием;

Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи и наоборот;

Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, в противном случае – как ограничение равенство;

Если какое либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.

Пример:

Прямая задача:

Двойственная задача:

В этой задаче – предельные оценки стоимости единицы каждого ресурса, целевая функция – оценка стоимости всех ресурсов, а каждое ограничение есть условие, что оценка ресурсов, идущих на производство продукции , не менее чем цена единицы продукции.

Взаимосвязь решений прямой и двойственной задач находится из трех теорем двойственности.

.2. 4 Теоремы двойственности.

Первая теорема двойственности:

Если одна из двойственных задач имеет оптимальное решение, то и другая задача имеет оптимальное решение, причем экстремальные значения целевых функций совпадают Z(X)=Z'(Y). Если одна из двойственных задач неразрешима вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Экономическое содержание первой теоремы двойственности: если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения и оценок ресурсов, при этом полная стоимость продукта, полученного в результате реализации оптимального плана, совпадает с суммарной оценкой ресурсов. Совпадения, значений целевых функций для соответствующих решений пары двойственных задач достаточно для того, чтобы эти решения были оптимальными. Это значит, что план производства и вектор оценок ресурсов являются оптимальными только тогда, когда полная стоимость произведенной продукции и суммарная оценка ресурсов совпадает.

Оценки выступают как инструмент сбалансирования затрат и результатов. Двойственные оценки обладают тем свойством, что они гарантируют рентабельность оптимального плана, т.е. равенство общей стоимости продукции и ресурсов обуславливает убыточность всякого другого плана отличающегося от оптимального. Двойственные оценки позволяют сопоставлять и сбалансировать затраты и результаты производства.

Вторая теорема двойственности:

Для того чтобы план Х* и Y* пары двойственных задач были оптимальными, необходимо и достаточно выполнение условий:

Эти условия называются условиями дополняющей нежесткости. Из них следует, что если какое-либо неравенство системы ограничений в одной из задач не обращается в строгое равенство оптимальным планом этой задачи, то соответствующий элемент оптимального плана двойственной задачи должен равняться нулю. Если какой-либо элемент оптимального плана одной из задач положителен, то соответствующее ограничение в двойственной задаче её оптимальным планом должно обращаться в строгое равенство, т.е.

если bj, то ;

если 0, то .

Аналогично,

если

если 0 то

Экономически это означает, что если по некоторому оптимальному плану X*= производства расход j-го ресурса меньше его запаса bj, то в оптимальном плане соответствующая двойственная оценка единицы этого ресурса равна нулю. Если же в некотором оптимальном плане оценок его j-й элемент больше нуля, то в оптимальном плане производства расход соответствующего ресурса равен его запасу. Отсюда следует вывод: двойственные оценки могут служить мерой дефицитности ресурсов. Дефицитный ресурс, т.е. полностью используемый по оптимальному плану производства, имеет положительную оценку, а избыточный ресурс, т.е. не используемый полностью имеет нулевую оценку.

Решение задач линейного программирования

геометрическим методом

Графический метод решения ЗЛП основан на следующих утверждениях.

Система ограничений ЗЛП геометрически представляет собой выпуклый многоугольник или выпуклую многоугольную область как пересечение полуплоскостей - геометрических образов неравенств системы.

Целевая функция Z = c1x1 + c2x2 геометрически изображает семейство параллельных прямых, перпендикулярных вектору нормали N(с1,с2). Эти прямые называются линиями уровня.

Линия уровня – это прямая, вдоль которой целевая функция принимает фиксированное значение.

Теорема. При перемещении линии уровня в направлении вектора нормали N значение целевой функции возрастает, в противоположном направлении - убывает.

Алгоритм графического метода решения ЗЛП.

В системе координат построить прямые по уравнениям, соответствующим каждому неравенству системы ограничений;

найти полуплоскость решения каждого неравенства системы (обозначить стрелками). Для определения полуплоскости необходимо выбрать любую контрольную точку, не лежащую на данной прямой. Подставить ее координаты в систему ограничений. Если неравенство выполняется, то нужно выбрать полуплоскость, содержащую контрольную точку. Если неравенство не выполняется нужно выбрать полуплоскость, не содержащую контрольную точку. В качестве контрольной точки рекомендуется выбирать точку с координатами (0;0);

найти многоугольник (многоугольную область) решений системы ограничений как пересечение полуплоскостей;

построить вектор нормали N. Начало вектора нормали в точке с координатами (0;0), конец вектора в точке с координатами (с1, с2);

через начало координат построить линию уровня, перпендикулярно к вектору нормали;

перемещать линию уровня параллельно самой себе по области решения в угловые точки, достигая max f при движении вектора N и достигая точки «выхода» (min f при движении достигая точки «входа»);

найти координаты точки max (min). Для этого необходимо решить систему уравнений прямых, которые пересекаются в этой точке или определить координаты по графику;

вычислить значение целевой функции в этой точке (ответ).

Задача. Решить графическим методом следующую задачу линейного программирования:

1. Найдем общую часть всех полуплоскостей решений. Получим, что область допустимых решений представляет собой четырехугольник

2. Построим вектор-градиент .

3. Построим прямую , проходящую через начало координат перпендикулярно .

4. Перемещаем прямую параллельно и пересечем ОДР. Последнее пересечение с ОДР будет в точке , которая соответствует максимуму целевой функции.

5.Определим координаты точки , решая систему.

Подставив координаты точки в целевую функцию, получим

Точка С (2,14; 0,85) является точкой максимума

Ответ: Fmax= 8,12 при x (2,14; 0,85)

Симплексный метод решения задач линейного программирования

Если в задаче три и более переменных, а в реальных экономических задачах как раз такая ситуация, то трудно представить наглядно графически область решений системы ограничений. Такие задачи решаются с помощью симплекс-метода (метода последовательных улучшений). По определенному правилу находится первоначальный опорный план (некоторая вершина области ограничений). Проверяется, является ли план оптимальным. Если да, то задача решена. Если нет, то переходим к другому, улучшенному плану – к другому базису. Значение целевой функции в новом базисе (в новой вершине) заведомо лучше, чем в предыдущем. Алгоритм перехода осуществляется с помощью некоторого вычислительного шага, который удобно записывать в виде таблиц, называемых симплекс-таблицами. Так как вершин конечное число, то за конечное число шагов мы приходим к оптимальному решению.

Еще раз заметим, что симплекс-метод применим для решения канонических задач ЛП, приведенных к специальному виду, т.е. имеющих базис (Базисным называется решение, соответствующее нулевым значениям свободных переменных), положительные правые части и целевую функцию, выраженную через небазисные переменные. Если задача не приведена к специальному виду, то нужны дополнительные шаги, о которых мы поговорим позже.

Рассмотрим алгоритм решения задачи симплекс-методом на конкретном примере задачи о планировании производства, предварительно построив модель и приведя ее к каноническому виду.

Задача (о планировании производства изделий).

Для изготовления изделий А и В склад может отпустить сырья не более 80 единиц. Причем на изготовление изделия А расходуется две единицы, а изделия В – одна единица сырья. Требуется спланировать производство так, чтобы была обеспечена наибольшая прибыль, если изделий А требуется изготовить не более 50 шт., а изделий В – не более 40 шт. Причем прибыль от реализации одного изделия А – 5 тыс. руб., а от одного изделия В – 3 тыс. руб.

Построим математическую модель, обозначив за – количество изделий А в плане, за – количество изделий В, тогда система ограничений будет выглядеть следующим образом:

Приведем задачу к каноническому виду, введя дополнительные переменные

I этап. Запись задачи в симплекс-таблицу.

Между системой ограничений задачи и симплекс-таблицей взаимно однозначное соответствие:

Строчек в таблице столько, сколько равенств в системе ограничений (+2); а столбцов столько, сколько переменных (+2).
Базисные переменные заполняют первый столбец, свободные и базисные – верхнюю строку таблицы.
Каждая строка таблицы соответствует уравнению.
Коэффициенты целевой функции записываются с противоположными знаками.
В правом нижнем углу первоначально записывается 0, если в функции нет свободного члена.( На этом месте (в правом нижнем углу) будет значение целевой функции, которое при переходе от одной таблице к другой должно увеличиваться). Итак, нашей системе ограничений соответствует табл. 1 и можно переходить ко II этапу решения.

Таблица 1

свобод. базис			-х3	-х4	-х5	правые части
	1	0	1	0	0	50	50/1=50
	0	1	0	1	0	40	-
	2	1	0	0	1	80	80/2=40 min
F	–5	–3	0	0	0	0

II этап. Проверка опорного плана на оптимальность.

Данной таблице соответствует опорный план: . Свободные переменные равны 0, а базисные переменные принимают значения чисел столбца свободных членов. Значение целевой функции

Наша задача проверить, является ли данный опорный план оптимальным, для этого необходимо просмотреть индексную строку – строку целевой функции F.

Возможны ситуации:

1) в индексной F–строке нет отрицательных элементов. Значит, план оптимален, можно выписать решение задачи. Целевая функция достигла своего оптимального значения, равного числу, стоящему в правом нижнем углу. Переходим к IV этапу;

2) в индексной строке есть хотя бы один отрицательный элемент, в столбце которого нет положительных. Тогда делаем вывод о том, что целевая функция неограниченно возрастает;

3) в индексной строке есть отрицательный элемент, в столбце которого есть хотя бы один положительный. Тогда переходим к III этапу, улучшаем опорный план, пересчитывая таблицу.

III этап. Улучшение опорного плана.

1. Из отрицательных элементов индексной F–строки выберем наибольший по модулю, назовем соответствующий ему столбец разрешающим и пометим .

2. Чтобы выбрать разрешающую строку, необходимо вычислить отношения элементов столбца свободных членов к только положительным элементам разрешающего столбца. Выбрать из полученных отношений минимальное. Соответствующий элемент, на котором достигается минимум, называется разрешающим. Будем выделять его квадратом.

В нашем примере, элемент – разрешающий. Строка, соответствующая этому элементу, тоже называется разрешающей.

Таблица 2

свобод. базис			-х3	-х4	-х5	правые части
	1	0	1	0	0	50	50/1=50
	0	1	0	1	0	40	-
		1	0	0	1	80	80/2=40 min
-F	–5	–3	0	0	0	0

3. Выбрав разрешающий элемент, делаем перечет таблицы по следующим правилам.

3.1. В новой таблице, таких же размеров, что и ранее, переменные при разрешающем элементе меняем местами, что соответствует смене базисов. В нашем примере: входит в базис, вместо , которая выходит из базиса, и теперь свободная (меняются местами элементы столбцов Х1 и Х5).

3.2. На месте разрешающего элемента (который теперь в столбце Х5)записываем обратное ему число

3.3. Элементы разрешающей строки делятся на разрешающий элемент.

3.4. Элементы разрешающего столбца делятся на разрешающий элемент и записываются с противоположным знаком

Таблица 3

свобод. базис		-х3	-х4	-х5	правые части
	0
	0			0
X1	1	0	0		40
-F	0

3.5. Все остальные элементы табл. 2.6 пересчитываем по правилу прямоугольника (в любом порядке).

Правило прямоугольника:

Пусть мы хотим посчитать элемент, например Соединяем пересчитываемый элемент мысленно с разрешающим, находим произведение.

Вычитаем произведение элементов, находящихся на другой диагонали получившегося прямоугольника. Разность делим на разрешающий элемент.

Итак, . Записываем 10 на место, где было 50.

Аналогично:

, , , .

Имеем в новом базисе пересчитанную табл. 2.8.

Таблица 4

свобод. базис		-х3	-х4	-х5	правые части
	0	1	0		10
	0	0	1	0	40	40/1=40
X1	1	0	0		40	40*2/1=80
-F	0	0	0		200

Базисными переменными теперь являются переменные . Значение целевой функции стало равно 200, т.е. увеличилось. Чтобы проверить данное базисное решение на оптимальность, надо перейти опять ко II этапу.

Для этого проверим индексную строку и, увидев в ней отрицательный элемент , назовем ему соответствующий столбец – разрешающим. Составим соотношения правых частей к только положительным элементам разрешающего столбца, выберем среди них минимальное: . Определим разрешающий элемент 1, теперь пересчет осуществляем согласно правилам 3.1–3.5.

свобод. базис			-х3	-х4	-х5	правые части
	0	0	1			30
	0	1	0	1	0	40
	1	0	0			20
-F	0	0	0			220

После пересчета таблицы убеждаемся, что в индексной строке последней таблицы нет отрицательных элементов, следовательно, задача решена, базисный план оптимален.

IV этап. Выписывание оптимального решения.

Если симплекс-метод остановился согласно пункту 1 II этапа, то решение задачи выписывается следующим образом. Базисные переменные принимают значения столбца правых частей соответственно. В нашем примере Свободные переменные равны 0: Значение целевой функции равно числу в правом нижнем углу таблицы: Итак,

Ответ к задаче: необходимо в план выпуска включить 20 изделий типа А, 40 изделий типа В, при этом прибыль будет максимальной и составит 220 руб. Переменная означает, что есть излишки по первому ограничению в количестве 30 ед., по смыслу этой задачи – это потенциальная возможность выпуска.

PAGE \* MERGEFORMAT 11

Экономико-математическое моделирование