ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ ЗОНЫ ПРОВОДИМОСТИ НА СТРУКТУРУ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ ПРИМЕСНЫХ ИОНОВ В КРИСТАЛЛАХ
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение
высшего профессионального образования
«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»
(ФГБОУ ВПО «КубГУ»)
Физико-технический факультет
Кафедра физики и информационных систем
Допустить к защите в ГАК
_____ . ____ . 2014 г.
Заведующий кафедрой
д-р физ-мат. наук, профессор
_______________Н. М. Богатов
ВЫПУСКНАЯ КВАЛИФИКАЦИОННАЯ РАБОТА БАКАЛАВРА
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ ЗОНЫ ПРОВОДИМОСТИ НА СТРУКТУРУ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ ПРИМЕСНЫХ ИОНОВ В КРИСТАЛЛАХ
Работу выполнил _____________________________ Дмитриев Денис Игоревич
Специальность 010700 – Физика
Научный руководитель
канд. физ.-мат. наук, доцент _________________________________ Е.Н.Тумаев
Нормоконтролер ________________________________________ П.И.Быковский
Краснодар 2014
РЕФЕРАТ
Выпускная квалификационная работа 67с., 8 рис., 20 источников.
ЗОНА ПРОВОДИМОСТИ, ЭНЕРГЕТИЧЕСКИЕ УРОВНИ, ОПТИЧЕСКИЙ ЭЛЕКТРОН ПРИМЕСНОГО ИОНА, КРИСТАЛЛИЧЕСКОЕ ПОЛЕ, КОРРЕЛЯЦИОННАЯ ЭНЕРГИЯ, 3–d ИОН.
Целью выпускной квалификационной работы является теоретическое и численное исследование спектроскопических свойств 3d - ионов в полупроводниковых матрицах.
В ходе выполнения выпускной квалификационной работы было показано, что влияние зоны проводимости на структуру энергетических уровней 3d1 - иона сводится к дальнейшему снятию вырождения для тетраэдрической позиции.
СОДЕРЖАНИЕ
|
[0.1] ВВЕДЕНИЕ
[0.2] В последнее время возникла необходимость в использовании квантовой электроники широкозонных полупроводниковых материалов, активированных ионами группы железа. Главной областью применения таких сред является
[0.3] создание новых магнитных материалов с новыми свойствами. Для этой цели двойные проводники типа A3B5 вводят ионы железа, кобольта, никеля, придавая полупроводнику магнитные свойства. Теоретические и экспериментальные аспекты создания и исследования таких сред нашли отражение в монографии Кикоина, Флюрова, изданной в Израиле.[1] Наряду с этим полупроводниковые материалы, активированные другим классом ионов группы железа, а именно титаном, ванадием, хромом, перспективны для применения в качестве комбинированных активных сред, для создания лазеров, люминесцентных источников света и т.п. Для таких сред определяющим свойством являются спектроскопические, а не магнитные свойства ионов. Таким образом, проблема исследования спектроскопических свойств, перечисленных 3d - ионов, является актуальной и составляет содержание настоящей выпускной квалификационной работы работы.
[0.4] Выпускная квалификационная работа состоит из введения, 4 глав и заключения. Во введении обосновывается актуальность работы.
[0.5] В 1 главе рассматривается теоретические подходы, используемые для исследования спектроскопических свойств примесных ионов в кристаллических матрицах.
[0.6] В настоящее время имеется проблема учета корреляционных эффектов при взаимодействии одиночного электрона с электронным ансамблем. Дело в том, что в ансамбле электронов распределение электронов по состояниям производится с учетом принципа Паули. Следовательно, изменение состояния отдельного электрона ведет к перестройке состояний электронного ансамбля. Проблема учета этого эффекта в настоящее время далека от своего решения и учитывается в основном эмпирическими методами. Строгие рассчеты существуют только для свободного газа электронов в ящике с кулоновским взаимодействием между ними. Соответствующие рассчеты были выполнены Гелл-Маном и Бракнером, являются по существу единственным вычислением корреляционной энергии из первых принципов. Поэтому в главе 2 проведен обзор эмперических формул для корреляционной энергии электронно-дырочной плазме в полупроводниках.
[0.7] В главе 3 приводится пример рассчета свойств двумерной электронно-дырочной плазмы из первых принципов, при помощи численных методов. Изложение базируется на оригинальной работе Васильченко А. А. и Тумаева Е. Н.[2] с целью применения этих методов для исследования спектроскопических свойств ионов в полупроводниках.
[0.8] В главе 4 развивается общая теория взаимодействия оптического электрона примесного иона с ансамблем электронов зоны проводимости. Рассчеты выполнены в одном электронном приближении, для которого получена величина для расщепления уровня энергии 3d1 - иона в тетраэдрической позиции. Величина полного расщепления уровней примесного иона складывается из вычисленной в главе 4 величины расщепления в элетронном приближении и приведенной в главах 2 и 3 величины корреляционной энергии. Обе эти энергии зависят от плотности носителей заряда в зоне проводимости и подбираются под конкретную полупроводниковую матрицу . Таким образом выпускная квалификационная работа состоит не только из вычисления расщепления уровней энергии в одноэлектронном приближении, но и учете коллективных эффектов. Насколько известно, автору и научному руководителю выпускной квалификационной работы в таком объеме задача исследования спектроскопических свойств не ставилась.
[0.9] 1 ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ИССЛЕДОВАНИЯ СПЕКТРОСКОПИЧЕСКИХ СВОЙСТВ ПРИМЕСНЫХ ИОНОВ В КРИСТАЛЛИЧЕСКИХ МАТРИЦАХ
[0.10] Теория кристаллического поля
[0.11] Учет кулоновского взаимодействия
[0.12] Учет спин-орбитального взаимодействия
[0.13] 3 КУЛОНОВСКИЕ КОРРЕЛЯЦИИ И ЭЛЕКТРОННО – ДЫРОЧНАЯ ЖИДКОСТЬ В ДВОЙНЫХ КВАНТОВЫХ ЯМАХ
|
2 Обзор теоретических исследований по учету корреляционных эффектов в многоэлектронных системах…………………………………………………......19
3 Кулоновские корреляции и электронно – дырочная жидкость в двойных квантовых ямах...……………………………………………………..………………….29
3.1 Модель………………………………….………………………………...31
3.2 Корреляционная энергия..………….……….………………….….........33
3.3 Уравнение состояния……………………………………........................38
3.4 Обсуждение результатов…………………………………………….….41
4 Расчет вклада кулоновского взаимодействия в энергию связанного оптического электрона примесного 3d – ионав полупроводниковых матрицах………45
4.1 Расчет вклада кулоновского взаимодействия оптического электрона примесного3d – иона с электронами зоны проводимости………………………..45
Заключение………………………………………………………………………….65
Список использованных источников……………………………………………..66
ВВЕДЕНИЕ
В последнее время возникла необходимость в использовании квантовой электроники широкозонных полупроводниковых материалов, активированных ионами группы железа. Главной областью применения таких сред является
создание новых магнитных материалов с новыми свойствами. Для этой цели двойные проводники типа A3B5 вводят ионы железа, кобольта, никеля, придавая полупроводнику магнитные свойства. Теоретические и экспериментальные аспекты создания и исследования таких сред нашли отражение в монографии Кикоина, Флюрова, изданной в Израиле.[1] Наряду с этим полупроводниковые материалы, активированные другим классом ионов группы железа, а именно титаном, ванадием, хромом, перспективны для применения в качестве комбинированных активных сред, для создания лазеров, люминесцентных источников света и т.п. Для таких сред определяющим свойством являются спектроскопические, а не магнитные свойства ионов. Таким образом, проблема исследования спектроскопических свойств, перечисленных 3d - ионов, является актуальной и составляет содержание настоящей выпускной квалификационной работы работы.
Выпускная квалификационная работа состоит из введения, 4 глав и заключения. Во введении обосновывается актуальность работы.
В 1 главе рассматривается теоретические подходы, используемые для исследования спектроскопических свойств примесных ионов в кристаллических матрицах.
В настоящее время имеется проблема учета корреляционных эффектов при взаимодействии одиночного электрона с электронным ансамблем. Дело в том, что в ансамбле электронов распределение электронов по состояниям производится с учетом принципа Паули. Следовательно, изменение состояния отдельного электрона ведет к перестройке состояний электронного ансамбля. Проблема учета этого эффекта в настоящее время далека от своего решения и учитывается в основном эмпирическими методами. Строгие рассчеты существуют только для свободного газа электронов в ящике с кулоновским взаимодействием между ними. Соответствующие рассчеты были выполнены Гелл-Маном и Бракнером, являются по существу единственным вычислением корреляционной энергии из первых принципов. Поэтому в главе 2 проведен обзор эмперических формул для корреляционной энергии электронно-дырочной плазме в полупроводниках.
В главе 3 приводится пример рассчета свойств двумерной электронно-дырочной плазмы из первых принципов, при помощи численных методов. Изложение базируется на оригинальной работе Васильченко А. А. и Тумаева Е. Н.[2] с целью применения этих методов для исследования спектроскопических свойств ионов в полупроводниках.
В главе 4 развивается общая теория взаимодействия оптического электрона примесного иона с ансамблем электронов зоны проводимости. Рассчеты выполнены в одном электронном приближении, для которого получена величина для расщепления уровня энергии 3d1 - иона в тетраэдрической позиции. Величина полного расщепления уровней примесного иона складывается из вычисленной в главе 4 величины расщепления в элетронном приближении и приведенной в главах 2 и 3 величины корреляционной энергии. Обе эти энергии зависят от плотности носителей заряда в зоне проводимости и подбираются под конкретную полупроводниковую матрицу . Таким образом выпускная квалификационная работа состоит не только из вычисления расщепления уровней энергии в одноэлектронном приближении, но и учете коллективных эффектов. Насколько известно, автору и научному руководителю выпускной квалификационной работы в таком объеме задача исследования спектроскопических свойств не ставилась.
В заключении приведены основные результаты выпускной квалификационной работы.
1 ТЕОРЕТИЧЕСКИЕ ПОДХОДЫ, ИСПОЛЬЗУЕМЫЕ ДЛЯ ИССЛЕДОВАНИЯ СПЕКТРОСКОПИЧЕСКИХ СВОЙСТВ ПРИМЕСНЫХ ИОНОВ В КРИСТАЛЛИЧЕСКИХ МАТРИЦАХ
Спектроскопические свойства примесных ионов переходных металлов в кристаллических матрицах являются результатом взаимодействия большого числа частиц, вследствие чего точное решение уравнений Шредингера для этих частиц не представляется возможным. Решение можно найти в рамках различных приближений. Так, в частности, очевидно, что влияние на примесный ион атомов решетки будет тем меньше, чем сильнее они удалены от примеси. Поэтому в приближенном гамильтониане примесного центра можно учесть влияние лишь наиболее близких к активатору атомов решетки.
Поскольку масса электронов на несколько порядков меньше массы ядер, а скорость электронов на несколько порядков превышает скорость даже самых легких ядер, то можно в нулевом приближении считать ядра покоящимися. В последующих приближениях с помощью теории возмущений можно учесть движение ядер. Такой подход получил название адиабатического приближения.
Пусть – совокупность координат всех электронов относительно центра инерции рассматриваемой системы, а – совокупность координат ядер. Гамильтониан системы имеет вид
(1.1)
где – оператор кинетической энергии электронов, –масса всех электронов, – оператор кинетической энергии ядер, – масса ядер, – оператор потенциальной энергии взаимодействия между всеми частицами.
В нулевом приближении задача сводится к решению уравнения Шредингера
(1.2)
при постоянных Индекс обозначает набор квантовых чисел, характеризующих стационарное состояние с энергией и волновой функцией
Если известны решения (1.2), то решения уравнения
(1.3)
можно искать в виде
(1.4)
Если подставить (1.4) в (1.3), умножить на и проинтегрировать по координатам электронов, то получим систему уравнений
(1.5)
оператор имеет вид
(1.6)
Рассматривая оператор как малый, систему (1.5) можно решать методом последовательных приближений. Физически требование малости означает слабую зависимость электронных волновых функций от ядерных смещений.
В нулевом (адиабатическом) приближении полагается равным 0, волновая функция системы принимает вид
(1.7)
где квантовые числа определяют состояния движения ядер. Для состояний электронов, характеризуемых квантовыми числами , получаем систему уравнений
(1.8)
Таким образом, адиабатическое приближение позволяет свести решаемую задачу к случаю неподвижных ядер.
- Теория кристаллического поля
В этом подразделе излагается теория кристаллического поля в приближении точечных зарядов, позволяющая теоретически приближенно описывать взаимодействие примесного иона с кристаллической решеткой, предполагая, что окружающие центральный ион лиганды являются неподвижными точечными зарядами. Приведены данные о волновых функциях электрона в случае группы симметрии системы .
В случае неподвижных ядер для нахождения энергетических уровней системы, ее волновых функций может с успехом применяться теория кристаллического поля. Ее основы были заложены Х.Бете в 1929 г. Основная идея теории кристаллического поля заключается в том, что гамильтониан ПЦ можно представить в виде линейной комбинации одноэлектронных операторов , [3] которые действуют только на угловые части волновых функций и при вращении координат всех электронов ПЦ преобразуются как неприводимые тензорные операторы:
. (1.6)
При описании квантовомеханических систем давно и плодотворно используются методы теории групп.[4] Гамильтониан системы, обладающей нетривиальной группой симметрии , инвариантен относительно преобразований пространства, переводящих эту систему в себя.[5] То есть решение уравнения Шредингера при преобразовании симметрии переходит также в некоторое, вообще говоря, другое решение уравнения Шредингера. Волновые функции и соответствующие им уровни энергии можно классифицировать по неприводимым представлениям группы . Если – размерность представления , соответствующего энергии , то уровень должен быть по крайней мере –кратно вырожден.[6]
Традиционно для теоретико-группового описания ПЦ в кристаллах используются представления группы симметрии октаэдра . Это связано с тем, что во многих случаях симметрию окружения ПЦ можно приближенно считать октаэдрической. Отклонение действительной симметрии от октаэдрической можно затем учесть методами теории возмущений.
Простейшим вариантом теории кристаллического поля является модель точечных зарядов, где все заряды предполагаются неподвижными, а взаимодействие между ними – электростатическим.
Рассмотрим водородный атом с единственным 3d-электроном, окруженный шестью точечными зарядами величины (здесь и далее полагаем , заряд электрона равен ). Направление осей координат показано на рисунке 1.

Рисунок 1.1 - Октаэдрическое окружение лигандов. Группа симметрии поля .
Расстояние между ПЦ и каждым лигандом равно . Оператор Гамильтона электрона центрального атома равен
, (1.7)
где – потенциальная энергия электрона относительно центрального ядра, расположенного в начале координат, – энергия электрона относительно кристаллического поля лигандов, – радиус-вектор электрона.
, (1.8)
– радиус-вектор –го лиганда.
Данное уравнение Шредингера может решаться с помощью теории возмущений. выражается через полиномы Лежандра следующим образом:
, (1.9)
– угол между и . Отсюда
, (1.10)
, (1.11)
, (1.12)
и – полярные координаты.
Волновые функции 3d-электронов имеют вид
. (1.13)
Между функциями будут отличны от нуля только следующие матричные элементы :
, (1.14)
, (1.15)
, (1.16)
, (1.17)
, (1.18)
. (1.19)
Решение характеристического уравнения показывает, что пятикратно вырожденный 3d-уровень свободного иона с энергией расщепляется кристаллическим полем на двукратно вырожденный уровень с энергией
(1.20)
и трехкратно вырожденный уровень с энергией
. (1.21)
Уровень при преобразованиях симметрии системы преобразуется по представлению группы , уровень – по представлению . Действительные базисные волновые функции пространства могут быть выбраны следующим образом:
, (1.22)
аналогично для пространства :
,
, (1.23)
.
- Учет кулоновского взаимодействия
Изложен способ перехода от случая единственного электрона к случаю нескольких электронов, взаимодействующих между собой. Рассмотрен метод расчета энергий получающихся многоэлектронных состояний, а также величин их расщепления в случае отклонения симметрии системы от октаэдрической.
Используя решение задачи об энергетических уровнях одного электрона в кристаллическом поле, легко получить энергии нескольких электронов
в этом же поле. Гамильтониан системы двух электронов, движущихся в поле, описанном выше, имеет вид:
, (1.24)
, (1.25)
где – расстояние между электронами, а операторы и действуют на электрон с номером .
Известно, что если и – орбитальные базисные функции неприводимых представлений группы и соответственно, то базисные функции неприводимых представлений , на которые распадается произведение Кронекера , выражаются через линейные комбинации произведений с помощью коэффициентов Клебша-Гордана группы :
. (1.26)
В пространстве спиновых функций аналогичную роль играют коэффициенты Вигнера для спина.
Если – собственные функции операторов , , а , то
, (1.27)
где – собственная функция операторов и с собственными значениями и соответственно, – спиновые коэффициенты Вигнера.
С помощью коэффициентов Вигнера и Клебша-Гордана легко получить двухэлектронные волновые функции, являющиеся базисными функциями , преобразующимися по представлению группы , которые будут собственными функциями операторов и с собственными значениями и соответственно:
(1.28)
.
Индекс различает разные представления, эквивалентные .
– (1.29)
определитель Слэтера.
Аналогичная –электронная функция строится через –электронную антисимметризацию выражения
(1.30)
Если предположить, что кристаллическое окружение не слишком сильно деформирует волновые функции ПЦ, и можно предположить, что они имеют вид
, (1.31)
то матричные элементы оператора кулоновского взаимодействия выражаются через параметры Рак , и (которые, в свою очередь, можно выразить через параметры Слэтера-Кондона ). Приближение –функций (1.31) также позволяет выразить матричные элементы оператора спин-орбитального взаимодействия через единственный параметр .
Во многих случаях симметрия окружения ПЦ отличается от . Тогда потенциал кристаллического поля представляется в виде суммы
, (1.32)
где имеет группу симметрии , а обладает более низкой симметрией, чем . Влияние на уровни энергии ПЦ можно учесть методами теории возмущений после учета других взаимодействий. Однако эффективность такого подхода вызывает обоснованные сомнения. Так, в работе [5] отмечено, что нахождение уровней энергии примесного иона Cr3+ в кристаллах ниобата лития, основанное на теории тетраэдрической симметрии, едва ли обеспечит исчерпывающее решение задачи интерпретации спектров хрома в этом кристалле. Это свидетельствует о необходимости адаптации формул теории кристаллического поля для случаев низкосимметричных позиций, выполненной в следующем разделе.
- Учет спин-орбитального взаимодействия
Оператор спин-орбитального взаимодействия
(1.33)
имеет для ионов переходных металлов величину, приблизительно на порядок меньшую, чем операторы кулоновского взаимодействия или кристаллического поля. Здесь
, (1.34)
– сферически симметричный потенциал электрона.
Однако сравним по порядку величины с поправочным оператором , характеризующим отклонение симметрии кристаллического поля от октаэдрической. Поэтому спин-орбитальное взаимодействие учитывается для ионов переходных металлов, как правило, в последнюю очередь.
Внешняя оболочка иона Cr3+ содержит три электрона. И оператор Гамильтона данной трехэлектронной системы инвариантен относительно действия оператора обращения времени.[6] Следовательно, по теореме Крамерса уровни энергии рассматриваемой системы должны быть как минимум двукратно вырождены.И поэтому учет разными авторами всех взаимодействий электронов, включая спин-орбитальное, приводит к вырожденным энергетическим уровням. Эксперимент также дает серию крамерсовых дублетов в спектре.
Величины расщеплений уровней спин-орбитальным взаимодействием выражаются через единственную постоянную спин-орбитального взаимодействия
(1.35)
Ее значение можно с достаточной точностью определить из сопоставления расчетных значений с экспериментом.[7] Поскольку спин-орбитальное взаимодействие для иона хрома в ниобате лития является малым, его мультиплеты расположены далеко друг от друга, и тонкая структура хорошо различима.
2 ОБЗОР ТЕОРЕТИЧЕСКИХ ИССЛЕДОВАНИЙ ПО УЧЕТУ КОРРЕЛЯЦИОННЫХ ЭФФЕКТОВ В МНОГОЭЛЕКТРОННЫХ СИСТЕМАХ
Одним их характерных квантовых эффектов, обусловленных тождественностью электронов в многоэлектронных системах, являются эффекты, связанные с корреляцией электронов. происхождение этих эффектов можно пояснить следующим образом. Если уровни энергии электронов заполнены в соответствии с принципом Паули, то изменение состояния любого электрона влияет на состояние всех остальных электронов системы одновременно. Наличие такого влияния приводит к появлению у системы электронов дополнительной энергии, которая называется корреляционной энергией. Поскольку при конструировании мнгоэлектронной волновой функции она строится как антисимметричная комбинация одноэлектронных волновых функций, что обуславливает появление обменной энергии, то корреляционная энергия оказывается самым тесным образом связана с обменной энергией, что позволяет рассматривать их сумму как единую обменно-корреляционную энергию.
Ввиду сложности задачи исследования системы многих взаимодействующих электронов, для ее учета используют различные модельные приближения, эмпирические формулы и т.п. Одной из немногих систем, для которой удается вычислить корреляционную энергию методом диаграмм Фейнмана, является теория электронного газа Гелл-Манна и Бракнера.[7] Другим подходом к расчету обменно-корреляционой энергии является использование численных методов, базирующихся на использовании уравнения Кона-Шэма (метод функционала плотности). Изложим ниже применение указанного метода к электрон-дырочной плазме в двумерных полупроводниках, т.е., на тонких пленках. Более конкретно, рассмотрим образование двойного электрического слоя в электронно-дырочной плазме.
Теорию функционала плотности можно легко обобщить на многокомпонентные системы. Так для двухкомпонентной системы (электроны и дырки) полная энергия запишется как
(2.)
где , – кинетическая энергия носителей, - электростатическая энергия, - обменно-корреляционная энергия. Варьируя выражение (2.1) по плотностям и , получим два уравнения Шредингера:
(2.)
где i=eh.
Здесь и далее используется экситонная система единиц: энергия измеряется в единицах , а длина в единицах , где - оптическая масса.
Таким образом, проблема сводится к решению двух одномерных нелинейных уравнений Шредингера для частиц в первой и во второй ямах, которые описываются потенциалами и и , где - обменно-корреляционный потенциал, а электростатический потенциал находится из уравнения Пуасcона :
(2.)
с граничными условиями:
, (2.)
где , , -двумерные плотности электронов и дырок, соответственно.
Чтобы упростить вычисления, далее будем считать, что заполнен только один уровень размерного квантования. Когда заполнен только нижний уровень размерного квантования, плотности носителей задаются выражениями:
, (2.)
Для обменно-корреляционной энергии используем приближение локальной
плотности:
(2.)
где ( - обменно-корреляционная энергия электронов и дырок на единицу объема. Тогда обменно-корреляционные потенциалы имеют вид:
, . (2.)
В общем случае вид выражения для неизвестен. В случае нейтральной электронно-дырочной плазмы для обменно-корреляционной энергии имеется аппроксимационная формула:
, (2.)
где , a=-4,8316 , b=-5,0879, c=0,0152, d=3,0426. Для однокомпонентной системы ( ne nh =0 ) будем использовать следующее выражение:
, (2.)
где - число эквивалентных долин.
В общем случае возьмем следующую аппроксимацию для :
(2.10)
где и - обменно-корреляционные энергии на частицу задаются формулами (2.10) и (2.9), соответственно, , ,
Для f (y) используется такое же выражение:
(2.11)
Предполагаем, что существует равновесие между поверхностью и объемом, тогда должны выполняться условия:
, (2.12)
, (2.13)
где - среднее удаление электронов (дырок) от поверхности полупроводника, - число эквивалентных долин, e и h- квазиуровни Ферми для электронов и дырок, . Таким образом , задавая и мы можем найти концентрации и для заданных значений .
Физическая причина образования второго слоя очень проста. Предположим, что первый слой является электронным, а второй дырочным. Тогда при освещении светом, когда и , падение потенциала в электронном слое происходит на расстоянии порядка нескольких экситонных радиусов и дырки смогут находиться вблизи электронного слоя. Переэкранировка внешнего электрического поля электронами будет гаситься дырками, причем дырки совместно с электронами будут сами создавать себе потенциальную яму.[8,16]
Оценим изменение полной энергии при добавлении к двумерному слою электронов двумерного слоя дырок плотности. Пусть слои находятся на расстоянии, тогда, считая, что носители образуют - слои, получаем для изменения электростатической энергии: . В кинетической энергии учитываем только энергию движения вдоль поверхности. Тогда получим для вклада кинетической энергии в : T. Для изменения обменно-корреляционной энергии запишем приближенное выражение: , где - средняя обменно-корреляционная энергия.
Таким образом, изменение полной энергии Et запишется в следующем виде:
Et=+4Nh2zeh+ Nh, (2.14)
Используя простую аппроксимацию, для и пренебрегая электростатической энергией , получаем необходимое условие для образования 2МЭДП:
, (2.15)
где - характерный размер волновой функции электронов,
- константа, численное значение которой порядка единицы.
Из выражения (2.15) следует, что наиболее стабильное состояние 2МЭДП будет наблюдаться для поверхностей с большими и .
Для более строгого определения условий существования 2МЭДП необходимо численно самосогласованно решить уравнения Кона-Шэма (2.1)-(2.9). Самосогласованные вычисления сделаны для различных поверхностей кремния. На рисунке 2.1 показаны волновые функции и эффективные потенциалы для поверхности кремния (100), причем в первом слое находятся дырки, а во втором электроны (h-e слой). Видно, что волновые функции электронов и дырок сильно перекрываются.[9]
Для того чтобы показать возможность образования второго слоя (например, электронного) необходимо вычислить среднюю энергию связи электрона и дырки:
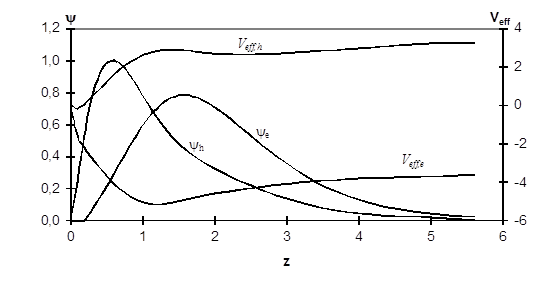
Рисунок 2.1 - Самосогласованные потенциалы и волновые функции электронов и дырок для поверхности кремния: =1012см-2, Ne=4*1011см-2.
Область существования 2МЭДП находится из условия. Видно, что существует область плотностей (а значит и область для квазиуровней Ферми e и h), в которой возможно образование 2МЭДП. Убывание средней энергии связи с возрастанием плотности (или) происходит в основном из-за возрастания кинетической энергии носителей вдоль поверхности полупроводника. Поэтому для поверхностей с большими эффективными продольными массами и (или) большим числом эквивалентных долин 2МЭДП может образовываться для более широкой области плотностей во втором слое. Отметим, что для поверхности существует критическая концентрация , выше которой образование 2МЭДП невозможно.
Именно для поверхности кремния имеется наибольшее число эквивалентных долин и, следовательно, кинетическая энергия носителей дает наименьший вклад в полную энергию.[10] Сравнение рисунков показывает, что средняя энергия связи электрона и дырки существенно больше для поверхности кремния.
Интересная особенность возникает в зависимости суммы квазиуровней Ферми электронов и дырок от концентрации носителей во втором слое (Рисунок 2.2).
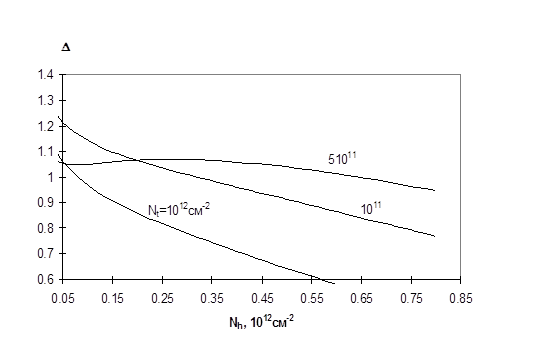
Рисунок 2.2 - Зависимость средней энергии связи электронов и дырок от концентрации дырок в кремнии.
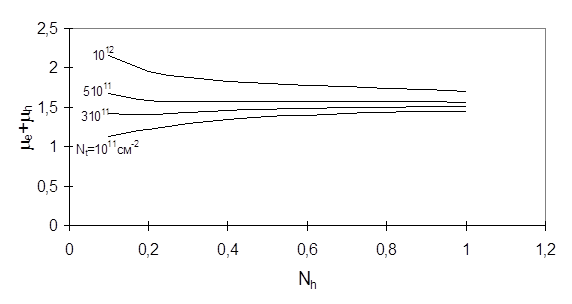
Рисунок 2.3 - Зависимость суммы квазиуровней Ферми от концентрации дырок во втором слое для eh-слоя на поверхности кремния.
При концентрациях сумма e + h увеличивается с возрастанием . Такая зависимость связана с тем, что при низких концентрациях главную роль играет обменно-корреляционное взаимодействие. Монотонное возрастание суммы квазиуровней Ферми с увеличением концентрации во втором слое может привести к пространственной неустойчивости во втором слое носителей. Условие устойчивости равновесия между поверхностью и объемом запишется в следующем виде:
(2.16)
где e + h, - число электронно-дырочных пар в объеме полупроводника, и - флуктуации плотности во втором слое и объеме полупроводника, соответственно.
При полной постоянной концентрации носителей величины и имеют противоположные знаки, поэтому при различных знаках у производных в выражении (2.16) состояние системы всегда будет устойчивым. При одинаковых знаках производных состояние может быть неустойчивым, поэтому в этом случае второй слой должен разбиваться на области с плотностью , при которой условие (2.16) выполняется. Очевидно, в этом случае возможно разбиение второго слоя на капли, которые могут не перекрываться друг с другом. При таком разбиении второй слой будет диэлектриком, и проводимость по второму слою будет отсутствовать, что подтверждается результатами эксперимента.
В работе найдено, что присм-2 проводимость поверхностных пар не наблюдается.[11,16] В этой работе исчезновение проводимости объясняется существованием фазового перехода плазма-жидкость, т. е. образованием объемных e-h капель, связанных со слоем поверхностного заряда.
В представленной здесь модели этот эффект объясняется разбиением на двумерные капли, которое происходит при . Расхождение экспериментального и теоретического значения, по-видимому, связано с уменьшением роли обменно-корреляционного взаимодействия в нашей модели. В случае, если взять в формуле (2.10) f(y)=1, тогда критическое значение плотности , ниже которой отсутствует проводимость, составляет приблизительно 21012см-2.
Из рисунке 2.2 также видно, что 2МЭДП может существовать только при нахождении квазиуровней Ферми электронов и дырок в достаточно узкой полосе. Как следует из результатов, представленных на рисунке 2.2, величины квазиуровней Ферми практически не имеют общих областей при различных . Это значит, что для данной интенсивности внешнего излучения 2МЭДП может существовать только в узком диапазоне величины , что противоречит результатам эксперимента. Это противоречие снимается, если в теории увеличить роль обменно-корреляционного взаимодействия. В частности , расчеты, выполненные с f(y)=1 (обменно-корреляционная энергия задается формулой (2.9), показали, что области существования 2МЭДП с различными сильно перекрываются.
Кроме полученных выше эффектов, на поверхности полупроводника возможно образование многослойной системы, т.е. системы состоящей из чередующихся слоев электронов и дырок. Отметим также, что 2МЭДП может образоваться на поверхности полупроводника при.
3 КУЛОНОВСКИЕ КОРРЕЛЯЦИИ И ЭЛЕКТРОННО – ДЫРОЧНАЯ ЖИДКОСТЬ В ДВОЙНЫХ КВАНТОВЫХ ЯМАХ
Многочастичные кулоновские корреляции в двойных квантовых ямах с пространственно разделенными электронами и дырками приводят к образованию вырожденной электронно-дырочной жидкости со средним расстоянием между частицами, меньшим размера изолированного экситона. Это состояние оказывается энергетически более выгодным, чем газ экситонов. Результаты получены в предположении, что в системе имеется много различных сортов электронов и дырок, что характерно, в частности, для многодолинных полупроводников. Обсуждается связь с экспериментами, в которых наблюдались люминесцирующие области в таких системах.
В последнее время резко возрос интерес к исследованию двойных квантовых ям (ДКЯ) в связи с возможностью экспериментальной реализации ДКЯ, в которых электроны и дырки расположены в пространственно разделенных областях, туннелирование между которыми является исчезающе малым.[12] Исследование пространственно разделенных электронов и дырок в ДКЯ было инициировано тем, что в таких системах возможно образование связанных состояний электрона и дырки (экситонов), с большим временем жизни . Это время на несколько порядков больше, чем время жизни экситонов в обычных трехмерных полупроводниках, что способствует возможности наблюдения их бозе-конденсации. Дальнейшие исследования таких систем показали, что их фазовая диаграмма может быть довольно сложной. В настоящей работе, вычисляется вклад кулоновских корреляций в энергию основного состояния многокомпонентной вырожденной электронно-дырочной плазмы в ДКЯ. В рассматриваемой модели ДКЯ предполагается, что электроны и дырки пространственно разделены. При этом электроны движутся в одном двумерном слое, а дырки –в другом, расположенном на расстоянии l от первого слоя. Рассматривается случай, когда электронно-дырочная плазма является многокомпонентной. При этом имеется различных сортов электронов и такое же количество сортов дырок, причем 1. При достаточно малой плотности системы, электроны и дырки образуют связанные состояния (экситоны). При достаточно низкой температуре система может рассматриваться как вырожденный бозе-газ. Однако с увеличением плотности электронно-дырочной плазмы n, когда среднее расстояние между частицами n 1/2 становится меньше или порядка радиуса изолированного экситона Rex , связанные состояния электронов и дырок разрушаются и система трансформируется в вырожденную сильно коррелированную плазму. Впервые вычисление корреляционной энергии многокомпонентной вырожденной электронно-дырочной плазмы в обычных трехмерных многодолинных полупроводниках с числом долин 1, основанное на отборе диаграмм по параметру 1/, было проведено в работе .
В данной главе показано, что многочастичные кулоновские корреляции приводят к существованию отрицательного минимума энергии основного состояния вырожденной электронно-дырочной плазмы в ДКЯ как функции плотности n. При этом минимум имеет место при такой плотности , при которой среднее расстояние между частицами является величиной, меньшей размера экситона, . Оказывается, что указанный минимум лежит ниже энергии основного состояния экситонного газа, так что энергия системы в расчете на одну частицу есть отрицательная величина, причем имеет значение, большее величины энергии связи экситона . Поэтому системе энергетически не выгодно находиться в состоянии с малой плотностью , при которой она представляет собой газ экситонов. В результате система оказывается в состоянии, которое представляет собой электронно-дырочную жидкость. При этом если полное число частиц таково, что плотность , то система является однородной, а если , то система распадается на капли жидкой фазы. Следует отметить, что образующаяся электронно-дырочная жидкость обладает сильными электронно-дырочными корреляциями вблизи поверхности Ферми.[13] Характерный радиус таких корреляций оказывается больше среднего расстояния между частицами. Следовательно данные корреляции не могут быть связаны с наличием бозе - частиц, каковыми являются экситоны. Возможность существования электронно-дырочных капель в полупроводниках была предсказана в работе. Затем это обстоятельство было многократно подтверждено в других теоретических и экспериментальных работах. В последнем пункте рассматривается кинетика образования капель электронно-дырочной жидкости в стационарном состоянии, оценивается радиус этих капель, обсуждается возможная связь полученных результатов с рядом имеющихся экспериментов.
3.1 Модель
Для описания многочастичных эффектов в пространственно разделенной электронно-дырочной плазме в ДКЯ предполагается, что электроны расположены в одном бесконечно тонком двумерном слое, а дырки – в другом. Ниже используется система единиц, в которой эффективный заряд электрона
, (3.1)
где – статическая диэлектрическая постоянная среды, k = 1 - постоянная Планка, m = 1 - эффективная масса электрона. При этом для простоты предполагается, что она равна эффективной массе дырки. Мы рассматриваем случай многокомпонентной электронно-дырочной плазмы. Число сортов электронов считается большой величиной ( 1).
В этом случае импульс Ферми и энергия Ферми для электронов и дырок одинаковы и равны
(3.2)
, (3.3)
где n – концентрация электронов.
Температура системы предполагается малой по сравнению с энергией Ферми (T F). Таким образом, электронно - дырочная плазма является вырожденной. Гамильтониан системы может быть записан в виде
, (3.4)
где – кинетическая энергия,
– кулоновское взаимодействие
(3.5)
(3.6)
Здесь = относятся к электронам, =1, –индекс сорта электрона, и –операторы рождения и уничтожения, k, k, q – двумерные импульсы.
3.2 Корреляционная энергия
В данной работе учет многочастичных корреляций сводится к вычислению собственно-энергетической части как суммы диаграмм, главных по параметру 1/ 1. Это означает, что при отборе диаграмм учитываются только те из них, которые в каждом порядке теории возмущений по кулоновскому взаимодействию максимальны по параметру 1/. Каждая фермионная петля вносит в диаграмму вклад, пропорциональный большому параметру . Такой отбор диаграмм, по существу, является 1/-разложением и приводит к главной последовательности диаграмм, формально совпадающей с последовательностью RPA – диаграмм.[14,20] Отбор диаграмм по параметру 1/ 1 приводит к системе самосогласованных уравнений, диаграммное представление которых показано на рисунке
Рисунок 3.1 - Самосогласованная система диаграммных уравнений для собственно-энергетической части функции Грина
Первое диаграммное уравнение определяет собственно-энергетическую часть, которую можно записать в виде:
(3.8)
Или в виде:
(3.9)
(3.10)
(3.11)
(3.12)
где - перенормированная мацубаровская функция Грина электрона, = /2, – мацубаровская частота, (, p) – собственно-энергетическая часть, µ - химический потенциал, Т-температура системы, S – площадь слоя, – вклад в собственно-энергетическую часть прямого кулоновского взаимодействия, – вклад обменного взаимодействия, – корреляционный вклад.
Перенормированное взаимодействие (, p), входящее в (3.11), удовлетворяет второму диаграммному уравнению, которое имеет вид
(3.13)
При этом поляризационный оператор не зависит от сорта частиц и равен
(3.14)
В случае взаимодействием можно пренебречь. Тогда решение уравнения (3.13) приобретает вид
(3.15)
Если же , то взаимодействие . В это случае решение уравнения (3.13) получается из решения (3.15) заменой поляризационного оперетора на удвоенный:.
Вклад прямого кулоновского взаимодействия (3.9) вычисляется точно
, (3.16)
поскольку и . Вычисление обменного вклада тоже легко приводится и дает величину
(3.17)
В дальнейшем будет показано, что этим членом можно пренебречь по параметру 1/ как в случае > 1, так и в случае .
Для того чтобы вычислить химический потенциал частиц как функцию концентрации n, найдем собственно-энергетическую часть (0, pF ), используя самосогласованную систему уравнений (3.8) – (3.11). Химический потенциал связан с собственно - энергетической частью и импульсом Ферми pF известным соотношением:
(3.18)
В выражении (3.11) для собственно-энергетической части в случае l 1 перенормированное взаимодействие U(k, ) имеет вид (11). Как было указано выше, в случае l 1 в выражении (3.15) поляризационный оператор заменяется на удвоенный. В обоих случаях главный вклад в интеграл для корреляционной составляющей собственно-энергетической части дают импульсы и частоты , что связано с малостью импульса Ферми из-за фактора 1/. Эти импульсы и частоты оказываются порядка и , что будет показано в дальнейшем.[17] В связи с тем что импульсы, дающие главный вклад в интеграл (3.11) для , велики по сравнению с импульсом Ферми ( ), перенормированное взаимодействие (k, ) (3.15) определяется асимптотикой поляризационного оператора при большой передаче импульса (k pF ):
(3.19)
В этом случае перенормированное взаимодействие (3.15) при l >> 1 имеет вид
(3.20)
В случае l << 1 оно получается из (3.20) заменой плотности n на удвоенную:
Вычисление корреляционного вклада (3.11) в собственно-энергетическую часть для внешних импульсов и частот и дает величину, не зависящую от и [18]. Как нетрудно убедиться, в случае l >> 1 оно приводит к интегралу
(3.21)
=
В случае l 1 корреляционная поправка получается из (3.21) заменой плотности n 2n, что фактически означает замену константы C C.
Главный вклад в интеграл (3.21), как мы и предполагали, воспользовавшись асимптотикой поляризационного оператора для больших импульсов, вносят импульсы и частоты . Для оценки последнего интеграла можно ввести новые переменные, и . После этого подынтегральное выражение перестает зависеть от n и полученый интеграл в новых переменных дает константу порядка единицы. Численная оценка константы пропорциональности С в выражении (3.21) дает величину С2.528.
Обменным вкладом (3.17) собственно-энергетическую часть можно пренебречь по сравнению с корреляционным вкладом , если , что и предполагается в дальнейшем. Подставляя полученные для собственно-энергетической части выражения в (3.18), получим выражение для химического потенциала при :
, (3.22)
где первый член есть кинетическая энергия , второй – поправка(12), связанная с прямым кулоновским взаимодействием, а последний корреляционная поправка (3.21). При выражение для химического потенциала получается из (3.22) заменой .
3.3 Уравнение состояния
Используя выражение (3.22) для химического потенциала, можно получить выражение для энергии на один электрон:
(3.23)
Тогда давление сильно вырожденной электронно-дырочной плазмы запишется в виде
(3.24)
Поскольку , в случае можно пренебречь вкладом от кинетической энергии по сравнению со вкладом прямого кулоновского взаимодействия . Легко показать, что при плотностях сжимаемость и система неустойчива. Для плотностей имеем , что означает устойчивость системы. Однако в интервале плотностей давление оказывается отрицательным. Наиболее энергетически выгодным является состояние, при котором энергия достигает минимального значения.[15] Последнее определяется условием . Это равенство определяет плотность энергетически выгодной фазы
(3.25)
Энергия на одну частицу для этой плотности определяется выражением
(3.26)
При дальнейшем увеличении плотности система остается в однородном состоянии при давлении P > 0. Сравним энергию (3.25) с энергией , приходящейся на один экситон в системе взаимодействующих экситонов. Энергия связи изолированного экситона при . Поскольку экситоны в ДКЯ отталкиваются, . Сравнивая эту оценку с выражением (3.26), приходим к выводу, что основное состояние электронно-дырочной жидкости, отвечающее плотности (3.25), оказывается энергетически выгоднее экситонного, если , причем радиус экситона . Следовательно, в этом случае при плотности зарядов имеем . При таких плотностях система не может рассматриваться как газ экситонов. Она является электронно-дырочной жидкостью.
В случае при нахождении уравнения состояния системы мы пренебрегли кинетической энергией в уравнении (3.22). Обратимся к противоположному случаю, . Втаком случае кинетической энергией пренебрегать нельзя. Теперь, плотность электронно-дырочной жидкости зависит от величины параметра и определяется выражением
(3.27)
Для этой плотности энергия на одну частицу
(3.28)
Энергия отрицательна, а ее модуль велик, . В то же время при энергия связи экситона . Сравнивая ex и eq , видим, что |eq| |ex | при l 1. Таким образом, и в этом случае электронно-дырочная жидкость обладает меньшей энергией на частицу, чем экситонное состояние. Кроме того, при l 1 экситонный радиус Rex ~ 1 превышает среднее расстояние между частицами n1/2, отвечающее плотности (3.27). В результате neqR2 1 и система представляет собой электронно-дырочную жидкость.
В промежуточном случае l ~ 1 и eq ~ ex ~ 1, т.е. электронно-дырочная жидкость и экситонная фаза обладают одинаковой по порядку величины энергией. Однако в этом случае и среднее расстояние между экситонами по порядку величины равняется экситонному радиусу. Поэтому концепция экситона теряет смысл. Таким образом, при любом соотношении между межплоскостным расстоянием l и боровским радиусом электронно - дырочная жидкость обладает меньшей энергией по сравнению с экситонным состоянием.
Интересно отметить, что если l 1, то кинетическая энергия, по порядку величины равная , не играет роли при установлении равновесного состояния. Электронно-дырочная жидкость при этом образуется в результате балланса между положительной “энергией конденсатора” (3.16) и внутрислоевой отрицательной корреляционной энергией (3.21). В данном случае как энергия основного состояния eq, так и равновесная концентрация neq не зависят от параметра . Последнее имеет место, несмотря на тот факт, что формально результат получен при 1. Это позволяет ожидать справедливости полученных результатов, по крайней мере качественно, и при ~ 1. Однако подобный вывод может быть подтвержден только численными расчетами.
3.4 Обсуждение результатов
Итак в данной главе рассмотрена многокомпонентная, двумерная электронно-дырочная плазма с пространственным разделением зарядов. Показано, что независимо от расстояния l между слоями электронно - дырочная жидкость обладает меньшей энергией на одну частицу, чем экситонный газ. В случае l 1 согласно уравнению (3.23) вкладом кинетической энергии в химический потенциал можно пренебречь. Тогда энергия электронно - дырочной системы складывается из двух частей. Первый вклад равен ln2. Он связан как с внутрислоевым e e и h h прямым кулоновским взаимодействием, так и с межслоевым e h кулоновским взаимодействием. Электрон - электронный и дырочно - дырочный вклады положительны и расходятся. Электрон - дырочный вклад отрицателен и также расходится. Вследствие электронейтральности эти три члена дают конечное значение ln2. Второй вклад есть отрицательная корреляционная энергия. Заметим, что в случае l 1 она связана только с e e- и h – h - взаимодействием. Эта энергия отрицательна, несмотря на то что внутри слоя частицы отталкиваются. Аналогичное обстоятельство имеет место в случае трехмерного электронного газа на однородном положительном фоне.
Обратимся теперь к возможной связи между полученными результатами и результатами ряда экспериментов, в которых наблюдаются фрагментированные люминесцирующие области в ДКЯ. Наличие таких областей иногда рассматривают как проявление бозе - конденсации экситонов. В некоторых работах люминесцирующие фрагменты ассоциируются с экситонной жидкостью, в которой экситоны рассматриваются как бозе - частицы, испытывающие эффективное притяжение на малых расстояниях. В реальных экспериментах фрагментация наблюдается, если nex R2 ~ 1. В этом случае проявление экситонных корреляций вблизи поверхности Ферми в некоторых работах интерпретируют как наличие экситонов, являющихся бозе-частицами. Однако по нашему мнению, люминесцирующие фрагменты не связаны с экситонами, а являются двумерными электронно - дырочными каплями, в которых на поверхности Ферми могут иметь место сильные электронно - дырочные корреляции экситонного типа.
В упомянутых экспериментах электронно-дырочная плазма в ДКЯ создается внешним оптическим источником. Если средняя плотность зарядов в созданной плазме меньше, чем neq, то однородное состояние системы неустойчиво и возникают нейтральные 2D электронно - дырочные капли. Положительный заряд последних сосредоточен в одном слое, а отрицательный – в другом. При этом плотность зарядов каждого знака есть neq, а заряженные области расположены одна над другой.
Оценим характерный радиус капли R. Для этого учтем, что время жизни пространственно разделенных электронов и дырок конечно. Тогда уменьшение полного заряда одного знака в капле (при сохранении нейтральности) есть R2neq /. С другой стороны, вне капель имеется поток экситонов j, непрерывно рождаемый внешним оптическим источником. Этот поток, попадая вовнутрь 2D-капли, увеличивает заряд в каждом слое на величину +2Rj. В состоянии динамического равновесия гибель и приход зарядов в капле компенсируют друг друга, приводя к зависимости
(3.29)
Очевидно, что понятие электронно-дырочной капли теряет смысл , если её радиус . По этой причине существует минимально пороговое значение потока
(3.30)
приводящего к образованию капли. Из уравнения (3.29) следует, что электронно-дырочные капли образуются, если поток j превышает некоторую критическую величину jc. Таким образом, если оптическая накачка слаба (j < jc ), то капля не успевает образоваться. Это коррелирует с упомянутыми экспериментами, в которых обнаружен минимальный порог накачки, при котором наблюдается фрагментация. Если накачка достаточно сильна, то рождается электронно-дырочная плазма с плотностью n >> neq. При этом капели не появляются, а устойчивое состояние системы является однородной электронно - дырочной жидкостью. Очевидно, что в данном случае давление P > 0 и для реализации такого состояния наличие стенок является необходимым.
В данной главе показано, что корреляционные эффекты обусловлены главным образом рассеянием в канале экранирования. Следует отметить, что исследовался другой тип электронно - дырочной жидкости. В этой работе минимум энергии как функции концентрации n зарядов в ДКЯ найден посредством вариационной процедуры и связан с экситонными корреляциями в канале рассеяния электрон – дырка. В нашей работе рассмотрение этих корреляций отвечало бы учету диаграмм, малых по параметру 1/. Строго говоря, наши результаты обоснованы только в случае 1. В то же время результаты работы фактически относятся к случаю = 2. Поэтому формально сравнение наших результатов является некорректным. По моему мнению, в работе недооценивается роль рассмотренных нами корреляционных эффектов. Однако последовательный учет корреляций в канале рассеяния электрон – дырка на фоне рассеяния в канале экранирования при = 2 может быть проведен только численно, что выходит за рамки данной работы. В то же время именно корреляции в канале рассеяния электрон – дырка ответственны за появление аномальных средних экситонного типа, приводящих к возникновению диэлектрической щели на поверхности Ферми[16,20].
4 РАСЧЕТ ВКЛАДА КУЛОНОВСКОГО ВЗАИМОДЕЙСТВИЯ В ЭНЕРГИЮ СВЯЗАННОГО ОПТИЧЕСКОГО ЭЛЕКТРОНА ПРИМЕСНОГО 3d – ИОНА В ПОЛУПРОВОДНИКОВЫХ МАТРИЦАХ
4.1 Расчет вклада кулоновского взаимодействия оптического электрона примесного 3d - иона с электронами зоны проводимости
(4.1)
(4.2)
(4.3)
(4.4)
Матричный элемент кулоновского взаимодействия оптического электрона примесного центра с электроном зоны проводимости
(4.5)
Оптический центр – одноэлектронный, состояние связанного электрона – 3d1 (ион Ti3+, V4+ и т.п., выбран для того, что бы не учитывать взаимодействие электронов в d-оболочке, методы такого учета хорошо разработаны)[17]. Взаимодействие с зоной изучено слабо.
Начальное состояние: связанный электрон в состоянии 3d1 , , , квантовое число принимает значения от –2 до +2 с интервалом единица. Волновую функцию начального состояния выбираем в виде водородоподобной функции, поскольку ее уточнение незначительно влияет на числовые значения радиальной части матричных элементов.
, (4.6)
где – радиальная часть волновой функции связанного оптического электрона,
– сферическая гармоника,
– набор угловых координат .
Волновую функцию электрона зоны проводимости выбираем в виде плоской волны
, (4.7)
где – принадлежащий зоне Бриллюэна волновой вектор электрона.
Конечное состояние характеризуется значением
(4.8)
для связанного электрона, и значением для плоской волны описывающей
конечное состояние электрона зоны проводимости, которое также выбираем в
виде плоской волны
(4.9)
Основанием для такого выбора являются следующие соображения. При температурах, близких к комнатной, средняя скорость движения электронов составляет величину порядка м/с, поэтому время между двумя последовательными соударениями электронов с ионами составляет порядка с, что меньше времен продольной и поперечной релаксации оптического электрона примесного центра.
В соответствии с принципом Паули выбираем волновую функцию начального и конечного состояния системы двух электронов в виде антисимметризованного произведения волновых функций связанного электрона и электрона зоны проводимости
(4.10)
. (4.11)
Тогда матричный элемент кулоновского взаимодействия электронов можно записать как разность кулоновского и обменного интегралов
(4.12)
где
(4.13)
– матричный элемент кулоновского взаимодействия, и
(4.14)
– матричный элемент обменного взаимодействия. Следует, однако отметить, что при вычислении обменной части мы пренебрегаем эффектами корреляции электронов в зоне проводимости, т.е., рассматриваем взаимодействие оптического электрона с одним из электронов зоны проводимости. Такое одноэлектронное приближение примнеяется достаточно часто. Дело в том, что учет корреляционных эффектов представляет собой сложную задачу. Если уровни энергии электронов заполнены в соответствии с принципом Паули. Наличие такого влияния приводит к появлению у системы электронов дополнительной энергии, которая называется корреляционной энергией. Поскольку при конструировании мнгоэлектронной волновой функции она строится как антисимметричная комбинация одноэлектронных волновых функций, что обуславливает появление обменной энергии, то корреляционная энергия оказывается самым тесным образом связана с обменной энергией, что позволяет рассматривать их сумму как единую обменно-корреляционную энергию.[18] Обзор корреляционных эффектов в системе электронов приведен в соответсвующем параграфе настоящей работы.
Рисунок 4.1 - Фейнмановская диаграмма, описывающая кулоновское взаимодействие связанного 3d1-электрона с электроном зоны проводимости
Рисунок 4.2 - Фейнмановская диаграмма, описывающая обменное взаимодействие связанного 3d1-электрона с электроном зоны проводимости
Вычислим матричный элемент , для чего напишем разложение потенциала кулоновского взаимодействия электронов по сферическим функциям
, (4.15)
где , – меньшее и большее из двух величин и , – угол между векторами и , и –полином Лежандра степени n, который можно представить в виде разложения в ряд по сферическим функциям
. (4.16)
Для плоской волны используем разложение следующего вида
, (4.17)
где
, (4.18)
и –функция Бесселя полуцелого порядка, которая выражается через элементарные функции.
Учитывая также, что в сферических координатах , где , получаем следующее выражение для
(4.19)
Полагаем , и обозначаем интеграл по через
. (4.20)
Согласно [19]
(4.21)
далее,
, (4.22)
то, используя соотношение ортогональности для сферических функций
, (4.23)
получаем
(4.24)
полагая в последней формуле , , получаем
(4.25)
Используя приведенные выше формулы, находим
(4.26)
тогда
. (4.27)
на следующем этапе вычислений выполняем усреднение по направлению волнового вектора , для чего используем формулу
. (4.28)
Поскольку
, (4.29)
то в формуле (4.27) остается только слагаемое с , . Следовательно, , . Тогда
(4.30)
На следующем этапе вычислений усредним выражение для матричного элемента по величине вектора , считая его принадлежащим зоне Бриллюэна, т.е., пренебрегая процессами переброса. При усреднении предполагаем, что абсолютная температура полупроводника равна нулю, и зона Бриллюэна представляет собой шар с радиусом, равным волновому числу Ферми . Тогда
(4.31)
Используя явный вид сферической функции Бесселя
, (4.32)
получаем
(4.33)
Вычисляя последний интеграл
(4.34)
получаем, что среднее значение сферической функции Бесселя равно
(4.35)
Для дальнейшего вычисления используем явный вид радиальной части волновой функции 3d1- состояния
, (4.36)
где а – боровский радиус.
Обозначим радиальную часть матричного элемента через
, (4.37)
где через обозначена функция
Поскольку через обозначено большее из , , приведенный интеграл разбивается на два слагаемых
, (4.38)
где
(4.39)
(4.40)
Тогда
(4.41)
Используя таблицы значений коэффициентов Клебша-Гордана [19], находим
,
получаем
при или 2, и при
Обозначая величину через B.
Тогда матрица энергий 3d1-электрона, взаимодействующего с электроном зоны проводимости, имеет вид :
В общем случае, секулярное уравнение имеет пять несовпадающих корней. Следовательно, в тетраэдрической позиции пятикратно вырожденный вырожденный 3d1 – ион расщепляется на пять синглетов, в отличии от октаэдрической позиции, в которой расщепление идет на два дублета и синглет.
Согласно общим принципам, всякое расщепление первоначально вырожденных уровней энергии связано с понижением симметрии. В данном случае выражение для матричного элемента кулоновского взаимодействия усреднено по направлению волнового вектора , что означает изотропное распределение электронов зоны проводимости, рассеянных на примесном центре. Казалось бы, эта изотропия не понижает первоначальную тэтраэдрическую симметрию, поэтому расщепления быть не должно. Однако, это не так. Дело в том, что элементарный акт взаимодействия оптического электрона с электроном зоны проводимости описывается гамильтонианом, симметрия которого представляет собой наложение аксиальной симметрии плоской волны и тэтраэдрической симметрии лигандов.
Рисунок 4.3 - Детальная картина расщепления энергетических уровней 3d1-электрона, обусловленная зоной проводимости
Рассчитаем и оценим значения величин, расщепленных уровней энергии, показанных на рисунке 4.3.
, ,(4.42)
, , (4.43)
где
(4.44)
(4.45)
(4.46)
(4.47)
где а- расстояние от центра тетраэдра до лигандов,
b- расстояние от примесного центра до плоскости основания тетраэдра.
z-эффективный заряд лигандов
e-заряд электрона
Найдем величину расщепления . Используя явный вид радиальной части волновой функции 3d1-электрона
, (4.48)
запишем величину
, (4.49)
где
, (4.50)
в виде
, (4.51)
или
(4.52)
Оценивая величину волнового числа Ферми qf как , где – концентрация электронов зоны проводимости, – полное число электронов, – объем полупроводника, можно заключить, что значение по порядку величины составляет , где – расстояние между атомами полупроводника. Следовательно, , поэтому в интеграле для можно положить
(4.53).
Тогда
, (4.54)
где – гамма-функция Эйлера, равная 720 при , и . Окончательно, . Для вычисления величины , равной
(4.55)
Заметим, что при больших r2 функция
(4.56)
приближенно равна , т.е., представляет собой убывающую осциллирующую функцию, поэтому вкладом в величину можно пренебречь. Следовательно
, (4.57)
Или, с учетом соотношения , получаем
, (4.58)
где через обозначена постоянная Ридберга , равная 13.6 эВ, и - боровский радиус. Тогда величина поправки к энергии оптического электрона составит величину порядка 10–4 эВ. Для регистрации такого расщепления требуются температуры порядка 1К.
Имеется основание считать, что вклад обменного взаимодействия мал по сравнению со вкладом кулоновского взаимодействия и не изменит качественно картину расщепления энергетических уровней 3d1-иона.
ЗАКЛЮЧЕНИЕ
В настоящей выпускной квалификационной работе проделана следующая работа:
1 Проведен литературный обзор, в результате которого было установлено, что в настоящее время проблема рассчета спектроскопических свойств 3d1- ионов с учетом как одночастичных и коллективных эффектов далека от своего решения.
2 Учитывая, что проблема рассчета корреляционной энергии систем электронов в настоящее время не решена, в работе приведены по литературным данным эмперические формулы для рассчета корреляционной энергии.
3 Произведен рассчет положений уровней энергии 3d- электрона с учетом кристаллического поля и электронов зоны проводимости, найдена величина энергии и составлена матрица энергий для тетраэдрической позиции.
4 Оценена величина расщепления уровня энергии для модельного полупроводника с шириной запрещеной зоны 1эВ.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1 L.A.Kikoin Transition Metal Impurities in Semiconductors (Electronic Structure and Physical Properties)/L.A.Kikoin, V.N.Fluerov, Singapore, World Scientific,1994,354ch.
2 Васильченко, А.А. Расчеты основного состояния квазидвумерной электронно-дырочной плазмы / А.А. Васильченко, Е.Н. Тумаев, Д.А. Ермохин
3 Малкин Б. З. Безызлучательные переходы в редкоземельных димерах в кристаллах CsCdBr3:RE3+ / Б. З. Малкин, Э. И. Байбеков // Физика и техника полупроводников. – 2001. – Т. 5. – № 6. – С. 1100–1112.
4 Ландау Л. Д. Теоретическая физика / Л. Д. Ландау, Е. М. Лифшиц. –М :Физматлит, 2003. –Т.5. -531с.
5 Эллиот Д. Симметрия в физике / Д. Эллиот, П. Допер. –М: Мир, 2001. –Т. 2. -414с.
6 Альтшулер С. А. Электронный парамагнитный резонанс соединений элементов промежуточных групп / С. А. Альтшулер, Б. М. Козырев. -М: Наука, 2002. -670с.
7 Selina N.V., Avanesov A.G., Lebedev V.A., Stroganova E.V., Tumayev E.N., Brik M.G., Special features of the phonon spectrum and non-radiative transitions in the Cr3+-doped ionic–covalent crystals. // Solid State Communications 2008, 146, 298.
8 Грибов.Л.А.Электронно-колебательные спектры многоатомных молекул/ Грибов.Л.А., Баранов В.И., Зеленцов Д.Ю. М.: Наука, 2000. С.197-201.
9 Sugano S., Tanabe Y. Multiples of Transition-Metal Ions in Crystals. Academic Press, N.-Y. and London, 2003, 285 pp.
10 Сущинский М. М. Спектры комбанационного рассеяния света молекул и кристаллов. – М.: Наука, 2000.-576 с.
11 Жижин Г.Н. Оптические колебательные спектры кристаллов/ Жижин Г.Н., Маврин Б.Н., Шабанов В.Ф. – М.: Наука, 2004.- 232 с.
12 Китайродский А.И. Молекулярные кристаллы. – М.: Наука, 2001. - 424 с.
13 Применение спектров комбинационного рассеяния / Под редакцией А.Андерсона и К.И. Петрова. – М.: Мир, 2000. – 586 с.
14 Борн М. Динамическая теория кристаллических решеток. - М.: ИЛ, 2000. – 488 с.
15 Zhizhin G.N. Optical spectra and lattice dynamics of molecular crystals. Vibrational spectra and structure / Zhizhin G.N., Muktarov E.I., Eds. J.R. Durig. A series of advances, V. 21.- Amsterdam: ELSEVIER, 2003.- 490 p.
16 Авадов Д.И. Изучение оптических свойств примесных ионов переходных металлов в кристаллах.-Краснодар, 2008, 99с.
17 Шаскольская М.П. Кристаллография. – М.: Высшая школа. 2000.- 391с.
18 Horning D.F. // J.Chem.Phys. - 2000. - V.16, №11. - P. 1063-2076.
19 Варшалович Д. А. Квантовая теория углового момента / Д. А. Варшалович, А. Н. Москалев, В. К. Херсонский. –М: Наука, 2000, 441с.
20 В.С. Бабиченко Кулоновские корреляции и электронно – дырочная жидкость в двойных квантовых ямах/В.С.Бабиченко, И.Я. Полищук,Письма в ЖЭТФ, том 97, вып.11, с.726-731.
eq
eq
,
,
,
0 F
ex
ex
ex
eq
ex
eq ex
4
ex
m
m'
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
m
m'
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 
EMBED Equation.DSMT4 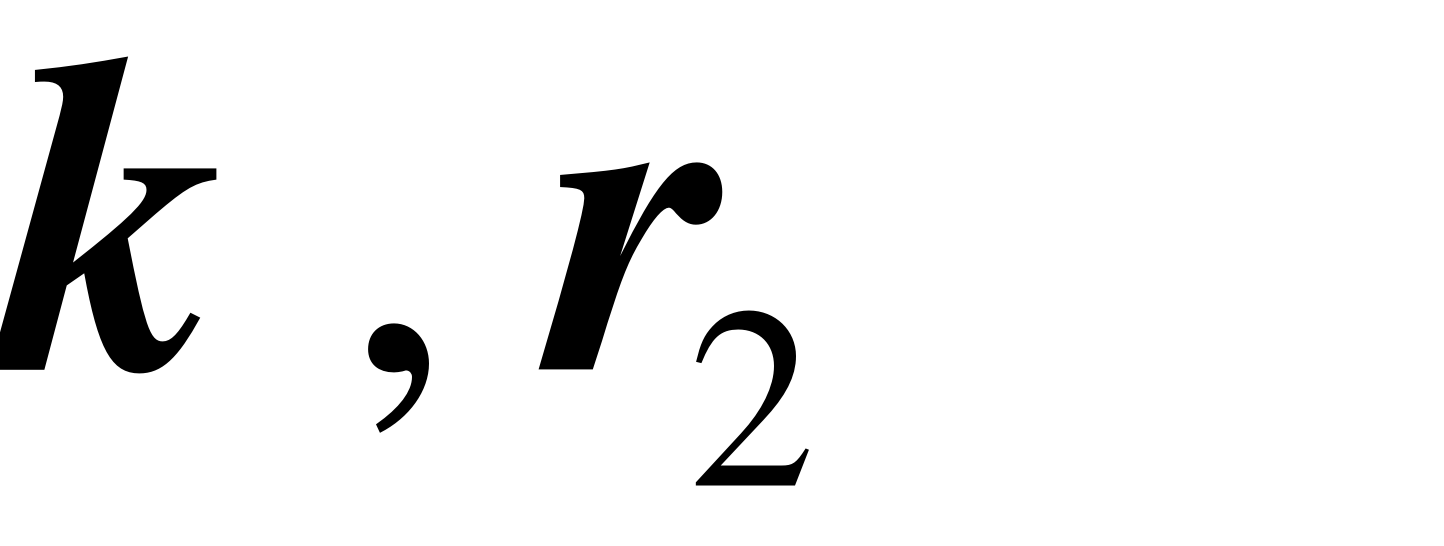
EMBED Equation.3 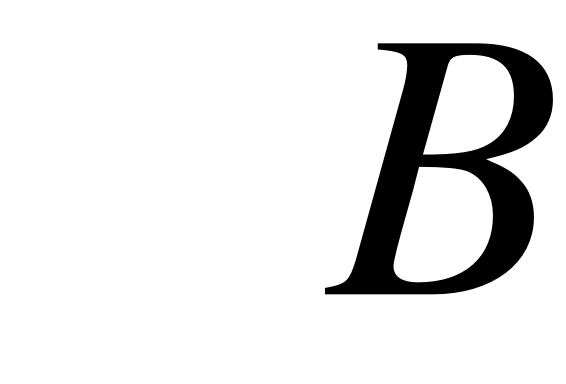
EMBED Equation.3 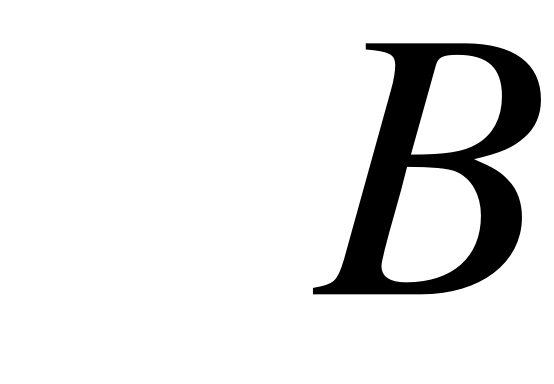
EMBED Equation.3 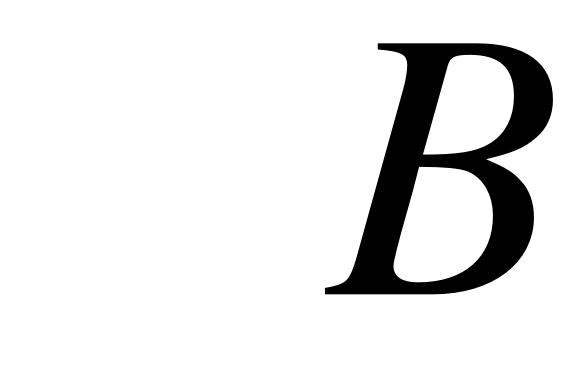
ТЕОРЕТИЧЕСКОЕ ИССЛЕДОВАНИЕ ВЛИЯНИЯ ЗОНЫ ПРОВОДИМОСТИ НА СТРУКТУРУ ЭНЕРГЕТИЧЕСКИХ УРОВНЕЙ ПРИМЕСНЫХ ИОНОВ В КРИСТАЛЛАХ