УСТРАНЕНИЕ ПОМЕХ ПРИ ИЗМЕРЕНИИ МАГНИТНЫХ ПОЛЕЙ БИОЛОГИЧЕСКИХ ОБЪЕКТОВ

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

«КУБАНСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ»

(ФГБОУ ВПО «КубГУ»)

Физико-технический факультет

Кафедра радиофизики и нанотехнологий

Допустить к защите в ГАК

_____ . ____ . 2014 г.

Заведующий кафедрой

д-р физмат. наук, профессор

_______________Г. Ф. Копытов

ДИПЛОМНАЯ РАБОТА

УСТРАНЕНИЕ ПОМЕХ ПРИ ИЗМЕРЕНИИ МАГНИТНЫХ ПОЛЕЙ БИОЛОГИЧЕСКИХ ОБЪЕКТОВ

Работу выполнил_________________ Коробейников Дмитрий Александрович

Направление 011800.62 Радиофизика

Научный руководитель

д-р физмат. наук, профессор_____________________________ Г. Ф. Копытов

Нормоконтролер _________________________________ М. А. Жужа

Краснодар 2014

СОДЕРЖАНИЕ

Введение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава 1. Литературный обзор . . . . . . . . . . . .. . . . . . . . . . . . . . . . . . . . . . . . .
§1.1 Область применения биомагнитометрии . . . . . . . . . . . . . . . . . . . . . . . .
§1.2 Современные разработки датчиков биомагнитного поля . . . . . . . . . . . .
§1.3 Методы борьбы с помехами . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава 2. Экспериментальная установка и методика эксперимента . . . .
§2.1 Нейрон и нейронные сети . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.1.1 Биологический нейрон . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.1.2 Модели . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.2 Базовая экспериментальная установка . . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.2.1 Установка исследуемой модели . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.2.2 Установка датчика поля . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
§2.3 Исполнение методов устранения помех . . . . . . . . . . . . . . . . . . . . . . . . . .
Глава 3. Экспериментальные результаты . . . . . . . . . . . . . . . . . . . . . . . .
§3.1 Снятие характеристик поля базовой установки . . . . . . . . . . . . . . . . . . . .
§3.2 Снятие характеристик поля помехозащищённой установки . . . . . . . . .
§3.3 Анализ эффективности системы устранения помех . . . . . . . . . . . . . . . .
Заключение . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Список использованных источников . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

ВВЕДЕНИЕ

Как известно, биологические объекты порождают электромагнитные поля различных частот, то есть выступают в роли биогенераторов теплового, электрического, магнитного, гравитационного полей. Измерение биоэлектрической активности упомянутых источников давно и уверенно заняло достойную нишу в медицинских, психологических, клинических исследованиях. Широкодоступны в плане наличия предложения и с относительно адекватной стоимостью такие измерительные приборы, как электрокардиографы, электроэнцефалографы как от зарубежных [1, 2], так и от отечественных производителей [3, 4].

Регистрация же биомагнитных сигналов существенно дополняет регистрацию электрических потенциалов. Их комбинация дает наиболее полную информацию об исследуемых процессах [5, 6].

Но огромный пласт работы в этом поле деятельности ещё не завершён. В настоящее время нет данных о статическом распределении проводимости в пространстве мозга живого человека. Существующие оценки очень приблизительны и не позволяют учесть имеющиеся пространственные неоднородности проводимости. А это очень существенно при расчёте, например, обратной задачи электроэнцефалографии [13] – описания распределения потенциалов, регистрируемых с поверхности головы дипольными источниками, расположенными в глубине мозга.

Важной проблемой измерения биомагнитных сигналов является следующее: независимо от вида источника, все биомагнитные сигналы и образуемые ими поля имеют очень низкую амплитуду по сравнению, например, с магнитной составляющей поля Земли [14] или полем среды. Это частично исправляется особыми методами экранирования (ферромагнитные, сверхпроводящие экраны) и активной защитой. Рывком вперёд здесь было изобретение сверхпроводящего квантового интерферометрического датчика (СКВИД) [15], в основе работы которого лежит эффект Джозефсона [16]. СКВИДы имеют рекордно высокую чувствительность к магнитному полю (до 10–15 Тл). Но СКВИДы обладают также рядом серьёзных недостатков (высокая стоимость, малая длина когерентности, сильная анизотропия электронных свойств). И большинство исследований проводятся с такими датчиками магнитного поля, как феррозондовый магнитометр, магнитометр с оптической накачкой, индукционные магнитометры, магнитометры с MEMS-датчиками.

Каждый из этих магнитометров обладает свойственным ему уровнем собственных шумов. Малость собственных шумов ещё не означает, что измерение МП биообъектов будет проведено с высоким разрешением: как уже было сказано, наряду с исследуемым биомагнитным полем в области измерения всегда присутствуют мешающие магнитные поля, или магнитные помехи.

В виду перечисленных особенностей биомагнитных сигналов, методам борьбы с помехами в этой области уделяется большое внимание. Ниже представлен один из возможных вариантов классификации этих методов.

Для того чтобы уменьшить влияние магнитных помех от искусственных источников, экспериментальные лаборатории, в которых проводятся биомагнитные измерения, по возможности размещают на большом удалении от промышленных предприятий и крупных населённых пунктов.

Другой способ уменьшения влияния внешних магнитных помех – создание специальных экспериментальных комнат, или камер с магнитной экранировкой.

Распространённый способ избавления от шума является использование дифференциального включения датчиков магнитометра. Применение дифференциальных схем измерения оправдано в том случае, когда источники помех находятся на расстоянии, которое существенно (не менее чем на два порядка) превышает расстояние между датчиками.

Современное развитие электронно-вычислительных технологий позволяет в режиме реального времени производить оцифровку поступающих аналоговых сигналов с высокой частотой дискретизации. Это ещё один повсеместно используемый метод борьбы с помехами: используется дополнительная обработка поступающего оцифрованного сигнала, такая как фильтрация сигнала в выбранном диапазоне частот с сохранением текущей фазы и амплитуды частотных составляющих сигнала.

При анализе нестационарного сигнала, когда важно определить момент изменения частотной составляющей, зачастую используются различные типы линейных фильтров, реализуемых в цифровой форме: аналоговые фильтры с бесконечной импульсной характеристикой, цифровые фильтры с бесконечной или с конечной импульсной характеристикой, характеризующиеся способами и особенностями задания передаточной характеристики. При этом возникает проблема, связанная с фазовым искажением сигнала после фильтрации, способом решения которой является использование алгоритма двойной фильтрации.

В качестве общего замечания следует отметить необходимость предварительного измерения уровня магнитных помех в месте измерения, снятия топологии МП, соблюдения правил магнитной гигиены (не производить накопления ферромагнитных материалов, приборов, электрических двигателей и машин) на месте или вблизи последующей установки магниточувствительных датчиков. При измерениях следует помнить, что смещение магниточувствительного датчика в пространстве при наличии неоднородного МП ведет к созданию дополнительных магнитных помех.

Целью данной работы: разработать модель и систему защиты биологических объектов от помех при измерении их магнитного поля.

Для достижения этой цели надо решить следующие задачи:

1. Дать обзор состояния вопроса

2. Предложить модель биологического объекта

3. На основе модели создать … и построить измерительный прибор.

Глава I. Литературный обзор

§1.1 Область применения биомагнитометрии

Задача неинвазивной визуализации структурных особенностей мозга человека и физиологической составляющей когнитивных процессов является междисциплинарной и очень важной для целого ряда областей науки о человеке – психологии, биологии, медицины, психофизиологии. Методами регистрации магнитной компоненты сигналов биологического происхождения добиваются очень ценной возможности бесконтактно получать в реальном времени трёхмерное распределение проводимости (которая изменяется в связи с электрическими и биохимическими процессами в мозге), а также даёт новые преимущества, например, для визуализации мозговой активности, недоступные с помощью других методов [7].

Такие методы, как магнитоэнцефалография (МЭГ) [8], магнитоиндукционная томография (МРТ) [9], магнитокардиография (МКГ) [10] активно развиваются в сфере применения в клинических исследованиях, методов обработки получаемых сигналов, поиска эффективных решений технической реализации датчиков и экранировки.

Основной ветвью современного биомагнетизма можно считать направление, связанное с регистрацией магнитных полей, порождаемых переменными биотоками. Почти все зарегистрированные в этом направлении биомагнитные феномены имеют аналоги в биоэлектрических явлениях. Самый сильный сигнал из порождаемых переменными биотоками у человека даёт сердце. Первая МКГ была зарегистрирована через 76 лет после регистрации первой ЭКГ. В среднем зубец R в МКГ равен 50 пТл, а в ЭКГ - 1000 мкВ.

Значимость этого направления увеличивается в связи с возможностью регистрации МКГ плода человека

Многообразие типов магнитометров позволяет остановиться на том, который соответствует поставленной задаче измерений, не привлекая без нужды дорогостоящие в производстве и эксплуатации магнитометры.

§1.2 Современные разработки датчиков биомагнитного поля

Многочисленные результаты лабораторных и клинических испытаний показывают, что эффективность использования ЭЭГ, МЭГ, МРТ, МЭГИ для регистрации и обработки ритмический активности биопотенциалов головного мозга человека даёт возможность в достаточно быстром темпе и с хорошей точностью заняться разработкой диагностических критериев и построением основы актуальных медицинских знаний, необходимых для диагностики функциональных нарушений и органической патологии внутренних органов.

В лаборатории экологической нейрокибернетики МНИЦ «Арктика» ДВО РАН разработан индукционный магнитоэнцефалограф (МЭГИ), который использовался затем в ряде экспериментов по диагностике заболеваний внутренних органов, основанных на регистрации и анализе ритмической (диффузной) активности головного мозга – преимущественно в лобной области. [8]

Созданный магнитоэнцефалограф представляет собой две дифференциальные пары катушек. Активные катушки расположены слева и справа в лобных областях, что создает идеальное монополярное отведение. Дифференциальные катушки помещены в теменной области и расположены над головой так, чтобы мозговые магнитные поля были значительно ослаблены: система полностью экранирована от внешнего магнитного поля.

Следует отметить некоторые особенности и явные преимущества рассматриваемого МЭГИ:

- работает в неэкранированном помещении

- не возникают проблемы с индифферентным электродом и артефактами, имеющими корни в ненадежности перехода электрод-гель-кожа.

- незначительная реакция на движение глаз и век с одной стороны и весьма сильная реакция на кашель, вербальные сигналы пациента

- забинтованная голова пациента, прямо или косвенно, не искажает картину измерений.

Упомянутое расположение катушек значительно уменьшило артефакты различного происхождения в области частоты менее 0,5 Гц и позволило увидеть устойчивую картину электромагнитного излучения головного мозга в диапазоне частот от 27 Гц до 0,13 Гц.

В исследованиях применялись цифровые усилители биопотенциалов с шумом в исследуемой полосе не более 1-2 мкВ, цифровой фильтрацией – подавлением сигнала выше 30 и ниже 0,1 Гц. Спектральная оценка проводилась с помощью быстрого преобразования Фурье (БПФ). При спектральном анализе использовалось программное разбиение частотной оси на 840 частотных полос (полосовая фильтрация). Ширина полосы непостоянна и составила 3 % от центральной частоты. Попавшие в полосу амплитуды спектральных частот в результате БПФ-преобразования интегрировались.

На выходе каждого полосового фильтра в результате операции суммации с временем 160 сек выделялись только повторяющиеся события. Именно так регистрировались длительнотекущие ритмические процессы и амплитуды их частот.

Примечательно, что упомянутый прибор, разработанный МНИЦ «Арктика» ДВО РАН, уже используется для некоторых медицинских исследований. Например, Владивостокским государственным медицинским университетом, который заявил целью своих исследований «выявить закономерные отличия данных спектрального анализа диффузной или глобальной магнитоэлектрической активности головного мозга пациентов с острой и хронической формами передней и задней ишемической оптической нейропатии, а также с травматической оптической нейропатией от данных практически здоровых исследуемых». [9]

Для высокого пространственного разрешения, измерения биосигналов порядка пика- и фемто-тесла требуются сенсоры плотного векторного поля. Исследователями из Германии представлен первый МЭМС сенсор, герметичный, созданный на основе магнитоэлектрических (МЭ) материалов с использованием многопластинчатой конструкции [12]. Сенсор показал высокие значения таких характеристик, как МЭ коэффициент – 2390 (В/м)/(А/м) и чувствительность 3800 В/Тл при резонансе на 7,1 кГц.

Эти результаты могут соперничать с работами над новейшими некапсулируемыми сантиметровыми МЭ сенсорами, которые при этом являются в 300 раз больше в размерах [21]. Было получено минимальное разрешение в 30 пТл и уровень шума в 27 пТл/Гц1/2 в резонансном режиме работы, что вполне пригодно для работы с биомагнитными сигналами и заметно превышает соответствующую характеристику других магнитных микросенсоров векторного поля. Делается прогноз, что улучшение вакуумной герметизации даст значительное повышение Q-фактора и ультранизкий уровень шума.

Магнитоэлектрический слой консоли был собран из 150 мм силиконовых пластин при использовании механической микрообработки поверхностей (ход обработки см. на рис. 1). Далее, на них были нанесены сочленительные перемычки (рис. 2). Инкапсуляция сенсора была проделана с помощью низкотемпературного TLP (transient-liquid phase) соединения пластин [13].

Рисунок 1 – Ход создания пластины на устройстве МЭМС

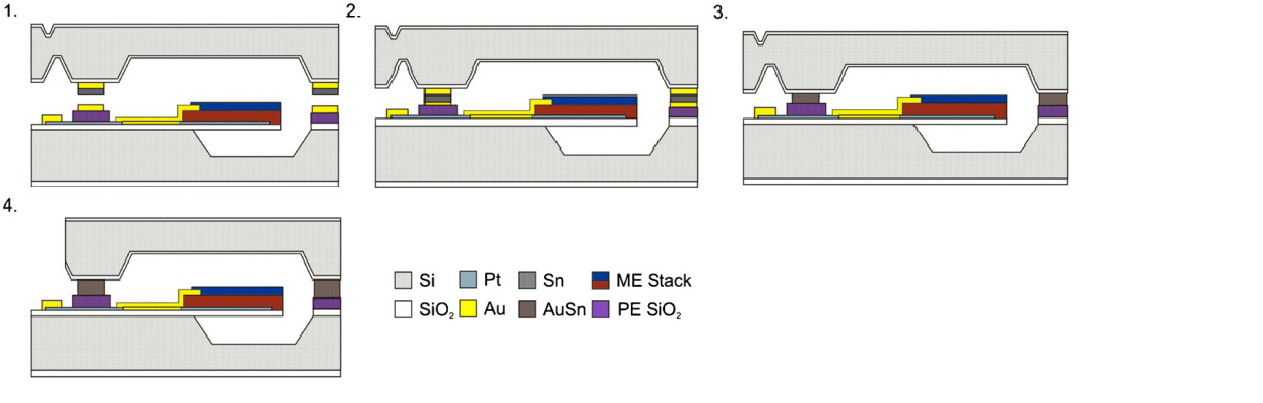Рисунок 2 – Последовательность соединения

Характеристики элементов сенсора были измерены с применением экранировки. Сенсор был помещен в две катушки. На одной катушке генерировалось постоянное магнитное поле смещения, чтоб ввести сенсор в оптимальное состояние [14]. Вторая катушка использовалась для воздействие другим магнитным полем с HAC, измеряемым. Ввиду низкой электроемкости сенсора, потребовалось усиливать заряд, чтоб измерить МЭ коэффициент и линейность.

Так, было измерено генерируемое напряжение выхода Uвых, а по нему – вычислено напряжение UME по формуле

,

где cf – емкость обратной связи, cs – емкость сенсора. Преобразователь Keithley 6221AC использовался как источник измеряемого поля с HAC. Плотность напряжения собственного шума была измерена анализатором динамического сигнала SR785.

Разрешение и линейность в резонансе показаны на рис. 3. За исключением ряда относительно сильных полей (выше 1 мкТл), сенсор линеен вплоть до 30 пкТл. Ниже отмеченных на графике точек, показания имеют рассеянные значения и отношение сигнал/шум стремится к нолю [15]. В сравнении с опубликованными результатами других микромагнитомеров, таких как датчики Холла, AMR, GMR, Лоренц резонаторы, micro-uxgates, разработанный сенсор показывает значительно лучший результат.

Рисунок 3 – Чувствительность и линейность сенсора

Так, работа, проделанная данной группой учёных, доказывает эффективность использования МЭ компонентов в микросенсорах в качестве сверхчувствительных датчиков магнитного поля.

2). Известно, что тонкослойные магнитоэлектрические (МЭ) сенсоры дают чувствительность порога 7,1 пТл/(Гц)1/2 на узких частотных полосах резонанса [16]. Очевидно, высокая чувствительность делает, как уже было замечено, сенсоры такого рода пригодными для измерения биомагнитных сигналов, в т.ч. МЭГ. С другой стороны, для биомагнитных измерений обычно требуется высокая чувствительность на широком, но очень низком частотном спектре – 0.1-100 Гц. К сожалению, на таких низких частотах, сильно отдалённых от частот резонансов, МЭ коэффициент резко уменьшается, а уровень шума – возрастает. Это ведёт к значительному снижению чувствительности. Учёные, часть которых участвовала в разработке высокочувствительного МЭМС, описанного выше, занялись решением проблемы снижения чувствительности, разработав для этого новый метод преобразования частоты [17].

Он позволяет проводить широкополосные измерения на низких частотах, устраняя нелинейные характеристики кривой магнитострикции. Данная технология даёт резонансно усиленную чувствительность на, фактически, произвольных частотах, причём значительно ниже резонансных. Измерения показывают, что чувствительность при 1 Гц может быть усилена по коэффициенту в порядок тысячи раз по сравнению с нерезонансным случаем при использовании описанной в работе технологии модуляции. Данный метод также открывает преимущества в ускорении работы сенсора, ликвидации механического шума и управлении системами такого рода сенсоров.

Так, из рассмотренных примеров можно видеть, что важная часть разработок вращается вокруг борьбы с помехами и повышением чувствительности создаваемых приборов.

§1.3 Методы борьбы с помехами

Мешающие магнитные поля можно подразделить на две категории: магнитные поля того же самого биологического объекта, не подлежащие исследованию в данном конкретном эксперименте, и магнитные поля, обусловленные внешними по отношению к объекту генераторами (естественного и искусственного происхождения). Из внешних магнитных полей наиболее сильным является естественное поле Земли, обусловленное электрическими токами в земной коре. Характеризуя интенсивность поля, обычно используют модуль вектора магнитной индукции (при использовании других характеристик делаются соответствующие оговорки). Постоянная составляющая магнитного поля Земли, или геомагнитного поля равна 50–70 мкТл (в зависимости от географического положения), причём около 80% этого значения определяется магнитным диполем, расположенном в центре земного шара. Пространственный градиент геомагнитного поля невелик – он составляет 10–20 пТл/м. Геомагнитное поле медленно изменяется во времени в результате планетарных взаимодействий и ионосферных процессов. Такие изменения наблюдаются в частотном диапазоне 10-4–102 Гц и зависят от географического положения, сезона и времени суток. Равномерность геомагнитного поля может быть заметно искажена под влиянием крупных предметов из ферромагнитного материала (элементы конструкций зданий из стали и т. п.).

Из искусственных источников магнитных помех наиболее сильным является сеть электропитания; она создаёт магнитное поле с амплитудой до нескольких сотен тысяч пикотесел и с градиентом 500–20000 пТл. Источниками магнитных помех являются так же различные технические устройства, двигатели, транспортные средства и предметы из материалов, хорошо проводящие электрический ток (в них индуцируются вихревые токи, порождающие магнитное поле). Магнитные помехи создаются также высокочастотными радиоволнами. Наконец, магнитные помехи самого низкого уровня порождаются электрическими токами, обусловленными тепловым шумом в электропроводящих телах.

Если помехи, вызванные внешними источниками (поля приборов, проводки, волны радиопередач), решаются широким спектром возможностей экранировки, то физиологические помехи – шумы, вызванные биологическими источниками и процессами, не попадающими в поле исследуемых – вызывают гораздо больше трудностей. Существует ряд методов, призванных снизить физиологические артефакты в записях биомагнитных сигналов, таких как полосовая фильтрация, фильтрация Кальмана («мускульный» и флуктуационный шумы), адаптивная фильтрация (АФ), вайвлет-преобразование и пр. Впрочем, каждый вид имеет свои недостатки и специфические ограничения в применении.

Электронный фильтр – это частотно-избирательное устройство, кото-рое служит для передачи (пропускания) сигналов в заданном диапазоне час-тот (полосе пропускания) и подавления сигналов в других диапазонах частот (полоса задерживания). Различают аналоговые фильтры, в которых обрабатываемый сигнал имеет аналоговую форму, и цифровые фильтры, предназначенные для обработки цифровых сигналов.

Аналоговый фильтр представляет линейную частотно-селективную цепь, поведение которой определяется операторной передаточной функцией. В общем случае для получения передаточной функции, обеспечивающей заданную форму частотных характеристик, используют методы оптимизации. На практике часто используют типовые передаточные функции, имеющие аналитическое решение. Перечислим наиболее распространённые передаточные функции, аппроксимирующие. АЧХ фильтра нижних частот.

1. Фильтр Баттерворта с максимально плоской амплитудно-частотной характеристикой.

2. Фильтр Чебышева с равноволновой характеристикой в полосе про-пускания.

3. Инверсный фильтр Чебышева с равноволновой характеристикой в полосе задерживания.

4. Эллиптический фильтр, имеющий равноволновые характеристики в полосе пропускания и полосе задерживания.

5. Фильтр Бесселя с фазочастотной характеристикой, близкой к линейной.

В задачах цифровой обработки сигналов выделяют этапы предварительной (первичной) и вторичной обработки сигналов. Это связано с тем, что в общем случае на входе системы обработки наблюдается смесь V(t) полезного сигнала x(t), некоторого шума n(t) и различных помех разной природы p(t):

V(t) = x(t) + n(t) + p(t),

где n(t) является характеристикой самого техничного устройства, а p(t) - некоторое искажающее воздействие самой физической среды, в которой распространяется сигнал (например, затухание). Важнейшей задачей предварительной обработки сигнала является подавление n(t) и p(t) (шума и помехи). Такая задача оптимального может быть решена только на основе использования избыточности представления исходного сигнала, а также имеющихся сведений о свойствах полезного сигнала, помехи и шума для увеличения вероятности правильного приёма.

Известны следующие методы фильтрации, обеспечивающие улучшение соотношения сигнал/помеха:

- метод накопления;

- частотная фильтрация;

- корреляционный метод;

- согласованная фильтрация;

- нелинейная фильтрация.

Все эти методы основаны на использовании различий свойств полезного сигнала и помехи.

Комплекс цифровой обработки сигналов содержит ЭВМ, специализированные устройства ввода и соответствующее программное обеспечение. В общем случае подобный комплекс должен также обеспечивать ввод, вывод и передачу сигналов различной физической природы.

Глава 2. Экспериментальная установка и методика эксперимента

§2.1 Нейрон и нейронные сети

§2.1.1 Биологический нейрон

Как известно, самая сложная и малоизученная часть человеческого организма – головной мозг. Физиология, гуморальная регуляция других органов принципиально прочих органов принципиально изучена. Мозг же является, во-первых, органом не только функциональным, но и управляющим, что уже значительно повышает его сложность и значимость.

Во-вторых, до сих пор он слабо описан как система со связями структуры и функционала. Если общеинтегративные функции и механизм обработки сенсорной информации известны достаточно хорошо, то даже элементарные когнитивные процессы изучены с этой точки зрения в очень малом количестве.

И, наконец, с точки зрения медицины мозг представляет собой неоднозначный объект исследований. С одной стороны, он даёт богатейшую возможность диагностирования засечёт наличия связей между состоянием определённых его частей и магнитным и электрическим полями, которые он образует. С другой стороны, эти связи очень сложны и здесь первым делом встаёт так называемая задача картирования головного мозга, что позволит определять индивидуальное местоположение и особенности областей мозга, отвечающих за те или иные функции. Сложность связей вызвана не только большим количеством нейронов, но и принципом работы нейронной сети: она представляет собой мощный статистический процессор (в отличие от систем, основанных на последовательной обработке и исполнении команд).

Один из наиболее эффективных методов изучения мозга – магнитоэнцефалография, она была описана в главе 1 данной работы.

Магнитное поле головного мозга вызывается суммой огромного количества электрических импульсов, проходящих по нейронным сетям.

Биологический нейрон состоит из тела диаметром от 3 до 100 мкм, содержащего ядро и отростки. Выделяют два вида отростков. Аксон обычно — длинный отросток, приспособленный для проведения возбуждения от тела нейрона. Дендриты — как правило, короткие и сильно разветвлённые отростки, служащие главным местом образования влияющих на нейрон возбуждающих и тормозных синапсов (разные нейроны имеют различное соотношение длины аксона и дендритов). Нейрон может иметь несколько дендритов и обычно только один аксон. Один нейрон может иметь связи с 20-ю тысячами других нейронов. Кора головного мозга человека содержит десятки миллиардов нейронов.

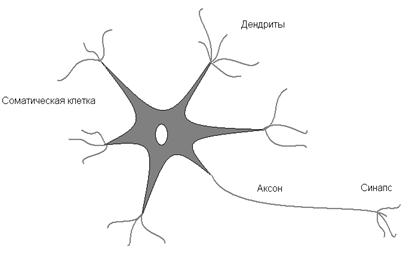
Биологический нейрон является важнейшим элементом клеток нервной системы и строительным материалом мозга. Нейроны существуют в нескольких форма, в зависимости от их назначения и дислокации, но в целом они схожи по структуре.

Каждый нейрон является устройством обработки информации, которое получает сигналы от других нейронов через специальную структуру ввода, состоящую из дендритов. Если совокупный входной сигнал превышает пороговый уровень, то клетка передаёт сигнал далее в аксон, а затем в структуру вывода сигнала, от которой он передаётся в другие нейроны. При переходе в возбужденное состояние в выходном отростке (аксоне) генерируется импульс возбуждения, распространяющийся по нему со скоростью от 1 до 100 м/с; в основе процесса распространения лежит изменение локальной проводимости мембраны аксона по отношению к ионам натрия и калия. Между нейронами нет прямых электрических связей. Перенос сигнала с аксона на входной отросток (дендрит) другого нейрона осуществляется химическим путём в специальной области – синапсе, где окончания двух нервных клеток подходят близко друг к другу. Некоторые из синапсов являются особыми, вырабатывающие сигналы обратной полярности для гашения сигналов возбуждения. В настоящее время интенсивно изучаются и глобальные аспекты деятельности мозга – специализация его больших областей, функциональные связи между ними и т.п. В то же время мало известно, как же осуществляется обработка информации на промежуточном уровне, в участках нейронной сети, содержащей всего десятки тысяч нервных клеток.

§2.1.1 Модели

Деятельность мозга связана с параллельной обработкой информации. К настоящему времени организация параллельных вычислений уже используется в ЭВМ, например, с матричными процессорами, представляющими собой сеть из более простых процессоров, имеющих собственную память. Техника параллельного вычисления заключается в том, что элементарный процессор «знает» лишь о состоянии своего малого элемента среды. Основываясь на этой информации, каждый процессор вычисляет состояние своего элемента в следующий момент времени. При этом отсутствует ограничение быстродействия, связанное со скоростью распространения сигналов. Работа матричного процессора устойчива по отношению к локальным повреждениям.

Следующим этапом в развитие идеи параллельных вычислений явилось создание вычислительных сетей. Такое своеобразное «сообщество» компьютеров напоминает многоклеточный организм, который «живет своей жизнью». При этом функционирование вычислительной сети как сообщества компьютеров не зависит от того, как именно устроен каждый отдельный компьютер, какими процессами внутри него обеспечена обработка информации. Можно представить себе сеть, состоящую из очень большого числа примитивных компьютеров, способных выполнять всего несколько операций и хранить в своей памяти мгновенные значения нескольких величин.

Рассмотрим общие принципы построения моделей нейрона и нейронных сетей.

При построении нейровидных систем можно выделить два основных подхода: так называемые подходы «сверху» и «снизу». Первый подход – подход «сверху» – предусматривает создание таких функциональных или информационных структур, которые моделируют процессы, происходящие в мозге человека во время восприятия информации. Внутренняя структура мозга при этом не учитывается. Поэтому нейронные элементы, которые используют подход «сверху», используются для изучения общих принципов функционирования мозга, а поэтому их структура может быть более сложной для выполнения большого количества операций. Второй подход предусматривает создание так называемых имитационных структур, то есть таких систем, структура которых подобна структуре мозга человека. Нейронные элементы для такого подхода должны быть простейшими, но в тоже время – достаточно точными, поскольку они будут использоваться для построения нейронных сетей.

Очевидно, в данной работе будет использоваться второй подход, так как для изучения магнитного поля объекта важно воспроизвести точное прохождение вызывающих его токов.

Кусок про компьютерное моделирование

Так, может показаться, что техническое моделирование нейрона и нейросетей неактуально и имеет мало приложений. Но это не так. Порой – как, например, в данной работе – требуется достаточно точное воспроизведение принципов работы нейросети, а не общее имитирование структурного функционирования.

Существует ряд схем, моделирующих определённые части нейрона отдельно: модель мембраны Люиса, модель мембраны Роя (обе являются реализацией теоретической модели мембраны Ходгкина и Хаксли).

Модель мембраны Люиса. We discuss here the model published by Lewis in 1964. Lewis realized the sodium and potassium conductances using electronic hardware in the form of active filters, as shown in the block diagram of Figure 10.1. Since the output of the model is the transmembrane voltage Vm, the potassium current can be evaluated by multiplying the voltage corresponding to GK by (Vm - VK). Figure 10.1 is consequently an accurate physical analog to the Hodgkin-Huxley expressions, and the behavior of the output voltage Vm corresponds to that predicted by the Hodgkin-Huxley equations.

The electronic circuits in the Lewis neuromime had provision for inserting (and varying) not only such constants as GK max, GNa max, VK, VNa, VCl, which enter the Hodgkin-Huxley formulation, but also h, m, n, which allow modifications from the Hodgkin-Huxley equations. The goal of Lewis's research was to simulate the behavior of a neuronal network, including coupled neurons, each of which is simulated by a neuromime; this is documented later in this chapter.

In the electronic realization the voltages of the biological membrane are multiplied by 100 to fit the electronic circuit. In other quantities, the original values of the biological membrane have been used. In the following, the components of the model are discussed separately.

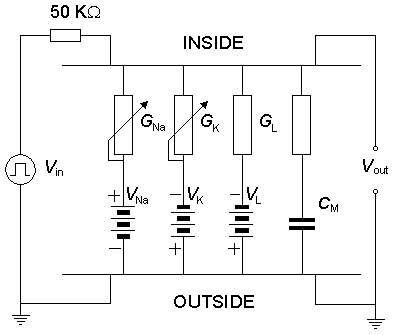
Люиса

Модель Роя. Guy Roy published an electronic membrane model in 1972 (Roy, 1972) and gave it the name "Neurofet." His model, analogous to Lewis's, is also based on the Hodgkin-Huxley model. Roy used FET transistors to simulate the sodium and potassium conductances. FETs are well known as adjustable conductors. So the multiplying circuit of Lewis may be incorporated into a single FET component (Figure 10.6).

In the Roy model the conductance is controlled by a circuit including an operational amplifier, capacitors, and resistors. This circuit is designed to make the conductance behave according to the Hodgkin-Huxley model. Roy's main goal was to achieve a very simple model rather than to simulate accurately the Hodgkin-Huxley model. Nevertheless, the measurements resulting from his model, shown in Figures 10.7 and 10.8, are reasonably close to the results obtained by Hodgkin and Huxley.

Figure 10.7 illustrates the steady-state values for the potassium and sodium conductances as a function of applied voltage. Note that for potassium conductance the value given is the steady-state value, which it reaches in steady state. For sodium the illustrated value is ; it is the value that the sodium conductance would attain if h remained at its resting level (h0). (The potassium and sodium conductance values of Hodgkin and Huxley are from tables 1 and 2, respectively, in Hodgkin and Huxley, 1952.)

The full membrane model was obtained by connecting the potassium and sodium conductances in series with their respective batteries and simulating the membrane capacitance with a capacitor of 4.7 nF and simulating the leakage conductance with a resistance of 200 k . The results from the simulation of the action pulse are illustrated in Figure 10.8.

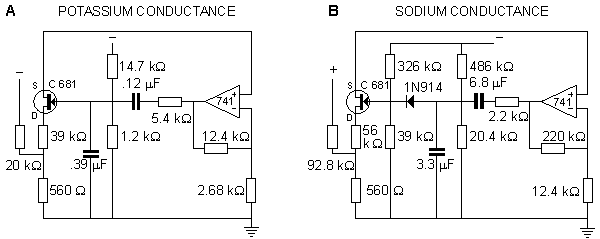Роя

Другой пример – модель потенциала действия на аксоне.

Но для изучения магнитного поля подходящей видится схема Л. Д. Хармона. Она описывает клетку как целую единицу, точно симулируя функционирование отдельного нейрона. Она достаточно проста при том, что выдаёт импульс действия такой, как и настоящий нейрон.

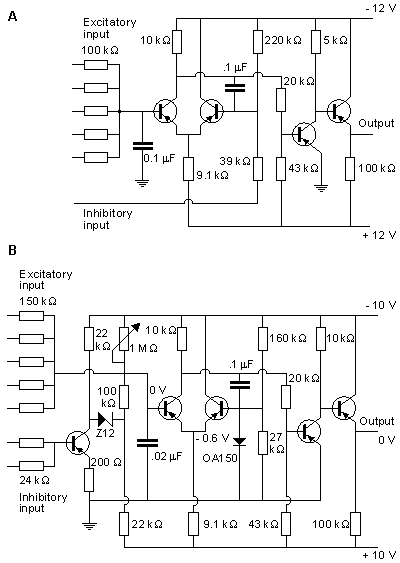
Хармон

Кроме описанной схемы, предложен ряд других вариантов моделей нейрона на лампах и транзисторах. Эти модели отличаются друг от друга как своими функциональными характеристиками, так и временными параметрами. Разработано также несколько вариантов моделей нейрона на магнитных элементах, в которых, используя частичное перемагничивание, легко имитировать пороговые свойства и процессы суммации входных воздействий.

§2.2 Базовая экспериментальная установка

§2.2.1 Установка исследуемой модели

Модель Хармона. The circuit of the Harmon neuron model is given in Figure 10.13. Figures 10.13A and 10.13B show the preliminary and more advanced versions of the circuit, respectively. The model is equipped with five excitatory inputs which can be adjusted. These include diode circuits representing various synaptic functions. The signal introduced at excitatory inputs charges the 0.02 µF capacitor which, after reaching a voltage of about 1.5 V, allows the monostable multivibrator, formed by transistors T1 and T2, to generate the action pulse. This impulse is amplified by transistors T3 and T4. The output of one neuron model may drive the inputs of perhaps 100 neighboring neuron models. The basic model also includes an inhibitory input. A pulse introduced at this input has the effect of decreasing the sensitivity to the excitatory inputs.

Strength-Duration Curve

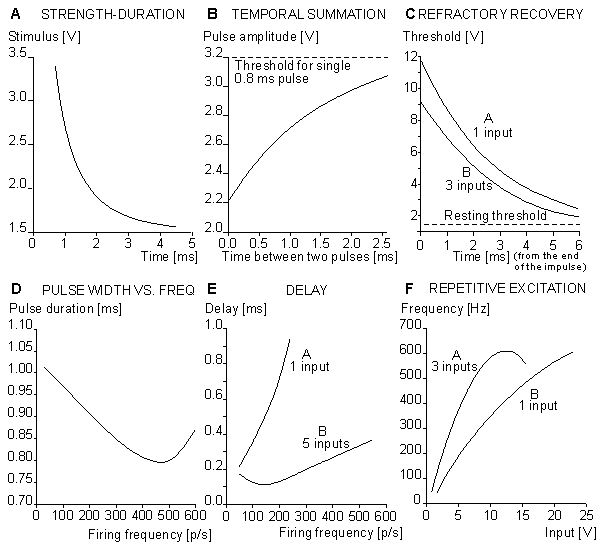
The Harmon model follows a strength-duration curve similar to that exhibited by the natural neuron. The time scale is approximately correct, but owing to the electric properties of circuit components, the voltage scale is much higher. The threshold voltage in the Harmon model is about Vth = 1.5 V, as described in Figure 10.14A. Latency

Because the model contains no internal circuit that specifically generates a latency, this phenomenon is totally described by the strength-duration curve which is interpreted as a stimulus-latency curve. The action pulse is generated only when the stimulus has lasted long enough to generate the action pulse. Temporal Summation

The model illustrates the stimulus threshold in the case of two consecutive stimulus pulses where the first pulse leaves the membrane hyperexcitable to the second. Figure 10.14B shows the required amplitude of two 0.8 ms pulses as a function of their interval, and one notes that the threshold diminishes with a reduced pulse interval, owing to temporal summation. In all cases the pulse amplitude is reduced from the value required for activation from a single pulse. Refractory Period (Recovery of Excitability)

The typical recovery of excitability of the model after an action pulse is shown in Figure 10.14C (curve A). This curve is similar to that for a biological neuron. The neuron model is absolutely refractory for about 1 ms - that is, the time of the output pulse. The relative refractory period starts after this (t = 0), and its time constant is about 1.7 ms. Curve A is obtained when the stimulus is applied at one input. Curve B represents the situation when the stimulus is simultaneously applied to three inputs (see Fig. 10.13). Output Pulse, Action Impulse

The output pulse obeys the all-or-none law, and its amplitude is quite stable. Its width is, however, to some degree a function of the pulse frequency. This dependence is given in Figure 10.14D. Delay

The delay refers, in this case, to the time between the onsets of the stimulus pulse and the output pulse. It is not the delay in the usual meaning of the term. In the model, the delay is a function of the integration in the input as well as the refractory condition. Curve A in Figure 10.14E represents the delay when a stimulus is applied to one input, and curve B when the stimulus is applied to all five excitatory inputs. Repetitive Excitation

Repetitive excitation refers to the generation of output pulses with a constant input voltage and frequency. Figure 10.14F, curve A, shows the frequency of the output pulse when the input voltage is connected to three inputs, and curve B when the input voltage is connected to one input. The output frequency follows the input only for high voltage inputs. As the input is reduced, pulses drop out, and the resulting output frequency is reduced compared to the input.

By connecting capacitors between the input and output ports of the neuron model, it is possible to realize much more complex functions. Harmon performed experiments also with combinations of many neuron models. Furthermore, Harmon investigated propagation of the action pulse by chaining models together. These neuron models can be applied to simulate quite complex neural networks, and even to model brain waves.

УСТРАНЕНИЕ ПОМЕХ ПРИ ИЗМЕРЕНИИ МАГНИТНЫХ ПОЛЕЙ БИОЛОГИЧЕСКИХ ОБЪЕКТОВ