Сопоставление правила порогового агрегирования и ранговых процедур

Веселова Ю.А.1

Введение

Правила коллективного выбора – процедуры принятия решений, учитывающие мнение множества агентов. В связи с развитием компьютерных технологий область коллективного выбора приобретает все большее значение в задачах автоматического агрегирования большого количества предпочтений, таких как электронные голосования, построения рейтингов, упорядочение ссылок в поисковых и рекомендательных системах и т.д. При этом как число альтернатив, так и число агентов может быть очень большим, что может быть значительным препятствием для применения того или иного правила ранжирования в силу большой вычислительной сложности. Поэтому аналитическое исследование свойств правил коллективного выбора, а также оценка сложности процедур имеет сегодня большую актуальность.

В работе мы рассматриваем алгебраические свойства правил коллективного выбора, основанных сумме взвешенных рангов и лексикографическом сравнении. К числу процедур, основанных на ранге, или порядковых, относятся правила простого большинства, правило одобряющего голосования, правило Борда. Все перечисленные процедуры упорядочивают альтернативы согласно сумме взвешенных рангов: чем больше сумма, тем более предпочтительным считается вариант. Отличие таких правил друг от друга заключается лишь в векторе весов различных рангов. Аксиоматика ранговых правил выбора была представлена в работе (Young, 1975). Правило коллективного выбора тогда и только тогда является ранговым, когда оно удовлетворяет одновременно свойствам анонимности, нейтральности и согласованности.

Лексикографическое сравнение используется в процедуре порогового агрегирования, математическая модель и аксиоматическое описание которой даны в работах (Aleskerov, Yakuba 2003, 2007) и (Aleskerov et al, 2010). Согласно правилу порогового агрегирования, низкие оценки вариантов не могут быть компенсированы более высокими оценками. Например, вариант, получивший оценки 3, 5, 5, хуже варианта, получившего три четверки. С другой стороны, возможность такой компенсации – одно из необходимых свойств правила Борда, являющегося типичным примеров ранговой процедуры.

В работе дан теоретический анализ свойств как уже известных, так и новых правил, основанных на суперпозиции ранговых и лексикографических процедур. Мы доказываем, что правило порогового агрегирования удовлетворяет всем аксиомам ранговых правил, а следовательно, существуют такие веса рангов, при которых результат соответствующего порядкового правила будет совпадать с результатом правила порогового агрегирования, и приводим схему построения такого вектора весов рангов.

Модель

Пусть - множество альтернатив, , - множество избирателей. Каждый избиратель каждой альтернативе дает некоторую оценку из множества оценок, такую функцию оценивания мы обозначим за . Считаем, что чем выше оценка, данная альтернативе, тем больше избиратель ее ценит. Теперь для каждой альтернативы определим вектор , -ый элемент которого, , будет равен количеству избирателей, давших альтернативе оценку . Множество всех возможных векторов оценок может быть упорядочено лексикографически следующим образом. Если существует номер такой, что для каждого выполнено и , то , то есть лексикографически доминирует . Такое отношение задает на множестве всех возможных векторов оценок линейный порядок, т.е. сравнимы все неодинаковые векторы. Согласно правилу порогового агрегирования (Aleskerov et al, 2010), альтернатива доминирует альтернативу , если . В то же время, если две альтернативы имеют одинаковые позиции в предпочтениях с точностью до перестановки избирателей, то они будут иметь и одинаковые векторы оценок. Следовательно, на множестве альтернатив заданное таким образом отношение задает слабый порядок. Классы эквивалентности в данном случае – множества альтернатив с одинаковыми векторными оценками.

Теперь рассмотрим формальное описание правил коллективного выбора, основанных на сумме взвешенных рангов, рассмотренное в (Saari, 2000) Для этого нам остается определить способ задания вектора весов рангов. При этом более высокая оценка должна иметь не меньший вес, а наихудшая оценка – нулевой. В правиле простого большинства учитываются только альтернативы, стоящие на первом месте в предпочтениях избирателей, т.е. те их них, которые получают максимальные оценки. Следовательно, вес всех оценок, кроме наивысшей, будет нулевым. Нормируя сумму весов к единице, получим следующий вектор . Для правила одобряющего голосования с квотой важны только альтернативы, которые находятся среди лучших альтернатив в предпочтениях избирателей, при этом вес всех наилучших оценок одинаков, поэтому нормированным вектором весов для данного правила будет

По правилу Борда за каждую оценку альтернатива получает баллов, за каждую оценку получает баллов, и т.д. вес -ой оценки равен . Следовательно, нормированный вектор весов рангов будет

Далее вектор оценок альтернативы скалярно умножается на вектор весов оценок для соответствующего правила . Альтернативы упорядочиваются согласно полученным значениям , т.е. варианты с большим значением доминируют варианты с меньшим значением.

Классы эквивалентных оценок ранговых процедур

Для порядковых правил коллективного выбора также существует проблема несравнимости вариантов. Так, по правилу простого большинства окажутся несравнимыми альтернативы, имеющие одинаковое количество наивысших оценок. Если рассматривать множество всех возможных векторов оценок, то эквивалентными будет считать те их них, которые дают одно и то же значение . Таким образом, мы получаем разбиение множества векторов оценок на непересекающиеся подмножества – классы эквивалентности. Количество таких классов для правила Борда равно .

Рассмотрим пример для и . На рисунках 1-3 изображены симплексы . Каждая точка на симплексе соответствует некоторому вектору . На рисунке 1 множества точек, объединенных в группы, - классы эквивалентности по рангу Борда, . Аналогично, классы эквивалентности по правилу простого большинства и по правилу одобряющего голосования с квотой изображены на рисунках 2 и 3.

Случай с тремя градациями оценок, , дает возможность наглядно продемонстрировать построение классов эквивалентных векторов оценок. Правило простого большинства и правило одобряющего голосования с квотой 1 являются двумя крайними случаями ранговых процедур и составляют базис пространства векторов весов для . Эквивалентные векторы оценок расположены на линиях уровней . Таким образом, угол под которым в симплексе идут линии уровня любого рангового правила, будет находиться между углами линий уровня правил простого большинства и правила одобряющего голосования.

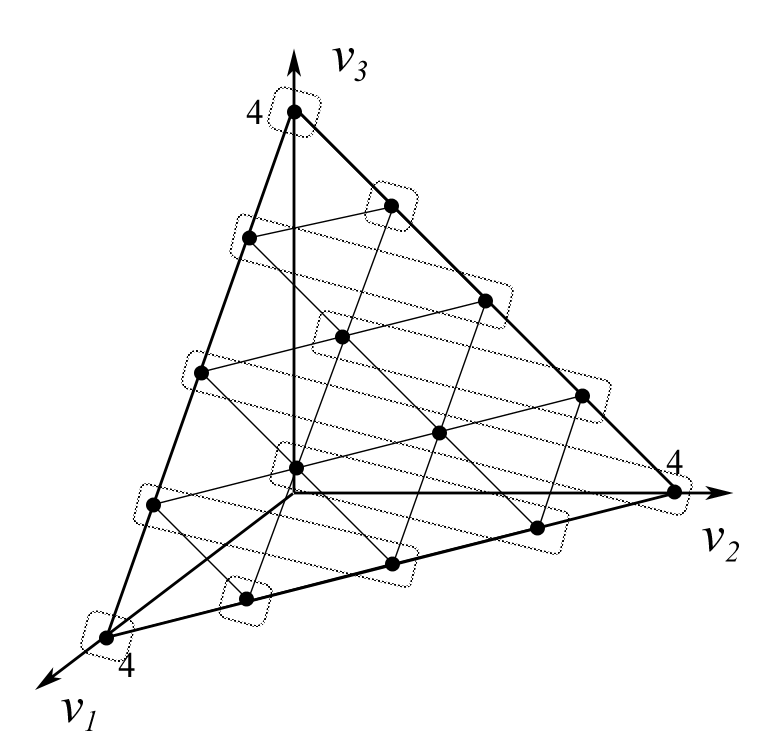
Рис. 1. Классы эквивалентности по правилу Борда.

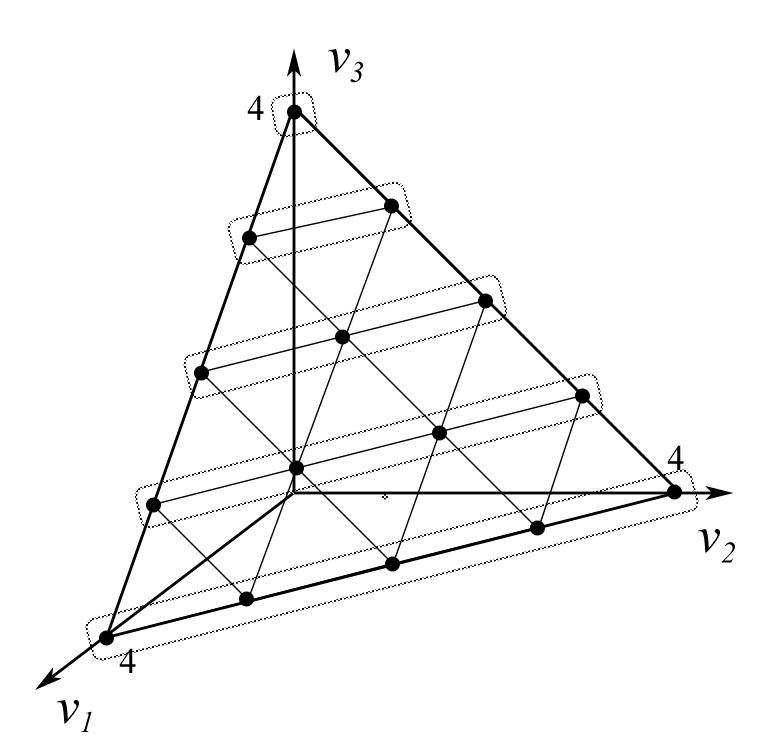
Рис. 2. Классы эквивалентности по правилу простого большинства.

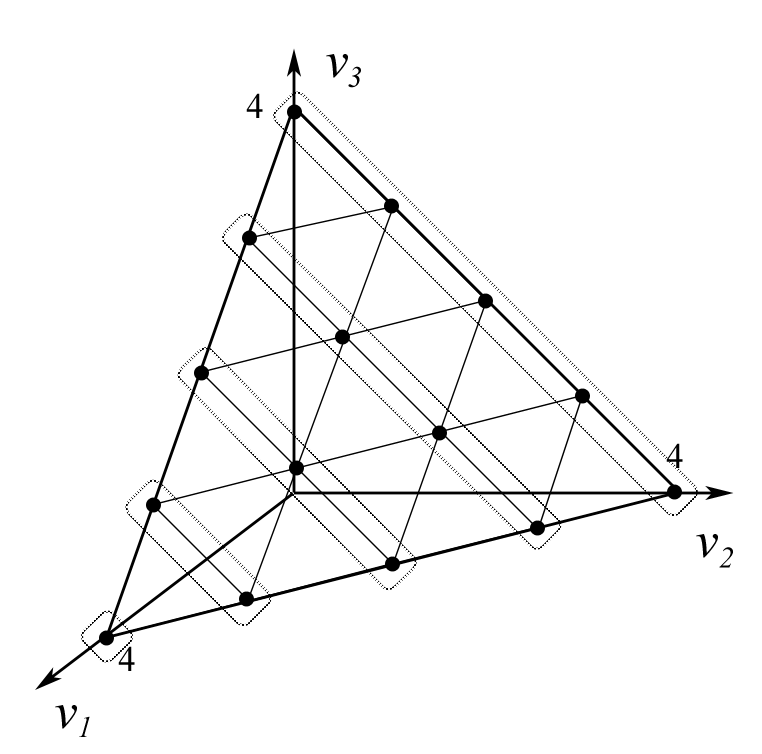
Рис. 3. Классы эквивалентности

по правилу одобряющего голосования с квотой .

Правило порогового агрегирования

Теперь рассмотрим геометрическую иллюстрацию упорядочения согласно правилу порогового агрегирования, представленную на рисунке 4. Каким образом следует подобрать веса, чтобы ранговая процедура давала аналогичное упорядочение?

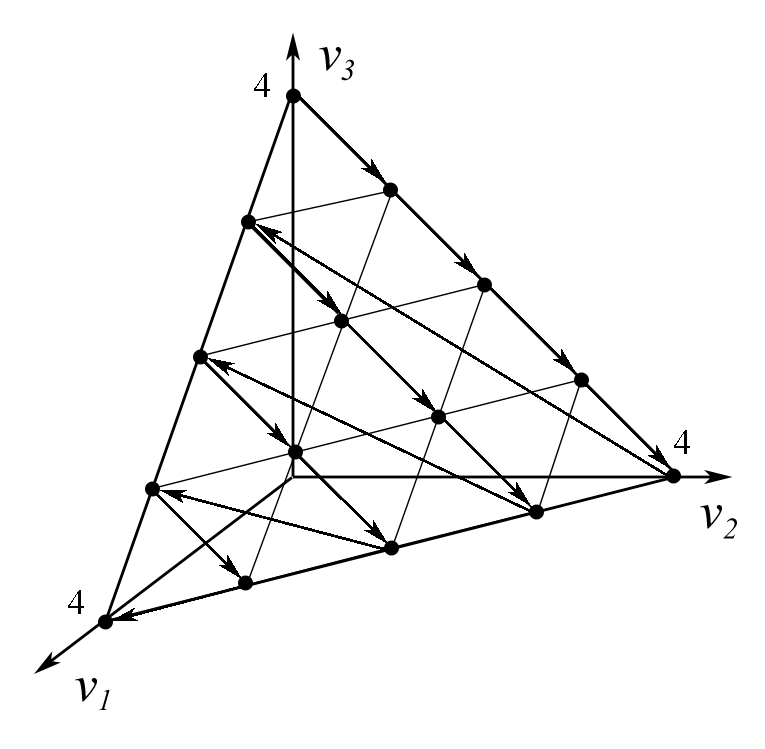
Рис. 4. Упорядочение векторов оценок согласно правилу

порогового агрегирования.

На рисунке 5 изображены линии уровня для ранговой процедуры, результат которой совпадает с правилом порогового агрегирования. Мы утверждаем, что в каждом случае существует континуум векторов весов рангов, удовлетворяющих нашему требованию.

Утверждение 1. Для ранговая процедура эквивалентна правилу порогового агрегирования тогда и только тогда, когда нормированный вектор весов равен

где .

Рис. 5. Линии уровня для ранговой процедуры, результат которой совпадает с правилом порогового агрегирования.

Мы выводим условия, при которых ранговая процедура дает то же самое упорядочение, что и правило порогового агрегирования в более общем случае, а также доказываем, что существует аналогичный способ подобрать веса для суперпозиции ранговых процедур и порогового правила. Результаты исследования обобщают математическую модель ранговых процедур, а также дают возможность упростить вычисление результата правила выбора, сведя более сложные правила к обычной процедуре с назначением весов оценок, что немаловажно при больших объемах данных.

Литература

Биркгоф Г., Барти Т.К. (2005), “Современная прикладная алгебра”, перевод с английского Ю.И.Манина, издательство “Лань”, Санкт-Петербург.
Кофман А. (1975), «Введение в прикладную комбинаторику», Главная редакция физико-математической литературы изд-ва “Наука”.
Aleskerov F, Chistyakov V, Kalyagin V. (2010), “Social threshold aggregations”, Social Choice Welfare Vol. 35: 627–646.
Aleskerov F.T., Yakuba V.I. (2003) “A method for aggregation of rankings of special form”, Abstracts of the 2nd international conference on control problems, IPU RAN, Moscow, Russia, 116.
Aleskerov F.T., Yakuba V.I. (2007) “A method for threshold aggregation of three-grade rankings”, Dokl Math 75: 322–324.
Gehrlein W.V., Lepelley D. (2011), “Voting Paradoxes and Group Coherence”, Springer-Verlag Berlin Heidelberg.
Saari, D.G. (2000), “Mathematical structure of voting paradoxes II: positional voting”, Journal of Economic Theory Vol. 15: 55-101.
Young, H.P. (1974), “Axiomatization of Borda’s rule”, Journal of Economic Theory, Vol. 9: 43-52.
Young, H.P. (1975), “Social Choice Scoring Functions”, Journal on Applied Mthematics, Vol. 28, No. 4: 824-838.

1 НИУ ВШЭ, Кафедра высшей математики на факультете экономики, Международная лаборатория анализа и выбора решений.

E-mail: yul-r@mail.ru

1 Такое правило обычно называют обратным правилом простого большинства.

Сопоставление правила порогового агрегирования и ранговых процедур