ПРИМЕНЕНИЕ СОПРЯЖЕННОЙ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ ДЛЯ АНАЛИЗА ПОКАЗАТЕЛЕЙ ПРОИЗВОДИТЕЛЬНОСТИ

А.В.Матвеенко

Санкт-Петербургский государственный университет

Санкт-Петербург

Повышение производительности – актуальная задача, стоящая перед российской и другими развивающимися и переходными экономиками. Ее решение затрудняется тем, что имеются сложные взаимосвязи между различными показателями производительности и эффективности, а возможности изменения показателей эффективности (таких как TFP и эффективности факторов) мало изучены (см., например, Prescott, 1998).

В работе устанавливается зависимость между показателями производительности труда, производительности капитала (капиталоотдачи) и показателями эффективности (TFP и эффективностями факторов) на основе понятия технологического меню (Jones, 2005) и понятия сопряженной функции (Rubinov, Glover, 1998).

Технологическое меню, по Джонсу, определяется как множество «локальных» технологий , максимизация по которым при заданных K, L дает «глобальную» производственную функцию:

. (1)

Здесь - производственная функция Леонтьева. Представление (1) интерпретируется следующим образом. Фирме (или стране) доступно некоторое множество леонтьевских технологий – технологическое меню . Располагая имеющимися факторами производства K, L, фирма (страна) выбирает из технологического меню леонтьевскую технологию так, чтобы, с ее помощью, получить максимальный выпуск. В результате, по технологическому меню получается производственная функция, стоящая в левой части равенства (1).

Сопряженная функция может быть описана следующим образом. Если F(K,L) – производственная функция, то cопряженная функция определена выражением

где .

В работе доказывается, что технологическое меню состоит из всевозможных пар средних производительностей труда и капитала, которые возможны при фиксированном TFP (или эффективностях факторов). Сопряженная функция, рассматриваемая как функция от средних производительностей, показывает значение TFP, при котором становится допустимой данная пара средних производительностей.

Получено соотношение между темпами прироста средних производительностей капитала, труда и TFP

, (2)

где - доли труда и капитала, соответственно.

Равенство (2) означает, что темп прироста производительности труда складывается из взятых с положительными коэффициентами темпа прироста TFP и темпа снижения капиталоотдачи. Таким образом, снижение капиталоотдачи (а не повышение) способствует росту производительности труда. Одновременное повышение производительности труда и капиталоотдачи может происходить лишь с ограниченным темпом прироста капиталоотдачи ().

По поводу изменения капиталоотдачи известен стилизованный факт, сформулированный в 1961 г. британским экономистом Н.Кальдором: отношение выпуска к капиталу постоянно. Если принять это предположение, то , и из (2) следует, что

, (3)

т.е. для стран, для которых справедлив данный стилизованный факт, производительность труда растет в раз быстрее, чем растет TFP.

Пусть теперь для какой-то страны величина мала по абсолютной величине, хотя . Если в (2) коэффициент мал, то можно пренебречь вторым слагаемым, тогда (3) выполняется как приближенное равенство.

Относительно соотношения долей труда и капитала (т.е. величины ) проводился в последние годы ряд исследований, которые показывают, что, в среднем, величина ниже в промышленно развитых странах, чем в развивающихся, причем во всех группах стран происходит постепенный рост этой величины (доля капитала растет, а доля труда снижается). Таким образом, можно ожидать, что равенство (3) выполняется как приближенное для многих промышленно развитых стран (к которым, в первую очередь, относится данный стилизованный факт Н.Кальдора, и для которых коэффициент относительно невелик), но равенство (3) будет неверным, по крайней мере, для некоторых развивающихся стран, и для них рост производительности труда существенно связан с изменением капиталоотдачи.

Так ли это на самом деле, мы наблюдаем на реальных данных по промышленно развитым (табл. 1) и развивающимся (табл. 2) странам.

Табл. 1. Темпы прироста TFP и производительностей факторов в некоторых промышленно развитых странах. (Расчет автора по результатам «учета роста»).

Страна	Период	Доля капитала	Темп прироста производитель- ности труда, %	Темп прироста TFP, %	Темп прироста капитало-отдачи, %
Великобри- тания	1947-73	0,38	3,68	1,94	-0,9	0,61
Германия	1947-73	0,39	6,31	3,74	-0,27	0,64
Италия	1947-73	0,39	5,1	3,35	0,67	0,64
Канада,	1947-73	0,44	3,6	1,75	-0,6	0,78
США	1947-73	0,4	2,43	1,35	-0,27	0,67
Франция	1947-73	0,4	5,07	2,95	-0,2	0,67
Великобри- тания	1960-90	0,39	2,66	1,3	-0,83	0,64
Германия	1960-90	0,4	3,63	1,57	-1,52	0,67
Италия	1960-90	0,38	3,9	1,97	-1,19	0,61
Канада	1960-90	0,45	1,7	0,46	-1,0	0,82
США	1960-90	0,41	0,92	0,41	-0,32	0,68
Япония	1960-90	0,42	5,16	1,97	-2,43	0,72

В таблице 1 рассматриваются промышленно развитые страны. Как видим, данные не подтверждают точно стилизованный факт Н.Кальдора о постоянстве капиталоотдачи: на самом деле, капиталоотдача падала во всех рассматриваемых в таблице 1 промышленно развитых странах, кроме Италии, где в 1947-73 гг. она возрастала. Однако, для ряда стран и периодов (Германия, США, Франция в 1947-73 гг., США в 1960-90 гг.) второе слагаемое в равенстве (2) весьма мало, и выполняется приближенно равенство (3)

В отличие от промышленно развитых стран, в большинстве рассмотренных развивающихся стран (табл. 2) капиталоотдача росла и, соответственно, темпы прироста средней производительности труда были ниже.

Табл. 2. Темпы прироста TFP и производительностей факторов в некоторых развивающихся странах. (Расчет автора по результатам «учета роста»).

Страна	Период	Доля капитала	Темп прироста производитель- ности труда, %	Темп прироста TFP, %	Темп прироста капитало-отдачи, %
Аргентина	1940-80	0,54	1,53	1,1	0,73	1,17
Бразилия	1940-80	0,45	4,04	1,85	-0,82	0,82
Венесуэла	1940-80	0,55	1,31	0,5	-0,16	1,22
Колумбия	1940-80	0,53	0,61	1,20	1,55	1,13
Мексика	1940-80	0,69	1,63	2,3	2,6	2,22
Чили	1940-80	0,52	1,72	1,5	1,3	1,08
Япония	1947-73	0,39	5,88	4,02	1,1	0,64

Если технический прогресс состоит в многократных разовых изменениях технологии, то траектория средних производительностей факторов (технологических коэффициентов), если принять предположение Солоу о постоянной норме накопления, будет такой, как показано на рис. 1.

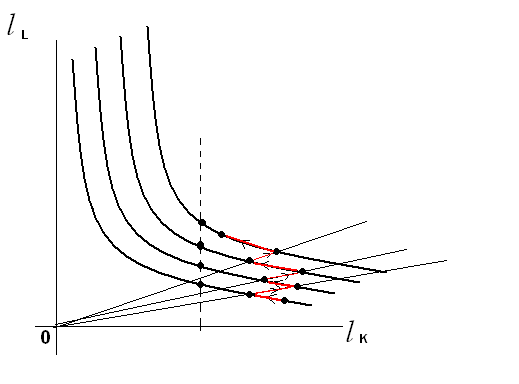Рис.1.

Таким образом, модель показывает, что производительность труда постоянно растет, а производительность капитала колеблется, но, если отдельные технологические сдвиги относительно невелики, имеет тренд снижения.

Такой характер технологических сдвигов, по-видимому, свойственен промышленно развитым странам. В развивающихся странах могут происходить более существенные изменения технологии. В таком случае, производительность капитала может иметь тренд роста.

Такой характер динамики подтверждается имеющимися данными.

Дано возможное объяснение различия реакций стран на снижение TFP во время экономического перехода или кризиса. Снижение TFP ведет к снижению производительности труда. Некоторым «противовесом» может быть снижение производительности капитала, достичь которого можно путем повышения капиталовооруженности при увольнении «лишних» работников или путем «углубления капитала» за счет иностранных инвестиций. Но такие меры будут работать не всегда. Некоторым странам не удастся повысить производительность труда в кризисный период, поскольку, если эластичность замещения мала, то производительность труда ограничена. Это объясняет, почему в период экономического перехода в конце 1980-х – первой половине 1990-х гг. в одних странах фирмы пытались повысить производительность труда за счет увольнений и инвестиций, а в других странах не было ни массовой безработицы, ни роста инвестиций. В переходных экономиках с преимущественно крупным производством (Россия, Украина, Казахстан) эластичность замещения была очень мала, а в переходных экономиках с высокой долей средних и мелких производителей (Польша, Венгрия) – значительно выше. Средняя производительность труда ограничена величиной, которая тем меньше, чем меньше эластичность замещения. В Польше и Венгрии можно было повысить производительность труда за счет «углубления капитала», тогда как в России, Украине, Казахстане производительность труда была существенно ограничена ввиду низкой эластичности замещения.

Так можно объяснить то, что в России в 1990-х годах не было скачкообразного роста безработицы, что было неожиданным. Р.И.Капелюшников (2001) пишет: «Как показывают данные, несмотря на большую глубину и продолжительность трансформационного кризиса относительные потери рабочих мест были в России либо такими же, либо даже меньшими, чем в странах Центральной Восточной Европы. Это – один из парадоксальных результатов развития российского рынка труда в переходный период».

Помимо TFP, рассматривается взаимосвязь эффективностей факторов со средними производительностями труда и капитала. Здесь также существенную роль играют технологическое меню и сопряженная производственная функция. Ставится вопрос, какое отношение эффективностей факторов оказывается «наилучшим» с точки зрения повышения производительностей. Оказывается, что это «наилучшее» отношение является решением уравнения, смысл которого в том, что «наилучшее» отношение эффективностей факторов совпадает с отношением долей факторов.

Литература

Ашманов С.А. 1984. Введение в математическую экономику. М., Наука.

Капелюшников Р.И. 2001. Российский рынок труда: адаптация без реструктуризации. М.,

ГУ-ВШЭ.

Jones C.J. 2005. The shape of production function and the direction of technical

change. Quarterly Journal of Economics. V. 120 (2), pp. 517-549.

Kim J. 2001. Total factor productivity growth in East Asia: implications for future growth.

Dongguk University, Seoul. http://www.cid.harvard.edu/events/papers/kim.pdf

Prescott E.C. 1998. Needed: A theory of total factor productivity. International Economic

Review, V. 39, pp. 525-551.

Rubinov A.M., Glover B.M. 1998. Duality for increasing positively homogeneous

functions and normal sets. Recherche Operationnele/Operations Research. V. 12 (2), pp.

105-123.

Solow R.M. 1956. A contribution to the theory of economic growth. Quarterly Journal of

Economics, V. 70, pp. 65-94.

Solow R.M. 1957. Technological change and the aggregate production function. Review of

Economics and Statistics, V. 39, pp.312-320.

PAGE \* MERGEFORMAT 1

ПРИМЕНЕНИЕ СОПРЯЖЕННОЙ ПРОИЗВОДСТВЕННОЙ ФУНКЦИИ ДЛЯ АНАЛИЗА ПОКАЗАТЕЛЕЙ ПРОИЗВОДИТЕЛЬНОСТИ