Моделирования территориальных процессов в российских городах методом географически взвешенной регрессии
Балаш О.С.
к.э.н., доц.,
кафедры высшей математики и информационных технологий
Саратовского института РГТЭУ
А.В. Харламов
ст. преподаватель
Саратовского государственного университета
Моделирования территориальных процессов в российских городах методом географически взвешенной регрессии
Условиями применения классической модели регрессии, используемой при анализе однородных объектов, являются некоррелированность ошибок, подчиняющихся нормальному распределению с нулевым средним и постоянной дисперсией. Но при моделировании процессов, имеющую большую территориальную неоднородность, классическая модель может давать неверный результат.
Для анализа пространственных данных обследуемую область разделяют на районы и для учета влияния этих областей в модель вводят фиктивные переменные. Зонирование зависит от выбора масштаба и определения вида границ. Различают районы с четкими и нечеткими границами.
При разделении исследуемой территории на зоны с четкими границами предполагают, что они определяют отличия в социально-экономических явлениях. Часто берут административные границы, но такое деление не всегда верно. Поэтому проблема выделения однородных зон ложится на исследователя. Субъективное и необоснованное определение границ может приводить к ошибочным результатам, и предпочтительнее использовать нечеткие границы.
Нечеткие границы означают, что каждый объект с той или иной вероятностью имеет возможность попасть в любую зону. Вероятность зависит от близости объекта к центру зоны и с увеличением расстояния уменьшается.
Кроме определения границ возникает проблема влияния масштаба выделяемых областей на значимость коэффициентов модели. Возможна ситуация, когда применяя различные масштабы или перегруппировывая зоны, получают различные и даже совершенно противоположные результаты в оценках и значимости параметров модели, что затрудняет выбор модели и трактовку результатов.
Для избежания этих трудностей, применяют метод географически взвешенной регрессии, который можно рассматривать как некоторое обобщение фиктивных переменных, позволяющий сгладить перечисленные проблемы и получать модель с непрерывно меняющейся структурой.
Модель географически взвешенной регрессии имеет вид:
. (1)
где пара переменных (ui,vi) представляет координаты точки (местоположение) i, ; yi - значение наблюдаемой зависимой переменной; - независимые детерминированные регрессоры, , p - число регрессоров;
- неизвестные коэффициенты, подлежащие оценке, ; - случайные ошибки.
Для вычисления оценок коэффициентов в местоположении i может использоваться метод наименьших квадратов. В целях выявления местных особенностей используются не все имеющиеся наблюдения, а только соседние с i. Предполагается, что регрессионные модели для соседних точек схожи, но могут варьироваться по территории. Степень близости учитывается с помощью весов wij. Вектор оценок коэффициентов для каждого местоположения i вычисляется:
,
где W(ui,vi) - диагональная матрица весовых коэффициентов размерности (nn):
.
Элемент матрицы wij, определяет степень влияния соседей j на зависимости в местоположении i. Матрица весовых коэффициентов вычисляется для каждого местоположения.
Так как расчеты коэффициентов проводятся для всех измерений, то в результате получают матрицу оценок параметров:
,
где i-ая строка представляет собой вектор оценок коэффициентов в точке (ui,vi), :
.
Для определения весовых коэффициентов используют методы административно-территориального деления, движущегося окна, фиксированных и адаптивных ядер.
Если административное деление раскрывает специфические закономерности, присущим административным единицам, то для точек, принадлежащих одному району, элемент весовой матрицы полагают равным единице и нулю в противном случае:
, если ();
, если ().
Если административные районы сформированы исторически и не отражают естественное расслоение объектов, то дискретные веса определяются с учетом расстояния между объектами. При этом задают предельно допустимую удаленность, то есть некоторое фиксированное расстояние b, относительно которого определяют категорию ближайшего соседа. Вес принимают равным единице, если расстояние dij между объектами не превосходит заданного расстояния b, и нулю в противном случае:
, если ;
, если .
Расстояние dij вычисляется как расстояние между точками на плоскости. Это так называемый метод движущегося фиксированного окна. b фиксировано и называется шириной окна или полосы пропускания.
Использование дискретного подхода при определении весов учитывает территориальную неоднородность, но влияние соседей, попавших в полосу пропускания, считается одинаковым. Во многих случаях влияние соседей уменьшается с увеличением расстояния. Поэтому более близким соседям придают больший вес, чем дальним. Подход, в котором веса строятся с учетом непрерывного изменения расстояния между исследуемыми объектами, называют ядерным. Наиболее часто применяют ядра Гаусса:
,
где dij - расстояние между местоположением i и соседом j, а b - ширина полосы пропускания.
Альтернативными вариантами являются ядра би-квадрат и три-куб:
,
Влияние соседей в непосредственной близости к местоположению практически равно единице и уменьшается при приближении к границе полосы пропускания.
Применим метод географически взвешенной регрессии для построения модели ценообразования на рынке недвижимости на примере модели стоимости однокомнатных квартир г. Саратова.
Информационной базой послужили данные о продажах однокомнатных квартир на вторичном рынке жилья (http://www.ks.sarbc.ru) за январь 2006 года. Численность выборки составила 1813 объектов.
Зависимой переменной является y - цена квартиры (тыс. руб.), регрессорами: x1 - жилая площадь, м2; x2 - площадь кухни, м2; x3 - дополнительная площадь, м2; x4 - логарифм расстояния, ln(м); x5 - расположение на первом этаже; x6 - расположение на последнем этаже; x7 - дом малой этажности; x8 - пятиэтажка; x9 - кирпичный дом; x10 - в хорошем или отличном состоянии; x11 - имеются балкон или лоджия.
В качестве центра г. Саратова выбран район Главпочтамта.
Глобальная линейная регрессионная модель, построенная по исходным, данным имеет вид:
Все коэффициенты при переменных оказались значимыми, как и вся модель в целом. Коэффициент детерминации R2=0,7 показывает, что модель объясняет только 70% имеющейся зависимости.
Для применения географически взвешенной регрессии в исходные данные были добавлены условные координаты объектов, полученные с помощью электронной базы данных «Все города России».
При построении весовой матрицы использовалась функция «три-куб», в качестве критерия оптимизации ширины «окна» - критерий Акайка:
,
где - оценка стандартного отклонения, .
Географически взвешенный метод дал следующие результаты.
Оптимальное число ближайших соседей, дающее минимум критерия Акайка, равно 295. Коэффициент детерминации R2=0,8.
Проанализируем значения полученных оценок коэффициентов при каждом регрессоре. Для удобства анализа представим результаты в виде таблиц, в которых значения оценок коэффициентов усреднены по целым значениям координат, а также представлены в виде диаграмм. Центр города располагается в квадрате Х=61, Y=32.
Оценки коэффициента при регрессоре «жилая площадь» показано в таблице 1 и на рисунке 1.
Таблица 1
Зависимость оценок коэффициентов регрессии от координат
|
|
координаты
|
|
|
|
|
Х
|
|
|
|
|
|
|
|
|
|
Жилая площадь
|
53
|
54
|
55
|
56
|
57
|
58
|
59
|
60
|
61
|
62
|
63
|
64
|
|
|
27
|
|
9.8
|
|
|
|
|
|
|
|
|
|
|
|
|
28
|
9.8
|
10.0
|
10.3
|
|
|
|
|
|
|
|
|
|
|
|
29
|
9.6
|
11.0
|
13.3
|
13.7
|
14.0
|
12.7
|
|
|
|
|
|
|
|
Y
|
30
|
10.3
|
12.9
|
14.2
|
13.6
|
14.7
|
16.4
|
18.6
|
|
|
|
|
|
|
|
31
|
|
|
|
13.0
|
15.7
|
17.2
|
19.7
|
22.4
|
17.4
|
11.6
|
13.5
|
|
|
|
32
|
|
|
|
|
14.1
|
16.6
|
23.2
|
28.4
|
21.4
|
14.1
|
14.1
|
|
|
|
33
|
|
|
|
11.2
|
|
12.0
|
15.7
|
20.3
|
19.1
|
|
15.7
|
|
|
|
34
|
|
|
|
11.9
|
11.5
|
11.8
|
14.7
|
|
16.6
|
15.2
|
16.6
|
16.8
|
|
|
35
|
|
9.7
|
10.9
|
11.9
|
12.9
|
9.8
|
|
|
12.4
|
|
|
16.7
|
|
|
36
|
|
9.1
|
8.6
|
|
12.2
|
11.2
|
8.9
|
8.6
|
|
|
|
|
Соответствующие уровни значимости представлены в таблице 2.
Таблица 2
Уровни значимости оценок при регрессоре «жилая площадь»
|
|
|
|
|
|
|
Х
|
|
|
|
|
|
|
|
|
|
t
|
53
|
54
|
55
|
56
|
57
|
58
|
59
|
60
|
61
|
62
|
63
|
64
|
|
|
27
|
|
0
|
|
|
|
|
|
|
|
|
|
|
|
|
28
|
0
|
0
|
0
|
|
|
|
|
|
|
|
|
|
|
|
29
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
Y
|
30
|
0
|
0
|
0
|
0
|
0
|
0
|
0
|
|
|
|
|
|
|
|
31
|
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0.005
|
0.001
|
|
|
|
32
|
|
|
|
|
0
|
0
|
0
|
0
|
0
|
0
|
0.001
|
|
|
|
33
|
|
|
|
0
|
|
0
|
0
|
0
|
0
|
|
0
|
|
|
|
34
|
|
|
|
0
|
0
|
0
|
0
|
|
0
|
0
|
0
|
0
|
|
|
35
|
|
0
|
0
|
0
|
0
|
0
|
|
|
0
|
|
|
0
|
|
|
36
|
|
0
|
0
|
|
0
|
0
|
0
|
0
|
|
|
|
|
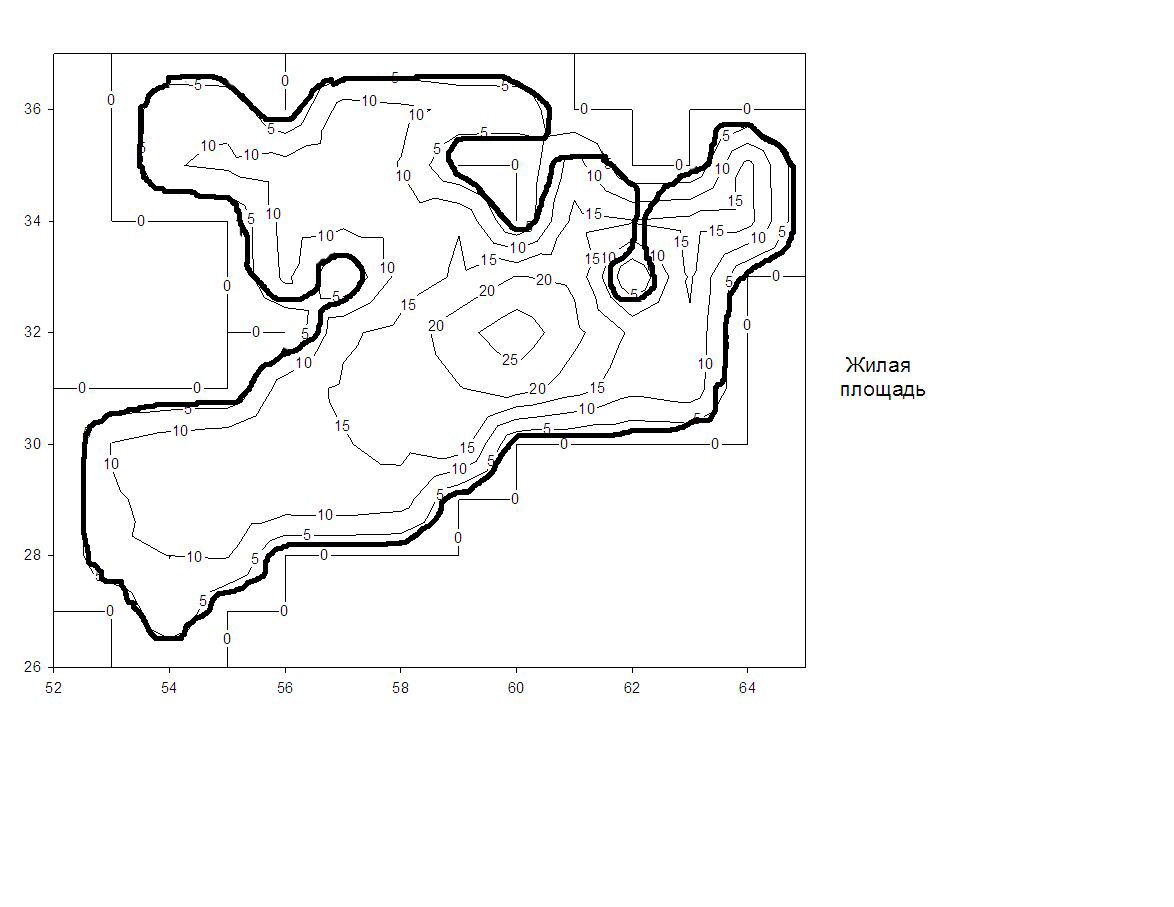
Рисунок 1 - Значения оценок коэффициента при регрессии «жилая площадь»
Как видно из рис.1 оценки коэффициента значимы на всей территории. В центральной части города выделяется квадрат с координатами X=60, Y=32 с самыми дорогими квартирами, практически по 30 тыс. рублей за квадратный метр. Около этого квадрата можно выделить некоторый район, стоимость метра жилой площади в котором превышает 20 тыс. рублей или находится в районе этого значения. Четко выделяются окраины города, где цена квадратного метра жилой площади порядка 10 тыс. рублей. Можно проследить дрейф убывающей цены от центра в направлении Ленинского района («левого верхнего» и «левого нижнего» углов представленной таблицы).
Аналогично рассчитаны показатели по остальным регрессорам.
Моделирования территориальных процессов в российских городах методом географически взвешенной регрессии