Анализ модели выбора вида потребительской субсидии
Сулима Алексей Сергеевич
asulima@bk.ru
Южный федеральный университет
г. Ростов-на-Дону
Анализ модели выбора вида потребительской субсидии.
В условиях финансового кризиса очевидна проблема рационализации и повышения эффективности бюджетных расходов в сфере субсидирования домохозяйств. В 2007г. социальная поддержка граждан составила 10,9%1 от общего дохода домохозяйств. При этом «вливание» денег в экономку в виде субсидий являются одним из механизмов вмешательства как сферу потребления, так и в сферу производства, поэтому определения оптимального вида выплат субсидий требует глубокого теоретического анализа.
Модель2, позволяющая сравнить виды выплат, основана на теории потребительского выбора и учитывает изменения бюджетного ограничения при трех основных способах начисления субсидий: на потребителя, на конкретного производителя и на производителя, но с правом выбора у получателя субсидии поставщика услуг. На наш взгляд, данная модель нуждается в дополнение системой критериев сравнения различного рода субсидий и на ее основе определения оптимального вида для потребителя, в этом и состоит цель данной работы. Проводить оценку какой из видов субсидии наиболее благоприятен для домохозяйств логично при помощи двух основных показателей: 1. изменение потребительского оптимума, т.е. какой вид субсидии приводит к стоянию наибольшей потребительской полезности; 2. широта потребительского выбора, т.е. при какой субсидии количество доступных товарных наборов становится максимальным.
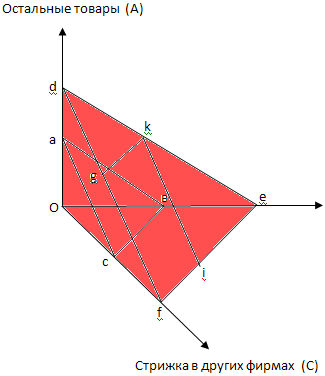
В начале проведем анализ на основе первого критерия, для этого построим в трехмерной системе координат бюджетные ограничения и кривые безразличия (рисунок 1). На этом рисунке треугольник авс отражает бюджетное ограничение потребителя до денежных льгот; def- бюджетное ограничение после введения субсидии на потребителя; kie – бюджетное ограничение при введение субсидии с прикреплением к конкретному поставщику; трапеция gkfe – площадь бюджетного ограничения при определении льготы с правом выбора поставщика.
Рисунок 1. Изменения потребительского оптимума.
До введения льгот оптимум потребителя находится в точке касания кривой безразличия 1 и бюджетного ограничения авс. Очевидно, что при введении субсидии потребителю станет доступно большее количество товаров и он окажется на более высокой кривой безразличия 2 и оптимум сместиться в плоскость DEF. Таким образом, видно, что субсидия увеличивает потребительскую полезность. К сожалению, используя кривые безразличия, невозможно выявить какой способ предоставления субсидии наилучший. Это связанно тем, что треугольники def, kei и трапеция kgfe лежат в одной плоскости DEF, следовательно, все эти наборы товаров обладают одинаковой полезностью для потребителя. Так, предположим обратное. Например, что наборы товаров составляющие kei имеют большую полезность чем наборы товаров из def, но это невозможно так как бюджетное ограничение def включает в себя все наборы из kei по построению. Следовательно, наше предположение не верно, и полезность для потребителя будет одинаковой. Из-за того, что все три вида субсидирования приводят к одинаковой потребительской полезности, постараемся посмотреть на субсидирование с иной точки зрения для потребителя.
Ведь для потребителя так же имеет значение широта выбора товаров и появление возможности приобрести товарные наборы, которые были не доступны для них до введение субсидий. Поэтому проведем оценку субсидирования с точки зрения широты выбора.
Заметим, что потребители могут покупать товарные наборы находящиеся не только на бюджетном ограничении, а сохранить часть дохода и приобрести наборы внутри него. Следовательно, широта потребительского выбора будет измеряться объемам фигуры, образованной осями координат ОХ, ОУ, ОZ и бюджетным ограничением. Рассмотрим соответствующие объемы фигур: на рисунке 2 V1 - объем до введения субсидии;
при введение субсидии с прикреплением к конкретному производителю широта потребительского выбора будет соответствовать объему V2, представленного на рисунке 3; при введении субсидии с правом выбора поставщика потребительский выбор увеличивается до объема V3(рисунок 4); на рисунке 5 изображен объем выбора V4 при выплате субсидии в денежной форме непосредственно потребителю. Очевидно что:
V1 <V2 <V3 <V4
Из выше изложенного можно сделать вывод о том, что с точки зрения максимизации полезности, безразлично в каком виде субсидия будет начисляться, но для домохозяйств, на мой взгляд, наилучший способ субсидирования - субсидия на потребителя, так как, именно эта форма обеспечит максимально широкий потребительский выбор (V4 наибольший объем) и позволит совершить выбор поставщиков товаров.
ЗАМЕЧЕНИЕ. О расположении бюджетного ограничения в системе координат
Стоит отметить, что немалое значение на модель выбора субсидии оказывает размещение в системе координат бюджетного ограничения. В статье при его построении на осях откладывалась максимально возможная сумма расходов на товар, которая составляла или доход потребителя (I) или доход + субсидия (I+r). Но в экономической теории на осях откладывается не располагаемая денежная сумма, а то количество товаров, которое может приобрести потребитель с учетом уровня цен. То есть: Qn=I/Pn или Qn=(I+r)/Pn, где n-соответствующий товар. Поэтому, необходимо посмотреть, как изменяться бюджетные ограничения при таком способе их построения.
Пусть цены на товар А (остальные товары), товар В (товар на который введена субсидия с прикрепление к определенному поставщику), товар С (товар на который введена субсидия с правом выбора поставщика) соответственно равны Ра, Рв, Рс. Так же, допустим, что цены не изменяются при введении субсидии. Так как, цена на товары А независима, от Рв и Рс, и при субсидировании его потребление увеличится на Qa = r/Pa, то интерес для нас будет представлять линия бюджетного ограничения расположенная в нижней полуплоскости на рисунке 1.
Рассмотрим ситуацию, когда Рв = Рс, то Qb= I/Pb= Qc=I/Pc , а изменение объемов потребления при введении субсидии будут составлять Qb= r /Рв = Qc = r/Pc. В данных условия рисунок бюджетных ограничений и соответствующие им координаты точек на осях (рисунок 6) не будут отличаться от рисунка1. Потребительский оптимум и объем потребительского выбора останутся такие же, как мы и рассматривали в первом замечании, для разных видов субсидий.
Рисунок6. Расположения бюджетных ограничений при Pc=Pb
Теперь, рассмотрим ситуацию, когда Рв < Рс и Рв >Рс. Из-за разницы в цене для потребителя будут доступны разное количество благ В и С, при этом, он сможет купить больше товаров В чем С при условии Рв < Рс, и наоборот, при ценовом условии Рв >Рс. Тогда можно наблюдать отклонение в положении бюджетной линии от ситуации, когда Qb=Qc (пунктирная линия на рисунке 7).
Рисунок 7. Расположение бюджетного ограничения при Рв < Рс и Рв >Рс.
Как видно при таких условиях основания площади наших бюджетных ограничений (треугольников и трапеци) будут смещаться соответственно в право или влево. Из-за изменения положения бюджетных ограничений, иначе чем при их построении по максимально возможной сумме расходов, произойдут изменения и в модели субсидирования. Теперь посмотрим как отреагируют наши критерии выбора субсидии (потребительский оптимум и широта потребительского выбора) на эти изменения.
С начало, проанализируем изменения оптимума потребителя. После введения субсидии при ценовых соотношениях Рв < Рс и Рв >Рс треугольник def, из рисунка 1, будет смещаться в плоскость расположенную ниже или выше относительно плоскости DEF. Следовательно, потребительский оптимум будет смещаться вмести с плоскостью на кривую безразличий либо с более высоким уровнем полезности, либо более низким. Из этого можно сделать вывод о том, что уровень цен конечно оказывает влияния на положение потребительского оптимума, но не стоит забывать что уровень и соотношении цен являются заданными параметрами при введение субсидии, а потребительская полезность не изменяется от вида субсидии. Таким образом, учет уровня цен не окажет влияния на выбор способа начисления субсидии.
Так же следует отметить, что новая конфигурация и иное размещение кривых безразличия на осях координат повлияет на объем потребительского выбора численно, но при этом сохраниться ранжирование объемов, которое мы определили выше: V1 <V2 <V3 <V4.
Таким образом, при рассмотрении модели в которой бюджетные ограничения откладывались на осях по количеству товаров, как принято в экономической теории, с корректировало рисунок и произошли изменения как в потребительском оптимуме, так и в объеме потребительского выбора. Но при этом можно сделать вывод о том, что субсидия на потребителя все равно более выгодна для домохозяйств при этой модели, так же как и в модели без учета уровня цен.
Список используемой литературы:
- Александрова А.Л. Теория и практика перехода к потребительской субсидии: зарубежный опыт// Институт экономики города.- 2003г.
- Фаминский И.П. Национальная экономика в условиях глобализации.- М.: Магистр, 2007.
- Федеральная служба государственной статистики // www.gks.ru
1 Федеральная служба государственной статистики // www.gks.ru
2 Александрова А.Л. Теория и практика перехода к потребительской субсидии: зарубежный опыт // Институт экономики города.- 2003г.
PAGE 5
2
1
i
k
g
f
e
d
О
в
с
а
Товар у конкретного поставщика (В)
Товары у остальных поставщиков (С)
стальные товары (А)
Рисунок 5
Рисунок 3
Рисунок 4
Рисунок 2
(0;Qc; Qb+Qb)
(Qa; Qd; 0)
(Qa;0;Qc)
(0;0; Qс)
(Qa;0;0)
(0;Qb+Qb;0)
(0;0;Qc+Qc)
(0;Qb;0)
(Qa+Qa;0;0)
Товар В
Товар С
Товар (А)
Товар С
Товар В
Qc>Qb
Товар С
Товар В
Qc=Qb
Товар С
Товар В
Qc<Qb
Анализ модели выбора вида потребительской субсидии