Некомпенсаторное агрегирование и рейтингование студентов

А. А. Гончаров, В. В. Чистяков

Государственный университет - Высшая школа экономики,

Нижегородский филиал

г. Нижний Новгород

2009 год

Некомпенсаторное агрегирование и рейтингование студентов*

1. Введение

На практике зачастую мнение коллектива индивидуумов или экспертов выражается при помощи различных шкал оценок, проставляемых каждым членом этого коллектива; например, “плохо, средне, хорошо” (при опросе общественного мнения или дегустации),

“1, 2, 3, 4, 5” (в школе, университете) и т.п. Задача агрегирования состоит в том, чтобы корректно описать коллективное мнение на основе полученных наборов из индивидуальных оценок. Усреднение полученных наборов оценок, которое по традиции наиболее часто используется, не всегда возможно, а в том случае, когда оно возможно, то приводит к интуитивно неадекватному результату. Так, при усреднении наборов оценок низкие оценки одного эксперта могут быть компенсированы средними или хорошими оценками других экспертов. Нас будут интересовать ситуации (в частности, в высшем образовании), когда такое компенсирование невозможно. Ясно, например, что отличные оценки студента технического вуза по иностранному языку никоим образом не компенсируют его плохие оценки по специальности, и тем более не говорят о том, что он/она – квалифицированный инженер. Таким образом, исследование индивидуальных предпочтений с учетом компенсаций (как в случае усреднения) и без учета компенсаций (как в последнем примере) и их сравнение является современной актуальной задачей.

Целью настоящей работы является сравнение и сопоставление двух диаметрально противоположных методов агрегирования предпочтений – компенсаторного с одной стороны, к которому относятся правило голосования Борда и его обобщения, и некомпенсаторного – с другой. В последнем методе низкие оценки участников оценивания не могут быть компенсированы никакими самыми высокими оценками и даже их количеством. Этот новый метод агрегирования был развит для трехградационных предпочтений (т.е. предпочтений, выражаемых оценками 1 – плохо, 2 – средне и 3 – хорошо) в серии недавних работ Ф.Т.Алескерова и В.И.Якубы (ГУ-ВШЭ, Москва) и их сотрудников [1]-[3], а затем обобщен на произвольное число оценок В.А.Калягиным и В.В.Чистяковым (НФ ГУ-ВШЭ, Нижний Новгород) [4]-[7]. Сравнение этих двух методов осуществляется на основе изучения поведения соответствующих функций предпочтения и их аксиоматических определений. Представляется ясным, что вне зоны самых высоких оценок и самых низких оценок эти методы ведут себя неодинаково, и выяснению подлежит поведение методов в промежуточных зонах. Полученные результаты применяются к новому рейтингованию студентов, обучающихся в НФ ГУ-ВШЭ, что позволяет сравнить новые рейтинговые оценки с традиционно используемыми. Отметим, что в новых рейтинговых оценках существенно используется некомпенсаторная природа агрегирования в смысле, указанном выше.

* Работа выполнена при поддержке внутреннего гранта Нижегородского филиала Государственного университета – Высшая школа экономики, номер 09-04.

1. Теоретические основы рейтингования

2.1. Стандартное рейтингование студентов ГУ-ВШЭ

Стандартное рейтингование студентов, утвержденное в ГУ-ВШЭ, опирается на 60 кредитов, распределенных между всеми изучаемыми студентами предметами, и основывается на рабочем плане студенческой группы за календарный год. В этом рабочем плане выделяются два типа предметов – неаккредитованные и аккредитованные. Неаккредитованные предметы не учитываются при подсчете рейтинга студентов. Обычно такими предметами являются факультативы, иностранный язык и физическая культура. Аккредитованные предметы имеют в рейтинге определенные зачетные единицы, называемые кредитами, сумма которых равняется 60. Количество кредитов у каждого предмета зависит от доли его времени в общей нагрузке студентов за год (в среднем в 1,5 раза больше числа модулей, отведенных на предмет). Поскольку в ГУ-ВШЭ принята десятибалльная система оценок, то максимальное число кредитов, которые студент может получить за один год, равно 600. В случае неуспешной сдачи экзамена по какому-либо предмету независимо от оценки за пересдачу экзамена в рейтинг студента по этому предмету записывается оценка 0 (нуль).

Математически значение рейтинга ГУ-ВШЭ можно записать в виде:

где xi – оценка студента за экзамен по предмету i, ri – зачетные единицы предмета и

k – количество предметов в годовой нагрузке. Отметим, что в силу сказанного выше,

0 r 600 и xi принимает значения 0, 4, 5, 6, 7, 8, 9, 10 (оценки 1, 2 и 3 не считаются “положительными” и играют такую же роль, как 0).

1. Средний балл

В большинстве вузов для рейтингования студентов используется обычный средний балл. В этом случае все зачетные единицы предметов ri одинаковы и равны 1/k.

Следует отметить, что рейтинг ГУ-ВШЭ имеет определенные преимущества по сравнению со средним баллом: он более адекватно учитывает успеваемость студентов по предметам своей специальности и учитывает нагрузку студента по каждому отдельному предмету в зависимости от количества часов, отведенных на предмет.

1. Некомпенсаторный метод рейтингования

Напомним, что при неуспешной сдаче студентом экзамена по определенному предмету

в рейтинг по этому предмету студенту записывается 0 баллов. Это означает, что низкие оценки не должны быть компенсированы высокими, и это обстоятельство следует учитывать при рейтинговании. В моделях некомпенсаторного агрегирования, развитых в работах, упомянутых во Введении, предложен следующий метод сравнения альтернатив

(в данном случае студентов) по их оценкам x=(x1,…,xn). Он основан на известном правиле сравнения альтернатив Leximin. Обозначим через vj(x) количество оценок j в векторе оценок x, где j принимает значения 0, 4, 5, 6, 7, 8, 9, 10. Скажем, что x=(x1,…,xn)строго предпочтительнее y=(y1,…,yn), если [v0(x)<v0(y)] или [v0(x)= v0(y) и v4(x)< v4(y)] или [v0(x)= v0(y) и v4(x)= v4(y) и v5(x)< v5(y)] или, и так далее, до [v0(x)= v0(y) и v4(x)= v4(y) и … и v8(x)= v8(y) и v9(x)< v9(y)]. Отметим, что сравнение количеств v_j(x) останавливается при j=9, поскольку v0(x)+ v4(x)+ v5(x)+…+ v9(x)+ v10(x)=n (размерность вектора x). Функция Ф, определенная на множестве всех альтернатив x, называется функцией предпочтения, если неравенство Ф(x)>Ф(y) выполнено тогда и только тогда, когда альтернатива x строго предпочтительнее альтернативы y в смысле, указанном выше. В работах [4] и [7] такую функцию Ф(x) удалось найти в явном виде:

где и .

В рамках нашей модели рейтингования студентов здесь n – число изучаемых предметов,

m =8 –количество оценок (в нашем случае 0, 4, 5, 6, 7, 8, 9, 10) и vj(x) – количество оценок j у студента x. Функция Ф(x) принимает натуральное значение на любом векторе х, равное порядковому номеру этого вектора в описанном выше строгом предпочтении. Кроме того, функция Ф обладает некоторыми оптимальными свойствами (типа симметрии, Парето-доминирования и др., подробнее см. [4], [7]).

Некомпенсаторное агрегирование рассматривается в нашей модели в двух вариантах:

а) когда число n равно числу предметов (без учета факультативов) в базовой нагрузке;

б) когда n=60 (по числу кредитов). Этот случай обусловлен тем, что оценка по предмету будет повторяться столько раз, сколько кредитов на него отведено в учебном плане.

1. Практические результаты

Результаты стандартного рейтингования ГУ-ВШЭ, рейтингования по среднему баллу и некомпенсаторное рейтингование при n=число предметов и n=60 наглядно продемонстрированы на следующих графиках. Все рейтинговые оценки получены с помощью компьютерной программы, написанной на языке С++, а графики и прочие проведенные расчеты были получены при помощи программы Microsoft Office Excel. Оценки взяты из реальных экзаменационных ведомостей студентов 2-го и 3-го курсов факультета Бизнес-информатики и прикладной математики НФ ГУ-ВШЭ за 2008-2009 г.

Табл. 1

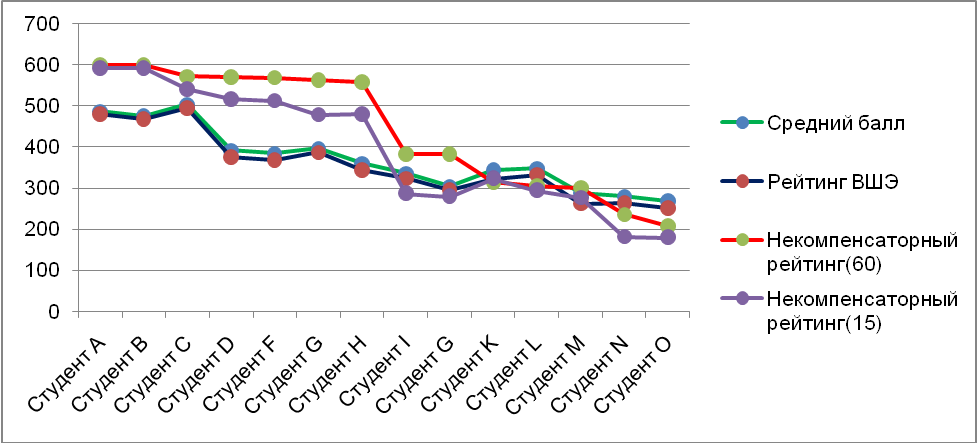
Табл. 2

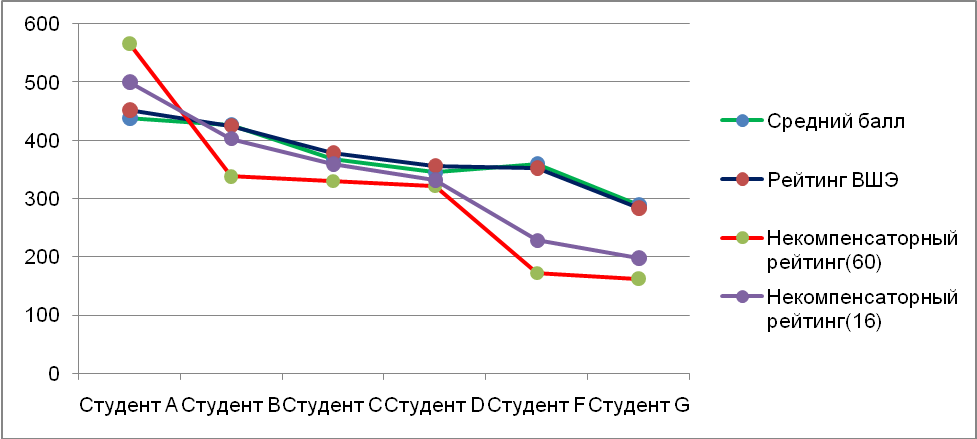
Табл. 3

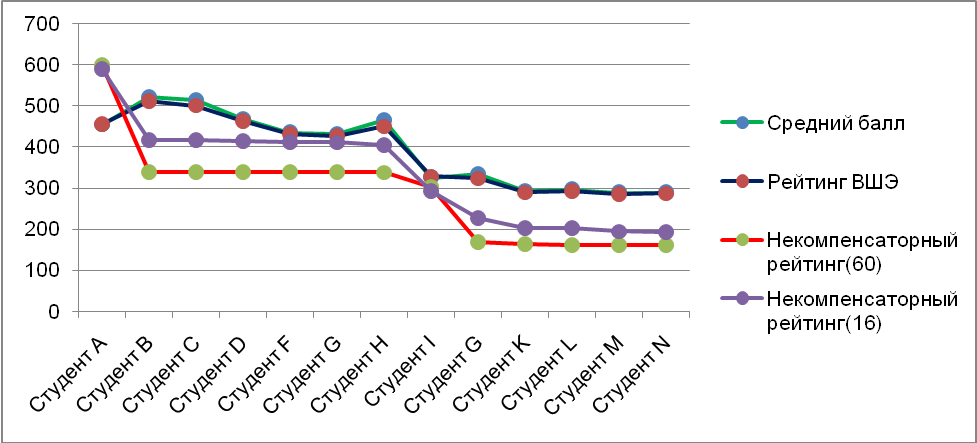
1. Заключение

Стандартный и некомпенсаторный подходы к рейтингованию студентов в подавляющем большинстве случаев дают одинаковое положение студентов в итоговом рейтинге (что может объясняться «разумностью» проставленных оценок за реально сданные предметы). Различие наблюдается, например, при анализе рейтинга для целей выдачи стипендии: в стандартном рейтинге студент (студент В в табл. 3) может иметь больший рейтинг (чем студент А в табл. 3) и при этом не получать стипендии, тогда как такое положение невозможно при некомпенсаторном подходе. Кроме того, при некомпенсаторном подходе возможно провести деление студентов на четкие группы: совсем плохие, середняки и отличники. Некомпенсаторный рейтинг с n=60 практически всегда ниже некомпенсаторного рейтинга при n<60, который в свою очередь ниже, чем средний балл и рейтинг ГУ-ВШЭ; последние два метода, как правило, дают сходные результаты. Таким образом, с точки зрения учета влияния низких оценок на результирующий рейтинг некомпенсаторный метод рейтингования более адекватен для практического применения.

Список используемой литературы

[1] Алескеров Ф.Т., Юзбашев Д.А., Якуба В.И. «Пороговое агрегирование трехградационных ранжировок.» Автоматика и телемеханика, N 1 (2007), 147-152.

[2] Алескеров Ф.Т., Якуба В.И. «Метод порогового агрегирования трехградационных ранжировок.» Докл. РАН, 413, N 2 (2007), 181-183.

[3] Aleskerov F., Yakuba V., Yuzbashev D. «A `threshold aggregation' of three-graded rankings.»
Math. Social Sci. 53 (2007), 106-110.

[4] Калягин В.А., Чистяков В.В. «Модель некомпенсаторного агрегирования с произвольным набором оценок.» Докл. РАН, 421, N 5 (2008), 607-610.

[5] Калягин В.А., Чистяков В.В. «Об определении функции предпочтений в задаче рейтингования при отсутствии компенсаций.» В кн.: Модернизация экономики и глобализация (отв. ред. Е.Г. Ясин). Гос. ун-т -- Высшая школа экономики. М.: Изд. дом ГУ ВШЭ, книга 3, 2009, 592-597.

[6] Калягин В.А., Чистяков В.В. «Аксиоматическая модель некомпенсаторного агрегирования.» Препринт WP7/2009/01. М: Изд. дом ГУ ВШЭ, 2009. – 76 с.

[7] Чистяков В.В. «Функция перечисления в многокритериальной задаче порогового агрегирования.» Труды Матем. центра им. Н.И. Лобачевского. Теория функций, ее прилож. И смежные вопр. Материалы 9-ой междунар. Казанской летней научной школы-конф. Казань: Изд-во Казан. матем. об-во, Том 38, 2009, 302-304.

PAGE 1

Некомпенсаторное агрегирование и рейтингование студентов