Оценки экономической эффективности перехода к достижимому потенциалу

Айвазян С.А., Афанасьев М.Ю., ЦЭМИ РАН, Москва

Методология построения модели производственного потенциала непрерывно совершенствуется, отражая развитие теории производства и теории X-эффективности. Одним из важных этапов стало понимание необходимости расширить набор факторов производства и, наряду с основными, рассматривать сопутствующие производственные факторы. Проявилась ограниченность детерминистской концепции производственного потенциала, так как некоторые сопутствующие факторы оказывают случайное воздействие на производственный процесс. Некоторые из них влияют на эффективность производства. К факторам эффективности относят, например, уровень мотивации персонала, его квалификацию, затраты на обучение. Идентификация степени воздействия факторов эффективности является одной их основных задач методологии стохастической границы [5,6], которая приводит к известной модели стохастического граничного производственного потенциала и позволяет получить оценки технической эффективности производства.

На основе предпосылки о том, что возможности воздействия на факторы эффективности ограничены, авторами предложен новый подход [1,2] к проектированию мероприятий, направленных на повышение эффективности производства. Его реализация предполагает оценку параметров модели исходного производственного потенциала, идентификацию факторов эффективности, оценку их воздействия на производственный процесс. При фиксированных затратах и возможностях целенаправленного воздействия в результате решения задачи оптимального управления определяются такие значения факторов эффективности, при которых ожидаемый экономический эффект от реализации мероприятия достигает максимального значения. Построение модели производственного потенциала на основе прогнозируемых значений факторов эффективности приводит к новому понятию «достижимый производственный потенциал», обобщающему понятие «граничный производственный потенциал».

Построены оценки математического ожидания экономического эффекта мероприятия, направленного на переход к достижимому производственному потенциалу, опирающиеся на два различных подхода к оценке фактического производственного потенциала. Первый основан на моделировании воздействия факторов эффективности как случайной величины, не зависящей от наблюдаемых результатов производственного процесса. Во втором подходе используется оценка эффективности, ожидаемая при фактически наблюдаемом результате. В среде Microsoft Excel созданы приложения, позволяющие строить методом имитации [1] функции распределения экономического эффекта. Предложенный подход развивает методологию стохастической граничной функции и расширяет сферу ее практического применения.

Для описания зависимости результатов производственного процесса от объемов основных факторов производства будем, как в [1,2], использовать производственную функцию в форме , где – фактический объем производства i-го объекта, i =1,…,N; – объем трудозатрат, – объем основных фондов на i-ом объекте, – параметры, – случайная величина, характеризующая результат случайных воздействий на i-й объект. Обозначим через , через , через - логарифмы значений остальных возможных факторов. Тогда

(1).

Концепция стохастической граничной производственной функции [5] приводит к разделению случайной составляющей на две компоненты, , где , - не зависимая от неотрицательная случайная величина, имеющая усеченное в нуле нормальное распределение с математическим ожиданием и дисперсией , т.е. , где - функция, характеризующая воздействие факторов эффективности; q =1,…,m - индекс фактора эффективности, - вектор значений факторов эффективности для i –го наблюдения; - вектор параметров. Если исключить из производственного процесса все факторы эффективности, то фактический объем производства повысится до уровня

(2).

Описанный таким образом результат производственного процесса при исключенном воздействии факторов эффективности принято называть граничным производственным потенциалом. Техническую эффективность i-го объекта, характеризующую отличие фактического результата производства от граничного, определяют по формуле . В качестве оценки величины обычно используют ожидаемое значение условного распределения (3),

где , , , - функция стандартного нормального распределения [5]. Можно использовать также безусловную оценку

(4).

Пусть случайная величина имеет неотрицательное распределение , где

(5).

Здесь – возможные изменения в значениях факторов эффективности, характеризующих i-й объект, – m-мерная область, определяющая множество всех допустимых значений факторов эффективности i-го объекта, - размер финансовых затрат, требуемых для изменения значения k-го фактора эффективности для i-го объекта на величину , а – затраты на повышение эффективности производства. Случайная величина (6),

характеризующая результат производственного процесса при исключенном воздействии управляемых факторов эффективности работе [1,2] получила название «достижимый производственный потенциал». Техническая эффективность достижимого потенциала относительно граничного оценивается величиной . В качестве оценки можно, по аналогией с (4), использовать ожидаемое значение

(7) ,

где .

Рассмотрим мероприятие M=, направленное на развитие производства. Здесь - множество допустимых значений факторов эффективности в результате реализации мероприятия для i-го объекта, -затраты на реализацию мероприятия. Экономическую эффективность мероприятия предлагается оценивать в соответствии с [4] как дисконтированный эффект, который определяется по формуле вида или . Здесь – цена продукта; - процентная ставка; -приращение объема производства, определяемое как разность между достижимым производственным потенциалом (6) и объемом производства (1), прогнозируемым без учета наблюдаемого результата производственного процесса; - приращение объема производства, определяемое как разность между достижимым производственным потенциалом (6) и объемом производства, прогнозируемым при ожидаемом уровне эффективности, соответствующем наблюдаемому объему производства ; величина определяется из уравнения . С учетом соотношений (3), (4) и (7) можно оценить ожидаемые значенияи.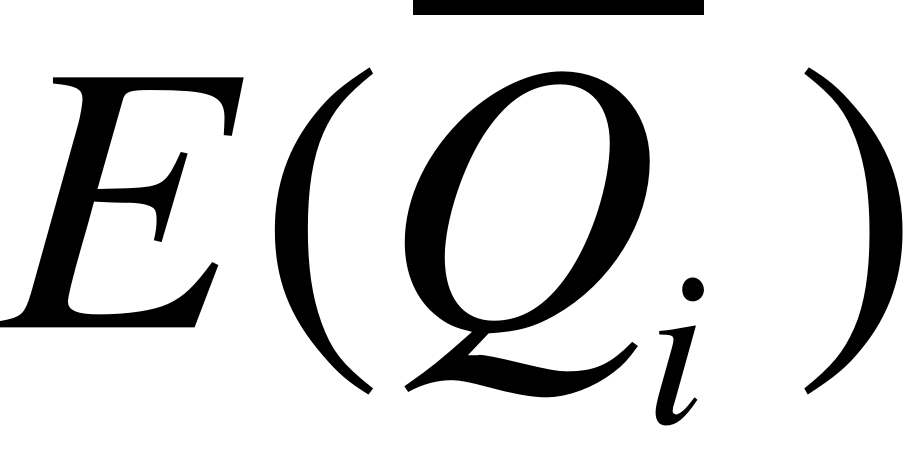

Оценки параметров , могут быть получены методом максимального правдоподобия: ,

где L – функция правдоподобия, , а и определены выше (i =1,…,N). Оценка определяется в результате решения задачи (5) при .

Для примера, описанного в [3], по 1093 наблюдениям за производственным объектом получены оценки и проведен анализ мероприятия по управлению факторами неэффективности. Учитывалось воздействие 15 факторов неэффективности, только 3 из которых считались управляемыми. На рисунке 1 ряд 1 (линия, огибающая снизу) содержит оценки эффективности , полученные без учета управляющих воздействий на факторы неэффективности и упорядоченные по убыванию. Ряд 2 содержит оценки эффективности для соответствующих наблюдений, полученные в результате построения модели достижимого потенциала c учетом управляющих воздействий на факторы неэффективности. Для тех наблюдений, для которых результаты решения задачи оптимального управления (7) привели к изменению значений функции неэффективности , оценки возросли. Для тех наблюдений, для которых значение функции неэффективности не изменилось, оценки остались прежними.

Рисунок 1. Оценки технической эффективности.

Построена функция распределения случайной величины :

Методом имитации Монте-Карло для производственного объекта, описанного в [3], а также для рекламных мероприятий в сфере кредитования построены распределения случайных величин и . Определены вероятности того, что мероприятия, направленные на повышение эффективности, не окупятся. Получены экспериментальные распределения и эффективности, учитывающие масштаб производства и позволяющие оценить риски при сравнении мероприятий, проводимых на разных производственных объектах.

Если наблюдения проводятся в различные моменты времени, то фактор времени следует учитывать в производственной функции при моделировании достижимого производственного потенциала. Для этого может быть использован более общий вид производственной функции: . Здесь - момент времени, в который проводится наблюдение , - параметр. В этом случае как множество допустимых значений факторов неэффективности в задаче (5), так и модель достижимого потенциала могут зависеть от времени.

На основе предлагаемого подхода могут быть рассчитаны корректные в методологическом отношении оценки мероприятий, направленных на повышение эффективности производства. Для их получения используются теоретически обоснованные и прошедшие практическую апробацию модели граничного и достижимого потенциалов.

Литература.

Айвазян С.А., Афанасьев М.Ю. (2009) Оценка экономической эффективности перехода к достижимому потенциалу. Прикладная эконометрика.
№ 3(15), c.43-55.
Айвазян С.А., Афанасьев М.Ю. (2007) Оценка мероприятий, направленных на управление факторами неэффективности производства. Прикладная эконометрика.
№ 4(8), c.27-41.
Афанасьев М. Ю. (2006) Модель производственного потенциала с управляемыми факторами неэффективности. // Прикладная эконометрика.
№ 4, с. 74–89.
Виленский П.Л., Лившиц В.Н., Смоляк С.А. (2008) Оценка эффективности инвестиционных проектов. Теория и практика. М., «ДЕЛО».
Aigner D.J., Lovell C.A.K. and Schmidt P. (1977) “Formulation and Estimation of Stochastic Frontier Production Function Models”, Journal of Econometrics, 6, 21-37.
Battese G.E., Coelli T.J. (1988) Prediction of Firm-level Technical Efficiencies with a Generalized Frontier Production Function and Panel Data // J. of Econometrics. Vol. 38, 387-399.

Оценки экономической эффективности перехода к достижимому потенциалу