Эффективное использование природных алмазов и теоремы вложения

Фридман Александр Абрамович.

ЦЭМИ РАН . Москва

1. Введение. Актуальность проблемы эффективного использования ресурсов общеизвестна. Она естественно возрастает, когда речь идет о таком редком и дорогостоящем ресурсе как природные алмазы.

О редкости драгметаллов и алмазов Таблица 1

Объемы мировой добычи в тоннах в 1980–2006 гг.
Годы	1980	1990	2000	2001	2002	2003	2004	2005	2006	2007
Золото	1210	2230	2550	2530	2550	2540	2420	2480	2370	2340
Платина		129	160	172	178	195	200	211	216	212
Алмазы	8,8	22,2	24.4	25,5	28,2	31,6	33,0	36,6	34,8	33,8
Ювелирные Алмазы	2,0	10.4	13,4	14,6	15,3	17,6	17,7	18,6	18,8	18,5

Источник: U.S. Geological Survey Minerals Yearbook. 2000–2007.

Из таблицы 1 видно, что годовой объем мировой добычи природных алмазов на порядок меньше годового объема мировой добычи платины и почти на два порядка меньше годового объема добычи золота, а редкость ювелирных алмазов еще выше. Заметим, что 1 карат (0,2г) хорошего ювелирного алмаза в 1000раз дороже 1 карата золота, а стоимость бриллианта массой 1 карат почти на порядок превосходит стоимость 1 карата алмаза. Более того, если стоимость золота растет прямо пропорционально его весу, то стоимость алмаза возрастает существенно нелинейно с увеличением его веса. Красноречивый пример – для получения 1 млн.долларов США в ноябре 2009г надо было бы иметь ~ 35 кг. золота, или ~23 кг.платины, либо ~115 г хороших алмазов по 1 карату каждый, либо хороших бриллиантов - всего 20 штук по 2 карата каждый и общим весом 8 граммов!!!

2. Задачи 1-4. Ниже излагается подход к решению проблемы эффективного использования природных алмазов при производстве бриллиантов, основанный на математическом моделировании алмазов и бриллиантов и решении нового класса оптимизационных задач о вложении одних тел в другие. Идея предлагаемого подхода носит достаточно общий характер и состоит в следующем. Если из выпуклого тела А можно реально сделать тело Б, то значит это тело Б можно как то разместить, расположить в теле А, т.е. вложить Б в А. Если это сделать оптимально, то мы приходим к задачам оптимального вложения тел, в частности оптимального вложения круглых бриллиантов в октаэдрический алмаз (ОА). (Понятие ОА раскрывается на стр.2.) Выбор именно этих задач объясняется тем, что ОА - это самые ценные алмазы в силу их строения и стоимости, а около 80-85 % производимых в мире бриллиантов – круглые.

Содержательно эти задачи можно сформулировать следующим образом.

Задача 1. В октаэдрический алмаз вложить круглый бриллиант максимального радиуса R

Задача 2 В октаэдрический алмаз А вложить круглый бриллиант максимального R,

а в оставшуюся часть А - бриллиант возможно большего радиуса r.

Задача 3 В октаэдрический алмаз вложить два круглых бриллианта с максимальным

суммарным весом.

Задача 4 В октаэдрический алмаз вложить два круглых бриллианта с максимальной

суммарной стоимостью

Здесь уместно отметить, что производство бриллианта напоминает работу скульптора, делающего из камня мысленно вложенную в него задуманную скульптуру, посредством отделения от камня ненужных с точки зрения результата частей камня, идущих в отходы. А что значит ненужных ?

3. О критерии эффективноcти производства бриллиантов

Алмаз – сырье высочайшей ценности, а при производстве бриллиантов около 50% каждого кристалла амаза идет в отходы. Отсюда родилась ориентация производства на минимизацию потерь. Это было близко психологии руководителей. Так сформировался весовой критерий эффективности – «Тот план и стратегия обработки алмазов лучше, при котором больше вес получаемых бриллиантов». На это было ориентировано производство, все показатели, премии и штрафы. Чтобы показать к чему это приводит, уместен следующий иллюстративный пример. Имеется кусок бумаги К для изготовления денежных знаков. Есть 2 варианта его использования :

А) из куска бумаги К можно сделать 10 купюр по 10 рублей и отходов бумаги будет 0, а сумма купюр -100 рублей.

Б) из К можно сделать всего 2 купюры по 500 рублей с большим отходом бумаги.

Если ориентироваться на конечный эффект - надо выбрать вариант Б, так как он дает больший доход, хотя при нем и отходы большие, но не ориентироваться же на 0 – ую величину отходов. Так и с алмазами – бриллианты производят и продают, чтобы получить за них больше валюты, а не минимизировать отходы при их изготовлении. В плановой экономике вокруг этого были дискуссии. Поэтому в комплексе задач 1- 4 фигурируют разные критерии, что позволило комплексно исследовать этот вопрос.

4. О моделировании ОА . Октаэдрический алмаз –это многогранник , получающийся из правильного октаэдра посредством сдвигов некоторых его граней параллельно самим себе. При этом число граней и углы между ними сохраняются (в невырожденных случаях).Такие многогранники называются октаэдрическими (ОМ). Их типичные виды представлены ниже.

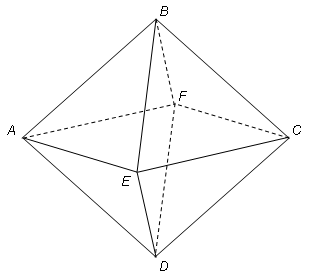
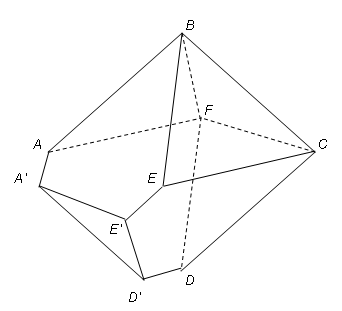
Рис .1 .Правильный октаэдр Рис. 2 Октаэдрический многогранник

(правильный октаэдрический многогранник) AEDAEDBFC

AEDBFC

Если в правильном многограннике (Рис.1) сдвинуть параллельно самой себе плоскость, содержащую грань АЕD, направляя ее движение во вне многогранника , то есть в направлении внешней нормали к АЕD (сдвигаемая плоскость переходит в плоскость, содержащую грань AED нового многогранника ) то мы получим многогранник AEDAEDBFC (Рис.2)

Еще более сложный пример ОМ можно получить, сдвигая (на Рис.2) параллельно себе плоскость, содержащую грань BFC и двигаясь вовне многогранника.

В наших работах были построены две модели ОА - комбинаторная и аналитическая в виде системы линейных неравенств. Нам удалось установить следующий факт.

Теорема 1 Каждый октаэдрический алмаз есть пересечение (общая часть) двух правильных тетраэдров, названных нами порождающими.

Ниже, на Рис.3 показано комбинаторное представление ОА в виде пересечения двух правильных порождающих тетраэдров

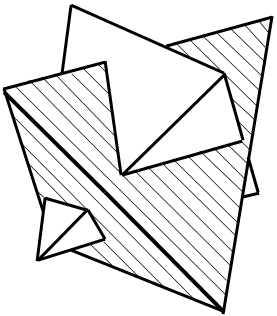
Рис 3 Октаэдрический алмаз как пересечение двух правильных тетраэдров

Такая комбинация тетраэдров называется звездой, которая однозначно задает ОА. Параллельные грани октаэдрического алмаза принадлежат разным порождающим тетраэдрам. Найдена полная система метрических параметров ОА - четыре толщины Li между 4 парами параллельных граней и две высоты двух правильных тетраэдров H1, H2, причем L1 + L2 +L3+L4 = H1+H2, а любые 5 их них линейно независимы.

Нами доказано, что любые 5 из указанных параметров определяют два ОА, являющихся зеркальным отражением друг друга. Каждому октаэдрическому алмазу O сопоставим его характеристику – вектор (О)= (L1, L2 L3 , L4, H1, H2), где L1, L2 L3 , L4, , – упорядоченные по возрастанию расстояния между параллельными гранями алмаза О, а H1, H2- высоты порождающих его тетраэдров. Эта характеристика (О ) октаэдрического алмаза является ключевым математическим инструментом при изучении различных свойств ОА , при доказательстве ряда теорем, связанных с алмазами, а также при исследовании и решении задач 1- 4 .

5. О модели круглого бриллианта (КБ) и идее тесного сырья

Круглый бриллиант (КБ) похож на тело вращения типа юлы. Вообще говоря, круглый бриллиант можно считать выпуклым многогранником и попытаться описать его системой двусторонних линейных неравенств. Но в силу сложной структуры КБ, имеющего 57 граней и более 150 вершин и ребер, попытка описать КБ таким многогранником и смоделировать процесс его вложения в ОА наталкивается на трудности:

- модель КБ-многогранника в виде системы неравенств весьма громоздка,

- в процессе решения задачи 1 пришлось бы следить за положением около 150 вершин

и ребер бриллианта, обязанных быть внутри кристалла.

Порождаемое таким обилием возможностей дерево ситуаций трудно обозримо, а сам вычислительный процесс – труднореализуем на ЭВМ.

Здесь оказалась плодотворной следующая идея. Для ее понимания приведем

стилизованный пример. Представим, что в прямоугольник П вложено тело (эллипс) Т, как показано на Рис. 4

A B