Применимо ли понятие «главного звена» к противодействию коррупции
Георгий Сатаров,
Фонд ИНДЕМ, Москва
Применимо ли понятие «главного звена»
к противодействию коррупции
В данном небольшом исследовании ставится вопрос о соотношении эффективности различных социальных институтов (в широком смысле этого слова) и коррупции. Ответ ищется с помощью анализа данных регулярных исследований Всемирного банка «World Governance Indicators» (далее – WGI). В рамках этого проекта Всемирный банк ежегодно, начиная с 1996 г., определяет и публикует значения шести рейтингов-индикаторов-индексов для более чем двухсот стран мира.
Таблица 1. Перечень рейтингов программы WGI Всемирного Банка. Приведены применяемый здесь код рейтинга, его английское название и русский перевод названия
|
Код
|
Русский перевод
|
Оригинальное название
|
|
VaA
|
Право голоса и подотчетность
|
Voice and Accountability
|
|
PSaAV
|
Политическая стабильность и ненасилие
|
Political Stability & Absence of Violence/Terrorism
|
|
GE
|
Эффективность управления
|
Government Effectiveness
|
|
RQ
|
Качество регулирования
|
Regulatory Quality
|
|
RoL
|
Верховенство закона
|
Rule of Law
|
|
CoC
|
Способность ограничивать коррупцию
|
Control of Corruption
|
Каждый индикатор откалиброван таким образом, чтобы он изменялся в диапазоне от -2,5 (наихудшее качество) до 2,5 (наилучшее качество).
Если просто вычислить коэффициенты линейной корреляции между указанными переменными (за некоторый год), то, чаще всего1, мы получим совокупность положительных коэффициентов, указывающих, как правило, на статистически значимую зависимость. Однако эта информация мало полезна по двум (как минимум) причинам. Первая: коэффициенты корреляции не указывают на причинно-следственную связь. Вторая: среди вычисленных корреляций многие могут оказаться ложными. Пример: между переменными CoC и PSaAV имеется корреляция равная 0, 687, подталкивающая к выводу, что чем выше стабильность, тем меньше коррупция (или наоборот – чем меньше коррупция, тем выше стабильность). Однако, если вычислить частную корреляцию между CoC и PSaAV при переменной RoL в качестве контролирующей, то выяснится, что корреляция между CoC и PSaAV падает до значения -0,147, т.е. до статистически незначимого значения, позволяющего сделать вывод об отсутствии непосредственного взаимовлияния между CoC и PSaAV и о влиянии RoL на две эти переменные и связь между ними.
Этот пример дает основание ставить следующую задачу: для набора шести переменных, определяемых в рамках проекта WGI, определить структуру влияния данных переменных друг на друга. Для решения этой задачи предлагается описанная ниже эвристическая процедура.
Рассмотрим матрицу корреляций между n переменными Пусть также – частная корреляция между i-й и j-й переменными при контролирующей t-й переменной.
Рассмотрим теперь величину , которая определяется выражением:
. (1)
Величина характеризует степень относительного смещения исходной корреляции до частной корреляции при использовании t-й контролирующей переменной. Тем самым оценивает степень влияния t-й переменной на i-ю и j-ю переменные и связь между ними. Чем выше значение , тем выше влияние.
Теперь введем две новыe переменные и . Первая образована усреднением переменных по i, а вторая – по j. Предполагается, что первая из двух новых переменных характеризует влияние t-й переменной на j-ю переменную и на ее взаимосвязи с остальными переменными; то же самое касается второй переменной применительно к i-й переменной. Чтобы упростить обозначения и дальнейшее конструирование введем новое обозначение Тем самым, мы получаем квадратную несимметричную матрицу в которой элемент характеризует влияние j-й переменной на i-ю переменную и ее взаимосвязи с n-2 остальными переменными. Осталось слегка преобразовать эту матрицу следующим образом:
(2)
Значения лежат в промежутке между -1 и 1. Величина показывает, в какой мере влияние j-й переменной на i-ю переменную и ее взаимосвязи превосходит влияние i-й переменной на j-ю. Если величина больше 0, то мы можем говорить, что j-я переменная влияет на i-ю. Если величина больше 0, то мы можем говорить, что j-я переменная влияет на i-ю. Если величина меньше 0, то мы можем говорить, что j-я переменная подвержена влиянию i-й переменной. Тем самым мы получили новую антисимметричную квадратную матрицу , которую мы можем называть матрицей взаимовлияний рассматриваемых переменных.
Завершим наше конструирование введением величины , которая образуется из величин усреднением по i (каждого столбца матрицы по ее строкам). Величина также меняется в пределах от -1 до 1. Она характеризует некоторую обобщенную влиятельность (если она больше 1) или подверженность влиянию (если она меньше 1) j-й переменной в наборе рассматриваемых n переменных.
Теперь вернемся к данным проекта WGI. В первую очередь рассмотрим значения индикатора для каждой из переменных из Таблицы 1, применив соответствующие расчеты к данным 2008 г., образованным следующими выборками стран: все страны, транзитные страны, развитые демократические страны, страны азиатского региона. Результаты указанных расчетов приведены на диаграмме Рисунка 1.

Рисунок 1. Профили значений коэффициента i, характеризующего влияние переменных рейтингов WGI на остальные по данным различных выборок
Диаграмма Рисунка 1 показывает как общие свойства различных выборок стран, так и их особенности. К общим свойствам, как легко убедиться относятся доминирующее влияние верховенства права (RoL) и подчиненное положение стабильности (PSaAV). Среди особенностей можно отметить низкое влияние качества нормативного регулирования (RQ) для развитых демократических стран и права голоса и подотчетности (VaA) для стран азиатского региона.
Теперь перейдем к основной теме данного сообщения. Для этого рассмотрим нессиметричную матрицу коэффициентов ij, характеризующих влияние одной переменной на другую, для каждой выборки. Из этой матрицы возьмем строки, соответствующие переменной «Контроль над коррупцией» (CoC), что позволит определить, какие из остальных переменных влияют в наибольшей степени на CoC. Результаты этих расчетов приведены на диаграмме Рисунка 2.
Профили на этой диаграмме в целом напоминают приведенные на предшествующем рисунке. Главный результат, касающийся поставленного выше вопроса, бросается в глаза: наибольшее влияние на эффективность контроля над коррупцией оказывает верховенство закона. Второе место досталось эффективности управления (GE). Этот факт не удивителен, поскольку, как принято считать, коррупция коренится именно в дефектах управления. Тем не менее, эффективность управления уступает, и весьма значительно, верховенству права. Интересно, что в наибольшей степени это касается транзитных стран, а значит и России. Но самое примечательное, что стандартные модернизационные проекты не уделяют должного внимания формированию современной правовой системы, концентрируясь на политических и экономических институтах, а также законодательстве, регулирующем эти институты. Между тем, они в большей степени подвержены влиянию верховенства права, нежели оказывают на него влияние. Если предлагаемые выводы верны, то это означает необходимость пересмотра стандартных стратегий модернизации.
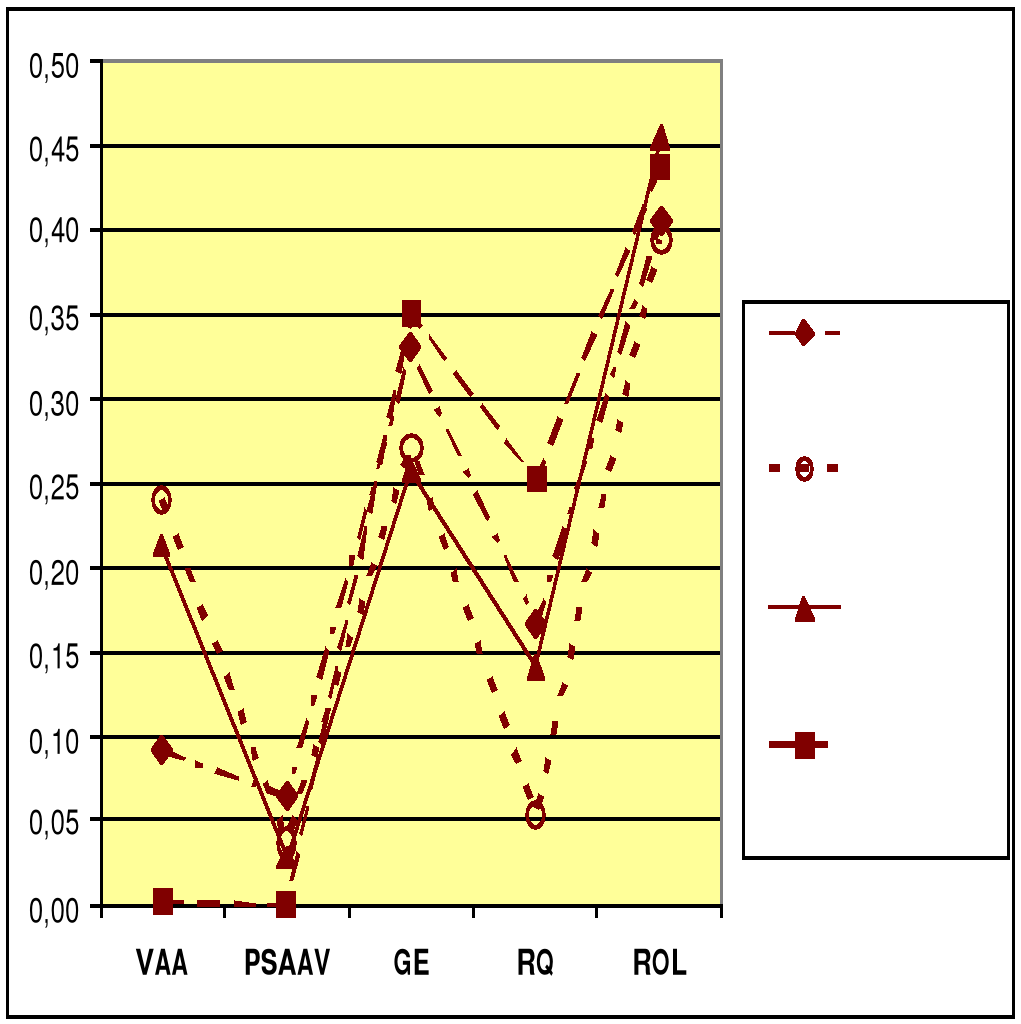
Рисунок 2. Профили значений коэффициента ij, характеризующего влияние переменных WGI на переменную «Контроль над коррупцией» (CoC) по данным различных выборок
В заключении отметим, что сходную эвристическую процедуру можно построить с помощью использования регрессионных коэффициентов в линейной модели. Она дает тот же основной результат – доминирующее объясняющее влияние верховенства права (RoL). Однако в остальном процедура существенно менее устойчива и систематически выдает слабо интерпретируемые результаты.
Использованная литература
D. Kaufmann, A. Kraay, and P. Zoido-Lobatn. Aggregating Governance Indicators (World Bank Policy Research Working Paper 2195) October 1999.
D. Kaufmann, A. Kraay, and P. Zoido-Lobatn/ Governance Matters (World Bank Policy Research Working Paper 2196) October 1999.
1 Понятно, что результат может зависеть (и это будет показано ниже) от выборки стран.
Применимо ли понятие «главного звена» к противодействию коррупции