РАСЧЁТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРИЧЕСКИХ СЛЕДЯЩИХ ПРИВОДОВ С ПРИМЕНЕНИЕМ ОПЕРАЦИОННОГО МЕТОДА РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

Реферат

РАСЧЁТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРИЧЕСКИХ

СЛЕДЯЩИХ ПРИВОДОВ С ПРИМЕНЕНИЕМ ОПЕРАЦИОННОГО МЕТОДА

РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ

В данной работе рассматривается подготовка к компьютерному расчёту динамических характеристик электрических следящих приводов (ЭСП) с применением операционного метода решения дифференциальных уравнений, изложенного в [1]. Примеры компьютерных программ расчёта динамических характеристик ЭСП приведены на сайте dinamikasistem.esy.es в поисковой системе mail.ru.

Метод основан на разложении на простейшие множители определителя операторного изображения динамической характеристики и представлении изображения динамической характеристики в виде суммы простейших дробей.

Метод применим к системам управления и их элементам, для которых справедливо следующее предположение. Эти системы (элементы) скачкообразно переходят через ряд состояний, в каждом из которых они описываются линейной дифференциальной системой уравнений (ЛДУ). Последовательность решений ЛДУ для реализованных состояний и даёт динамическую характеристику.

К таким системам относятся следящие приводы. Устойчивый следящий привод после отработки заданного достаточного большого начального рассогласования приходит в состояние, соответствующее линейной модели, но перед этим он проходит через состояния с насыщением усилителя, с ограничением тока в ЭСП, часто с насыщением сигнала рассогласования.

Подготовка исходных материалов для составления программы расчёта динамических характеристик ЭСП включает:

- составление расчётной схемы системы управления или элемента;

- определение числа учитываемых нелинейностей и, как следствие, числа учитываемых состояний системы управления или элемента;

- составление ЛДУ для всех учитываемых состояний и приведение ЛДУ к виду уравнений состояния и уравнений выхода;

- определение условий перехода между состояниями;

- определение передаточной функции для состояния, соответствующего линейной модели;

- определение диапазона изменяемых параметров и задание фиксированных параметров.

Уравнения состояния связывают функции ,…,…, характеризующие внутреннее состояние реактивных элементов системы, с входными сигналами единичной амплитуды ,…,…. Величина - аргумент, время от момента перехода системы в рассматриваемое состояние. Величина - порядок системы ЛДУ, а также порядок описываемой системы.

Алгебраические уравнения выхода выражают все функции, которые не являются функциями состояния, через входные сигналы и функции состояния.

Внутреннее состояние реактивных элементов во многих случаях описывается двумя функциями. Из них в качестве функций уравнений состояния будем принимать функции, обладающие лучшей непрерывностью, например, напряжение, а не ток конденсатора. При расчёте динамических характеристик ЭСП в качестве функций уравнений состояния приняты ток обмотки с индуктивностью исполнительного электродвигателя, ЭДС обмотки электродвигателя, угол поворота вала объекта, напряжения корректирующих конденсаторов. При таком выборе, если отсутствуют импульсные входные сигналы или импульсные взаимодействия между частями ЭСП, то функции уравнений состояния непрерывны, что облегчает расчёты.

В общем случае уравнения состояния системы порядка приводим к виду

где - производные первого порядка от функций , , - коэффициенты при функциях состояния, - входной сигнал единичной амплитуды, - амплитуда входного сигнала, - коэффициенты при входном сигнале.

Используемый вид уравнений состояния удобен для применения операторного преобразования Лапласа.

Уравнения выхода в общем случае будем записывать в виде

В приведённых выражениях - число уравнений выхода, - функции выхода, , - коэффициенты при функциях состояния, - коэффициенты при входном сигнале.

В этой части статьи выполним первые четыре этапа подготовки исходных материалов для устройств, общих для всех ЭСП. Такими устройствами являются силовая часть с объектом регулирования и датчик ошибки, показанные на рисунке 1. Рассмотрим также режимы ограничения тока исполнительного двигателя ЭСП.

На рисунке 1 обозначены:

– угол задающего воздействия,

– угол поворота вала объекта,

ДО – датчик ошибки,

– крутизна входного устройства датчика ошибки,

– выходное напряжение датчика ошибки,

СО – силовая часть и объект регулирования,

УМ – безинерционный усилитель мощности,

– входной сигнал УМ,

ИД – исполнительный двигатель,

– активное сопротивление обмотки ИД,

– индуктивность обмотки ИД,

– э. д. с. обмотки ИД,

ТП – тахогенератор, связанный с валом ИД,

– выходное напряжение ТП, пропорциональное угловой скорости ИД,

Р – механическая передача (редуктор),

ОР – объект регулирования,

– резистор токовой обратной связи,

– ток обмотки ИД,

– напряжение токовой обратной связи.

Далее для краткости слова «угловая», «угловое» применительно к скоростям и ускорениям писать не будем.

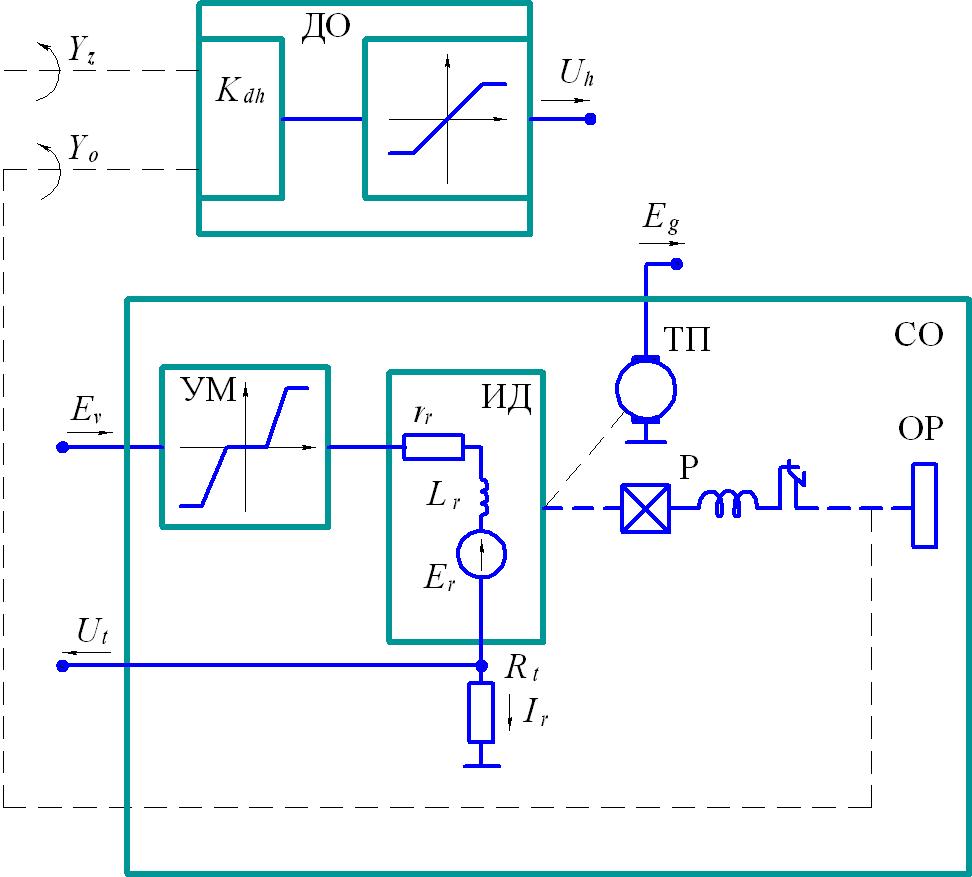
Рисунок 1. Функциональная схема датчика ошибки ДО и силовой части с

усилителем мощности и объектом регулирования СО

В силовой части с объектом регулирования отдельно рассмотрим электрическую цепь усилителя мощности и обмотки ИД и механическую часть, включающую ротор ИД, объект и передачу между ними.

1. Электрическая цепь усилителя мощности и обмотки ИД

Для цепи УМ и обмотки ИД будем определять ток , который является функцией состояния, а также функции выхода:

– выходное напряжение УМ,

– фиктивное выходное напряжение УМ,

– напряжение токовой обратной связи.

Напряжение не зависит от состояний устройства и равно

. (1-1)

Будем использовать также обозначения:

- коэффициент усиления УМ в линейной зоне,

- половина зоны нечувствительности, приведённая к выходу УМ, смысл этой величины пояснён на рисунке 2, где величина отложена на оси ,

- суммарное сопротивление

- электромагнитная постоянная времени

- абсолютная величина напряжения насыщения УМ.

На рисунке 2 показан примерный вид напряжений , в зависимости от напряжения .

Как следует из графика выходного напряжения УМ , устройство может находиться в одном из пяти состояний, которым дадим условные обозначения:

- выходное напряжение УМ в насыщении, отрицательное, равное минимальному значению ,

- выходное напряжение УМ в линейной зоне отрицательное,

- УМ в зоне нечувствительности, выходное напряжение равно нулю,

- выходное напряжение УМ в линейной зоне положительное,

- выходное напряжение УМ в насыщении, положительное, равное максимальному значению ,

Фиктивное выходное напряжение УМ представляет собой выходное напряжение УМ при отсутствии зоны нечувствительности и ограничения выходного напряжения. Это напряжение используется для определения условий перехода между состояниями.

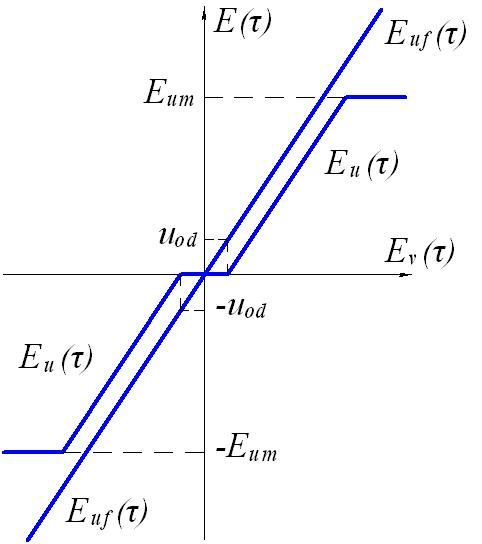
Рисунок 2. Вид характеристики вход - выход

усилителя мощности

Для всех состояний устройства

. (1-2)

Далее предполагаем, что для всех состояний выходное сопротивление УМ равно нулю.

Для состояния уравнение выходного напряжения УМ и уравнение напряжений цепи УМ и обмотки ИД имеют вид

Разделим второе уравнение на и применим введённое ранее обозначение . Получим уравнение состояния с производной от функции состояния

. (1-3)

Для состояния уравнение выходного напряжения УМ и уравнение напряжений цепи УМ и обмотки ИД имеют вид

, (1-4)

откуда

. (1-5)

Это уравнение превратится в уравнение состояния, когда для конкретной схемы ЭСП функцию выразим через другие функции состояния.

Для состояния получим уравнения, аналогичные уравнениям для состояния

, (1-6)

. (1-7)

Для состояния получим уравнения

, (1-8)

. (1-9)

Для состояния получим уравнения

, (1-10)

. (1-11)

Запишем условия, при которых устройство находится в текущем состоянии.

Для состояния и .

Для состояния .

При нарушении одного из условий нахождения в текущем состоянии происходит переход в другое состояние. Приведённые далее условия переходов между состояниями состоят из двух частей: собственно условия перехода и условия, требующего, чтобы при переходе не была превышена заданная абсолютная погрешность функции, определяющей момент перехода.

Условия переходов между состояниями и , и :

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и .

В приведённых выражениях - допустимая абсолютная погрешность функции .

В частном случае зона нечувствительности может отсутствовать, при этом величина равна нулю. Условия переходов между состояниями , и в случае, когда величина больше нуля:

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и .

Если величина равна нулю, то отрицательное и положительное выходные напряжения УМ в линейной зоне соответствуют одному состоянию. Будем считать вариант нулевых значений лишь частным случаем задания зоны нечувствительности. Чтобы не вводить дополнительное состояние при нулевой зоне нечувствительности, будем использовать состояния , с переходами между ними:

переход -

и ,

переход -

и .

Переходы между состояниями , являются искусственными, они вызваны не процессами в системе, а использованной методикой расчёта.

2. Механическая передача между ИД и объектом

Рассмотрим последовательно четыре варианта механической передачи:

- механическая передача без упругих деформаций и без люфта;

- механическая передача с упругими деформациями без люфта;

- механическая передача без упругих деформаций с люфтом;

- механическая передача с упругими деформациями и с люфтом.

Для варианта механической передачи без упругих деформаций и без люфта ротор объект и механическую передачу будем рассматривать как одно механическое тело. Для варианта механической передачи с упругими деформациями или (и) с люфтом будем рассматривать механическую систему из двух тел, ротора и объекта. Считаем, что моменты инерции, моменты трения вращающихся частей механической передачи после пересчёта учтены в соответствующих параметрах ротора. При этом момент вязкого трения ротора может полностью определяться моментами вязкого трения (для движения с постоянной скоростью) вращающихся частей механической передачи.

Считаем, что параметры ротора приведены к углу объекта. При этом обозначения моментов, моментов инерции и угловых величин, относящихся к ротору и приведённых к углу объекта, содержат индекс «o». Упоминать о приведении к углу объекта параметров с индексом «o» в обозначении далее не будем.

Состояния устройства в значительной мере определяются действием моментов трения покоя и скольжения.

Далее используем следующую модель действия моментов трения.

При движении механического тела без изменения знака скорости момент трения скольжения имеет постоянное значение, равен номинальному моменту скольжения и направлен против направления скорости.

В неподвижном состоянии момент трения покоя направлен против приложенного к объекту суммарного внешнего момента и равен ему по величине. Это выполняется до тех пор, пока приложенный момент не превысит значение номинального момента трения покоя, после чего начинается движение с ускорением, пропорциональным разности между приложенным моментом и номинальным моментом трения скольжения.

Когда при движении происходит изменение знака скорости, то механическое тело продолжит движение, если приложенный момент превышает значение номинального момента трения скольжения, в противном случае механическое тело остановится.

Значение номинального момента трения покоя может несколько превышать значение номинального момента трения скольжения или быть ему равным.

Введение номинального момента трения покоя, отличающегося по величине от номинального момента трения скольжения, не влияет на ЛДУ, а отражается только на условиях переходов из состояния покоя. По этой причине далее, полагая, что моменты трения покоя и скольжения равны, различия между ними не делаем и применяем общее название «момент трения».

Для всех вариантов механической передачи получим ЛДУ состояния с производными от функций состояния:

- э. д. с. ротора;

- угол объекта.

Для механической передачи с упругими деформациями или (и) с люфтом получим также уравнения ЛДУ состояния с производными от функций состояния:

- разность между углом объекта и углом ротора,

- скорость объекта.

С учётом уравнений с производной от функции состояния , полученных в разделе 1, система ЛДУ механической передачи без упругих деформаций и без люфта имеет третий порядок. Система ЛДУ других вариантов механической передачи имеет пятый порядок.

Будем определять функции выхода:

- угол ротора,

- скорость ротора,

- ускорение объекта,

- ускорение ротора,

- э. д. с. тахогенератора ТП,

- эквивалентный ток начала движения ротора в механической передаче с упругими деформациями,

- эквивалентный ток начала движения объекта в механической передаче с упругими деформациями.

Будем использовать обозначения:

- момент инерции объекта,

- момент инерции ротора (и механической передачи),

- суммарный момент инерции объекта и ротора

- момент трения объекта,

- момент постоянной нагрузки объекта,

- момент трения ротора,

- суммарный момент трения объекта и ротора

- передаточное отношение механической передачи,

- коэффициент пропорциональности между моментом и током ИД,

- эквивалентный ток, пропорциональный моменту трения объекта,

- эквивалентный ток, пропорциональный моменту трения ротора,

- эквивалентный ток, пропорциональный моменту трения объекта и ротора

- эквивалентный ток, пропорциональный моменту постоянной нагрузки объекта,

- коэффициент вязкого трения объекта,

- коэффициент вязкого трения ротора,

- суммарный коэффициент вязкого трения объекта и ротора

- коэффициент пропорциональности между скоростью ИД и его э. д. с.,

- коэффициент пропорциональности между скоростью ИД и э. д. с. тахогенератора ТП,

- электромеханическая постоянная времени

- электромеханическая постоянная времени при отсоединённом объекте

- коэффициент упругой деформации механической передачи,

- коэффициент вязкого трения механической передачи при упругой деформации.

Приведём формулы, которые действительны для всех вариантов механической передачи.

, (2-1)

, (2-2)

, (2-3)

, (2-4)

, (2-5)

Если ротор неподвижен, справедливы следующие выражения:

, (2-6)

, (2-7)

, (2-8)

, (2-9)

Если объект неподвижен, справедливы следующие выражения:

, (2-10)

. (2-11)

Для механической передачи с упругими деформациями или (и) с люфтом действительны следующие выражения:

, (2-12)

. (2-13)

Из выражений (2-1) и (2-2), (2-13) следуют два уравнения состояния механической передачи с упругими деформациями или (и) с люфтом:

, (2-14)

. (2-15)

Если объект неподвижен, уравнения состояния механической передачи с упругими деформациями или (и) с люфтом (2-14), (2-15) принимают вид:

, (2-16)

. (2-17)

2.1 Механическая передача без упругих деформаций и без люфта

Для этого варианта механической передачи справедливы выражения:

, (2-18)

, (2-19)

. (2-20)

При наличии момента трения выделим три состояния, для которых будем использовать условные обозначения:

- объект (и ротор) неподвижен;

- объект движется с отрицательной скоростью;

- объект движется с положительной скоростью.

Из выражений (2-2), (2-19) следует уравнение состояния для механической передачи без упругих деформаций и без люфта.

. (2-21)

Выражение для скорости объекта имеет вид

, (2-22)

Для определения ускорения далее будем использовать формулу, которая следует из (2-5), (2-20)

. (2-23)

Уравнения (2-21)… (2-23) будем применять для состояний , .

В состоянии действительны выражения (2-6)… (2-11). Первое из них является уравнением состояния. Второе уравнение состояния определяются выражением, которое следует из (2-21) и (2-7)

. (2-24)

Уравнение моментов на валу объекта для состояния , то есть при движении с отрицательной скоростью

. (2-25)

Далее для наглядности вместо моментов будем применять пропорциональные им эквивалентные токи , определённые ранее.

К левой части (2-25) применим подстановку с использованием (2-1), (2-2), (2-19). Получим

. (2-26)

Аналогичное уравнение для состояния отличается только знаком перед последним членом.

Коэффициент вязкого трения представим в виде отношения

, (2-27)

где использованы обозначения:

- номинальная скорость ИД, приведённая к валу объекта,

- момента вязкого трения при номинальной скорости ИД,

- номинальная скорость ИД,

- эквивалентный ток, пропорциональный моменту .

Номинальную скорость ИД (рад/с) можно определить, зная номинальную частоту вращения ИД (об /мин):

Используя введённое ранее обозначение , выражение (2-27), уравнение (2-26) (и аналогичное уравнение для состояния ), приведём к виду уравнения состояния с производной от функции

, (2-28)

Из (2-28) определим и подставим в (2-5). Получим выражение для ускорения ротора

. (2-29)

В (2-28), (2-29) знак «+» соответствует состоянию , знак «» соответствует состоянию .

Ускорение объекта согласно (2-20) равно ускорению ротора.

Устройство находится в состоянии , если момент трения не равен нулю и момент, развиваемый ИД, в сумме с моментом, приложенным к объекту, недостаточны для начала движения. Используя обозначения эквивалентных токов, условия действия уравнений состояния запишем в виде:

и .

В состоянии устройство находится, если скорость и, соответственно, э. д. с. не положительна

В состоянии устройство находится, если

Из приведённых неравенств получим условия переходов между состояниями , , :

переход -

и :

переход -

и ;

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

В приведённых выражениях , - допустимые абсолютные погрешности функций , .

Если момент трения равен нулю, устройство имеет одно состояние. Будем считать этот вариант лишь частным случаем для задаваемых значений момента трения. Чтобы не вводить дополнительное состояние при нулевом моменте трения, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

Эти переходы являются искусственными, они вызваны не процессами в системе, а использованной методикой расчёта. Аналогичные переходы будем использовать и далее в подразделах 2.2, 2.3.

Величина задаёт гистерезис при переходе, она должна быть меньше, чем , и больше, чем погрешность, с которой компьютер вычисляет функцию .

Если отработка начального рассогласования происходит с колебаниями относительно заданного положения, то при нулевом моменте трения амплитуда колебаний скорости стремится к нулю с выполнением переходов между состояниями , . Введение величины прекращает выполнение таких переходов и, соответственно, сбой счёта при очень малой амплитуде колебаний скорости.

2.2 Механическая передача с упругими деформациями без люфта

Функциональная схема для расчёта механической передачи с упругими деформациями без люфта приведена на рисунке 3.

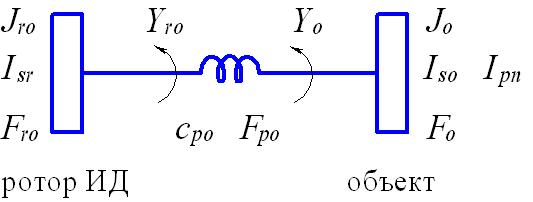
Рисунок 3. Функциональная схема механической передачи

с упругими деформациями без люфта

На рисунке стрелками показаны положительные направления углов вала ротора ИД и вала объекта . Такие же направления имеют скорости и ускорения.

Ротор имеет момент инерции . К ротору приложен момент трения , который будем учитывать, используя эквивалентный ток , и момент вязкого трения ротора (и механической передачи), который характеризуется коэффициентом .

Механическая передача характеризуется коэффициентом упругой деформации и коэффициентом вязкого трения при деформации .

Объект имеет момент инерции . К объекту приложены момент трения , момент вязкого трения объекта, который характеризуется коэффициентом и момент постоянной нагрузки . Моменты , будем учитывать, используя эквивалентные токи , .

Нелинейностями, определяющими число состояний устройства, являются моменты трения ротора и объекта.

Выделим девять состояний устройства, которым дадим условные обозначения:

- ротор и объект неподвижны;

- ротор движется с отрицательной скоростью, объект неподвижен;

- ротор движется с положительной скоростью, объект неподвижен;

- ротор неподвижен, объект движется с отрицательной скоростью;

- ротор и объект движутся с отрицательной скоростью;

- ротор движется с положительной скоростью, объект движется с отрицательной скоростью;

- ротор неподвижен, объект движется с положительной скоростью;

- ротор движется с отрицательной скоростью, объект движется с положительной скоростью;

- ротор и объект движутся с положительной скоростью.

Для состояний , , , в которых ротор неподвижен, действует уравнение состояния (2-6), а функции , равны нулю согласно выражениям (2-8), (2-9).

Используя рисунок 3, уравнения моментов на валу ротора для состояний , , , когда ротор движется с отрицательной скоростью, запишем в виде:

. (2-30)

Из (2-15) определим

. (2-31)

Выражение (2-31), а также и из (2-2) подставим в (2-30). Полученное выражение приведём к виду:

. (2-32)

Аналогичное уравнение для состояний , , отличается только знаком перед членом в правой части.

Для удобства сопоставления результатов расчётов члены (2-31), содержащие , , , , приведём к относительному виду.

Коэффициент вязкого трения ротора представим как отношение момента вязкого трения ротора при номинальной скорости ИД к номинальной скорости ИД :

, (2-33)

где использовано обозначение эквивалентного тока , пропорционального моменту .

Следуя методике [2], введём обозначение постоянной времени механической передачи

. (2-34)

Преобразуем отношение

, (2-35)

где использовано обозначение коэффициента относительного затухания механической передачи под действием момента вязкого трения при упругой деформации

. (2-36)

Применив к (2-32) и к аналогичному уравнению для состояний , , ранее введённое обозначение , а также (2-33)…(2-36),.получим уравнение состояния

. (2-37)

Чтобы определить ускорение ротора, из уравнения (2-37) выразим и подставим в (2-5)

. (2-38)

В (2-37), (2-38) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Для состояний , , , в которых объект неподвижен, действуют уравнения состояния (2-16), (2-17), а функции , равны нулю согласно выражениям (2-10), (2-11).

Используя рисунок 3, уравнения моментов на валу объекта для состояний , , , когда объект движется с отрицательной скоростью, запишем в виде:

. (2-39)

Подставив (2-1) и (2-31) в (2-39), получим:

.(2-40)

Аналогичное уравнение для состояний , , отличается только знаком перед последним членом в правой части.

Коэффициент вязкого трения объекта представим как отношение момента вязкого трения объекта при номинальной скорости ИД к номинальной скорости ИД :

, (2-41)

где использовано обозначение эквивалентного тока , пропорционального моменту .

Применив к (2-40) и к аналогичному уравнению для состояний , , обозначения (2-34), (2-36), (2-41),.получим уравнение состояния

. (2-42)

Чтобы определить ускорение объекта, из уравнения (2-42) выразим и подставим в (2-4)

. (2-43)

В (2-42), (2-43) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Переход из состояния покоя ротора к состоянию движения с отрицательной скоростью произойдёт, если правая часть уравнения (2-30), или, что эквивалентно, правая часть уравнения (2-38) станет меньше нуля. В правой части уравнения (2-38) в момент перехода член, содержащий функцию , равен нулю, поэтому условие перехода имеет вид

. (2-44)

Приведём (2-44) к виду

Используя первые три слагаемых этого неравенства, введём функцию , которую будем использовать для определения условий переходов между состояниями ротора.

. (2-45)

Таким образом, переход из состояния покоя ротора к состоянию движения с отрицательной скоростью, используя функцию , запишем в виде:

В целом, условия переходов между состояниями ротора , , , в которых буква соответствует состоянию объекта и заменяет одну из букв , , , имеют вид, аналогичный условиям переходов в подразделе 2.1:

переход -

и ;

переход -

и ;

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

Если момент трения ротора равен нулю, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

В приведённых выражениях , - допустимые абсолютные погрешности функций , . Величина задаёт гистерезис при переходе, она должна быть меньше, чем , и больше, чем погрешность, с которой компьютер вычисляет функцию .

Переход из состояния покоя объекта к состоянию движения с отрицательной скоростью произойдёт, если правая часть уравнения (2-43) станет меньше нуля. В правой части уравнения (2-43) в момент перехода член, содержащий функцию , равен нулю, поэтому условие перехода приведём к виду с эквивалентными токами без этой функции

Используя первые три слагаемых этого неравенства, введём функцию , которую будем использовать для определения условий переходов между состояниями объекта.

. (2-46)

Условия переходов между состояниями объекта , , , в которых буква соответствует состоянию ротора и заменяет одну из букв , , , имеют вид, аналогичный условиям переходов между состояниями ротора

переход -

и ;

переход -

и ;

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

Если момент трения объекта равен нулю, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

2.3 Механическая передача без упругих деформаций с люфтом

Кинематическая схема взаимных положений объекта и ротора ИД механической передачи без упругих деформаций с люфтом приведена на рисунке 4. Для удобства угловые перемещения заменены линейными, стрелка на рисунке показывает направление, принятое положительным для угловых функций.

На рисунке 4 а) приведено положение, в котором люфт не выбран, а углы объекта и ротора равны. Это положение при нулевых значениях углов принято в качестве исходного.

На рисунке 4 б) приведено положение, в котором люфт выбран, объект отстаёт от ротора на минимальную величину , равную минус , где - половина величины люфта.

На рисунке 4 в) приведено положение, в котором люфт выбран, объект опережаёт ротор на максимальную величину , равную .

Обозначение на рисунке 4 со значениями 1 и -1 введено как признак взаимного положения объекта и ротора при выбранном люфте.

Нелинейностями, определяющими число состояний устройства, являются люфт, моменты трения ротора и объекта.

На основании рисунка 4 выделим двенадцать состояний устройства. Три состояния соответствуют положению, когда люфт выбран и совпадают с состояниями механической передачи без упругих деформаций и без люфта , , . Девять состояний соответствуют положению, когда люфт не выбран и совпадают с состояниями механической передачи с упругими деформациями без люфта , , , , , , , , .

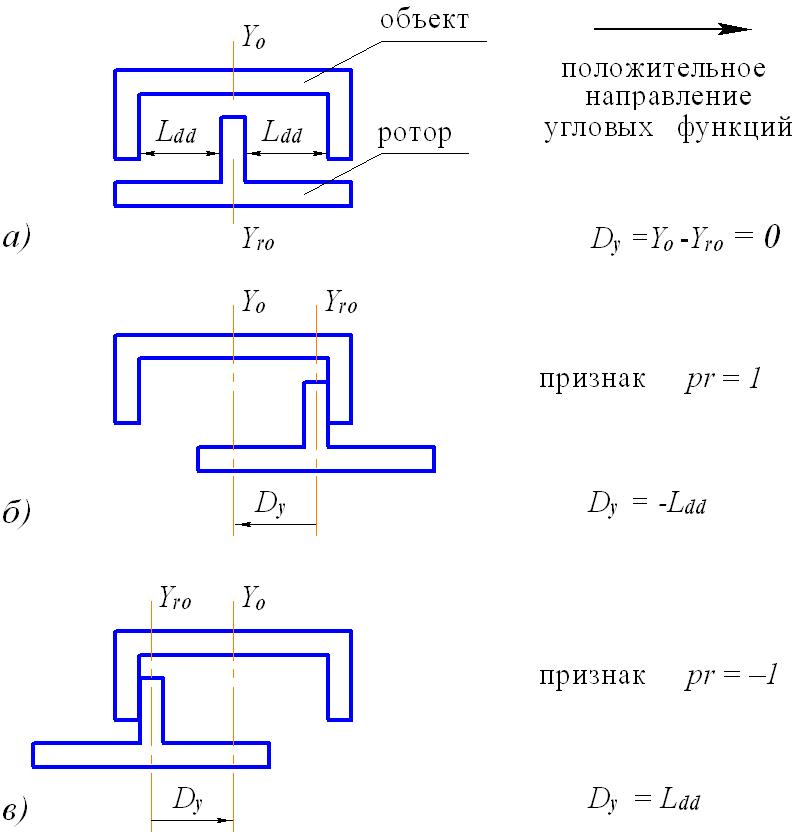
Рисунок 4. Кинематическая схема положений объекта и

ротора в механической передаче с люфтом:

а) - люфт не выбран, углы объекта и ротора совпадают;

б) - люфт выбран, угол объекта меньше угла ротора;

в) - люфт выбран, угол ротора меньше угла объекта

2.3.1 Уравнения и функции

Для состояний , , , , в которых ротор неподвижен, функции , , равны нулю согласно выражениям (2-7)…(2-9). Действует уравнение состояния (2-6).

Для состояний , , , , в которых объект неподвижен, функции , равны нулю согласно выражениям (2-10), (2-11). Действуют уравнения состояния (2-16), (2-17).

Для состояний , , , в которых люфт не выбран, а скорость ротора отрицательна, уравнение моментов на валу ротора имеет вид

Для состояний , , уравнение моментов отличается знаком перед последним членом.

Применив к уравнению моментов для состояний , , , , , ранее введённое обозначение , а также (2-2), (2-5), (2-33),.получим уравнение состояния

. (2-47)

Выражение для ускорения получим аналогично выражению (2-38)

. (2-48)

В (2-47), (2-48) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Для состояний , , , в которых люфт не выбран, а скорость объекта отрицательна, уравнение моментов на валу объекта имеет вид

Для состояний , , уравнение моментов отличается знаком перед последним членом.

Применив к уравнению моментов для состояний , , , , , выражения (2-1), (2-41),.получим уравнение состояния

. (2-49)

Выражение для ускорения получим аналогично выражению (2-43)

. (2-50)

В (2-49), (2-50) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Для состояний , , , в которых люфт выбран, уравнения совпадают с уравнениями механической передачи без упругих деформаций и без люфта при

Не совпадают углы 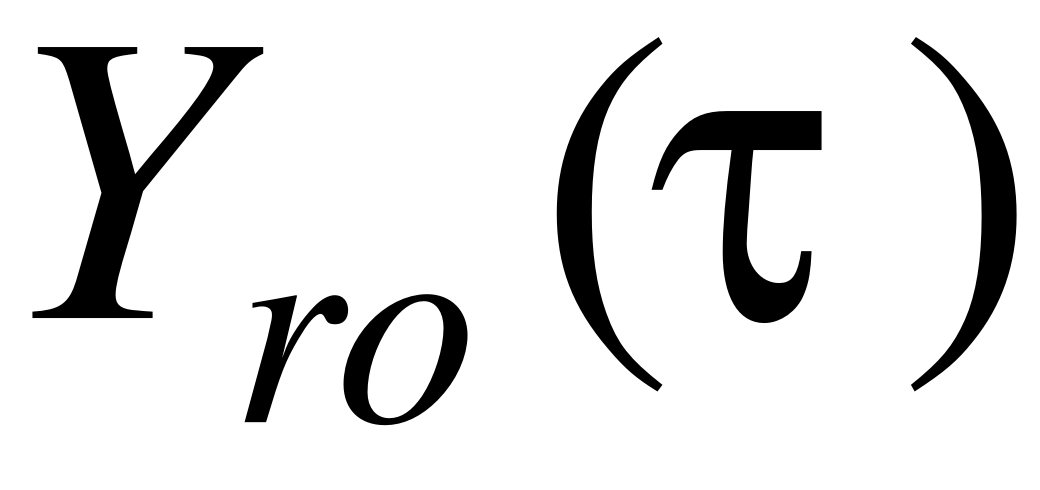и 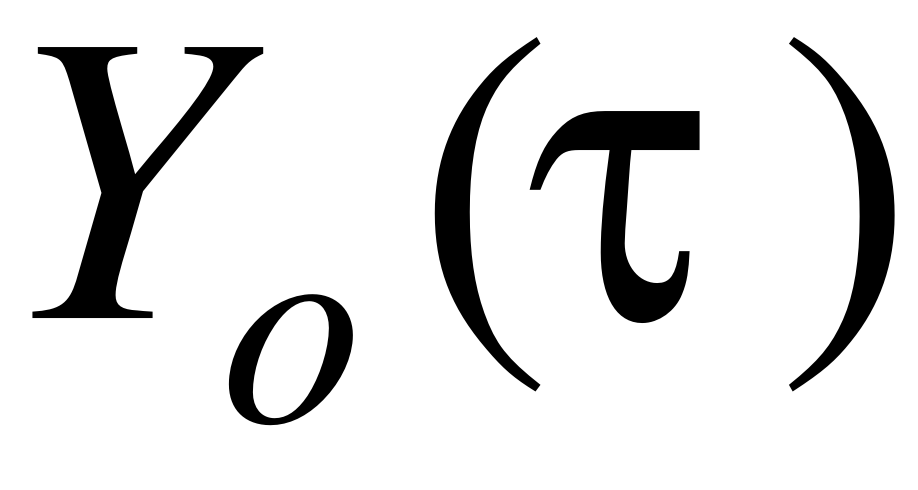. Если люфт выбран, как показано на рисунке 4 б), то

Если люфт выбран, как показано на рисунке 4 в), то

Чтобы обеспечить непрерывность расчёта функций состояния при переходах, сохраним порядок ЛДУ таким, каким он был при невыбранном люфте. Функции , будем учитывать как функции состояния.

Для состояний , ,

. (2-51)

Для состояния из (2-6) и (2-22) получим

. (2-52)

Для состояний , из (2-28) и (2-22) получим

. (2-53)

В (2-53) знак «+» соответствует состоянию , знак «» соответствует состоянию .

В уравнениях (2-28) и (2-53) функции , и коэффициенты при , , отличаются на один постоянный множитель .

2.3.2 Условия переходов между состояниями с невыбранным люфтом

Условия переходов между состояниями с невыбранным люфтом , , , , , , , , аналогичны соответствующим переходам механической передачи с упругими деформациями без люфта.

Условия переходов между состояниями ротора , , , в которых буква соответствует состоянию объекта и заменяет одну из букв , , , имеют вид:

переход -

и ;

переход -

и ;

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

Если момент трения ротора равен нулю, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

Условия переходов между состояниями объекта , , , в которых буква соответствует состоянию ротора и заменяет одну из букв , , , имеют вид:

переход -

и ;

переход -

и ;

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

Если момент трения ротора равен нулю, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

переход -

и и ;

переход -

и и ;

переход -

и и ;

переход -

и и .

Переходы из состояния отсутствуют, так как к объекту приложен постоянный момент.

Если момент трения объекта равен нулю, будем использовать состояния , с переходами между ними:

переход -

и ;

переход -

и .

В приведённых выражениях - допустимая абсолютная погрешность функции . Величина задаёт гистерезис при переходе, она должна быть меньше, чем , и больше, чем погрешность, с которой компьютер вычисляет функцию .

2.3.3 Условия переходов между состояниями при выборке люфта. Удар

Переход из состояния, когда люфт не выбран, в состояние с выбранным люфтом в положение, изображённое на рисунке 4 б), может произойти, если скорость объекта меньше скорости ротора .

Переход в положение, изображённое на рисунке 4 в), может произойти, если скорость объекта больше скорости ротора .

Соответственно формулируем условия переходов между состояниями при выборке люфта.

Переход из состояния в состояния , , из состояния в состояния , , из состояния в состояние , из состояния в состояния , , , из состояния в состояние в положение, изображённое на рисунке 4 б)

и и . (2-54)

Переход из состояния в состояния , , из состояния в состояние , из состояния в состояния , , из состояния в состояния , , , из состояния в состояние в положение, изображённое на рисунке 4 в)

и и . (2-55)

В приведённых выражениях - допустимая абсолютная погрешность функции .

При выборке люфта нужно формировать признак взаимного положения объекта и ротора, он необходим при обратных переходах.

При переходе в положение, изображённое на рисунке 4 б) будем формировать признак , при переходе в положение, изображённое на рисунке 4 в) будем формировать признак .

Переход из состояния, когда люфт не выбран, в состояние с выбранным люфтом в механической передаче без упругих деформаций сопровождается ударом.

Удар – это предельный случай взаимодействия тел механической системы, в результате которого изменяются скорости и кинетические энергии тел, а взаимодействие происходит за малое по сравнению с другими процессами системы время.

Удар представляет собой импульсное воздействие, которое вызывает скачкообразное изменение функций состояния системы. В рассматриваемой системе скачкообразно изменяются скорость объекта и э. д. с. ротора , пропорциональная изменяющейся скорости ротора . Скачкообразное изменение и вызывает соответствующее изменение зависящих от них функций выхода.

Рассматривают два предельных случая: абсолютно упругий удар, в результате которого суммарная кинетическая энергия тел сохраняется, и абсолютно неупругий удар, в результате которого скорости тел становятся одинаковыми [3].

В случае абсолютно упругого удара угловые скорости вращающихся тел после удара определяют из условия сохранения суммарной кинетической энергии и условия сохранения момента импульса относительно оси вращения, которые для системы из объекта и ротора запишем соответственно в виде:

, (2-56)

, (2-57)

где

, - скорости объекта до и после удара,

, - скорости ротора до и после удара.

Для абсолютно неупругого удара угловые скорости вращающихся тел после удара определяют из условия сохранения момента импульса относительно оси вращения (2-57) и условия равенства угловых скоростей после удара, в данном случае

, (2-58)

Закон сохранения момента импульса справедлив для замкнутой системы, то есть системы, в которой отсутствуют внешние воздействия на соударяющиеся тела.

На практике этот закон распространяют на незамкнутые системы, обосновывая это тем, что при ударе возникают большие силы, необходимые для того, чтобы за очень малое время изменить скорости объектов, поэтому действием значительно меньших сил за малое время удара можно пренебречь.

В замкнутой системе после абсолютно неупругого удара тела сохраняют одинаковую скорость.

В незамкнутой системе после абсолютно неупругого удара скорости тел выравниваются, затем их скорости могут быть одинаковыми, но могут отличаться, то есть произойдёт обратный переход к люфту.

Далее будем рассматривать только абсолютно неупругий удар.

Из уравнений (2-57), (2-58) определим

. (2-59)

Далее, используя (2-2), найдём

. (2-60)

Если до удара ротор был неподвижен (исходное состояние или ) и, если выполняется условие

то после удара считаем, что произошёл переход к состоянию , или, если выполняется условие

то после удара считаем, что произошёл переход к состоянию , в противном случае считаем, что произошёл переход к состоянию . Таким образом, учитывается влияние моментов трения как внешних по отношению к механической системе объект – ротор воздействий.

Если до удара скорость ротора не была равна нулю, то состояние после удара определяем по значению функции , вычисленной по формулам (2-59), (2-60).

Если вычисленная функция больше , то принимаем, что произошёл переход к состоянию , если функция меньше, чем минус , то принимаем, что произошёл переход к состоянию , в противном случае считаем, что произошёл переход к состоянию .

Определённое таким образом состояние или не окончательное. Необходимо учесть влияние вращающего момента ИД, пропорционального току , как внешнего по отношению к механической системе объект – ротор воздействия.

Из состояния возможен обратный переход к состоянию . Из состояния возможен обратный переход к состоянию . Необходимые условия для таких переходов рассмотрены в пункте 3.3.4.

Для случая, когда до удара скорость ротора не была равна нулю, учёт влияния моментов трения будет выполнен компьютерной программой в следующей точке счёта. Отдельного рассмотрения этот случай не требует.

2.3.4 Условия переходов из состояний с выбранным люфтом

В начале рассмотрим условия, определяющие нахождение устройства в состоянии с выбранным люфтом. Нарушение одного из этих условий вызывает переход к другому состоянию.

В состоянии , когда ротор и объект неподвижны, устройство находится, если выполняются условия, исключающие совместное движение:

Кроме того, в положении, изображённом на рисунке 4 б), устройство находится, если

а в положении, изображённом на рисунке 4 в), устройство находится, если

Последние четыре неравенства исключают движение ротора и объекта по отдельности.

В состоянии , когда скорость ротора и объекта отрицательна, устройство находится, если выполняется условие

В положении, изображённом на рисунке 4 б), устройство находится, если

Последнее неравенство исключает переход к состоянию с люфтом. Подставив в это неравенство выражения (2-48), (2-50) для ускорений и учитывая (2-19), (2-2), приведём его к виду

Введём обозначение эквивалентного тока

. (2-61)

Тогда неравенство, исключающее переход к состоянию с люфтом в положении, изображённом на рисунке 4 б), запишем в виде

В положении, изображённом на рисунке 4 в), устройство находится, если

или

В состоянии , когда скорость ротора и объекта положительна, устройство находится, если выполняется условие

При этом в положении, изображённом на рисунке 4 б), устройство находится, если

или с учётом (2-48), (2-50), (2-19), (2-2), (2-61)

В положении, изображённом на рисунке 4 в), устройство находится, если

или

Условия переходов из состояния :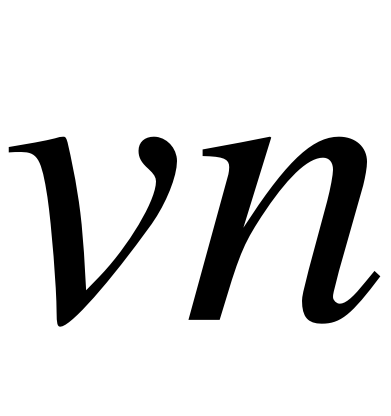

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и .

Условия переходов из состояния :

переход 1 -

и и и ,

переход 1 -

и и и ,

переход 2 -

и и и и ,

переход 2 -

и и и и ,

переход -

и и и и и ,

переход 3 -

и и и и и ,

переход 1 -

и и ,

переход 2 -

и и .

Условия переходов из состояния :

переход 1 -

и и и и ,

переход 1 -

и и и и ,

переход 2 -

и и и ,

переход 2 -

и и и ,

переход -

и и и и и ,

переход 3 -

и и и и и ,

переход 1 -

и и ,

переход 2 -

и и .

2.4 Механическая передача c упругими деформациями и с люфтом

Нелинейностями, определяющими число состояний устройства, являются люфт, моменты трения ротора и объекта.

В положении, когда люфт не выбран, девять состояний устройства , , , , , , , , совпадают с состояниями механической передачи без упругой деформации с люфтом, рассмотренными в подразделе 2.3.

Действительны уравнения (2-47)…(2-50) и условия переходов между состояниями с невыбранным люфтом, приведённые в пункте 2.3.2.

Если люфт выбран, как показано на рисунке 4 б), то действуют девять состояний устройства, аналогичные состояниям механической передачи с упругими деформациями без люфта. Присвоим этим состояниям условные обозначения , , , , , , , , .

Если люфт выбран, как показано на рисунке 4 в), то действуют девять аналогичных состояний. Присвоим этим состояниям условные обозначения , , , , , , , , .

Для состояний , , , , , , в которых

ротор неподвижен, действует уравнение состояния (2-6), а функции , равны нулю согласно выражениям (2-8), (2-9).

Для состояний , , , , , , в которых объект неподвижен, действуют уравнения состояния (2-16), (2-17), а функции , равны нулю согласно выражениям (2-10), (2-11).

Уравнения для состояний , , , , , , в которых скорость ротора не равна нулю, а люфт выбран в сторону, изображённую на рисунке 4 б), получим, если в (2-37), (2-38) функцию заменим суммой :

. (2-62)

. (2-63)

В (2-62), (2-63) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Уравнения для состояний , , , , , , в которых скорость объекта не равна нулю, а люфт выбран в сторону, изображённую на рисунке 4 б), получим, если в (2-42), (2-43) функцию заменим суммой :

. (2-64)

Чтобы определить ускорение объекта, из уравнения (2-42) выразим и подставим в (2-4)

. (2-65)

В (2-64), (2-65) знак «+» соответствует состояниям , , , знак «» соответствует состояниям , , .

Уравнения для состояний , , , , , , в которых скорость ротора не равна нулю, а люфт выбран в сторону, изображённую на рисунке 4 в), можно получить, если в (2-37), (2-38) функцию заменить разностью .

Аналогично, уравнения для состояний , , , , , , в которых скорость объекта не равна нулю, а люфт выбран в сторону, изображённую на рисунке 4 в), можно получить, если в (2-42), (2-43) функцию заменить разностью .

Определённые таким образом уравнения будут отличаться от уравнений (2-62) … (2-65) только знаком перед слагаемым, содержащим .

Определим функции , , которые используются для переходов между состояниями. Соответствующие выражения получим, если в (2-45), (2-46) функцию заменим суммой для случая, когда люфт выбран в сторону, изображённую на рисунке 4 б):

. (2-66)

. (2-67)

Аналогично, функции для случая, когда люфт выбран в сторону, изображённую на рисунке 4 в) можно получить, если в (2-45), (2-46) функцию заменить разностью . В этом случае функции , будут отличаться от функций (2-66), (2-67) только знаком перед слагаемым, содержащим .

Для определённых таким образом функций , действительны все условия переходов между состояниями, приведёнными в подразделе 2.2, если совпадают первые три буквы в обозначениях состояний.

Например, переходу - подраздела 2.2 соответствует переход - , когда люфт выбран в сторону, изображённую на рисунке 4 б), или переход - , когда люфт выбран в сторону, изображённую на рисунке 4 в).

При выборке люфта с переходом из состояния в состояние (где и заменяют одну из букв , , ) действует условие (2-54). При этом формируется признак .

Условие обратного перехода из состояния в состояние :

и и .

При выборке люфта с переходом из состояния в состояние действует условие (2-55). При этом формируется признак .

Условие обратного перехода из состояния в состояние :

и и .

В приведённых выражениях - допустимая абсолютная погрешность функции .

3. Датчик ошибки

Под датчиком ошибки (ДО) будем подразумевать устройство, которое вырабатывает электрический сигнал , зависящий от угловой ошибки ЭСП . Датчик ошибки может выполнять и преобразование электрического сигнала, например, усиление, ограничение по амплитуде, фазочувствительное выпрямление в случае применения первичных датчиков переменного тока.

Уравнение сигнала ошибки

, (3-1)

- угол поворота задающего вала,

- угол поворота вала объекта.

Сигнал ошибки может принимать значения в пределах от минус до + . Значения минус и + включать в рабочий диапазон сигнала ошибки не будем.

Рассмотрим два вида характеристик вход – выход ДО: характеристику с тремя линейными зонами, изображённую на рисунке 5, и характеристику с одной линейной зоной, изображённой на рисунке 6.

3.1 Характеристики и условия переходов ДО с тремя линейными зонами

Характеристика , изображённая на рисунке 5, состоит из семи участков: линейный участок - , участки насыщения - и - , линейный участок - , участки насыщения - и - , линейный участок - .

Соответствующим состояниям дадим условные обозначения: , и , , и , .

На рисунке 5 изображена также характеристика фиктивного выходного напряжения , которую будем использовать для определения переходов между состояниями ДО. Характеристика состоит из трёх линейных участков: - , - , - .

Разделение состояний, соответствующих участкам характеристики с насыщением, на два состояния и , и является искусственным, оно вызвано необходимостью определить зоны действия участков характеристики .

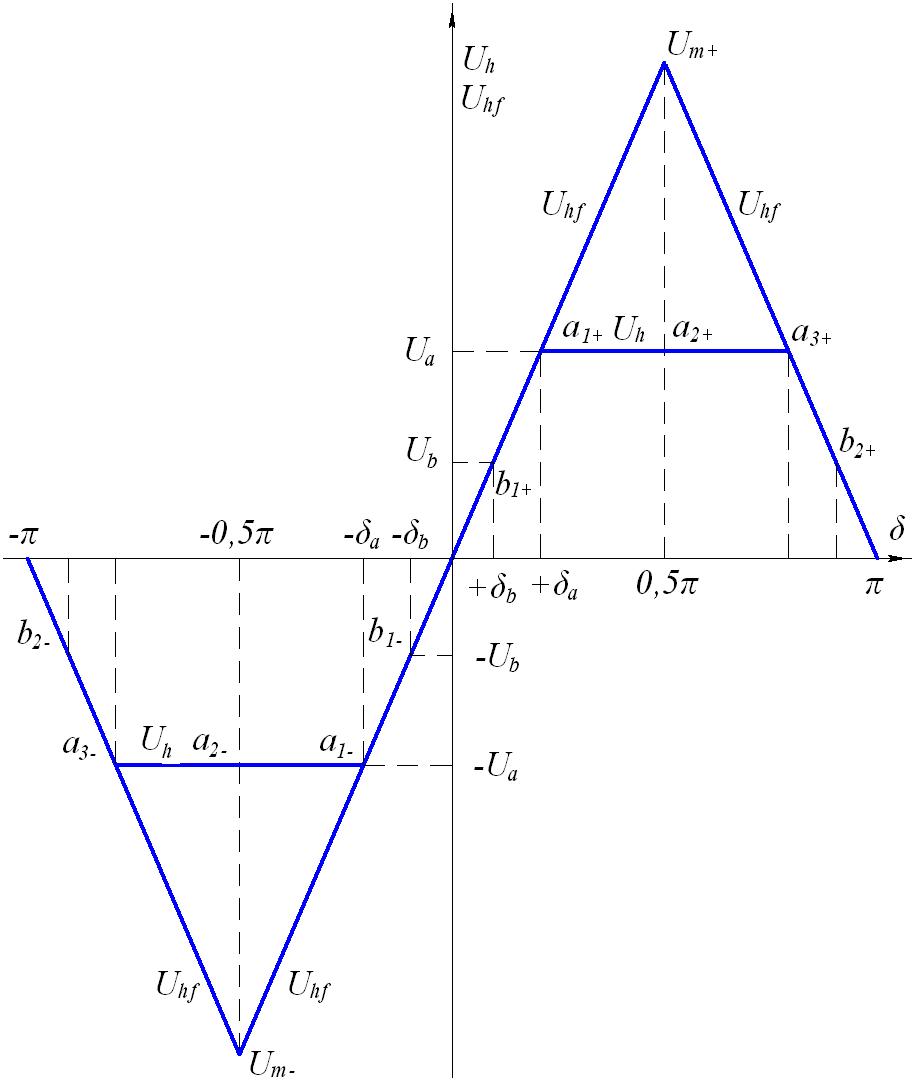
Рисунок 5. Характеристики вход – выход датчика ошибки ДО

с тремя линейными зонами

Характеристика , изображённая на рисунке 5, аппроксимирует характеристику ДО, которая формируется с применением пары синусно-косинусных вращающихся трансформаторов (СКВТ) или сельсинов.

Пусть, например, в соответствии со схемой ДО, приведённой на рисунке 1, СКВТ вырабатывает напряжение переменного тока

где - амплитуда выходного напряжения СКВТ- приёмника.

Напряжение поступает в фазочувствительный выпрямитель с коэффициентом передачи и с ограничением выходного напряжения на уровне и минус .

Таким образом, состояния , , , , формируются ограничением выходного напряжения фазочувствительного выпрямителя, а состояния , , - характеристикой пары СКВТ и коэффициентом передачи .

Крутизну характеристики ДО для состояния примем равной произведению

, (3-2)

где - крутизна выходного напряжения пары СКВТ при нулевом значении сигнала ошибки :

(В/рад).

Уравнения характеристик ДО, изображённых на рисунке 5:

состояние

, (3-3)

состояние

Уравнение характеристики для состояния (3-3) должно соответствовать отрицательной обратной связи ЭСП. Как видно из рисунка 5 и приведённых выражений, уравнение характеристики для состояний , должно соответствовать положительной обратной связи ЭСП.

Условия переходов между состояниями , , , , , , :

переход -

и и ,

переход -

и и ,

переход -

и ,

Переход -

и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

Переход -

и и ,

Переход -

и ,

Переход -

и ,

переход -

и и ,

переход -

и и .

В приведённых неравенствах и - допустимые абсолютные погрешности функций , .

3.2 Характеристики и условия переходов ДО с одной линейной зоной

Характеристика , изображённая на рисунке 6, состоит из трёх участков: участок насыщения - , линейный участок - , участок насыщения - .

Соответствующим состояниям дадим условные обозначения , , .

На рисунке 6 изображена также характеристика фиктивного выходного напряжения , которую будем использовать для определения переходов между состояниями ДО. Характеристика линейна во всём диапазоне и на участке - совпадает с характеристикой .

Характеристики, изображённые на рисунке 6, могут формироваться с использованием преобразователя цифра – напряжение (ПЦН). Если величина младшего разряда ПЦН меньше статической ошибки ЭСП, то дискретностью выходного сигнала ПЦН можно пренебречь.

Участки насыщения характеристики, изображённой на рисунке 6, могут формироваться как характеристикой ПЦН, так и ограничением выходного напряжения электронного согласующего усилителя, на вход которого поступает сигнал ПЦН.

Далее для определённости будем считать, что действует второй вариант формирования участков насыщения.

Крутизну характеристики ДО для состояния примем равной произведению

, (3-4)

где - крутизна первичного датчика, например, ПЦН,

- крутизна согласующего усилителя в составе ДО.

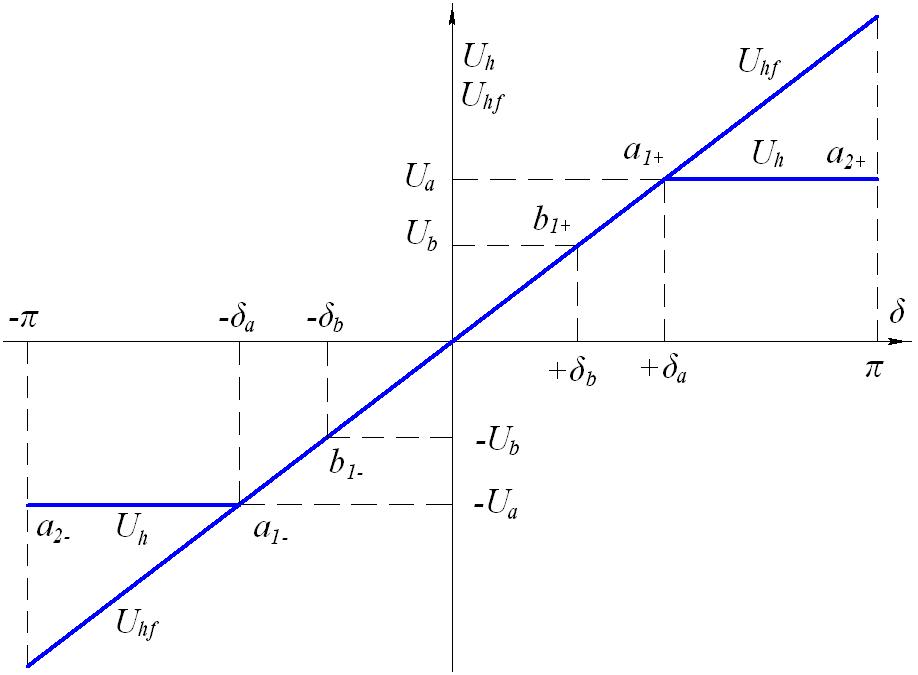
Рисунок 6. Характеристики вход – выход датчика ошибки ДО

с одной линейной зоной

Уравнения характеристик ДО, изображённых на рисунке 6:

состояние

, (3-5)

состояние

Уравнение функции для всех состояний имеет вид

Условия переходов между состояниями , , :

переход -

и ,

переход -

и ,

переход -

и ,

Переход -

и ,

4 Изменение структуры ЭСП в зависимости от выходного сигнала датчика ошибки

Рассмотренные в разделе 3 состояния датчиков ошибки (ДО) соответствуют линейной модели ЭСП. В некоторых случаях для повышения качества отработки начального рассогласования зону действия состояния уменьшают.

Это достигается в общем случае применением коммутирующего устройства, содержащего компаратор и аналоговые ключи. На вход компаратора поступает выходной сигнал ДО . Если сигнал по модулю становится больше уровня , меньшего, чем , то устройство изменяет структуру ЭСП, например, вводит дополнительную отрицательную обратную связь (ООС).

В простейшем случае может быть использована нелинейность характеристики диодов или стабилитронов для уменьшения крутизны сигнала, пропорционального ошибке ЭСП, при этом компаратор и аналоговые ключи не требуются.

Устройство, изменяющее структуру ЭСП, не входит в состав ДО, но, поскольку, его работа зависит от выходного сигнала ДО, то изменение состояний ДО и такого устройства будем рассматривать совместно, используя характеристики ДО, приведённые на рисунках 5 и 6.

4.1 Характеристики и условия переходов при использовании ДО с тремя линейными зонами

В рассматриваемом случае характеристика , изображённая на рисунке 5, состоит из одиннадцати участков: линейные участки - , - , участки насыщения - и - , линейные участки - , - , - , участки насыщения - и - , линейные участки - , - .

Соответствующим состояниям дадим условные обозначения: , , , , , , , , , , .

Для состояний , , , уравнения характеристик ДО совпадают с уравнениями характеристик, приведённых в подразделе 3.1 для соответственно состояний , , , . Уравнения характеристик остальных состояний совпадают с уравнениями для одноимённых состояний подраздела 3.1.

Условия переходов между состояниями , , , , , , , , , , :

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и ,

переход -

и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и и ,

переход -

и ,

переход -

и ,

переход -

и и ,

переход -

и и .

переход -

и и ,

переход -

и и .

В приведённых неравенствах , и - допустимые абсолютные погрешности функций , при переходах.

4.1 Характеристики и условия переходов при использовании ДО с одной линейной зоной

В случае применения устройства, изменяющего структуру ЭСП в зависимости от выходного сигнала ДО с одной линейной зоной, их совместная характеристика (рисунок 6) состоит из пяти участков: участок насыщения - , линейные участки - , - , - , участок насыщения - .

Соответствующим состояниям дадим условные обозначения , , , , .

Для состояний , , уравнения характеристик ДО совпадают с уравнениями характеристик, приведённых в подразделе 3.2 для состояния . Уравнения характеристик остальных состояний совпадают с уравнениями для одноимённых состояний подраздела 3.2.

Условия переходов между состояниями , , , , :

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и .

5 Состояния с ограничением тока ИД

Обмотка применяемых в ЭСП ИД в большинстве случаев имеет малое активное сопротивление, поэтому при пуске и торможении необходимо ограничивать величину тока ИД. Исключение представляют асинхронные двухфазные управляемые ИД, их обмотка управления имеет сравнительно большое сопротивление, поэтому ограничения тока не требуется. Такие ИД имеют малый кпд, они выпускаются на небольшие мощности.

Рассмотрим два варианта ограничения тока: перевод ИД в режим противовключения и перевод ИД в режим динамического торможения.

По эффективности ограничения тока оба варианта равноценны. В реализации второй вариант несколько проще.

5.1 Ограничение тока переводом ИД в режим противовключения

Принцип ограничения тока поясним с помощью рисунка 7.

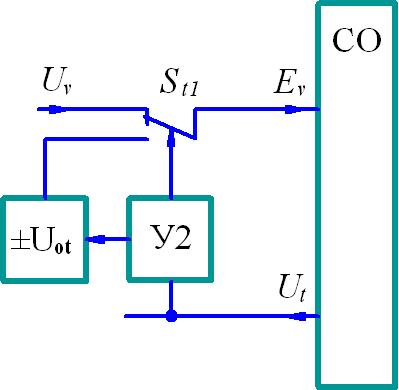
Рисунок 7. Схема ограничения тока переводом ИД в режим противовключения

В состав ЭСП входит коммутирующее устройство У2, содержащее компаратор. На вход У2 поступает сигнал , пропорциональный току ИД. При достижении током установленной предельной величины коммутирующее устройство У2 с помощью аналогового ключа отключает от входа УМ управляющий входной сигнал и подключает входной сигнал + или минус . Полярность входного сигнала такова, что приводит к уменьшению тока ИД. При достижении током другой величины, несколько меньшей, чем предельная величина, управление УМ от сигнала восстанавливается.

В общем случае ограничение тока проявляется в многократном срабатывании коммутирующего устройства У2.

Таким образом, по отсутствию или наличию ограничения тока ЭСП имеет три состояния: ограничение тока отсутствует, действует ограничение отрицательного значения тока, действует ограничение положительного значения тока. Присвоим этим состояниям условные обозначения , , .

Предполагается, что величина сигнала задана достаточно большой, чтобы перевести УМ в режим насыщения напряжения. Тогда в состоянии цепь УМ и обмотки ИД описывается уравнениями (1-10), (1-11), а в состоянии - уравнениями (1-8), (1-9).

Предполагается также, что после выхода из режима ограничения тока цепь УМ и обмотки ИД возвращается к тому состоянию, которое было до перехода к режиму ограничения тока.

Переходы между состояниями отсутствия или наличия ограничения тока:

переход -

и ,

переход -

и ,

переход -

и ,

переход -

и .

В приведённых неравенствах , и - соответственно верхнее предельное значение ограничения тока, нижнее предельное значение ограничения тока и допустимая абсолютная погрешность функции при переходах.

5.2 Ограничение тока переводом ИД в режим динамического торможения

Принцип ограничения тока поясним с помощью рисунка 8. Сигнал поступает на вход УМ с выхода предварительного инвертирующего усилителя, выполненного на операционном усилителе .В состав ЭСП входит коммутирующее устройство У2, содержащее компаратор. На вход У2 поступает сигнал , пропорциональный току ИД. При достижении током установленной предельной величины коммутирующее устройство У2 с помощью аналогового ключа отключает сигналы, ранее поступавшие на вход предварительного усилителя через резисторы , и подключает сигнал отрицательной обратной связи по току, поступающий через резистор . В результате происходит уменьшение величины тока. При достижении током другой величины, несколько меньшей, чем предельная величина, управление предварительного усилителя восстанавливается.

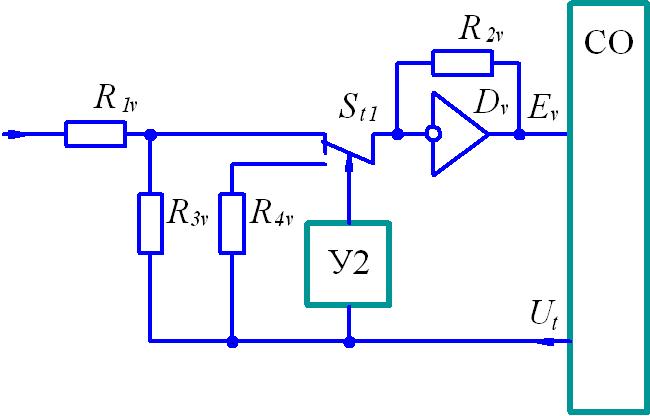
Рисунок 7. Схема ограничения тока переводом ИД в режим динамического торможения

Как и в подразделе 5.1, ограничение тока в общем случае проявляется в многократном срабатывании коммутирующего устройства У2.

Таким образом, по отсутствию или наличию ограничения тока ЭСП имеет два состояния: ограничение тока отсутствует, и ограничение тока действует. Присвоим этим состояниям условные обозначения , .

Переход в режим ограничения тока влияет на уравнения состояний , , на состояние цепи УМ и на переходы между состояниями цепи УМ, рассмотренными в разделе 1.

Уравнение токов на входе предварительного усилителя запишем в виде:

откуда

Подставим это выражение в (1-4)…(1-7).

. (5-1)

. (5-2)

Уравнения (5-1), (5-2), взятые со знаком «+» перед последним членом, действительны для состояния , уравнения (5-1), (5-2), взятые со знаком «–» перед последним членом, действительны для состояния .

Введём фиктивное выходное напряжение УМ при ограничении тока ЭСП . Фиктивное выходное напряжение УМ представляет собой выходное напряжение УМ в условиях действия ограничения тока ЭСП при отсутствии зоны нечувствительности и ограничения выходного напряжения:

. (5-3)

Это напряжение используется для определения состояния УМ при переходе к режиму ограничения тока ЭСП. В режиме ограничения тока ЭСП при определении условий перехода между состояниями УМ, приведёнными в разделе 1, взамен напряжения также следует использовать напряжение .

Уравнение (5-3) действительно для всех состояний УМ.

Переходы между состояниями отсутствия или наличия ограничения тока:

переход - ,

и и ,

переход - ,

и и ,

переход - ,

и и ,

переход - ,

и и .

СПИСОК ЛИТЕРАТУРЫ

1 Панарин Г. М. Расчёт динамических характеристик систем управления с применением операционного метода решения дифференциальных уравнений. http://www.twirpx.com/files/automation/tau/ft.article/

2 Динамика электромашинных следящих систем. М., «Энергия». 1967. 408 с. Авт.: Е. С. Блейз, Ю. Н. Семёнов, Б. К. Чемоданов, Н. М. Якименко.

3 Савельев И. В. Курс общей физики: Учебное пособие. Т.1. Механика. Scask.ru.

PAGE 1

РАСЧЁТ ДИНАМИЧЕСКИХ ХАРАКТЕРИСТИК ЭЛЕКТРИЧЕСКИХ СЛЕДЯЩИХ ПРИВОДОВ С ПРИМЕНЕНИЕМ ОПЕРАЦИОННОГО МЕТОДА РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ