Машинная модель взволнованной водной поверхности и её обратного отражения разработанного ЭВМ

Курсовая работа

Введение

Важным этапом в разработке эффективных алгоритмов дистанционного мониторинга параметров взволнованной морской поверхности является исследование особенностей формирования пространственно-временной структуры отраженных полей декаметрового радиодиапазона и статистических характеристик радиолокационных отражений.

Для успешного решения основной задачи – выявления новых информативных признаков рассеянного сигнала позволяющих повысить точность измерений спектральных характеристик морского волнения необходимо провести ряд натурных экспериментов по зондированию поверхности моря с борта летательного аппарата. Такие натурные эксперименты чрезвычайно дорогостоящие мероприятия, а в связи со стремительным развитием вычислительной техники, им появилась хорошая альтернатива – моделирование. В связи с этим было выбрано направление по созданию адекватной математической модели рассеяния электромагнитных волн протяженными шероховатыми поверхностями.

Решение обратной задачи рассеяния электромагнитных волн шероховатой поверхностью сводится к определению комплексной амплитуды отраженного поля. Ряд приближенных методов определения поля, основываются на решении интегральных уравнений Максвелла. Такое решение получено Кирхгофом и является строгой математической формулировкой принципа Гюйгенса-Кирхгофа, согласно которому каждая точка, в которой возбуждается электромагнитное поле, может рассматриваться как источник вторичной сферической волны. Однако, извлечение и анализ таких данных осложняется тем, что рассеивающие свойства объекта локации зависят от ряда факторов, меняющихся в широких пределах.

Использование в качестве зондирующих сигналов, сигналов со сложным спектральным составом (сверхширокополосных (СШП) сигналов, сигналов с внутриимпульсной модуляцией и т.д.), позволяет повысить разрешающую способность по пространственным координатам.

Феноменологическая модель рассеяния ЭМВ протяженной поверхностью
1. Дискретное представление протяженной поверхности

В качестве протяженной поверхности будем рассматривать морскую поверхность. Сложную волновую поверхность в промежутке квазистационарности и на участке квазиоднородности, можно представить моделью Лонге-Хиггинса []

где al - амплитуда элементарной плоской волны; l - начальная фаза элементарной волны, распределенная равномерно в интервале [–; ].

Согласно такой модели морская поверхность – есть линейная суперпозиция плоских поверхностных волн, имеющих различные амплитуды, частоты, направления распространения относительно главного направления распространения морских волн и случайные начальные фазы.

Каждая элементарная волна подчиняется всем законам классической гидродинамики.

Амплитуды плоских волн определяются двумерным энергетическим спектром волнения , приращениями волновых чисел и направлений

В качестве частотного спектра будем использовать спектр В. Пирсона и Л. Мошковица, рекомендованный международной конференцией опытных бассейнов в качестве стандартного.

;;;,

где V – скорость ветра.

Для построения реализации квазипериодической поверхности удобно оперировать частотным спектром, выраженным в длинах волн . Тогда выражение (1.1) можно записать в следующей форме

Фрагмент реализации поверхностной волны, рассчитанная с использованием выражения , приведен на (вид сверху) и на (изометрическая проекция). На стрелкой показано направление главного распространения, пунктиром – фронт распространения волн. Реализация получена для скорости ветра 6 м/с и направления главного распространения 0=30.

рис. .

Однако для оценки адекватности динамической РЛХ необходимо иметь априорно известный энергетический частотно-направленный спектр. В качестве такого «эталонного» энергетического спектра волнения будем рассматривать спектр имеющий Гауссову огибающую частотного спектра.

где 0 – центральная длина волны; – ширина спектра по уровню 0,707; – параметрическое решение уравнения .

Фрагмент реализации поверхностной волны, рассчитанная с использованием выражения и , приведен на (вид сверху) и на (изометрическая проекция). На стрелкой показано направление главного распространения, пунктиром – фронт распространения волн.

рис. .

Динамическая импульсная характеристика отражения поверхности

Известно, что сверхширокополосные РЛХ являются наиболее общей характеристикой объекта радиолокации. Подобные характеристики могут быть получены как отклик цели на тестовое сверхширокополосное воздействие – функцию Дирака (t) [, ]. Таким образом, импульсная характеристика представляет собой поле, рассеянное объектом при падении сферической монохроматической волны единичной амплитуды. На практике формирование тестового сигнала вида (t) практически не осуществимо, поэтому необходимо изыскивать возможности описания сверхширокополосных РЛХ адекватно используемому зондирующему сигналу. Это означает, что сверхширокополосные РЛХ должны быть определены в диапазоне частот большим или равным ширине спектра воздействия. В этом случае, речь идет о так называемой «сглаженной» импульсной характеристики [, ].

Таким образом, длительность тестового импульса для получения сглаженной импульсной характеристики определяется минимальным интервалом дискретизации зондирующего сигнала T выбранного согласно теореме Котельникова. Таким образом, для получения адекватной сглаженной импульсной характеристики необходимо чтобы частота ее дискретизации была равна или превышала удвоенную максимальную частоту в спектре предполагаемого зондирующего сигнала.

Передающая система излучает зондирующий сигнал, который представляет прямоугольный импульсный сигнал единичной амплитуды с длительностью T. Пространственно-избирательные характеристики передающей системы Fr пока принимать во внимание не будем, частотно-избирательные характеристики передающей системы в данном случае не учитываются. Т.е. излучающая система не вносит искажений в амплитудный и фазовый спектр зондирующего сигнала а, следовательно, не искажает его форму. Излучаемая сферическая волна имеет два фронта соответствующие переднему и заднему фронту зондирующего импульса. Таким образом, интервал наклонных дальностей R=cT, будет определять участок отражения поверхности в конкретный момент времени (см. ).

По мере распространения зондирующего сигнала в различные моменты времени будут освещаться различные участки поверхности. Не трудно представить, что на интервале участок отражения будет представлен окружностью, при участком отражения будет кольцо, по мере распространения радиус кольца будет увеличиваться, а его ширина уменьшаться.

рис. .

Отсечение поверхности реализовано на основе модифицированного для полярных координат алгоритма быстрого отсечения. Листинг алгоритма приведено ниже.

unit ISCUtilsUnit;

interface

uses

SysUtils, Math, Precisions, ErrorHandle;

// should be included in all units in project

{$I 'Defaults.inc'}

function CircleClipping (var x0, y0, x1, y1 : TFloatValue;

const Cx0, Cy0, R, DeltaR : TFloatValue) : Boolean;

// function clip two polar points and compute realated Cartesian coordinates

function ClipSample (var aR_0 : TFloatValue;

var aX_0 : TFloatValue;

var aY_0 : TFloatValue;

var aZ_0 : TFloatValue;

var aR_1 : TFloatValue;

var aX_1 : TFloatValue;

var aY_1 : TFloatValue;

var aZ_1 : TFloatValue;

const aSlantRange : TFloatValue;

const aSlantRangeDelta : TFloatValue;

const aHeight : TFloatValue;

const aCoordinateX : TFloatValue;

const aCoordinateY : TFloatValue

) : Boolean;

// returns distance between two spatial points

function GetDistance (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue) : TFloatValue;

// returns cosine of angle between tangent plane and triangle plane

// for more see

// "К построению 3х мерной ИХП (Форма тока на треугольнике - решение задачи).mcd"

function GetCosGamma (const A_triangle, B_triangle, C_triangle : TFloatValue;

const A_tangent, B_tangent, C_tangent : TFloatValue) : TFloatValue;

// compute plane coefficients A, B, C, D using three spatial points

// for more see

// "К построению 3х мерной ИХП (Форма тока на треугольнике - решение задачи).mcd"

procedure GetPlaneCoef (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue;

const x2, y2, z2 : TFloatValue;

var A_plane : TFloatValue;

var B_plane : TFloatValue;

var C_plane : TFloatValue;

var D_plane : TFloatValue

);

// returns area of triangle

function GetTriangleArea (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue;

const x2, y2, z2 : TFloatValue): TFloatValue;

// represent approximation of antenna pattern

function AntennaPatternApprox (

const aAlpha : TFloatValue; // azimuth

const aBeta : TFloatValue; // tilt angle

const aBeamWidth : TFloatValue // beam width on 0.5 level

) : TFloatValue;

implementation

function CircleClipping (var x0, y0, x1, y1 : TFloatValue;

const Cx0, Cy0, R, DeltaR : TFloatValue) : Boolean;

var

CC_x0, CC_y0, CC_x1, CC_y1,

sRange : TFloatValue;

Code, Visible : Byte;

////////////////////////////////////////////////////////////////////////////////

procedure Clip0_Top;

var

k, a, b, c, D,

sX, sY : TFloatValue;

begin

k := (CC_y1 - CC_y0)/(CC_x1 - CC_x0);

a := 1 + k*k;

b := 2*k*(CC_y0 - k*CC_x0 - Cy0) - 2*Cx0;

c := Cx0*Cx0 - R*R + SQR(CC_y0 - k*CC_x0 - Cy0);

D := b*b - 4*a*c;

sX := (-b + SQRT(D))/(2*a);

sy := k*(sX - CC_x0) + CC_y0;

CC_x0 := sX;

CC_y0 := sY;

end;

////////////////////////////////////////////////////////////////////////////////

procedure Clip0_Bottom;

var

k, a, b, c, D,

sX, sY : TFloatValue;

begin

k := (CC_y1 - CC_y0)/(CC_x1 - CC_x0);

a := 1 + k*k;

b := 2*k*(CC_y0 - k*CC_x0 - Cy0) - 2*Cx0;

c := Cx0*Cx0 - SQR(R + DeltaR) + SQR(CC_y0 - k*CC_x0 - Cy0);

D := b*b - 4*a*c;

if (D<0) then

begin

D := -D;

{$IFDEF DODEBUG}

ErrorHandle.WtiteToLog (sErrorLogFilePath,

Format ('Determinant is negative x0=%g, y0=%g, x1=%g, y1=%g; X0=%g, Y0=%g',

[CC_x0,CC_y0, CC_x1, CC_y1, Cx0, Cy0]));

{$ENDIF}

end;

sX := (-b - SQRT(D))/(2*a);

sy := k*(sX - CC_x0) + CC_y0;

CC_x0 := sX;

CC_y0 := sY;

end;

////////////////////////////////////////////////////////////////////////////////

procedure Clip1_Top;

var

k, a, b, c, D,

sX, sY : TFloatValue;

begin

k := (CC_y0 - CC_y1)/(CC_x0 - CC_x1);

a := 1 + k*k;

b := 2*k*(CC_y1 - k*CC_x1 - Cy0) - 2*Cx0;

c := Cx0*Cx0 - R*R + SQR(CC_y1 - k*CC_x1 - Cy0);

D := b*b - 4*a*c;

sX := (-b - SQRT(D))/(2*a);

sy := k*(sX - CC_x1) + CC_y1;

CC_x1 := sX;

CC_y1 := sY;

end;

////////////////////////////////////////////////////////////////////////////////

procedure Clip1_Bottom;

var

k, a, b, c, D,

sX, sY : TFloatValue;

begin

k := (CC_y0 - CC_y1)/(CC_x0 - CC_x1);

a := 1 + k*k;

b := 2*k*(CC_y1 - k*CC_x1 - Cy0) - 2*Cx0;

c := Cx0*Cx0 - SQR(R + DeltaR) + SQR(CC_y1 - k*CC_x1 - Cy0);

D := b*b - 4*a*c;

if (D<0) then

begin

D := -D;

{$IFDEF DODEBUG}

ErrorHandle.WtiteToLog (sErrorLogFilePath,

Format ('Determinant is negative x0=%g, y0=%g, x1=%g, y1=%g; X0=%g, Y0=%g',

[CC_x0,CC_y0, CC_x1, CC_y1, Cx0, Cy0]));

{$ENDIF}

end;

sX := (-b + SQRT(D))/(2*a);

sy := k*(sX - CC_x1) + CC_y1;

CC_x1 := sX;

CC_y1 := sY;

end;

////////////////////////////////////////////////////////////////////////////////

begin

Code := 0;

Visible := 0; // segment is invisible

Result := False;

CC_x0 := x0;

CC_y0 := y0;

CC_x1 := x1;

CC_y1 := y1;

// Code evaluation for segment

sRange := Hypot(Cx0 - CC_x1, Cy0 - CC_y1);

if sRange < R then Code := Code + 1 else

if sRange >= R + DeltaR then Code := Code + 2;

sRange := Hypot(Cx0 - CC_x0, Cy0 - CC_y0);

if sRange < R then Code := Code + 4 else

if sRange >= R + DeltaR then Code := Code + 8;

// direct clipping for all of 9 cases

case Code of

$00: inc(Visible);

$01: begin

Clip1_Top;

Inc(Visible);

end;

$02: begin

Clip1_Bottom;

Inc(Visible);

end;

$04: begin

Clip0_Top;

Inc(Visible);

end;

$05: Exit; // skipped

$06: begin

Clip0_Top;

Clip1_Bottom;

Inc(Visible);

end;

$08: begin

Clip0_Bottom;

Inc(Visible);

end;

$09: begin

Clip0_Bottom;

Clip1_Top;

Inc(Visible);

end;

$0A: Exit; // skipped

else

HandleError ('{07A7DBA4-FFFA-4A45-A112-2E73C38E7613}', 'Wrong circle clipping code!');

end;

if Visible > 0 then

begin

x0 := CC_x0;

y0 := CC_y0;

x1 := CC_x1;

y1 := CC_y1;

Result := True;

end;

function ClipSample (var aR_0 : TFloatValue;

var aX_0 : TFloatValue;

var aY_0 : TFloatValue;

var aZ_0 : TFloatValue;

var aR_1 : TFloatValue;

var aX_1 : TFloatValue;

var aY_1 : TFloatValue;

var aZ_1 : TFloatValue;

const aSlantRange : TFloatValue;

const aSlantRangeDelta : TFloatValue;

const aHeight : TFloatValue;

const aCoordinateX : TFloatValue;

const aCoordinateY : TFloatValue

) : Boolean;

var

tmpR_0 : TFloatValue;

tmpR_1 : TFloatValue;

tmpK_0 : TFloatValue;

tmpK_1 : TFloatValue;

begin

tmpR_0 := aR_0;

tmpR_1 := aR_1;

Result := CircleClipping (aR_0, aZ_0, // first radial point

aR_1, aZ_1, // second radial point

0, aHeight, // relative carrier coordinats

aSlantRange,

aSlantRangeDelta

);

if Result then

begin

if tmpR_0 <> 0 then

tmpK_0 := aR_0/tmpR_0

else

tmpK_0 := 1;

tmpK_1 := aR_1/tmpR_1;

aX_0 := aCoordinateX + (aX_0 - aCoordinateX) * tmpK_0; // similar triangles

aY_0 := aCoordinateY + (aY_0 - aCoordinateY) * tmpK_0; // similar triangles

aX_1 := aCoordinateX + (aX_1 - aCoordinateX) * tmpK_1; // similar triangles

aY_1 := aCoordinateY + (aY_1 - aCoordinateY) * tmpK_1; // similar triangles

end;

function GetDistance (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue) : TFloatValue;

begin

Result := SQRT (SQR(x1 - x0) + SQR(y1 - y0) + SQR(z1 - z0));

end;

function GetCosGamma (const A_triangle, B_triangle, C_triangle : TFloatValue;

const A_tangent, B_tangent, C_tangent : TFloatValue) : TFloatValue;

begin

Result := (

A_triangle * A_tangent

B_triangle * B_tangent

C_triangle * C_tangent

)

SQRT(

(

A_triangle * A_triangle

B_triangle * B_triangle

C_triangle * C_triangle

)

(

A_tangent * A_tangent

B_tangent * B_tangent

C_tangent * C_tangent

)

);

end;

procedure GetPlaneCoef (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue;

const x2, y2, z2 : TFloatValue;

var A_plane : TFloatValue;

var B_plane : TFloatValue;

var C_plane : TFloatValue;

var D_plane : TFloatValue

);

begin

A_plane := (y1 - y0)*(z2 - z0) - (z1 - z0)*(y2 - y0);

B_plane := (z1 - z0)*(x2 - x0) - (x1 - x0)*(z2 - z0);

C_plane := (x1 - x0)*(y2 - y0) - (y1 - y0)*(x2 - x0);

D_plane := - (x0*A_plane + y0*B_plane + z0*C_plane);

end;

function GetTriangleArea (const x0, y0, z0 : TFloatValue;

const x1, y1, z1 : TFloatValue;

const x2, y2, z2 : TFloatValue): TFloatValue;

var

a, b : TFloatValue;

CosPhi : TFloatValue;

begin

a := GetDistance (x0, y0, z0,

x1, y1, z1);

b := GetDistance (x0, y0, z0,

x2, y2, z2);

// see "К построению 3х мерной ИХП (Форма тока на треугольнике - решение задачи).mcd"

CosPhi := GetCosGamma (x1 - x0, // l1

y1 - y0, // m1

z1 - z0, // n1

x2 - x0, // l2

y2 - y0, // m2

z2 - z0 // n2

);

Result := 0.5*ABS (a*b

SQRT (1 - CosPhi*CosPhi) // sine Phi

);

end;

function AntennaPatternApprox (

const aAlpha : TFloatValue; // azimuth

const aBeta : TFloatValue; // tilt angle

const aBeamWidth : TFloatValue // beam width on 0.5 level

) : TFloatValue;

begin

Result := exp (

-1.38 * (

aAlpha*aAlpha +

aBeta*aBeta

(aBeamWidth*aBeamWidth)

);

end;

end.

Известно, что подобный алгоритм имеет линейную временную сложность. Применение алгоритма быстрого отсечения позволяет получить объем разрешения , а также рассматривать поверхность в виде непрерывной функции.

Сглаженная импульсная характеристика отражения подстилающей поверхности есть временная зависимость напряжения в согласованной нагрузке приемной антенны, как реакции поверхности на излученный тестовый импульс [].

где N – общее количество ЭО участка отражения в объеме разрешения ; – напряжение в согласованной нагрузке приемной антенны, полученное от воздействия i-го ЭО; (х) - функция Дирака.

Используя выражение была рассчитана импульсная характеристика отражения морской поверхности, сплошная линия см. , . На , пунктиром представлена импульсная характеристика отражения, рассчитанная по аналитическим выражениям. Графики представлены в относительных задержках.

рис. .

Из приведенных графиков видно, что результат моделирования хорошо согласуется с аналитическим расчетом.

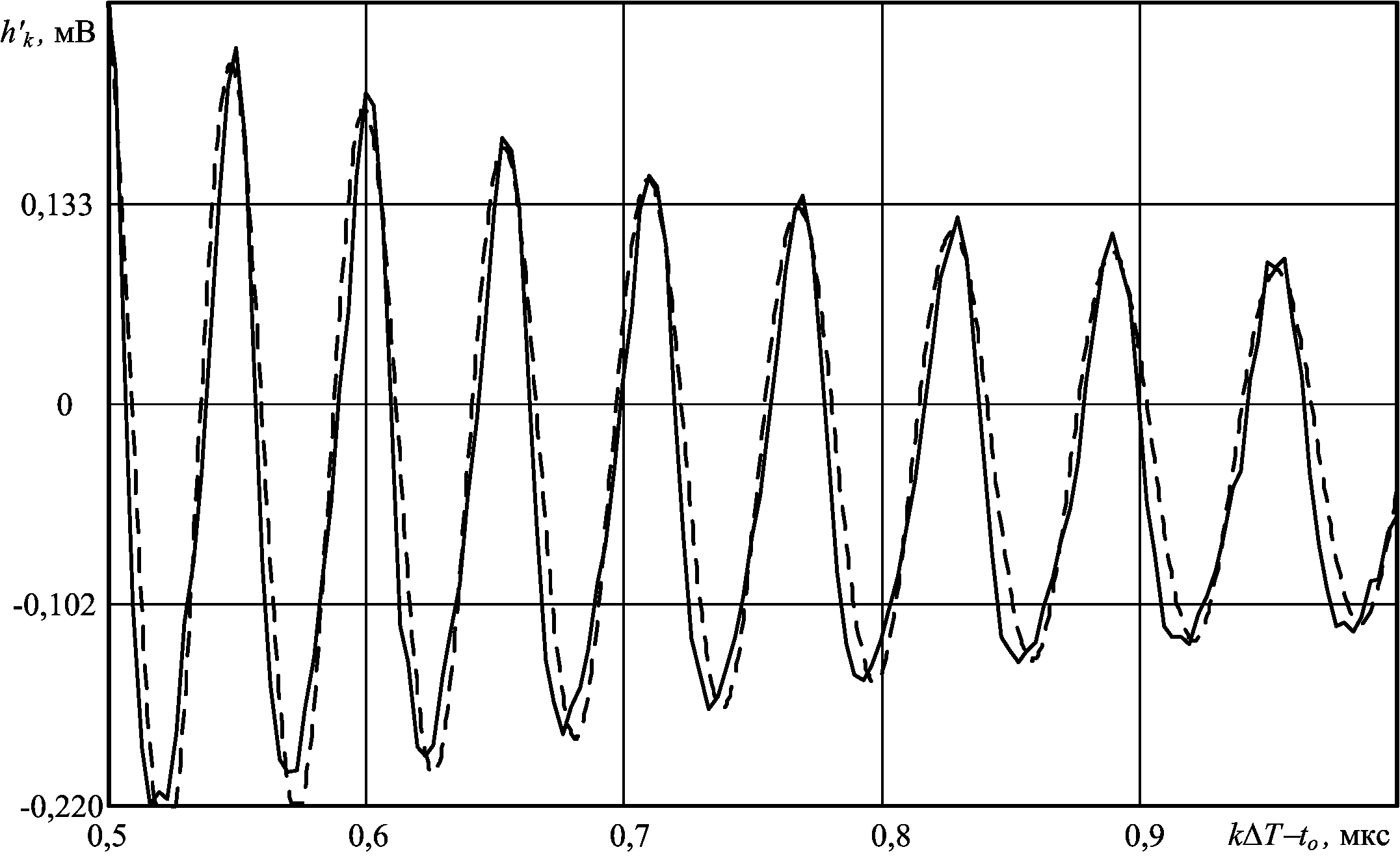
рис. .

Отсчеты отраженного от поверхности сигнала будем искать в виде дискретной свертки отсчетов импульсной характеристики и зондирующего сигнала

где N – количество отсчетов сглаженной импульсной характеристики отражения поверхности.

Отчеты сигнала представлены следующей общей записью:

где Ak – отсчеты амплитуды зондирующего сигнала; k – отсчеты круговой частоты; k – отсчеты фазы.

Листинг программы получения отчетов зондирующего сигнала приведен ниже.

unit SignalUnit;

interface

uses

Windows, Messages, SysUtils, Precisions, Math, ErrorHandle, XpDOM,

ModuleHandleUnit, ThreadPoolHandle, CommonUtils, MathUtils, DataStorageUnit,

FFTUnit, ISCUnit, MiscellaneousUnit;

// should be included in all units in project

{$I 'Defaults.inc'}

{$I '..\StrConst.inc'}

resourcestring

rsComputeMaxBandFrequencyError = 'The following error occurred while computing '+

'maximum band frequency';

rsComputeSignalSampleError = 'The following error occurred while processing %d sample with'+#13+

'signal kind "%s"';

type

TSignalKind = (stSimpleImpulse, stLFM, stOptimum);

pOptimumParams = ^TOptimumParams;

TOptimumParams = record

CarrierFrequency : TFloatValue;

CarrierHeight : TFloatValue;

SpectrumCentralWaveLenght : TFloatValue;

end;

// Class TSignal implements probe signal

TSignal = class (TCustomModule, IDataTimeDomain, IDataFreqDomain,

ISignalDataOut, IOpimalFilterFreqDomain)

private

// inner all model parameters.

// should only be used as a data storage.

// all parameters involved in computations

// should have an alias, i.e.

// tmpNodes := FxmlParameters.DocumentElement.SelectNodes ('XPath string');

// tmpNode := tmpNodes.Item(0).Attributes.GetNamedItem('Attribute name');

// FAlias := tmpNode.NodeValue;

// ...

// FAlias := FAlias + SQR(FAlias) - Power (FAlias, 5);

//---------------------------------------

// Alias definitions

//---------------------------------------

SignalKind : TSignalKind; // Signal Type to use

Height : TFloatValue; //Carrier Height

PulseDuration : TFloatValue; // Duration of signal

CarrierFrequency : TFloatValue; // Carrier Frequency of signal

FrequencyDeviation : TFloatValue; // FM Deviation of signal

OptimumCarrierHeight : TFloatValue; // Carrier Height for optimum signal

OptimumSurfaceWaveLenght : TFloatValue; // WaveLenght in Surface Spectrum

// for optimum signal

Amplitude : TFloatValue; // Signal Amplitude

InitialPhase : TFloatValue; // Infill Initial Phase

MaxBandFrequency : TFloatValue; // Maximal Frequency in probe signal

// spectrum (мы препарируем импульсную хар-ку

// под наш диапазон, определяемый максимальной

// частотой в спектре зондирующего сигнала)

ObservationPeriod : TFloatValue; // Observation Period

SamplesPerPeriod : TFloatValue; // Quantity of samples per Signal Wave period

AbsoluteTimeDelay : Boolean; // Show Absolute or Relative (t=t-2*H/c) delays

AdjustTimeDelay : Boolean; // Correct time delay for optimum signal

//---------------------------------------

// End of alias definitions

//---------------------------------------

TimeDiscrete : TFloatValue; // Time discrete of signal

SamplesCount : TIntValue; // Count of spatial intervals

Samples2NCount : TIntValue; // Count of spatial intervals

// closest to 2^N, needed for DFFT

SignalSamples : TFloat2DData; // alias of Signal data

EnvelopeSamples : TFloat2DData; // alias of signal envelope data

AmplitudeSamples : TFloat2DData; // alias of signal amplitude data

// optimum signal only

PhaseSamples : TFloat2DData; // alias of signal phase data

// optimum signal only

FilterPhaseSamples : TFloat2DData; // alias of filter phase data

// optimum signal only

procedure PrepareData (const aOwnerThread : IPooledThread; aData : Pointer);

procedure ComputeSamples (const aOwnerThread : IPooledThread; aData : Pointer);

function GetSamples : TFloat2DData; stdcall;

function GetAmplitudeSamples : TFloat2DData; stdcall;

function GetPhaseSamples : TFloat2DData; stdcall;

function GetFilterPhaseSamples : TFloat2DData; stdcall;

function IDataFreqDomain.GetAmplitudeSamples = GetAmplitudeSamples;

function IDataFreqDomain.GetPhaseSamples = GetPhaseSamples;

function IOpimalFilterFreqDomain.GetAmplitudeSamples = GetAmplitudeSamples;

function IOpimalFilterFreqDomain.GetPhaseSamples = GetFilterPhaseSamples;

function GetMaxBandFrequency : TFloatValue; stdcall;

protected

procedure DoAccomplish; override;

public

procedure RenewParameters; override;

procedure Execute; override;

end;

implementation

function FrequencyToTimeDelay (AbscissValue : TFloatValue; Data : TIntValue): TFloatValue;

var

a, b : TFloatValue;

begin

with pOptimumParams (Data)^ do

begin

b := 2*CarrierHeight/c;

a := c*pi/SpectrumCentralWaveLenght;

Result :=b/Sqrt(1-Sqr(a/(2*pi*AbscissValue)));

end;

function OptimumDeviation (AbscissValue : TFloatValue; Data : TIntValue): TFloatValue;

begin

with pOptimumParams (Data)^ do

Result := FrequencyToTimeDelay (CarrierFrequency - AbscissValue/2, Data) -

FrequencyToTimeDelay (CarrierFrequency + AbscissValue/2, Data);

end;

{TSignal}

procedure TSignal.RenewParameters;

begin

inherited RenewParameters;

if not Assigned (Parameters) then

begin

HandleError ('{8CAE3FF9-8576-452F-9472-B8215DAE429D}', 'Parameters object is not assigned');

Exit;

end;

SignalKind := TSignalKind (GetIntegerParameter (Parameters, 'Signal',

'SignalKind', 0));

Height := GetFloatParameter (Parameters, 'Carrier', 'Height', 0);

PulseDuration := GetFloatParameter (Parameters, 'Signal', 'PulseDuration', 0);

CarrierFrequency := GetFloatParameter (Parameters, 'Signal',

'CarrierFrequency', 0);

FrequencyDeviation := GetFloatParameter (Parameters, 'Signal',

'FrequencyDeviation', 0);

OptimumCarrierHeight := GetFloatParameter (Parameters, 'Signal',

'OptimumCarrierHeight', 0);

OptimumSurfaceWaveLenght := GetFloatParameter (Parameters, 'Signal',

'OptimumSurfaceWaveLenght', 0);

Amplitude := GetFloatParameter (Parameters, 'Signal',

'Amplitude', 0);

InitialPhase := GetIntegerParameter (Parameters, 'Signal',

'InitialPhase', 0)*pi/180;

MaxBandFrequency := GetFloatParameter (Parameters, 'Signal',

'MaxBandFrequency', 0);

ObservationPeriod := GetFloatParameter (Parameters, 'Signal',

'ObservationPeriod', 0);

SamplesPerPeriod := GetIntegerParameter (Parameters, 'Signal',

'SamplesPerPeriod', 0);

AbsoluteTimeDelay := Boolean(GetIntegerParameter (Parameters, 'Signal',

'AbsoluteTimeDelay', 0));

AdjustTimeDelay := Boolean(GetIntegerParameter (Parameters, 'Signal',

'AdjustTimeDelay', 0));

end;

procedure TSignal.Execute;

begin

inherited Execute;

// disable graphs

SetGraphAccess (Self.Name, False);

// add initial task

ThreadPool.AddTask (PrepareData, nil, Name);

end;

procedure TSignal.PrepareData (const aOwnerThread : IPooledThread; aData : Pointer);

var

BandWidthParams : pOptimumParams;

PointsNumber : TIntValue;

Points : pCrossSectionPoints;

begin

FProgress := 0;

FTaskDescription := LoadStringRes (ModulesMatrix.UILocaleInstance, rsSignalInitialization);

aOwnerThread.Synchronize(DoProgress);

//---------------------------------------

// Start of procedure body

//---------------------------------------

// assign loaded parameters to local module variables

RenewParameters;

try

case SignalKind of

stSimpleImpulse :

MaxBandFrequency := CarrierFrequency;

stLFM :

MaxBandFrequency := CarrierFrequency + FrequencyDeviation/2;

stOptimum :

begin

GetMem (BandWidthParams, SizeOf (TOptimumParams));

ZeroMemory (BandWidthParams, SizeOf (TOptimumParams));

try

// assign parameters

BandWidthParams^.CarrierFrequency := CarrierFrequency;

BandWidthParams^.CarrierHeight := OptimumCarrierHeight;

BandWidthParams^.SpectrumCentralWaveLenght := OptimumSurfaceWaveLenght;

// get cross points

Points := nil;

PointsNumber := GetCrossSectionPoints (0,

2*(CarrierFrequency

- c/(2*OptimumSurfaceWaveLenght)

)

- 0.25e6, // see "Ширина спектра оптимального сигнала 22_11_02.mcd"

// maximum pulse duration should be less then 8 microsecond

0.25e6,

PulseDuration,

OptimumDeviation,

TIntValue (BandWidthParams),

Points);

try

if PointsNumber > 0 then

MaxBandFrequency := CarrierFrequency + Points^[0].X/2;

finally

FreeMem (Points, PointsNumber * SizeOf (TFloatPoint));

end;

finally

FreeMem (BandWidthParams, SizeOf (TOptimumParams));

end;

end; // end of case

except

HandleError ('{4BF27520-03B8-40DE-8533-94DA46F64897}', rsComputeMaxBandFrequencyError);

raise; // raise nested exeption

end;

// set MaxBandFrequency parameter

SetFloatParameter (Parameters, 'Signal', 'MaxBandFrequency', MaxBandFrequency);

//dT = 1/(Fmax*n)

TimeDiscrete := 1/(MaxBandFrequency * SamplesPerPeriod);

//N = T/dT

SamplesCount := Round(ObservationPeriod*(MaxBandFrequency * SamplesPerPeriod)) + 1;

Samples2NCount := 1 shl (Ceil(Log2(SamplesCount)));

if not Assigned (SignalSamples) then

begin

SignalSamples := TFloat2DData.Create (2, Samples2NCount);

SignalSamples.Comment := 'Signal samples';

OuterData.Add (SignalSamples);

end

else

SignalSamples.AllocateMemory (2, Samples2NCount);

// clear previous data

SignalSamples.Clear;

if not Assigned (EnvelopeSamples) then

begin

EnvelopeSamples := TFloat2DData.Create (2, Samples2NCount);

EnvelopeSamples.Comment := 'Envelope samples';

OuterData.Add (EnvelopeSamples);

end

else

EnvelopeSamples.AllocateMemory (2, Samples2NCount);

// clear previous data

EnvelopeSamples.Clear;

if not Assigned (AmplitudeSamples) then

begin

AmplitudeSamples := TFloat2DData.Create (2, Samples2NCount);

AmplitudeSamples.Comment := 'Amplitude samples';

OuterData.Add (AmplitudeSamples);

end

else

AmplitudeSamples.AllocateMemory (2, Samples2NCount);

// clear previous data

AmplitudeSamples.Clear;

if not Assigned (PhaseSamples) then

begin

PhaseSamples := TFloat2DData.Create (2, Samples2NCount);

PhaseSamples.Comment := 'Signal phase samples';

OuterData.Add (PhaseSamples);

end

else

PhaseSamples.AllocateMemory (2, Samples2NCount);

// clear previous data

PhaseSamples.Clear;

if not Assigned (FilterPhaseSamples) then

begin

FilterPhaseSamples := TFloat2DData.Create (2, Samples2NCount);

FilterPhaseSamples.Comment := 'Signal phase samples';

OuterData.Add (FilterPhaseSamples);

end

else

FilterPhaseSamples.AllocateMemory (2, Samples2NCount);

// clear previous data

FilterPhaseSamples.Clear;

//---------------------------------------

// End of procedure body

//---------------------------------------

// execute next task

ThreadPool.AddTask (ComputeSamples, nil, Name);

end;

procedure TSignal.ComputeSamples (const aOwnerThread : IPooledThread; aData : Pointer);

var

i : TIntValue;

T0 : TFloatValue;

Tadjust : TFloatValue;

BandWidthParams : pOptimumParams;

begin

case SignalKind of

stSimpleImpulse : //Simple Pulse Signal

begin

for i := 0 to Samples2NCount - 1 do

try

if (i >= 0) and (i*TimeDiscrete <= PulseDuration) then

begin

EnvelopeSamples.Value^[1,i] := Amplitude;

SignalSamples.Value^[1,i] := Amplitude * cos (2*pi*

CarrierFrequency

TimeDiscrete*i

InitialPhase);

end

else

begin

EnvelopeSamples.Value^[1,i] := 0;

SignalSamples.Value^[1,i] := 0;

end;

if AbsoluteTimeDelay then

begin

EnvelopeSamples.Value^[0,i] := TimeDiscrete*i + 2*Height/c;

SignalSamples.Value^[0,i] := EnvelopeSamples.Value^[0,i];

end

else

begin

EnvelopeSamples.Value^[0,i] := TimeDiscrete*i;

SignalSamples.Value^[0,i] := EnvelopeSamples.Value^[0,i];

end;

except

HandleError ('{BDEE41D8-D42F-4A5E-A12C-999510134D59}',

Format (

rsComputeSignalSampleError,

[

'simple impulse'

]

)

);

raise; // raise nested exeption

end; // end of for

ModulesMatrix.Module[ModuleID].NextGroupID := 1;

end;

stLFM : //LFM Signal

begin

for i := 0 to Samples2NCount - 1 do

try

if (i >= 0) and (i*TimeDiscrete <= PulseDuration) then

begin

EnvelopeSamples.Value^[1,i] := Amplitude;

SignalSamples.Value^[1,i] := Amplitude

* cos (

2*pi*

(

(CarrierFrequency - FrequencyDeviation/2)

* TimeDiscrete*i

+ (

FrequencyDeviation/PulseDuration

* Sqr(i*TimeDiscrete)

)/2

)

);

end

else

begin

EnvelopeSamples.Value^[1,i] := 0;

SignalSamples.Value^[1,i] := 0;

end;

if AbsoluteTimeDelay then

begin

EnvelopeSamples.Value^[0,i] := TimeDiscrete*i + 2*Height/c;

SignalSamples.Value^[0,i] := EnvelopeSamples.Value^[0,i];

end

else

begin

EnvelopeSamples.Value^[0,i] := TimeDiscrete*i;

SignalSamples.Value^[0,i] := EnvelopeSamples.Value^[0,i];

end;

except

HandleError ('{BDEE41D8-D42F-4A5E-A12C-999510134D59}',

Format (

rsComputeSignalSampleError,

[

'LFM signal'

]

)

);

raise; // raise nested exeption

end; // end of for

ModulesMatrix.Module[ModuleID].NextGroupID := 1;

end;

stOptimum : // Optimum Signal

begin

GetMem (BandWidthParams, SizeOf (TOptimumParams));

ZeroMemory (BandWidthParams, SizeOf (TOptimumParams));

try

BandWidthParams^.CarrierFrequency := CarrierFrequency;

BandWidthParams^.CarrierHeight := OptimumCarrierHeight;

BandWidthParams^.SpectrumCentralWaveLenght := OptimumSurfaceWaveLenght;

if AdjustTimeDelay then Tadjust := PulseDuration*1.5

else Tadjust := 0;

T0 := FrequencyToTimeDelay (CarrierFrequency, LongInt(BandWidthParams));

for i := 0 to Samples2NCount - 1 do

try

if (i/(TimeDiscrete * Samples2NCount) >=

CarrierFrequency -(MaxBandFrequency - CarrierFrequency)) and

(i/(TimeDiscrete * Samples2NCount) <= MaxBandFrequency) then

begin

AmplitudeSamples.Value^[1,i] := 2*pi*i

(c*TimeDiscrete * Samples2NCount)

Power (

1-Sqr(

c*2*pi/OptimumSurfaceWaveLenght

)

(

4* Sqr (

2*pi*i

(

TimeDiscrete

* Samples2NCount

)

3/4

);

PhaseSamples.Value^[1,i] := -2*pi*i

(TimeDiscrete*Samples2NCount)

(T0 + Tadjust)

OptimumCarrierHeight/c

* Sqrt (

4* Sqr (

2*pi*i

/ (

TimeDiscrete

Samples2NCount

)

- Sqr(

c*2*pi/OptimumSurfaceWaveLenght

)

);

FilterPhaseSamples.Value^[1,i] := -(-2*pi*i

(TimeDiscrete*Samples2NCount)

(T0)

OptimumCarrierHeight/c

* Sqrt (

4* Sqr (

2*pi*i

/ (

TimeDiscrete

Samples2NCount

)

- Sqr(

c*2*pi/OptimumSurfaceWaveLenght

)

));

end

else

if (i/(TimeDiscrete * Samples2NCount) >= 1/TimeDiscrete -

(CarrierFrequency +(MaxBandFrequency - CarrierFrequency))) and

(i/(TimeDiscrete * Samples2NCount) <= 1/TimeDiscrete -

(CarrierFrequency -(MaxBandFrequency - CarrierFrequency))) then

begin

AmplitudeSamples.Value^[1,i] := (

2*pi/TimeDiscrete

2*pi*i

(TimeDiscrete * Samples2NCount)

)/c

Power (

1-Sqr(

c*2*pi

OptimumSurfaceWaveLenght

)

(

4* Sqr (

2*pi/TimeDiscrete

2*pi*i

(

TimeDiscrete

Samples2NCount

)

3/4

);

PhaseSamples.Value^[1,i] := -(

2*pi/TimeDiscrete

2*pi*i/(TimeDiscrete*Samples2NCount)

)

(T0 + Tadjust)

+ OptimumCarrierHeight/c

* Sqrt (

4* Sqr (

2*pi/TimeDiscrete

2*pi*i

(

TimeDiscrete

Samples2NCount

)

- Sqr(

c*2*pi

OptimumSurfaceWaveLenght

)

);

FilterPhaseSamples.Value^[1,i] := (

2*pi/TimeDiscrete

2*pi*i/(TimeDiscrete*Samples2NCount)

)

(T0)

+ OptimumCarrierHeight/c

* Sqrt (

4* Sqr (

2*pi/TimeDiscrete

2*pi*i

(

TimeDiscrete

Samples2NCount

)

- Sqr(

c*2*pi

OptimumSurfaceWaveLenght

)

);

end

else

begin

AmplitudeSamples.Value^[1,i] := 0;

PhaseSamples.Value^[1,i] := 0;

end;

AmplitudeSamples.Value^[0,i] := i/(TimeDiscrete * Samples2NCount); // frequency

PhaseSamples.Value^[0,i] := AmplitudeSamples.Value^[0,i];

except

HandleError ('{BDEE41D8-D42F-4A5E-A12C-999510134D59}',

Format (

rsComputeSignalSampleError,

[

'Optimum signal'

]

)

);

raise; // raise nested exeption

end; // end of for

finally

FreeMem (BandWidthParams, SizeOf (TOptimumParams));

end;

ModulesMatrix.Module[ModuleID].NextGroupID := 2;

end;

end; // end of case

// execution of module is finished

aOwnerThread.Synchronize(DoAccomplish);

end;

function TSignal.GetSamples : TFloat2DData;

begin

Result := SignalSamples;

end;

function TSignal.GetAmplitudeSamples : TFloat2DData;

begin

Result := AmplitudeSamples;

end;

function TSignal.GetPhaseSamples : TFloat2DData;

begin

Result := PhaseSamples;

end;

function TSignal.GetFilterPhaseSamples : TFloat2DData;

begin

Result := FilterPhaseSamples;

end;

function TSignal.GetMaxBandFrequency : TFloatValue;

begin

Result := MaxBandFrequency;

end;

procedure TSignal.DoAccomplish;

begin

// enable graphs

SetGraphAccess (Self.Name, True);

inherited;

end;

end.

Проверка знаний
1. Какая модель энергетического спектра используется в работе:

Лапласа.	`Гаусса.
Фурье.	`Пирсона-Мошковица.

Чем определяется объем разрешения моноимпульсной радиолокационной системы:
1. `Шириной диаграммы направленности по азимуту.
2. `Длительностью зондирующего импульса.
3. Частотой Доплера.
4. `Шириной диаграммы направленности по углу места.
  1. Дайте определение импульсной характеристики:
есть реакция линейной стационарной системы на входное воздействие вида функции Хевисайда.
`есть реакция линейной стационарной системы на входное воздействие вида дельта-функция.
есть обратное преобразование Фурье от частотного коэффициента передачи по мощности.
есть прямое преобразование Фурье от комплексного частотного коэффициента передачи.
1. Как определить отклик линейной стационарной системы во временной области на входное воздействие зная ее импульсную характеристику:
`воспользоваться интегралом Дюамеля.
воспользоваться теоремой Винера-Хинчина.
`провести прямое преобразование Фурье импульсной характеристики и входного воздействия, полученные результаты перемножить и провести обратное преобразование Фурье.
провести обратное преобразование Фурье импульсной характеристики и входного воздействия, полученные результаты разделить и провести прямое преобразование Фурье.
Результаты моделирования рассеяния радиолокационных сигналов

Отраженный от поверхности сигнал имеет множество информативных параметров. К ним относятся начальная фаза высокочастотного заполнения, временная задержка отраженного сигнала, форма его огибающей и т.д. Наибольший интерес представляет исследование изменения формы огибающей отраженного сигнала по сравнению с излученной. Моделирование не накладывает каких либо ограничений на зондирующий сигнал. Это означает, что для исследования мы можем пользоваться любыми классами радиотехнических сигналов. В качестве зондирующего сигнала будем использовать простой импульсный радиосигнал и оптимально согласованный с поверхностью радиосигнал. Для выяснения основных устойчивых зависимостей между параметрами морской поверхности и параметрами огибающей рассеянного на этой поверхности сигнала, энергетический спектр поверхности будет состоять из единственной гармоники.

Зондирующий сигнал – простой импульсный радиосигнал

На - представлено семейство мощностных огибающих отраженного сигнала иллюстрирующих зависимость амплитуды некогерентной составляющей от высоты полета носителя. Первые 4 семейства представлены в абсолютных значениях и нормированных, последующие только в нормированных.

рис. .

На - представлено семейство мощностных огибающих отраженного сигнала иллюстрирующих зависимость амплитуды некогерентной составляющей от длины поверхностной волны. Семейства представлены в абсолютных значениях.

рис. .

На - представлено семейство мощностных огибающих отраженного сигнала иллюстрирующих зависимость амплитуды некогерентной составляющей от высоты поверхностной волны. Семейства представлены в абсолютных значениях.

рис. .

Из рисунков видно, что с возрастанием высоты волнения, растет и величина некогерентной составляющей в отраженном сигнале. Удобным оценочным параметром в данном случае является отношение некогерентной составляющей к когерентной. Такая оценка исключает влияние различных факторов (затухание в атмосфере, изменение коэффициента усиления приемного тракта, мощности передатчика и т.д.) на точность измерения, так как она является относительной.

Увеличение высоты полета уменьшает амплитуды обеих составляющих. Это связано с уменьшением энергии принимаемого сигнала. Однако следует отметить, что отношение между составляющими остается неизменным. Так как излучаемая волна является сферической, поэтому амплитуды отраженного сигнала пропорциональны 1/z0 . Как видно из графика, с уменьшением высоты полета носителя, уменьшается разрешающая способность составляющих по времени задержки.

Изменение длины поверхностной волны, рабочей длины волны, высоты полета, приводит к изменению временного положения некогерентного импульса относительно когерентного. Задержка между ними определяется следующим аналитическим выражением

Зондирующий сигнал – оптимально согласованный с поверхностью радиосигнал

На - представлено семейство мощностных огибающих отраженного сигнала иллюстрирующих зависимость амплитуды некогерентной составляющей от высоты полета носителя. Семейства представлены в нормированных величинах.

рис. .

Из графиков видно, что соотношения, отмеченные для зондирующего сигнала представленного простым радиосигналом, сохраняются и для оптимально согласованного зондирующего сигнала. Нужно отметить более высокую разрешающую способность составляющих по времени задержки, что в свою очередь позволяет решать задачу восстановления спектральных характеристик волнения неконтактным методом.

Список использованных источников

М.С. Лонге-Хиггинс. Статистический анализ случайно движущейся поверхности. // Ветровые волны. Под ред. Ю.М. Крылова. М.: Иностранная литература, 1962г. 218с.

. М.Е. Варганов, Ю.С. Зиновьев, Л.Ю. Астанин и др.; под ред. Л.Т. Тучкова, Радиолокационные характеристики летательных аппаратов, М., Радио и связь, 2005г., 236с.

. Е.А. Штагер, Рассеяние радиоволн на телах сложной формы, М., Радио и связь, 2006г., 184с.

. В.Т. Лобач, М.В. Потипак, Модельные исследования радиолокационного отражения сложных сигналов взволнованной морской поверхностью, Материалы 13 Международной Крымской конференции "СВЧ Техника и телекоммуникационные технологии" КрыМиКо'2013 стр.760-762.

. В.Т. Лобач, М.В. Потипак, Получение импульсной характеристики отражения морской поверхности средствами математического моделирования, Материалы XXIII Всероссийского симпозиума «Радиолокационное исследование природных сред» 2005 стр.103-110.

Машинная модель взволнованной водной поверхности и её обратного отражения разработанного ЭВМ