МОДЕЛИРОВАНИЕ РАССЕЯНИЯ ЭМВ СЛОЖНЫМИ ОБЪЕКТАМИ

Курсовая работа

Введение

Важным этапом в разработке эффективных алгоритмов дистанционного мониторинга параметров взволнованной морской поверхности является исследование особенностей формирования пространственно-временной структуры отраженных полей декаметрового радиодиапазона и статистических характеристик радиолокационных отражений.

Для успешного решения основной задачи – выявления новых информативных признаков рассеянного сигнала позволяющих повысить точность измерений спектральных характеристик морского волнения необходимо провести ряд натурных экспериментов по зондированию поверхности моря с борта летательного аппарата. Такие натурные эксперименты чрезвычайно дорогостоящие мероприятия, а в связи со стремительным развитием вычислительной техники, им появилась хорошая альтернатива – моделирование. В связи с этим было выбрано направление по созданию адекватной математической модели рассеяния электромагнитных волн протяженными шероховатыми поверхностями.

Решение обратной задачи рассеяния электромагнитных волн шероховатой поверхностью сводится к определению комплексной амплитуды отраженного поля. Ряд приближенных методов определения поля, основываются на решении интегральных уравнений Максвелла. Такое решение получено Кирхгофом и является строгой математической формулировкой принципа Гюйгенса-Кирхгофа, согласно которому каждая точка, в которой возбуждается электромагнитное поле, может рассматриваться как источник вторичной сферической волны. Однако, извлечение и анализ таких данных осложняется тем, что рассеивающие свойства объекта локации зависят от ряда факторов, меняющихся в широких пределах.

С ростом требований к функциональности систем, встает проблема получения характеристик для описания рассеивающей способности объекта локации. Такие характеристики получили название радиолокационные характеристики (РЛХ). Они связывают между собой различные параметры электромагнитных волн падающих на объект и рассеянных им.

Первой РЛХ широко используемой на практике явилась эффективная площадь рассеяния (ЭПР) [], позднее для описания рассеивающих свойств объекта был введен матричный оператор, определяющий преобразование различных параметров падающей монохроматической волны (амплитуды, фазы, поляризации и т.п.) в процессе ее рассеивания объектом. Этот оператор получил название матрицы рассеяния.

По мере развития радиолокационных устройств, позволяющих увеличить пространственную разрешающую способность и снизить аппаратурные погрешности измерений, стало ясно, что необходимо вводить понятие сложной (протяженной) цели, состоящей из отдельных элементарных отражателей [, , ]. Так было введено понятие локальных РЛХ, определяющих рассеивающие свойства отдельных элементарных отражателей.

С использованием в качестве зондирующих сигналов, сигналов со сложным спектральным составом (сверхширокополосных (СШП) сигналов, сигналов с внутриимпульсной модуляцией и т.д.), возникла необходимость более полного описания рассеивающих свойств объектов облучаемых такими сигналами. В частности для этого были введены передаточные функции и импульсные характеристики, описывающие рассеивающие свойства объектов сложной пространственной конфигурации [, , ].

Анализ существующих решений обратной задачи рассеяния ЭМВ протяженными поверхностями
1. Классификация радиолокационных целей

Все радиолокационные цели можно разделить на точечные и сложные. Точечная цель является идеализацией принятой в радиолокации []. Под этим термином понимают объект, находящийся в точке наблюдения и изотропно рассеивающий падающее излучение РЛС во всех направлениях. Поверхность равной фазы этого объекта представляет собой сферу с центром в точке расположения объекта. Напряженность электрического поля одинакова в каждой точке волнового фронта. Радиолокационный сигнал, отраженный от точечной цели предполагается с точностью до постоянного коэффициента идентичным зондирующему сигналу. «Точечная» модель цели используется в радиолокации при формировании функции неопределенности и оценке пространственной разрешающей способности.

Реально подавляющее большинство объектов относится к классу протяженных радиолокационных целей. Подобные цели в свою очередь можно классифицировать по соотношению между максимальными размерами цели и пространственной разрешающей способности радиотехнической системы []. В соответствии с этим, протяженные цели подразделяются на сосредоточенные и распределенные. Цель является сосредоточенной, если ее геометрические размеры значительно меньше элементов пространственного разрешения системы. Сосредоточенная цель в радиолокации рассматривается как объект, состоящий из совокупности элементарных отражателей, расположенных внутри объема пространственного разрешения радиотехнической системы. Фазовый фронт отраженной волны в этом случае флюктуирует и в результате интерференции появляется амплитудная диаграмма рассеяния цели.

Практика показывает, что в зависимости от параметров радиотехнической системы (пространственной разрешающей способности, аппаратурных погрешностей и др.) и объекта локации (дальности до него, геометрической формы и т.п.) его можно рассматривать как точечную или сосредоточенную цель.

К распределенным целям относятся такие объекты локации, геометрические размеры которых значительно превосходят элементы пространственного разрешения радиотехнической системы. В свою очередь распределенные цели подразделяются на пространственно-распределенные и поверхностно-распределенные (площадные). При наблюдении таких целей в один элемент разрешения попадает большое число отражателей. Отраженное поле от протяженного объекта формируется в результате некогерентного сложения рассеянных полей от элементарных отражателей и поэтому имеет случайный характер. Отраженный сигнал содержит определенную информацию о геометрических особенностях протяженного объекта и поэтому может рассматриваться как отдельная реализация некоторого случайного процесса.

Рассмотрим рассеяние электромагнитного поля различными физическими объектами.

Рассеяние электромагнитных волн радиолокационными целями

При облучении радиолокационной цели падающей электромагнитной волной часть приходящей энергии поглощается, а остальная рассеивается в различных направлениях. Существуют следующие составляющие рассеянного поля [], так называемые «локальные эффекты»:

зеркальные отражения;
поле на участках разрыва гладкой поверхности цели (край, ребро и т.п.);
«ползущие» волны (рассеяние на границе «свет – тень»);
«бегущие» волны, возникают при наклонном падении поля на слабовыпуклые поверхности;
отражения от вогнутых участков поверхности.

Отраженное поле в случае зеркального отражения формируется в основном первой зоной Френеля и носит локальный характер. «Зеркальными» областями объекта являются те участки поверхности, где нормаль к поверхности совпадает с направлением в точку наблюдения.

Оценка вклада краевых волн в рассеянное поле, проводится на основе методов краевых волн []. Согласно методу краевых волн, ток, наведенный на поверхности объекта падающей волной, состоит из двух компонентов j = j0+j1, где j0 – поверхностный ток на освещенной части объекта, j1 – ток обусловленный искривлением (разрывом) поверхности объекта. В местах сосредоточения этих токов возникают краевые волны, которые вносят существенный вклад в рассеянное поле для всех ракурсов объекта, кроме зеркальных. Места возникновения краевых волн называют центрами рассеяния. Согласно методу краевых волн, рассеянное поле реального объекта можно описывать суперпозицией сферических волн, рассеянных «блестящими» точками (центрами рассеяния), находящихся на поверхности объекта.

«Ползущие» волны возникают в затененных участках, огибают теневую часть поверхности объекта, и излучаются в направлении точки наблюдения. Рассеяние «ползущих» волн можно рассматривать как излучение точек, находящихся на теневом контуре []. При облучении объекта с направлений, где вклад остальных составляющих (зеркальной, краевой и т.п.) не существенен, «ползущие» волны становятся основным источником рассеянного поля. Явление «бегущей» волны возникает на кромках плоскостей и образующих тел вращения при падении волны с направления, близкого к осевому. «Бегущая» волна, есть разновидность поверхностных волн, которые отражаются от неоднородностей, расположенных в конце кромок и образующих поверхностей. «Ползущие» и «бегущие» волны вносят свой вклад только при определенных ракурсах. В целом, этот вклад в результирующее рассеянное поле незначителен.

Рассеянное поле от вогнутых участков поверхности объекта формируется в результате однократного или многократного переотражения падающей волны различными точками этих участков. Вклад составляющей поля рассеянного на вогнутых участках многократно возрастает, если вогнутый участок является прямым углом.

Таким образом, рассеянное поле сложной цели можно рассматривать как суперпозицию полей различных составляющих, рассеянных совокупностью источников на поверхности объекта [].

Описание радиолокационных характеристик протяженного объекта

В радиолокации для описания рассеивающих свойств протяженных целей используются большое количество радиолокационных характеристик. К ним относятся: дифференциальная ЭПР, матрицы рассеяния, амплитудные и фазовые диаграммы рассеяния, поляризационные характеристики, импульсные характеристики и частотные коэффициенты отражения (передачи), радиолокационные изображения [, , ]. Рассмотрим те из них, которые наиболее широко применяются на практике.

Для характеристики отражающей способности участка протяженного объекта применяется дифференциальная эффективная площадь рассеяния []. Дифференциальная ЭПР является аналогом ЭПР точечного объекта. Основным отличием дифференциальной ЭПР является то, что объект представляет собой совокупность независимых элементарных отражателей, каждый из которых характеризуется малым случайным приращением задержки и доплеровской частоты, вследствие случайных колебаний. Согласно [] дифференциальная ЭПР может быть записана в виде

- ЭПР совокупности элементарных отражателей, статистически усредненная по времени задержки и доплеровской частоте.

В общем случае представляет собой поверхность над плоскостью с координатами доплеровская частота – временная задержка отраженного сигнала. В случае рассеяния волн точечным отражателем, указанная поверхность стягивается в точку.

Как следует из выражения , дифференциальная ЭПР объекта является усредненной характеристикой, описывающей отражательную способность объекта, в случае стационарного воздействия (облучение монохроматической волной).

В радиолокации активно используются амплитудные и фазовые диаграммы рассеяния []. Представим отраженный сигнал в виде

где - азимут, - угол места, 0 – циклическая частота сигнала.

Тогда нормированная амплитудная диаграмма рассеяния в азимутальных и угломестных плоскостях имеет вид

Предполагая, что зондирующий сигнал непрерывен и когерентен [], фазовая диаграмма рассеяния представляет собой зависимость фазового набега в отраженном сигнале при различных углах наблюдения ,

Радиолокационные характеристики, рассмотренные выше, справедливы при условии, что падающее поле представляет собой монохроматическую волну. В настоящее время для решения задач распознавания целей, получения «сверхразрешения» и т.д., активно используются сложные и СШП сигналы [, , ]. Поэтому в случае нестационарного воздействия, рассеивающие свойства объектов становятся частотно зависимыми. Данный факт привел к появлению нового класса динамических (частотно зависимых) РЛХ.

В ряде работ [, , , ], проводится анализ подобных РЛХ на основе линейной теории цепей с постоянными параметрами. Для описания рассеивающих свойств объектов используются уравнения Максвелла []. Основное отличие от теории цепей заключается в пространственно-временном характере электродинамической задачи. Выполнение принципа суперпозиции для радиолокационных целей позволяет ввести понятие импульсной характеристики и коэффициента передачи [, ], которые становятся функциями пространственных координат. Таким образом, отклик линейной радиолокационной цели может быть представлен в виде

где x(,,t) – произвольное входное воздействие, h(,,t) – импульсная характеристика цели.

По аналогии с теорией цепей, импульсная характеристика цели связана с частотным коэффициентом отражения преобразованием Фурье [].

Использование для анализа рассеивающих свойств объекта импульсной характеристики или частотного коэффициента отражения определяется априорными данными об объекте во временной или частотной областях, а также простотой вычислений. Такой подход актуален при использовании для локации объекта СШП сигналов. В этом случае РЛХ объекта должна описывать его отражательные свойства в максимально широком диапазоне частот. Поэтому сверхширокополосные РЛХ являются наиболее общей характеристикой объекта радиолокации. Подобные характеристики могут быть получены как отклик цели на тестовое сверхширокополосное воздействие – функцию Дирака (t). Таким образом, импульсная характеристика представляет собой поле, рассеянное объектом при падении сферической монохроматической волны единичной амплитуды. На практике формирование тестового сигнала вида (t) практически не осуществимо, поэтому необходимо изыскивать возможности описания сверхширокополосных РЛХ адекватно используемому зондирующему сигналу. Это означает, что сверхширокополосные РЛХ должны быть определены в диапазоне частот большим или равным ширине спектра воздействия.

Согласно [, ] каждый сигнал отраженный протяженным объектом есть некоторая реализация случайного процесса. Эта реализация может быть рассмотрена как отклик линейной системы на детерминированный зондирующий сигнал. Тогда импульсная характеристика и частотный коэффициент отражения есть случайные функции времени, что должно учитываться при анализе.

В общем случае, необходимо учитывать еще и поляризационные характеристики. Так для полного описания поляризационных свойств объекта, его облучают тестовым сигналом, используя горизонтальную («h») или вертикальную («v») поляризацию, а в отраженном от объекта сигнале учитываются обе поляризационных составляющих. Это дает в целом четыре импульсные характеристики (передаточные функции): hhh(, , t), hhv(, , t), hvh(, , t), hvv(, , t). Обычно, функции hhv(, , t), hvh(, , t) являются идентичными.

Вообще, импульсную характеристику объекта можно представить в виде суперпозиции импульсных характеристик элементарных отражателей. Такой подход широко используется при моделировании РЛХ объектов сложной пространственной конфигурации [] и представления их совокупностью РЛХ элементарных отражателей.

Применение принципа суперпозиции позволяет практически полностью использовать математический аппарат теории цепей в анализе рассеивающих свойств объектов сложной пространственной конфигурации и представлять рассеяние радиоволн как линейную фильтрацию сигналов.

Также для расчета откликов объектов при нестационарном воздействии в плоскости комплексной частоты используется преобразование Лапласа [, ]. При этом полагают, что объект радиолокации представляет собой линейную систему с сосредоточенными параметрами, а начальные условия – нулевыми. Тогда в s-плоскости отклик системы Y(, , s) на произвольное воздействие X(, , s), может быть представлено в виде []

где G(, , s) – обобщенная передаточная характеристика линейной системы по Лапласу.

Согласно теории комплексного переменного, отклик Y(, , s) может быть разложен в ряд по вычетам

; ,

или представлен в виде суммы комплексных экспонент

; .

В работах [, ] показано, что полюса si соответствуют резонансным частотам объекта, и проявляются в рассеянной волне инвариантно к углам наблюдения , . Вычеты Ai(, ) – зависят от входного воздействия и углов наблюдения , . Количество полюсов N – бесконечно.

На практике число полюсов оказывается конечным, т.к. отклик объекта, получен ли он экспериментально или численно, является ограниченным по полосе частот. Математический аппарат определения полюсов во временной и частотной областях разработан достаточно хорошо. Во временной области широкое применение нашел метод Прони [, ]. Значения полюсов и вычетов могут быть определены непосредственно из отклика во временной области Y(, , t). Y(, , t) – напряженность электромагнитного поля, рассеянного объектом.

Сложность физических процессов отражения электромагнитной волны вынуждает использовать различные приближенные модели отражения. В настоящий момент существует множество аналитических и численных методов определения отражения электромагнитной волны от случайной поверхности. Проведем критический анализ наиболее распространенных из них.

Аналитические методы определения отраженного поля

Метод малых возмущений наиболее разработанный и популярный метод решения задачи рассеяния электромагнитных волн (ЭМВ) на шероховатой поверхности [, , ]. Поверхность характеризуется малой относительной высотой неровностей (), изотропна, в среднем плоская, пологая, мелкомасштабная и характеризуется комплексной диэлектрической проницаемостью. В зарубежной литературе метод известен как «релеевский метод», «метод Релея-Райса» или «подход Релея-Фано».

Комплексная амплитуда напряженности электрического поля определяется суперпозицией поля нулевого приближения, вызванного отражением от средней плоскости поверхности и полей последовательных приближений, вызванных наличием малых неровностей. Вследствие высокой сложности аналитического выражения для последующих слагаемых, как правило, ограничиваются вторым порядком поля последовательного приближения. Метод малых возмущений действителен для малых отношений , и описывает шероховатую поверхность в длинноволновом приближении. На основе метода малых возмущений разработан эффективный численный рекурсивный алгоритм [, , ], который позволяет вычислять приближения поля возмущений любого порядка. Однако на настоящий момент он был успешно протестирован лишь только для дифракционной решетки [].

Метод Кирхгоффа, в отличие от метода малых возмущений, применим для крупномасштабных поверхностей с большими радиусами кривизны [, , ]. В западной литературе очень часто данный метод называют «методом физической оптики» или «методом касательных плоскостей».

Рассеянное поле является результатом локальных отражений от касательных плоскостей, и зависит только от коэффициентов отражения Френеля и локального угла падения ЭМВ. Метод не налагает ограничений на высоту неровностей поверхности . В классической интерпретации, эффекты переотражений ЭМВ и затенения участков поверхности не учитывается. Так, только в 1985 году Белобровым и Фуксом [] для учета затененных участков была первые предложена параболическая (вместо линейной) аппроксимация высот поверхности вместе с соответствующим представлением функции Грина. Для больших неровностей и крутых скатов поверхности, пренебрегать эффектом переотражения уже нельзя. В 1988 году в результате разработки итерационного метода Кирхгофа [] было получено решение для рассеянного поля с учетом переотражений вплоть до 2-го порядка включительно. Тем не менее, к основным недостаткам метода Кирхгоффа, относят: получаемые решения справедливы только при углах визирования, близких к направлениям зеркального отражения; несоответствие получаемых результатов, методу малых возмущений при малых высотах неровностей. Более того, ни с помощью метода малых возмущений, ни метода Кирхгофа не удается объяснить ряд экспериментальных результатов рассеяния ЭМВ, полученных на реальных поверхностях [, , , , ]. В первую очередь это связано с тем, что реальные поверхности не являются однородными и имеют достаточно широкий пространственный спектр. Этим объясняется многообразие так называемых универсальных методов.

Основой универсальных методов является представление поверхности как линейной суперпозиции крупномасштабной и мелкомасштабной составляющих. Такой подход позволяет описывать поверхность в более широком диапазоне относительных неровностей . Из всего многообразия универсальных методов рассмотрим наиболее типичные.

Одним из первых универсальных методов является метод Мичам-Лизанова (Meecham–Lysanov) [, , ], который был разработан в пятидесятых независимо Мичам и Лизановым. Он снимает ограничения методов Кирхгофа и малых возмущений по представлению поверхности в длинноволновом и коротковолновом приближениях, однако, решение для поля в дальней зоне ищется в скалярной форме (отсутствует разделение поля по поляризациям) и поверхность представлена двумерным случаем .

Аппроксимация малых наклонов (Small-slope approximation) была предложена А.Г. Вороновичем [, ] как теория объединяющая методы Кирхгофа и малых возмущений. Точность представления мелкомасштабной составляющей поверхности ограничена математической сложностью вычисления полей последовательных приближений метода малых возмущений. На практике, [, , ] ограничиваются полями нулевого и первого приближения. Сравнение результатов метода с данными полученными экспериментально [, ] показало, что при учете только поля нулевого приближения, значительно расширяется диапазон применимости по сравнению с методом малых возмущений. Однако в этом случае, аппроксимация малых наклонов дает неудовлетворительные результаты в случае наличия больших неровностей по сравнению с методом Кирхгоффа. Этот недостаток нивелируется в случае учета полей нулевого и первого приближения, однако при этом многократно возрастает трудоемкость вычислений, но даже при этом не учитываются локальные эффекты. Численное решение для трехмерной поверхности было получено сравнительно недавно [] и только для случая, когда плотность вероятности ординаты волны в фиксированной точке поверхности определяется нормальным законом распределения.

Учет локальных эффектов в методе аппроксимации малых наклонов, был предложен А.Г. Вороновичем []. В основе лежит метод Мичам-Лизанова, однако, решение для поля в дальней зоне ищется в векторной форме. Тем не менее, вследствие высокой трудоемкости вычислений, численные результаты получены только для двумерного случая [, , , ].

Операторный метод разложения в ряд был изложен в 1991 году [] для двумерного случая, и нашел дальнейшее развитие в работах [, ], учитывая трехмерный случай и представление поверхности диэлектриком. Основной принцип операторного метода заключается в выражении отраженного от поверхности поля в виде поверхностного интеграла Грина-Гельмгольца. Такой подход справедлив исключительно для плоской волны, и показывает лучшие результаты по сравнению с методами Кирхгофа и малых возмущений [], однако локальные эффекты не учитываются.

Двухполупериодный подход (full-wave approach). Поверхность рассматривается как нижняя граница полубесконечного волновода, а отраженное поле представлено разложением в ряд в базисе локальных волн. Неизвестные коэффициенты ряда удовлетворяют дифференциальному уравнению распространения в поперечном направлении, так называемому телеграфному уравнению для волновода [, ]. После дополнительных допущений, уравнение может быть решено методом последовательных приближений. Двухполупериодный подход по существу является двумерным случаем. Все попытки расширить метод до трехмерного, приводят к еще более упрощающим допущениям, которые математически не всегда строгие. В работе [] проводится сравнение данного подхода с другими приближенными методами. Показано, что точность двухполупериодного подхода полностью покрывает метод малых возмущений, для случая малых неровностей. Однако для крупномасштабных поверхностей, точность не удовлетворительна, в сравнении с методом Кирхгоффа. По сравнению с другими универсальными методами двухполупериодный подход является достаточно сложным как в аналитическом, так и в вычислительном плане, а итоговая точность получаемых результатов оказывается хуже, чем у других рассмотренных методов.

Метод объемов (volumetric method) это приближенный метод, суть которого сводится к представлению шероховатой границы раздела двух однородных сред, определенным пространственным распределением диэлектрической проницаемости. Данный метод основывается на приближении Борна (Born approximation), которое в свою очередь применимо в случае, когда диэлектрические проницаемости сред сравнимы [, ]. Однако самым слабым местом приближения Борна является несовместимость его результатов с данными метода малых возмущений при малых величинах неровностей поверхности. Это является следствием отсутствия учета отражений приближением Борна, что делает это подход бесполезным при «критических углах» – поверхностном отражении []. Тем не менее, метод объемов применяется в частных случаях, например в случае плоской границы двух сред, он позволяет быстро получить нужный результат.

Метод интегральных уравнений (integral equation method) был разработан в 1980-х как метод объединяющий метод малых возмущений и метод Кирхгоффа []. Основой метода является итерационный метод Кирхгоффа. Тем не менее, в отраженном поле присутствуют и так называемые «корректирующие составляющие» зависящие от статистических характеристик рассматриваемой шероховатой поверхности []. В работах [, , ] показано, что точность метода интегральных уравнений снижается при больших углах визирования (малых углах скольжения) а также при малых радиусах кривизны поверхности.

Из рассмотренного выше можно заключить, что как такого универсального в широком смысле аналитического подхода для решения задачи рассеяния ЭМВ шероховатой поверхности не существует. Это в свою очередь связано с тем, что реальные поверхности не являются однородными и имеют достаточно широкий пространственный спектр, необходимость учета локальных эффектов еще более усложняет и без того громоздкие аналитические выражения. Зачастую имеет место следующая ситуация, теоретически подход проработан очень глубоко, но практически применить его в реальных условиях оказывается не возможным.

При построении аналитического решения авторы продумывают аспект о практической применимости получаемого выражения. Итогом их работы выступает конечная аналитическая запись результата, пригодная для численного решения. В большинстве случаев получаемое аналитическое выражение просчитывают с некоторыми допущениями и упрощениями в угоду облегчения математических вычислений.

Например, в работе [] приводится результаты полученные с помощью аналитического метода Кирхгоффа для идеально отражающей поверхности представленной одной пространственной волной в оптическом диапазоне. Была получена зависимость усредненного коэффициента отражения от угла визирования. Далее с помощью численных методов авторам удалось решить задачу рассеяния для произвольной поверхности. Реализация поверхностной волны с гауссовым распределением высот получена методом статистических эквивалентов.

В работах [, , ], получено распределение амплитуды некогерентной составляющей поля отраженного от многослойной поверхности методом малых возмущений в оптическом диапазоне ЭМВ. Модель поверхности представлена тремя средами с различными диэлектрическими проницаемостями, разделенными двумя границами разделов сред [, ]. В качестве поверхности в статье [] использовалась модель «диэлектрик на проводящей подложке». В качестве зондирующего сигнала во всех работах использовалась плоская монохромная волна. В связи с высокой вычислительной сложностью задачи, аналитическое решение получено только для полей первого приближения для каждой из границ разделов сред. Распределение амплитуд некогерентной составляющей отраженного поля было рассчитано с помощью численных методов по итоговому аналитическому выражению.

В работе [] приведено решение интеграла по объему методом Монте-Карло. Изначально комплексная амплитуда отраженного поля от сосредоточенной цели была записана в общей интегральной форме с использованием приближения Борна (метод объемов). Сосредоточенная цель представляет собой совокупность отражателей с различными диэлектрическими проницаемостями вписанных в сферу. Отраженное поле было получено численным решением интеграла по методу Монте-Карло.

В работе [] рассмотрен численный метод определения амплитуды и фазы отраженного от поверхности электромагнитного поля, основанный на точном решении общего интегрального уравнения Гельмгольца методом моментов. Особенность метода состоит в положении, что ток, наведенный на поверхность, имеет локальную природу. Это позволяет разделить полную матрицу моментов на диагонально доминирующую матрицу, определяющую сильное взаимодействие, и разреженную отвечающую за слабое взаимодействие []. Дальнейшие операции проводятся только с матрицей описывающей сильное взаимодействие, что позволяет значительно сократить объем вычислений. Существуют следующие ограничения рассматриваемого метода: падающая ЭМВ имеет только горизонтальную поляризацию, поверхность двумерна и идеально проводящая, реализация поверхностной волны строится методом статистических эквивалентов.

В основном, все рассмотренные выше работы имеют раздел «моделирование», которое на практике сводится к численному решению интегрально-дифференциальных уравнений для определенных условий.

Тем не менее, существенно расширить границы применимости аналитических методов позволяют физические модели, о которых пойдет речь далее, основанные на описании реальных физических процессов рассеяния ЭМВ структурами сложной геометрической конфигурации.

Физические модели рассеяния электромагнитных волн

Основой математических моделей электромагнитного взаимодействия является строгая математическая формулировка физического явления в виде системы интегрально-дифференциальных уравнений Максвелла. Методологические различия в решении таких систем уравнений формируют некоторый базис математических моделей. Как было указано выше, зачастую, для анализа полей рассеяния объектами сложной пространственной конфигурации необходимо вводить различные упрощения и допущения при решении системы уравнений Максвелла. Применение чисто математических приемов совместно с пониманием физики электродинамических процессов рассеяния, привело к созданию так называемых физических моделей [, ]. Наибольший интерес представляют феноменологические и аналоговые модели.

Феноменологическая модель строится на основании непосредственного наблюдения процесса. В основном, широкое распространение получили феноменологические модели основанные на лучевых представлениях полей рассеяния и модели базирующиеся на принципе Гюйгенса-Френеля. Первая модель подчиняется принципам геометрической оптики [, ]. В этом случае, предполагают, что размеры объекта должны быть много больше длины волны, фронт падающей волны должен быть плоским, а дифракционное поле порождается только частью падающих лучей. Точность решения во многом зависит от области пространства примыкающего к освещенной части поверхности объекта.

Согласно второй феноменологической модели рассеянное поле формируется на основании постулатов физической оптики [, ], при этом, каждая точка волнового фронта рассеянного поля рассматривается как источник вторичных сферических волн. В итоге, рассеянное поле представляет собой суперпозицию волновых фронтов с учетом не только амплитуд, но и пройденных расстояний. Анализ литературы, приведенный ниже, показал, что подобный тип модели до сих пор не нашел широкого применения в связи с тем, что достаточно сложно точно определить фазы и амплитуды вторичных волн. Обычно, фазы вторичных волн принимают одинаковыми в пределах заданной зоны, это в свою очередь уменьшает вычислительную сложность модели, и как следствие, ведет к снижению точности []. Поиск компромисса между точностью модели и ее сложностью привел к появлению аналоговых моделей.

Наблюдение явлений подобных исследуемому, формирует аналоговую модель. Такой моделью принято называть модель «блестящих» точек [], согласно которой, рассеянное поле формируется совокупностью точечных целей, расположенных на поверхности объекта [].

Показано [, , , ], что отражение радиоволн от тел сложной геометрической формы носит локальный характер, т.е. на поверхности объекта возникает небольшое количество участков с интенсивным отражением. Характерной поверхностью с участками локального отражения в сантиметровом диапазоне длин волн является морская поверхность []. Таким образом, участок морской поверхности или любой другой пространственно сложный объект можно представить в виде совокупности участков локального отражения. Следовательно, в результате такого представления общее поле, рассеянное объектом, есть суперпозиция полей отдельных локальных источников. Такая модель получила название модель локальных источников. Каждый участок локального отражения имеет свою амплитудную и фазовую характеристику рассеяния, что усложняет получение результирующего поля.

Дальнейшим развитием модели локальных источников стала модель Де Лано []. Ее основное отличие от модели локальных источников, заключается в вероятностном описании характеристик поля локальных участков отражения. В частности, оказывается, что напряженности отраженного от сложной цели поля распределены по нормальному закону, что существенно облегчает анализ.

Основными недостатками обеих моделей является проблема выбора участков локального отражения на поверхности объекта, и как следствие, не высокая точность расчета отраженного поля. Поэтому основными критериями адекватности таких моделей служат сопоставления результатов моделирования либо с результатами достоверного эксперимента, либо с результатами точного (или асимптотически точного) аналитического решения.

Из-за ограниченности вычислительных ресурсов, не так давно, аналоговые модели обладали рядом неоспоримых преимуществ, среди которых основным козырем была скорость вычислений. В настоящее время ситуация изменилась. С увеличением мощностей ЭВМ, феноменологические модели стали использоваться все чаще. Основная причина кроется в том, что феноменологические модели описывают непосредственно само явление или эффект, а не оперируют с его аналогом и, следовательно, более тонко передают взаимодействие электромагнитных волн с объектом. Так в работах [, , , ] расчет отраженного поля происходит на основании фацетной модели цели в сантиметровом диапазоне длин волн. Объект локации представлен в виде триангулированной сетки, т.е. локальными элементами сцены считаются плоские треугольные пластины, вершины которых лежат на поверхности объекта. Результирующее дифракционное поле рассеяния радиолокационной сцены в целом определяется путем когерентного суммирования локальных полей рассеяния отдельных элементов принадлежащих различным элементам сцены. Методы физической теории дифракции особенно удобны с точки зрения дальнейшего повышения точности вычисления полей рассеяния [].

В основе каждой модели помимо электродинамических аспектов лежат технологические расчеты объекта сложной пространственной конфигурации. Так, например, для модели "блестящих" точек необходимо знание их относительного расположения, а для лучевых моделей необходима информация о нормали в каждой точке рассеяния. От уровня сложности топологии объекта зависит выбор модели и ее реализация в виде алгоритмической процедуры.

В работах [, ] рассмотрен еще один тип модели построенной по методу статистических эквивалентов. В [] получена двухмерная плотность распределения вероятности амплитуды и фазы поля, рассеянного в обратном направлении точечным изотропным отражателем, расположенным вблизи статистически шероховатой границы раздела двух сред. В работе [] огибающая отраженного от поверхности радиолокационного сигнала считается распределенной по нормальному закону. Полезный сигнал рассматривается в виде узкополосного случайного процесса, у которого огибающая определяется затуханием, например, в растительном покрове.

Таким образом, с помощью различных физических моделей можно описать рассеивающие способности объекта. Выбор конкретной модели зависит от априорных данных, заданной точности и т.п.

Исходя из описанных выше преимуществ, в качестве модели рассеяния электромагнитных волн была выбрана феноменологическая модель, на базе которой была получена импульсная характеристика поверхности.

Проверка знаний
1. Распределенная радиолокационная цель это:
объект, геометрические размеры которого значительно меньше элементов пространственного разрешения системы.
`объект локации, геометрические размеры которого значительно превосходят элементы пространственного разрешения радиотехнической системы.
объект, находящийся в точке наблюдения и изотропно рассеивающий падающее излучение РЛС во всех направлениях.
объект, находящийся в точке наблюдения и анизотропно рассеивающий падающее излучение РЛС в обратном направлении.
1. Дайте определение дифференциальной эффективной площади рассеяния объекта:
отношение поверхностной плотности потока энергии, падающей на цель, к потоку (мощности) электромагнитной энергии, отражаемой целью в направлении радиоэлектронного средства.
статистически усредненная по времени задержки и доплеровской частоте характеристика, описывающая отражательную способность объекта, в случае нестационарного воздействия.
отношение потока (мощности) электромагнитной энергии, отражаемой целью в направлении радиоэлектронного средства, к поверхностной плотности потока энергии, падающей на цель.
`статистически усредненная по времени задержки и доплеровской частоте характеристика, описывающая отражательную способность протяженного объекта, в случае стационарного воздействия.
1. Требования метода малых возмущений к характеристикам поверхности:
поверхность характеризуется малыми наклонами крупномасштабных неровностей, анизотропна, в среднем плоская.
поверхность характеризуется крупномасштабными неровностями, с большими радиусами кривизны, изотропна и характеризуется комплексной диэлектрической проницаемостью.
`поверхность характеризуется малой относительной высотой неровностей, изотропна, в среднем плоская, пологая, и характеризуется комплексной диэлектрической проницаемостью.
поверхность представлена шероховатой границей раздела двух однородных сред, с определенным пространственным распределением диэлектрической проницаемости.
1. Формирование рассеянного поля феноменологической моделью:
рассеянное поле формируется совокупностью точечных целей, расположенных на поверхности объекта, т.е. на поверхности объекта возникает небольшое количество участков с интенсивным отражением.
`рассеянное поле формируется на основании постулатов физической оптики, при этом, каждая точка волнового фронта рассеянного поля рассматривается как источник вторичных сферических волн. В итоге, рассеянное поле представляет собой суперпозицию волновых фронтов с учетом не только амплитуд, но и пройденных расстояний.
рассеянное поле есть вероятностное описание характеристик поля локальных участков отражения, в частности напряженности отраженного от сложной цели поля оказываются распределены по нормальному закону.
рассеянное поле формируется на основании постулатов геометрической оптики, а рассеянное поле представляет собой суперпозицию волновых фронтов с учетом не только амплитуд, но и пройденных расстояний.

Феноменологическая модель рассеяния ЭМВ протяженной поверхностью
1. Дискретное представление протяженной поверхности

В качестве протяженной поверхности будем рассматривать морскую поверхность. Сложную волновую поверхность в промежутке квазистационарности и на участке квазиоднородности, можно представить моделью Лонге-Хиггинса []

где al - амплитуда элементарной плоской волны; l - начальная фаза элементарной волны, распределенная равномерно в интервале [–; ].

Согласно такой модели морская поверхность – есть линейная суперпозиция плоских поверхностных волн, имеющих различные амплитуды, частоты, направления распространения относительно главного направления распространения морских волн и случайные начальные фазы.

Каждая элементарная волна подчиняется всем законам классической гидродинамики.

Амплитуды плоских волн определяются двумерным энергетическим спектром волнения , приращениями волновых чисел и направлений

В качестве частотного спектра будем использовать спектр В. Пирсона и Л. Мошковица, рекомендованный международной конференцией опытных бассейнов в качестве стандартного.

;;;,

где V – скорость ветра.

Для построения реализации квазипериодической поверхности удобно оперировать частотным спектром, выраженным в длинах волн . Для перехода от спектра к , необходимо учитывать соответствующий якобиан преобразования [].

, .

На приведен энергетический спектр волнения рассчитанный по выражению для скорости ветра 6 м/с и направления главного распространения 0=30.

рис. .

Согласно [, ] дисперсия волновых ординат морской поверхности связана с частотно-направленным частотным спектром волнения соотношением

С учетом известной связи высоты волны 3-х процентной обеспеченности со среднеквадратическим отклонением ординат морской поверхности запишем

Для записи выражения (1.1) в дискретном виде необходимо провести дискретизацию энергетического спектра волнения . Для этого необходимо определить минимальную длину волны в частотном спектре min, а также ширину частотного спектра в длинах волн s. Ввиду необходимости получения универсального инструмента для определения ширины спектра имеющего произвольную форму был разработан численный алгоритм определения пересечения произвольной непрерывной функции одной переменной с заданным уровнем. Алгоритм приведен в Приложении 1.

Приращения по пространственным длинам волн и по угловому спектру теперь могут быть записаны в следующем виде

где l – количество спектральных составляющих в частотном спектре волнения; – количество спектральных составляющих в угловом спектре волнения.

Согласно (1.2) справедлива следующая запись

Тогда выражение (1.1) можно записать в следующей форме

Фрагмент реализации поверхностной волны, рассчитанная с использованием выражения и , приведен на (вид сверху) и на (изометрическая проекция). На стрелкой показано направление главного распространения, пунктиром – фронт распространения волн. Реализация получена для скорости ветра 6 м/с и направления главного распространения 0=30.

рис. .

Однако для оценки адекватности динамической РЛХ необходимо иметь априорно известный энергетический частотно-направленный спектр. В качестве такого «эталонного» энергетического спектра волнения будем рассматривать спектр имеющий Гауссову огибающую частотного спектра.

где 0 – центральная длина волны; – ширина спектра по уровню 0,707; – параметрическое решение уравнения .

рис. .

На приведен энергетический спектр волнения рассчитанный по выражению для H3%=1 м и направления главного распространения 0=30.

рис. .

Радиолокационный портрет протяженной поверхности

Было отмечено выше, что поверхность любого трехмерного объекта можно описать фацетной моделью, т.е. представить в виде аппроксимации полигональной сеткой. Ячейкой такой сетки является элементарный отражатель (фацет). Локальными элементами сцены считаются плоские отражатели, вершины которых лежат на поверхности объекта. Результирующее дифракционное поле рассеяния радиолокационной сцены в целом определяется путем когерентного суммирования локальных полей рассеяния отдельных элементов принадлежащих различным элементам сцены. Было отмечено, что вклад в результирующее поля рассеяния вносят следующие «локальные эффекты»: зеркальное рассеянное поле от гладких элементов радиолокационной сцены; дифракционное поле от острых кромок элементов сцены, участков разрыва гладкой поверхности цели; «ползущие» волны; «бегущие» волны; переотражения электромагнитных волн между элементами сцены.

Геометрия задачи представлена на . Плоскость xOy является средней плоскостью морской поверхности. В точке O(x0, y0, z0,) находится передающая система, характеризующаяся пространственной диаграммой направленности Fr, в точке O`(x1, y1, z1,) находится приемная система с диаграммой направленности Fs. Морская поверхность задана дискретными отчетами согласно выражения . Пространственный параллелограмм (ABCD) представляет собой отражательную площадку. Из точки O(x0, y0, z0,) распространяется сферическая волна.

рис. .

Фронт падающей сферической ЭМВ в окрестностях отражательной площадки можно представить локально плоским при выполнении критерия дальней зоны. Критерий дальней зоны для i-ой отражательной площадки имеющей линейный размер Li можно записать в виде

где s - минимальная длина волны зондирующего сигнала.

Под линейным размером площадки Li понимается максимальная диагональ пространственного параллелограмма (ABCD).

В области трехмерного моделирования и конструирования в качестве ячейки полигональной сетки широко используется треугольник. Это позволяет добиться наилучшей точности аппроксимации объектов сложной геометрической конфигурации.

Поскольку точки A, B, C и D в общем случае не лежат в одной плоскости пространственный параллелограмм целесообразно представить в виде двух треугольников .

Сформируем поляризационный базис падающей локально плоской волны в окрестности каждого из треугольников. Падающая на каждый из треугольников плоская волна характеризуется вектором поляризации и направляющим вектором (единичный орт радиус-вектора ). Орт определяет направление вертикальной поляризации в базисе падающей волны и характеризует амплитуду вертикальной составляющей вектора напряженности электрического поля в окрестностях каждого треугольника. Орт задает направление горизонтальной поляризации.

рис. .

Направление распространения каждой из отраженных волн на приемную систему с локальным вектором поляризации характеризуется направляющим вектором , который проводится из средней точки треугольника в точку расположения приемной системы. Поляризационный базис представляет локально плоскую волну рассеянную каждым из треугольников.

Предполагается, что треугольный элемент обладает вполне определенными электродинамическими свойствами. В общем случае электродинамические параметры задаются с помощью комплексной диэлектрической проницаемости и магнитной проницаемости . Треугольный элемент может обладать многослойным покрытием с различными диэлектрическими проницаемостями. В дальнейшем под элементарным отражателем (ЭО) будем подразумевать треугольники, образованные из пространственного параллелограмма (см. ).

Рассеивающие свойства ЭО описывает однопозиционная матрица рассеяния []

Здесь – элементы матрицы рассеяния i-ого ЭО для случая линейной поляризации, представляют собой комплексные коэффициенты отражения в базисах падающей и отраженной волн. – комплексная амплитуда напряженности рассеянного ЭО поля в базисе ; – комплексная амплитуда напряженности электрического поля в базисе ; Т – символ транспонирования.

Комплексный характер элементов матрицы рассеяния непосредственно указывает на учет фазовых набегов. Абсолютные значения аргументов всех элементов матрицы определяются расстоянием между приемной системой и ЭО. Поэтому такой фазовый множитель может быть вынесен за знак матрицы. В связи с этим в [] вводится понятие абсолютной и относительной матрицах рассеяния. Запишем однопозиционную относительную матрицу рассеяния в следующем виде

В дальнейшем будем использовать только «относительные» элементы матрицы рассеяния .

В результате анализа выражения было выявлено, что поверхность является непрерывной. Анализ геометрии задачи показал, что при минимальной высоте расположения приемной и передающей системы определяющейся режимом работы радиолокатора, эффект затенения поверхности проявляется только за границами участка квазиоднородности и квазистационарности поверхности. Таким образом, можно заключить, что поле рассеяния протяженного объекта заданного выражением в окрестности приемной системы будет равно сумме рассеянных полей зеркального отражения совокупности ЭО этой поверхности, а также вкладу поля от переотражений между элементами сцены.

Энергетические соотношения для рассеянного поля

В соответствии с выражением для определения поля рассеяния в первую очередь необходимо вычислить комплексные коэффициенты отражения матрицы рассеяния ЭО, которые определяются соотношением []

В соответствии с методикой, изложенной в работах [-] для вычисления комплексного коэффициента отражения плоского треугольника полигональной модели, был использован метод ФО, согласно которому поле на поверхности треугольника определяется в результате векторной суммы падающего на плоскость поля и поля отраженного от плоскости треугольника по законам геометрической оптики (ГО). Выражение для комплексного коэффициента отражения треугольника, полученное на основе метода ФО и соотношения имеет вид

где – вектора локального базиса треугольника, – орты поляризационного базиса падающей волны, – вектор нормали к плоскости треугольника, – разностный направляющий вектор, – вершины треугольника, , – коэффициенты отражения от плоскости треугольника для вертикальной и горизонтальной поляризаций, – проекция разностного вектора на плоскость треугольника, причем .

В случае если треугольник покрыт многослойным радиопоглощающим покрытием, коэффициенты отражения , вычисляются на основе метода ГО [-]. Иначе , представляют собой коэффициенты отражения Френеля для треугольника из однородного материала. Выражение получено с использованием метода Гордона, согласно которому поверхностный интеграл источников на плоскости треугольника заменяется криволинейным интегралом по контуру, ограничивающему треугольник.

Плотность потока мощности локально плоской падающей волны в направлении на i-й ЭО в дальней зоне определяется выражением []

где Ом – волновое сопротивление среды; Pr – мощность излученного сигнала; Dr – КНД передающей антенной системы; Fri – значение нормированной диаграммы направленности передающей системы в направлении на i-й ЭО.

Комплексная амплитуда напряженности электрического поля в окрестности i-го ЭО с учетом сферической падающей волны можно записать как

где – вектор поляризации передающей антенны в базисе .

Вектор комплексной напряженности поля, рассеянного ЭО, в точке расположения приемной антенны с учетом выражения и можно записать как

Тогда напряжение в согласованной нагрузке приемной антенны, полученное от воздействия i-го ЭО, определяется произведением величины напряженности его электрического поля рассеяния на модуль действующей высоты антенны.

где hai – модуль действующей высоты приемной антенны; Ds – КНД приемной антенной системы; Fsi – значение нормированной диаграммы направленности приемной системы в направлении на i-й ЭО.

Дискретное представление динамической импульсной характеристики отражения поверхности

Раннее было отмечено, что сверхширокополосные РЛХ являются наиболее общей характеристикой объекта радиолокации. Подобные характеристики могут быть получены как отклик цели на тестовое сверхширокополосное воздействие – функцию Дирака (t). Таким образом, импульсная характеристика представляет собой поле, рассеянное объектом при падении сферической монохроматической волны единичной амплитуды. На практике формирование тестового сигнала вида (t) практически не осуществимо, поэтому необходимо изыскивать возможности описания сверхширокополосных РЛХ адекватно используемому зондирующему сигналу. Это означает, что сверхширокополосные РЛХ должны быть определены в диапазоне частот большим или равным ширине спектра воздействия. В этом случае, речь идет о так называемой «сглаженной» импульсной характеристики.

Таким образом, длительность тестового импульса для получения сглаженной импульсной характеристики определяется минимальным интервалом дискретизации зондирующего сигнала T выбранного согласно теореме Котельникова. Таким образом, для получения адекватной сглаженной импульсной характеристики необходимо чтобы частота ее дискретизации была равна или превышала удвоенную максимальную частоту в спектре предполагаемого зондирующего сигнала.

В соответствии с геометрией задачи (см.) передающая система излучает зондирующий сигнал, который представляет прямоугольный импульсный сигнал единичной амплитуды с длительностью T. Пространственно-избирательные характеристики передающей системы Fr пока принимать во внимание не будем, частотно-избирательные характеристики передающей системы в данном случае не учитываются. Т.е. излучающая система не вносит искажений в амплитудный и фазовый спектр зондирующего сигнала а, следовательно, не искажает его форму. Излучаемая сферическая волна имеет два фронта соответствующие переднему и заднему фронту зондирующего импульса. Таким образом, интервал наклонных дальностей R=cT, будет определять участок отражения поверхности в конкретный момент времени (см. ).

По мере распространения зондирующего сигнала в различные моменты времени будут освещаться различные участки поверхности. Не трудно представить, что на интервале участок отражения будет представлен окружностью, при участком отражения будет кольцо, по мере распространения радиус кольца будет увеличиваться, а его ширина уменьшаться.

рис. .

Сглаженная импульсная характеристика отражения подстилающей поверхности есть временная зависимость напряжения в согласованной нагрузке приемной антенны, как реакции поверхности на излученный тестовый импульс

где N – общее количество ЭО участка отражения в объеме разрешения ; (х) - функция Дирака.

Выберем сферическую систему координат. Начало координат совместим с точкой O(x0, y0, z0,) (см. ). Рассмотрим граничные условия для получения отчетов импульсной характеристики , а также определим и .

Выше было рассмотрено, что морское волнение можно рассматривать как эргодический стационарный случайный процесс только на участке квазистационарности и квазиоднородности []. Протяженность такого участка Lsu обычно изменяется в пределах 10-12 километров. Следовательно, максимальная наклонная дальность, при которой анализ рассеивающих свойств поверхности имеет смысл можно определить как

где, – коэффициент определяющий максимальную высоту волнения, находится в пределах 1,2-1,5.

Очевидно, что проводить анализ в области пространства, где отсутствует поверхность также не целесообразно. Поэтому минимальную наклонную дальность, с которой будет начинаться анализ рассеивающих свойств поверхности, определим следующим образом

Исходя из геометрии задачи , определим , для этого необходимо найти проекцию ширины кольца дальности RA max и RA min на ось Ox.

где R – текущая наклонная дальность, RA – ширина зоны анализа поверхности.

рис. .

На представлены два случая распространения фронтов зондирующего импульса. Первый случай иллюстрирует расположение фронтов при , второй при . Очевидно, что при отсутствии пересечения задним фронтом в точках B1 и C1, RA min=0.

На приведено поведение ширины зоны анализа поверхности на участке Lsu. Максимальное значение RA обуславливается тем, что в этот момент, зондирующий импульс длительностью T формирует максимальное пятно рассеяния на поверхности.

Для нахождения обратимся к . Очевидно, что

где l – длина дуги проекции элементарной площадки ABCD на плоскость xOy; выражен в градусах.

рис. .

Для точного представления поверхности, необходимо чтобы размеры проекции элементарной площадки A`B`C`D` были постоянны. Это условие достигается при использовании адаптивной дискретизации по углу, путем установления длины дуги l равной постоянному значению. Очевидно, что . Учитывая тот факт, что поверхность задается моделью Лонге-Хиггинса

где Ns – количество отсчетов на период пространственной волны.

На приведено поведение на участке Lsu.

Теперь можно записать координаты точек элементарной площадки ABCD A(xA, yA, zA,), B(xB, yB, zB,), C(xC, yC, zC,), D(xD, yD, zD,)

где ; ; Ta – время наблюдения; - количество циклов моделирования.

рис. .

Таким образом, координаты вершин первого ЭО составляющего отражательную площадкуABCD будут P1=A, P2=B, P3=C, второго ЭО P1=A, P2=D, P3=C.

Предварительно оценим количество ЭО которые будут участвовать в формировании отклика поверхности в согласованной нагрузке приемной антенны

На приведено изменение Nel на участке Lsu. Общее количество ЭО данной сцены 1100х106 штук.

рис. .

Используя выражение была рассчитана импульсная характеристика отражения морской поверхности, сплошная линия см. , . На , пунктиром представлена импульсная характеристика отражения, рассчитанная по аналитическим выражениям (3.14) и (3.17).

рис. .

Графики представлены в относительных задержках, .

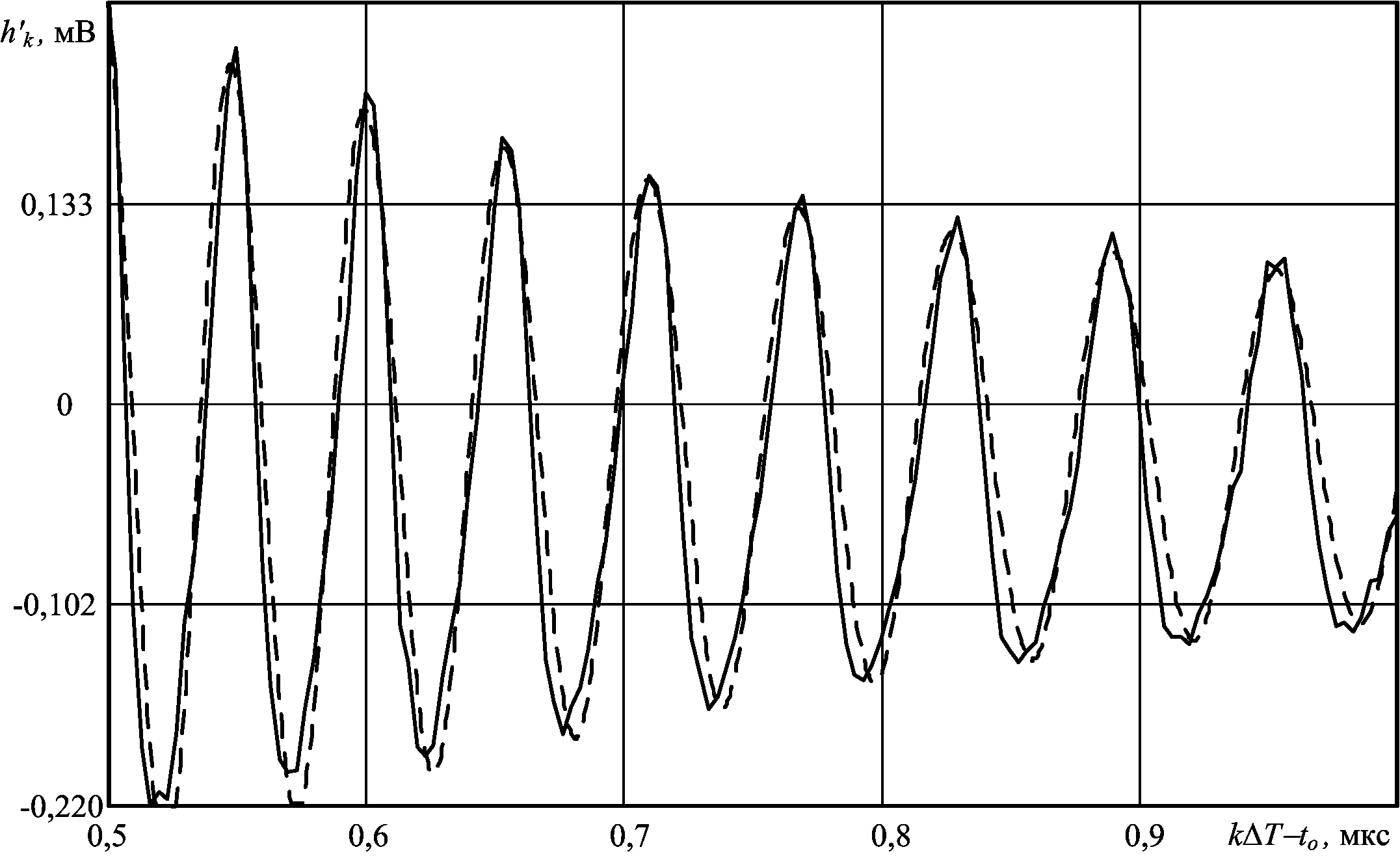
рис. .

Из приведенных графиков видно, что результат моделирования хорошо согласуется с аналитическим расчетом.

Отсчеты отраженного от поверхности сигнала будем искать в виде дискретной свертки отсчетов импульсной характеристики и зондирующего сигнала

где N – количество отсчетов сглаженной импульсной характеристики отражения поверхности.

Список использованных источников

. А.А. Гарнакерьян, В.Г. Захаревич, В.Т. Лобач Г.С. Панатов, А.В. Явкин, Радиоокенаграфическое, навигационное и информационное обеспечение гидроавиации, Таганрог: ТРТУ, 1997. 258 с.

. T. Elfouhaily, C.A. Guerin, A critical survey of approximate scattering wave theories from random rough surfaces, Waves in Random and Complex Media, 14, R1-R40, 2005.

. O.P. Bruno, F. Reitich, Numerical solution of diffraction problems: a method of variation of boundaries, J. Opt. Soc. Am. 10 1168–75, 1993.

. O.P. Bruno, F. Reitich, Numerical solution of diffraction problems: a method of variation of boundaries II. Finitely conducting gratings, Pade approximants, and singularities, J. Opt. Soc. Am. 10 2307–16, 1993.

. O.P. Bruno, F. Reitich, Numerical solution of diffraction problems: amethod of variation of boundaries. III. Doubly periodic gratings, J. Opt. Soc. Am. 10 2551–62, 1993.

. А.В. Белобров, И.М. Фукс, Дифракционные поправки к методу Кирхгофа в задаче рассеяния на неровной поверхности - Diffraction corrections to the Kirchoffs method in the problem of scattering on the rough surface, 31 с. ил. 21 см Харьков ИРЭ 1985.

. Y.Q. Jin, Multiple scattering from a randomly rough surface, J. Appl. Phys. 63 1286–92, 1988.

. А.А. Гарнакерьян, А.С. Сосунов, Радиолокация морской поверхности, Ростов н/Д: РГУ, 1978. 142 с.

. O.P. Bruno, A. Sei, M. Caponi, High-order high-frequency solutions of rough surface scattering problems, Radio Science, Vol 37, No 4, pp 2-1 - 2-13, 2002.

. W.C. Meecham, Fourier transform method for the treatment of the problem of the reflection of radiation from irregular surfaces, J. Acoust. Soc. Am. 28 370–7, 1956.

. Y.P. Lysanov, About one approximate solution of the problem of acoustic wave scattering by a rough interface, Sov. Phys.—Acoust. 2 190–8, 1956.

. A.G. Voronovich, Small-slope approximation in wave scattering by rough surfaces, Soviet Physics JETP, Vol. 62, 65-70, 1985.

. A.G. Voronovich, Wave Scattering from Rough Surfaces, 2nd ed., Springer-Verlag, 1999.

. V.I. Tatarskii, The expansion of the solution of the rough-surface scattering problem in powers of quasislopes, Waves Random Media 3 127–46, 1993.

. S.T. McDaniel, A small-slope theory of rough surface scattering, J. Acoust. Soc. Am. 95 1858–64, 1994.

. M.S. Gilbert, J.T. Johnson, A study of the higher-order small-slope approximation for scattering from a Gaussian surface, Waves Random Media 13 137–43, 2003.

. A.G. Voronovich, Non-local small-slope approximation for wave scattering from rough surfaces, Waves Random Media 6 151–67, 1996.

. S.L. Broschat, E.I. Thorsos, A preliminary study of the nonlocal small-slope approximation, J. Acoust. Soc. Am. 100 2702, 1996.

. S.L. Broschat, E.I. Thorsos, An investigation of the small slope approximation for scattering from rough surfaces 2 numerical studies, J. Acoust. Soc. Am. 101 2615–25, 1997.

. S.L. Broschat, Reflection Loss from a Pierson-Moskowitz sea surface using the nonlocal small-slope approximation, IEEE Trans. Geosci. Remote Sens. 37 632–4, 1999.

. H. Kim, J.T. Johnson, Radar images of rough surface scattering: Comparison of numerical and analytical models, IEEE Trans. Antennas Propag. 50 94–100, 2002.

. D.M. Milder, An improved formalism for wave scattering from rough surface, J. Acoust. Soc. Am. 89 529–41, 1991.

. D.M. Milder, T Sharp, An improved formalism for wave scattering from rough surface: numerical trials in three dimensions, J. Acoust. Soc. Am. 91 2620–6, 1992.

. R.A. Smith, The operator expansion formalism for electromagnetic scattering from rough dielectric surfaces, Radio Sci. 31 1377–85, 1996.

. E. Bahar, Full-wave solutions for the depolarization of the scattered radiation by rough surfaces of arbitrary slope, IEEE Trans. Antennas Propag. 29 443–54, 1981.

. E. Bahar, Y. Zhang, A new unified full wave approach to evaluate the scatter cross sections of composite random rough surfaces, IEEE Trans. Geosci. Remote Sens. 34 973–80, 1996.

. R.E. Collin, Electromagnetic scattering from perfectly conducting rough surfaces (a new full wavemethod), IEEE Trans. Antennas Propag. 40 1466–77, 1992.

. G. Vineyard, Grazing-incidence diffraction anf the distorted-wave approximation for the study of surfaces, Phys. Rev. B 26 4146–59, 1982.

. A.K. Fung, G.W. Pan, An integral equation method for rough surface scattering, Proc. Int. Symp. on Multiple Scattering of Waves in Random Media and Random Surfaces 701–14, 1986.

. J.L. Alvarez-Perez, An extension of the IEM/IEMM surface scattering model, Waves Random Media 11 307–29, 2001.

. K.S. Chen, T.D. Wu, A.K. Fung, A study of backscattering from multi-scale rough surface, J. Electromagn. Waves Appl. 12 961–79, 1998.

. F. Mattia, Backstattering properties of multiscale rough surfaces, J. Electromagn. Waves Appl. 13 493–527, 1999.

. D. Lemaire, P. Sobieski, C. Craeye, A. Guissard, Two-scale models for rough surface scattering: Comparison between the boundary perturbation method and the integral equation method, Radio Science, Vol. 37, No. 1, 1-1 - 1-16, 2002.

. I. Simonsen, D. Vandembroucq, S. Roux, Electromagnetic wave scattering from conducting self-affine surfaces: an analytic and numerical study, J. Optical Society of America A, Vol. 18, Issue 5, pp. 1101-1111, 2001.

. A. Soubret, G. Berginc, C. Bourrely, Backscattering enhancement of an electromagnetic wave scattered by two-dimensional rough layers, J. Optical Society of America A, Vol. 18, Issue 11, pp. 2778-2788, 2001.

. A. Soubret, G. Berginc, C. Bourrely, A new application of reduced Rayleigh equations to electromagnetic wave scattering by two-dimensional randomly rough surfaces, Physical Review B, 63 245411 - http://hal.archives-ouvertes.fr/hal-00119509/en/, 2001.

. I Simonsen, A.A. Maradudin, Numerical simulation of electromagnetic wave scattering from planar dielectric films deposited on rough perfectly conducting substrates, Optics Communications, Volume 162, Number 1, pp. 99-111, 1999.

. А.А. Коростелев, Н.Ф. Клюев, Ю.А. Мельник и др.; под ред. В.Е. Дулевича, Теоретические основы радиолокации, М., Сов. Радио, 1978г., 608с.

. М.Е. Варганов, Ю.С. Зиновьев, Л.Ю. Астанин и др.; под ред. Л.Т. Тучкова, Радиолокационные характеристики летательных аппаратов, М., Радио и связь, 1985г., 236с.

. Е.А. Штагер, Рассеяние радиоволн на телах сложной формы, М., Радио и связь, 1986г., 184с.

. В.А. Боровиков, Б.Е. Кинбер, Геометрическая теория дифракции, М., Связь, 1978г., 248с.

. Е.М. Кенно, Д.Л. Моффатт, Аппроксимация переходных и импульсных переходных характеристик, ТИИЭР № 8, т. 53, 1965г.

. А.С. Кузнецов, Б.А. Стрюков, Построение РЛ изображений проводящих объектов при короткоимпульсном зондировании, Радиотехника №4, 1988г.

. П.Я. Уфимцев, Метод краевых волн в физической теории дифракции, М., Сов. радио, 1962г., 234с.

. В.Г. Небабин, В.В. Сергеев. Методы и техника радиолокационного распознавания. М.: Радио и связь, 1984г., 152с.

. В.И. Кошелев, В.Т. Сарычев, С.Э. Шипилов, В.П. Якубов. Оценивание информационных характеристик радиолокационных объектов при сверхширокополосном зондировании. «Журнал Радиоэлектроники» № 6, 2001г.

. Ю.В. Кузнецов, В.Ю. Щекатуров, А.Б. Баев, Сравнительная характеристика алгоритмов оценки параметров резонансной модели объектов, Вестник МАИ, том 4, N2, с. 70-76, 1997г.

. Г.Т. Марков, Б.М. Петров, Г.П. Грудинская, Электродинамика и распространение радиоволн, учебн. пособие для вузов, М. Сов. радио, 1969г., 376с.

. С.И. Баскаков, Радиотехнические цепи и сигналы, М., Высшая школа, 1983г., 535с.

. B.E. Barrowes, C. Ao, F.L. Teiseira, Jin Au Kong, Leung Tsang, Monte Carlo simulation of electromagnetic wave propagation in dense random media with dielectric spheroids, IEICE Trans., Vol. E83-C, No. 12, pp. 1797–1802, 2000.

. D.J. Donohue, H.C. Ku, D.R. Thompson, J Sadowsky, Direct numerical simulation of electromagnetic rough surface and sea scattering by an improved banded matrix iterative method, Johns Hopkins APL Technical Digest Volume 18(2), 204–216, 1997.

. L. Tsang, C.H. Chan, K. Pak, H. Sangani, Monte-Carlo Simulations of Large-Scale Problems of Random Rough Surface Scattering and Applications to Grazing Incidence with the BMIA/Canonical Grid Method, IEEE Trans. Antennas Propagat. 43, 851–859, 1995.

. N. Reul, B. Chapron, WP1100 - Improvements in emissivity models, SMOS-Salinity Data Processing Study, ESA Contract n°15165/01/NL/SF, 2001.

. Справочник по радиолокации, пер. с англ., под ред. М. Сколника, т.1, М. Сов. радио, 1977г., 455.

. Ф.Г. Басс, И.М. Фукс, Рассеяние волн на статистически неровной поверхности, М. Наука, 1972г., 424с.

. А.Б. Борзов, Р.П. Быстров, А.В. Соколов, Анализ радиолокационных характеристик объектов сложной пространственной конфигурации, Журнал Радиоэлектроники № 1, 1998г.

. А.Б. Борзов, А.В. Соколов, В.Б. Сучков, Методы цифрового моделирования радиолокационных характеристик сложных объектов на фоне природных и антропогенных образований. «Зарубежная радиоэлектроника. Успехи современной радиоэлектроники» № 5, 2001г.

. А.Б. Борзов, А.В. Соколов, В.Б. Сучков, Цифровое моделирование входных сигналов систем ближней радиолокации от сложных радиолокационных сцен, "Журнал Радиоэлектроники" № 4, 2004г.

. Г.Н. Андреев, О.А. Логвин, Статистические модели отраженных от поверхности радиолокационных сигналов. «Методы и средства дистанционного радиозондирования». Моск. Гос. Техн. ун-т гражд. Авиации. М., 1995.

. В.В. Леонтьев, Вероятностная модель рассеяния сантиметровых радиоволн объектом вблизи взволнованной морской поверхности. «Радиотехника» № 4, 1998г.

. Л.В. Лабунец, Н.Н. Анищенко, А.Р. Яруллин, Математическое моделирование переходных характеристик 3D- объектов в радиолокационной системе ближнего действия. Радиотехника и электроника № 3, Т. 51. С. 279-302., 2006.

. Ю.М. Крылов, Спектральные методы исследования и расчета ветровых волн. Л.: Гидрометеоиздат, 1966г., 256с.

М.С. Лонге-Хиггинс. Статистический анализ случайно движущейся поверхности. // Ветровые волны. Под ред. Ю.М. Крылова. М.: Иностранная литература, 1962г. 218с.

МОДЕЛИРОВАНИЕ РАССЕЯНИЯ ЭМВ СЛОЖНЫМИ ОБЪЕКТАМИ