Обоснование оценок искомых параметров и их ошибок

PAGE \* MERGEFORMAT 1

Реферат

1. Оценки искомых параметров и их ошибок. Прямые измерения

Обратимся к обоснованию оценок измерений и их погрешностей. Подчеркнем, что определение систематических ошибок не является задачей статистики. Это инструментальная проблема. Поэтому в дальнейшем систематическую ошибку мы исключаем. Впрочем, мы все-таки будем ее вкратце касаться.

Пусть проводятся измерения какой-то величины . В результате N экспериментов имеем выборку N измеренных величин , и нам нужно определить какие-то параметры на основе этих измерений. Будучи некоторой функцией , искомые параметры, в свою очередь, будут некоторыми случайными величинами. Очевидно, их закон распределения будет как-то зависеть от закона распределения . Будем считать, что оценка соответствующих параметров является «хорошей», если она удовлетворяет следующим условиям.

1. Является состоятельной, т.е. при оценка сходится к самому параметру (который, вообще говоря, неизвестен).

2. Является несмещенной, т.е. поскольку мы используем не сам искомый параметр, а его оценку, то мы не должны делать систематической ошибки в сторону его завышения или занижения, иными словами математическое ожидание этого параметра должно равняться ему самому.

Является эффективной, в том смысле, что несмещенная оценка обладала бы наименьшей дисперсией.

Пусть мы имеем N измерений некоторой величины , которую представим в виде:

(1)

где, как и раньше, Q есть математическое ожидание, есть случайная величина – погрешность. Закон распределения случайной величины нам неизвестен. Известно лишь, что . Наша задача – оценить среднее значение Q и ошибку этого среднего. В качестве математического ожидания естественно взять среднее арифметическое

(2)

т.к. согласно закону больших чисел эта оценка будет состоятельной и несмещенной.

Дисперсия Q (т.е. разброс в определении истинного значения, обозначим дисперсию ) согласно центральной предельной теореме (см. 2.8) равна:

(3)

где 2 есть дисперсия . Если нам как-то определить 2, то мы могли бы найти дисперсию среднего значения, т.е. его разброс. Тогда среднее значение искомой величины мы представили бы в виде: . Такая запись означала бы, что с вероятностью примерно 68% среднее значение искомой величины лежит в пределах относительно найденного значения Q.

Перейдем к определению 2. На первый взгляд для нее представляется естественной взять следующую оценку :

(4)

Можно показать, что эта оценка состоятельна, а также для нормального закона распределения (3) будет минимальной, т.е оценка разброса эффективная. Но расчеты (детали можно найти, например, в книге Вентцель) показывают, что эта оценка является смещенной, а именно, несмещенная оценка должна получаться путем замены (4) на следующее выражение:

(5)

Для больших выборок поправочный коэффициент стремится к единице. Его имеет смысл вводить для небольших выборок.

Обратим внимание на следующее обстоятельство. В нашей задаче мы имели один искомый параметр Q. И в (5) в знаменателе имеем величину N-1. Если бы мы решали задачу с несколькими искомыми параметрами, скажем, p, то, как показывают исследования, вместо N-1 мы бы имели N-p. Эта величина называется количеством степеней свободы. При большом числе определяемых параметров, очевидно, следует учитывать количество степеней свободы, особенно если число измерений невелико.

Резюмируем сказанное. Величина , которая характеризует разброс погрешности , еще называется погрешностью единичного измерения. Погрешностью измерения среднего значения является . Она оказывается существенно меньше, чем (1.4).

Обоснование среднего как наилучшей оценки

Пусть на основании измерений мы имеем выборку . Наша задача – найти наилучшие оценки для Q и . Если нам известно, что результаты измерений описываются нормальным законом, то мы могли бы вычислить вероятность получения значений . Так, вероятность того, что заключена в интервале вблизи фактически измеренного значения равна:

аналогично записываем для других . Вероятность того, что в процессе N измерений мы будем иметь те , которые и были получены в эксперименте, равна:

(6)

Очевидно, здесь делается предположение о независимости измерений! Кроме того, мы сократили на .

Важно отметить, что величины - это измеренные, т.е. известные нам значения. Неизвестны здесь среднее Q и дисперсия . Задача и состоит в том, чтобы их найти. Решение, очевидно, состоит в следующем: Наилучшей оценкой для искомых параметров будет оценка, при которой вероятность их реализации будет максимальной. В статистике это называется принципом максимального правдоподобия. Максимум достигается при минимуме показателя, т.е. . Дифференцируя, получим: , или . Для оценки дисперсии, дифференцируем вероятность (6):

Отсюда:

На первый взгляд, последняя оценка противоречит сказанному ранее, когда в знаменателе вместо N фигурировало количество степеней свободы N-1. В действительности должно фигурировать именно N-1, что можно доказать более точными расчетами (см. курс Вентцель). Качественная причина такой замены состоит в том, что в оценке дисперсии используется не истинное значение Q, а его оценка, которая заключает в себе уже некоторую погрешность.

На приведенном ниже рисунке 1 поясняется процесс измерения, как реализация (красные точки) из возможного ряда значений, имеющих соответствующий разброс. Этот разброс и есть разброс отдельного измерения.

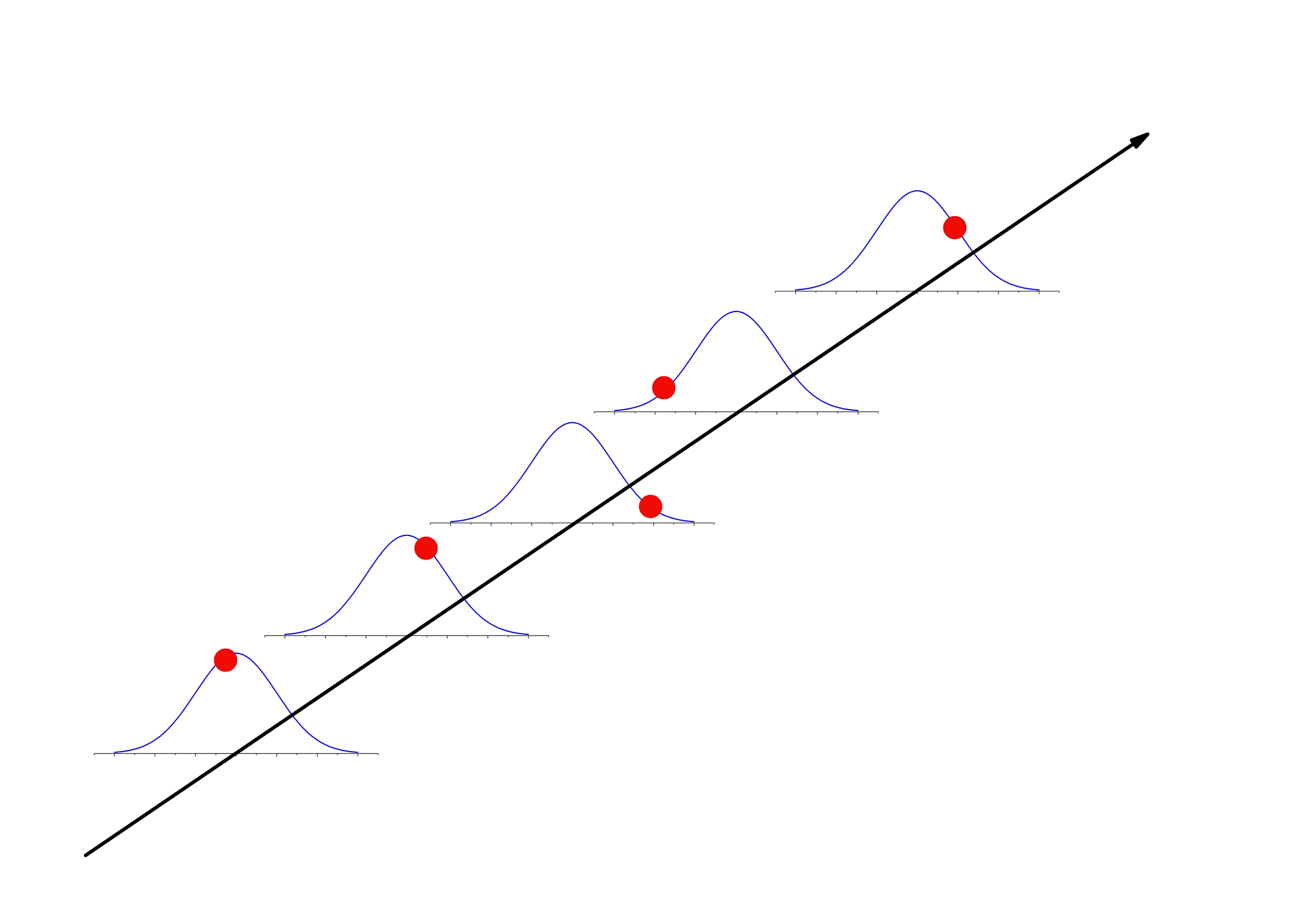
Рис. 1. Качественное пояснение разброса отдельных измерений.

Здесь возникает такой вопрос: увеличивая число измерений, мы можем определить искомую величину, казалось бы, с какой угодно точностью. Этот абсурдный вывод можно опровергнуть следующим образом. Во-первых, мы с самого начала не учитывали систематическую (т.е. инструментальную) погрешность. Очевидно, если случайная погрешность сравнялась с систематической, то дальше уже нет смысла ее уменьшать, накапливая число измерений. Следует поработать над конструкцией приборов с целью уменьшения систематической погрешности. Кроме того, в приведенных выше рассуждениях принималось, что измерения независимые. Если измерения делаются на одном и том же приборе, то абсолютной независимости гарантировать нельзя. В этом случае возникает некоторая зависимость между измерениями, и это тоже налагает определенный предел на количество измерительной информации. Наконец, любопытно сделать следующую оценку. Предположим, что, тем не менее, путем увеличения числа измерений, мы с помощью грубых приборов пытаемся выполнить тонкие измерения, например, с помощью обычной линейки определить размер атома. Примем, что для измерений с помощью линейки = 1 мм. Т.к. размер атома порядка 10-7 мм, чтобы достичь нужной точности, нам следует выполнить порядка 1014 измерений. Если мы предположим, что одно измерение делается в течение 1 секунды, нам потребуется лет: три миллиона лет!

Итак, на грубых приборах невозможно получить точных результатов. С помощью статистических методов можно лишь улучшить наивные оценки статистических погрешностей типа (1.3).

2. Обоснование оценок ошибок в косвенных измерениях

Независимые измерения

Ниже мы дадим вероятностное обоснование формуле (1.7). Итак, имеем измеряемые величины x и y. Нас интересует наилучшая оценка величины z с ее ошибками, которая связана с предыдущими соотношением . Представим , где Х есть среднее, а есть случайная добавка. Аналогично запишем для других величин. Будем считать, что случайные добавки распределены по нормальному закону. Тогда вероятность

Аналогично для . Мы здесь не выписываем нормировочных коэффициентов. Поскольку и независимы, то вероятность получения любых и равна

(7)

Сделаем в последнем выражении замену переменных: от и вначале перейдем к переменным и (очевидно, среднеквадратичные разбросы новых переменных: и ). Тогда . Теперь сделаем замену в (7): от и перейдем к переменным и . Путем простых, но громоздких преобразований можно показать:

, где .

Плотность распределения их вероятности будет:

где

(8)

имеет смысл дисперсии . Поскольку нас интересует вероятность появления некоторого при любом (при этом и независимы), то плотность распределения вероятности

Таким образом, величина также распределена по нормальному закону с разбросом , определяемым формулой (8).

Формула (8) легко обобщается на произвольную функциональную зависимость (см.1.8).

Еще раз напомним, что в этом разделе речь шла об оценке ошибок в случае, когда исходные величины независимые.

Выше речь шла о случайных погрешностях. Как в окончательном ответе учесть систематические ошибки? Суммарная ошибка, учитывающая как случайную, так и систематическую погрешность, может быть оценена либо как простая сумма ошибок (аналогично (1.3)), либо как корень квадратный из суммы квадратов (аналогично (8)). Обосновать ту или иную формулу, по крайней мере, в общем виде не представляется возможным. Очевидно, последняя оценка будет несколько меньше первой.

Доверительный интервал. Надежность оценок

Оценкой ошибок процесс обработки опытов еще не заканчивается. Необходимо еще выяснить надежность выполненных оценок. Это особенно важно в случае небольших выборок, но не только. Поясним сказанное. Как уже говорилось, в качестве оценки для математического ожидания принимается среднее арифметическое. Если число экспериментов велико, то с большой вероятностью среднее арифметическое будет близко к математическому ожиданию. Но при малом числе экспериментов, замена математического ожидания средним арифметическим может привести к некоторой погрешности, т.к. среднее арифметическое меняется в зависимости от числа элементов в выборке. Доверительный интервал и служит для целей оценки качества определения параметров.

Вначале рассмотрим введение доверительного интервала в асимптотическом приближении бесконечно большого числа экспериментов. Пусть для искомого параметра q в результате серии экспериментов получена оценка . Мы хотим оценить возможную ошибку. Назначим некоторую большую вероятность , такую, что с этой вероятностью событие можно было бы считать достоверным, и найдем такое значение , для которого вероятность отклонения оценки от искомого параметра в пределах этого значения будет равна , т.е.:

Это означает, что диапазон возможных ошибок при замене q на Q с большой вероятностью равен относительно Q. Вероятность попадания искомой величины вне этот диапазон, равная 1- будет мала. Вероятность принято называть доверительной вероятностью, интервал от до - доверительным интервалом. Еще этот интервал понимают как интервал значений, не противоречащих опыту. События, не попадающие в указанный интервал, имеют малую вероятность и считаются противоречащими опыту.

Как, задав , найти доверительный интервал? Для этого надо знать закон распределения величины . Как правило, он не известен, но центральная предельная теорема дает основания принять его нормальным. Тогда:

(9)

Здесь

Сделав в интеграле замену: , его можно привести к виду

, (10)

где использовано обозначение

- эта функция называется функцией Лапласа или функцией ошибок (в справочниках она может нормироваться по-разному).

Т.о., решая трансцендентное уравнение (10), находим для принятого . В математических справочниках приводятся таблицы решений уравнения типа (10), записанного в виде:

, где минус первая степень означает функцию, обратную к . Через эту величину доверительный интервал выражается следующим образом:

(11)

Перейдем к рассмотрению точной теории, учитывающей число экспериментов. Здесь принимается, что изучаемая величина описывается точно нормальным распределением. В этом случае доказана теорема, что величина подчиняется т.н. t – распределению Стьюдента с N-1 степенями свободы, обозначим это распределение (соответствующее выражение можно найти в книгах по теории вероятности и статистике). Далее рассуждения повторяются, только вместо функции (10) в уравнении, аналогичном (10), будет присутствовать функция . Из соответствующего уравнения опять находится коэффициент , который теперь будет функцией не только принятого уровня вероятности , но и от количества степеней свободы N-1(если искомых параметров р штук, то количество степеней свободы равно N-p). Доверительный интервал снова оценивается по формуле (11).

Аналогично можно рассчитать доверительный интервал и для дисперсии.

В практических применениях часто используют решение уравнения (9) с функцией Стьюдента. Соответствующие таблицы в зависимости от и N-p (p - число определяемых параметров) приводятся в руководствах по статистике и теории вероятностей. С их помощью можно оценить надежность статистических оценок. Так поступают часто даже в тех случаях, если закон распределения искомой величины неизвестен.

Каким принять уровень надежности? Не существует математических методов расчета уровня надежности. Это зависит от конкретной ситуации. Ранее было введено понятие стандартной ошибки. Это означает, что вероятностью 68% ожидаемая величина попадает в интервал и с вероятностью 32% не попадает. 32% - это почти половина от 68%. Надежность оценки в этом случае невелика. Общепринятым считается, что во многих случаях можно считать оценку надежной, если искомая величина попадает в доверительный интервал с вероятностью 95% и лишь с вероятностью 5% оказывается вне его. Для N-1=10 этому уровню надежности соответствует (для ). Таким образом, доверительный интервал примерно в (так и говорят: «две сигмы») соответствует примерно 95%-ому уровню надежности. В некоторых случаях требуется более высокий уровень надежности, скажем, 99% (в качестве примеров приведем следующие ситуации: ответственные или дорогостоящие – космические – эксперименты, или когда вероятность гибели людей отлична от нуля). Тогда доверительный интервал выбирают существенно больше, например, три сигмы.

Из понятия доверительного интервала вытекают несколько важных следствий.

1. Основываясь на этих представлениях, мы можем принять, что те измерения, которые сильно отклоняются от среднего значения, ошибочны. В качестве границы, отделяющей сильные отклонения от приемлемых, часто принимают - «правило трех сигм». Это правило используется для отбрасывания «подозрительных» данных.

2. Пусть оцененное в результате экспериментов значение какой-то величины есть , тогда как ожидаемое значение есть (частным значением может быть . С помощью t – распределения Стьюдента мы можем ответить на такой вопрос: приемлемо ли полученное значение ? Еще говорят так: можем проверить нуль гипотезу о том, что . Сокращенно пишут так: « против » (здесь буква Н от английского слова гипотеза – hypothesis). Для проверки гипотезы, во-первых, задается уровень надежности , скажем, 95%; во-вторых, вычисляется отношение . Далее, по таблицам находится (это значение коэффициента Стьюдента называют еще критическим). Если оцененное значение окажется больше критического , то гипотеза, что отвергается (в статистических исследованиях обычно избегают выражения «принять гипотезу» и предпочитают обсуждать вопрос отвергнуть или не отвергнуть).

Изложенная методика количественной оценки качества измерений будет использована далее.

3. Коэффициент корреляции

Выше, при выводе формул для ошибок в косвенных измерениях, мы предполагали, что соответствующие непосредственно измеряемые (случайные) величины являются независимыми. Здесь мы дадим количественную меру для оценки зависимости случайных величин.

Пусть мы имеем две случайные величины и . Для систем случайных величин, так же как и для одной, вводятся числовые характеристики – моменты. Обозначим плотность распределения вероятностей этих величин через . Смысл ее понятен: есть вероятность одновременного попадания и в соответствующие интервалы.

Начальными моментами порядка называется математическое ожидание:

(12)

Отсюда математическим ожиданием для величин и является: ; .

Центральным моментом порядка называется математическое ожидание:

(13)

Отсюда дисперсии ; . Они характеризуют рассеивание случайной точки (с координатами ) в направлении соответствующих осей.

Помимо приведенных моментов из формулы (13) вытекает существование еще одного момента второго порядка

, (14)

который называется смешанным или корреляционным моментом случайных величин , который описывает связь между случайными величинами. Для того, чтобы в этом убедиться, покажем, что для независимых случайных величин он равен нулю. Действительно, для независимых случайных величин функция плотности распределения вероятностей есть произведение вероятностей для каждой величины, т.е. . Тогда

(15)

Напоминаем, что угловые скобки здесь означают усреднение. Поскольку и, то из (4.4) следует, что в этом случае .

Итак, для независимых случайных величин корреляционный момент равен нулю. Обратное, вообще говоря, неверно. Равенство нулю корреляционного момента еще не означает, что величины независимые.

Рассмотрим другой предельный случай зависимых величин. Пусть . Для этого случая для вычисления корреляционного момента вместо двойного интеграла будет простой интеграл:

(16)

Это выражение можно симметризовать следующим образом. Из (13) в случае зависимых величин имеем: . Отсюда: . Подставляя его в (16), имеем:

. (17)

В практических расчетах вместо корреляционного момента часто используют коэффициент корреляции , который определяется следующим образом:

(18).

Очевидно, в случае независимых величин вслед за корреляционным моментом коэффициент корреляции равен нулю. В случае линейно зависимых величин с помощью (4.5, 4.6) получим:

(19).

Отсюда видно, что коэффициент корреляции равен единице, если у растет вместе с х, и минус единице, если убывает.

В общем случае, т.е. произвольной вероятностной зависимости между величинами, коэффициент корреляции оказывается заключен в пределах: . Если коэффициент корреляции положителен, то говорят о положительной корреляции, отрицателен – об отрицательной.

4. Оценка погрешности в косвенных измерениях. Зависимые величины

Теперь мы можем дать формулу оценки погрешности в случае косвенных измерений, когда измеряемые величины являются зависимыми (точнее, коррелированными), т.е. обобщить формулу (19). Напомним, пусть мы измеряем величины x и y, а нас интересует величина . Мы хотим получить рецепт расчета погрешности , если известны погрешности x и y и известно, что они не являются независимыми. Как и в Теме 1 разложим , здесь использовано представление и , где и - случайные величины, характеризующие разброс измеряемых величин вокруг истинных значений X и Y. Используя это представление, вычислим дисперсию :

Как и выше здесь использованы обозначения . Очевидно, . Окончательно,

(20)

Эта формула обобщает расчет ошибок в косвенных измерениях, если непосредственно измеряемые величины являются коррелированными.

Лишние данные

В разделе 1 было показано, что погрешность измерения среднего равна , где есть дисперсия ошибок, есть число измерений. Там же был сформулирован парадокс: поскольку при мы можем сделать ошибку сколь угодно малой, то можно ожидать, что с помощью грубых приборов можно производить измерения со сколь угодно большой точностью. Один из ответов был такой: в этих рассуждениях предполагалось, что инструментальной ошибкой мы можем пренебречь. Очевидно, если случайная ошибка сравнивается с инструментальной (систематической), то дальше накапливать измерения просто нет смысла. Оказывается, что корреляции между ошибками в процессе измерений также накладывают ограничение на число измерений.

С этой целью рассмотрим такую демонстрационную задачу. Пусть нас интересует некоторая случайная величина

(21)

Обратим внимание на то, что индексом i отмечается i-я случайная величина x.

Далее как обычно большими буквами будем обозначать средние соответствующих величин. Тогда

Дисперсия

(22)

Обозначим стоящее под знаком суммы выражение: . Эту величину называют ковариационной матрицей. В частном случае она будет равна ковариационному коэффициенту.

Допустим, что

(23)

Где есть дисперсия х (в нашем демонстрационном расчете принимаем ее постоянной), r есть коэффициент корреляции между различными х (его тоже принимаем постоянным). Из приведенного выражения видно, что ковариационная матрица имеет одинаковых значений, равных (они располагаются на диагонали), и, соответственно значений, равных . Таким образом:

(24)

Рассмотрим следствие из формулы (24). Предположим, что - некоторые измеряемы величины. Как правило, для их случайной составляющей предполагается некоторый закон распределения, при этом для простоты полагают, что они независимые, т.е. (некоррелированные величины). Отсюда дисперсия интересующей нас величины равна: . Но если коэффициент парной корреляции отличен от нуля, то стандартное отклонение интересующей нас величины растет с гораздо быстрее. Отсюда вытекает ограничение на нужное количество измерений:

(25)

Аналогично можно показать (Эльясберг), что при наличии корреляций между ошибками в различных измерения одной и той же величины среднее значение интересующей нас величины имеет стандартное отклонение:

; при . (26)

В настоящее время нередко проводятся эксперименты с большим количеством измерений. Особенно это стало возможно в компьютерную эру. При этом, в процессе обработке молчаливо предполагается, что различные измерения являются независимыми. Из последней формулы видно, к каким ошибкам это может привести. Очевидно, оптимальное значение измерений получается согласно (25).

Вместе с тем, следует отметить, что, если коэффициент корреляции между измерениями в последовательной серии мал, то на практике его очень трудно бывает оценить.

Резюме. Результат (26) указывает, что к понятию состоятельности оценки надо относиться с осторожностью. Действительно, оно выполняется лишь асимптотически, когда число экспериментов . Но в этом случае начинают сказываться корреляции между измерениями. Тогда оценка может стать неэффективной, т.к. при погрешность выражается не формулой , а формулой , согласно которой погрешность вовсе не убывает с ростом числа экспериментов.

Это вывод говорит о том, что к оценкам, получаемым методами математической статистики надо относиться с осторожностью. Некоторые авторы даже утверждают, что понятие состоятельной оценки является мифом ХХ века!

Литература

Бисноватый-Коган Г.С.: Релятивистская астрофизика и физическая космология. - М.: КРАСАНД, 2011

Паркер Ю.Н.: Беседы об электрических и магнитных полях в космосе. - Ижевск: Ижевский институт компьютерных исследований, 2010

Самойленко П.И.: Теория и методика обучения физике. - М.: Дрофа, 2010

Верходанов О.В.: Радиогалактики и космология. - М.: ФИЗМАТЛИТ, 2009

Горелов А.А.: Концепции современного естествознания. - М.: Юрайт, 2009

Кирьянов В.И.: Описание фазовых состояний Вселенной через фундаментальные постоянные. - М.: ЛИБРОКОМ, 2009

Колесниченко А.В.: Турбулентность и самоорганизация . - М.: БИНОМ, 2009

Котельников В.А.: Собрание трудов. - М.: ФИЗМАТЛИТ, 2009

Под ред. В.Д. Кузнецова: Солнечно-земная физика. - М.: ФИЗМАТЛИТ, 2009

Фортов В.Е.: Экстремальные состояния вещества. - М.: ФИЗМАТЛИТ, 2009

Яценко А.С.: Оптические спектры N- и O-подобных ионов. - Новосибирск: Наука, 2009

Котельников В.А.: Собрание трудов. - М.: Физматлит, 2008

Гопка В.В.: Вселенная и человек. - Новосибирск: Сибмедиздат НГМУ, 2007

Гопка В.В.: Так сколько же вселенных? По крайней мере не меньше двух!. - Запорожье: Днепровский металлург, 2007

Кондратьев А.С.: Задачи по термодинамике, статистической физике и кинетической теории. - М.: ФИЗМАТЛИТ, 2007

Сивухин Д.В.: Общий курс физики. - М.: Физматлит, 2006

Братухин Э.Н.: Физическая вселенная. Вариант второй (гипотеза). - М.: Антиква, 2004

PAGE \* MERGEFORMAT 1

Обоснование оценок искомых параметров и их ошибок