Метод наименьших квадратов
PAGE 2
Реферат
Метод наименьших квадратов
Содержание
Вероятностное обоснование МНК как наилучшей оценки
Прямая и обратная регрессии
Общая линейная модель. Многофакторные модели
Доверительные интервалы для оценок МНК
Дисперсионный анализ
Взвешенный МНК
Литература
Вероятностное обоснование МНК как наилучшей оценки
Рассмотрим следующую задачу. Пусть из теоретических соображений мы знаем, что
. Пусть мы провели измерений и получили выборку пар . Наша задача – найти коэффициенты .
Если изобразить результаты измерений на графике, то они не лягут в точности на прямую. Будет некоторый разброс. Поэтому можно сказать, что наша задача состоит и в том, чтобы провести прямую наилучшим образом. Начнем с простейшего подхода.
В дальнейших рассуждениях пренебрежем ошибкой в . Будем считать, что вся ошибка заключена в . Представим результаты измерений следующим образом: , где есть случайная величина со средним значением ноль. Будем подбирать искомые коэффициенты из соображений, чтобы случайная добавка была наименьшей. Введем с этой целью невязку и найдем минимум невязки:
Эти уравнения называются в теории МНК нормальными уравнениями. Они и служат для определения искомых коэффициентов.
Перепишем их следующим образом:
Решение этих уравнений имеет вид:
Полученная линия называется линией аппроксимации по методу наименьших квадратов, еще говорят линией регрессии у по х.
В стандартных учебниках обычно на этом и заканчивается изложение метода НК. Однако до завершения еще далеко. Во-первых, следует оценить ошибки коэффициентов, найти для них доверительные интервалы. Во-вторых, следует оценить качество регрессии. Все это достаточно тонкие и сложные вопросы. Но их надо решать.
Перейдем к оценке ошибок коэффициентов. Для этого сделаем некоторые предварительные замечания и преобразуем найденные выражения.
Введем средние значения для : , аналогично : .
Вычислим:
аналогично для
Тогда
Перепишем теперь коэффициенты. Для
Последняя сумма равна нулю, и окончательно имеем:
Это соотношение следует рассматривать таким образом:
Мы приняли, что основная ошибка заключена в у, а х не флуктуируют. Последнюю формулу мы можем рассматривать как линейную комбинацию у, в которой х выступают как фиксированные неслучайные числа. Если предположить, что yi и yj между собой независимы и дисперсия , то мы уже получали, что дисперсия b
Как оценить ? Очевидно,
На самом деле – это смещенная оценка, т.к. вместо истинных значений и подставляются лишь их оценки. Более детальные расчеты показывают, что вместо надо подставить : 2 здесь потому, что в задаче 2 искомых параметра и . Тогда правильная оценка для дисперсии будет:
.
Если бы в задаче было бы р искомых параметров, то надо было бы записать:
.
Этим и заканчивается оценка ошибки коэффициента .
По аналогии можно показать, что дисперсия коэффициента равна:
Чтобы убедиться в том, что значения коэффициентов, полученные МНК, являются наилучшими, применим принцип максимального правдоподобия. Опять же пренебрежем погрешностью в и будем считать, что вся погрешность заключена в . Примем, что i –й результат измерений – это есть какое-то конкретное случайное число, случайная реализация из бесконечного набора случайных чисел. Этот набор случайных чисел подчиняется нормальному закону распределения и характеризуется разбросом, или стандартным отклонением . Будем считать, что стандартное отклонение во всех измерениях одинаковое, т.е. . И последнее: считаем, что результаты измерений между собой независимые. Тогда вероятность получить в результате измерений набор чисел равна:
Наилучшую оценку для и даст . И мы приходим к нормальным уравнениям для и .
После того, как найдены коэффициенты и , дифференцируя вероятность по , находим выражение для нее, совпадающее с тем, что мы использовали выше, где уже учтено количество степеней свободы.
Прямая и обратная регрессии
Перепишем расчетные формулы в несколько иной форме. Дополнительно к приведенным формулам введем:
и корреляционный момент:
.
Тогда формулы для коэффициентов регрессии можно переписать в следующем виде:
, . Само уравнение регрессии принимает вид:
.
Если принять за независимую переменную у, а за зависимую х, то можно показать, что уравнение регрессии примет вид:
.
Здесь надо учесть, что .
Обратите внимание, что последнее уравнение не получается из предыдущего путем простого выражения х через у. Если нарисовать графики этих двух регрессий, то мы будем иметь следующее:
Покажем, что в общем случае эти две регрессии не совпадают. С этой цель рассчитаем :
Чтобы прямые совпадали, должен равняться нулю, или: . В каком случае это возможно? Для этого учтем, что
, . Учитывая выражение для корреляционного момента через коэффициент корреляции: , получаем: .
Вывод: прямая и обратная регрессии совпадают только в том случае, если коэффициент корреляции равен 1. В противном случае нельзя поступать так: скажем, нашли регрессию у по х, т.е. зависимость у от х. После этого, если нам надо найти какое-то значение х, просто в полученное уравнение подставляем соответствующее значение у и находим обратное решение. В действительности нужно поступить по-другому. Надо вначале построить обратную регрессию х по у. И уже из этой регрессии находить х при нужном значении у.
Пример
Исследования распределения тяжелых элементов в галактическом диске Wielen et al. 1996.
Содержание тяжелых элементов в звездах часто характеризуется интегральной величиной, которую называют металличностью:
По данным о рассеянных скоплениях:
соответственно, градиент у них получился .
По данным о распределении звезд по возрастам, но теперь в окрестности Солнца, они построили зависимость:
, здесь - возраст звезды в млрд лет. После этого они предложили модель химической эволюции галактического диска:
В качестве примера, иллюстрирующего, как будет меняться со временем по галактическому диску металличность, они на основе своей формулы построили такой рисунок:
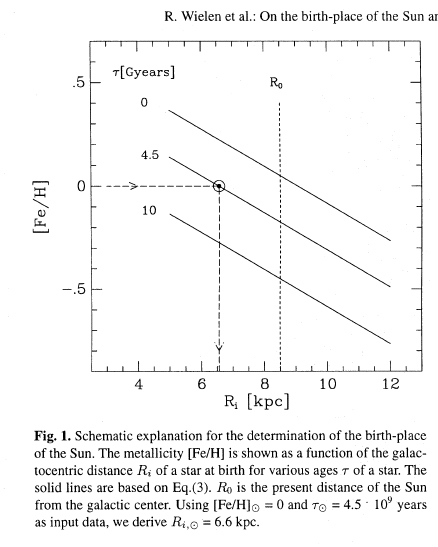
И далее сделали удивительный вывод. Они решили, что найденная модель позволяет определять места рождения звезд, т.е.:
Приняв для Солнца его возраст и металличность (по определению, для Солнца она равна нулю), авторы получили, что в момент рождения оно находилось примерно на 1.9 кпк ближе к галактическому центру, нежели его современное расстояние.
Ошибка при этом у них оценивалась примерно в 1 кпк. Так что на уровне стандартного отклонения и даже почти 2 этот радиальный сдвиг Солнца достоверен. Они же развили теорию диффузии звездных орбит по радиусу галактики. Эта работа в свое время вызвала огромный резонанс. Многие авторы считали, что она решает ряд проблем, как Солнца, так и Галактики. Авторы этой работы – известные специалисты. Их авторитет и большое количество ссылок создали видимость, что здесь все правильно. Но оказалось, что это не так.
Во-первых, эту работу покритиковал известнейший специалист в области исследований химического состава звезд – Тварог.
1. Он обратил внимание на то, что выборка Вилена и др. не является представительной. Еще говорят так: не является репрезентативной.
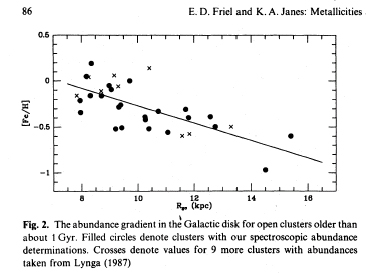
Посмотрите, где заканчиваются данные в этой работе: они охватывают область кпк и не заходят во внутреннюю область, откуда, по мнению Вилена и др., Солнце продиффундировало к нынешнему положению.
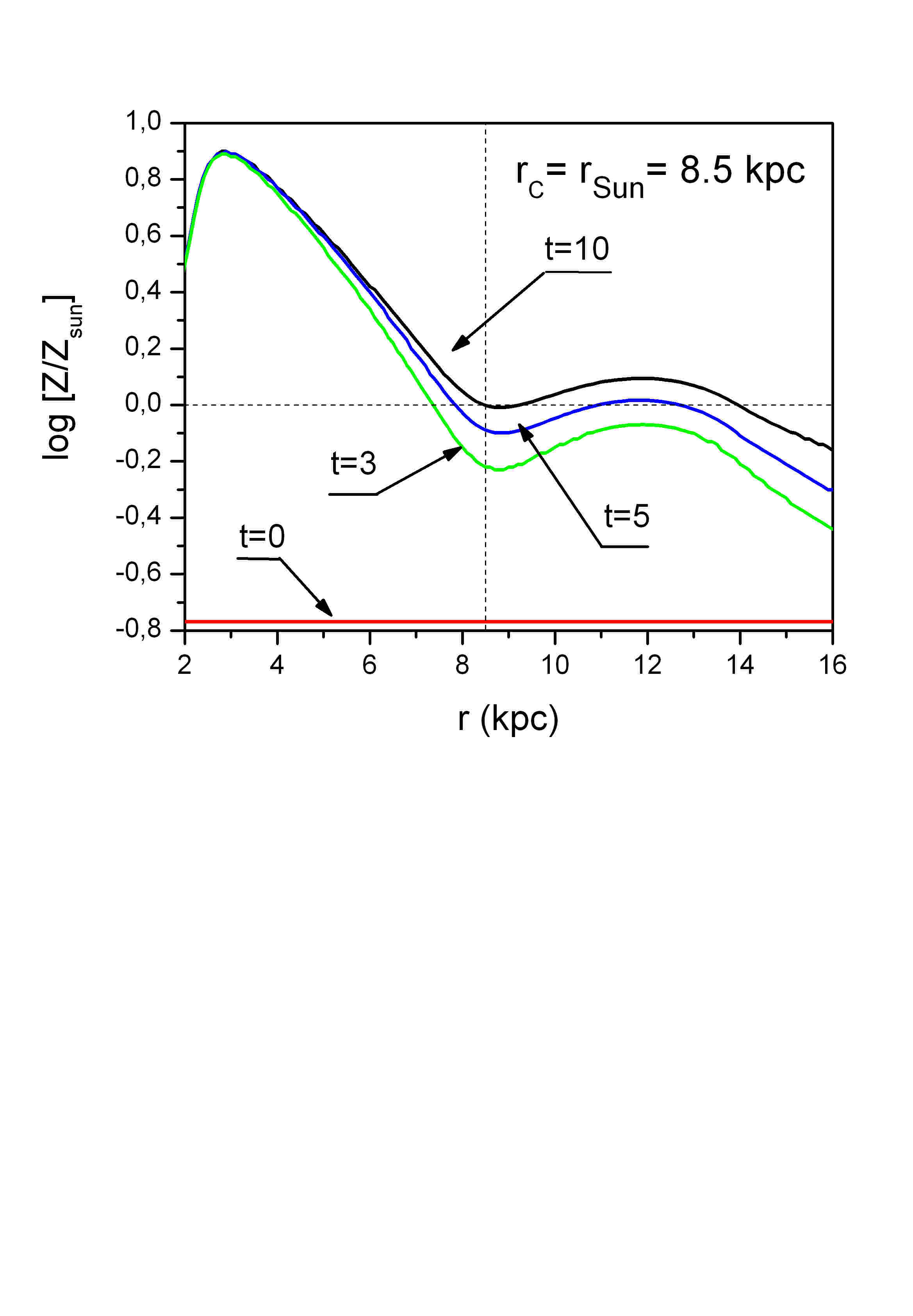
2. Авторы заложили крайне упрощенную модель распределения тяжелых элементов в виде линейной функции с единым в значительной части диска галактики градиентом. Такое представление ниоткуда не следует, и более поздние работы, в частности, наши с И.А. и моим постоянным соавтором на протяжении уже 10 лет из ин-та Астрономии при университете Сан Паулу (Бразилия) Ж.Лепиным показывают, что радиальное распределение тяжелых элементов в галактических дисках вовсе не описывается линейной функцией. Более того, распределение деформируется со временем.
3. И еще одна деталь. Вилен с соавторами упустили, что из прямой регрессии нельзя делать обратные расчеты. Мои расчеты показывают, что если по тем же данным построить регрессионную зависимость от , то получается совершенно другой результат:
Если эту формулу привести к виду, аналогичному Вилену и др., то получим:
Отсюда . С учетом стандартной погрешности в определении расстояний кпк, приведенное выше смещение можно считать недостоверным.
В обсуждаемой работе много других предположений, которые вызывают недоумение, но я не буду на них останавливаться.
Общая линейная модель. Многофакторные модели
Приведенную схему можно обобщить на произвольное число независимых переменных. Пусть у нас есть набор переменных . Их называют «объясняющие» переменные. И мы имеем линейное соотношение:
Допустим, что из серии экспериментов мы получили мерных векторов . Наша задача – найти коэффициенты . Опять же будем считать, что все ошибки заключены в .
Поставленная задача решается путем минимизации невязки, но уже методами матричного исчисления. Соответствующие формулы можно найти в литературе, которую я привел в начале курса.
Под величинами можно понимать какие-то функции, например, разложение функции в виде ряда по степеням , или по каким-то другим функциям, например, синусам – косинусам – тогда это есть ряд Фурье для представления искомой функции и т.д. Важной особенностью обсуждаемого представления является то, что искомые параметры – коэффициенты - входят в модельное представление линейным образом. Поэтому такие модели называются линейными. Подчеркну еще раз: зависимость от может быть нелинейной, но если искомые коэффициенты входят линейно, то модель называется линейной. Выделенность линейной модели связана с тем, что в этом случае есть однозначный рецепт, как искать параметры модели и как рассчитывать погрешности.
Как поступать, если искомые коэффициенты входят нелинейно? В некоторых случаях задача имеет скрытую линейность и может быть приведена к линейной путем замены переменных. Например: Очевидно, путем логарифмирования получаем: . Далее в качестве зависимой переменой выбирается , а вместо искомой величины ищется . Очевидно, модель в действительности является линейной. Однако, здесь надо помнить, что законы распределения и отличаются. Впрочем, это требуется для детального расчета погрешностей. Если ограничиться простейшим подходом, то эти тонкости можно опустить.
Как поступать, если задача не приводится к линейной, т.е. является существенно нелинейной. Здесь возникают, по крайней мере, 2 проблемы.
1. Как найти минимум невязки? Здесь, в свою очередь, возникают 2 вопроса.
Во-первых, с помощью какого алгоритма искать минимум? Существуют специальные методы поиска минимумов в случае многомерных нелинейных задач.
Во-вторых, минимумов может быть несколько. Действительно, в линейной модели невязка есть квадратичная форма от искомых параметров. В этом случае минимум будет единственный. В нелинейной модели, как уже говорилось, минимумов может быть несколько. Спрашивается, какой минимум принять за решение? Ответ может быть двоякий. Либо ищется глобальный минимум, либо выбирается тот минимум, который отвечает дополнительным связям.
2. Как вычислить ошибки? Аналитических выражений для ошибок в общем случае нет. Ошибки ищутся путем линеаризации невязки по искомым параметрам вблизи минимума.
Пример. Определение параметров галактического вращения.
аналогично:
Разлагаем в ряд Тейлора угловую скорость:
; .
Разлагая угловую скорость до любого порядка, в принципе, можно найти кривую вращения для любых расстояний с любой точностью. Ограничения накладываются имеющимися данными и требованием, чтобы коэффициенты были достоверные.
Доверительные интервалы для оценок МНК
После построения регрессии нужно еще определить ее качество.
Начнем с рассмотрения доверительных интервалов для искомых коэффициентов. Мы нашли уже стандартные отклонения для коэффициентов a и b:
; .
Для определения доверительных интервалов воспользуемся критерием Стьюдента. Назначим какой-то уровень надежности, (скажем, ). Находим по таблицам соответствующее значение . Тогда доверительные интервалы будут: ; .
Теперь мы можем проверить следующую гипотезу: предположим, что для коэффициентов мы ожидаем некоторое значение. По-видимому, наиболее актуально – нулевое значение того или иного параметра. Скажем, в задаче Хаббла о законе расширения Вселенной, коэффициент a равен нулю. Допустим, что, не зная этого из теории, как оно и было в истории с Хабблом, мы предположили общую линейную модель со свободным членом, отличным от нуля. После обработки экспериментов, мы находим оба коэффициента. Определяем доверительные интервалы. И теперь можем рассмотреть нуль гипотезу: (в частном случае ) против альтернативы . Идея такая: вычисляется
. Это значение сравнивается с табличным . Очевидно, если , то - гипотеза отбрасывается. Впрочем, Если не попадает в интервал , то это и означает, что на принятом уровне вероятности -гипотеза отвергается.
Аналогичная работа проводится с другими коэффициентами. После того, как недостоверные коэффициенты установлены, их следует исключить из рассмотрений и повторить расчеты. И т.д. Однако на этом обработка не заканчивается. Поясню сказанное следующим примером. Предположим, мы рассматриваем следующую модель:
. При этом, нам заранее не известна наибольшая степень показателя k. Более того, какие-то слагаемые в этой сумме могут и не присутствовать, иными словами, какие-то коэффициенты bi могут быть равными нулю. Как определить максимальную степень икса, и какие коэффициенты следует исключить из рассмотрения. Во-первых, указанием на включение или не включение того или иного слагаемого может служить критерий Стьюдента. Во-вторых, для окончательного решения вопроса следует убедиться, что та или иная аппроксимация является наилучшей (по крайней мере, среди рассмотренных вариантов).
Дисперсионный анализ
Начнем с понятия о дисперсионном анализе регрессии. Разберем это понятие на примере линейной зависимости. Согласно МНК можем представить:
, где . Здесь второе соотношение – найденное уравнение регрессии, есть случайная величина со средним, равным нулю. Усредняя, находим:
. Введем: и . Обратить внимание на малые и большие буквы. Через эти обозначения уравнение регрессии можно записать так:
. Кроме того: .
Вычислим теперь такую сумму:
.
Покажем, что средняя сумма равна нулю.
В принятых обозначениях , поэтому действительно .
Окончательно интересующая нас сумма может быть разбита на 2 части:
Чтобы проанализировать смысл полученного разбиения, нарисуем график:
Во-первых, заметим, что регрессионная прямая всегда проходит через средние значения.
Во-вторых, смысл первой суммы есть вариация зависимой переменной около среднего значения, которая объясняется регрессией. Вторая сумма – это та часть вариации, которая регрессией не объясняется. Отсюда видно, что качество регрессии тем лучше, чем меньше доля второй суммы по отношению к исходной. Для случая зависимости от одной переменной (ее еще называют предиктором), можно показать, что:
, где есть коэффициент корреляции между х и у. Можно еще записать так:
. Отсюда видно, если не будет случайных ошибок, то . Величину еще называют коэффициентом детерминации. По смыслу сказанного ясно, что он позволяет судить о качестве регрессионной модели.
С учетом степеней свободы коэффициент детерминации определяется так:
Другой взгляд на то, что показывает коэффициент детерминации. Регрессионная прямая, как уже отмечалось, проходит через средние значения. Она может проходить либо под углом к оси абсцисс, либо горизонтально. В первом случае мы имеем, что между х и у есть некоторая зависимость. Во втором – зависимость отсутствует. Коэффициент детерминации позволяет сделать выбор между этими двумя возможностями.
Какова количественная мера того, что коэффициент детерминации значим? Заметим здесь, что если в задаче один предиктор, то ответ на этот вопрос дается с помощью критерия Стьюдента. Коэффициент детерминации сохраняет свое значение и в случае многофакторного анализа, но в этом случае используется несколько другая статистика – статистика Фишера.
Типичная задача. Пусть мы имеем какое-то регрессионное уравнение, скажем,
. Под понимаю какой-то объясняющий предиктор. Спрашивается, все ли к предикторов должны участвовать в модели, или какие-то m штук в модель не входят, т.е. соответствующие коэффициенты равны нулю? В последнем случае модель имеет вид:
.
Задача решается следующим образом. Вначале строится первая модель и находится коэффициент детерминации, обозначим его . Затем строится вторая модель без m предикторов и находится коэффициент детерминации . Затем вычисляется величина
.
Эта величина подчиняется статистике Фишера с (m,N-k-1) степенями свободы. Как и для коэффициента Стьюдента, для нее рассчитаны таблицы. Работа с ними строится так. Назначается заданный уровень значимости. По таблицам находится критическое значение F-статистики Фишера с соответствующим количеством степеней свободы. Если рассчитанное значение превосходит критическое, то нулевая гипотеза, заключающаяся в том, что рассматриваемые m переменных не входят в модель, отвергается. Собственно говоря, из структуры для F видно, что если исключены m каких-то переменных и при этом коэффициент детерминации мало изменился, то это и означает, что добавление этих переменных мало меняет остатки. Соответственно, эти переменные можно и не включать. Но если разность будет большой, то это означает, что изменение остатков существенное, существен вклад этих m предикторов, и исключать их неправомерно.
На практике не исключают сразу несколько предикторов, а анализируют по очереди.
Приведу такой пример. Пусть процесс описывается функцией , а мы, не зная этого, моделируем его функцией . В силу того, что в экспериментальных данных будут погрешности, скорее всего, все коэффициенты будут отличны от нуля. Но после построения регрессии общего вида, следует проверить достоверность коэффициентов по критерию Стьюдента, формулировав нулевую гипотезу для каждого коэффициента. Затем, выбрав недостоверный коэффициент, исключить его. Построить новую регрессию, и с помощью статистики Фишера убедиться, что исключение соответствующего коэффициента было значимо.
Собственно говоря, в этом и состоит дисперсионный анализ.
Взвешенный МНК
До сих пор явно или неявно предполагалось, что дисперсия погрешностей , т.е. постоянная величина. Однако, это сильная идеализация. В примере с кривой вращения галактики выражение для лучевой компоненты скорости имеет вид: . Уже из этого выражения ясно, что чем дальше от нас отстоит звезда, тем больше будет погрешность в измерении скорости. Следовательно, надо это каким-то образом учесть.
Другой пример. Часто измерения на графике приводят погрешностями – барами.
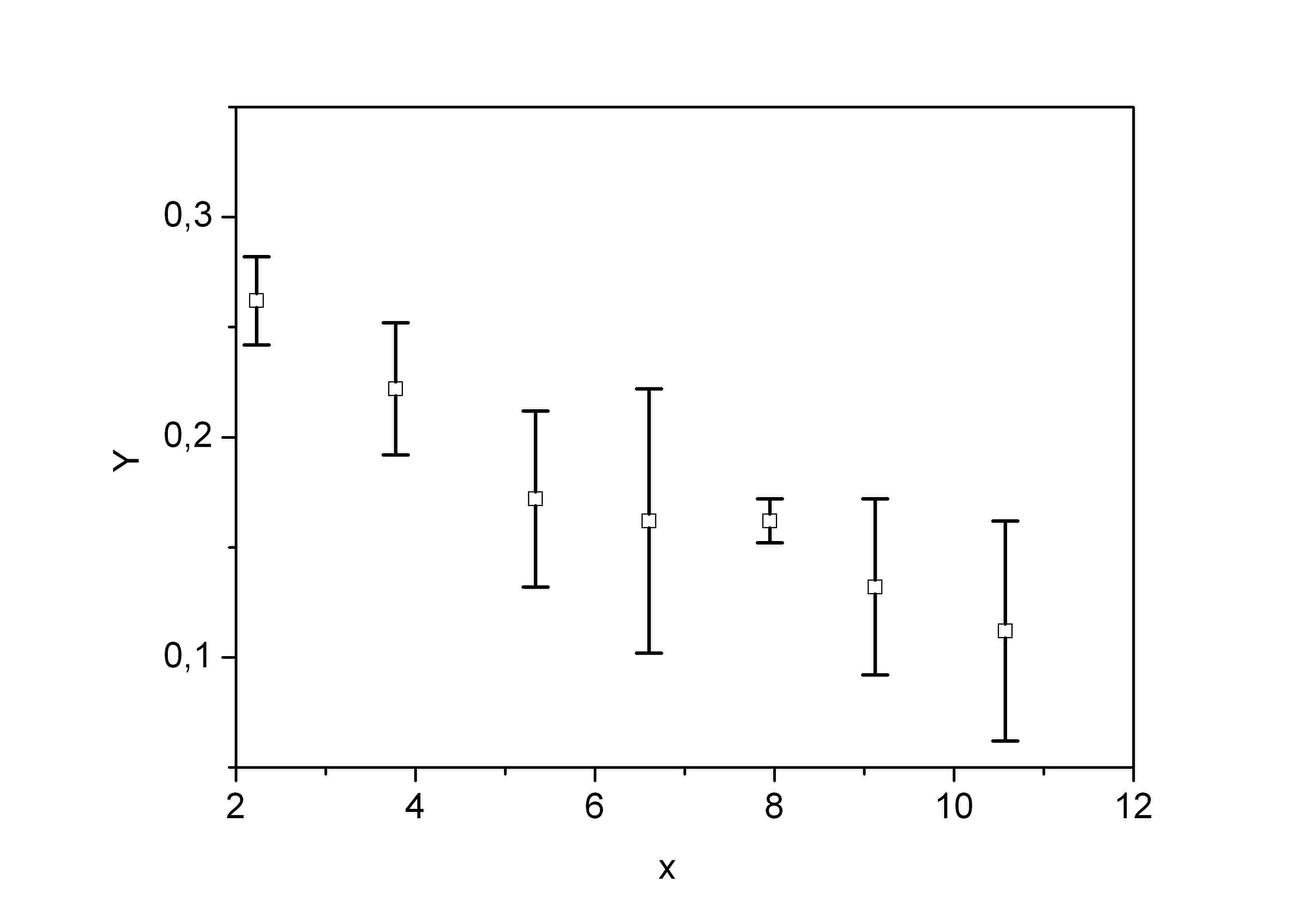
Из этого рисунка видно, что некоторые значения имеют большую ошибку, некоторые – маленькую. Это значит, что те, которые имеют маленькую ошибку, должны иметь больший вес, чем те, которые имеют большую ошибку.
Как учесть эту ошибку в МНК? Если результаты измерений представлены с ошибками, как это показано на последнем рисунке, то поступать следует таким образом.
Допустим, что разброс (или среднеквадратичное отклонение) и-того измерения есть . Введем вес : , где пока неизвестная величина.
Вместо отклонения измерений от регрессии введем новое так, что:
.
Ясно, что дисперсия и-того измерения будет: .
Далее, составляем невязку относительно .
. И минимизируем ее.
В примере с кривой вращения можно поступить так. Из структуры формулы можно высказать предположение: . Тогда в качестве веса берем: , делаем замену переменных, вводим новую невязку, находим минимум.
Литература
1. Битнер, Г.Г. Теория вероятностей: Учебное пособие / Г.Г. Битнер. - Рн/Д: Феникс, 2012. - 329 c.
2. Большакова, Л.В. Теория вероятностей для экономистов: Учебное пособие / Л.В. Большакова. - М.: ФиС, 2009. - 208 c.
3. Гмурман, В.Е. Теория вероятностей и математическая статистика: Учебное пособие для бакалавров / В.Е. Гмурман. - М.: Юрайт, 2013. - 479 c.
4. Горлач, Б.А. Теория вероятностей и математическая статистика: Учебное пособие / Б.А. Горлач. - СПб.: Лань, 2013. - 320 c.
5. Калинина, В.Н. Теория вероятностей и математическая статистика: Учебник для бакалавров / В.Н. Калинина. - М.: Юрайт, 2013. - 472 c.
6. Климов, Г.П. Теория вероятностей и математическая статистика / Г.П. Климов. - М.: МГУ, 2011. - 368 c.
7. Колемаев, В.А. Теория вероятностей и математическая статистика: Учебник / В.А. Колемаев, В.Н. Калинина. - М.: КноРус, 2013. - 376 c.
8. Колесников, А.Н. Теория вероятностей в финансах и страховании / А.Н. Колесников. - М.: Анкил, 2008. - 256 c.
9. Кочетков, Е.С. Теория вероятностей в задачах и упражнениях: Учебное пособие / Е.С. Кочетков, С.О. Смерчинская. - М.: Форум, 2011. - 480 c.
10. Кочетков, Е.С. Теория вероятностей и математическая статистика: Учебник / Е.С. Кочетков, С.О. Смерчинская, В.В. Соколов. - М.: Форум, НИЦ ИНФРА-М, 2013. - 240 c.
11. Краснов, М.Л. Вся высшая математика. Т. 5. Теория вероятностей. Математическая статистика. Теория игр: Учебник / М.Л. Краснов, А.И. Киселев, Г.И. Макаренко [и др.]. - М.: ЛКИ, 2013. - 296 c.
12. Кремер, Н.Ш. Теория вероятностей и математическая статистика: Учебник для студентов вузов / Н.Ш. Кремер. - М.: ЮНИТИ-ДАНА, 2012. - 551 c.
13. Лебедев, А.В. Теория вероятностей и математическая статистика: Учебное пособие / Л.Н. Фадеева, А.В. Лебедев; Под ред. проф. Л.Н. Фадеева. - М.: Рид Групп, 2011. - 496 c.
14. Лунгу, К.Н. Сборник задач по высшей математике. 2 курс: С контрольными работами: Ряды и интегралы. Векторный и комплексный анализ. Дифференциальные уравнения. Теория вероятностей. Операционное исчисление / К.Н. Лунгу, В.П. Норин, Д.Т. Письменный; Под ред. С.Н. - М.: Айрис-пресс, 2011. - 592 c.
15. Мхитарян, В.С. Теория вероятностей и математическая статистика: Учебник для студентов учреждений высшего профессионального образования / В.С. Мхитарян, В.Ф. Шишов, А.Ю. Козлов. - М.: ИЦ Академия, 2012. - 416 c.
EMBED Equation.3 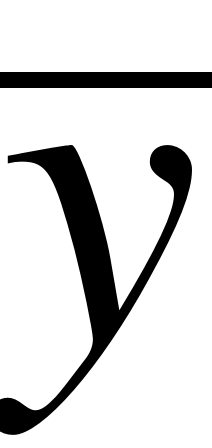
EMBED Equation.3 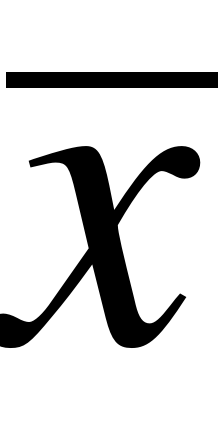
EMBED Equation.3 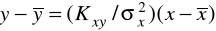
EMBED Equation.3 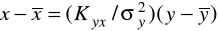
r
R0
0R0
R
l
Метод наименьших квадратов