Элементы теории вероятностей
PAGE \* MERGEFORMAT 5
Реферат
Элементы теории вероятностей
Содержание
1. События. Вероятность
2. Непрерывные случайные величины
3. Числовые характеристики случайных величин
4. Нормальный закон
5. Понятие функции случайной величины
6. Центральная предельная теорема
7. Закон больших чисел
Литература
1. События. Вероятность
Случайные ошибки следует описывать методами теории вероятностей. Ниже будут приведены некоторые основные сведения из теории вероятностей. Тут надо сказать, что само понятие вероятности базируется на интуитивных представлениях. Мы не будем вводить формально строгих определений, а последуем как раз интуитивным представлениям.
К случайным относятся события, предсказать конкретную реализацию которых невозможно. Причина невозможности предсказаний может быть разной – то ли это внутренняя природа явлений (как в случае с квантовыми явлениями), то ли это следствие нашего неполного знания. Оговоримся лишь о следующем: теория вероятности и статистика рассматривают не любые случайные события, а лишь те, которые обладают т.н. статистической устойчивостью.
Введем определения. Событием называется конкретная реализация некоторого эксперимента, скажем, измерение какой-то величины. Набор всевозможных событий – результатов данного эксперимента – образует полную группу событий. События называются несовместными, если никакие два из них не могут произойти вместе.
Как оценить вероятность реализации того или иного события? Наиболее просто она оценивается тогда, когда полная группа событий может быть представлена как совокупность N равновозможных случаев, а рассматриваемое событие А состоит в реализации одного из n этих случаев. Тогда вероятность этого события Р(А) находится по формуле:
(1)
Эта величина имеет смысл частоты реализации события А. Очевидно, вероятность реализации какого-то события заключена в пределах от 0 до 1. Ноль означает, что событие невероятное. Единица – достоверное.
Результат определения частоты реализации какого-то события в разных сериях может оказать различным. При малом числе экспериментов разброс может быть значительным. Однако, по мере увеличения числа экспериментов он может стремиться к некоторому пределу. Такие события называют статистически устойчивыми. Они и являются предметом теории вероятностей. События, не обладающие этим свойством, называют неопределенными, и теорией вероятности они не рассматриваются.
Суммой двух событий А и В называется событие С, состоящее в выполнении или события А, или В или обоих вместе. Записывается так: С = А + В. Это определение очевидным образом распространяется на несколько событий.
Произведением двух событий (А и В) называется событие С, состоящее в совместном выполнении события А и В. Опять же, это определение очевидным образом распространяется на несколько событий.
Часто полезно бывает изображать событие как множество точек на плоскости, см. рис 1.
Рис. 1. Сумма и произведение событий.
Для дальнейшего нам важно уметь рассчитывать вероятности для суммы и произведения событий, если известны вероятности исходных событий.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий. Для доказательства этой теоремы подсчитывается частота событий А и В. Поскольку события несовместны, то суммарная частота реализации этих событий и дает вероятность суммы событий. Очевидно, она равна сумме вероятностей. Можно также воспользоваться рис. 1 для вывода этой формулы. Действительно, пусть события А и В будут подмножеством некоторого множества D. Вероятность события А мы можем оценить как отношение «площади» А к «площади» D. Соответственно и для события В. Тогда вероятность для суммы несовместных событий будет равна приведенной выше формуле.
Как подсчитать вероятность суммы совместных событий? Пользуясь последним методом, легко сообразить, что она равна:
(2)
Как вычислять вероятность произведения событий? Введем вначале определение независимых событий. Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Можно показать, что обратное утверждение верно, если выполняется прямое.
Вероятность произведения двух событий Р(АВ) равна:
, (3)
где Р(В|А) – т.н. условная вероятность реализации события В при условии, что событие А имело место. Здесь как раз и учитывается, что события А и В могут быть зависимыми. Приведенная формула легко доказывается с использованием понятия частот. Пусть мы имеем N возможных исходов, из них событию А благоприятны k случаев, событию В – m случаев. Число перекрывающихся случаев – благоприятных одновременно и событию А и событию В (в приведенных выше терминах это и есть произведение событий АВ) пусть будет n. Тогда:
;
Условная же вероятность будет равна отношению числу n перекрывающихся событий, благоприятных и для А и для В, но теперь уже не к N, а к k случаям, благоприятным для события А, т.е.
.
Подстановка этих соотношений в (3) приводит к тождеству.
Соотношение (3) можно было бы переписать в виде:
Если событие А не зависит от события В, то это записывается так: . Отсюда имеем вероятность произведения независимых событий:
(4)
Это чрезвычайно важная для прикладных задач формула, т.к. часто априорно принимается, что случайные события – измерения – являются независимыми. Если это предположение не выполняется (а на практике часто так бывает), отсюда могут проистекать некорректные, и даже ошибочные оценки измеряемых величин (см. ниже).
2. Непрерывные случайные величины
Выше речь шла о дискретных случайных величинах. Если случайная величина является непрерывной, т.е. она может принимать любые значения на числовой оси, а не только целые (пример – стрельба по мишени, в этом случае координата точки попадания снаряде есть непрерывная случайная величина), то мы уже не можем ввести частоту появления конкретного значения. Для непрерывной случайной величины можно говорить о вероятности попадания ее в некоторый интервал. Скажем, рассматриваем случайную величину . Мы можем говорить о вероятности попадания ее в интервал от до . Т.к. есть функция , то мы всегда можем представить ее в виде: , где функция имеет смысл плотности распределения вероятности попадания случайной величины в оговоренный выше интервал значений. Далее, для простоты изложения примем, что наша случайная величина изменяется от - и до +. Интеграл
(5)
есть вероятность того, что попадает в интервал значений от - до . Если , то Р = 0, т.е. вероятность того, что значение случайной величины никуда не попало на числовой оси равно нулю – это невероятное событие. Если , то Р = 1. Иными словами, реализация любого значения - достоверное событие. Еще говорят, что вероятность Р нормирована на 1. Этому условию по определению всегда должна удовлетворять вероятность. Выполнения его добиваются путем введением соответствующего множителя в функции . Из сказанного выше вытекает еще одно условие на функцию плотности распределения вероятности: она должна достаточно быстро спадать на бесконечности, чтобы быть интегрируемой.
3. Числовые характеристики случайных величин
Математическое ожидание:
Величина
(6)
называется математическим ожиданием. По существу, - это среднее значение с учетом веса реализации текущего значения . Чтобы пояснить понятие веса, примем здесь, что - дискретная величина. Пусть данное значение - обозначим его x’ реализовалось n раз. При вычислении среднего это значение даст вклад (n/N)x'. Величина n/N (уже известная нам частота реализации данного события) и есть вес. Приведенное выше выражение (6) есть обобщение сказанного на непрерывную случайную величину. Здесь роль веса (или частоты) играет fdx.
Величина
(7)
называется моментом порядка S (математическое ожидание есть момент первого порядка).
Моменты являются числовыми характеристиками вероятностных свойств изучаемой случайной величины. На практике функция плотности распределения вероятности может быть определена не всегда, поэтому вместо нее могут быть использованы моменты. Нередко ограничиваются первыми двумя или тремя моментами (третий момент описывает асимметрию функции плотности распределения вероятности).
Чрезвычайно важной особенностью моментов является то, что они обладают свойством устойчивости: с увеличением числа экспериментов N вычисленные по конкретной выборке моменты, флуктуируя, стремятся к своим средним значениям.
4. Нормальный закон
На рис. 2 приведена (наиболее) часто встречающаяся функция плотности распределения вероятности Гаусса, выражающая т.н. нормальный закон распределения
(8)
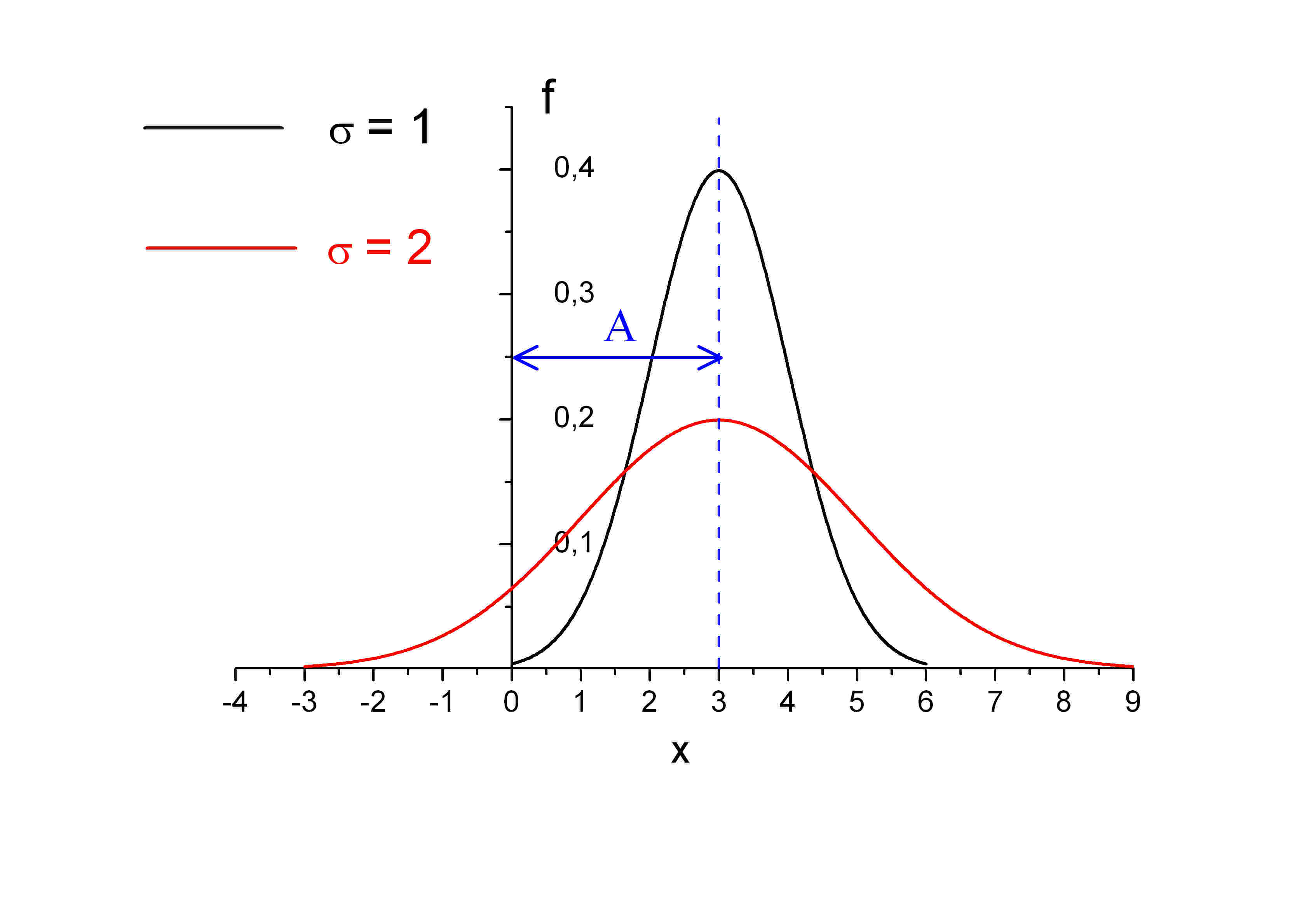
Рис 2 – функция плотности распределения вероятности для нормального закона
Величина есть площадь элементарной трапеции под графиком. Ее смысл – вероятность попадания случайной величины в соответствующий интервал. Максимум есть наиболее вероятное значение, т.к. при одном и том же вероятность попадания в соответствующий диапазон здесь будет больше, чем в другом месте. Если какая-то величина описывается приведенным выше нормальным законом, то ее среднее
, (9)
При вычислении этого интеграла делается замена переменных , отсюда
. Тогда: , и
с учетом того, что интеграл от нечетной функции по симметричным относительно нуля пределам равен нулю, а также известного из курса курс математического анализа интеграла Эйлера-Пуассона
получается приведенное значение для среднего.
Аналогично показывается, что функция плотности распределения вероятности удовлетворяет условию нормировки:
Смысл ее в том, что вероятность реализации какого-либо значения случайной величины х равна 1.
Второй момент вычисляется также:
(10)
Он называется дисперсией.
Если А = 0, то такую функцию плотности и, соответственно, моменты называют центрированными (в этом случае максимум функции плотности располагается при х = 0). В дальнейшем мы будем в основном пользоваться центрированными функциями.
Обсудим теперь смысл величины . Из рисунка видно, что она характеризует ширину охватываемой графиком области. Ее называют среднеквадратичным, или стандартным, отклонением х от среднего значения. Она, очевидно, характеризует меру разброса х относительно среднего. Для дальнейшего важно, что:
(11)
Иными словами: вероятность попадания случайной величины, описываемой нормальным законом распределения, в интервал от – до + составляет примерно 68%, соответственно, непопадания – 32%. Полезно также помнить, что вероятность того, что случайная величина будет заключена в пределах ±2 примерно равна 95%, в пределах ±3 – 99,7%. В последних двух случаях можно сказать: маловероятно, чтобы случайная величина выходила за указанные пределы.
5. Понятие функции случайной величины
Рассмотрим важную с точки зрения практического применения задачу. Пусть имеется непрерывная случайная величина с плотностью распределения . Нас интересует задача нахождения плотности распределения величины , связанной с соотношением: . Обозначим искомую функцию .
Решение задачи зависит от того, как ведет себя функция - возрастает, убывает или колеблется. Рассмотрим первый случай. Если величина попадает в интервал от до , то, соответственно, величина попадает в интервал . Далее, есть вероятность попадания величины в указанный интервал. При этом вероятность для попасть в соответствующий интервал есть . Поскольку вероятности совпадают, можем записать:
Далее надо сделать замену переменных: , где есть функция, обратная . Делаем замену переменных в предыдущем выражении:
Аналогично находится выражение для убывающей функции. В этом случае в правой части появляется знак минус. Эти два случая могут быть объединены одной формулой:
Случай осциллирующей функциональной связи можно найти в руководствах по теории вероятности.
Следствия.
1. Компьютерные генераторы случайных чисел, как правило, генерируют последовательности с равномерным распределение плотности. Полученные формулы позволяют пересчитывать их в последовательности, подчиняющиеся любым законам распределения.
Пусть случайная величина подчинена нормальному закону, а случайная величина связана с ней линейной функцией: . Требуется найти закон ее распределения.
Из условия: , отсюда . Тогда:
Мы здесь сделали замену , чтобы уточнить, что это дисперсия х, при этом обозначение для среднего значения х оставили прежнее. Из последнего выражения видно, что закон распределения тоже нормальный с числовыми характеристиками: среднее значение (математическое ожидание) ; среднеквадратичное .
6. Центральная предельная теорема
Мы остановились подробно на нормальном законе распределения случайной величины по ряду соображений. В курсах теории вероятности (см. Худсон, стр. 54) доказывается т.н. центральная предельная теорема. Суть ее состоит в следующем. Пусть случайная величина х имеет среднее значение А и дисперсию Если дисперсия конечная, то при стремлении числа реализаций случайной величины (или еще говорят ее выборки) N к бесконечности распределение <x> будет стремиться к нормальному закону со средним А и дисперсией . Там же доказывается важнейшая формула:
(12)
где z и есть случайная величина, распределенная по нормальному закону с нулевым средним и единичной дисперсией (поскольку <x> связано с z линейным соотношением, то <x> тоже будет распределено по нормальному закону). Крайне важно отметить следующее. При формулировке и доказательстве теоремы не делается никаких предположений о законе распределения самой величины х, кроме предположения о конечности дисперсии (см. Худсон).
В других формулировках (см., например, Вентцель) доказывается, что если мы имеем N независимых случайных величин, то совместная их вероятность также стремится к нормальному закону распределения.
Центральная предельная теорема – важнейшая теорема статистики. Она как раз и служит основанием того, что так много внимания уделяется нормальному закону распределения. Впрочем, в ряде случаев возможны и другие законы.
7. Закон больших чисел
Другая важная теорема – это т.н. закон больших чисел (теорема Чебышева). Опыт человечества еще с древнейших времен демонстрирует поразительную устойчивость массовых явлений, когда реализуется большое число однородных опытов со случайными воздействиями. При этом случайные воздействия компенсируются, а средние величины (в наших терминах – моменты, т.е. математическое ожидание, дисперсия) мало подвержены случайным изменениям (или, как говорят, флуктуациям). Этот практический результат и составляет содержание теоремы Чебышева (или закона больших чисел):
При достаточно большом числе независимых опытов среднее арифметическое наблюденных значений случайной величины сходится (по вероятности) к ее математическому ожиданию.
Литература
1. Андронов, А.М.; Копытов, Е.А.; Гринглаз, Л.Я. Теория вероятностей и математическая статистика; СПб: Питер - Москва, 2004. - 461 c.
2. Битнер Г. Г. Теория вероятностей; Феникс - Москва, 2012. - 336 c.
3. Большакова Л. В. Теория вероятностей для экономистов; Финансы и статистика - Москва, 2009. - 208 c.
4. Боровков А. А. Теория вероятностей; Либроком - Москва, 2009. - 656 c.
5. Боровков А.А. Теория вероятностей; Мир - Москва, 1986. - 395 c.
6. Вентцель Е. С., Овчаров Л. А. Теория вероятностей и ее инженерные приложения; Высшая школа - Москва, 2010. - 480 c.
7. Вентцель Е.С., Овчаров Л.А. Теория вероятностей; Высшая школа - Москва, 1976. - 616 c.
8. Глиненко В. И. Теория вероятностей; Государственное учебно-педагогическое издательство - Москва, 1986. - 138 c.
9. Гмурман В.Е. Теория вероятностей и математическая статистика; Наука - Москва, 1980. - 541 c.
10. Горлач Б. А. Теория вероятностей и математическая статистика; Лань - Москва, 2013. - 320 c.
11. Калинина В. Н. Теория вероятностей и математическая статистика; Юрайт - Москва, 2013. - 480 c.
12. Колмогоров А.Н., Юшкевич А.П. Математика XIX века (том 1): математическая логика, алгебра, теория чисел, теория вероятностей; СПб. [и др.] : Питер - Москва, 1978. - 246 c.
13. Кочетков Е. С., Смерчинская С. О. Теория вероятностей в задачах и упражнениях; Форум - Москва, 2008. - 480 c.
14. Крупин В. Г., Туганбаев А. А. Теория вероятностей; Факториал Пресс - Москва, 2006. - 128 c.
15. Левкович В. Л. Теория вероятностей; Издательство Академии наук БССР - Москва, 2007. - 104 c.
16. Луценко А. И. Теория вероятностей; Феникс - Москва, 2009. - 256 c.
17. Нельсон Е. Радикально элементарная теория вероятностей; РГГУ - Москва, 1995. - 145 c.
18. Ниворожкина, Л.И.; Морозова, 3.А. Теория вероятностей и математическая статистика; Эксмо - Москва, 2008. - 432 c.
19. Прохоров Ю. В., Розанова Ю. А. Теория вероятностей; Главная редакция физико-математической литературы издательства "Наука" - Москва, 2003. - 496 c.
PAGE \* MERGEFORMAT 5
C = A + B
A
B
A
C = A B
Элементы теории вероятностей