Спектроскопия кристаллов

Реферат

Неприводимые представления и классификация нормальных колебаний

Нормальные колебания вводятся при рассмотрении малых колебаний, т.е. колебаний вблизи положения равновесия как таких колебаний, которые 1) совершаются по гармоническому закону(i=1, 2…) 2) каждая нормальная координата относится не к одной какой-либо частице, а ко всем сразу, т.е. все частицы достигают одновременно максимального отклонения и проходят через минимумы одновременно, 3) нормальные координаты независимы, т.е. энергия одного колебания не может перейти в энергию других нормальных колебаний, 4) кинетическая и потенциальная энергия колеблющейся системы должна равняться сумме кинетических и потенциальных энергий отдельных нормальных колебаний.

Представление группы – сопоставление каждому элементу группы определенной матрицы. Совокупность этих матриц дает представление:

k= 1,2,…f.

Неприводимое представление – число преобразующихся друг через друга функций базиса не может быть уменьшено никаким линейным преобразованием.

Характер представления – сумма диагональных членов матрицы. Всякое приводимое представление может быть разложено на неприводимые, т.е. матрица приведена к квазидиагональному виду.

Характеры различных неприводимых представлений удовлетворяют соотношению ортогональности:, g – порядок группы или число элементов в группе.

Зная характеры приводимого и неприводимого представлений можно определить, сколько раз данное неприводимое представление встречается в приводимом:

где - характер неприводимого представления, g – порядок группы, - характер приводимого представления.

А теперь перейдем к классификации нормальных колебаний по неприводимым представлениям. Оно основано на теореме Вигнера.

Теорема Вигнера.

Каждому уровню энергии соответствует неприводимое представление группы симметрии.

При действии преобразования симметрии на волновую функцию, удовлетворяющую уравнению Шредингера, должна получиться волновая функция, удовлетворяющая этому уравнению Шредингера.

2) Эти волновые функции, относящиеся к одному значению энергии, образуют представление группы.

3) Это представление, относящееся к одному значению энергии уровня, неприводимо по построению, т.к. эти преобразующиеся друг через друга волновые функции должны относиться к одному значению энергии.

Таким образом, каждому уровню энергии системы соответствует неприводимое представление, размерность его равна кратности вырождения уровня, которая определяет сколько волновых функций или нормальных координат соответствует данному уровню (двукратно вырожденной частоте соответствуют две волновые функции, две нормальных координаты).

Эти соображения дают возможность произвести классификацию собственных колебаний молекулы без того, чтобы решать сложную задачу о конкретном определении ее нормальных координат. Для этого надо найти представление, осуществляемое всеми колебательными координатами – полное представление. Это полное представление приводимо, и разлагая его на неприводимые части, мы определим кратность собственных частот и свойства симметрии соответствующих колебаний. Одно и тоже неприводимое представление может входить в приводимое несколько раз. Это означает, что имеется несколько различных частот одинаковой кратности и симметрии.

Для нахождения полного представления в качестве функций базиса возьмем не нормальные координаты, а компоненты ui векторов смещения ядер от их положений равновесия, так как характеры представления инвариантны относительно линейного преобразования функций базиса.

При вычислении характера элемента G группы надо рассмотреть только те ядра, положения равновесия которых остаются на месте при данном преобразовании симметрии.

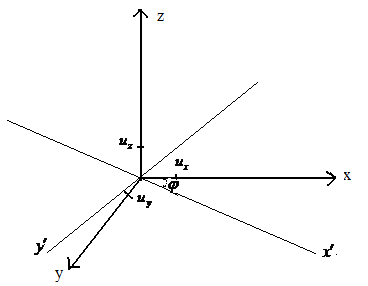
Рассмотрим поворот С() на угол вокруг оси. Ux,uy,uz – компоненты вектора смещения некоторого ядра, положение равновесия которого находится на самой оси и поэтому не затрагивается поворотом.

Ux=ux cos+ uy cos( 90 - )

Uy=-ux cos( 90 - ) + uy cos

Uz= uz

Характер – сумма диагональных элементов …. матрицы

1 + 2 cos. Если на оси Nc атомов, то суммарный характер Nc( 1 + 2 cos). Это характер, соответствующий преобразованию 3N смещений. Выделим из него часть, соответствующую поступательному и вращательному движению как целого. Поступательное перемещение определяется вектором u центра инерции молекулы, соответствующая часть характера 1 + 2 cos. Поворот определяется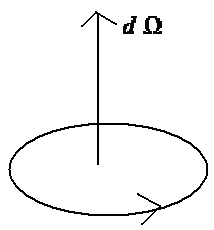

вектором d - аксиальный вектор, по величине равный углу поворота и направленный вдоль оси поворота. По отношению к поворотам аксиальный вектор ведет себя как обычный вектор, поэтому соответствующий характер равен 1 + 2 cos.

(С)= ( Nc-2 ) ( 1 + 2 cos ) – характер поворота в колебательном представлении. Для тождественного преобразования Е характер равен (Е)=3N – 6, Nc=N.

Для зеркального поворота ux = ux cos + uy sin

Uy = -ux sin + uy cos

Uz= - uz

Характер равен - 1 + 2cos. Характер зеркального поворота в полном представлении

Ns ( -1 + cos).

Вектору смещения центра инерции молекулы соответствует характер – 1 + 2cos. Аксиальный вектор d при отражении в плоскости h не меняется, а при отражении в плоскости v изменяется на обратный.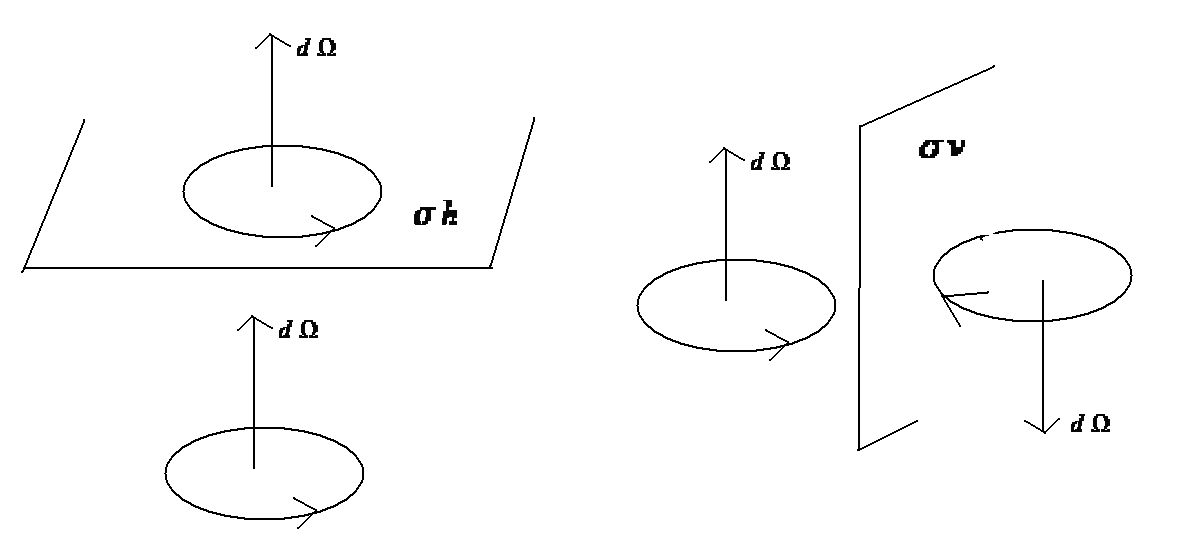

S()=C() h = C(+ ) I, h= C() I, C() = 1 + 2cos, а при инверсии аксиальный вектор не меняется.

- 1 + 2cos + 1 – 2cos

Характер зеркального поворота в колебательном представлении равен (S)= Ns( - 1 + 2cos). N,

После определения характеров полного или механического представления остается разложить его на неприводимые части по формуле

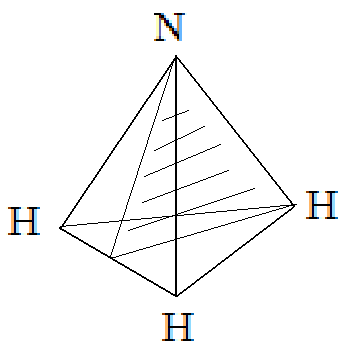
Пример. Произвести классификацию нормальных колебаний молекулы аммиака NH3. Точечная группа молекулы аммиака C3v. Выписываем характеры точечной группы из таблиц

C3v	E	2C3	3
A1	1	1	1
A2	1	-1	-1
E	2	1	0

Число инвариантных атомов, т.е. атомов остающихся на месте при данном преобразовании симметрии, для тождественного преобразования Е – 4 , для операции поворота на 120 градусов C3 -1 и для отражения в плоскости - 2. Характеры полного колебательного представления:

0)=6

Разлагаем это приводимое представление на неприводимые части по формуле , где g – порядок группы или число элементов симметрии в группе, - характер приводимого представления, - характер неприводимого представления. Для аммиака g=6. Число, показывающее, сколько раз неприводимое представление А1 входит в приводимое представление nA1=1/6(6+6)=2. nA2=1/6(6-6)=0. nE=1/6(12)=2. То есть у молекулы аммиака должно быть 2 полносимметричных колебаний, преобразующихся по представлению А1, и две двукратновырожденных частоты, преобразующихся по представлении Е.

Правила отбора для колебательных спектров

Получим правила отбора для матричных элементов различных величин, характеризующих систему, с помощью теории групп.

Теорема: Пусть - одна из волновых функций базиса неприводимого неединичного представления группы симметрии. Тогда ее интеграл по всему пространству тождественно обращается в нуль.

Интеграл инвариантен относительно преобразования симметрии.

Просуммируем по всем элементам группы G.

dq=k в силу ортогональности матричных элементов различных неприводимых представлений:

отличен от нуля, если подынтегральное выражение содержит единичное представление. Если волновая функция относится к приводимому представлению, то разложим ее по неприводимым представлениям. Интеграл разобьется на сумму интегралов различных неприводимых представлений, равных нулю за исключением случая, когда волновая функция относится к единичному представлению.

Пусть f - оператор скалярной физической величины. Он инвариантен относительно преобразований симметрии. Матричный элемент скалярной физической величины

где и нумеруют различные термы, i,k нумеруют волновые функции, относящиеся к одному представлению. D- произведение неприводимых представлений, соответствующих и . Это прямое произведение двух представлений не содержит единичное:

но следовательно у скалярной физической величины отличны от нуля матричные элементы лишь для переходов между состояниями одинакового типа (относящиеся к одному неприводимому представлению).

Если А – вектор, то Ax,Ay,Az преобразуются по представлению DA. Матричный элемент векторной физической величины отличен от нуля, если представление D по которому преобразуется подинтегральное выражение, содержит единичное представление. Оно содержит единичное представлнение, если в

содержится

Применим вышеуказанные правила к конкретным матричным элементам дипольного момента и поляризуемости.

Наличие линии в спектре поглощения, связанной с переходом из квантового состояния с квантовым числом v1 в состояние v2 определяется матричным элементом

где M(Q) – оператор дипольного момента, соответствующий линейной комбинации из MxMyMz

Mx= My=, Mz= где e - заряд -го атома.

В результате преобразования симметрии Mx, My, Mz преобразуются как координаты. Характер (-+1+2cos). Положительный знак берется для собственных вращений (E,C2,C3C4,C6), отрицательный – для несобственных вращений (Sn=,I,S3,S4,S6).

Обычно переходы рассматривают из основного состояния в возбужденное, а основное состояние полносимметричное, одномерное, поэтому произведение волновых функций преобразуется по неприводимому представлению, соответствующего волновой функции то-есть верхнего состояния. Для отличия от нуля матричного элемента дипольного момента нужно, чтобы было отлично от нуля число, показывающее сколько раз неприводимое представление содержится в приводимом представлении, соответствующем линейной комбинации из Mx, My, Mz, т.е. интеграл отличен от нуля, если

не равно нулю. Интенсивность линии отлична от нуля, когда первая производная от дипольного момента по нормальной координате не равна нулю.

Наличие линии в спектре комбинационного рассеяния (СКР) связано с переходом молекулы из состояния я колебательным квантовым числом v1 в состояние с колебательным квантовым числом v2 и определяется матричным элементом поляризуемости

где Q) – линейная комбинация компонент тензора поляризуемости. Характер, соответствующий линейной комбинации компонент тензора поляризуемости, берем без вывода и он равен

Для отличия от нуля матричного элемента поляризуемости, необходимо, чтобы число, показывающее сколько раз представление, соответствующее произведению волновых функций v1v2 , содержалось в представлении компонент тензора поляризуемости, было отлично от нуля.

не равно нулю. Для отличия от нуля интенсивности линии СКР необходимо отличие от нуля первой производной компонент тензора поляризуемости по нормальной координате .

Обозначение одномерных представлений А и В, двумерных –Е, трехмерных F.

А и В – симметричное и антисимметричное представление относительно Сn – оси поворота n-го порядка.

А1 и А2 – симметричное и антисимметричное представление относительно оси 2-го порядка перпендикулярной Сn.

Представление симметричное относительно инверсии – g, антисимметричное относительно инверсии – u.

Одним штрихом обозначают представление симметричное относительно плоскости отражения h, двумя штрихами – антисимметричное относительно h.

Методы теоретико-группового анализа фундаментальных колебаний кристалла.

Теоретико-групповые методы анализа фундаментальных колебаний кристаллов позволяют однозначно определить число колебаний, их тип симметрии, а также проанализировать их активность, указать условия их наблюдения в том или ином физическом процессе.

Существует а) общий метод (ОМ) классификации колебаний кристаллов, основанный на построении полного колебательного представления с последующим разложением этого представления по неприводимым представлениям группы симметрии кристалла, в) метод позиционной симметрии (ПС), для применения которого нужно использовать корреляционные таблицы.

К основным элементам симметрии кристаллов неограниченных размеров относятся параллельные переносы в некоторых направлениях, повороты на некоторые углы, зеркальные отражения, винтовые оси и плоскости скольжения.

Совокупность всех элементов симметрии кристаллов образует пространственную группу. Для трехмерных кристаллов существует 230 пространственных групп.

Каждая пространственная группа имеет подгруппу трансляций, образованную всеми векторами решетки . Трансляции состоят в том, что координаты всех частиц в кристалле получают приращение n. Базисными векторами являются а1, а2, а3, которые совпадают с осями x, y, z, а их модули равны отрезкам а1, а2, а3.

Если взять в кристалле произвольную точку и произвести над ней трансляции, определяемые всеми векторами n, то получится система точек, которую называют простой решеткой Браве, т.е. совокупность всех преобразований (инверсия, повороты и отражения), которые переводят любой вектор n подгруппы трансляции в вектор n` той же подгруппы образуют точечную группу симметрии погруппы трансляции. В связи с этим подгруппы трансляций подразделяются на 7 сингоний:

триклинная (S2=Ci),
моноклинная (C2h),
ромбическая или тригональная D2d,
ромбоэдрическая D3d,
тетрагональная или квадратная D4h,
гексагональная D6h,
кубическая Oh.

Кроме трансляционной симметрии кристаллы обладают некоторой симметрией направлений (повороты на углы кратные 60, 90, инверсия и их сочетание). Совокупность элементов симметрии, переводящих каждое направление в кристалле в ему эквивалентное, образует __точечную группу кристалла.

Точечная группа решетки Браве (точечная группа подгруппы трансляций) как правило выше точечной группы кристалла. В частности, центр инверсии всегда имеется у точечной группы решетки Браве, а в точечной группе кристалла его может не быть.

Элементы симметрии пространственной группы переводят все точки кристалла в эквивалентные, а элементы симметрии группы направлений – каждое направление в эквивалентное. Существуют 32 точечных группы, соответственно которым кристаллы подразделяются на 32 кристаллических класса.

Все элементы симметрии пространственной группы можно представить в виде произведения трансляции на элементы симметрии некоторй группы, которую называют фактор-группой по подгруппе трансляций. Фактор-группа изоморфна точечной группе кристалла, которая содержит вращательную часть всех операторов пространтвенной группы.

Отличие фактор-группы и изоморфной точечной группы кристалла в том, что в фактор-группе остаются такие элементы симметрии, как винтовые оси и плоскости скольжения. Вследствие изоморфизма любое представление точечной группы кристалла является также представлением фактор-группы. Поэтому при исследовании неприводимых представлений вместо фактор-группы можно рассматривать точечную группу симметрии кристалла.

При инфракрасном поглощении (ИК) и комбинационном рассеянии (КР) возбуждаются при однофотонном возбуждении колебания кристалла, нормальные координаты которых преобразуются по неприводимым представлениям пространственной группы с волновым вектором k=0 (k=

- длинноволновые колебания ).

Колебания с волновым векором k=0 происходят синхронно во всех элементарных ячейках, так как u(0)/u(na)=expikna=1.

Все элементарные ячейки колеблются одинаково, поэтому достаточно рассмотреть колебания одной элементарной ячейки. Багавантам в своей книге даёт удобный метод рассмотрения длинноволновых колебаний с k=0. Он рассматривает преобразования элементарной ячейки под действием элементов симметрии пространственной группы, содержащие трансляции меньшие постоянной решетки.

Группа симметрии элементарной ячейки эквивалентна группе симметрии волнового вектора k=0. Группой симметрии нулевого вектора является группа, харктеризующая кристаллический класс кристалла. Поэтому методы классификации нормальных колебаний по неприводимым представлениям остаются такими же, как и для молекул.

Сущность общего метода классификации колебаний заключается в нахождении полного колебательного представления с последующим разложением его по неприводимым представлениям фактор-группы кристалла.

Характер полного колебательного представления h) определяется следующим образом

где h – элемент симметрии фактор-группы кристалла, ur(h) – число атомов, которые после действия операции r остаются на месте на месте с точностью до вектора примитивной трансляции, - угол поворота при действии операции r. Знак + выбирается положительным для собственных вращений, отрицательный – для несобствеенных вращений (поворот с отражением).

Мы будем рассматривать молекулярные кристаллы, которые состоят из тех же молекул, из которых вещество состоит в жидкой и газообразной фазах. Все колебания в молекулярных кристаллах можно разбить на а) внутренние колебания атомов друг относительно друга, при которых не перемещается центр тяжести, - сильная связь, = 400 -4000 см-1. При комнатной температуре kT порядка 100 см-1, т.е. при комнатной температуре они не возбуждены. Температура и другие воздействия мало влияют на эти частоты, они сохраняются при изменении агрегатного состояния вещества, мало зависят от волнового вектора k.

Б) Внешние колебания – это колебания групп частиц друг относительно друга или колебания решетки, соответствующие вращательным и поступательным свободы. Частоты внешних колебаний порядка 100 см-1 зависят от температуры, волнового вектора, возбуждены при комнатной температуре, не встречаются в парах и растворах.

В действительности оба рода колебаний являются колебаниями решетки и строго не могут быть отделены друг от друга. Но в первом приближении такое разделение возможно и даёт значительное упрощение при исследовании колебаний.

В молекулярных кристаллах с молекулами в элементарной ячейке и атомов в молекуле 3 -3 оптических ветвей, 3 акустических ветви, 6 колебаний решетки, 3 соответствуют вращательному движению, 3 -3 –трансляциям.

3 6 внутренних колебаний.

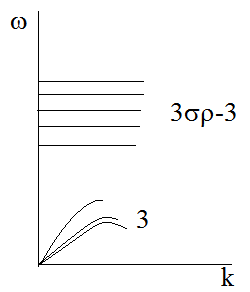
Мода колебаний – определенный тип колебаний с определенной частотой и волновым вектором, т.е. точка на дисперсионной кривой. Колебательные моды при нулевом колебательном векторе называются фундаментальными модами, а их частоты – фундаментальными частотами.

После нахождения характеров полнового представления, разлагаем его по неприводимым представлениям фактор-группы и определяем число колебаний и их тип симметрии. Полное число колебаний равно числу степеней свободы элементарной ячейки.

Для молекулярных кристаллов ввели внешние или решеточные колебания и внутренние колебания.

Формула для нахождения числа решеточных колебаний трансляционного типа с волновым вектором k=0 с данной симметрией:

Ni=1/g

Формула для нахождения числа решеточных колебаний вращательного типа:

Ni=1/g

- число атомов в элементарной ячейке, s – число групп, на которые разбивается атомов по величине сил, действующих между атомами. uG(s) – число инвариантных групп относительно преобразования G.uG(s) – 1 вычитается чистая трансляция, v – число одноатомных групп, не имеющих вращательных степеней свободы.

Число внутренних колебаний равно полному числу колебаний минус число чистых трансляций и число решеточных колебаний трансляционного и вращательного типа.

Метод позиционной симметрии.

Внутренние колебания кристалла по частотам близки к колебаниям соответствующих свободных молекул, но в в кристалле уровни, соответствующие свободным молекулам, расщепляются в результате понижения симметрии (Бете) и резонансного взаимодействия молекул (Давыдов). Изменяются правила отбора для спектров, поляризация. Очень часто на практике имеется молекулярный кристалл, для него известны частоты колебаний молекул, необходимо найти, как изменяются эти колебания в кристалле (расщепление и поляризация). Здесь используется метод позиционной симметрии, предложенный Хэлфордом.

В элементарной ячейке каждый атом занимает вполне определенное положение. Набор операций симметрии, оставляющих данную точку расположения атома на месте, образует точечную группу позиционной симметрии этого атома. Группа позиционной симметрии является подгруппой точечной группы кристалла.

Хэлфордом были перечислены возможные варианты позиционной симметрии и число точек, одновременно имеющих данную позиционную симметрию для всех пространственных групп. Например, для пространственной группы D2h16 (кристалл халькоперита AgGaS2 имеются следующие группы позиционной симметрии 2S4(2), 2C2(4), C1(8). 2S4(2) означает, что в данном кристалле возможны два набора атомов (коэффициент перед S4(2)), имеющих позиционную симметрию S4 и в каждом наборе находится по два атома (число в скобках). Сопоставляя найденные из эксперимента координаты атомов с возможными, найдем позиции атомов Ag – S4(2), Ga – S4(2) и 4S – C2(4).

Мы уже отмечали, что группа позиционной симметрии является подгруппой точечной группы кристалла. С другой стороны, центр масс молекулы остаётся инвариантным, поэтому позиционная группа

должна быть подгруппой изолированной точечной группы молекулы. Связь между движениями изолированной молекулы и соответствующими движениями в кристалле может быть установлена с помощью сравнения характеров для молекул, позиционных или местных групп и фактор-групп или с помощью таблиц корреляции.

Так как местная или локальная группа симметрии молекулы является подгруппой фактор-группы, то часть элементов фактор-грппы совпадает с элементами симметрии местной группы.

Если некоторый элемент симметрии R* фактор-группы не совпадает с любым элементом симметрии местной группы Rm, то действие операции R* на волновую функцию сводится к замене её на другую волновую функцию. Следовательно, матрица элемента R*, соответствующая предсавлению фактор-группы, не имеет отличных от нуля диагональных элементов. Поэтому характеры элементов симметрии местной группы во всех представлениях равны нулю. Если операция R* фактор-группы совпадает с операцией Rm местной группы, то связь между характерами соответствующих представлений в обеих группах где - число молекул в элементарной ячейке. Итак, характер любого элемента симметрии точечной группы кристалла, соответствующий молекулярному терму местной группы, вычисляется по формуле:

где - число молекул в элементарной ячейке, f(R) – характер точечной группы кристалла в представлении волновых функций молекулы, f(Rm) – характер местной группы в представлении молекулярных волновых функций.

В общем случае вычисленные характеры f® относятся к приводимым представлениям точечной группы симметрии кристалла, которые можно разложить по характерам неприводимых представлений точечной группы симметрии кристалла l®.

где суммирование по всем неприводимым представлениям точечной группы кристалла,

nl=1/g где суммирование по всем элементам точечной группы кристалла.

Для нахождения правил отбора в ИКС и СКР кристалла можно пользоваться формулами, выведенными для молекул, так как компоненты дипольного момента или тензора поляризуемости при трансляциях преобразуются как при тождественном преобразовании,а при зеркальном скольжении они преобразуются как при простом или зеркальном повороте.

Для иллюстрации применения теории групп к исследованию колебательных спектров кристаллов рассмотрим кристалл кальцита CaC03, MgC03, NaN03, KN03.

Ca (1,2), C(3,4),O( 5 – 10). Группы CO3 – плоские треугольники, повернутые 60 градусов друг относительно друга.

M=2,

Найдем инвариантные атомы.

Е (1)(2)(3)……..(10).

2S6 – повороты на 60 градусов и трансляции вдоль оси. Первый атом обменивается со вторым, но они не различаются, третий обменивается с четвёртым.

2S6 {(1) (2) (3,4) (5,9,7,8,6,10)

(2) (3,4) (5,10,6,8,7,9)

2C3 (1) (2) (3) (4) (5,6,7) (8,9,10)

I – инверсия в 1-ом атоме (1) (2) (3) (4) (5,8) (7,10) (6,8)

3v – три плоскости скольжения, которые делят расстояние между соседними атомами кислорода.

(1,2) (3,4) (5,8) (6,10) (7,9)

(1,2) (3,4) (5,10) (6,9) (7,8)

(1,2) (3,4) (5,9) (7,10) (6,8)

3C2 – три оси второго порядка, которые делят углы между плоскостями скольжения пополам.

(1,2) (3) (4) (7) (10) (5,6) (8,9)

(1,2) (3) (4) (5) (8) (9,10) (7,6)

(1,2) (3) (4) (6) (9) (5,7) (8,10)

D3d5	E2S62C3i3v3C2	Ni T T R n	СКР	ИКС
A1g	1 1 1 1 1 1	1 0 0 0 1	Акт.	Запр.
A2g	1 1 1 1 -1 -1	3 0 1 1 1	Запр.	Запр.
A1u	1 -1 1 -1 -1 1	2 0 1 1 0	Запр.	Запр.
A2u	1 -1 1 -1 1 -1	4 1 1 0 2	Запр.	Разр.
Eu	2 1 -1 -2 0 0	6 1 2 1 2	Запр.	Разр.
Eg	2 -1 -1 2 0 0	4 0 1 1 2	Акт.	Запр.
uR(ni)	10 2 4 2 0 4
uR(s)	4 2 4 2 0 2
uR(s-v)	2 0 2 0 0 2
	30 0 0 -6 0 -4
	3 0 0 -3 1 -1
	9 0 0 -3 -1 -1
R’)	6 0 0 0 0 -2
(СКР)	6 0 0 6 2 2

Далее, зная частоты свободных ионов, найти, какие частоты будут проявляться в ИКС и СКР кристалла CaCO3. Пространственная группа D3d5, группа симметрии свободного иона D3h, локальная группа C3v. Частоты колебаний иона CO3 :

1063 cm-1 A1’, 878 cm-1 A2”, 1415 cm-1 E’, 650 cm-1 E’.

Локальные группы пространственной группы D3d5:

С1(12), 2D3(1), C3v(2), 2C2h(3), 2C6(6), C3(6).

Таблица характеров точечной группы симметрии свободного иона CO3:

D3h E 2C3 3C2 h 2S3 3v

A1’ 1 1 1 1 1 1

A2’ 1 1 -1 1 1 -1

E’ 2 -1 0 2 -1 0

A1” 1 1 1 -1 -1 -1

A2” 1 1 -1 -1 1 1

E” 2 -1 0 -2 1 0

Таблица характеров локальной группы C3v:

C3v E 2C3 3v

A1 1 1 1

A2 1 1 -1

E 2 -1 0

Найдем, какой терм соответствует A1’ группы симметрии свободного иона в локальной группе C3v. Для этого найдем, сколько раз представление A1 C3v содержится в представлении A1’ D3h:

nA1=1/6(1+2+3)=1; nA2=1/6(1+2-3)=0; nE=1/6(2-2+0)=0

То есть терму A1’ свободной молекулы соответствует терм локальной группы А1. Найдем характеры приводимого представления фактор-группы, соответствующего терму A1’

суммирование по всем элементам симметрии фактор-группы.

E 2S6 2C3 I 3v 3C2

2 0 2 0 2 0

Найдем, сколько раз каждое неприводимое представление фактор-группы содержится в приводимом, число элементов симметрии группы g=12.

nA1g=1/12(2+4+6)=1; nA2g=1/12(2+4-6)=0; nA1u=1/12(2+4-6)=0; nA2u=1/12(2+4+6)=1; nEu=1/12(4-4)=0; nEg=1/12(4-4)=0.

A1’=A1g+A2u. Таким образом, мы нашли расщепление терма свободного иона A1’ в кристалле.

Литература

Магомедов М.Н.: Изучение межатомного взаимодействия, образования вакансий и самодиффузии в кристаллах. - М.: ФИЗМАТЛИТ, 2010

: Сквозь магический кристалл. - М.: Наше наследие, 2009

МГУ им. М.В. Ломоносова, Геологический фак-т ; Отв. ред. В.С. Урусов: Проблемы кристаллологии. - М.: ГЕОС, 2009

Под ред.: Ц.Фукуды, П.Рудольфа, С. Уды ; Пер. с англ. под ред. Б.В. Шульгина: Выращивание кристалловолокон из расплава. - М.: ФИЗМАТЛИТ, 2009

Ярославцев А.Б.: Химия твердого тела. - М.: Научный мир, 2009

Зайцев О.С.: Химия. - М.: Академия, 2008

Кормилицын О.П.: Механика материалов и структур нано- и микротехники. - М.: Академия, 2008

Лебедев В.И.: Физика фазовых переходов в дефектных и малоразмерных кристаллах. - Ставрополь: СевКавГТУ, 2008

Уваров Н.Ф.: Композиционные твердые электролиты. - Новосибирск: СО РАН, 2008

Ковалевский М.Ю.: Статистическая механика квантовых жидкостей и кристаллов. - М.: ФИЗМАТЛИТ, 2006

авт.-сост.: А.А. Смоликов, М.А. Трубицын: Основы кристаллохимии. - Белгород: БелГУ, 2003

Вейль Г.: Симметрия. - М.: Едиториал УРСС, 2003

Плесков Ю.В.: Электрохимия алмаза. - М.: Едиториал УРСС, 2003

РАН; Ин-т кристаллографии им. А.В. Шубникова; Ин-т проблем химической физики; Геологический ин-т Кольского научного центра; МО РФ; Санкт-Петербургский гос. ун-т; Московский гос. ун-т; Н.В. Чуканов, И.В. Пеков, А.Е. Задов и др.; Отв. ред. Д.Ю. Пущаров: Минералы группы лабунцовита. - М.: Наука, 2003

Иродов И.Е.: Задачи по квантовой физике. - М.: Лаборатория Базовых Знаний, 2002

Сост.: В.А. Тихомирова, А.И. Черноуцан: Очерки о кристаллах. - М.: Бюро Квантум, 2002

Е.А. Туров, А.В. Колчанов, В.В. Меньшенин и др. : Симметрия и физические свойства антиферромагнетиков. - М.: Физматлит, 2001

Спектроскопия кристаллов