МЕТОДЫ ОПТИМИЗАЦИИ. АЛГОРИТМЫ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ

Контрольно-практическая работа

МЕТОДЫ ОПТИМИЗАЦИИ. АЛГОРИТМЫ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ


Содержание

Введение………………………………………………………………….

4

1. Математическое программирование. Основные понятия…..………...

5

2. Элементы выпуклого анализа…………………………………………...

8

2.1. Выпуклые множества……………………………………………….

8

2.2. Выпуклые функции…………………………………………………

9

3. Линейное программирование…………………………………………..

15

3.1.Свойства задач линейного программирования…………………….

18

3.2. Симплекс-метод…………………………………………………….

24

3.3. Построение начальной симплекс-таблицы………………..............

30

4. Теория двойственности в линейном программировании……..............

34

5. Нелинейное программирование………………………………………..

41

5.1. Задача условной оптимизации с ограничениями-равенствами…..

41

5.2. Задачи условной оптимизации с ограничениями-неравенствами

43

5.3. Выпуклое программирование………………………………………

45

6. Метод возможных направлений………………………………………..

50

Литература…………………………………………………………………..

52

Введение

Целью контрольной работы является предоставление знаний и навыков построения математических оптимизационных моделей, их анализа и выбора подходящего метода решения.

В первом разделе работы вводится общая задача математического программирования и основные понятия, связанные с экстремальными задачами, проводится классификация задач математического программирования. Второй раздел посвящен изложению основ выпуклого анализа. Теория выпуклого анализа используется в последующих разделах при изложении линейного и выпуклого программирования.

В третьем и четвертом разделах излагается теория линейного программирования и численный метод решения линейных оптимизационных задач – симплексный метод. При изложении материала приводятся доказательства основных теоретических результатов, и дается теоретическое обоснование симплекс-метода.

Пятый и шестой разделы посвящены нелинейным задачам математического программирования с ограничениями. В пятом разделе излагается теория множителей Лагранжа для задач с ограничениями-равенствами и задач с ограничениями-неравенствами. В шестом разделе изложен численный метод решения регулярной задачи выпуклого программирования.

Особо следует отметить присутствие во всех разделах контрольно-практической работы алгоритмического описания аналитического и численного подходов к решению задач.


1. Математическое программирование. Общие понятия

Задача математического программирования состоит в отыскании экстремума некоторой функции в области, заданной ограничениями в виде равенств и (или) неравенств.

Формально задача математического программирования записывается следующим образом:

Ограничения:

(1.1)

Оптимизируемую функцию называют целевой функцией, функцией цели или критерием задачи (критерием эффективности).

Если все функции, входящие в задачу (1.1) линейные, то получаем задачу линейного программирования. В противном случае – это задача нелинейного программирования. Если целевая функция квадратичная, а ограничения линейны, то имеет место задача квадратичного программирования.

Задача математического программирования без ограничений называется задачей безусловной оптимизации, в противном случае задачей условной оптимизации.

Если в задаче (1.1) есть требование целочисленности переменных, то получаем задачу целочисленного программирования.

Согласно введенным обозначениям приведем следующие определения.

Определение 1.1. Допустимым решением задачи (1.1) называется точка , удовлетворяющая всем ограничениям задачи.

Множество допустимых решений задачи называют областью допустимых решений (ОДР).

Определение 1.2. Допустимое решение называется оптимальным решением задачи, если оно доставляет целевой функции максимальное (минимальное) значение.

Определение 1.3. Оптимальное значение целевой функции – это максимальное (минимальное) значение целевой функции в ОДР.

В дальнейшем будем использовать следующие обозначения и понятия: En – n-мерное евклидово пространство, элементом которого является точка , норма евклидова пространства , скалярное произведение двух векторов (x,y)=.

Если матрица будет обозначена буквой A, то ее элементы будем обозначать , строку с номером i - (индекс внизу), а i – й столбец - (индекс вверху).

Тогда -окрестностью точки в пространстве En является множество

.

Пусть Х – некоторое множество в пространстве En . Точка является внутренней точкой множества Х, если существует -окрестность этой точки, состоящая только из точек множества Х.

Точка является граничной точкой множества Х, если в любой окрестности этой точки есть точки, как принадлежащие множеству Х, так и не принадлежащие ему.

Точка является предельной точкой множества Х, если в любой окрестности этой точки содержится бесконечно много точек из Х.

Множество Х – замкнутое, если ему принадлежат все его предельные точки.

Множество Х – ограниченное, если ему не принадлежат бесконечно удаленные точки.

Различают локальные и глобальные экстремумы. Глобальный экстремум достигается в точке из ОДР, если в ней целевая функция достигает наибольшего (наименьшего) значения в ОДР. Локальный экстремум достигается в точке из ОДР, если существует окрестность этой точки, в которой целевая функция достигает наибольшего (наименьшего) значения. Очевидно, что всякий глобальный экстремум является локальным. Поэтому, если глобальный экстремум существует, то его можно искать среди локальных экстремумов. Далее будем предполагать, что речь идет о глобальном экстремуме, если противное не оговаривается особо.

Теорема Вейерштрасса. Всякая непрерывная функция на ограниченном, замкнутом множестве из пространства En достигает своего наибольшего и наименьшего значений.

2. Элементы выпуклого анализа

Познакомимся с понятием выпуклого множества, дадим определение выпуклой функции, рассмотрим некоторые свойства выпуклых функций, приведем критерии выпуклости функций. Эти понятия в методах оптимизации играют важную роль, так как используются при изложении разделов линейного программирования и выпуклого программирования.

2.1. Выпуклые множества

Определение 2.1. Выпуклой комбинацией двух точек называется точка

, где .

Геометрическая интерпретация: выпуклая комбинация двух точек является параметрическим уравнением отрезка, соединяющего точки .

Пример. Даны две точки =(1, 10, -2), =(-3, 4, 6). Параметрическое уравнение задает выпуклую комбинацию этих точек. После элементарных преобразований получим

=(1-4, 10-6, -2+8), .

Середина отрезка находится в точке, соответствующей, то есть в точке =(-1,7,2).

Определение 2.2. Выпуклой комбинацией m точек называется точка =, где , и .

Введем понятие выпуклого множества, используя определение 2.1 для выпуклой комбинации.

Определение 2.3. Множество X называется выпуклым, если вместе с любыми двумя точками , принадлежащими этому множеству, ему принадлежит и их выпуклая комбинация.

Так как выпуклая комбинация двух точек геометрически определяет отрезок в пространстве , соединяющий эти точки, то имеет место и такое определение: множество X называется выпуклым, если вместе с любыми двумя точками , принадлежащими этому множеству, ему принадлежит и отрезок их соединяющий.

Примеры выпуклых множеств: круг является выпуклым множеством, выпуклый многоугольник. По определению выпуклым множеством считают множество, состоящее из одной точки, а также пустое множество.

Теорема 2.1. Пересечение выпуклых множеств является выпуклым множеством.

Теорема 2.2. Множество X является выпуклым тогда и только тогда, когда выпуклая комбинация любых m (m 2) точек из этого множества принадлежит этому множеству.

2.2. Выпуклые функции.

Определение 2.4. Пусть функция определена на выпуклом множестве X . Функция называется выпуклой (вогнутой) на выпуклом множестве X, если для любых двух точек выполняется неравенство

), где . (2.2)

Определение 2.5. Если неравенство (2.2) выполняется как равенство только при =0 и =1, то функция называется строго выпуклой (строго вогнутой) на выпуклом множестве X.

Рассмотрим некоторые свойства выпуклых функций.

Теорема 2.3. Неотрицательная линейная комбинация функций, выпуклых на выпуклом множестве X, является выпуклой функцией на этом множестве.

Теорема 2.4. Если функция выпуклая на выпуклом множестве X, то функция вогнутая на этом множестве.

Теорема 2.5. Если функция выпуклая на отрезке [a,b] и монотонно не убывает, а функция выпуклая на выпуклом множестве X и [a,b], то суперпозиция функций выпуклая на X.

Доказательства теорем 3-5 рекомендуется провести самостоятельно.

Познакомимся с теоремой о связи выпуклого множества с выпуклой функцией. Эта теорема играет важную роль в постановке задач выпуклого программирования.

Рассмотрим множество, которое задается функцией , определенной на множестве X , и константой С .

Теорема 2.6. Если выпуклая функция на выпуклом множестве то множество выпуклое.

Доказательство. Возьмём произвольные точки , и построим их выпуклую комбинацию: , где . Докажем, что .

Основываясь на выпуклости функции, получаем: , , то есть . Из выпуклости множества X следует, что . Следовательно, , и множество выпуклое.

Для проверки функции на выпуклость будем использовать критерии, формулировку которых рассмотрим ниже.

Рассмотрим некоторую функцию , определенную на выпуклом множестве Выберем произвольную точку и направление, задаваемое вектором Выбирая соответствующим образом длину вектора s, можно добиться того, что точка при любом значении скалярной величины .

Одномерным сечением функции f(x) называется функция скалярного аргумента , где .

Рис.2.1. Одномерное сечение функции

Сформулируем критерий выпуклости функции, в основе которого лежит понятие одномерного сечения функции.

Теорема 2.7. Рассмотрим некоторую функцию , определенную на выпуклом множестве Функция – выпуклая на множестве тогда и только тогда, когда всякое её одномерное сечение есть выпуклая на отрезке [0,1] функция.

Предположим, что – дважды непрерывно дифференцируемая функция на множестве , и сформулируем критерии выпуклости гладких функций

Теорема 2.8. Следующие четыре утверждения эквивалентны.

1) Функция – выпуклая на выпуклом множестве .

2) , где - выпуклое множество.

3) монотонно неубывающая функция на [0,1].

4) Матрица Гессе неотрицательно определена во всех точках области Х. .

Дадим пояснения к сформулированным утверждениям из теоремы 2.8.

Пояснение к утверждению 2. На рисунке 2.2 изображены график функции в виде кривой MA и касательная к этой кривой в точке M ().

Рис. 2.2. Иллюстрация утверждения 2.

, ,

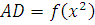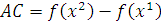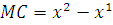
Из 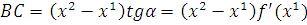. Условие 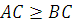эквивалентно условию 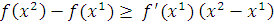. В результате получена геометрическая интерпретация утверждения 2 для случая, когда : всякая касательная к выпуклой функции в области Х лежит ниже графика этой функции.

Пояснение к утверждению 3. Одномерное сечение задает функция . Производная этой функции , вторая производная , где - матрица Гессе. Из утверждения 3 следует, что , то есть матрица в любой точке области Х неотрицательно определена.

Пояснение к утверждению 4. Матрица Гессе функции состоит из производных второго порядка этой функции. Если смешанные производные непрерывны, то они равны, и матрица H(x) симметричная.

Матрица - неотрицательно определена в точке x тогда и только тогда, когда в этой точке .

Если , и только, если , то называется положительно определённой матрицей.

При применении утверждения 4 рекомендуется использовать критерий положительной определенности матрицы и (или) критерий неотрицательной определенности матрицы:

1. Действительная симметричная матрица будет положительно определена тогда и только тогда, когда все ее угловые миноры положительны.

2. Действительная симметричная матрица будет неотрицательно определена тогда и только тогда, когда все ее главные миноры неотрицательны (то есть миноры, составленные из элементов матрицы после вычеркивания из нее строк и столбцов с одинаковыми номерами).

Алгоритм проверки выпуклости функции на основе утверждения 4

  1. Построить матрицу Гессе для данной функции.
  2. Найти значения всех угловых миноров.

Если среди них встретится отрицательный минор, то функция не является выпуклой, и алгоритм завершает работу.

Если все угловые миноры положительны, то делаем вывод о строгой выпуклости функции, и алгоритм завершает работу.

  1. Вычислить те главные миноры, которые не являются угловыми. Если они все окажутся неотрицательными, то функция выпуклая, иначе она не является выпуклой. Алгоритм завершает работу.

Пример. Найдите область выпуклости функции .

Построим матрицу Гессе . Угловые миноры матрицы равны: и ; главный минор, не являющийся угловым, равен 6. Функция будет выпуклой в области, где все найденные миноры неотрицательны. Следовательно, область выпуклости определяется системой неравенств: , .

Отсюда, получаем , и . Второе неравенство определяет область внутри параболы, вершина которой находится в точке (0,1/2), ветви опущены вниз. Так как все точки этой области удовлетворяют неравенству , то именно она является областью выпуклости функции .

3. Линейное программирование

Определение 3.1. Задачей линейного программирования называют задачу оптимизации линейной функции в области, задаваемой линейными ограничениями-неравенствами и (или) линейными ограничениями-равенствами.

Математическая модель задачи линейного программирования в общем виде:

, ,

, , (3.1)

, ,

, , где .

В дальнейшем, будем выделять две специальные формы задач линейного программирования: каноническую форму и стандартную (симметричную).

Определение 3.2. Говорят, что задача ЛП имеет каноническую форму, если все ограничения являются равенствами и все входящие в задачу переменные ограничены по знаку:

, , (3.2)

, .

Используя векторы , , и матрицу , математическую модель (3.2) можно переписать в виде:

( 3.3)

При этом является обозначением i-й строки матрицы A, векторное неравенство означает, что все координаты вектора неотрицательны, то есть . Задачу (3.3) можно переписать в виде:

,

, , . (3.4)

Определение 3.3. Говорят, что задача ЛП имеет стандартную (симметричную) форму, если все ограничения являются неравенствами и все входящие в задачу переменные ограничены по знаку:

, , (3.5)

, .

В векторной форме эту задачу можно переписать в виде:

,

, (3.6)

, .

Требование, решить задачу линейного программирования, означает следующее: если задача разрешима, то необходимо найти среди допустимых решений задачи оптимальные решения и вычислить оптимальное значение целевой функции; если задача неразрешима, то требуется установить причину ее неразрешимости.

Используя эквивалентные преобразования из таблицы 3.1, можно всегда данную задачу ЛП свести к требуемому виду. Это позволяет, не нарушая общности, при изложении теории или практики ориентироваться на одну из указанных форм задач ЛП.

Таблица 3.1 - Эквивалентные преобразования

Название преобразования

До преобразования

После преобразования

Преобразование неравенства в равенство

,

Преобразование неравенства в равенство

,

Переход от решения задачи минимизации к решению задачи максимизации

Переход от свободной переменной к переменным, ограниченным по знаку

3.1.Свойства задач линейного программирования

Обозначим область допустимых решений задачи

.

Теорема 3.1. Область допустимых решений (ОДР) задачи линейного программирования X есть многогранное замкнутое выпуклое множество.

Доказательство основывается на том, что, во-первых, все предельные точки принадлежат этому множеству, и, во-вторых, выпуклая комбинация любых двух точек из этого множества так же принадлежит ему.

Упражнение. Подробное доказательство провести самостоятельно.

Определение 3.4. Базисным решением системы называется точка , если она является решением этой системы, и ее ненулевым координатам соответствуют линейно-независимые столбцы матрицы .

Координаты базисного решения можно всегда разбить на 2 группы так, что в одной группе все координаты будут равны нулю, а координатам другой группы будут отвечать линейно-независимые столбцы матрицы . При этом координаты первой группы будем называть небазисными, а координаты 2-й группы – базисными переменными.

Пример. Рассмотрим систему линейных уравнений

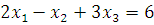
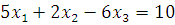
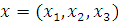
Столбцы матрицы A имеют вид , , .

Из этих столбцов можно сформировать только 2 базиса , . Пара не образует базис, так , и, значит, столбцы линейно зависимы. Базису соответствует следующее разбиение вектора : , -базисные переменные, - небазисная переменная. При определении базисного решения =0. Тогда переменные , можно найти, решив систему

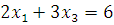
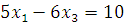
Таким образом, получим базисное решение .

Найдем базисное решение, отвечающее базису . Небазисная переменная =0, тогда базисные переменные , найдем из системы. Получим еще одно базисное решение. Других базисных решений у данной системы нет.

Определение 3.5. Опорным решением системы называется базисное решение системы, у которого все координаты неотрицательны.

Так, в предыдущем примере были найдены два базисных решения, из них только является опорным решением системы.

Предположим, что ранг матрицы . Тогда, у базисного (и опорного, если оно таковым является) решения системы количество базисных переменных равно . Если среди них есть равные нулю, то базисное (опорное) решение называют вырожденным. В противном случае говорят о невырожденном базисном (соответственно опорном) решении.

На рисунке 3.1 изображена область допустимых решений и некоторые из базисных решений. Они представлены не окрашенными и окрашенными точками пересечения прямых, ограничивающих область. Из них опорными решениями являются вершины области X.

Вершиной (крайней точкой) выпуклого множества называется точка из этого множества, которую нельзя представить в виде выпуклой комбинации двух других точек этого множества.

X

- опорные решения, - базисные решения, не являющиеся опорными

Рис.3.1. Геометрическая интерпретация базисного и опорного решений.

Теорема 3.2. Всякое опорное решение системы является вершиной (крайней точкой) ОДР множества и наоборот.

Доказательство. Пусть А-матрица размера , и ранг .

Предположим, что координаты допустимого решения системы упорядочены так, что , где .

Тогда, система в точке примет вид

. (3.7)

Дано: - опорное решение, то есть , и столбцы линейно независимы. Докажем, что – вершина.

Предположим противное, пусть - не является вершиной выпуклого множества . Тогда существуют две другие точки такие, что (3.8)

Из равенства (3.8) следует, что если , то и . Следовательно, , , и верны равенства , .

Вычитая из одного равенства другое, получим: . Так как , то и столбцы линейно зависимы. Получено противоречие, доказывающее, что сделанное предположение не верно, и – вершина.

Дано, что вершина области . Докажем, что – опорное решение системы .

По определению области Х имеем 0, и теперь достаточно доказать, что - базисное решение. Доказывать будем методом от противного.

Пусть не является базисным решением, тогда столбцы линейно зависимы. Это означает, что существуют коэффициенты , среди которых есть не равные 0, и для которых . (3.9)

Сложим равенство с равенством (3.9), предварительно умножив его на величину . Получим . А если вместо сложения выполнить вычитание, то получим при любом .

Покажем существование , при котором точки и , то есть являются допустимыми решениями.

Для этого решим систему неравенств относительно переменной для .

Проведем преобразования

для = и >0.

И так, получены две точки , и . Это означает, что представима в виде выпуклой комбинации точек , то есть не вершина. Но это противоречит условию теоремы.

Основная теорема линейного программирования. Если задача линейного программирования разрешима, то среди её оптимальных решений всегда есть вершина (опорное решение).

Доказательство проведем методом от противного. Пусть задача линейного программирования разрешима, но среди ее оптимальных решений нет вершины.

Пусть оптимальное решение, которое по сделанному предположению не является опорным.

Тогда можно построить точки и , которые являются допустимыми для значений , удовлетворяющих условию (см. доказательство предыдущей теоремы). Покажем, что если точки являются допустимыми, то они являются и оптимальными. Для определенности предположим, что рассматривается задача максимизации. По определению оптимального решения , .

Откуда следует, что , , и точки - оптимальные решения.

Выберем . Тогда, в точке , или в точке , по меньшей мере, одна из координат с номером j , где обратится в ноль. В результате получим оптимальное решение, у которого, по крайней мере, на одну нулевую координату больше, чем у точки . Так как по предположению новое оптимальное решение не является опорным, то можно выполнить действия, аналогичные проведенным ранее. Получим новое оптимальное решение, у которого еще на одну или более станет больше нулевых координат.

Действуя таким образом, получим оптимальное решение, у которого все координаты или все, кроме одной, равны нулю. Это решение является по определению опорным, а по предположению таковым быть не может. Полученное противоречие означает, что было сделано неверное предположение и среди оптимальных решений есть вершина.

Теорема 3.3. Если точки являются оптимальными решениями задачи линейного программирования, то их выпуклая комбинация , где , так же оптимальное решение этой задачи.

3.2. Симплекс-метод

Симплексный метод предназначен для решения задач линейного программирования. Его реализация предполагает поиск оптимального решения среди опорных решений (вершин). Поэтому при изложении метода остановимся на способе описания опорного решения и соответствующем ему представлении системы уравнений в виде симплексной таблице. Сформулируем критерий оптимальности опорного решения, и подробно изложим правило перехода к следующему опорному решению, если есть необходимость в продолжении симплекс-метода.

Рассмотрим задачу линейного программирования в каноническом виде:

, .

Предположим, что матрица A имеет размер mn, где m<n, и ранг матрицы равен m. Тогда количество опорных решений у системы не превосходит значения . Опираясь на основную теорему ЛП, приходим к выводу, что оптимальное решение нужно искать среди опорных решений.

Возьмем m линейно-независимых столбцов матрицы и образуем из них квадратную матрицу . Очевидно, что определитель . Оставшиеся столбцы объединим в матрицу 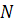. Обозначим - множество номеров тех столбцов, из которых составлена матрица B, - множество номеров столбцов, из которых составлена матрица N.

Разобьем вектор на 2 части: базисные переменные образуют вектор =, небазисные переменные вектор =.

Тогда, систему уравнений можно переписать в виде или . Если используем обозначения , , то получим

. (3.10)

О системе линейных уравнений (3.10) говорят, что она имеет жорданову форму.

Рассмотрим базисное решение системы , отвечающее базису 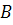: =0, из равенства (3.10) . Если , то – опорное решение системы.

Выразим значение целевой функции в произвольной допустимой точке через значение целевой функции в точке . ====, то есть

=, где . (3.11)

Координаты вектора называют оценками замещения или просто оценками.

Замечание. Если использовать формулу (3.11) для нахождения оценок, соответствующих базисным переменным, то получим . Приходим к выводу: оценки замещения, соответствующие базисным переменным, равны 0.

Содержательная интерпретация оценки замещения . Оценка () определяет величину, на которую увеличится (уменьшится) значение целевой функции при переходе в точку, получаемую из опорного решения заменой нулевого значения p-й небазисной координаты на единицу.

Систему линейных уравнений (3.11) и соответствующее опорное решение можно записать в виде таблицы (рис.3.1) , которую далее будем называть симплексной. Окрашенные области таблицы заполняются именами переменных, остальные – числовыми значениями.

Z

f

Рис.3.1. Структура симплексной таблицы.

Критерий оптимальности. Невырожденное опорное решение будет оптимальным решением тогда и только тогда, когда все оценки замещения не отрицательны.

Доказательство.

Дано: – оптимальное решение. Доказать: .

Докажем это от противного. Пусть среди оценок, отвечающих небазисным переменным, есть оценка , где . Построим новое допустимое решение, не обязательно опорное, при котором значение целевой функции больше, чем в точке . Обозначим эту точку .

Положим , где , и для остальных . Чтобы эта точка удовлетворяла ограничениям задачи, найдем базисные переменные из системы (3.10) , или .

Потребуем, чтобы координаты точки были неотрицательны: . Это векторное неравенство можно переписать в виде системы неравенств

для . (3.12)

Рассмотрим два возможных случая.

1). В p-м столбце симплексной таблицы нет положительных чисел, то есть для . Тогда для выполняются при любом > 0.

2). В p-м столбце симплексной таблицы есть положительные числа. Тогда, решив систему (3.12), получим неравенство для определения : =. (3.13)

При этом , так как опорное решение предполагается невырожденным.

Сравним значения целевой функции в точках и , используя формулу (3.11):

=. Так как > 0 и , то >, и точка не является оптимальным решением, но это противоречие.

Дано: . Доказать: – оптимальное решение.

По формуле (3.11) значение функции цели в произвольной допустимой точке выражается через значение в точке : =. Так как в области допустимых решений , и по условию , то . Следовательно, в точке функция достигает максимального значения.

Следствие 1. Для вырожденного опорного решения условие не отрицательности оценок является лишь достаточным условием его оптимальности.

Следствие 2. (Признак неразрешимости 2-го рода). Если в симплекс-таблице среди оценок есть отрицательная, и в соответствующем ей столбце нет положительных чисел, то целевая функция неограниченна сверху в ОДР.

Доказательство. Пусть . Тогда можно построить точку (см. доказательство критерия оптимальности), которая является допустимой при любом > 0. При этом =. Тогда устремив , мы получим .

Следствие 3. Если в симплекс-таблице есть отрицательная оценка, и в соответствующем ей столбце есть положительные числа, то можно перейти к другому опорному решению. Если исходное опорное решение невырожденное, то при переходе к новому опорному решению будет иметь место возрастание целевой функции.

Доказательство. Для этого нужно получить симплексную таблицу, отвечающую опорному решению, взяв = . Если старое опорное решение не вырожденное, то и >0.

Тогда k-я координата точки станет равной 0, p-я станет равной , и эта точка станет опорным решением. При построении новой таблицы переменные и меняем местами, то есть k-ю координату переводим во множество небазисных переменных на место p-й координаты, которую делаем базисной.

При этом меняется значение целевой функции =, откуда, . Все остальные числовые значения из новой симплекс-таблицы получаем в результате жордановых преобразований относительно элемента , который далее будем называть главным. Соответственно k-ю строку и p-й столбец, будем называть главными.

Жордановы преобразования симплекс-таблицы

Главный элемент выбирается из столбца p с отрицательной оценкой по правилу =. Главная строка и главный столбец определяются главным элементом, который стоит на их пересечении. Жордановы преобразования относительно выбранного главного элемента требуют выполнения следующих действий.

  1. Поменять местами переменные, стоящие в главной строке и в главном столбце.
  2. Главный элемент заменить ему обратным.
  3. Все остальные элементы главной строки разделить на главный элемент.
  4. Все остальные элементы главного столбца разделить на главный элемент и поменять у них знаки на противоположные.
  5. Все оставшиеся элементы пересчитать по правилу, сходному с правилом вычисления определителя второго порядка (в качестве главной диагонали нужно брать ту, на которой стоит главный элемент), и разделить на главный элемент.

Замечание. Во всех перечисленных действиях используйте числа из старой таблицы, а результаты вычислений записывайте в новую таблицу.

Алгоритмическое описание симплекс-метода

Предположим, что известно некоторое опорное решение и построена соответствующая ему симплекс-таблица. В этих условиях приведем алгоритмическое описание симплекс-метода.

  1. Если оценки симплекс-таблицы неотрицательны, то таблица оптимальная, и соответствующее ей опорное решение оптимальное.

Полагая всякую небазисную переменную равной нулю, а базисную равной элементу из столбца свободных членов, получаем оптимальное опорное решение. Алгоритм завершает работу.

  1. Если в таблице есть столбец с отрицательной оценкой, и все элементы в нем не положительны, то оптимальное решение не существует, так как целевая функция неограниченна сверху в ОДР (Неразрешимость 2). Алгоритм завершает работу.
  2. Если в таблице есть столбец с отрицательной оценкой, и в нем есть положительные элементы, то среди этих элементов выбираем главный. Для этого найдем для каждого такого элемента частное от деления правой части ограничения на этот элемент. Полученные частные сравним для того, чтобы главным элементом выбрать тот, которому соответствует наименьшее частное. Главный элемент определяет главную строку и главный столбец, так как он стоит на их пересечении.
  3. Выполним жордановы преобразования симплекс-таблицы относительно выбранного главного элемента и перейдем к пункту 1.

3.3. Построение начальной симплекс-таблицы

Если ограничения имеют вид равенств в жордановой форме с неотрицательными числами в правых частях или элементарно приводятся к такому виду эквивалентными преобразованиями, то построение начальной симплекс-таблицы не вызывает трудностей. Для этого достаточно в качестве базисных переменных выбрать те, что соответствуют столбцам, образующим с точностью до порядка следования единичную матрицу.

1. Рассмотрим задачу линейного программирования вида:

, , и пусть .

Если перейти к каноническому виду, то получим

, ,.

Полученная система ограничений имеет опорное решение, отвечающее базису, состоящему из столбцов единичной матрицы 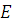. Этим решением является точка , где , . Переменные, составляющие вектор , - это небазисные переменные, а переменные, составляющие вектор , - базисные. Соответствующая этому опорному решению симплекс-таблица выглядит следующим образом

f

2. Рассмотрим задачу линейного программирования в каноническом виде

, ,

и предположим, не нарушая общности, что в этой задаче .

Рассмотрим случай, когда матрица A содержит набор столбцов, образующих единичную матрицу. Для определенности будем считать, что это первые m столбцов, то есть . Опорное решение, отвечающее базису E, определяется таблицей

f

3. Рассмотрим общий случай, когда построение симплекс-таблицы не является таким простым, как в случае 1 или 2. При этом будем для построения начальной симплекс-таблицы использовать метод искусственного базиса.

Метод искусственного базиса

Дана задача, которую далее будем называть исходной,

(3.14)

, , и пусть .

Чтобы построить начальную симплексную таблицу, требуется систему уравнений привести к жордановой форме с неотрицательными правыми частями.

Для этой цели построим вспомогательную задачу

(3.15)

, , ,

где - новые переменные, которые будем называть искусственными.

Сформулируем теоремы, определяющие свойства вспомогательной задачи и ее связь с исходной задачей.

Теорема 3.4. Вспомогательная задача (3.15) всегда разрешима.

Доказательство. Точка , у которой , всегда является допустимой для задачи (3.15). Целевая функция этой задачи ограничена сверху в области допустимых решений этой задачи, так как Следовательно, задача (3.15) разрешима.

Теорема 3.5. У исходной задачи существует допустимое решение тогда и только тогда, когда у вспомогательной задачи максимальное значение целевой функции равно нулю.

Доказательство.

У исходной задачи есть допустимое решение. Пусть это будет точка . Тогда , . Рассмотрим точку , где . Эта точка является допустимой для вспомогательной задачи и в ней целевая функция вспомогательной задачи равна нулю, то есть своему наибольшему значению. Отсюда, .

Пусть , и он достигается в точке . Тогда , , . Значит, , и точка является допустимым решением исходной задачи.

Следствие 1. Если оптимальное значение целевой функции вспомогательной задачи отрицательно, то у исходной задачи ограничения противоречивы (неразрешимость первого рода, Нр1).

Следствие 2. Если оптимальное значение целевой функции вспомогательной задачи равно 0, то из оптимальной симплекс-таблицы вспомогательной задачи можно построить начальную симплекс-таблицу исходной задачи. Здесь возможны 3 случая.

  1. Ранг матрицы ограничений исходной задачи , и задача невырожденная. Тогда, решив вспомогательную задачу, получим симплекс-таблицу, в которой искусственные переменные будут принадлежать множеству небазисных переменных. Для получения начальной симплекс-таблицы исходной задачи нужно вычеркнуть столбцы с искусственными переменными и пересчитать нижнюю строку таблицы оценок, используя целевую функцию исходной задачи
  2. Ранг матрицы ограничений исходной задачи , и задача невырожденная. Тогда, решив вспомогательную задачу, получим симплекс-таблицу, в которой среди базисных переменных будут некоторые искусственные переменные. В строках, где базисной переменной является искусственная переменная, все элементы будут равны 0. Эти строки будут соответствовать тем уравнениям, которые являются линейной комбинацией остальных. Для перехода к первому случаю, нужно вычеркнуть строки, о которых шла речь выше.
  3. Пусть ранг матрицы ограничений исходной задачи , и задача вырожденная. Тогда после решения вспомогательной задачи, можем получить симплексную таблицу, в которой среди базисных переменных будут некоторые искусственные переменные. Однако, в отличие от 2-го случая в этих строках будут элементы не равные нулю. Чтобы искусственную переменную вывести из базиса, достаточно выбрать в такой строке любой отличный от нуля элемент главным и выполнить относительно этого главного элемента жордановы преобразования таблицы. После того, как все искусственные переменные окажутся выведенными из числа базисных переменных, придем к таблице, отвечающей 1-му случаю.

Алгоритм построения начальной симплекс-таблицы с помощью метода искусственного базиса.

1. Используя эквивалентные преобразования, преобразуйте данную задачу к каноническому виду с неотрицательными правыми частями.

2. Постройте вспомогательную задачу. Для этого из исходной преобразованной задачи возьмите только ограничения. Прибавьте к левым частям ограничений новые переменные , которые далее будем называть искусственными. Если до введения искусственных переменных матрица ограничений имела некоторые столбцы для единичной матрицы, то дублировать их введением искусственных переменных не обязательно. В качестве целевой функции вспомогательной задачи возьмите сумму искусственных переменных со знаком минус и потребуйте ее максимизации.

3. Решите вспомогательную задачу симплекс-методом.

4. Если оптимальное значение целевой функции вспомогательной задачи окажется отрицательным числом, то сделайте вывод: исходная задача не имеет допустимых решений (неразрешимость 1). Перейдите к пункту 6.

5. Если оптимальное значение целевой функции вспомогательной задачи равно нулю, то используйте полученную оптимальную таблицу вспомогательной задачи и постройте начальную симплексную таблицу для исходной задачи. Для этого в таблице вычеркните столбцы с искусственными небазисными переменными и пересчитайте заново оценки, используя целевую функцию исходной задачи.

6. Завершите работу алгоритма.

4. Теория двойственности в линейном программировании

Определение 4.1. Парой симметричных двойственных задач называются задачи

Задачи (4.1), (4.2) являются взаимно двойственными задачами.

Для построения двойственной задачи рекомендуется выполнить действия:

  1. Если в исходной задаче требуется максимизировать целевую функцию, то все ограничения-неравенства преобразовать к виду « ».
  2. Если в исходной задаче требуется минимизировать целевую функцию, то все ограничения-неравенства преобразовать к виду « ».
  3. Построить двойственную задачу, воспользовавшись таблицей 2. При этом, если исходная задача - это задача 1, то двойственной к ней является задача 2, и наоборот.

Таблица 4.1 - Общая схема построения двойственной задачи

Задача 4.1

Переменные, соответствующие ограничениям задачи 4.1.

Переменные, соответствующие ограничениям задачи 4.2.

Задача 4.2

Таблица 4.2 - Пример построения двойственной задачи

Задача А

Переменные, соответствующие ограничениям задачи А.

Переменные, соответствующие ограничениям задачи В.

Задача В

1-я теорема двойственности. Двойственные задачи одновременно разрешимы или неразрешимы. В случае разрешимости оптимальные значения целевых функций этих задач равны.

Доказательство. Предположим, что задача (4.1) имеет оптимальное решение. Тогда эту задачу можно решить симплекс-методом. Для этого приведем задачу (4.1) к каноническому виду

(4.3)

Обозначим: вектор переменных , матрица , вектор коэффициентов функции f(x) . Тогда задачу (4.3) можно переписать в виде

(4.4)

Решим полученную задачу симплекс-методом и найдем оптимальное решение, определяемое следующей симплекс-таблицей.

Z

f

Элементы таблицы связаны с параметрами задачи (4.4) следующим образом

, , , и .

Рассмотрим точку и покажем, что она является оптимальным решением задачи (4.1). Для этого покажем, что удовлетворяет ограничениям этой задачи. Действительно, по определению . Тогда, = , или =. Из последнего уравнения получим при =, и =, если .

Значение целевой функции двойственной задачи в точке y* равно максимальному значению целевой функции задачи (4.4), так как . Следовательно, - оптимальное решение двойственной задачи, то есть она разрешима.

Аналогично, можно доказать, что из разрешимости задачи (4.2) следует разрешимость задачи (4.1).

Следствие. Если двойственные задачи разрешимы, то по оптимальной симплексной таблице, полученной при решении задачи (4.1), можно найти оптимальное решение двойственной задачи (4.2): = , .

Преобразуем ограничения симметричных двойственных задач в равенства, получим

2-я теорема двойственности. Допустимые решения двойственных задач являются оптимальными решениями этих задач тогда и только тогда, когда они удовлетворяют условиям дополняющей нежесткости .

Вторую теорему двойственности можно использовать для того, чтобы проверить, является ли заданное допустимое решение одной из пары симметричных двойственных задач оптимальным решением этой задачи.

Алгоритм проверки допустимого решения задачи (4.1) на оптимальность с помощью условий дополняющей нежесткости

  1. Дана точка - допустимое решение задачи (4.1). Преобразуем ограничения симметричных двойственных задач в равенства и получим задачи (4.5) и (4.6).
  2. Подставим точку в ограничения задачи (4.5), и найдем вектор , координаты которого будут неотрицательными числами.
  3. Выпишем систему условий дополняющей нежесткости в виде уравнений . В этой системе неизвестными являются . Из этой системы найдем те из них, что равны 0.
  4. Подставим найденные в ограничения задачи (4.6). Получим систему, состоящую из уравнений и неравенств. Если эта система имеет решение, то найденный вектор , и только он является оптимальным решением двойственной задачи, а вектор оптимальным решением исходной задачи.

Алгоритм проверки допустимого решения задачи (4.2) на оптимальность с помощью условий дополняющей нежесткости

  1. Дана точка - допустимое решение задачи (4.2). Преобразуем ограничения симметричных двойственных задач в равенства и получим задачи (4.5) и (4.6).
  2. Подставим точку в ограничения задачи (4.6) и найдем вектор , координаты которого будут неотрицательными числами.
  3. Выпишем систему условий дополняющей нежесткости в виде уравнений . В этой системе неизвестными являются . Из этой системы найдем те из них, что равны 0.
  4. Подставим найденные в ограничения задачи (4.5). Получим систему, состоящую из уравнений и неравенств. Если эта система имеет решение, то найденный вектор , и только он является оптимальным решением двойственной задачи, каковой здесь является задача (1), а вектор оптимальным решением исходной задачи (2).

Замечание. Отрицательный результат проверки еще не означает, что двойственные задачи не разрешимы.

Экономическая интерпретация двойственных переменных

Перепишем симметричные двойственные задачи в виде

=

(4.7)

=

(4.8)

Задачу (4.7) можно интерпретировать как задачу оптимальной организации технологического процесса. При этом переменная определяет объем продукции, выпускаемой по j-й технологии, - цену за единицу продукции, произведенной по j-й технологии. Матрицу А называют технологической матрицей, так как ее элемент равен количеству ресурса i-го вида, затрачиваемого на производство единицы продукции по j-й технологии. Величина - это запас i-го ресурса.

Функция g измеряется в тех же единицах, что и функция f , а, следовательно, двойственная переменная измеряется в единицах стоимости на единицу ресурса. Следовательно, можно интерпретировать как цену единицы i-го ресурса.

Вывод: двойственные переменные определяют теневые цены ресурсов.

О влиянии изменения запаса ресурса на оптимальную прибыль производства

Пусть запас к-го ресурса увеличен на единицу, то есть к-е ограничение задачи (4.7) теперь имеет вид . Это повлечет изменение целевой функции двойственной задачи, которая приобретет вид . Предположим, что такое изменение целевой функции не привело к изменению оптимального решения задачи (4.8). Значит, оптимальное значение новой целевой функции определяется подстановкой в нее оптимального решения : =. Так как по первой теореме двойственности до увеличения запаса , а после изменения запаса , то получаем, что .

Вывод: увеличение запаса к-го ресурса на единицу приводит к увеличению оптимальной прибыли на величину теневой цены этого ресурса.

Экономическая интерпретация условий дополняющей нежесткости.

Пусть план производства определяется вектором . Если , то i-й ресурс при реализации плана расходуется полностью и потому является дефицитным. Из условия дополняющей нежесткости произведение . Отсюда следует,что теневая цена недефицитного ресурса равна нулю.

Верно и такое утверждение: если цена ресурса не равна 0, то ресурс дефицитный.

Теперь рассмотрим условия дополняющей нежесткости . Если , то , то есть . А это означает, что цена производимого по j-й технологии продукта равна затратам на вложенные в него ресурсы.

Если , то . Этот результат приводит к выводу: если цена производимого по j-й технологии продукта больше затрат на вложенные в него ресурсы, то такой продукт не производится.

5. Нелинейное программирование

5.1. Задача условной оптимизации с ограничениями-равенствами (задача Лагранжа)

Рассмотрим задачу минимизации целевой функции, в которой все ограничения заданы в виде равенств

(5.1)

Построим функцию, которую назовем функцией Лагранжа,

, (5.2)

переменные, называют множителями Лагранжа.

Если функции , непрерывно дифференцируемы, то верна следующая теорема.

Теорема Лагранжа (необходимые условия). Если точка является локальным оптимальным решением задачи (5.1), то существует вектор множителей Лагранжа такой, что точка есть стационарная точка функции Лагранжа.

Эта теорема позволяет, решив систему уравнений найти точки , и затем среди полученных точек отобрать оптимальные решения задачи (5.1). Но при этом используются достаточные условия оптимальности. Получим их. Сравним значения целевой функции в точках и , где - вектор приращений. Тогда, если и - допустимые решения, то , и .

Разложим функцию в ряд Тейлора, получим = В точке выполняются необходимые условия из теоремы и, следовательно, . Итак, , где вектор приращений удовлетворяет условиям . Если функции разложить в ряд Тейлора до слагаемых первого порядка малости, то условия, накладываемые на приращения, приобретут вид . Полученный результат сформулируем в виде теоремы.

Теорема 5.1 (достаточные условия). Если стационарная точка функции Лагранжа, и в этой точке 0(0) для всех приращений , удовлетворяющих уравнениям , то в точке достигается локальный минимум (максимум).

Алгоритм решения задачи Лагранжа

  1. Преобразуйте задачу к виду (5.1), когда правые части ограничений нули.
  2. Постройте функцию Лагранжа.
  3. Найдите все стационарные точки функции Лагранжа.
  4. Каждую стационарную точку проверьте на оптимальность, используя достаточные условия оптимальности.

5.2. Задачи условной оптимизации с ограничениями-неравенствами

Рассмотрим задачу, в которой ограничения являются нестрогими неравенствами

(5.3)

Функция Лагранжа для этой задачи: , где переменные , - множители Лагранжа.

Определение 5.1. Точка , где , называется седловой точкой функции Лагранжа, если в этой точке выполняются неравенства для всех .

Лемма. Если - седловая точка функции Лагранжа, то и .

Доказательство. Для седловой точки выполняется неравенство , или для любого

. (5.4)

Перепишем неравенство (5.4) для точки , определив ее координаты по формуле . Получим , а так как k выбирали произвольно, то этот результат верен для любого k. Это означает, что .

Теперь перепишем неравенство (5.4) для точки , определив ее координаты по формуле . Получим для произвольного k. С другой стороны по определению седловой точки , и , что было доказано выше. Следовательно, для всех k, то есть .

Следующая теорема устанавливает связь между седловой точкой функции Лагранжа и оптимальным решением.

Первая теорема Куна-Таккера. Если седловая точка функции Лагранжа, то оптимальное решение задачи (5.3).

Доказательство. По определению седловой точки , и . Учитывая вид функции Лагранжа и лемму, получаем для , а значит тем более для . При этом . Тогда, , и . А это означает, что - оптимальное решение задачи (5.3).

Контр-пример к первой теореме Куна-Таккера.

Приведем пример задачи, функция Лагранжа которой не имеет седловой точки:

Функция Лагранжа для этой задачи имеет вид . У данной задачи единственное допустимое решение, которое является оптимальным решением Покажем, что при точка не является седловой, то есть не выполняется для всех неравенство

. (5.5)

Действительно, если , то из неравенства (5.5) получаем , что верно не для всех . Если и , то (5.5) преобразуется к виду , и вновь приходим к выводу, что неравенство (5.5) выполняется не для всех .

5.3. Выпуклое программирование

Определение 5.2. Задачей выпуклого программирования называется задача минимизации выпуклой функции на выпуклом множестве, или преобразуемая в таковую эквивалентными преобразованиями.

Очевидно, что задача (5.3) является задачей выпуклого программирования при условии, что все входящие в нее функции – выпуклые. Если все ограничения задачи (5.1) линейные, а целевая функция выпуклая, то эта задача то же будет задачей выпуклого программирования.

Задачи выпуклого программирования наделены свойством одноэкстремальности: всякий локальный минимум выпуклой функции на выпуклом множестве является глобальным. Поэтому в задачах выпуклого программирования речь всегда будет идти о глобальном минимуме.

Приведем различные математические модели задач выпуклого программирования.

Рассмотренная в контрпримере задача является задачей выпуклого программирования. Но, несмотря на это, функция Лагранжа не имеет седловую точку. Поэтому обратная (вторая теорема Куна –Таккера) верна для задач выпуклого программирования только при дополнительном требовании. И это – требование регулярности задачи. Введем это понятие.

Определение 5.3. Ограничение задачи (5.3) называется регулярным, если существует допустимое решение задачи , при котором .

Определение 5.4. Если все ограничения задачи регулярные, то говорят о регулярности самой задачи.

Вторая теорема Куна –Таккера. Для любого оптимального решения x* регулярной задачи выпуклого программирования (5.3) существует вектор множителей Лагранжа y* такой, что (x*, y*) – седловая точка функции Лагранжа.

Условия седловой точки для гладких функций (условия Куна-Таккера)

Теоремы Куна-Таккера дают метод нахождения оптимального решения задачи (5.3) через поиск седловых точек функции Лагранжа. Поэтому особый интерес вызывают условия, определяющие седловые точки. Получим эти условия для непрерывно дифференцируемых функций.

Предположим, что все функции в задаче (5.3) выпуклые и непрерывно дифференцируемые. Тогда можно сформулировать необходимые и достаточные условия седловой точки функции Лагранжа, называемые условиями Куна-Таккера.

Теорема 5.2. Точка является седловой точкой функции Лагранжа задачи выпуклого программирования тогда и только тогда, когда в ней выполняются условия Куна-Таккера:

, , (5.6)

, .

Доказательство.

Точка седловая и в ней по переменной x достигается минимум в области и максимум по переменной y в области . Следовательно, если , то частная производная в точке либо равна 0, либо положительна. Если , то частная производная в точке равна 0. Это можно записать, используя условие дополняющей нежесткости , для .

В векторной форме этот результат выглядит так , .

Аналогично выводится группа условий для переменной y.

В условиях Куна-Таккера , а функция , являясь неотрицательной линейной комбинацией выпуклых функций, - выпуклая функция. Из теоремы об эквивалентных условиях выпуклости из выпуклости функции следует

.

Используя равенство , и неравенство , получаем для всех . И так, доказано неравенство для всех .

Вспомним вид функции Лагранжа: . Из условий Куна-Таккера , . Следовательно, для всех . Или для всех . Доказано, что точка - седловая.

В таблице 5.1 приведены условия Куна-Таккера для общей задачи выпуклого программирования:

(5.7)

где

Таблица 5.1 - Условия Куна-Таккера к задаче (5.7)

Ограничение задачи

Соответствующие ограничению условия Куна-Таккера в точке

, ,

, ,

Если исходная задача является задачей выпуклого программирования, функции в задаче непрерывно дифференцируемы, а ограничения регулярные, то можно любую данную точку проверить на оптимальность.

Алгоритм проверки точки на оптимальность

  1. Преобразовать задачу к виду (5.7), выписав все функции .
  2. Проверить выпуклость всех функций, входящих в ограничения-неравенства, и линейность, входящих в ограничения-равенства. Доказать регулярность каждого из нелинейных ограничений.
  3. Выписать условия Куна-Таккера, подставив в них координаты точки .
  4. Если полученная система имеет решение , то - седловая точка функции Лагранжа, а - оптимальное решение задачи (5.7) по 1-й теореме Куна-Таккера. В противном случае по второй теореме Куна-Таккера не является оптимальным решением. Проверка завершается.

6. Метод возможных направлений

Это – численный метод решения регулярной задачи выпуклого программирования. Был предложен Г. Зойтендейком.

Рассмотрим задачу выпуклого программирования в виде

(6.1)

Обратите внимание: ограничения на знак переменных в постановке задачи не выделены в отдельные ограничения, и поэтому они могут быть в задаче (тогда они рассматриваются наравне с остальными ограничениями), а могут отсутствовать.

Общая схема метода возможных направлений

1. Преобразовать задачу к виду (6.1), выписав все функции .

2. Проверить выпуклость всех функций. Доказать регулярность каждого из нелинейных ограничений.

3. Выбрать произвольно точку , удовлетворяющую ограничениям задачи.

Положить k=0.

4. Построить в точке конус возможных направлений спуска .

5. Если конус - пустое множество, то делаем вывод о том, что точка является оптимальным решением задачи (6.1), и алгоритм завершает работу.

6. Выбрать в точке из конуса возможных направлений спуска направление .

7. Выбрать в точке при выбранном направлении длину шага .

8. Перейти в новую точку .

9. Присвоить k=k+1. Перейти к пункту 4.

Построение конуса возможных направлений спуска в точке .

1. Найти номера тех ограничений, которые в точке выполняются как строгие равенства: .

Это множество номеров можно разделить на два непересекающихся подмножества: и -линейная функция} и

и -нелинейная функция}.

В построении конуса будут участвовать только ограничения с этими номерами.

2. Конус возможных направлений спуска задается системой неравенств

Выписать систему неравенств, задающую конус в точке .

Выбор направления из конуса возможных направлений спуска

1. Если антиградиент целевой функции принадлежит полученному конусу, то полагаем . Переходим на пункт 4.

2. Если в конусе существует направление, ближайшее к антиградиенту целевой функции, то выбираем его. Переходим на пункт 4.

3. Выбираем любое направление из конуса.

4. Направление выбрано.

Выбор длины шага

Длину шага выбираем после выбора направления путем решения задачи

. (6.2)

В задаче (6.2) минимизация проводится по переменной .


Литература

  1. Сухарев А.Г., Тимохов А.В., Федоров В.В. Курс методов оптимизации.2-е издание. М.: ФИЗМАТЛИТ, 2005.
  2. Вентцель Е.С. Исследование операций. Задачи, принципы, методология. М.: Высш. шк.,2011.
  3. Таха Х. Введение в исследование операций.7-е издание. М.: Вильямс,2007.
  4. Афанасьев М.Ю., Суворов Б.П. Исследование операций в экономике: модели, задачи, решения: Учеб. Пособие. М.: ИНФА-М, 2013
  5. Моисеев Н.Н., Иванилов Ю.П., Столярова Е.М.. Методы оптимизации. М.: Наука, 1978.
  6. Васильев Ф.П. Численные методы решения экстремальных задач: Учеб. пособие. М.: Наука, 1981.
  7. Зинченко А.Б., Сантылова Л.И. Индивидуальные задания по курсу “Методы оптимизации” (часть 1): Метод.указания для студентов вечернего отделения мех.-мат.фак.-Ростов н/Д: РГУ,2003.
  8. Зинченко А.Б., Сантылова Л.И. Индивидуальные задания по курсу “Методы оптимизации” (часть 2): Метод.указания для студентов мех.-мат.фак. Ростов н/Д: РГУ,2003.
  9. Зинченко А.Б., Сантылова Л.И. Индивидуальные задания по курсу “Методы оптимизации” (части 3): Метод.указания для студентов мех.-мат.фак. Ростов н/Д: РГУ,2006.
  10. Землянухина Л.Н., Сантылова Л.И. Индивидуальные задания по курсу “Методы оптимизации” (части 4): Метод.указания для студентов мех.-мат.фак. Ростов н/Д: РГУ,2006.
  11. Землянухина Л.Н., Зинченко А.Б., Сантылова Л.И., Макмак С.М. Линейное программирование и смежные вопросы (часть 1): Метод.указания для студентов мех.-мат.фак. по курсу “Методы оптимизации”. Ростов н/Д: РГУ, 2008.
  12. Л.Н. Землянухина, А.Б. Зинченко, Л.И. Сантылова, Макмак С.М. Линейное программирование и смежные вопросы (часть 2): Метод.указания для студентов мех.-мат.фак. по курсу “Методы оптимизации”. Ростов н/Д: РГУ, 2008.
  13. Л.Н. Землянухина, А.Б. Зинченко, Л.И. Сантылова. Линейное программирование и смежные вопросы (часть 3): Метод.указания для студентов мех.-мат.фак. по курсу “Методы оптимизации”. Ростов н/Д: РГУ, 1998.
  14. Сантылова Л.И. Вариационное исчисление и методы оптимизации. Руководство по решению задач (часть 1): Метод.указания. Ростов н/Д: РГУ, 2006.

Дополнительная литература

  1. Волков И.К. и др. Введение в исследование операций. М.:Изд-во МГТУ им. Баумана, 2000.
  2. Вагнер Г. Основы исследования операций. Т.1-3.– М.:Мир,1973.
  3. Давыдов Э.Г.. Исследование операций. М. 1990.
  4. Реклейтис Г. и др. Оптимизация в технике. М. Мир, 1986.
  5. Химмельблау Д. Прикладное нелинейное программирование. М.: Мир, 1975.

МЕТОДЫ ОПТИМИЗАЦИИ. АЛГОРИТМЫ. ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ