АБСОЛЮТНАЯ И РОБАСТНАЯ УСТОЙЧИВОСТЬ
Реферат
АБСОЛЮТНАЯ И РОБАСТНАЯ УСТОЙЧИВОСТЬ
Содержание
1. Понятие абсолютной устойчивости
2. Критерий абсолютной устойчивости Попова
3. Исследование абсолютной устойчивости при неустойчивой линейной части
4. Круговой критерий Воронова
5. Робастная устойчивость
Литература
1. Понятие абсолютной устойчивости
Метод абсолютной устойчивости применяется для исследования устойчивости нелинейных систем, когда значения характеристик нелинейных элементов известны неточно. Неполнота информации может быть связана с погрешностью изго�товления, с пренебрежением некоторыми факторами, со старением элементов и т.п. Для того чтобы гарантировать устойчивость сис�тем, несмотря на неполную информацию о нелинейностях, было введено понятие абсолютной устойчивости. С этой же целью вводятся классы нелинейностей [4]. Для примера, на рис 1 показаны нелинейности из класса . По определению к этому классу относятся все нелинейные функции, график которых располагается между прямыми и , где .
а б
Рис.1.
Чаще всего используются следующие разновидности классов нелинейностей данного типа: [0; k], (рис. 1,б); класс (рис. 2,а); класс [k1; k2] причем , (рис. 2,б). Существуют и другие классы нелинейностей, определяемые более сложными выражениями [2, 4].
Практически, класс той или иной нелинейности должен быть выбран таким образом, чтобы в процессе старения, износа элементов системы или при любых других естественных изменениях нелинейность сохраняла свою принадлежность к исходному классу.
Определение. Система называется абсолютно ус�тойчивой, если её единственное положение равновесия асимптотически устойчиво в целом при любой нели�нейности из заданного класса.
2. Критерий абсолютной устойчивости Попова
Для исследования абсолютной устойчивости предложен ряд критериев абсолютной устойчивости. Наибольшее распространение из них получили следующие два: критерий устойчивости В. М. Попова и круговой критерий, предложенный А. А. Вороновым.
а б
в
Рис. 2
Критерий Попова используется для исследования абсолютной устойчивости систем с нелинейностью из класса [0, k], где . Для применения этого критерия структурная схема системы приводится к виду, показанному на рис. 3.
Уравнения системы
(1)
, (2)
(3)
где – управление, – вектор состояний.
Перейдя в (1) и (3) к изображениям по Лапласу, получим
. (4)
Рис. 3
Критерий В. М. Попова может применяться лишь в тех случаях, когда выполняются следующие условия:
а) ,
б) ,
в) Линейная система, полученная из нелинейной при замене на , устойчива асимптотически, то есть удовлетворяет критерию Гурвица или Найквиста при всех [0; k].
Критерий Попова. Нелинейная система, показанная на рис.3, является абсолютно устойчивой, если выполнены указанные выше условия а) – в), и при всех [0, ] выполняется неравенство:
[(1+)] (5)
Здесь – произвольное число.
Критерий Попова является достаточным.
Геометрическая форма критерия Попова. Для графического исследования системы на абсолютную устойчивость строят годограф Попова , который определяется по формуле:
()=()+().
Здесь () и () – вещественная и мнимая части , т.е. =()+(). Напомним, что именно по строится годограф Найквиста для линейной части системы, показанной на рис 3. Для примера на рис. 4 показаны годографы Попова и Найквиста , для одной и той же системы.
Рис. 4
Графический вариант критерия Попова состоит в следующем: Если через точку можно провести прямую так, чтобы годограф Попова располагался полностью справа от неё, то система абсолютно устойчива.
На рис. 5 показаны годографы Попова, построенные для абсолютно устойчивой системы (рис. 5,а) и системы не являющейся абсолютно устойчивой (рис. 5,б).
а б
Рис. 5
Путем исследования годографа Попова установлено [25. С. 185], что если линейная часть системы представляет собой последовательное соединение инерционных звеньев и не более одного интегрирующего звена, то соответствующий годограф Попова будет выпуклым (рис. 5,б). При этом предельное значение при котором система абсолютно устойчива по критерию Попова, будет совпадать со значением , даваемым критерием устойчивости Найквиста, если нелинейность заменить прямой . Поэтому, если линейная часть нелинейной системы имеет указанный вид, то для исследования абсолютной устойчивости можно применять критерий Найквиста вместо критерия Попова.
Пример 1. Исследовать на абсолютную устойчи�вость систему, схема которой показана на рис. 6.
Рис. 6
Нелинейность принадлежит сектору [0; 10], т.е. [0; 10].
Решение. Для решения задачи построим годограф Попова. Для этого сначала выделим вещественную и мнимую части . Имеем
.
Задаваясь значениями частоты , составим таблицу 1.
Таблица 1
|

|
0
|
1
|
|
5
|
|
|
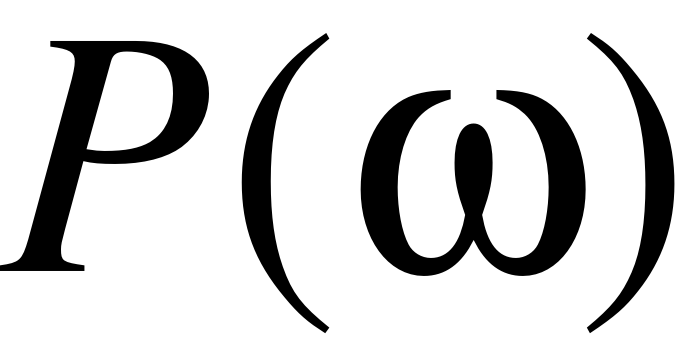
|
0,5
|
0,1
|
0
|
0,06
|
0
|
|
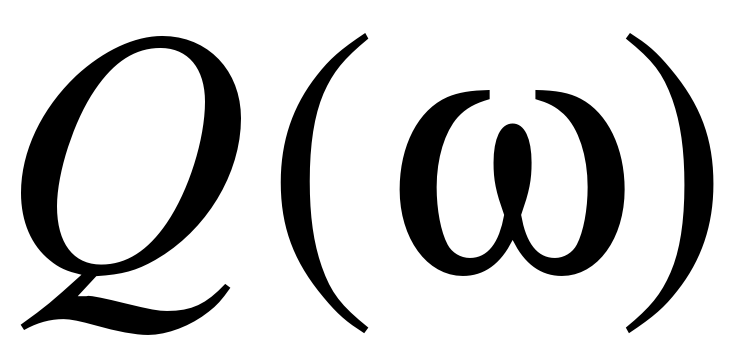
|
0
|
3
|
–0,25
|
–1,5
|
0
|
|
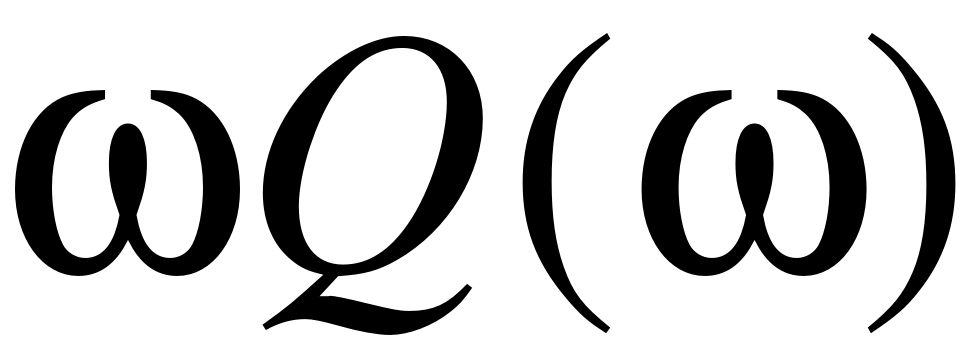
|
0
|
3
|
–0,37
|
3
|
0
|
Соответствующий годограф Попова построен на рис. 7. Как видно, в данном случае можно провести прямую через точку (–0,1; j0) так, что годограф Попова будет располагаться справа от неё. Следовательно, рассмат�риваемая система абсолютно устойчива.
Рис. 7
Пример 2. Исследовать на абсолютную устойчивость систему, структурная схема которой показана на рис. 3, а передаточная функция линейной части
Нелинейность [0; 5], т.е. k = 5.
Решение. Так как линейная часть представляет собой последова�тельное соединение инерционных звеньев, то для ре�шения задачи можно воспользоваться критерием Найквиста. На рис. 8 показан общий вид расположения годографа Найквиста для систем с передаточной функцией задан�ного вида.
Рис. 8
Очевидно, для решения задачи в данном случае достаточно сравнить зна�чения с величиной при k = 5. Поэтому запишем и найдем частоту . Имеем
Приравнивая мнимую часть знаменателя в этом выражении к нулю, полу�чим
.
Отсюда . Тогда . Условие (5), в соответствии с рис. 8, выполняется, если , т.е. если . Следовательно, рассматриваемая система абсолютно устойчива при .
Не трудно видеть, что если линейная часть нелинейной системы представляет собой последова�тельное соединение инерционных звеньев и одного интегрирующего звена, то исследование абсолютной устойчивости значительно упрощается, так как вместо критерия Попова можно применять критерий Найквиста.
3. Исследование абсолютной устойчивости при неустойчивой линейной части
Все известные критерии абсолютной устойчивости сформулированы для случая, когда линейная часть системы асимптотически устойчива. Поэтому при неустойчивой линейной части для обеспечения возможности применения критериев абсолютной устойчивости, необходимо сначала преобразовать систему так, чтобы линейная часть преобразованной системы была устойчивой. Для этой цели обычно применяют дополнительную обратную связь.
Рассмотрим, например, систему, схема которой приведена на рис. 9,а [25], где передаточная функция
(6)
а нелинейность относится к классу [0,2; 6], т.е. .
Найти условия, при которых данная система абсолютно устойчива.
Линейная часть в данном случае неустойчива, поэтому введем дополнительные связи с коэффициентом передачи , как показано на рис. 9,а. Так как введённые связи компенсируют друг друга, то полученная схема эквивалентна исходной. Затем перенесём вход положительной обратной связи с выхода системы на выход сравнивающего элемента, как показано на рис. 9,б. Из-за переноса через сравнивающий элемент эта связь станет отрицательной, но результирующая система будет, по-прежнему, эквивалентна исходной.
а
б
в
Рис. 9
Передаточная функция с учетом (6) и нелинейность эквивалентной схемы (рис. 9,в) определяются по формулам
(), ()=()–.
Очевидно в рассматриваемом случае
, (7)
Так как система с () (7) должна быть устойчивой, то рассматриваемая система может быть абсолютно устойчивой, если только и .
Имея в виду применение критерия Попова, примем . Тогда , а из условия следует неравенство или .
В рассматриваемом случае порядок линейной части равен двум, поэтому при и годограф Попова будет располагаться в четвертом и третьем квадранте, как показано на рис. 7. При этом прямую Попова через точку (–1/5,8; j0) можно всегда провести так, что критерий Попова будет выполняться.
Итак, рассматриваемая система будет абсолютно устойчива при и .
4. Круговой критерий Воронова
Критерий Воронова позволяет исследовать абсолютную устойчивость, когда нелинейность удовлетворяет условиям:
[ k1; k2], , .
Определение. Если ()[ k1; k2], и выполняется условие
, (8)
где , , то линейная система абсолютно устойчива.
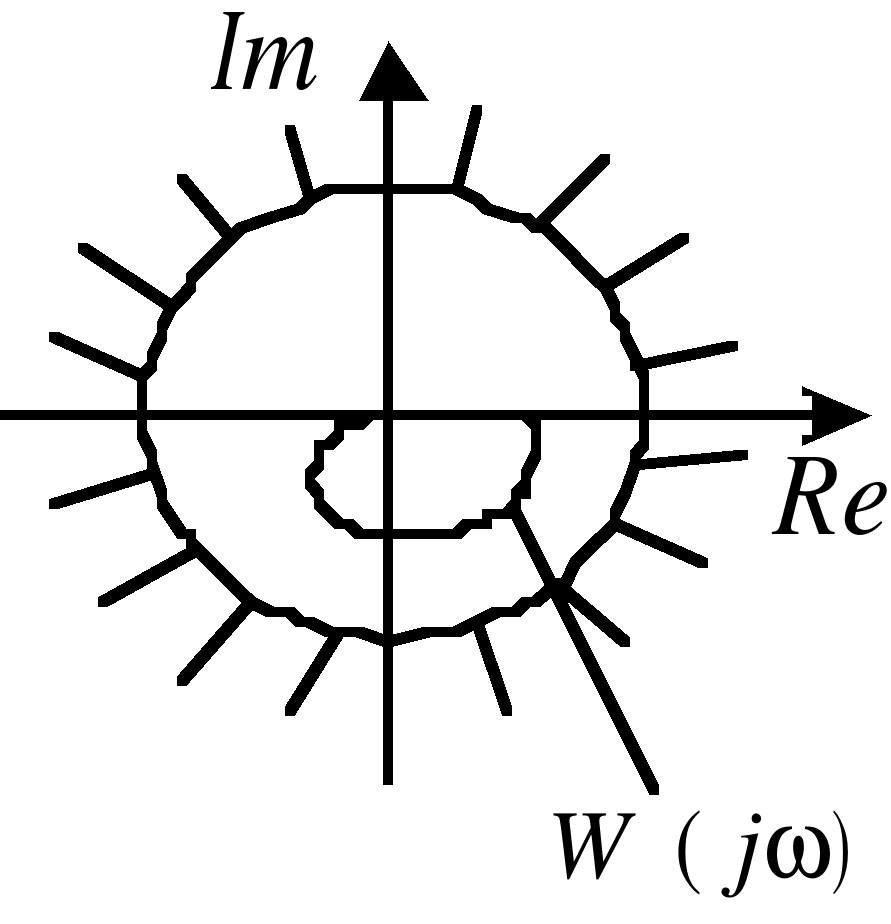
Графически условие (8) критерия Воронова заключается в том, что для абсолютной устойчивости нелинейной системы достаточно, чтобы годограф Найквиста линейной части системы (рис. 3) не «заходил» в запретную область, как показано на рис. 10 и рис. 11–13. На рис. 10 эта область является кругом и показана штриховкой.
На рис. 10 – 13 заштрихованы “запретные области” как для нелинейности (а), так и для годографа Найквиста линейной части системы (б), соответственно.
Рис. 10
а б
Рис. 11
а б
Рис.12
а б
Рис. 13
Круговой критерий Воронова проще в применении, но дает более жесткие («более достаточные») условия абсолютной устойчивости. Поэтому его целесообразно применять, когда или , т.е. в тех случаях, когда невозможно применить критерий Попова.
5. Робастная устойчивость
Абсолютная устойчивость, как отмечалось выше, связана со стремлением учесть неопределенности, возникающие при описании нелинейностей, входящих в модели динамических систем. Однако в общем случае линейные элементы также могут содержать неопределенности, так как параметры их моделей также определяются с некоторыми погрешностями. В связи с этим вводится, так называемая, робастная устойчивость систем управления.
Неопределенности в определении параметров системы, таких как постоянные времени или коэффициенты передачи приводят к тому, что точные значения этих параметров оказываются неизвестными. Фактически, всегда известно лишь, что значения этих параметров лежат в некоторых пределах: , . Подчеркнем, что сами коэффициенты , постоянные времени и другие параметры системы считаются при этом постоянными.
Это приводит к тому, что в отношении, например, коэффициентов характеристического полинома и других параметров различных моделей системы управления известными оказываются лишь интервалы, в которых лежат их значения.
Например, коэффициенты характеристического полинома
(9)
линейной системы могут быть заданы соотношениями
или . (10)
Заданные таким способом коэффициенты называются интервальными, а разность – интервалом. Верхние и нижние значения рассчитываются по верхним , и нижним , значениям коэффициентов , методами интервальной математики [22].
Обычно интервальный полином -го порядка записывается следующим образом
. (11)
В технических приложениях различные погрешности, неопределенности чаще всего определяются относительной погрешностью. Поэтому и коэффициенты характеристического полинома часто задаются своими расчетными значениями , найденными с некоторой относительной погрешностью %, т.е. . При таком задании коэффициентов их верхние и нижние значения определяются очевидными соотношениями:
, . (12)
В связи с этим в дальнейшем будем считать, что заданы верхние и нижние значения коэффициентов характеристического полинома (11) исследуемой системы управления. Относительные погрешности % могут быть одинаковыми для всех коэффициентов, т.е. , .
Определение. Динамическая система с характеристическим полиномом (11) является робастно устойчивой, если она является асимптотически устойчивой в целом при любых значениях постоянных коэффициентов , из интервалов (10).
Для оценки робастной устойчивости систем с интервальными параметрами обычно используется критерий, предложенный В.Л. Харитоновым [22]. Этот критерий позволяет свести задачу исследования робастной устойчивости динамических систем к задаче исследования гурвицевости некоторых полиномов. С этой целью сначала составляются четыре полинома Харитонова следующего вида:
,
,
,
. (13)
Каждый из этих полиномов имеет степень, равную степени интервального полинома (11), а их коэффициенты равны граничным значениям интервальных коэффициентов этого полинома.
Критерий Харитонова. Динамическая система с интервальным характеристическим полиномом (11) является робастно устойчивой, если все четыре полинома Харитонова (13) являются гурвицевыми.
Таким образом, для исследования робастной устойчивости некоторой системы с интервальными параметрами , необходимо найти интервальный характеристический полином этой системы в форме (11), затем составить четыре полинома Харитонова (13) и проверить удовлетворяют ли они критерию Гурвица или Рауса.
Пример 3. Исследовать робастную устойчивость системы с характеристическим полиномом
.
Решение. Полиномы Харитонова в данном случае имеют вид
, ,
, . (14)
В данном случае степени полиномов Харитонова . Поэтому
вместо критерия Гурвица можно воспользоваться критерием асимптотической устойчивости Вышнеградского.
Напомним, что в соответствии с критерием Вышнеградского полином третьей степени является гурвицевым, если все его коэффициенты больше нуля, и произведение его «средних» коэффициентов больше произведения «крайних» коэффициентов.
Применяя этот критерий к полиномам (14), найдем, что в данном случае все четыре полинома Харитонова (14) являются гурвицевыми. Следовательно, рассматриваемая система является робастно устойчивой.
Рассмотрим на конкретном примере задачу оценки робастной устойчивости системы 3-го порядка при задании относительной точности настройки её параметров.
Пример 4. Оценить робастную устойчивость системы с характеристическим полиномом
(15)
при 5% и 2% погрешности реализации его коэффициентов.
Решение. При точных (расчетных) значениях коэффициентов данная система, очевидно, является асимптотически устойчивой. Действительно, все коэффициенты полинома (15) больше нуля, а произведение его «средних» коэффициентов равно 186, что больше произведения «крайних» коэффициентов, равного 160. Поэтому в соответствии с критерием Вышнеградского система устойчива.
При реализации коэффициентов с погрешностью 5% согласно (12) граничные значения интервалов равны:
, ,
, ,
, ,
, .
Следовательно, интервальный полином рассматриваемой системы в данном случае имеет вид
,
а соответствующие полиномы Харитонова
, ,
, .
В данном случае первый, второй и четвертый полиномы удовлетворяют критерию Вышнеградского, а третий – не удовлетворяет, так как 2,8558,9=167,865, а 8,421=176,4.
Таким образом, при реализации коэффициентов с погрешностью 5% рассматриваемая система не является робастно устойчивой.
При реализации коэффициентов с погрешностью 2% граничные значения интервалов равны:
, ,
, ,
, ,
, .
а соответствующие полиномы Харитонова
, ,
, .
При этом неравенства критерия Вышнеградского имеют вид: 185,93>159,94; 185,93>159,94; 178,63>166,46; 193,15>153,64.
Таким образом, при реализации коэффициентов с погрешностью 2% все четыре полинома Харитонова удовлетворяют критерию Вышнеградского, т.е. в этом случае рассматриваемая система является робастно устойчивой.
Литература
1. Бубнов, В.А. Линейная алгебра: компьютерный практикум / В.А. Бубнов, Г.С. Толстова, О.Е. Клемешева. - М.: ЛБЗ, 2012. - 168 c.
2. Бурмистрова, Е.Б. Линейная алгебра, дифференциальное исчисление функций одной переменной: Учебник для студ. высш. учеб. заведений / Е.Б. Бурмистрова, С.Г. Лобанов. - М.: ИЦ Академия, 2010. - 336 c.
3. Гомонов, С.А. Математика. Линейная алгебра: Учебно-справочное пособие / С.А. Гомонов. - М.: Форум, НИЦ ИНФРА-М, 2013. - 144 c.
4. Горлач, Б.А. Линейная алгебра: Учебное пособие / Б.А. Горлач. - СПб.: Лань, 2012. - 480 c.
5. Демидович, Б.П. Сборник задач по математике для втузов. В 4-х т.Т. 1. Линейная алгебра и основы математического анализа: Учебное пособие для втузов / Б.П. Демидович. - М.: Альянс, 2011. - 480 c.
6. Епихин, В.Е. Аналитическая геометрия и линейная алгебра. Теория и решение задач: Учебное пособие / В.Е. Епихин, С.С. Граськин. - М.: КноРус, 2013. - 608 c.
7. Ильин, В.А. Линейная алгебра и аналитическая геометрия: Учебник / В.А. Ильин, Г.Д. Ким. - М.: Проспект, 2012. - 400 c.
8. Канатников, А.Н. Линейная алгебра: Учебник для вузов / А.Н. Канатников, А.П. Крищенко; Под ред. В.С. Зарубин. - М.: МГТУ им. Баумана, 2006. - 336 c.
9. Кожухов, И.Б. Сборник задач по математике для втузов. В 4-х т.Т. 1. Векторная алгебра и аналитическая геометрия. Определители и матрицы системы линейных уравнений. Линейная алгебра. Основы общей алгебры: Учебное пособие для втузов / И.Б. Кожухов. - М.: Физматлит, 2009. - 288 c.
10. Кочетков, Е.С. Линейная алгебра: Учебное пособие / Е.С. Кочетков, А.В. Осокин. - М.: Форум, 2012. - 416 c.
11. Лунгу, К.Н. Сборник задач по высшей математике. 1 курс: С контрольными работами: линейная алгебра; аналитическая геометрия; основы математического анализа; комплексные числа / К.Н. Лунгу, Д.Т. Письменный, С.Н. Федин, Ю.А. Шевченко. - М.: Айрис-пресс, 2011. - 576 c.
12. Михалев, А.А. Линейная алгебра и аналитическая геометрия: Учебное пособие для студ. учреждений высш. проф. образования / А.А. Михалев, И.Х. Сабитов. - М.: ИЦ Академия, 2013. - 256 c.
13. Просветов, Г.И. Линейная алгебра и аналитическая геометрия: Задачи и решения: Учебно-практическое пособие / Г.И. Просветов. - М.: Альфа-Пресс, 2009. - 208 c.
14. Рудык, Б.М. Линейная алгебра: Учебное пособие / Б.М. Рудык. - М.: НИЦ ИНФРА-М, 2013. - 318 c.
15. Скрыдлова, Е.В. Линейная алгебра: Учебное пособие / Е.В. Скрыдлова, О.О. Белова. - Рн/Д: Феникс, 2012. - 142 c.
16. Шевцов, Г.С. Линейная алгебра: теория и прикладные аспекты: Учебное пособие / Г.С. Шевцов. - М.: Магистр, НИЦ ИНФРА-М, 2013. - 528
EMBED Equation.3
EMBED Equation.3 
EMBED Equation.3 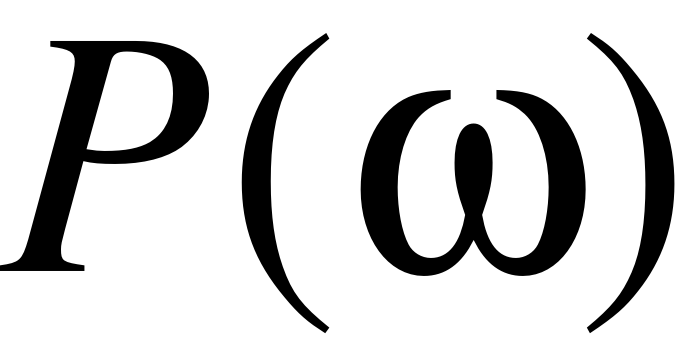
EMBED Equation.3 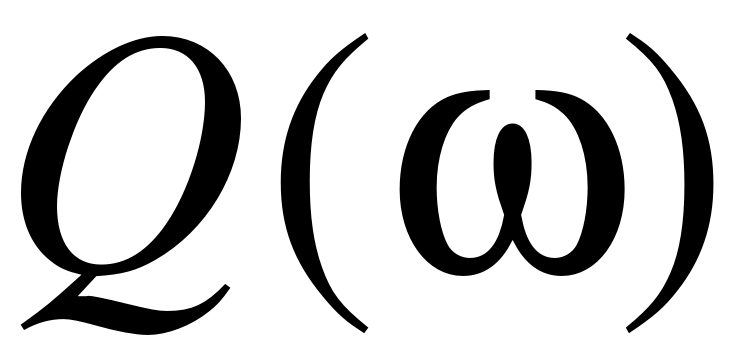
EMBED Equation.3 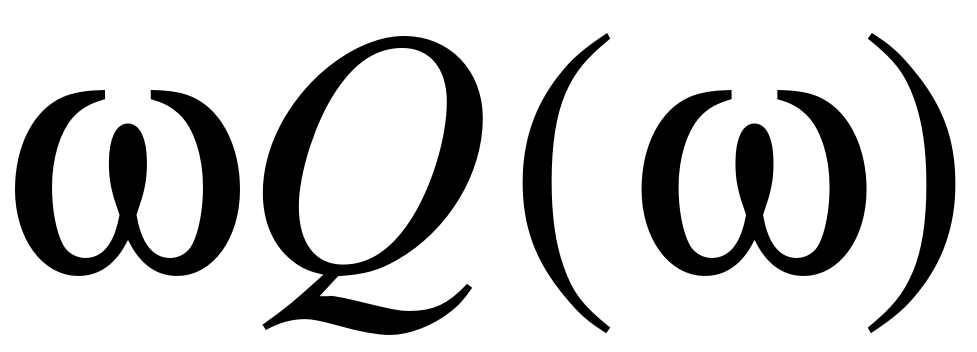
EMBED Equation.3
EMBED Equation.3
EMBED Visio.Drawing.6
EMBED Visio.Drawing.6
EMBED Visio.Drawing.6 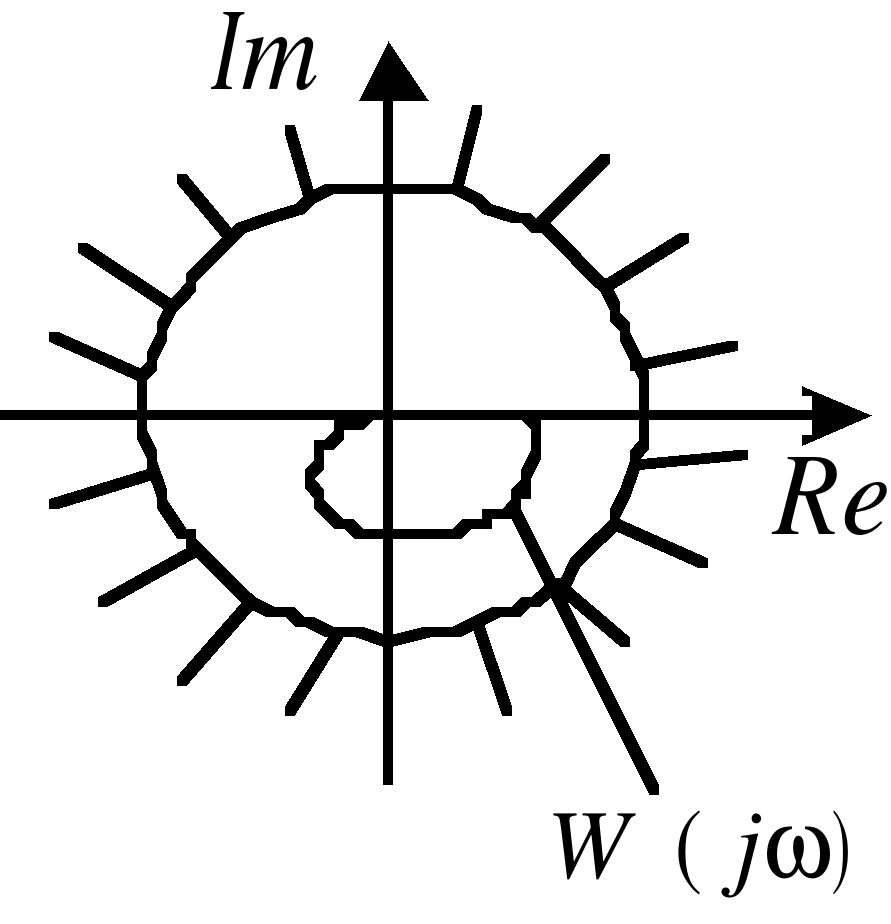
АБСОЛЮТНАЯ И РОБАСТНАЯ УСТОЙЧИВОСТЬ