СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ

Контрольная работа

Содержание

1. Задача синтеза цифровых устройств управления

2. Модальное дискретное управление

3. Модальное управление с запаздыванием

4. Синтез дискретных систем по заданным показателям качества

Литература

1. Задача синтеза цифровых устройств управления

В тех случаях, когда замкнутая дискретная система, составленная из функционально необходимых элементов, является неустойчивой, или её показатели качества не удовлетворяют требуемым, возникает задача её коррекции или задача синтеза устройства управления.

В настоящее время наиболее рациональным путем построения устройств управления является использование управляющих вычислительных машин или специализированных цифровых вычислителей (ЦВ) – микропроцессоров или микроЭВМ.

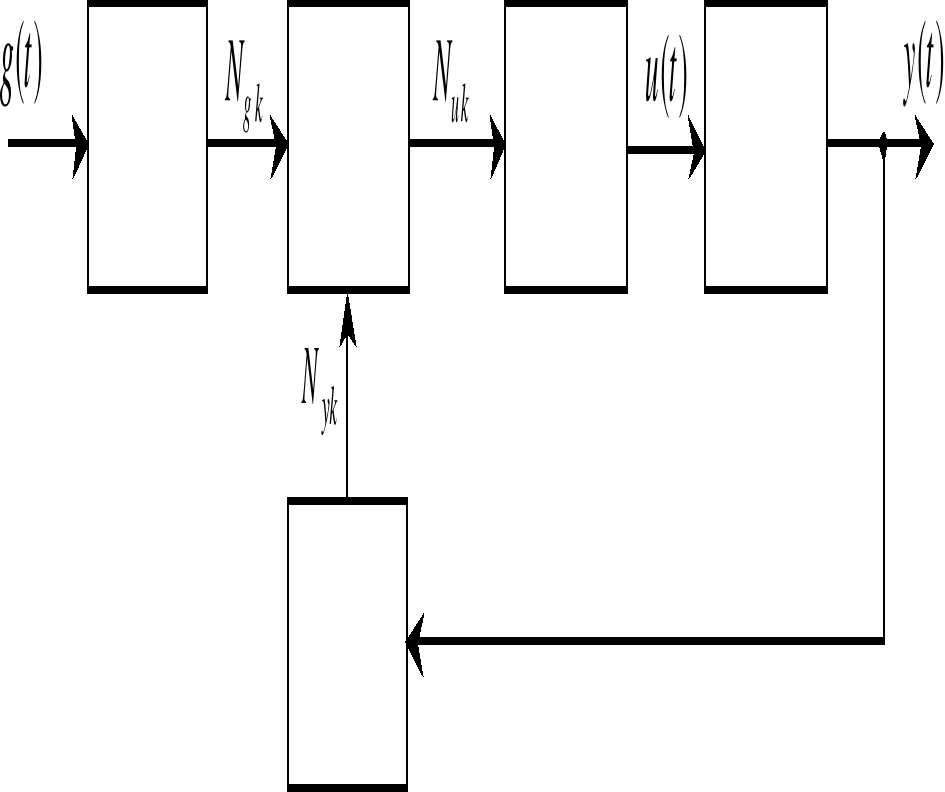
Система с цифровым управлением, кроме собственно цифрового вычислителя (ЦВ) и непрерывной части (НЧ), включает, как показано на рис. 1, аналого-цифровой и цифро-аналоговый преобразователи (АЦП и ЦАП). При работе системы АЦП формируют двоичные коды , , соответствующие дискретным значениям , непрерывных величин , в моменты времени , кратные периоду квантования по времени T, т.е. ,

Рис. 1

Вычислитель ЦВ периодически (тоже с периодом T ) по соответствующему алгоритму рассчитывает значения управления , двоичные коды которого с помощью ЦАП преобразуются в непрерывное управление , поступающее на непрерывный объект управления (НЧ).

Обычно число разрядов АЦП и ЦАП достаточно велико, так что квантованием по уровню можно пренебречь (по крайней мере, в первом приближении). В этом случае сигналы на выходах АЦП и ЦВ можно считать решетчатыми функциями , , , которые соответствуют непрерывным сигналам , , [5].

Коды на входе ЦАП изменяются только в моменты времени , , поэтому его выходной сигнал можно рассматривать как последовательность импульсов постоянной длительности T и переменной амплитуды . Этот факт является одной из отличительных особенностей систем с ЦВМ.

Коэффициенты передачи АЦП – и ЦАП – обычно выбираются так, что .

Поэтому при расчетах систем с цифровым управлением АЦП можно рассматривать как идеальные ключи, работающие с периодом T, а ЦАП – как формирователь прямоугольных импульсов. Длительность этих импульсов равна периоду квантования по времени T, а амплитуда .

Это позволяет представить расчетную схему системы с цифровым управлением в виде, показанном на рис. 2.

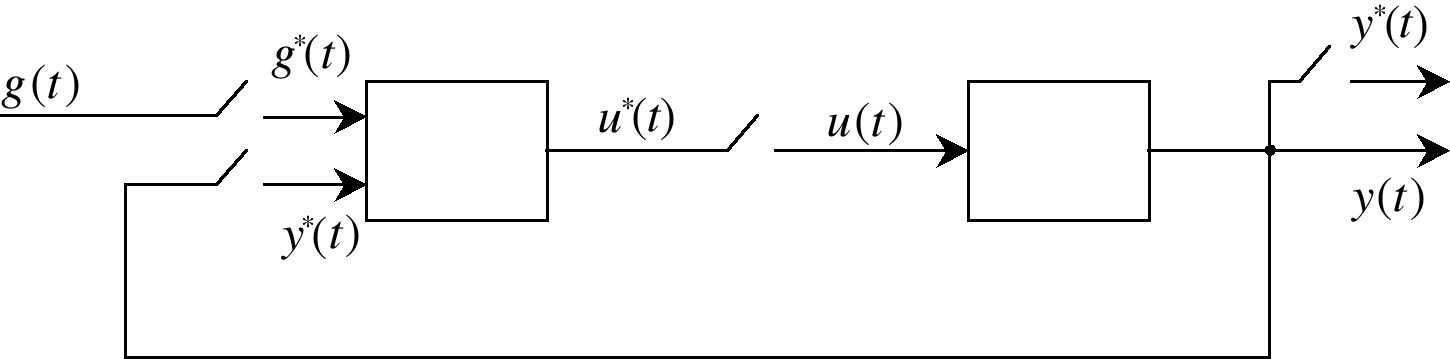
Рис. 2.

На этом рисунке ЦУУ – это совокупность АЦП и ЦВ, а ПНЧ – приведенная непрерывная часть – совокупность ЦАП и НЧ. Если непрерывная часть системы имеет передаточную функцию , то приведенная непрерывная часть системы, согласно (14.21) описывается передаточной функцией

Коды управления вычисляются цифровым вычислителем в соответствии с некоторым алгоритмом. Этот алгоритм может выбираться на основе часто используемых типовых законов управления. Например, это может быть П-закон, при котором алгоритм вычисления управления имеет вид

, (1)

где – отклонение, сигнал ошибки системы, – параметр настройки цифрового устройства управления, реализующего П-закон. Очень часто алгоритм ЦУУ строится на основе ПИ-закона, при котором

. (2)

Здесь и – также параметры настройки ЦУУ, реализующего ПИ-закон. Создаются алгоритмы работы ЦУУ и на основе других типовых законов управления.

Как видно, при цифровой реализации указанных законов в соответствии с выражениями (1), (2) учитывается запаздывание на такт. Это запаздывание обусловлено затратами времени на преобразование сигналов датчиков в цифровую форму, выполнение необходимых математических операций по расчету управления и обратное преобразование цифровых кодов в непрерывное управляющее воздействие.

Если время мало по сравнению с периодом T следования импульсов , то им обычно пренебрегают. В этом случае в правых частях выражений (1), (2) и аналогичных им индекс заменяется индексом k.

Чаще всего, однако, быстродействие современных ЦВ является

недостаточно высоким, так что указанное запаздывание необходимо учитывать. В дальнейшем будем считать, что запаздывание близко к периоду следования импульсов управления, т.е.

. (3)

Именно в этих случаях в дискретных алгоритмах учитывается запаздывание на один такт или один период T.

При выбранном законе управления, например в виде (1) или (2), задача синтеза сводится к определению численных значений его параметров настройки.

Однако в общем случае для обеспечения повышенных требований к качеству системы (например, второй или третий порядок астатизма, небольшое время регулирования и перерегулирование) простейшие законы управления оказываются недостаточными. В этом случае применяют более сложные алгоритмы вычисления , процедура синтеза которых включает определение и структуры, и параметров ЦУУ. Ниже рассматриваются некоторые из таких методов синтеза.

2. Модальное дискретное управление

При синтезе модального дискретного управления обычно предполагается, что объект управления (ОУ) задан своими уравнениями в переменных состояния, например, вида

, , (4)

где элементы матрицы A и векторов b и c имеют известные численные значения.

Однако при модальном управлении, в отличие от схемы, изображенной на рис. 2, в ЦВ вместо кодов управляемой переменной поступают формируемые АЦП также с периодом T коды , соответствующие значениям всех переменных состояния , ОУ, которые измеряются специальными датчиками.

Дискретное модальное управление, по аналогии с непрерывным, ищется в виде

. (5)

Коэффициенты необходимо выбрать таким образом, чтобы корни характеристического уравнения замкнутой системы (4), (5) имели заданные значения.

Управление (5) является идеализированным в том смысле, что оно не учитывает указанных выше затрат времени в управляющем устройстве на измерение и преобразование сигналов, а также на расчет управления. Следовательно, управление (5), как отмечалось выше, можно применять, если указанные затраты времени, по крайней мере на порядок, меньше периода квантования T, и их влиянием на свойства системы управления можно пренебречь.

Рассматривая далее модальное управление, будем предполагать, что все переменные состояния измеряются, преобразуются АЦП и поступают в ЦУУ.

Для вывода соотношений, позволяющих вычислить значения коэффициентов в равенстве (5), найдем уравнение дискретной системы с модальным управлением. Для этого подставим равенство (5) в уравнение (4). В результате будем иметь

. (6)

Далее найдем характеристический полином замкнутой системы (6). Переходя в равенстве (6) к z-изображениям при нулевых начальных условиях и проведя очевидные преобразования, получим

. (7)

Отсюда следует, что характеристический полином замкнутой системы (6) определяется выражением

. (8)

С использованием свойств определителей [7. С. 192] правую часть этого равенства можно представить так

, (9)

где

(10)

– характеристический полином заданного объекта управления (4). При этом полином имеет степень и содержит ровно n произвольных коэффициентов,

Степень характеристического полинома замкнутой системы также равна т.е. равна числу варьируемых коэффициентов в управлении (5). Поэтому выбором этих коэффициентов можно обеспечить любые заданные значения корней характеристического полинома (8) или (9).

В общем случае это можно осуществить, если объект (4) является полностью управляемым, т. е. если , где матрица . При этом процедура расчета коэффициентов из (5) полностью аналогична этой процедуре в непрерывном случае (см. § 7.2).

В частности, если заданное уравнение (4) объекта представлено в канонической управляемой форме [5. С. 35], то полином

. (11)

В этом случае коэффициенты в соответствии с выражениями (9) – (11) определяются по формулам

, , (12)

где – коэффициенты желаемого полинома, корни которого равны заданным (желаемым) полюсам замкнутой системы.

Пример 1. Для объекта

(13)

найти управление (5), при котором корни характеристического уравнения замкнутой системы будут равны , .

Решение. Прежде всего, отмечаем, что в данном случае уравнение объекта представлено в канонической управляемой форме, поэтому коэффициенты его характеристического полинома равны ; , а корни , . Так как один из корней больше единицы по модулю, то заданный объект без управления является неустойчивым. Поэтому модальное управление должно быть стабилизирующим.

Желаемый полином, корни которого равны заданным, очевидно, имеет вид

т.е. ; .

В данном случае уравнение объекта представлено в канонической управляемой форме, поэтому по формулам (12) находим

, .

Следовательно, искомое модальное управление определяется выражением

Проверим полученный результат. Подставляя найденное управление в уравнение (13) при , получим

Отсюда следует, что характеристический полином синтезированной системы равен

Таким образом, при найденном управлении корни характеристического уравнения (полюсы) замкнутой системы имеют заданные значения, т. е. качество процесса управления соответствует заданным полюсам.

3. Модальное управление с запаздыванием

Предположим теперь, что быстродействие ЦВ не велико, поэтому время на преобразование сигналов и расчет управления, в соответствии с условием (3), сравнимо с периодом квантования. В этом случае запаздыванием пренебречь нельзя и модальное управление берется в следующей форме:

. (14)

Здесь для вычисления значения управления, соответствующего моменту времени , используются данные, полученные в -м такте. Уравнение замкнутой системы (4), (14), очевидно, имеет вид

Запишем это уравнение в z-изображениях при нулевых начальных условиях ()

Умножим обе части этого равенства на z и приведем подобные. В результате получим

Снова используя указанное выше свойство определителей, заключаем, что в данном случае характеристический полином замкнутой системы определяется выражением

. (15)

Отсюда следует, что при наличии запаздывания в ЦУУ на один такт степень характеристического полинома замкнутой системы равна , а число варьируемых коэффициентов модального управления с запаздыванием (14), по-прежнему, . Следовательно, для обеспечения произвольного расположения всех корней характеристического полинома не хватает одного коэффициента.

Поэтому при использовании управления (14) (с запаздыванием на один такт) можно обеспечить только такое расположение корней характеристического уравнения (15) замкнутой системы, при котором один из коэффициентов её характеристического полинома равен соответствующему коэффициенту характеристического полинома (10) заданного дискретного объекта управления (4).

Рассмотрим процедуру расчета коэффициентов в управлении (14) на следующем примере.

Пример 2. Предположим объект управления тот же, что и в предыдущем примере, т.е. описывается уравнениями (13). Найти одно из возможных дискретных модальных управлений с запаздыванием на такт, при котором обеспечивается устойчивость замкнутой системы.

Решение. В данном случае , поэтому в соответствии с выражением (14) управление

. (16)

При этом характеристический полином замкнутой системы согласно (15), с учетом того, что , равен

Так как

то подставляя в предыдущее выражение, найдем

. (17)

Таким образом, корни характеристического полинома замкнутой системы нужно задать так, чтобы их сумма равнялась 1,5. При этом для обеспечения устойчивости замкнутой системы модуль каждого из них, в соответствии с условием (14.46), должен быть меньше единицы.

В данном случае корни можно задать, например, так: ;

; . Тогда желаемый полином

. (18)

Сравнивая полиномы (18) и (17), получаем

; .

Следовательно, искомое управление с запаздыванием на такт имеет вид .

Как и выше, для проверки полученного результата подставим найденное управление в уравнение объекта (13). В результате получим

Перейдя в этом выражении к z-изображениям, найдем, что характеристический полином синтезированной замкнутой системы определяется выражением

Сравнивая полученный полином с выражением (18), заключаем, что синтезированная дискретная система имеет заданные при её синтезе корни характеристического уравнения.

На основе изложенного можно заключить, что в случае дискретного модального управления с запаздыванием на такт не всегда можно обеспечить заранее заданное расположение полюсов дискретной системы.

Действительно, если коэффициент характеристического полинома (10) заданного объекта (4) не будет равен сумме n заданных чисел, то задача определения коэффициентов управления (14), очевидно, не будет иметь решения. В этих случаях для построения модального управления необходимо более точно учитывать запаздывание, вносимое АЦП, ЦВ и ЦАП, непосредственно при выводе уравнения дискретной модели объекта.

Отметим также, что при синтезе астатических систем с модальным управлением выбор желаемых корней характеристического полинома должен удовлетворять дополнительному условию астатизма заданного порядка дискретных систем управления (см. § 14.8).

Кроме того, как отмечалось выше, для реализации модального управления типа (5) или (14) необходимо прямое измерение всех переменных состояния объекта управления.

В целом же можно считать, что модальное управление при определенных условиях позволяет обеспечить желаемое расположение полюсов дискретных САУ, но предполагает доступность прямому измерению всех переменных состояния системы. При этом для получения приемлемого качества процесса управления необходимо выбирать желаемые значения полюсов так, чтобы переходный процесс системы был близок к желаемому. Как правило, это требует нескольких итераций. В этом смысле рассмотренный далее метод синтеза по желаемым показателям качества является более рациональным, тем более, что он не требует измерения переменных состояния.

4. Синтез дискретных систем по заданным показателям качества

В рассматриваемом ниже методе синтеза предполагается, что в соответствии с техническим заданием необходимо синтезировать систему управления с астатизмом первого порядка по задающему воздействию и с определенными первичными показателями качества такими, как время регулирования и перерегулирование. Фактически здесь требуется найти разностное уравнение, описывающее алгоритм работы ЦУУ, при котором указанные первичные показатели качества синтезируемой замкнутой системы будут не хуже заданных.

Перейдем к изложению метода синтеза. При этом будем считать, что структура проектируемой системы управления соответствует, приведенной на рис. 1, причем выполняются все указанные в начале данной главы предположения в отношении АЦП и ЦАП так, что расчетную схему синтезируемой системы с цифровым управле-

нием можно представить в виде, показанном на рис. 3.

Рис. 3

Передаточная функция дискретного объекта управления (ДОУ) может быть получена описанными в § 14.3 способами либо из уравнений в переменных состояния непрерывной части системы по формулам (14.3) – (14.10), (14.15), либо на основе его передаточной функции по формуле (14.21) (см. § 14.4).

При цифровом управлении длительность импульсов ЦАП равна периоду следования Т, поэтому эта формула значительно упрощается и принимает вид

, (19)

где Z – символ z-преобразования, а T – период следования импульсов на выходе ЦУУ, , – некоторые полиномы.

В дальнейшем будем считать, что эти полиномы известны. Обозначим , .

Равенству (19) соответствует следующее уравнение вход-выход дискретного объекта управления:

. (20)

Так как, согласно рис. 3, на вход ЦУУ поступают переменные и , а на его выходе формируется , то уравнение ЦУУ с учетом запаздывания на период можно записать так:

, (21)

где , , – некоторые неизвестные полиномы. Именно эти полиномы должны быть найдены в результате решения задачи синтеза, так как переход от уравнения (21) к соответствующему алгоритму работы ЦУУ типа (1), (2) или (16) при выполнении условий физической реализуемости не представляет каких-либо сложностей.

Множитель в правой части (21), в соответствии с условием (3), учитывает запаздывание на такт, которое возникает в ЦУУ из-за указанных выше затрат времени на определение . Поэтому условия физической реализуемости уравнения (21) имеют вид

, . (22)

Для удобства введем обозначения , , . Тогда условия (22) будут эквивалентны неравенствам

, . (23)

В общем случае степени и коэффициенты полиномов , и в (21) можно определить, исходя из различных условий. Например, это можно сделать по указанным в главе 14 условиям астатизма и минимальной, конечной длительности переходных процессов.

Ниже коэффициенты указанных полиномов отыскиваются по условиям астатизма первого порядка по отношению к задающему воздействию , заданным значениям времени регулирования , перерегулирования и, конечно, по условиям устойчивости.

Перейдем к изложению соответствующей методики синтеза дискретных систем (20), (21) с ЦУУ.

Необходимые качества синтезируемой системы управления учитываются в процедуре синтеза с помощью желаемой передаточной функции

, (24)

где и – некоторые полиномы, а k – целое число.

В рассматриваемом методе синтеза функция (24) оп-

ределяется по передаточной функции вспомогательной непрерывной системы, порядок астатизма которой по отношению к задающему воздействию – , время регулирования – и перерегулирование – совпадают с заданными значениями этих показателей , и для проектируемой дискретной системы (20), (21) с ЦУУ.

Передаточная функция определяется следующим образом. Из табл. 6.1 нормированных передаточных функций по степени n полинома А(z) из (20), порядку астатизма и перерегулированию выбираются коэффициенты , нормированной передаточной функции

. (25)

Здесь – временной масштабный коэффициент.

Из этой же таблицы выбирается значение времени регулирования , которое используется для вычисления требуемого значения коэффициента по формуле

, (26)

Подставляя полученное значение в (25), найдем желаемую передаточную функцию , т.е.

. (27)

Далее находятся полиномы и желаемой передаточной функции (24) дискретной системы по формуле, аналогичной (19):

. (28)

Z-преобразование в (28) можно также выполнить описанным в разделе 14.3 способом по формулам (14.3) – (14.10), (14.15), записав соответствующие передаточной функции уравнения в переменных состояния.

Таким образом, с помощью соотношений (25)–(28) определяются полиномы и желаемой передаточной функции (24), при которой проектируемая дискретная система имеет требуемые порядок астатизма, перерегулирование и длительность переходных процессов (при запаздывании в ЦУУ на один период). При этом параметр k остается пока неизвестным.

Следующий этап рассматриваемой методики синтеза связан с реализацией найденной передаточной функции , т.е. с определением полиномов , и из уравнения ЦУУ (21). Эти полиномы удобнее всего определить путем приравнивания и передаточной функции системы (20), (21). При этом для выполнения условий физической реализуемости передаточной функции рассматриваемой системой с частично заданной структурой (рис. 3) числитель и знаменатель этой передаточной функции необходимо [5] умножить на полином . В результате получим

. (29)

Здесь – вспомогательный множитель, и k – определяемые ниже параметры, а полином

, (30)

где – коэффициент при старшей степени полинома из уравнения объекта (20).

Будем предполагать, что нули этого полинома удовлетворяют условию

, , (31)

т.е. на комплексной плоскости они располагаются внутри окружности единичного радиуса.

Если нули полинома , найденного для заданного объекта управления, не удовлетворяют условию (31), то имеются две возможности проведения синтеза. Во-первых, можно изменить конструкцию объекта так, чтобы условие (31) оказалось выполненным. Во-вторых, можно выбрать полином в (24) так, чтобы среди его нулей оказались все те нули полинома , которые не удовлетворяют условию (31). Разумеется, для этого необходимо несколько видоизменить изложенную выше методику выбора . Причем система с соответствующей передаточной функцией должна иметь требуемые показатели качества процесса управления. Этот случай применительно к синтезу непрерывных устройств управления рассмотрен в работе [9].

При выполнении условия (31) полиномы , и

определяются следующим образом.

Из условия равенства знаменателей в (29) вытекает с учетом представления (30) полиномиальное уравнение

. (32)

В общем случае непрерывная часть синтезируемой системы может содержать некоторое число чистых интеграторов. Поэтому полином можно всегда представить следующим образом

, (33)

где – число единичных нулей полинома , т.е. число чистых интеграторов в непрерывной части, причем , а такой полином, что .

С другой стороны, синтезируемая замкнутая система должна иметь порядок астатизма по задающему воздействию, равный . Поэтому в соответствии с уравнением (32), при условии, что , полиномы и имеют вид

, , (34)

где , а , – вспомогательные полиномы.

С учетом (34) полиномиальное уравнение (32) переходит в следующее:

, (35)

где полиномы

, . (36)

При решении полиномиальных уравнений типа (35) сначала определяются степени и искомых полиномов , . При этом необходимо учесть следующие ограничения (условия физической реализуемости передаточных функций в замкнутой системе с частично заданной структурой [5]):

– индекс желаемой передаточной функции замкнутой системы должен быть не меньше индекса заданной части с учетом запаздывания на такт в ЦУУ, т.е.

, (37)

где , ;

– степени полиномов и должны быть не больше степени полинома , т.е.

, ; (38)

– число коэффициентов полиномов , должно быть неменьше числа уравнений в алгебраической системе эквивалентной полиномиальному уравнению (35) , т.е.

; (39)

– степень полинома в левой части (35) должна быть равна степе-

ни полинома в его правой части, т.е.

. (40)

Учет всех ограничений (37) – (40) при условиях и приводит к следующим соотношениям, которые определяют искомые параметры и степени полиномов:

, , (41)

, . (42)

При этом , а степень .

Обозначим – степень полинома , т.е. , а также коэффициенты полиномов

, , (43)

, . (44)

С учетом введенных обозначений (36), (43) и (44) систему алгебраических уравнений, эквивалентную полиномиальному уравнению (35), можно записать [5] следующим образом:

. (45)

В результате решения системы (45) определяются численные значения коэффициентов и полиномов (43), а затем по (34) находятся сами полиномы , .

Из условия равенства числителей в (29) вытекает следующее соотношение

. (46)

Таким образом, приведенные соотношения (22) – (46) позволяют найти полиномы , и и записать уравнение ЦУУ (21) с численными коэффициентами.

Для получения разностного уравнения ЦУУ, описывающего алгоритм вычисления значений управления , необходимо умножить обе части полученного уравнения (21) на , а затем перейти к оригиналам.

Вытекающее из полученного разностного уравнения выражение, определяющее как функцию предыдущих значений измеряемых переменных задающего воздействия, управления и управляемой переменной, т.е. равенство , , , является искомым алгоритмом работы ЦУУ.

В тех случаях, когда измеряемыми являются g и или y и уравнение (21) или соответствующее ему разностное уравнение преобразовываются соответствующим образом.

На этом формальная процедура синтеза САУ с ЦУУ заканчивается. Однако для завершения процесса синтеза необходимо промоделировать полученную систему и убедиться, что полученный алгоритм работы ЦУУ обеспечивает требуемые показатели качества процесса управления. При этом целесообразно объект управления моделировать по его непрерывной модели в переменных состояния, а ЦУУ по его алгоритму функционирования с учетом квантования по уровню и по времени.

Рассмотрим изложенную методику синтеза дискретных САУ на конкретном примере.

Пример 3. Найти алгоритм функционирования ЦУУ, обеспечивающего астатизм первого порядка по задающему воздействию, время регулирования не более 3 с и перерегулирование не более , в системе управления с передаточной функцией непрерывной части

. (47)

При этом период квантования с, а измеряемыми переменными

являются отклонение и управляемая переменная y.

Решение. Подставляя заданные и в выражение (19) и выполняя z-преобразование (с помощью методики, изложенной в § 14.4), получим

Следовательно, в рассматриваемом случае полиномы , , а их степени , . При этом по (22) , а полином ; по (33) , а полином .

Нуль полинома , очевидно, равен , т.е. удовлетворяет условию (31). Поэтому желаемую передаточную функцию будем искать в виде (24) с произвольным полиномом .

Так как в данном случае , , а %, то в соответствии с изложенной выше методикой выбираем из табл. 6.1 коэффициенты нормированной передаточной функции астатической системы второго порядка: , , и с. Поэтому по формуле (26) при с и с находим . Подставляя значения , , и , , в формулы (25) и (27), получим

Выполняя z-преобразование в соответствии с выражением (28), найдем полиномы , , т.е. , а .

Здесь целесообразно проверить, удовлетворяют ли полученные значения коэффициентов полиномов и условию астатизма первого порядка (14.56). В нашем случае имеем , т.е. указанное условие удовлетворяется.

Отметим, что при указанном способе определения полиномов и , оно может не выполняться лишь из-за ошибок округления. Поэтому при не выполнении условия (14.56) необходимо округлить коэффициенты этих полиномов так, чтобы указанное условие выполнялось.

Переходим к расчету полиномов , и . В нашем случае поэтому по формуле находим , а по формулам (36) – (44) получаем , , , , , , , , , . Далее по (45) записываем систему

Решение этой системы с учетом равенств (43) и (34) приводит к полиномам

, .

Затем по формуле (46) находим и, подставляя в (21) найденные выражения для полиномов, получим разностное уравнение ЦУУ

. (48)

Поскольку по условиям синтеза измеряются переменные и y, заменим в этом уравнении g по формуле . В результате уравнение (48) примет вид

. (49)

Для получения алгоритма ЦУУ умножим обе части уравнения (49) на , раскроем скобки, перейдем к оригиналам и перенесем в правую часть все слагаемые, кроме . В результате получим

. (50)

Полученное выражение представляет собой алгоритм вычисления значений управляющего воздействия для заданного объекта (47). Как видно, для вычисления цифровым устройством управления, которое происходит в течении -го такта, необходимы только измеренные в этом же -м такте и предыдущие значения воздействия , управляемой переменной , а также два предыдущих значения управляющего воздействия.

Отметим, что все предыдущие значения переменных, как и значения всех постоянных коэффициентов из равенства (50) хранятся в памяти ЦУУ.

Для оценки качества синтезированной системы из равенств (47) и (50) определим уравнение вход-выход замкнутой системы

После сокращения на множитель и перехода к разностному уравнению, получим

Полагая здесь и подставляя начальные значения управляемой переменной , , а также значения воздействия , можно найти реакцию синтезированной системы (47), (49) на внешние воздействия. В частности, при , и , получим значения переходной функции .

Результаты расчета переходной функции синтезированной системы приведены в табл. 1.

Таблица 1

k	0	1	2	3	4
	0	0	0,7076	1,04314	1,02417
k	5	6	7	8	9
	0,99918	0,99825	0,9999	1,00011	1,00002

Как видно, синтезированная система является астатической, её перерегулирование не превышает 5 % , а время регулирования не более трех секунд, что соответствует заданным требованиям.

Литература

1.Воронов А.А. Основы теории автоматического управления. Автоматическое регулирование непрерывных линейных систем / Воронов А.А. – 2-е изд., перераб. – М.: Энергия, 2010. – 309 с.

2. Воронов А.А. Основы теории автоматического управления. Особые линейные и нелинейные системы / Воронов А.А. – 2-е изд., перераб. – М.: Энергоиздат, 2001. – 303 с.

3. Бесекерский В.А. Теория систем автоматического управления / Бесекерский В.А., Попов Е.П. – 4-е изд., перераб. и доп. – СПб: Профессия, 2003. – 752 с.

4. Ким Д.П. Теория автоматического управления. Т.1. Линейные системы / Ким Д.П. – М.: Физматлит, 2013. – 288 с.

5. Лукас В.А. Теория управления техническими системами / Лукас В.А. – 3-е изд., перераб. и доп. – Екатеринбург: УГГГА, 2012. –675 c.

6. Бабаков Н.А. Теория автоматического управления. Ч.1 Теория линейных систем автоматического управления / Бабаков Н.А., Воронов А.А., Воронова А.А. – 2-е изд., перераб. и доп. – М.: Высшая школа, 2006. – 367 с.

7. Юрьевич Е.И. Теория автоматического управления / Юрьевич Е.И. – 2-е изд., перераб. и доп. – Л.: Энергия, 2008. – 416 с.

8. Дорф Р.К. Современные системы управления/ Дорф Р.К., Бишоп Р.Х. – М.: Лаборатория базовых знаний, 2004. – 831 с.

9. Методы классической и современной теории автоматического управления. Т.1 Математические модели, динамические характеристики и анализ систем автоматического управления / под ред.

Пупкова К. А., Егупова Н. Д. – 2-е изд., перераб. и доп. – М.: Издво МГТУ, 2004. – 655 с.

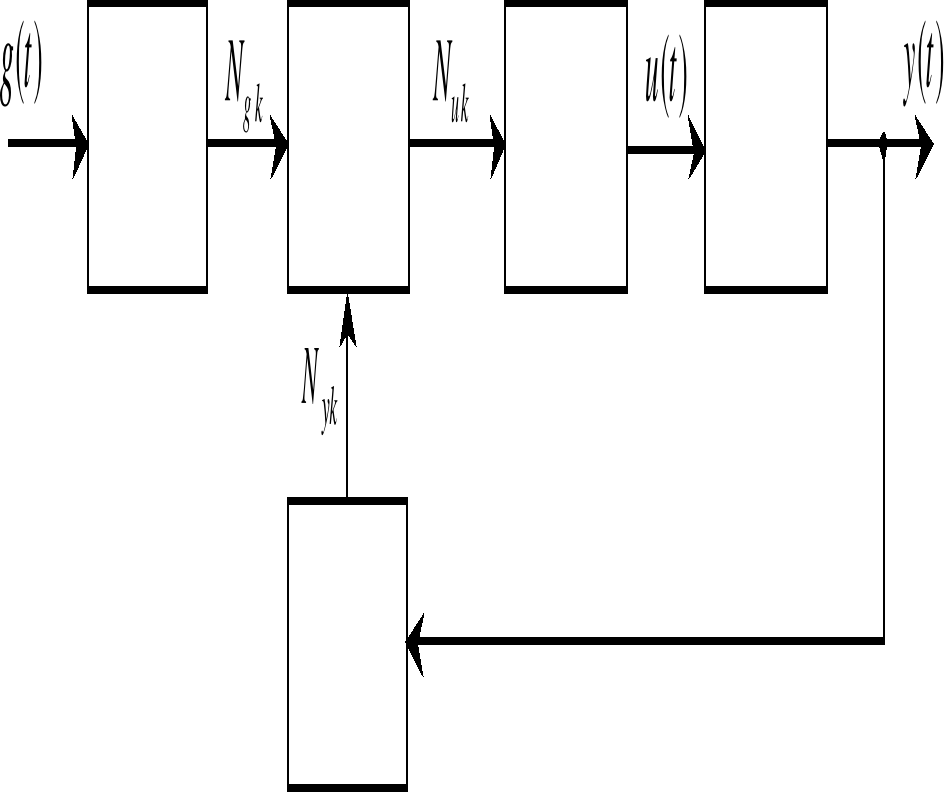
EMBED Visio.Drawing.6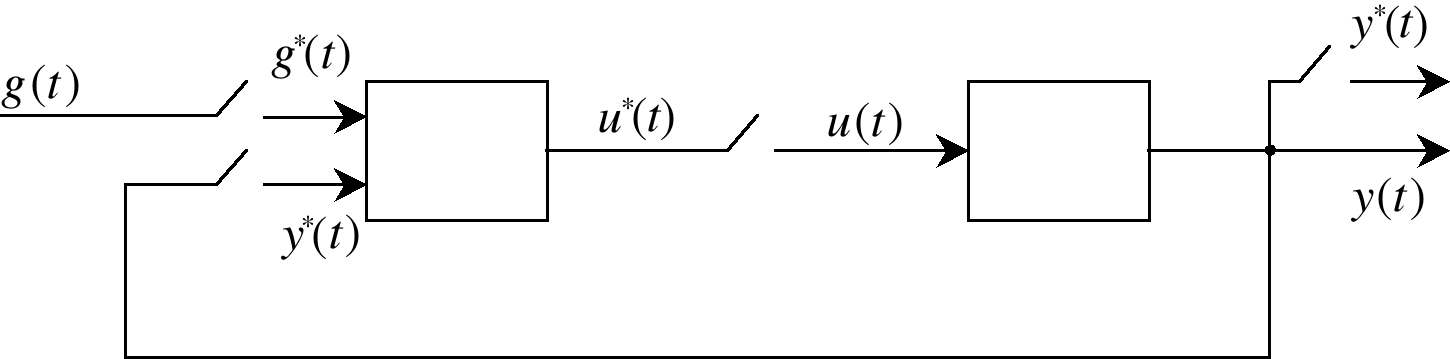

СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ УПРАВЛЕНИЯ