Зависимость часового заработка одного рабочего от общего стажа работы после окончания учебы путем построения уравнения парной линейной регрессии
Контрольная работа по эконометрике
7 вариант
Исходные данные
Имеются данные о часовом заработке 1 рабочего Y и общем стаже работы после окончания учебы Х .
|
№
|
X
|
Y
|
|
1
|
22,4
|
53,4
|
|
2
|
8,9
|
8
|
|
3
|
13,3
|
15+№=22
|
|
4
|
18,3
|
29,5
|
|
5
|
13,8
|
32
|
|
6
|
11,7
|
14,7
|
|
7
|
19,5
|
13
|
|
8
|
15,2
|
11,3
|
|
9
|
14,4
|
18
|
|
10
|
22
|
11,8
|
|
11
|
16,4
|
35-№=28
|
|
12
|
18,9
|
16
|
|
13
|
16,1
|
29,5
|
|
14
|
13,3
|
23,1
|
|
15
|
17,3
|
55
|
Задание
Исследовать зависимость часового заработка одного рабочего от общего стажа работы после окончания учебы путем построения уравнения парной линейной регрессии
.
Предварительный анализ данных
- Вычислите и проанализируйте описательные статистики(выборочные средние,медиану, моду, среднее квадратичное отклонение) для переменных Х и У .
- Постройте поле корреляции (диаграмму рассеяния) и сформулируйте гипотезу о форме связи.
- Вычислите парный коэффициент корреляции между переменными. Интерпретируйте полученные результаты: соответствуют ли знаки коэффициента вашим ожиданиям? Модель парной регрессии:
- Найти оценки и параметров модели парной линейной регрессии и . Записать полученное уравнение регрессии.
- Проверить значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента и сделать выводы о значимости этих оценок.Значимо ли уровень образования влияет на заработок?
- Определить интервальные оценки коэффициентов и с надежностью 0,95. Сделайте вывод о точности полученных коэффициентов.
- Рассчитайте стандартную ошибку регрессии. Сделать вывод о точности полученного уравнения регрессии.
- Определить коэффициент детерминации R2 и сделать вывод о качестве подгонки уравнения регрессии к исходным данным.
- Рассчитать среднюю ошибку аппроксимации и сделайте выводы о качестве уравнения регрессии.
- Рассчитать прогнозное значение результата , если значение фактора X будет больше на 15% его среднего уровня .
- Дать экономическую интерпретацию коэффициентов парной регрессии.
Решение
- Вычислим описательные статистики(выборочные средние, медиану, моду, среднее квадратичное отклонение) для переменных Х и У , для этого составим таблицу:
|
N
|
X
|
Y
|
Х-Хср
|
(Х-Хср)2
|
У-Уср
|
(У-Уср)2
|
(Х-Хср)(У-Ycp)
|
|
1
|
22,4
|
53,4
|
6,3
|
39,69
|
29,05
|
843,9025
|
183,015
|
|
2
|
8,9
|
8
|
-7,2
|
51,84
|
-16,35
|
267,3225
|
117,72
|
|
3
|
13,3
|
22
|
-2,8
|
7,84
|
-2,35
|
5,5225
|
6,58
|
|
4
|
18,3
|
29,5
|
2,2
|
4,84
|
5,15
|
26,5225
|
11,33
|
|
5
|
13,8
|
32
|
-2,3
|
5,29
|
7,65
|
58,5225
|
-17,595
|
|
6
|
11,7
|
14,7
|
-4,4
|
19,36
|
-9,65
|
93,1225
|
42,46
|
|
7
|
19,5
|
13
|
3,4
|
11,56
|
-11,35
|
128,8225
|
-38,59
|
|
8
|
15,2
|
11,3
|
-0,9
|
0,81
|
-13,05
|
170,3025
|
11,745
|
|
9
|
14,4
|
18
|
-1,7
|
2,89
|
-6,35
|
40,3225
|
10,795
|
|
10
|
22
|
11,8
|
5,9
|
34,81
|
-12,55
|
157,5025
|
-74,045
|
|
11
|
16,4
|
28
|
0,3
|
0,09
|
3,65
|
13,3225
|
1,095
|
|
12
|
18,9
|
16
|
2,8
|
7,84
|
-8,35
|
69,7225
|
-23,38
|
|
13
|
16,1
|
29,5
|
0
|
0
|
5,15
|
26,5225
|
0
|
|
14
|
13,3
|
23,1
|
-2,8
|
7,84
|
-1,25
|
1,5625
|
3,5
|
|
15
|
17,3
|
55
|
1,2
|
1,44
|
30,65
|
939,4225
|
36,78
|
|
Сумма
|
241,5
|
365,3
|
|
196,14
|
|
2842,418
|
271,41
|
|
Среднее
|
16,1
|
24,35333
|
|
|
|
|
|
выборочные средние
Хмах=22,4, Хмин=8,9
R=22.4-8.9=13.5
Медиана Xme=15.65
Мода Хмо=13,3
Дисперсия
среднее квадратичное отклонение
- Построим поле корреляции и сформулируем гипотезу о форме связи.
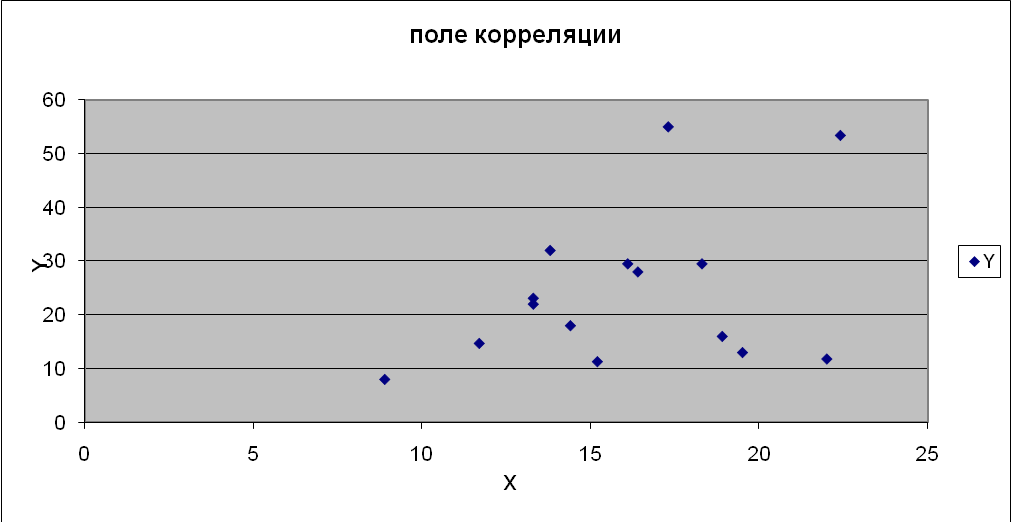
Анализируя данное поле корреляции можно сделать следующие выводы:
- между переменными Х и Y наблюдается прямая зависимость: с ростом Х значения Y увеличиваются.
- точки располагаются близко к прямой линии, т. Е. можно предположить , что связь между переменными линейная.
3. Вычислим парный коэффициент корреляции между переменными.
связь между часовым заработком 1 рабочего Y и общим стажем работы после окончания учебы Х прямая и слабая.
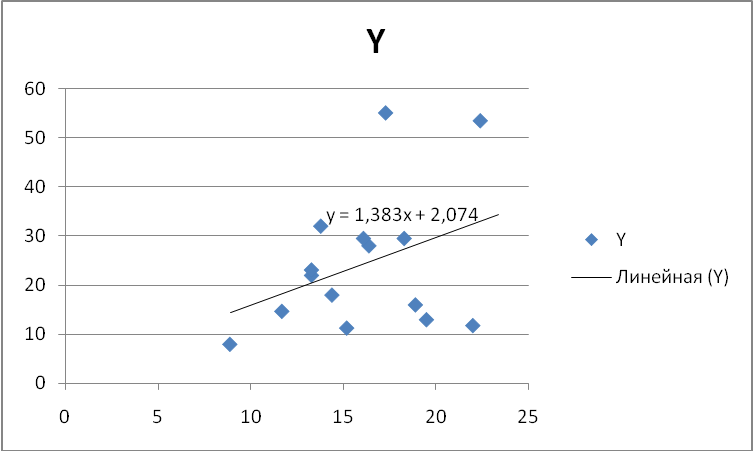
4. Найдем оценки и параметров модели парной линейной регрессии и .
Определим параметры линейной зависимости вида
Для расчета параметров , , коэффициента детерминации , оценки значимости уравнения результаты вспомогательных расчетов представим в виде таблицы.
|
N
|
X
|
Y
|
XY
|
X2
|
Y2
|
|
1
|
22,4
|
53,4
|
1196,16
|
501,76
|
2851,56
|
|
2
|
8,9
|
8
|
71,2
|
79,21
|
64
|
|
3
|
13,3
|
22
|
292,6
|
176,89
|
484
|
|
4
|
18,3
|
29,5
|
539,85
|
334,89
|
870,25
|
|
5
|
13,8
|
32
|
441,6
|
190,44
|
1024
|
|
6
|
11,7
|
14,7
|
171,99
|
136,89
|
216,09
|
|
7
|
19,5
|
13
|
253,5
|
380,25
|
169
|
|
8
|
15,2
|
11,3
|
171,76
|
231,04
|
127,69
|
|
9
|
14,4
|
18
|
259,2
|
207,36
|
324
|
|
10
|
22
|
11,8
|
259,6
|
484
|
139,24
|
|
11
|
16,4
|
28
|
459,2
|
268,96
|
784
|
|
12
|
18,9
|
16
|
302,4
|
357,21
|
256
|
|
13
|
16,1
|
29,5
|
474,95
|
259,21
|
870,25
|
|
14
|
13,3
|
23,1
|
307,23
|
176,89
|
533,61
|
|
15
|
17,3
|
55
|
951,5
|
299,29
|
3025
|
|
Сумма
|
241,5
|
365,3
|
6152,74
|
4084,29
|
11738,69
|
|
Среднее
|
16,1
|
24,35333
|
410,1827
|
272,286
|
782,5793
|
Сначала рассчитаем коэффициент
Используя полученное значение рассчитаем
Запишем полученное уравнение регрессии
Расчетные значения переменной у рассчитаем подстановкой значений Х в данное уравнение
|
N
|
X
|
Y
|
ур
|
Y-yp
|
(Y-yp)2
|
(Y-yp)2/Y
|
|
1
|
22,4
|
53,4
|
33,0768
|
20,3232
|
413,0325
|
7,73469
|
|
2
|
8,9
|
8
|
14,3523
|
-6,3523
|
40,35172
|
5,043964
|
|
3
|
13,3
|
22
|
20,4551
|
1,5449
|
2,386716
|
0,108487
|
|
4
|
18,3
|
29,5
|
27,3901
|
2,1099
|
4,451678
|
0,150904
|
|
5
|
13,8
|
32
|
21,1486
|
10,8514
|
117,7529
|
3,679778
|
|
6
|
11,7
|
14,7
|
18,2359
|
-3,5359
|
12,50259
|
0,850516
|
|
7
|
19,5
|
13
|
29,0545
|
-16,0545
|
257,747
|
19,82669
|
|
8
|
15,2
|
11,3
|
23,0904
|
-11,7904
|
139,0135
|
12,30208
|
|
9
|
14,4
|
18
|
21,9808
|
-3,9808
|
15,84677
|
0,880376
|
|
10
|
22
|
11,8
|
32,522
|
-20,722
|
429,4013
|
36,38994
|
|
11
|
16,4
|
28
|
24,7548
|
3,2452
|
10,53132
|
0,376119
|
|
12
|
18,9
|
16
|
28,2223
|
-12,2223
|
149,3846
|
9,336539
|
|
13
|
16,1
|
29,5
|
24,3387
|
5,1613
|
26,63902
|
0,903018
|
|
14
|
13,3
|
23,1
|
20,4551
|
2,6449
|
6,995496
|
0,302835
|
|
15
|
17,3
|
55
|
26,0031
|
28,9969
|
840,8202
|
15,28764
|
|
Сумма
|
241,5
|
365,3
|
|
|
2466,857
|
113,1736
|
|
Среднее
|
16,1
|
24,35333
|
|
|
164,4572
|
7,544905
|
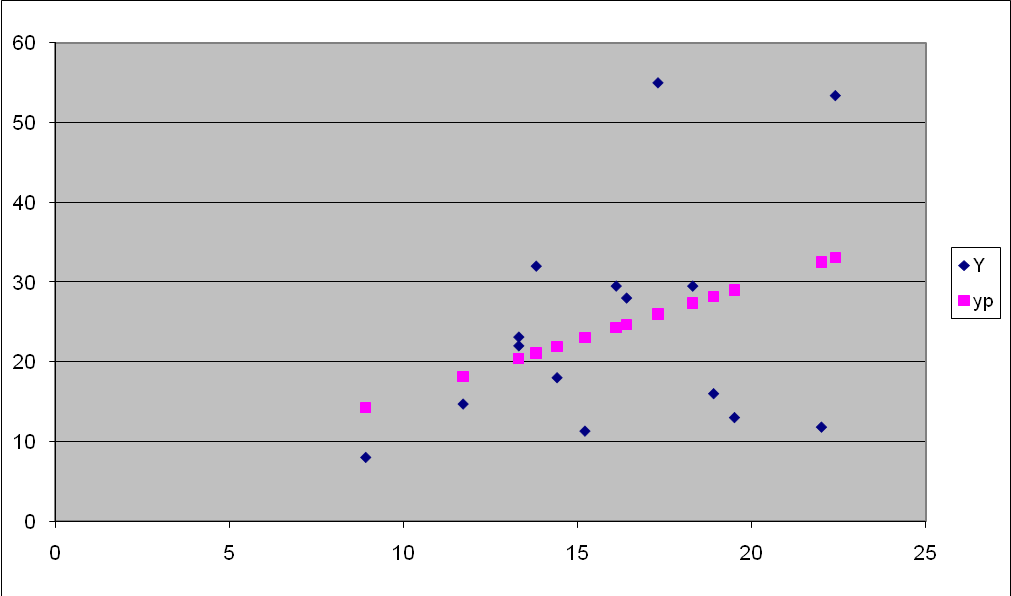
5. Проверим значимость оценок коэффициентов и с надежностью 0,95 с помощью t-статистики Стьюдента
Для оценки значимости уравнения необходимо рассчитать стандартную ошибку регрессии S и S
В среднем истинное значение может отклоняться от значения =1,387 на величину 0,984.
Рассчитаем значение статистики параметра
Значение t =1,41tкр=2,228 , поэтому параметр не является значимым.
Аналогично рассчитаем для параметра
Значение t =0,123<tкр=2,228 , поэтому параметр не является значимым.
5. Определим интервальные оценки коэффициентов и с надежностью 0,95.
Построим доверительные интервалы для параметра для уровня доверия q=0,95.
Построим доверительные интервалы для параметра для уровня доверия q=0,95.
6. Определим коэффициент детерминации R2 и коэффициент корреляции rxy. Сделать выводы о качестве уравнения регрессии.
Таким образом R2=0.133, т.е. на 13,3% дисперсия зависимой переменной у объясняется изменением переменной х, а 86,7% изменения у объясняется влиянием других факторов.
Рассчитаем коэффициент корреляции
Значение коэффициента корреляции 0,365 свидетельствует о том что связь между х и у слабая и прямая.
7. Проверим при уровне значимости 0,05 значимость уравнения регрессии с помощью F-статистики Фишера и сделать выводы о значимости уравнения регрессии.
Оценку значимости уравнения регрессии проведем с помощью F-критерия Фишера:
R2- коэффициент детерминации
Fтабл=4,98 для =0,05; k1=k=1;k2=n-k-1=10
F=1,99Fтабл=4.98
Уравнение регрессии с вероятностью 0,95 статически не значимое
- Рассчитаем среднюю ошибку аппроксимации и сделаем выводы о качестве уравнения регрессии.
В среднем на 50,26 % отличаются расчетные значения от фактических. Так как А=50,2610% то качество подгонки не достаточно хорошее.
- Рассчитаем прогнозное значение результата , если значение фактора X будет больше на 15% его среднего уровня .
Х среднее равно 16,1
Хпрогн=16,1+15%=18,51
- Дать экономическую интерпретацию коэффициентов парной регрессии.
Построенное уравнение регрессии
позволяет выполнить анализ взаимосвязи исследуемых показателей.
Экономический смысл параметра состоит в следующем- при изменении переменной х на единицу значение переменной у изменится в среднем на величину .
Определим коэффициент эластичности у по х.
Это означает что при изменении переменной х на 1 % на 91,7% изменится значение у.
Дополнительно решим задание в программе Microsoft Excel:
|
ВЫВОД ИТОГОВ
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Регрессионная статистика
|
|
|
|
|
|
|
|
|
Множественный R
|
0,363495
|
|
|
|
|
|
|
|
|
R-квадрат
|
0,132129
|
|
|
|
|
|
|
|
|
Нормированный R-квадрат
|
0,06537
|
|
|
|
|
|
|
|
|
Стандартная ошибка
|
13,77526
|
|
|
|
|
|
|
|
|
Наблюдения
|
15
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Дисперсионный анализ
|
|
|
|
|
|
|
|
|
df
|
SS
|
MS
|
F
|
Значимость F
|
|
|
|
|
Регрессия
|
1
|
375,5654
|
375,5654
|
1,979182
|
0,182931
|
|
|
|
|
Остаток
|
13
|
2466,852
|
189,7578
|
|
|
|
|
|
|
Итого
|
14
|
2842,417
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Коэффициенты
|
Стандартная ошибка
|
t-статистика
|
P-Значение
|
Нижние 95%
|
Верхние 95%
|
Нижние 95,0%
|
Верхние 95,0%
|
|
Y-пересечение
|
2,074854
|
16,23041
|
0,127837
|
0,900234
|
-32,9888
|
37,13852
|
-32,9888
|
37,13852
|
|
Переменная X 1
|
1,383757
|
0,983596
|
1,406834
|
0,182931
|
-0,74117
|
3,508687
|
-0,74117
|
3,508687
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ВЫВОД ОСТАТКА
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Наблюдение
|
Предсказанное Y
|
Остатки
|
Стандартные остатки
|
|
|
|
|
|
|
1
|
33,071
|
20,329
|
1,53147
|
|
|
|
|
|
|
2
|
14,39029
|
-6,39029
|
-0,48141
|
|
|
|
|
|
|
3
|
20,47882
|
1,521185
|
0,114597
|
|
|
|
|
|
|
4
|
27,3976
|
2,102402
|
0,158383
|
|
|
|
|
|
|
5
|
21,17069
|
10,82931
|
0,815818
|
|
|
|
|
|
|
6
|
18,2648
|
-3,5648
|
-0,26855
|
|
|
|
|
|
|
7
|
29,05811
|
-16,0581
|
-1,20973
|
|
|
|
|
|
|
8
|
23,10795
|
-11,808
|
-0,88954
|
|
|
|
|
|
|
9
|
22,00095
|
-4,00095
|
-0,30141
|
|
|
|
|
|
|
10
|
32,5175
|
-20,7175
|
-1,56074
|
|
|
|
|
|
|
11
|
24,76846
|
3,23154
|
0,243446
|
|
|
|
|
|
|
12
|
28,22785
|
-12,2279
|
-0,92118
|
|
|
|
|
|
|
13
|
24,35333
|
5,146667
|
0,38772
|
|
|
|
|
|
|
14
|
20,47882
|
2,621185
|
0,197465
|
|
|
|
|
|
|
15
|
26,01384
|
28,98616
|
2,183651
|
|
|
|
|
|
Зависимость часового заработка одного рабочего от общего стажа работы после окончания учебы путем построения уравнения парной линейной регрессии