ПОЛЯРИЗАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ДЕФЕКТАМИ ПРОСТРАНСТВА-ВРЕМЕНИ, КАК ТЕСТ ПО ФИКСАЦИИ ПАРАМЕТРОВ НАРУШЕНИЯ ЛОРЕНЦ-ИНВАРИАНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

ПОЛЯРИЗАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ДЕФЕКТАМИ ПРОСТРАНСТВА-ВРЕМЕНИ, КАК ТЕСТ ПО ФИКСАЦИИ ПАРАМЕТРОВ НАРУШЕНИЯ ЛОРЕНЦ-ИНВАРИАНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ.

1. Введение

Поиск нарушения Лоренц – инвариантности (LV) [1] для физических полей материи является актуальной задачей физики наших дней. Действительно, уравнения фундаментальных полей материи Лоренц – инвариантны. Они содержат только один параметр, непосредственно характеризующий вакуум этих полей, - массу. Если последовательно придерживаться геометрических идей в физике (а под знаком этих идей создана вся фундаментальная физика 20 в [2]), то надо потребовать объединения физических полей материи с гравитационным полем, как это завещал А. Эйнштейн [3]. Такое объединение требует отхода от идей локальности в физике и привлечения концепции струн [4]. Геометрически струны представляют собой многомерные колеблющиеся поверхности, на которых возбуждены волновые моды колебаний, при специфической процедуре квантования соответствующие элементарным частицам.

Благодаря идеям Замолодчикова [5], Когана [6], Мавроматоса [7], Эллиса [8] и других ученых, сегодня существует общий математический формализм струн Лиувилля, последовательно реализующий концепцию объединения взаимодействий. Для подтверждения этих теоретических идей требуется так редуцировать этот формализм к низким энергиям, чтобы он был в хорошем согласии с наблюдениями и экспериментами. Кроме того, новая теория должна приводить к экспериментальным следствиям, которых не могло быть в теориях более низкого уровня. Энергии современных ускорителей не хватает для постановки экспериментов по проверке следствий теории струн. Остается использовать с этой целью астрофизические тесты [9]. И действительно, теория с LV нарушением предсказывает появление у полей второго вакуумное параметра (второй массы), которую в состоянии измерить физические приборы при энергиях 10 Тэв и выше [9],[10].

Особо мощное излучение, свойство которого можно тестировать на присутствие в нем артефактов теории струн, излучают космологические гамма – всплески (GRB).. Гамма – всплеск представляет собой мощный выброс энергии от рождающихся в ранние моменты, близкие к моменту «первого света» во Вселенной, сверхновых. Эти сверхновые принадлежат «хозяйским галактикам» [11]. Через минуты после взрыва на этом месте возникает более устойчивое послесвечение выброшенной всплеском плазмы, которое анализируется оптическими обсерваториями [12]. (см рис. (1, 2)).

В предыдущих сборниках Баксанской школы весь этот комплекс идей был подробно проанализирован в серии статей автора (см., например, [13, 14]).

Новая идея поиска LV состоит в использовании для этого эффекта двойного лучепреломления электромагнитных волн в пространстве- времени расширяющейся Вселенной, который постепенно выходит на первый план в качестве арены поиска параметров LV нарушения.

2. Эволюция электромагнитных волн в расширяющейся Вселенной.

Здесь и ниже будем пользоваться естественной системой единиц

измерения =с=1. При относительно низких энергиях E( =

Гэв, = - масса Планка [3] ), теория струн редуцирутся до привычных земным экспериментаторам понятий. Этими понятиями являются :

1) четырехмерное пространство-время ;

2) квантовые частицы и волны;

3) малые (в пределе точечные) дефекты четырехмерного пространства-времени.

Кванты полей, сталкиваясь с дефектами, становятся квазичастицами с неклассическими дисперсионными соотношениями, характерными для сред с дефектами.

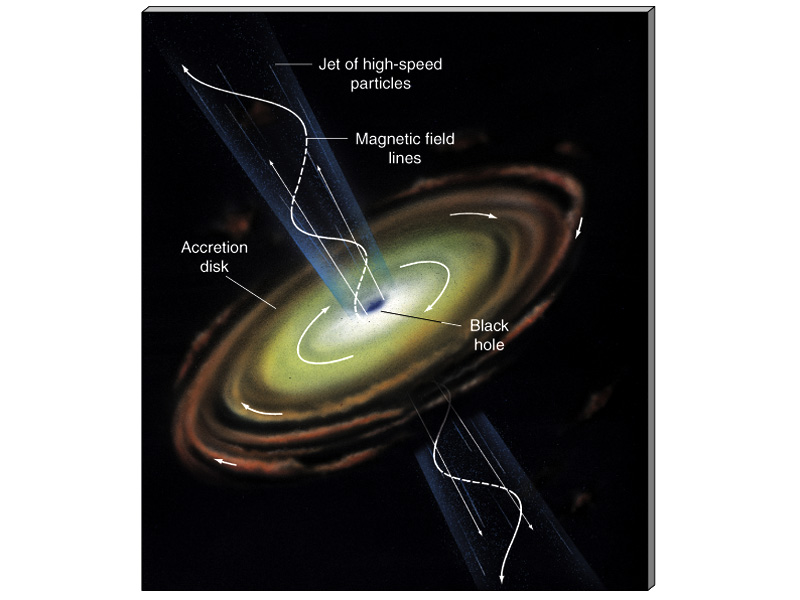
. Рис.1. Модель космологического гамма – всплеска в виде джета ( направленного выброса, перпендикулярного плоскости аккреционного диска центральной черной дыры ). Заряженные частицы высокой энергии движутся по винтовой линии вокруг магнитного поля иизлучают электромагнитные волны.

Выберем для расширяющегося пространства – времени синхронную

метрику Фридмана [3]:

Рис. 2. Плазменное послесвечение гамма всплеска в центре картинки. После корокого времени излучения центрального джета всплеск гаснет, а возбужденные ионы нагретой им плазмы начинают излучать элекромагнитный спектр с характеристиками, индуцированными погасшим всплеском. Это и есть плазменное послесвечение.

(1)

где a(t) – масштабный фактор Вселенной.

Пусть – частота, P- импульс электромагнитной волны.

Классическое дисперсионное соотношение для электромагнитных волн в этих обозначениях принимает вид:

= P (2)

Модифицируем его для рассматриваемого случая Вселенной с дефектами. Общая дисперсионная формула для Вселенной с фотонами – квзичастицами тогда примет вид:

(3)

где f(P) - поправка к дисперсионному соотношению. При низких энергиях эта поправка может быть разложена в ряд по малому параметру или , так как для ультрарелятивистских частиц .

Выберем в качестве коэффициента разложения функции f(P) по импульсу P неизвестное заранее число , которое должно быть определено из экспериментов со светом при рассматриваемых энергиях

E<<. Тогда, уравнение (3) можно переписать в виде разложения в степенной ряд [15]:

, (4)

где знаки () соответствуют лево (право) поляризованным фотонам. В расширяющейся Вселенной импульс фотона уменьшается в отношении

(5)

здесь - значение масштабного фактора в настоящее время, k – волновое число.

Теперь можно выписать дисперсионное соотношение (4) в явном виде:

(6)

Применим эти уравнения к послесвечению гамма – всплесков. Эти объекты удалены от Земли на тысячи мегапарсек. Сотая часть этого излучения строго линейно поляризована [16]. Если предположить, что эта поляризация обязана интересующим нас струнным эффектам, то именно информация о ней, поставляемая матрицами поляризационных приборов, должна содержать информацию о новых струнных эффектах.

Введем единицы измерения, используемые в космологии [17]:

1) - значение постоянной расширения Вселенной (постоянной Хаббла) в наш момент времени.

2) - красное смещение космологического объекта, определяющее расстояние до него.

С другой стороны, эта величина определяется по спектрам удаляющихся космологических объектов, которые сильно смещены к красному краю, по сравнению с лабораторными спектрами аналогичных элементов на Земле:

(7)

где наблюдаемая длина волны, длина волны земного эталона с такими же свойствами.

Рассмотрим электромагнитную волну с модифицированным (6) дисперсионным соотношением, свободно распространяющуюся в расширяющейся Вселенной. Допустим, что эта волна была излучена

послесвечением GRB c известными физическими свойствами

Дисперсионные свойства этой волны описаны формулой (4). При энергиях много меньше планковских для электромагнитного поля сохраняется принцип суперпозиции. В общем случае, вектор – потенциал этой переменной волны имеет вид:

, (8)

где векторы поля есть [18] :

(9)

вектор - потенциал линейно-поляризованной части электромагнитной волны.

(10)

вектор – потенциал циркулярно - поляризованной части волны. Здесь использованы обозначения:

- относительная доля в волне ее циркулярной поляризованной части.

- волновое число волны, пришедшей по оси координат «z».

Латинские индексы пробегают значения i=0,1,2,3, а векторы поляризации определены стандартным образом :

, (11)

Выражение (8) легко переписать через квантовую струнную поправку к дисперсионному соотношению.

(12)

Тогда (8) примет вид:

, (13)

где поправка к фазе волны

(14)

записывается с помощью поправки к частоте (6).

С помощью (8) компоненты электромагнитного поля волны рассчитываются как

(15)

и имеют вид:

(16)

(17)

(18)

(19)

Поляризационная матрица волны считается по стандартным формулам [19] с учетом малости циркулярной поляризации гамма – всплесков в оптическом , рентгеновском, гамма - диапазонах:

(20)

Явный вид этой матрицы есть:

(21)

Эта матрица составлена из поляризационных параметров Стокса:

(22)

Это излучение поляризовано, причем поляризация волны, с высокой степенью точности, остается линейной в процессе ее распространения:

(23)

Далее будет показано, что оптические измерения каждой из компонент вектора параметров Стокса, могут выявить их осцилляции с модулирующей частотой , и тем самым, зафиксировать математически эффект LV. Можно попытаться угадать величину этого эффекта по величине расстройки фазы , составив ее из фундаментальных констант в предположении, что предполагаемый эффект вызван LV:

(24)

где спектральная длина волны, для которой искомый эффект становится существенным.

3. Параметры поляризационной сферы Пуанкаре, вектор Стокса электромагнитной волны с LV нарушением.

Для анализа поляризованного излучения в оптической и рентгеновской спектроскопии используется четырехмерный вектор Стокса [20] :

(25)

Величина I обозначает общую интенсивность излучения. Поляризацонные параметры Q,U,V определены ниже. Представление Стокса дает более детальную картину распространения волны в расширяющемся пространстве-времени и позволяет рассчитать сразу 3 поляризационных параметра (вместо одного, к примеру, угла вращения плоскости поляризации излучения) и восстановить структуру поляризации излучения, которая не сводится просто к повороту одной плоскости поляризации волны при ее распространении в пространстве.

Вводя определение степени поляризации p, а также углов сферической системы координат можно определить поляризационную сферу

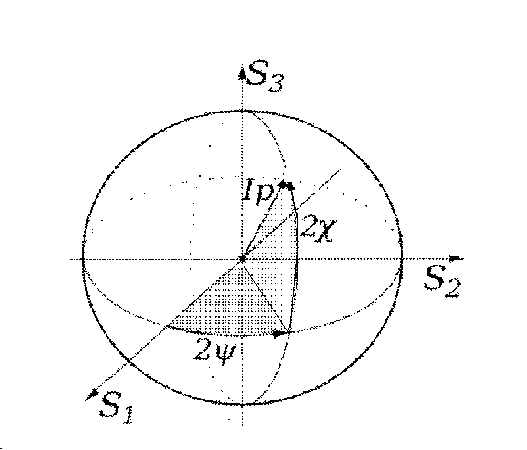
Рис.3. Рисунок сферы Пуанкаре, предназначенной для

графического представления поляризационных параметров электромаг -

нитного излучения. Плоскость , которой соответствует угол

,- отображение поляризационного эллипса. Повороту эллипса в простра-

нстве соответствует угол

Пуанкаре с координатами (Ip, ) (см. рис.3). Широтный угол сферы физически соответствует углу поляризационного эллипса излучения [20] .

Границы изменения угла , угол 0соответствует вращению плоскости поляризации поляризационного эллипса.

По определению, введенные параметры сферы Пуанкаре связаны между собой соотношениями:

(26)

(27)

(28)

В фиксированном базисе для поля (16)-(19) поляризационные параметры имеют вид:

(29)

(30)

(31)

(32)

С помощью (29)-(32) рассчитаем углы поляризационной сферы , :

(33)

Таким образом, все параметры поляризационной сферы Пуанкаре, используемые для анализа приходящего от источника электромагнитного излучения, удалось связать с фазой электромагнитной волны, приходящей от источника излучения.

Из (29)-(32) следует, что при малой циркулярной поляризации, электромагнитная волна в высокой степени линейно поляризована:

(34)

3. Вклад геометрии пространства – времени в поляризационные свойства излучения.

Рассчитаем расстройку фазы для общепринятой сегодня плоской модели Вселенной в зависимости от красного смещения Z. Уравнения Фридмана для изотропной Вселенной в этой модели имеют вид [21] :

(35)

где - значение постоянной Хаббла в наш момент времени, другие постоянные, входящие в (35) образуют вектор -параметров с координатами , .

Здесь плотность энергии материи, плотность «темной энергии», - критическая плотность Вселенной. Рассчитаем фазу с помощью (14), (35). Формула (35) дает возможность выразить

dt через dZ, а потом провести в явном виде интегрирование (14). Получим выражение:

(36)

где

, (37)

Откуда видно, что при малых красных смещениях Z<<1 вклад геометрии пространства времени в поляризацию излучения отсутствует. Поэтому, его не следует искать для объектов внутри Галактики.

4. Электромагнитное излучение поля с LV нарушением, принимаемое от оптического послесвечения GRB.

Принимаемое от послесвечений GRB электромагнитное излучение линейно поляризовано во всех диапазонах с длиной волны, меньшей, чем в радио диапазоне. Эта поля ризация является верхней границей, за которой могут скрываться эффекты LV. Согласно данным по послевечениям GRB, в [22] была построена фитирующая кривая для преставленной в работе выборке этих источников. Она дала для поляризованой фракции излучения значение p~ значениях поляризационных углов с вероятностью . При построенной по иным принципам выборке излучения от послесвечений есть надежда зафиксировать LV эффект.

Так как параметры Стокса являются (29)-(32) осциллирующими тригонометрическими функциями с фазой, обратно пропорциональной квадрату длины волны излучения то частота осцилляций будет возрастать при переходе от длинноволновой к коротковолновой части спектра. Общей составляющей излучения послесвечений будут являться осцилляции с переменной длиной и ограниченной (16)- (18) амплитудой. Это предсказание носит общий характер для излучения с любой длиной волны от послесвечений GRB. Поэтому, тщательно разыскиваемый сегодня с помощью различной аппаратуры таинственный LV эффект может быть обнаружен с помощью стационарного оборудования оптических обсерваторий.

Подставляя выражения физических констант в выражение для (36) для фазы , получим оценку:

(38)

Теория и наблюдения показывают, что циркулярная часть поляризации

послесвечений GRB подавлена [22], [23]. То есть, . Тогда поляризационные параметры сферы Пуанкаре (26) - (28) имеют вид:

(39)

(40)

V=0 (41)

То есть, параметры Q,U можно рассматривать, как базисные, для центральной плоскости сферы Пуанкаре, а угол поворота поляризационной плоскости на сфере подавлен. При изменяющемся во времени масштабном факторе Вселенной a(t) эти параметры синфазно осциллируют, поддерживая саму плоскость в неизменном положении, как при отсутствии расширения a=const. Линейная часть поляризации определяется стандартно и равна теперь

(42)

В ряде работ [24], [25] разными методами были получены ограничения на параметр Лоренц- нарушения Из формулы (38) следует, что фаза становится сравнимой с единицей при длинах волн

То есть, осцилляции квантовой природы, рассмотренные выше, должны наблюдаться в ультрафиолетовом или рентгеновском диапазоне излучения послесвечений в рассчитанном выше окне длин волн . Удобно представить графики значений поляризационных параметров в осях, нормированных на полную амплитуду поляризованного излучения послесвечений, то есть :

Достаточно сделать это для одного из параметров (к примеру, для параметра U), в силу их однотипной зависимости от осциллирующих тригонометрических функций. Такое представление позволяет получать детальную информацию об этих осцилляциях в компактном виде.

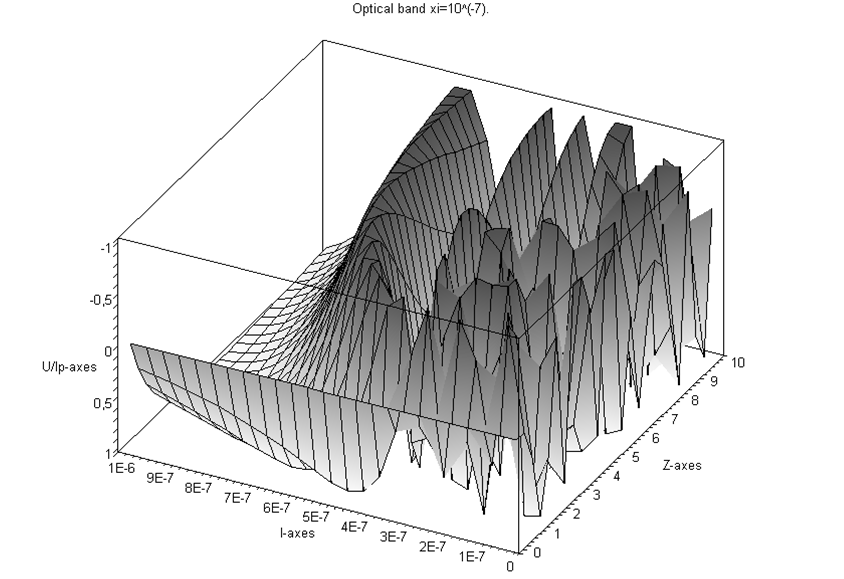
Рис. 4. Зависимость осцилляций поляризационного пара

метра U от длины волны излучения l и красного смещения Z.

Этот график помогает правильно сделать выборку послесвечений

гама – источников ,необходимую для постановки эксперимента по

измерению параметра .

Для определения точных значений постоянной (постоянной LV нарушения ) необходимо максимально точно определить точку начала осцилляций поляризационных параметров в зависимости от длины волны спектра послесвечений.

Теоретические предсказания для определения параметров осцилляций получаются после численного расчета по формулам (36), (37) и представлены на графиках (см рис.4, рис.5).

В последнем графике особый интерес представляет точка начала осцилляций в спектре. Осцилляции начинаются именно для тех длин волн, для которых фаза (36) сравнивается с единицей по порядку величины. Для выявления этого эффекта должен быть поставлен эксперимент по изучению спектра популяции гамма –всплесков, отоб- ранных в соответствии с критериями, предложенными здесь, с уче-

Рис.5. Зависимость поляризационного параметра U от

длины волны излучения l при значении красного смещения Z=1. Осцил-

ляции параметра I, на рисунке, позволяют количественно рассчитать

эффект LV нарушения Лоренц - инвариантности и осуществить изме-

рение параметра в удобной для постановки эксперимента форме.

том их красного смещения Z, и из поляризационных спектральных данных выделена и вычтена фоновая составляющая. То есть, спектры должны подвергнуться предварительной обработке с учетом предска-

заний теории.

5. Заключение.

Для определения типа теории поля при высоких энергиях, в частности, для выяснения вопроса о том, является она струнной или нет, необходимо развернуть серию поляризационных экспериментов по всему спектру излучения послесвечений - оптическому, ультрафиолетовому, рентгеновскому и гамма- диапазону длин волн. Определенные заявки на использование метода сферы Пуанкаре в гамма - диапазоне сделаны в препринтах американских теоретиков

( см. например, [26] ). То есть, логика развития теории требует постановки корректного эксперимента, в ходе которого полезная информация об осцилляции оптических параметров Пуанкаре была бы отделена от фона, несмотря на разный характер и величину экспериментальных ошибок в различных областях спектра электромагнитного излучения.

Список литературы.

1 Мурзин В.С., Астрофизика космических лучей.- М: МГУ, 2007,

1. .

2. Вайнберг . С. Квантовая теория поля. М: Физматлит, 2003, -

644с.

3. Мизнер Ч.,Торн У, Дж. Уилер Дж.. Гравитация, т1. М: Мир 1977,

-474с.

4. Каку М . Введение в теорию суперструн. М: Мир, 1999, -623сс.

5. Инстантоны, струны и конформная теория поля. / Под ред.

Белавина А.А., М:Физматлит, 2002, 441 стр.

6. Kogan I. I., Mavromatos N.E., et. al. hep-ph/9606102, v1.

7 N.E. Mavromatos N. E. , M. Sakellariadou, Phys. Lett. B., v.652, -

2007, pp. 97-102.

8. Ellis J. hep. -th. / 0710.0777 v1.

9. Jacobson et. al. Ann. of Phys. v..321, 2006, pp. 150-196.

10. Кладоркляйнгротхаус Г.В., Цюбер K.. Астрофизика

элементарных частиц.М: УФН, 2000,- 488сс.

11. Gamma ray bursts./ Vedrenne, Gilbert, Atteia, Jean Luck . Jointy

published with Praxis Publishing, UK, 2009, 584pp.

12. Постнов К.А., УФН., т. 169, №5, 1999, с. 545-588; Засов А.В.,

Постнов КА. Общая Астрофизика. Фрязино:2006, 493сс.

13. Гришкан Ю.С.Труды БМШ ЭТФ №6,, т.1. сс. 59-76, М:2006.

14. Гришкан Ю.С.Труды БМШ ЭТФ №7,, т.1. сс. 72-87, М:2007.

15. Mattingly D. gr-qc, /0802.1561, v. 1.

16. Pirnomonte S. et. al. Astron. Astrophys. v. 491, 2008, pp. 183-188.

17. Вайнберг С., Гравит ация и космология. М:Мир, 1975,- 682 сс.

18. Горбунов Д.С., Рубаков В.А.. Введение в теорию ранней

Вселенной и Большого взрыва- М: издательство ЛКИ, 2008.

19. Ландау Л.Д., Лифшиц Е.М.. Теория поля. М: Наука, 1973,

-504сс.

20. van de Hulst H.C., Light scattering by small particles. Dover Pub-

lications, New York, 1981.

21. Гришкан Ю.С. Труды БМШ ЭТФ №3,, т.2. сс. 69-85,

Нальчик:2004 .

22. Lazzati D. et. al. Astron. Astrophys., v. 410, 2003, pp. 823-831.

23. Asaf P. E. , Waxman. Apj, v. 638, 2006, pp 1187-1188; astro-ph/

040784, v2, Druft version Augaust , 2008.

24. Zhong Fan Yi. et. al. Mon. Not. Roy. Astron. Soc. v. 387, pp. 92-96.

25. Galaverni M, Sigl G, Phys.Rev. D. 78, 2008, pp. 021102- 021106.

26. Kostelecky V.A., Mewes M, hep-ph./ 0607084 v1.

ПОЛЯРИЗАЦИЯ ЭЛЕКТРОМАГНИТНЫХ ВОЛН ДЕФЕКТАМИ ПРОСТРАНСТВА-ВРЕМЕНИ, КАК ТЕСТ ПО ФИКСАЦИИ ПАРАМЕТРОВ НАРУШЕНИЯ ЛОРЕНЦ-ИНВАРИАНТНОСТИ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ