Piramidali Tartiblash

BUXORO DAVLAT UNIVERSITETI

FIZIKA-MATEMATIKA FAKULTETI

AMALIY MATEMATIKA YO’NALISHI

ALGORITMLAR NAZARIYASI FANIDAN

MAVZU: Piramidali Tartiblash

Bajardi: Suvonov Nurbek

Rahbar: Shafiyev T.

MUNDARIJA:

Mavzuning dolzarbligi

Bu ishda ikki vazifa – algoritmlarning dastur effektivligiga qanday ta’sir etishi va turli xil algoritmlarning analizini o’rganishdir. Ba’zi bir zamonaviy dasturiy ta’minotlarga e’tibor qilsak, ularning ayrim tuzuvchilari na dasturning ishlash effektivligiga va na xotiraning aql bilan ishlatilishiga e’tibor qilishadi. Ularning fikricha, dastur ko’p joy olsa, foydalanuvchi qo’shimcha xotira sotib olishga majbur bo’ladi yoki yangi tezroq ishlaydigan komyuter sotib oladi.

Lekin kompyuterlarning tezligi cheksiz kattalashmaydi. U simli kabelda elektronlarning harakat tezligi bilan, optik kabellarda yorug’likning tarqalish tezligi bilan va hisoblashda qatnashadigan kompyuterlar orasidagi aloqa kanallarining komutativlik tezligi bilan chegaralanadi. Boshqa cheklovlar kompyuter imkoniyatlari bilan bog’liq emas, balki qo’yilgan masalaning murakkablik darajasiga bog’liq. Shunday masalalar mavjudki, ularni yechish uchun eng tez ishlaydigan algoritmlar qo’llanilganda ham odam umri yetmaydi. Bu masalalar orasida yaqinroq javob olish uchun algoritmlar kerak bo’ladigan, juda zarurlari ham mavjud.

Piramidali tartiblashga kirish

Piramidali tartiblashning asosiga piramida deb nomlangan Binarli daraxtning maxsus tipi kiradi. Bunday daraxtning har qanday daraxtchasiga ildizning ahamiyati uning avlodlariddan har birining ahamiyatidan ko’ra kattaroq. Har bir tugunning bevosita avlodlari tartiblashtirilmagan, shuning uchun ba’zida chap bevosita avlod o’ngidan ko’ra ko’proq ahamiyatga ega ba’zida esa aksincha. Piramida o’zicha to’liq daraxtni tasvirlaydi, unga yangi darajaning to’ldirilishi faqat oldindagi darajaning to’liq to’ldirilganidan keyin boshlanadi. Hamma tushunchalar esa bitta darajada chapdan o’ngga to’ldiriladi.

Tartiblash piramidaning qurilishidan boshlanadi. Shunda ro’yxatning maksimal elementi daraxtning tepasida ma’lum bo’ladi. Chunki tepa ildizlari albatta kamroq bo’lishi kerak. Keyin esa ildiz ro’yxatning oxirgi elementi bo’lib yoziladi, piramida esa olib tashlangan maksimalli element bilan qayta shakllanadi, natijada, ildizda miqdori bo’yicha ikkinchi element ma’lum bo’ladi. U ro’yxatcha nusxalanadi protsedura hamma elementlar ro’yxatga qaytmaguncha takrorlanadi. Tegishli algoritmning korinishi shunday

Piramidani tuzish:

for i=1 to N do

piramida ildizini ro’yxatga nusxalash

piramidani qayta shakllantirish

end for

Bu algoritmda ba’zi bir detallarni aniqlash lozim. Biz piramidaning tuzilishi va qayta shakllanishining protsedurasi nimadan iborat ekanligini aniqlashimiz mumkin: bu esa algoritmni natijalashga ta’sir qiladi.

Bizni algoritmni amalga oshirish qiziqtiradi. Binarli daraxtni yaratishda nakladli satrlar ro’yxatining oshishi bilan o’sadi, lekin ro’yxat bilan band bo’lgan o’rindan foydalanish mumkin. Oxirgidan oldingi darajadagi bitta tugundan tashqari har bir ichki tugunda ikkita bevosita avlod borligini hisobga olsak, ro’yxatni piramidaga “qayta qurish” mumkin. Keying aks ettirish talab qilingan piramidani shakllantirishga imkon beradi. g raqami bilan ro’yxat elementining bevosita avlodlarini 2i va 2i+1 vaziyatga yozamiz. Shuni ko’ramizki, hamma avlodlar vaziyatlari natijasida har xil bo’ladilar, biz bilamizki, agar 2i>N bo’lsa, unda g tuguni barg bo’lib qoladi, agar 2i=N bo’lsa, unda g tugunda baravar bitta avlod bo’ladi. 1-rasmda piramida va uning ro’yxatli taqdimi ko’satilgan.

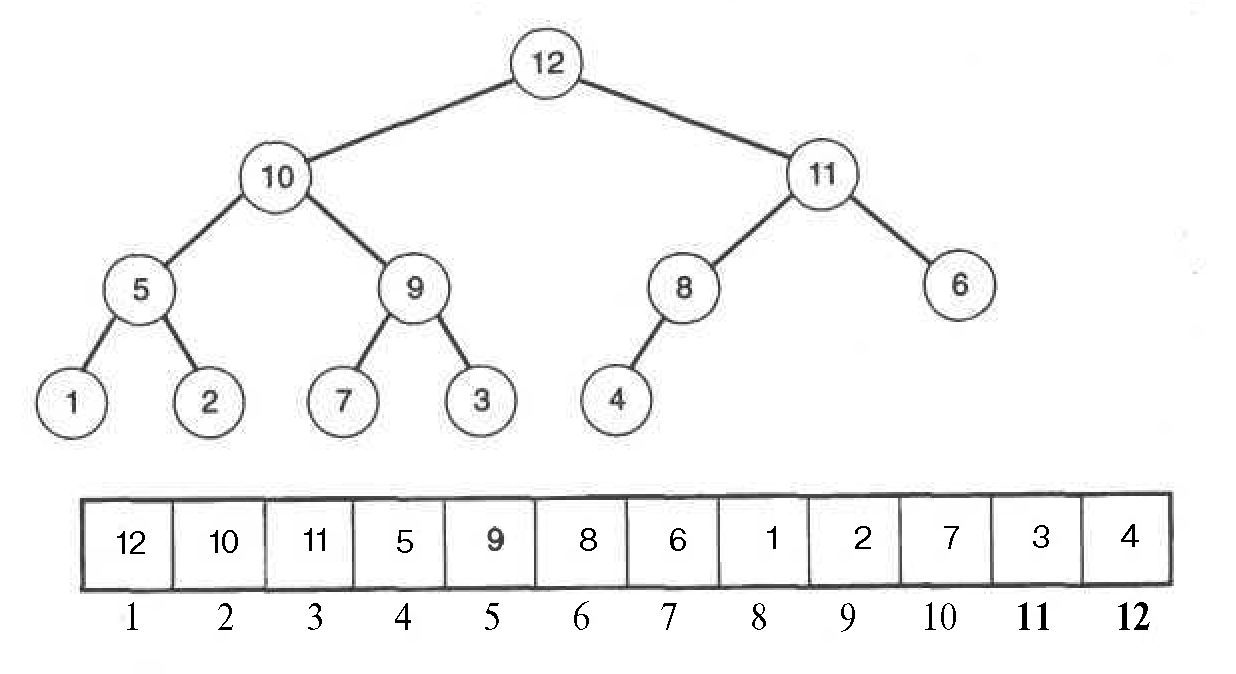
1-rasm. Piramida va uning ro’yxatli ko’rinishi

Piramidani qayta shakllantirish.

Ildizdan ko’proq elementning nusxalashida ildizli tugun ozod bo’lib qoladi. Biz bilamizki, unga ikkita bevosita avlodlardan kattasi tushishi kerak va biz uning o’rniga kim turishini ko’rib chiqishimiz kerak. Shunda piramida to’liq daraxtga iloji borich yaqin qolipga keladi. Piramidaning qayta shakllanishini biz eng ko’p elementdan uning pastki darajasida boshlaymiz. Natijada daraxtning pastki qismidan tugunlar bab-baravar yig’ishtiriladi. Agar buni kuzatmasak, hamma katta ahamiyat piramidaning bir qismida bo’lsa, unda piramida, balanslashadi va algoritm natijaviyligi tushadi. Natijada mana nimani olamiz:

FixHeap (list, root, bound)

List tartiblanadigan ro’yxat/piramida

Root piramida ildizining raqami

Key piramidaga qo’yiladigan kalit qiymati

Bound piramidaning o’ng chegarasi(nomer)

Vacant=root

While 2*vacant<=bound do

LargerChild = 2*vacant

// bevosita avlodlarning ikkitasidan eng kattasini qidirish

If (largerChild < bound) and (list [largerChild + 1])>

List [largerChild + 1]) then

largerChild = largerChild + 1

end if

// bugungi avloddan yuqoriroq kalit topiladimi?

If key > list [largerChild] then

//ha, sikl tugaydi

Break

Else

// yo’q, bevosita katta avlod

// ko’tarish lozim

List [vacant] = list [largerChild]

Vacant = largerChild

End if

End while

List [vacant] = key

Bu algoritm parametrlariga qaraganda shunday savol paydo bo’lishi mumkin. Nima uchun o’zgaruvchi root kerak? Haqiqatan ham protsedura rekursiv emas ekan. Piramida ildizi doima birinchi element bo’lishi kerak, lekin biz ko’ramizki bu qo’shimcha parametr piramidani pastdan yuqoriga qurishga imkon beradi. O’ng chegaraning ahamiyati piramidadan ro’yxatga elementlarni ko’chirishda piramidaning qisilishi uchun kiritiladi.

Piramidani qurish

FixHeap funksiyasiga bizning yondoshishimiz piramidaning boshlang’ich holatini shakllantirishga imkon beradi. har qanday ikkita qiymatlarni ozod tugunning barglari deb tushunishimiz mumkin. Chunonchi hamma elementlar barglar bo’lib hisoblanadilar, ro’yxatning ikkinchi yarmi bilan nimadir qilish zaruriyati yo’q. biz barglardan oddiy kichik piramidalar qurishimiz mumkin, keyin esa ro’yxatga hamma qiymatlar tushmaguncha ularni sekin asta birga terish kerak. Keyingi davr bu protsudurani amalga oshirishga imkon beradi.

For i = N/2 down to 1 do

FixHeap(list, i, list[i], N)

End for

Natijaviy algoritmi

Yozilgan hamma bo’laklarni birga qo’shib, piramida ro’yxati elementlarini ko’chirish bo’yicha kerakli operatsiyalarni amalga oshirib, natijaviy algoritmni olamiz.

for i=N/2 down to 1 do

FixHeap(list,i,list[i],N)

end for

for i=N down to 2 do

max=list[1]

FixHeap(list,l,list[i] ,i-l)

list [i]=max

end for

Eng yomon holat tahlili

FixHeap protsedurasining tahlilidan boshlaymiz. Chunonchi algoritmning qolgan qismi asosida quriladi. Piramidaning har bir darajasida algoritm ikkita bevosita avlodlarni, shuningdek bevosita avlodlar va kalitdan kattasini taqqoslaydi. Bu degani D chuqurlikdagi piramida uchun taqqoslash soni 2D2 oshmaydi. Piramidaning tuzilishi bosqichida biz avval oxirdan ikkinchi darajaning har bir tuguni uchun FixHeap protsedurani chaqirtiramiz. Ya’ni qurilgan piramidalar 1 chuqurlikka egalar. Keyin u pastdan uchinchi darajaning har bir tuguni uchun chaqirtiriladi. Ya’ni piramidalar 2 chuqurlikda quriladi. Oxirgi qadamda ildiz darajasida [log2N] chuqurlikda piramida shakllangan bo’ladi. Bizga faqat har bir o’tishda FixHeap protsedurasi tugunlarining ham 1 soni uchun chaqirtirish kerakligini sanash qoldi. Tugunning ildizi darajasida uzel bitta, ikkinchi darajasida esa unda ikkita o’g’li bo’ladi. Keyingi darajaning tugunlari soni to’rttadan oshmaydi. Keyingisida esa sakkizdan. Bu natijalarni birga chiqarib quyidagilarni olamiz:

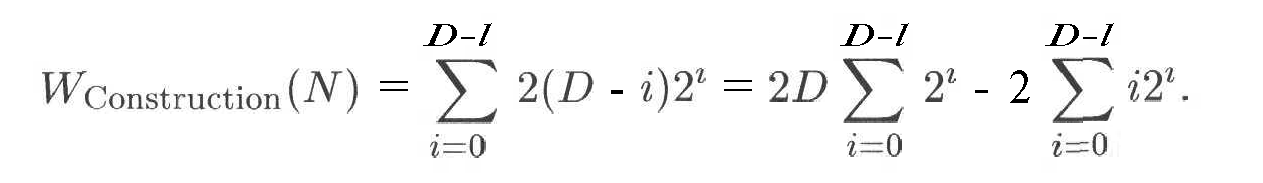
Bu esa quyidagini beradi:

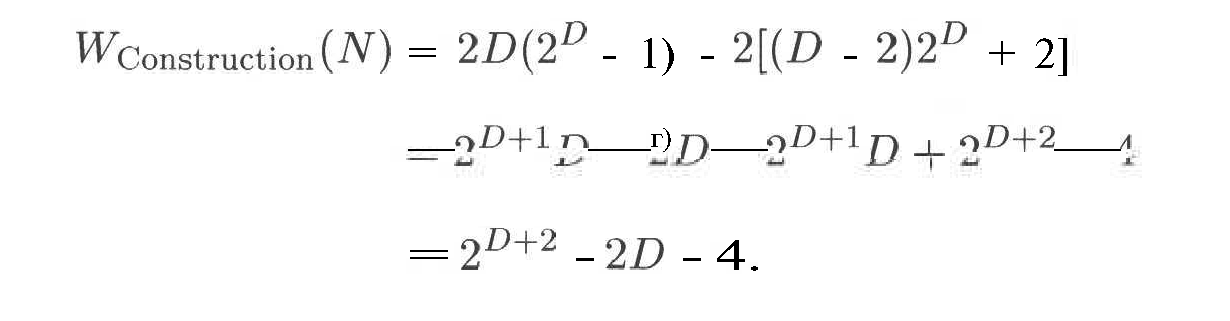
D – log2N ni qo’yib quyidagilarni olamiz:

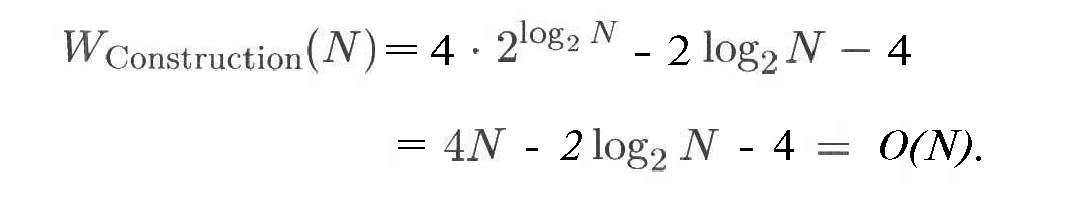
Shu uchun piramidani qurish bosqichi ro’yxat elementlarining soni bo’yicha chiziqli murakkablikka egadir.

Endi algoritmning asosiy davrini ko’rib chiqamiz. Bu siklda biz piramidadan bitta elementni yo’q qilamiz, keyin esa FixHeap protsedurasini chaqiramiz. Davr piramidada bitta element qolguncha bajariladi. Elementlarning soni har bir o’tishda bittaga kamayadi, piramidaning chuqurligi qanday o’zgaradi? Biz aytib o’tganimizdek hamma piramidaning chuqurligi [log2N] ga teng. Shu uchun agar piramidada K tugunlari qolgan bo’lsa, unda uning chuqurligi [log2K] ga teng. Taqqoslash sonlari esa 2 marta ko’p. bu degani eng yomon vaziyatda siklda quyidagi operatsiyalar bajariladi:

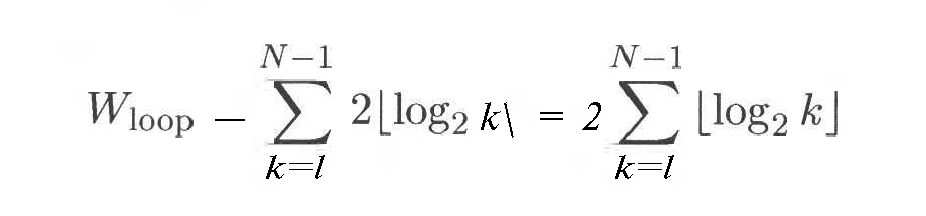
Lekin bu yig’indi uchun bitta standart ifoda yo’q.

Bu to’siqni qanday o’tish mumkinligini ko’ramiz. k=1 da [log2k] ga egamiz. K 2 yoki 3 ga teng bo’lganda [log2k]=1 bo’ladi. Keyinchalik 4 dan 7 gacha k da [log2k]=2 va 8 dan 15 gacha k da [log2k]=3 bo’ladi. Shuni sezamizki, har bir vaziyatda j natijasi argumentning Y qiymatga ega bo’ladi. Bu qoida piramidaning hamma darajalari uchun rioya qilinadi. Undan agar uto’liq bo’lmasa, oxirgisi istisno qilinadi. Bu bosqichda N-2(log2N) ta element bo’ladi.

Shu uchun oxirgi tenglikni shu shaklda ko’chirish mumkin:

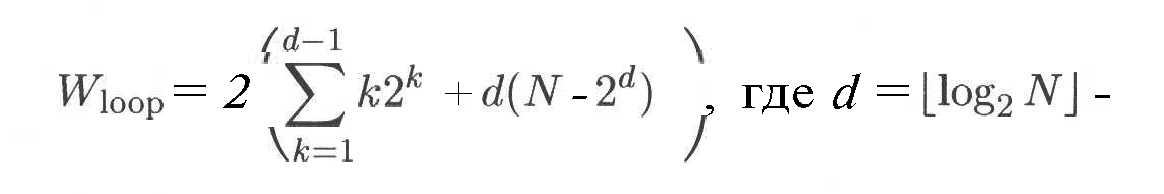
Bu esa quyidagini beradi:

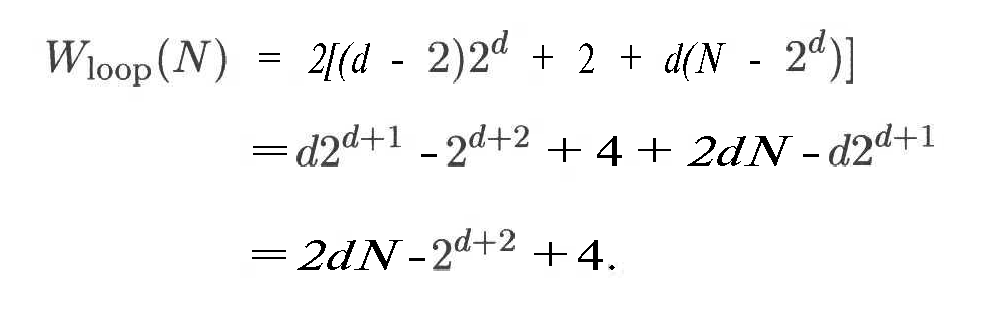
D – log2N ni qo’yib quyidagilarni olamiz:

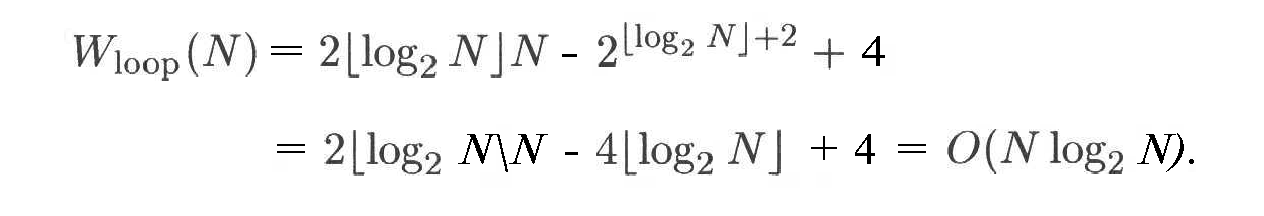
Yakunlovchi natijani olish uchun sikl va qurish protseduralarining murakkabliklarini qo’shish kerak. Natijada quyidagilarga ega bo’lamiz:

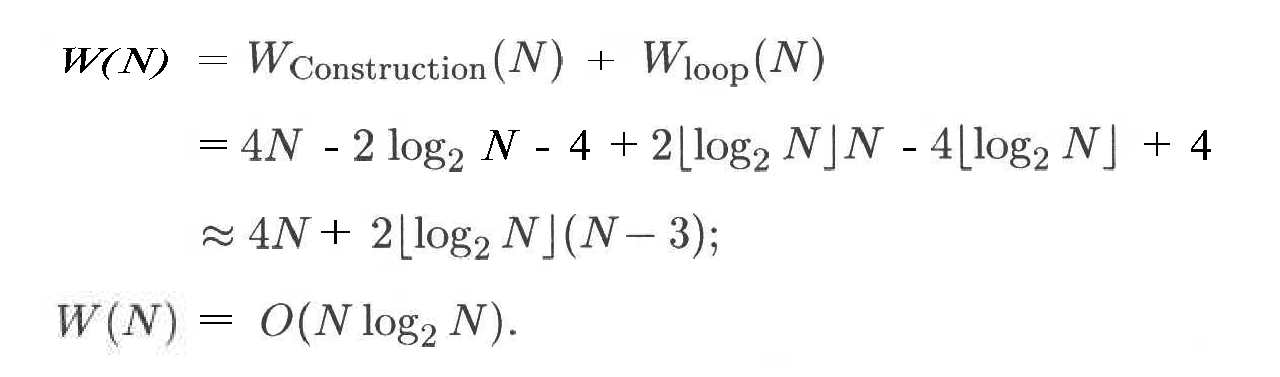
O’rta holat tahlili

O’rta vaziyatning tahlili uchun piramidali tartiblashga biz noodatiy usulni qo’llaymiz. Eng yaxshi vaziyatdan boshlaymiz. Unda oxirgi massivda qiymatlar teskari tartibda joylashgan. Bunday joylashish to’gri piramidani avtomatik ravishda berishini tekshirish murakkab emas. Shuning uchun FixHeap protsedurasining har birini chaqirtirilishida elementlar to’g’ri joylashganligini tasdiqlovchi baravar 2 ta taqqoslash bajariladi. Chunonchi FixHeap protsedurasi taxminan elementlarining yarmisi uchun chaqirtiriladi. Shunda ham bir chaqirish ikkita taqqoslashni talab qiladi. Piramidani qurish bosqichida N ga yaqin, eng yomon holatda qancha bo’lsa, shuncha. taqqoslash bajariladi.

Shuni aytib o’tamizki elementlarning boshlang’ich joylashishiga bog’liq bo’lmagan boshlang’ich bosqichining natijalari doim piramida bo’ladi. Shu uchun for siklining har bir vaziyatida eng yomon holatdagi kabi unda ham shuncha marta bajariladi: tartiblash ro’yxatini olish uchun bizga piramidadan har vaqtda uni qayta shakllantirib, hamma elementlarini olish kerak. Eng yaxshi holatda piramidali tartiblash N+N logN ta taqqoslash talab qiladi. Uning murakkabligi O(NlogN) bo’ladi.

Shunday qilib, piramidali tartiblash uchun eng yaxshi va eng yomon holatlar murakkabliklari O(NlogN)ga teng. Bu shuni anglatadiki, o’rta holat murakkabligi ham O(NlogN) ga teng bo’lishi shart.

Piramidali tartiblashning abstrakt shakli

Bu bo’limda biz piramidalli deb nomlangan tartiblash algoritmini ko’rib chiqamiz uning bajarish vaqti yomon holatda o’rtadagi kabi O(NlogN) tartibga ega. Bu algoritmni ko’pgina INSERT, DELETE, EMPTY va MIN operatorlaridan foydalanib, abstrakt (umumlashtirilgan) shaklda yozish mumkin. Tartiblangan elementlarni saqlash uchun foydalanadigan rekursiv (yozuv tipi) ko’pgina elementlari tartiblashga tegishli bo’lgan elementlar ro’yxatini L orqali belgilaymiz. MIN operatori yozuvlarining kalitli maydonida qo’llaniladi, ya’ni MIN(S) kalitning minimali ahamiyati bilan ko’pgina S dan yozuvni qaytaradi. Quyida biz piramidali tartiblash algoritmida qayta tuzadigan tartiblashning abstrakt algoritmi ko’rsatilgan.

1.1-listing. Tartiblashning abstrakt algoritmi

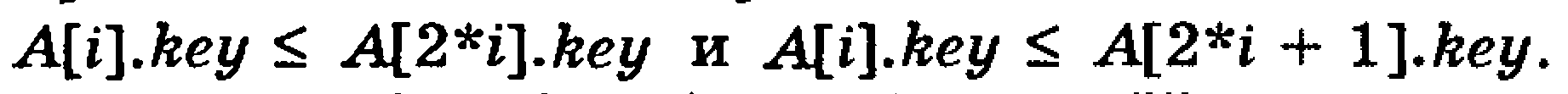
O(logN) bajarish vaqti bilan ko’plab operatorlarni amalga oshirishga yordam beruvchi ikki-uch daraxt kabi shunday ma’lumotlarning har xil tuzilishlarini ko’rsatadilar. Agar L ro’yxati N elementlarga ega bo’lsa, unda bizning abstraktli algoritm INSERT operatorlarining n bajarilishini, MIN operatorlarining n bajarilishini, EMPTY operatorlarining n+1 bajarilishini talab qiladi. Shunday qilib, agar ma’lumotlarning to’g’ri keladigan tuzilishidan foydalansak, algoritm bajarilishining umumiy vaqti O(NlogN) tartibga egadir. Qisman tartiblangan daraxtning berilgan tuzilishi berilgan algoritm uchun to’g’ri keladi. Qisman tartiblangan daraxtni biz to’da ko’rinishida A massivga taqdim etish mumkin, ularning elementlari

tengsizlikka bo’ysunadilar. Agar i indeksi bilan “o’g’illarni” quyidagi kabi 2i va 2i+1 indekslari bilan elementlar intepritatsiya qilinsa, unda A massivi balanslangan ikki karrali daraxtni shakllantiradi. Unda ota-onalar kalitlarning qiymati hech qachon o’g’illari kalitlari qiymatidan ustun kelmaydi.

Tartiblangan daraxt O(logN) bajarishi vaqti bilan INSERT va DELETE, MIN operatorlarini qo’llaydi. Lekin qisman tartiblashtirilgan daraxt bilan DELETE umumiy operatorini bajarish mumkin emas. Doimo yomon holatda yo’q qilishning chiziqli vaqtini talab qiluvchi alohida element topiladi. Shu sababli kalitlarning minimal qiymatlariga ega bo’lgan elementlar faqat yo’q qilinadi. Shu uchun (4) va (6) satrlarning elementini qaytaradigan bitta DELETEMIN operatori bilan birlashtirish mumkin. Shunday qilib, qisman tartiblangan daraxtning berilgan tuzilishidan foydalanib O(NlogN) vaqtda tartiblashni abstrakt algoritmni bajarish mumkin. Yo’q qilinadigan elemenlardan qochish uchun algoritmda yana bitta o’zgarishni qilish lozim. Xato (i<n) elementlariga faqat i ga ega bo’lganda ham ko’pgina S doimo A massivining yuqori qismida to’da shaklida qisman tartiblangan daraxt uchun eng kichik element doimo A[1] uyasida saqlanadi. Ko’pgina S dan yo’q qilingan elimentlarni tezkor tartibda tartiblangan Ai [i+1],…., A[n] uyachalarda saqlash mumkun edi ,yani A[i+1]>=]A[i+2]>=,…>=A[n] tengsizliklar bajarilishi uchun chunonchi A[1] vaA[i] elimentlar ichida kichik bo’libxisoblansa unda DELETEMIN operatorining natijaviyligini oshirish uchun A[1] va A[i] odiy joylashtirishmumkun A[i+1](eliment A[i+1]dan kura kichik emas u ko’pgina Sdan oldingi qadamda kabi yo’q qilingan edi ) unda kamayib ketish tartibida xilga ajratib A[i], ..,A[n] ketma ketligini olamiz . Endi A[i]…A[i-1] elimentlarning joylashishi bilan shug’ilanshi kerak .

Chunonchi A[1] yangi eliment qisman tariblashtirilgan daraxtning tuzilishini bo’zishi sababli uni DELETEMIN muolajasida qiladioganday daraxt shohlari shohlari bo’yicha pastga “yetalash” kerak Bu yerda maqsad bu mualajadan tashqari aniqlangan A massivdan operatsiya qilinadigan pushdowndan (pastga italash)dan biz foydalanamiz . Joyini almmashtirishning ketma-ketligi yordamini berilgan muolaja A[first] elimentni kerakli vaziyatgacha daraxt bo’yicha pastga “yitalaydi”. Tartiblashda bizning algoritmimizning vazyatini qisman tartiblashtirilgan daraxtni tiklash uchun first=1 uchun pushdown muolajasini chaqirtirish kerak .

1.2 – listing. Pushdown protsedurasi

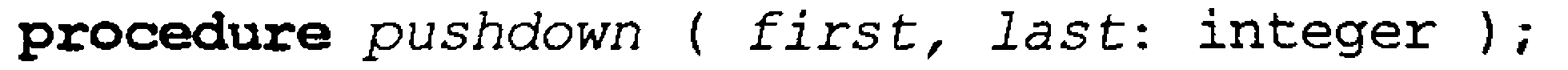
{A(first) …,..A(last) elimentlari qisman tartiblashtirgan daraxtdan iborat A(first) va uning o’g’illaridan tashqari pushdown muolajasi var qismi tartiblangan daraxtni tiklaydi}

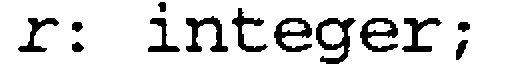{ A[first] ning vaziyatini ko’rsatadi}

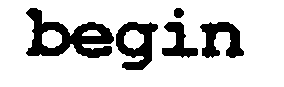
{ r vaziyatida element 2*r vaziyatida birta o’g’ilga ega}

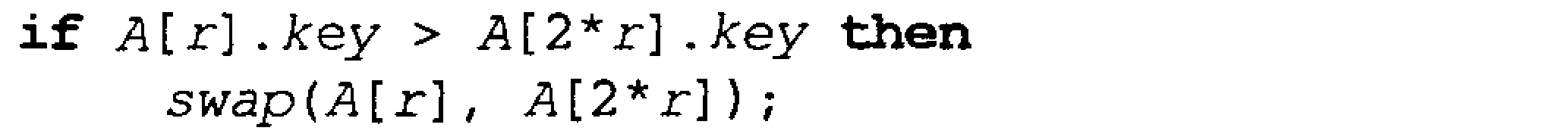
r:= last { (while) siklidan muddatdan oldingi chiqish.}

End

Else {r vaziyatida eliment 2*r va 2*r+1 vaziyatlarida ikkita o’g’lilga ega}.

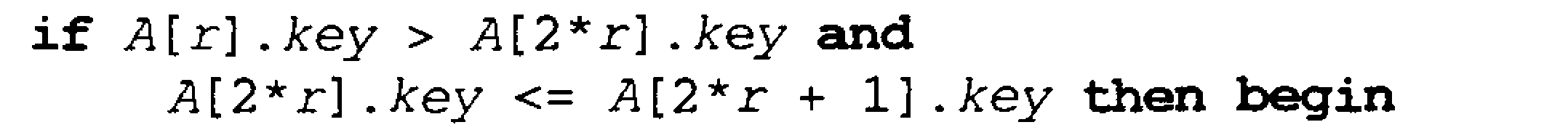
{joyini r-vaziyatda chap o’g’li bilan elimentning almashtirish.}

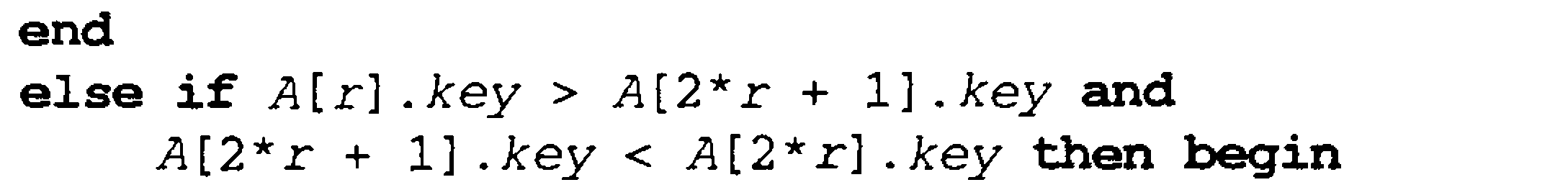
{ r-vaziyatda o’ng o’g’li bilan elementning almashtirish}

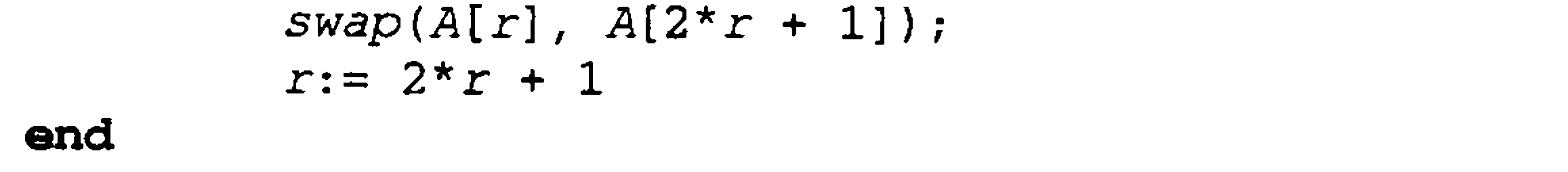
else {r-vaziyatida eliment qisman tartiblashtirilgan daraxtni bo’zmaydi}

r:=last {(while) siklidan chiqish.}

(4) va (6) satirlar bilan shug’ulanamiz satirning minimally elimentning tanlovi oddiy- bu faqat A[1] elimentidir.

(5)satrda pechat operatorini chiqarish uchun biz hozirgi to’dada A[1] va A[i] elementlarining o’rinlarini almashtirdik.Hozirgi to’dadan minamalli elementni yo’q qilish shuningdek oson. Hozirgi to’daning uchini ko’rsatuvchi i kursorni birga kamaytirish kerak. Keyin esa A[1]…..,A[i-1]todaning qisman tartiblashtirgan daraxtda tartibni tiklash uchun pushdown muolajasini chaqirtirish kerak.

(3) satrida tekshirish o’rniga s bo’sh bo’lib hisoblanmaydimi,yo’qmi hozirgi to’daning oxiriga ko’rsatuvchi i kursor ahamiyatini tekshirish mumkin. Endi esa satr(1)(2) satrlarda operatorlar bajarilishining usulini ko’rib chiqish qoldi.Boshdan boshlab L royxati elemantlarini A massivga ixtiyoriy tartibda joylashtirish mumkin.

Birinchi qiqisman tartiblashtirilgan daraxtni yaratish uchun hamma j=n/2,n/2-1,… uchun pushdown (j,n) muomalajasini ketma-ket chaqirtirish kerak.Pushdown (j,n) muolajani chaqishdan keyin quriladigan daraxtning avval tartiblashtirgan qismida tartib buzilmaydi,chunki daraxtga qo’yiladigan yangi element tartibga yangi buzulishlarni kiritmaydi, chunonchi u faqat o’zining “kichik” o’g’li bilan joyini almashtiradi.heapsort muolajasining to’liq kodi(piramidali xilga ajratish) ko’rsatilgan.

1.3 – listing. Piramidali tartiblash protsedurasi.

{A[1] …A[n] massiv elementlarini kamayish tartibida xilga ajratadi }

var i ;integer

{A massivida kursor}

begin

{qisman tartiblashtirilgan daraxtni yaratish}

{to’dadan minimal elementni yo’q qilish}

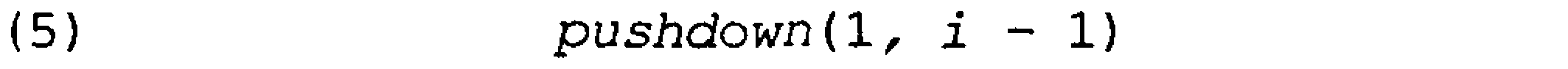
{Qisman tartiblashtirilgan daraxtni tikash}

end

end; (heapsort)

Piramidali tartiblash abstrakt shaklining tahlili

Avvalo pushdovn pratsedurasining bajarish vaqtini baholaymiz While davrining qismi(yani bu davirning alohida interatsiyasi)

Hisobga olingan vaqtda bajariladi har bir interatsiyadan kiyin uzgaruvchi r hech bo’lmaganda o’z ahamiyatini ikki baravar kupaytiradi .shuning uchun r ning boshlang’ch ahamiyati first gat eng, I interatsiyadan kiyin r>=firs*2i.lost/2 tengsizligi bajarilsa bu shart bajariladi

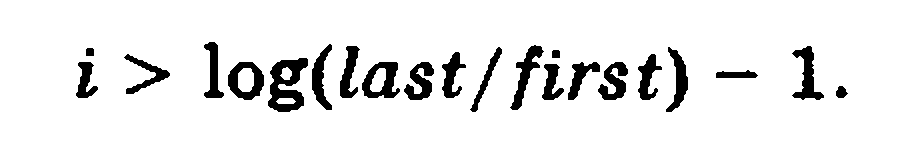(1)

Oxirgi tengsizlikni shunday kuchirish mumkun:

Binobarin ,pushdown protsedurasida while davri iteratsiyalar soni log(last/first) dan oshmaydi.

Chunonchi, first 1 va last n, unda (1) dan O(log n) dan ko’ra katta bo’lmagan tartib bo’yicha 1.3 listingning (2) va (5) satrlarda pushdown protsedurasining har bir chaqiruviga vaqt sarf qilinardi. Aftidan, (1), (2) satrlarning for sikli n/2 marta bajariladi. Shuning uchun bu sikl bajarilishining umumiy vaqti O(n log n) tartibga egadir. (3) va (5) satrlarda davr n-1 marta bajariladi. Binobarin, hamma joyda almashtirishni bajarishga (4) satrda O(n) tartibining vaqti sarf qilinadi, qisman tartiblangan daraxtning tiklashiga (5) satrda O(n log n). Shu yerdan kelib chiqadiki, (3)-(5) satirlarda davrini bajarishning umumiy vaqti O(nlogn) tartibga ega va shunday .

Xulosa

Heapsort mualajasi eng yomon vaziyatda O(nlogn) tartibning bajarish vaqtiga ega, o’rtacha uning tez xilga ajratishdan ko’ra vaqti ancha yomonroq ush tartibga ega bo’lsa ham Piramidali tartiblash nazariy rejada qiziqdir chunonchi bu O(nlogn) bajarish vaqti eng yomon vaziyatda ega bo’lgan biz tomondan birinchi ko’rib chiqilgan algoritimdir. Amaliy vaziyatlarda bu algoritim ruyxatining ajralishi emas balki faqat eng kichik k elimentlarni tanlab olish kerak bo’lganda foydalidir , shunda k da esa n ancha kam . oxirgi xulosada (1),(2) satirlarda haqiqatda davirning bajarish vaqti O(n) tartibga egadir. Agar (3)-(5) davirning faqat k itiratsiyasiyalarini qilish kerak bo’lsa , undaO(klogn) tartibning vaqti shunga sarf qilinadi .Shu uchun minimal elimentlarning k tanlovi heapsort pratsedura O(n+klogn) tartibida bajaradi. Shu erdan kelib chiqadiki, k<=n/logn dab u operatsiya bajariladi O(n) tartibda vaqt talab qilinadi.

Foydalanilgan adabiyotlar:

1. Дж. Макконел

Основы современных алгоритмов

М: Москва. 2001

1. А. Ахо, Дж. Хопкрофт, Дж. Ульман
   Построение и анализ вычислительных алгоритмов
   М.: Мир, 1979
2. А. Ахо, Дж. Хопкрофт, Дж. Ульман
   Структуры данных и алгоритмы
   М.: Вильямс, 2000
3. М. Гэри, Д. Джонсон
   Вычислительные машины и труднорешаемые задачи
   М.: Мир, 1982
4. Емеличев В.А
   Лекции по теории графов
   М.: Наука, 1990
5. Т. Кормен, Ч. Лейзер, Р. Ривест
   Алгоритмы. Построение и анализ
   МЦНМО, Москва, 1999
6. Кристофидес Н
   Теория графов. Алгоритмический подход
   М.: Мир, 1978
7. Л. Ловас, М. Пламмер
   Прикладные задачи теории графов
   М.: Мир, 1998
8. Липский В
   Комбинаторика для программистов
   М.: Мир, 1988
9. Новиков Ф.А
   Дискретная математика для программистов
   СПб.: Питер, 2001
10. Э. Рейнгольд, Ю. Нивергельт, Н. Део
    Комбинаторные алгоритмы
    М.: Мир, 1980

PAGE \* MERGEFORMAT 1

Piramidali Tartiblash